Finite-Basis-Set Approach to the Two-Center Heteronuclear Dirac Problem
Abstract
:1. Introduction
2. Method
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| c.s.o. | Coordinate system’s origin |
| TC | Two-center |
| MA | Monopole approximation |
| QED | Quantum electrodynamics |
References
- Verma, P.; Mokler, P.; Bräuning-Demian, A.; Bräuning, H.; Kozhuharov, C.; Bosch, F.; Liesen, D.; Hagmann, S.; Stöhlker, T.; Stachura, Z.; et al. Probing superheavy quasimolecular collisions with incoming inner shell vacancies. Nucl. Instrum. Methods Phys. Res. Sect. B 2006, 245, 56–60. [Google Scholar] [CrossRef]
- Verma, P.; Mokler, P.; Bräuning-Demian, A.; Kozhuharov, C.; Bräuning, H.; Bosch, F.; Liesen, D.; Stöhlker, T.; Hagmann, S.; Chatterjee, S.; et al. Spectroscopy of superheavy quasimolecules. Radiat. Phys. Chem. 2006, 75, 2014–2018. [Google Scholar] [CrossRef]
- Hagmann, S.; Stöhlker, T.; Kozhuharov, C.; Shabaev, V.; Tupitsyn, I.; Kozhedub, Y.; Rothard, H.; Spillmann, U.; Reuschl, R.; Trotsenko, S.; et al. Electron Spectroscopy In Heavy-Ion Storage Rings: Resonant and Non-Resonant Electron Transfer Processes. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2011; Volume 1336, p. 115. [Google Scholar]
- Zhu, B.; Gumberidze, A.; Over, T.; Weber, G.; Andelkovic, Z.; Bräuning-Demian, A.; Chen, R.J.; Dmytriiev, D.; Forstner, O.; Hahn, C.; et al. X-ray emission associated with radiative recombination for Pb82+ ions at threshold energies. Phys. Rev. A 2022, 105, 052804. [Google Scholar] [CrossRef]
- Hillenbrand, P.M.; Hagmann, S.; Kozhedub, Y.S.; Benis, E.P.; Brandau, C.; Chen, R.J.; Dmytriiev, D.; Forstner, O.; Glorius, J.; Grisenti, R.E.; et al. Single and double K-shell vacancy production in slow Xe54+,53+-Xe collisions. Phys. Rev. A 2022, 105, 022810. [Google Scholar] [CrossRef]
- Ter-Akopian, G.M.; Greiner, W.; Meshkov, I.N.; Oganessian, Y.T.; Reinhardt, J.; Trubnikov, G.V. Layout of new experiments on the observation of spontaneous electron–positron pair creation in supercritical Coulomb fields. Int. J. Mod. Phys. E 2015, 24, 1550016. [Google Scholar] [CrossRef]
- Ma, X.; Wen, W.; Zhang, S.; Yu, D.; Cheng, R.; Yang, J.; Huang, Z.; Wang, H.; Zhu, X.; Cai, X.; et al. HIAF: New opportunities for atomic physics with highly charged heavy ions. Nucl. Instrum. Methods Phys. Res. Sect. B 2017, 408, 169–173. [Google Scholar] [CrossRef]
- Gumberidze, A.; Stöhlker, T.; Beyer, H.; Bosch, F.; Bräuning-Demian, A.; Hagmann, S.; Kozhuharov, C.; Kühl, T.; Mann, R.; Indelicato, P.; et al. X-ray spectroscopy of highly-charged heavy ions at FAIR. Nucl. Instrum. Methods Phys. Res. Sect. B 2009, 267, 248–250. [Google Scholar] [CrossRef]
- Soff, G.; Greiner, W.; Betz, W.; Müller, B. Electrons in superheavy quasimolecules. Phys. Rev. A 1979, 20, 169–193. [Google Scholar] [CrossRef] [Green Version]
- Becker, U.; Grün, N.; Scheid, W.; Soff, G. Nonperturbative Treatment of Excitation and Ionization in U92+ + U91+ Collisions at 1 GeV/amu. Phys. Rev. Lett. 1986, 56, 2016–2019. [Google Scholar] [CrossRef]
- Eichler, J. Theory of relativistic ion-atom collisions. Phys. Rep. 1990, 193, 165–277. [Google Scholar] [CrossRef]
- Rumrich, K.; Soff, G.; Greiner, W. Ionization and pair creation in relativistic heavy-ion collisions. Phys. Rev. A 1993, 47, 215–228. [Google Scholar] [CrossRef] [Green Version]
- Ionescu, D.C.; Belkacem, A. Relativistic Collisions of Highly-Charged Ions. Phys. Scr. 1999, T80, 128. [Google Scholar] [CrossRef]
- Tupitsyn, I.I.; Kozhedub, Y.S.; Shabaev, V.M.; Deyneka, G.B.; Hagmann, S.; Kozhuharov, C.; Plunien, G.; Stöhlker, T. Relativistic calculations of the charge-transfer probabilities and cross sections for low-energy collisions of H-like ions with bare nuclei. Phys. Rev. A 2010, 82, 042701. [Google Scholar] [CrossRef] [Green Version]
- Tupitsyn, I.I.; Kozhedub, Y.S.; Shabaev, V.M.; Bondarev, A.I.; Deyneka, G.B.; Maltsev, I.A.; Hagmann, S.; Plunien, G.; Stöhlker, T. Relativistic calculations of the K-K charge transfer and K-vacancy production probabilities in low-energy ion-atom collisions. Phys. Rev. A 2012, 85, 032712. [Google Scholar] [CrossRef] [Green Version]
- Maltsev, I.A.; Shabaev, V.M.; Popov, R.V.; Kozhedub, Y.S.; Plunien, G.; Ma, X.; Stöhlker, T.; Tumakov, D.A. How to Observe the Vacuum Decay in Low-Energy Heavy-Ion Collisions. Phys. Rev. Lett. 2019, 123, 113401. [Google Scholar] [CrossRef] [Green Version]
- Popov, R.V.; Shabaev, V.M.; Telnov, D.A.; Tupitsyn, I.I.; Maltsev, I.A.; Kozhedub, Y.S.; Bondarev, A.I.; Kozin, N.V.; Ma, X.; Plunien, G.; et al. How to access QED at a supercritical Coulomb field. Phys. Rev. D 2020, 102, 076005. [Google Scholar] [CrossRef]
- Voskresensky, D.N. Electron-Positron Vacuum Instability in Strong Electric Fields. Relativistic Semiclassical Approach. Universe 2021, 7, 104. [Google Scholar] [CrossRef]
- Müller, B.; Rafelski, J.; Greiner, W. Solution of the Dirac equation with two Coulomb centres. Phys. Lett. B 1973, 47, 5–7. [Google Scholar] [CrossRef]
- Rafelski, J.; Müller, B. The critical distance in collisions of heavy ions. Phys. Lett. B 1976, 65, 205–208. [Google Scholar] [CrossRef]
- Rafelski, J.; Müller, B. Magnetic Splitting of Quasimolecular Electronic States in Strong Fields. Phys. Rev. Lett. 1976, 36, 517–520. [Google Scholar] [CrossRef]
- Lisin, V.; Marinov, M.; Popov, V. Critical distance for the electron two-center problem. Phys. Lett. B 1977, 69, 141–142. [Google Scholar] [CrossRef]
- Lisin, V.; Marinov, M.; Popov, V. Critical electron state in heavy-ion collisions. Phys. Lett. B 1980, 91, 20–22. [Google Scholar] [CrossRef]
- Yang, L.; Heinemann, D.; Kolb, D. An accurate solution of the two-centre Dirac equation for H+2 by the finite-element method. Chem. Phys. Lett. 1991, 178, 213–215. [Google Scholar] [CrossRef]
- Parpia, F.A.; Mohanty, A.K. Numerical study of the convergence of the linear expansion method for the one-electron Dirac equation. Chem. Phys. Lett. 1995, 238, 209–214. [Google Scholar] [CrossRef]
- Deineka, G. Application of the Hermitian basis of B-splines for solution of diatomic molecular problems by the Hartree-Fock-Dirac method. Opt. Spectrosc. 1998, 84, 159–164. [Google Scholar]
- Matveev, V.; Matrasulov, D.; Rakhimov, H.Y. Two-center problem for the dirac equation. Phys. At. Nucl. 2000, 63, 318–321. [Google Scholar] [CrossRef]
- Kullie, O.; Kolb, D. High accuracy Dirac-finite-element (FEM) calculations for H 2+ and Th 2 179+. Eur. Phys. J. D 2001, 17, 167–173. [Google Scholar] [CrossRef]
- Ishikawa, A.; Nakashima, H.; Nakatsuji, H. Solving the Schrödinger and Dirac equations of hydrogen molecular ion accurately by the free iterative complement interaction method. J. Chem. Phys. 2008, 128, 124103. [Google Scholar] [CrossRef] [Green Version]
- Artemyev, A.N.; Surzhykov, A.; Indelicato, P.; Plunien, G.; Stöhlker, T. Finite basis set approach to the two-centre Dirac problem in Cassini coordinates. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 235207. [Google Scholar] [CrossRef]
- Ishikawa, A.; Nakashima, H.; Nakatsuji, H. Accurate solutions of the Schrödinger and Dirac equations of H2+, HD+, and HT+: With and without Born–Oppenheimer approximation and under magnetic field. Chem. Phys. 2012, 401, 62–72. [Google Scholar] [CrossRef]
- Tupitsyn, I.I.; Mironova, D.V. Relativistic calculations of ground states of single-electron diatomic molecular ions. Opt. Spectrosc. 2014, 117, 351–357. [Google Scholar] [CrossRef]
- Mironova, D.; Tupitsyn, I.; Shabaev, V.; Plunien, G. Relativistic calculations of the ground state energies and the critical distances for one-electron homonuclear quasi-molecules. Chem. Phys. 2015, 449, 10–13. [Google Scholar] [CrossRef] [Green Version]
- Artemyev, A.N.; Surzhykov, A. Quantum Electrodynamical Corrections to Energy Levels of Diatomic Quasimolecules. Phys. Rev. Lett. 2015, 114, 243004. [Google Scholar] [CrossRef]
- Artemyev, A.N.; Surzhykov, A.; Yerokhin, V.A. Ab initio QED calculations in diatomic quasimolecules. Phys. Rev. A 2022, 106, 012813. [Google Scholar] [CrossRef]
- Kotov, A.A.; Glazov, D.A.; Malyshev, A.V.; Vladimirova, A.V.; Shabaev, V.M.; Plunien, G. Ground-state energy of uranium diatomic quasimolecules with one and two electrons. X-ray Spectrom. 2020, 49, 110–114. [Google Scholar] [CrossRef] [Green Version]
- Kotov, A.A.; Glazov, D.A.; Shabaev, V.M.; Plunien, G. One-Electron Energy Spectra of Heavy Highly Charged Quasimolecules: Finite-Basis-Set Approach. Atoms 2021, 9, 44. [Google Scholar] [CrossRef]
- Parpia, F.A.; Mohanty, A.K. Relativistic basis-set calculation for atoms with Fermi nuclei. Phys. Rev. A 1992, 46, 3735. [Google Scholar] [CrossRef]
- Shabaev, V.M.; Tupitsyn, I.I.; Yerokhin, V.A.; Plunien, G.; Soff, G. Dual Kinetic Balance Approach to Basis-Set Expansions for the Dirac Equation. Phys. Rev. Lett. 2004, 93, 130405. [Google Scholar] [CrossRef] [Green Version]
- Rozenbaum, E.B.; Glazov, D.A.; Shabaev, V.M.; Sosnova, K.E.; Telnov, D.A. Dual-kinetic-balance approach to the Dirac equation for axially symmetric systems: Application to static and time-dependent fields. Phys. Rev. A 2014, 89, 012514. [Google Scholar] [CrossRef] [Green Version]
- Yerokhin, V.A.; Shabaev, V.M. First-order self-energy correction in hydrogenlike systems. Phys. Rev. A 1999, 60, 800–811. [Google Scholar] [CrossRef]
- Glazov, D.A.; Volotka, A.V.; Shabaev, V.M.; Tupitsyn, I.I.; Plunien, G. Screened QED corrections to the g factor of Li-like ions. Phys. Lett. A 2006, 357, 330. [Google Scholar] [CrossRef]
- Artemyev, A.N.; Shabaev, V.M.; Tupitsyn, I.I.; Plunien, G.; Yerokhin, V.A. QED Calculation of the 2p3/2-2p1/2 Transition Energy in Boronlike Argon. Phys. Rev. Lett. 2007, 98, 173004. [Google Scholar] [CrossRef] [Green Version]
- Volotka, A.V.; Glazov, D.A.; Tupitsyn, I.I.; Oreshkina, N.S.; Plunien, G.; Shabaev, V.M. Ground-state hyperfine structure of H-, Li-, and B-like ions in the intermediate-Z region. Phys. Rev. A 2008, 78, 062507. [Google Scholar] [CrossRef] [Green Version]
- Artemyev, A.N.; Shabaev, V.M.; Tupitsyn, I.I.; Plunien, G.; Surzhykov, A.; Fritzsche, S. Ab initio calculations of the 2p3/2-2p1/2 fine-structure splitting in boronlike ions. Phys. Rev. A 2013, 88, 032518. [Google Scholar] [CrossRef]
- Malyshev, A.V.; Glazov, D.A.; Shabaev, V.M.; Tupitsyn, I.I.; Yerokhin, V.A.; Zaytsev, V.A. Model-QED operator for superheavy elements. Phys. Rev. A 2022, 106, 012806. [Google Scholar] [CrossRef]
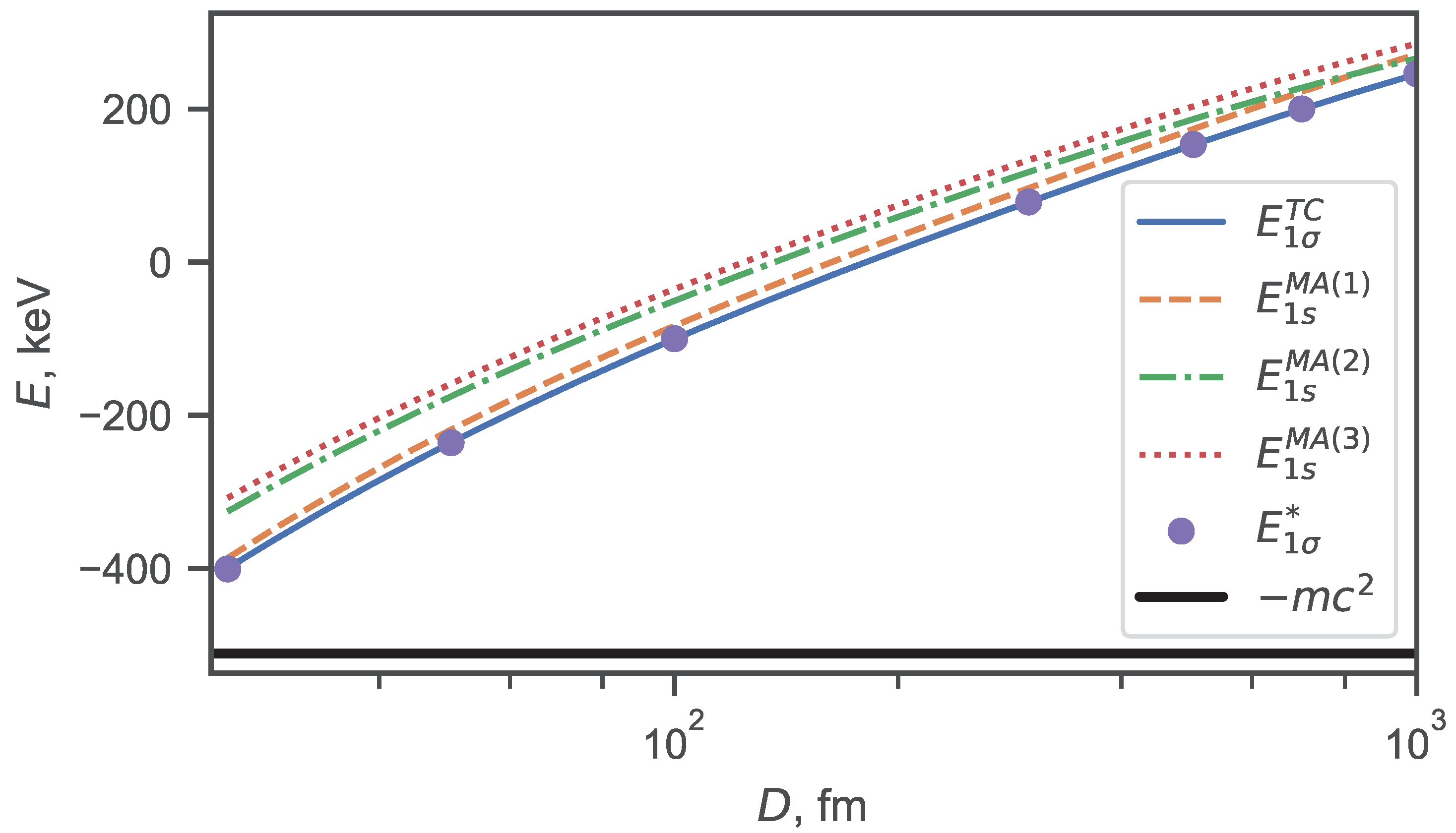
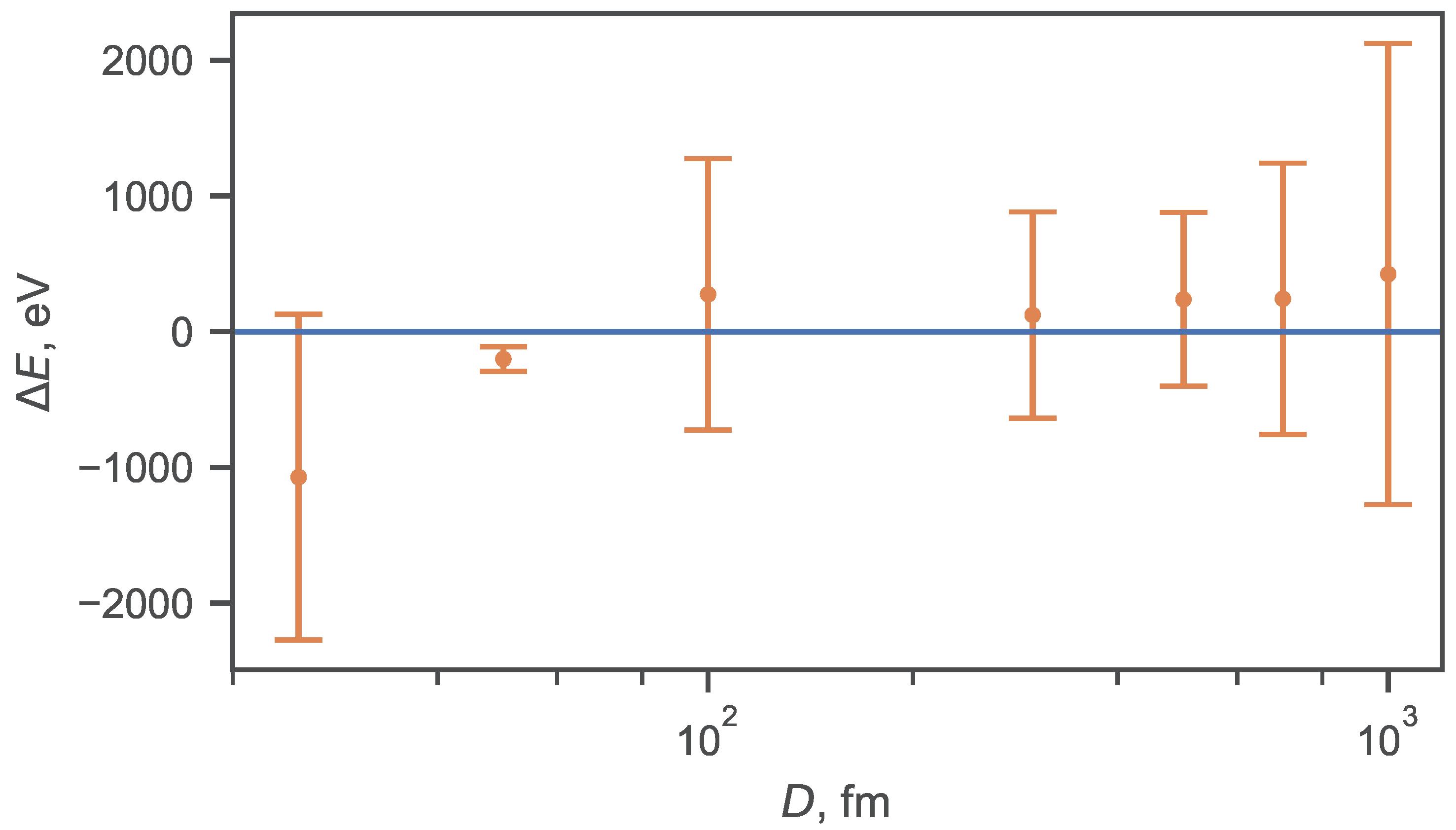
| D, fm | ||||||
|---|---|---|---|---|---|---|
| Bi–Au | ||||||
| 15 | −237,546 | −234,358 | −196,293 | −192,512 | 6900 | −6025 |
| 25 | −171,018 | −164,778 | −128,136 | −123,948 | 5236 | −3830 |
| 50 | −79,797 | −70,861 | −39,310 | −34,999 | 3376 | −1849 |
| 100 | 6199 | 16,418 | 44,424 | 48,863 | 2071 | −827 |
| 300 | 137,579 | 150,276 | 173,231 | 178,322 | 800 | −187 |
| 500 | 198,231 | 213,083 | 230,800 | 236,409 | 451 | −81 |
| 700 | 237,280 | 254,069 | 266,215 | 272,260 | 290 | −43 |
| 1000 | 276,703 | 296,127 | 300,037 | 306,662 | 169 | −21 |
| U–Pb | ||||||
| 25 | −399,528 | −386,390 | −325,462 | −307,855 | 7378 | −6230 |
| 50 | −235,560 | −218,680 | −175,040 | −158,648 | 4446 | −2722 |
| 100 | −100,275 | −83,130 | −50,315 | −35,068 | 2570 | −1113 |
| 300 | 78,437 | 96,786 | 117,862 | 133,471 | 928 | −227 |
| 500 | 153,372 | 173,899 | 186,844 | 203,557 | 512 | −95 |
| 700 | 199,857 | 222,639 | 227,866 | 245,689 | 325 | −50 |
| 1000 | 245,476 | 271,658 | 265,930 | 285,332 | 188 | −24 |
| Cf–U | ||||||
| 50 | −491,640 | −459,027 | −383,320 | −366,680 | 6003 | −4189 |
| 80 | −329,591 | −298,922 | −242,676 | −228,241 | 4007 | −2162 |
| 100 | −263,819 | −234,379 | −184,810 | −171,155 | 3285 | −1566 |
| 200 | −91,283 | −64,537 | −30,027 | −17,722 | 1701 | −551 |
| 250 | −43,071 | −16,584 | 13,759 | 25,933 | 1349 | −386 |
| 500 | 91,335 | 119,363 | 134,508 | 147,097 | 594 | −115 |
| 700 | 149,097 | 179,309 | 184,223 | 197,470 | 372 | −59 |
| 1000 | 204,297 | 238,194 | 229,390 | 243,724 | 212 | −28 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kotov, A.A.; Glazov, D.A.; Malyshev, A.V.; Shabaev, V.M.; Plunien, G. Finite-Basis-Set Approach to the Two-Center Heteronuclear Dirac Problem. Atoms 2022, 10, 145. https://doi.org/10.3390/atoms10040145
Kotov AA, Glazov DA, Malyshev AV, Shabaev VM, Plunien G. Finite-Basis-Set Approach to the Two-Center Heteronuclear Dirac Problem. Atoms. 2022; 10(4):145. https://doi.org/10.3390/atoms10040145
Chicago/Turabian StyleKotov, Artem A., Dmitry A. Glazov, Aleksei V. Malyshev, Vladimir M. Shabaev, and Günter Plunien. 2022. "Finite-Basis-Set Approach to the Two-Center Heteronuclear Dirac Problem" Atoms 10, no. 4: 145. https://doi.org/10.3390/atoms10040145
APA StyleKotov, A. A., Glazov, D. A., Malyshev, A. V., Shabaev, V. M., & Plunien, G. (2022). Finite-Basis-Set Approach to the Two-Center Heteronuclear Dirac Problem. Atoms, 10(4), 145. https://doi.org/10.3390/atoms10040145





