Collinear Laser Spectroscopy of Helium-like 11B3+
Abstract
:1. Introduction
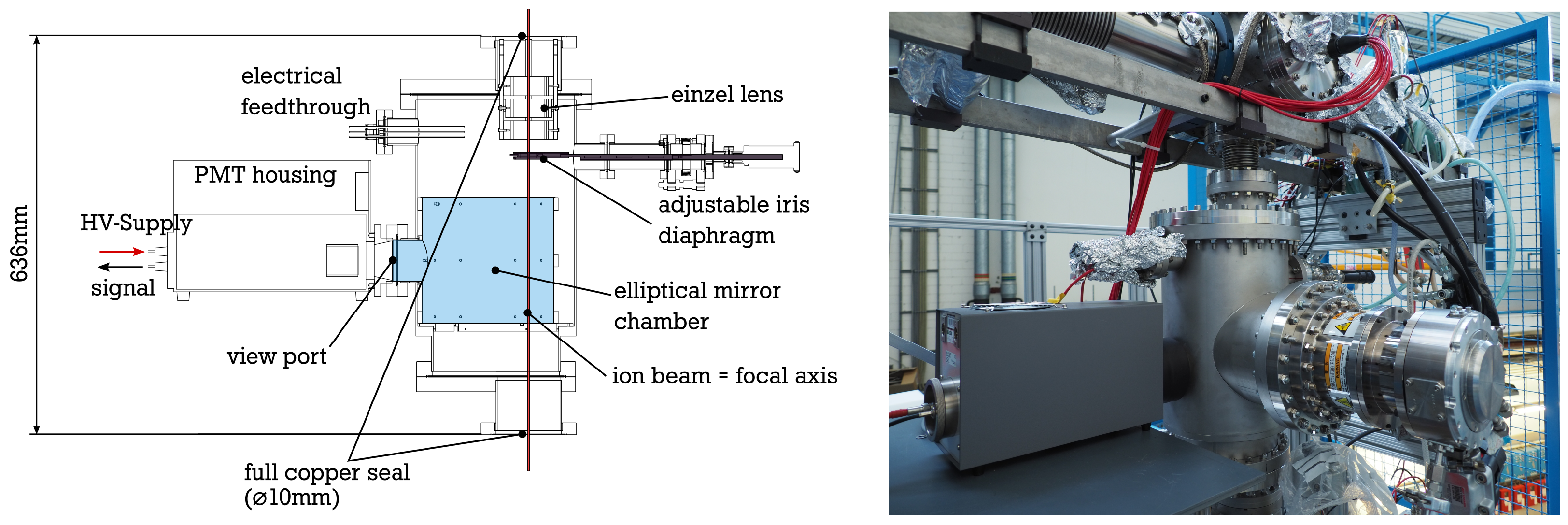
2. Experimental Setup
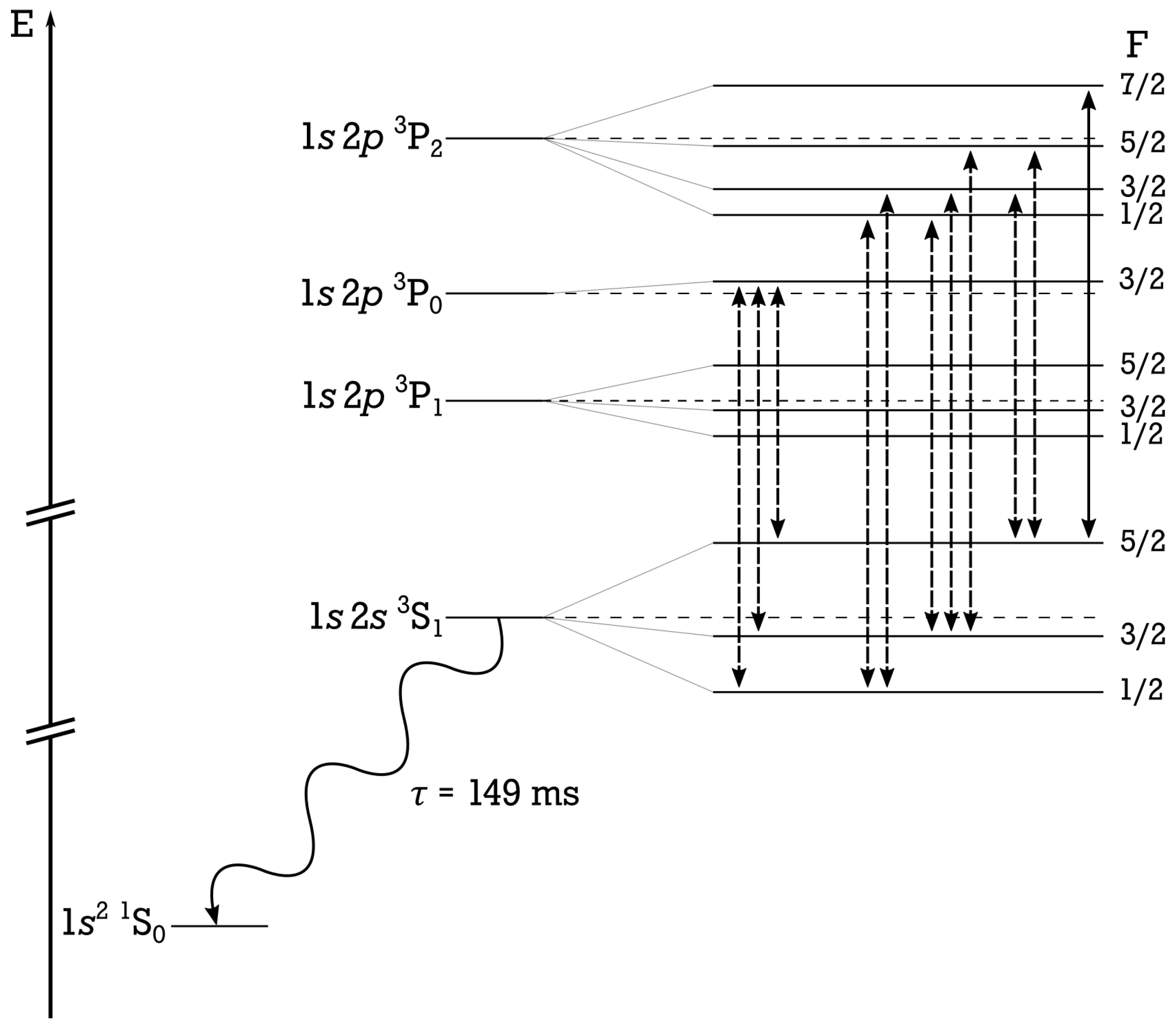
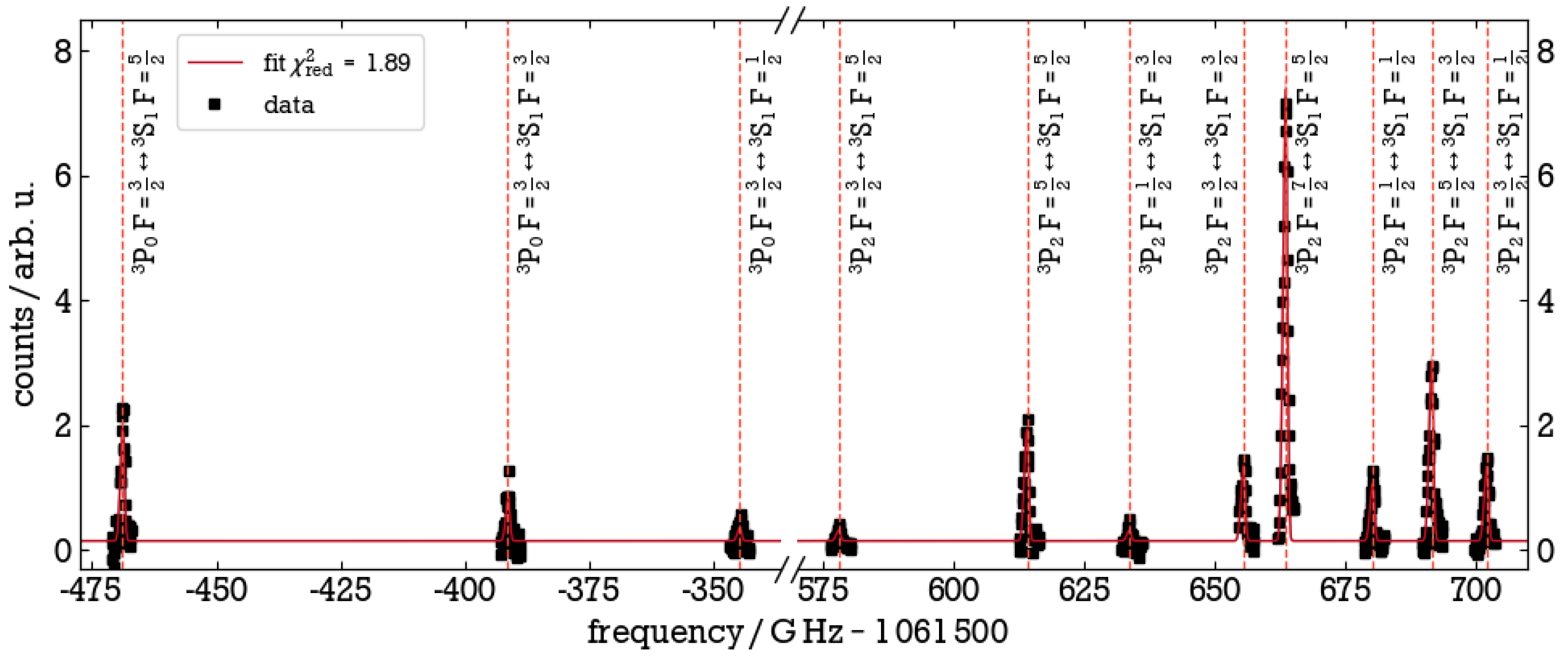
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blaum, K.; Dilling, J.; Nörtershäuser, W. Precision atomic physics techniques for nuclear physics with radioactive beams. Phys. Scr. 2013, T152, 014017. [Google Scholar] [CrossRef] [Green Version]
- Campbell, P.; Moore, I.D.; Pearson, M.R. Laser spectroscopy for nuclear structure physics. Prog. Part. Nucl. Phys. 2016, 86, 127–180. [Google Scholar] [CrossRef]
- Lu, Z.T.; Mueller, P.; Drake, G.W.; Nörtershäuser, W.; Pieper, S.C.; Yan, Z.C. Colloquium: Laser probing of neutron-rich nuclei in light atoms. Rev. Mod. Phys. 2013, 85, 1383–1400. [Google Scholar] [CrossRef] [Green Version]
- Maaß, B.; Hüther, T.; König, K.; Krämer, J.; Krause, J.; Lovato, A.; Müller, P.; Pachucki, K.; Puchalski, M.; Roth, R.; et al. Nuclear Charge Radii of 10,11B. Phys. Rev. Lett. 2019, 122, 182501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stovall, T.; Goldemberg, J.; Isabelle, D.B. Coulomb form factors of 10B and 11B. Nucl. Phys. 1966, 86, 225–240. [Google Scholar] [CrossRef]
- Schaller, L.A.; Schellenberg, L.; Ruetschi, A.; Schneuwly, H. Nuclear charge radii from muonic X-ray transitions in beryllium, boron, carbon and nitrogen. Nucl. Phys. A 1980, 343, 333–346. [Google Scholar] [CrossRef]
- Maaß, B.; Müller, P.; Nörtershäuser, W.; Clark, J.; Gorges, C.; Kaufmann, S.; König, K.; Krämer, J.; Levand, A.; Orford, R.; et al. Towards laser spectroscopy of the proton-halo candidate boron-8. Hyperfine Interact. 2017, 238, 25. [Google Scholar] [CrossRef]
- Antognini, A.; Bacca, S.; Fleischmann, A.; Gastaldo, L.; Hagelstein, F.; Indelicato, P.; Knecht, A.; Lensky, V.; Ohayon, B.; Pascalutsa, V.; et al. Muonic-Atom Spectroscopy and Impact on Nuclear Structure and Precision QED Theory. arXiv 2022, arXiv:2210.16929. [Google Scholar] [CrossRef]
- Udem, T.; Huber, A.; Gross, B.; Reichert, J.; Prevedelli, M.; Weitz, M.; Hänsch, T.W. Phase-Coherent Measurement of the Hydrogen 1S-2S Transition Frequency with an Optical Frequency Interval Divider Chain. Phys. Rev. Lett. 1997, 79, 2646–2649. [Google Scholar] [CrossRef]
- Beyer, A.; Maisenbacher, L.; Matveev, A.; Pohl, R.; Khabarova, K.; Grinin, A.; Lamour, T.; Yost, D.C.; Hänsch, T.W.; Kolachevsky, N.; et al. The Rydberg constant and proton size from atomic hydrogen. Science 2017, 358, 79–85. [Google Scholar] [CrossRef]
- Fleurbaey, H.; Galtier, S.; Thomas, S.; Bonnaud, M.; Julien, L.; Biraben, F.; Nez, F.; Abgrall, M.; Guéna, J. New Measurement of the 1S − 3S Transition Frequency of Hydrogen: Contribution to the Proton Charge Radius Puzzle. Phys. Rev. Lett. 2018, 120, 183001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pohl, R.; Antognini, A.; Nez, F.; Amaro, F.D.; Biraben, F.; Cardoso, J.M.; Covita, D.S.; Dax, A.; Dhawan, S.; Fernandes, L.M.; et al. The size of the proton. Nature 2010, 466, 213–216. [Google Scholar] [CrossRef] [PubMed]
- Pohl, R.; Nez, F.; Fernandes, L.M.P.; Amaro, F.D.; Biraben, F.; Cardoso, J.M.R.; Covita, D.S.; Dax, A.; Dhawan, S.; Diepold, M.; et al. Laser spectroscopy of muonic deuterium. Science 2016, 353, 669–673. [Google Scholar] [CrossRef] [PubMed]
- Krauth, J.J.; Schuhmann, K.; Ahmed, M.A.; Amaro, F.D.; Amaro, P.; Biraben, F.; Chen, T.l.; Covita, D.S.; Dax, A.J.; Diepold, M.; et al. Measuring the α-particle charge radius with muonic helium-4 ions. Nature 2021, 589, 527–531. [Google Scholar] [CrossRef] [PubMed]
- Karr, J.P.; Marchand, D.; Voutier, E. The proton size. Nat. Rev. Phys. 2020, 2, 601–614. [Google Scholar] [CrossRef]
- Yerokhin, V.A.; Patkóš, V.c.ě.; Pachucki, K. Relativistic corrections to the Bethe logarithm for the 2 3S and 2 3P states of He. Phys. Rev. A 2018, 98, 32503. [Google Scholar] [CrossRef] [Green Version]
- Patkóš, V.; Yerokhin, V.A.; Pachucki, K. Nonradiative α7m QED effects in Lamb shift of helium triplet states. Phys. Rev. A 2021, 103, 042809. [Google Scholar] [CrossRef]
- Yerokhin, V.A.; Patkóš, V.; Pachucki, K. QED calculations of energy levels of heliumlike ions with 5 ≤ Z ≤ 30. Phys. Rev. A 2022, 106. [Google Scholar] [CrossRef]
- Anton, K.R.; Kaufman, S.L.; Klempt, W.; Moruzzi, G.; Neugart, R.; Otten, E.W.; Schinzler, B. Collinear Laser Spectroscopy on Fast Atomic Beams. Phys. Rev. Lett. 1978, 40, 642–645. [Google Scholar] [CrossRef]
- Imgram, P.; König, K.; Krämer, J.; Ratajczyk, T.; Maaß, B.; Müller, P.; Sommer, F.; Nörtershäuser, W. High-precision collinear laser spectroscopy at the Collinear Apparatus for Laser Spectroscopy and Applied Physics (COALA). Hyperfine Interact. 2020, 241, 48. [Google Scholar] [CrossRef]
- Müller, P.; König, K.; Imgram, P.; Krämer, J.; Nörtershäuser, W. Collinear laser spectroscopy of Ca+: Solving the field-shift puzzle of the 4s 2S1/2⟶ 4p 2P1/2,3/2 transitions. Phys. Rev. Res. 2020, 2, 043351. [Google Scholar] [CrossRef]
- Neugart, R.; Billowes, J.; Bissell, M.L.; Blaum, K.; Cheal, B.; Flanagan, K.T.; Neyens, G.; Nörtershäuser, W.; Yordanov, D.T. Collinear laser spectroscopy at ISOLDE: New methods and highlights. J. Phys. G 2017, 44, 064002. [Google Scholar] [CrossRef]
- König, K.; Krämer, J.; Geppert, C.; Imgram, P.; Maaß, B.; Ratajczyk, T.; Nörtershäuser, W. A new Collinear Apparatus for Laser Spectroscopy and Applied Science (COALA). Rev. Sci. Instrum. 2020, 91, 081301. [Google Scholar] [CrossRef]
- Dinneen, T.P.; Berrah-Mansour, N.; Berry, H.G.; Young, L.; Pardo, R.C. Precision measurements of relativistic and QED effects in helium-like boron. Phys. Rev. Lett. 1991, 66, 2859–2862. [Google Scholar] [CrossRef] [PubMed]
- Sokolov, A.; Herfurth, F.; Kester, O.; Stoehlker, T.; Thorn, A.; Vorobjev, G.; Zschornack, G. SPARC EBIT—A charge breeder for the HITRAP project. J. Instrum. 2010, 5, C11001. [Google Scholar] [CrossRef] [Green Version]
- Andelkovic, Z.; Herfurth, F.; Kotovskiy, N.; König, K.; Maaß, B.; Murböck, T.; Neidherr, D.; Schmidt, S.; Steinmann, J.; Vogel, M.; et al. Beamline for low-energy transport of highly charged ions at HITRAP. Nucl. Instrum. Methods Phys. Res. Sect. A 2015, 795, 109–114. [Google Scholar] [CrossRef]
- Andelkovic, Z.; Cazan, R.; Nörtershäuser, W.; Bharadia, S.; Segal, D.M.; Thompson, R.C.; Jöhren, R.; Vollbrecht, J.; Hannen, V.; Vogel, M. Laser cooling of externally produced Mg ions in a Penning trap for sympathetic cooling of highly charged ions. Phys. Rev. A 2013, 87, 033423. [Google Scholar] [CrossRef] [Green Version]
- Buß, A. Development of Fluorescence Detectors for Laser Spectroscopy Experiments at GSI/FAIR, and Measurement of Hyperfine Transitions between the 23P and 23S States in Helium-like Boron. Ph.D. Thesis, WWU Münster, Münster, Germany, 2022. [Google Scholar]
- Mohr, K.T. First laser spectroscopy of Mg+ at CRYRING@ESR and He-Like Boron at HITRAP. Ph.D. Thesis, TU Darmstadt, Darmstadt, Germany, 2022. [Google Scholar] [CrossRef]
- Malbrunot-Ettenauer, S.; Kaufmann, S.; Bacca, S.; Barbieri, C.; Billowes, J.; Bissell, M.L.; Blaum, K.; Cheal, B.; Duguet, T.; Ruiz, R.F.G.; et al. Nuclear Charge Radii of the Nickel Isotopes 58--68,70Ni. Phys. Rev. Lett. 2022, 128, 022502. [Google Scholar] [CrossRef]
- König, K.; Imgram, P.; Krämer, J.; Maaß, B.; Mohr, K.; Ratajczyk, T.; Sommer, F.; Nörtershäuser, W. On the performance of wavelength meters: Part 2 – frequency-comb based characterization for more accurate absolute wavelength determinations. Appl. Phys. B 2020, 126, 86. [Google Scholar] [CrossRef]
- Drake, G.W.F. Theory of Relativistic Magnetic Dipole Transitions: Lifetime of the Metastable 23S State of the Heliumlike Ions. Phys. Rev. A 1971, 3, 908–915. [Google Scholar] [CrossRef] [Green Version]
- Krieger, A.; Nörtershäuser, W.; Geppert, C.; Blaum, K.; Bissell, M.L.; Frömmgen, N.; Hammen, M.; Kreim, K.; Kowalska, M.; Krämer, J.; et al. Frequency-comb referenced collinear laser spectroscopy of Be+ for nuclear structure investigations and many-body QED tests. Appl. Phys. B 2017, 123, 15. [Google Scholar] [CrossRef] [Green Version]
- Renth, L.; Imgram, P.; Krämer, J.; König, K.; Lellinger, T.; Maaß, B.; Müller, P.; Ratajczyk, T.; Nörtershäuser, W. First experiments with a laser ablation source at the COALA setup. Hyperfine Interact. 2020, 241, 56. [Google Scholar] [CrossRef]
- Johnson, W.R.; Cheng, K.T.; Plante, D.R. Hyperfine structure of 23P levels of heliumlike ions. Phys. Rev. A 1997, 55, 2728–2742. [Google Scholar] [CrossRef]
- Stone, N.J. Table of nuclear magnetic dipole and electric quadrupole moments. At. Data Nucl. Data Tables 2005, 90, 75–176. [Google Scholar] [CrossRef]
- Yerokhin, V.A.; Pachucki, K. Theoretical energies of low-lying states of light helium-like ions. Phys. Rev. A 2010, 81, 022507. [Google Scholar] [CrossRef] [Green Version]
- Schiff, B.; Accad, Y.; Pekeris, C.L. Correction to the n3P1 Levels of the Helium Isoelectronic Sequence Owing to Mixing with the n1P1 State. Phys. Rev. A 1973, 8, 2272–2273. [Google Scholar] [CrossRef]
- Drake, G.W. Theoretical energies for the n = 1 and 2 states of the helium isoelectronic sequence up to Z = 100. Can. J. Phys. 1988, 66, 586–611. [Google Scholar] [CrossRef]
- Chen, M.H.; Cheng, K.T.; Johnson, W.R. Relativistic configuration-interaction calculations of n =2 triplet states of heliumlike ions. Phys. Rev. A 1993, 47, 3692–3703. [Google Scholar] [CrossRef]


| 2 – 2 | Ref. | |
|---|---|---|
| Schiff, 1973 | [38] | |
| Drake, 1988 | [39] | |
| Dinnéen (exp.), 1991 | [24] | |
| Chen, 1993 | [40] | |
| Yerokhin, 2010 | [37] | |
| Yerokhin, 2022 | [18] | |
| This work (exp.) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohr, K.; Buß, A.; Andelkovic, Z.; Hannen, V.; Horst, M.; Imgram, P.; König, K.; Maaß, B.; Nörtershäuser, W.; Rausch, S.; et al. Collinear Laser Spectroscopy of Helium-like 11B3+. Atoms 2023, 11, 11. https://doi.org/10.3390/atoms11010011
Mohr K, Buß A, Andelkovic Z, Hannen V, Horst M, Imgram P, König K, Maaß B, Nörtershäuser W, Rausch S, et al. Collinear Laser Spectroscopy of Helium-like 11B3+. Atoms. 2023; 11(1):11. https://doi.org/10.3390/atoms11010011
Chicago/Turabian StyleMohr, Konstantin, Axel Buß, Zoran Andelkovic, Volker Hannen, Max Horst, Phillip Imgram, Kristian König, Bernhard Maaß, Wilfried Nörtershäuser, Simon Rausch, and et al. 2023. "Collinear Laser Spectroscopy of Helium-like 11B3+" Atoms 11, no. 1: 11. https://doi.org/10.3390/atoms11010011
APA StyleMohr, K., Buß, A., Andelkovic, Z., Hannen, V., Horst, M., Imgram, P., König, K., Maaß, B., Nörtershäuser, W., Rausch, S., Sánchez, R., & Weinheimer, C. (2023). Collinear Laser Spectroscopy of Helium-like 11B3+. Atoms, 11(1), 11. https://doi.org/10.3390/atoms11010011






