1. Introduction
The Coulomb singularity in the hamiltonian may appear as a challenge in electronic structure calculations. Singularity-adapted Slater type-atomic orbitals (STO) basis is the usual solution to this, and Gaussian-type contracted basis functions (GTO) have turned out to be useful with sufficient accuracy. The latter one is more popular due to other practical advantages.
Pseudopotentials removing the singularity are another possible solution to this problem. In this case, the core electrons do not play an essential role in the problem at hand or valence electrons are expanded in plane waves, like with heavy elements or periodic crystalline systems. In those cases, the pseudopotentials typically replace the nuclei and a number of core electrons with their charge distribution, and possibly, some other core properties.
One-dimensional interpolating wavelets have been used for atomic computations, for example, in Ref. [
1]. Fischer and Defranceschi [
2] have also solved hydrogen-like atoms with wavelets. In Ref. [
1], we used ordinary Deslauriers–Dubuc interpolating wavelets [
3,
4,
5] defined on the whole real axis, so including the negative real axis in the computations. We handled the singularity at the origin by excluding the scaling function at the origin from the basis. We used the nonstandard operator form for the various operators needed in the computations. We computed the Schrödinger equation of hydrogenlike atoms (ions) and Hartree–Fock equations of some light many-electron atoms (helium, lithium, beryllium, neon, sodium, magnesium, and argon). In this article, we repeat similar computations for hydrogen and helium atoms, but using a different method to handle the singularity of the potential and only one resolution level. We handle the singularity by computing the Schrödinger and Hartree–Fock equations for a range of variables
, which does not contain the origin. Here,
r is the position coordinate. The range
is neglected for hydrogen, and for helium, its contribution to the Slater integrals is computed using the hydrogenic orbitals.
Arias [
6] developed formalism for electronic structure calculations with interpolating wavelets so that matrix elements of the operators are computed as usual, and overlap matrices are used in the matrix form of the Schrödinger equation. On the other hand, we use the interpolating dual scaling functions and wavelets for the computation of matrix elements.
One-dimensional interpolating multiresolution analysis in space
consisting of uniformly continuous bounded functions in
was conducted in Ref. [
4]. One-dimensional interpolating multiresolution analysis in space
consisting of continuous functions in
and vanishing at infinity was constructed in [
5]. Both of these constructions are based on Deslauriers–Dubuc functions [
3]. Donoho [
5] constructs wavelets on a finite real interval, too. We compute the eigenenergies of hydrogen atom 1s, 2s, and 2p orbitals and helium atom configurations
,
, and
with the EPP method Exact Pseudopotential Method (EPP) using both the Galerkin method with interpolating wavelets and the finite difference method.
We denote the pointwise product of functions f and g by . We use atomic units throughout this article () and denote the atomic unit of energy by (Hartree).
4. Combination of EPP with Finite Difference Method
The Schrödinger and Hartree–Fock equations are converted to matrix equations using the biorthogonality relations of interpolating wavelets [
1]. We compare these computations with the Finite Difference Method, which is a straightforward method for solving differential equations. The spatial and time domains are discretized, and the derivative at a point is computed with a stencil applied to the nearby points. This way the differential equation is converted to a matrix equation. The Laplacian operator is approximated by
where
h is the discretization step size.
We discretize the Schrödinger Equation (
23) at points
,
, where
J is the number of actual computation points and
is the grid spacing. We define the discretized potential by
. The boundary condition at the end of the interval is set by
. We have
for
. We handle case
by extrapolating
linearly from
and
. We obtain
from which it follows that
. Hence, the difference equation for
is
In order to discretize the exchange operator
we need to discretize the integral operators
and
We define
and
where
. When
f is a real function, we define
. Now, the matrix of the exchange integral operator is computed by
where
is computed as in the case of wavelets,
and
5. Results
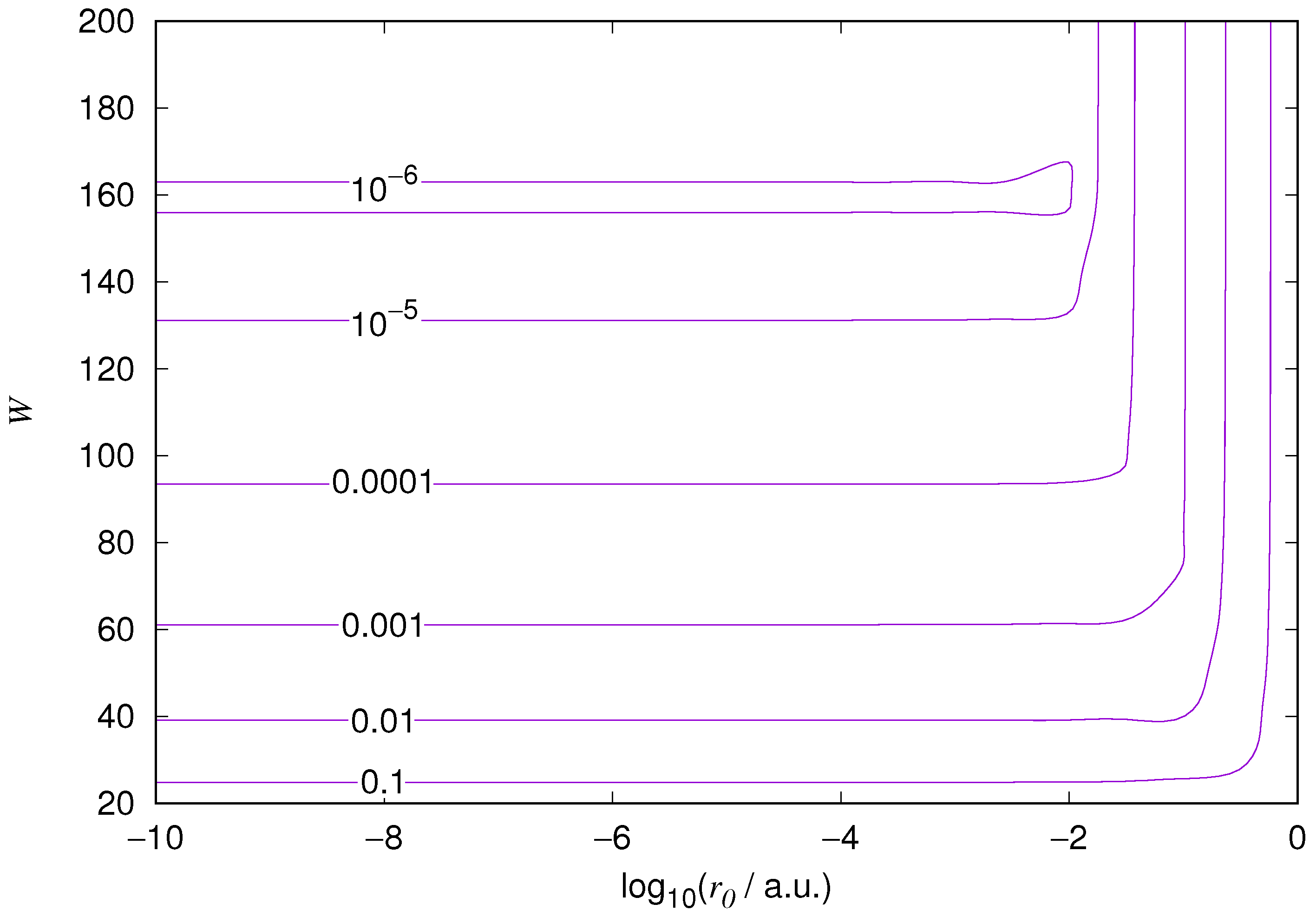
We demonstrate the EPP method by performing computations where the EPP radius
and the basis size
W are varied. We actually select a length scale
and conduct a change of variables
in Equations (
23) and (
31)–(
35). The length scale
u specifies how many atomic units of length a length unit in our own coordinate system is. Here,
R is the size of the computation domain. For hydrogen 1s, we have
, for hydrogen 2s and 2p
, for He
, and for He 1s2s
and
. We also set
for the basis set (see
Section 2), and hence
u is equal to the grid spacing
. The relative errors of the quantities are given as
The amount of discontinuity of a computed wavefunction at point is measured by computing the relative error of the computed wavefunction value compared to the hydrogenic wavefunction value .
The results for the ground state of the hydrogen atom are presented in
Figure 1 and
Figure 2, for the 2s state in
Figure 3 and
Figure 4, and for the 2p state in
Figure 5 and
Figure 6. The results of the ground state of the helium atom are presented in
Figure 7 and
Figure 8. The results for
are given in
Figure 9 and the results for
in
Figure 10. As expected, the energy results are best for large values of
W and small values of
. Using 200 basis functions for the helium ground state and computing the atom energies for
,
shows that atom energies are equal up to seven decimal places for
. Similar computation for the hydrogen 1s orbital shows that the H 1s energy is equal to
up to seven decimal places for
. For hydrogen 2s and 2p, the corresponding limit is
, too.
We also found that when the number of basis functions is sufficiently large for a given system, there is an approximate threshold value so that reducing below it does not make the accuracy of the computed energy better. When the number of basis functions is sufficiently large and is sufficiently small, the hydrogenic orbitals are approximately continuous at .
The most accurate computations are in the upper left corners of the figures. The orbitals of He 1s2s, except He 1s2s
1s, are not continuous at all at
, and no continuity plots are presented for them. The computation results and exact results are given in
Table 1. For the EPP–Galerkin method the best energies (largest basis and smallest
) of the computed systems are presented. The OIW–Galerkin results with same number of basis functions and grid spacing the same order of magnitude as for the most accurate EPP results are given, too. The accuracies of both of the methods depend on the grid spacing. The EPP–Galerkin method gives better results with the same number of basis functions and larger grid spacing. The results of the Finite Difference Method are also given. Note that for He 1s2s systems, the OIW–Galerkin method with a basis set of 601 functions and finest grid point distance
gives
and
, which are approximately the same as the results of the EPP–Galerkin method.
Some of the computations using the diagonalization of the Hamiltonian operator yield an unphysical state for the minimum eigenvalue. For 1s and 2s orbitals, this eigenvalue seems to be about
(in atomic units) and the corresponding eigenvector
. For the hydrogen 2p orbital, the unphysical eigenvector does not appear. The unphysical state remains the same during the HF iteration of
,
, and
. The physical admissibility of the wavefunctions
was characterized by the condition
We checked this condition by extrapolating solutions
polynomially at
. Actually, we extrapolate polynomially
at
using some points
s near 0. Note that Fischer and Defranceschi [
2] also find unphysical states in wavelet computations of hydrogen-like atoms. Their iteration scheme yields an unphysical result that is actually the mathematical ground state corresponding to the pseudopotential.
6. Discussion
The EPP–Galerkin method gives seven correct decimal places for the hydrogenic 1s orbital, six correct decimal places for the hydrogenic 2s and 2p orbitals, and four correct decimal places for He . For He 1s2s and , we obtain energies close to the HF limit. The OIW–Galerkin method with the finest grid spacing gives energies with two to five correct decimal places. The grid size of OIW–Galerkin calculations is smaller compared to the EPP–Galerkin calculations. The Finite Difference Method yields rather inaccurate results even though the grid spacing is considerably smaller compared to the EPP–Galerkin calculations.
To our surprise, the EPP Hartree–Fock total energy of the He excited state configuration
is lower than the exact energy including correlations. This has been observed earlier in Ref. [
10], and Cohen and Kelly [
11] have shown that the reason is the nonorthogonality of this particular state and the ground state
. Thus, the kind of "orbital relaxation" of the excited HF state
lowers the total energy by mixing a little of the ground state with the excited state wave function. In the present case, the EPP overlap integral of these two states is 0.0274, and there are obvious ways to work out the pure excited states, but this is out of the scope of this study.
We were able to obtain results near the Hartree–Fock limit by using a large enough basis and small enough parameter . It turns out that the EPP–Galerkin method yields better methods than the OIW–Galerkin method and considerably better results than the Finite Difference Method.