Background and Blended Spectral Line Reduction in Precision Spectroscopy of EUV and X-ray Transitions in Highly Charged Ions
Abstract
:1. Introduction
2. Spectroscopy in the EBIT
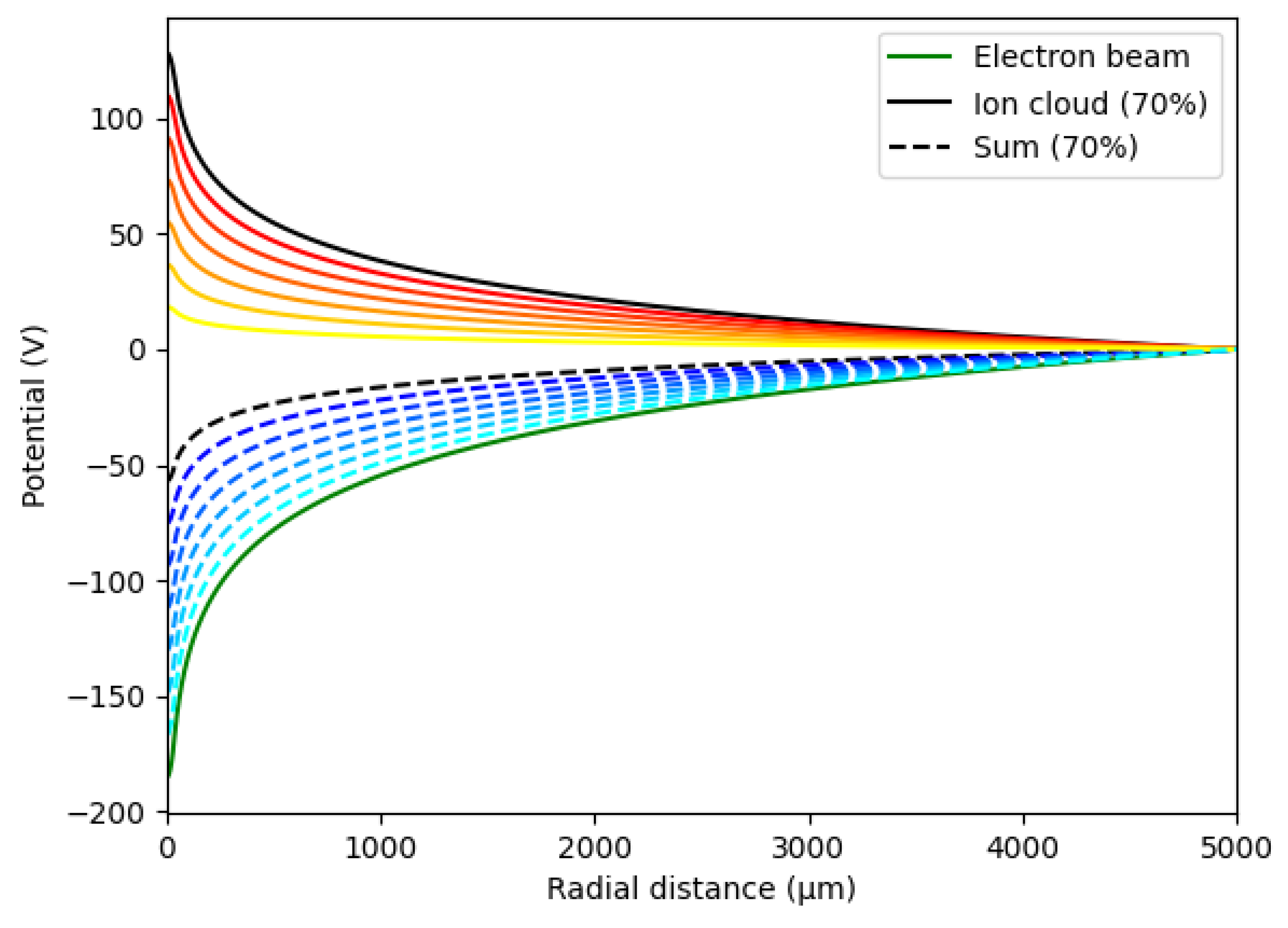
3. Ion Cloud Confinement
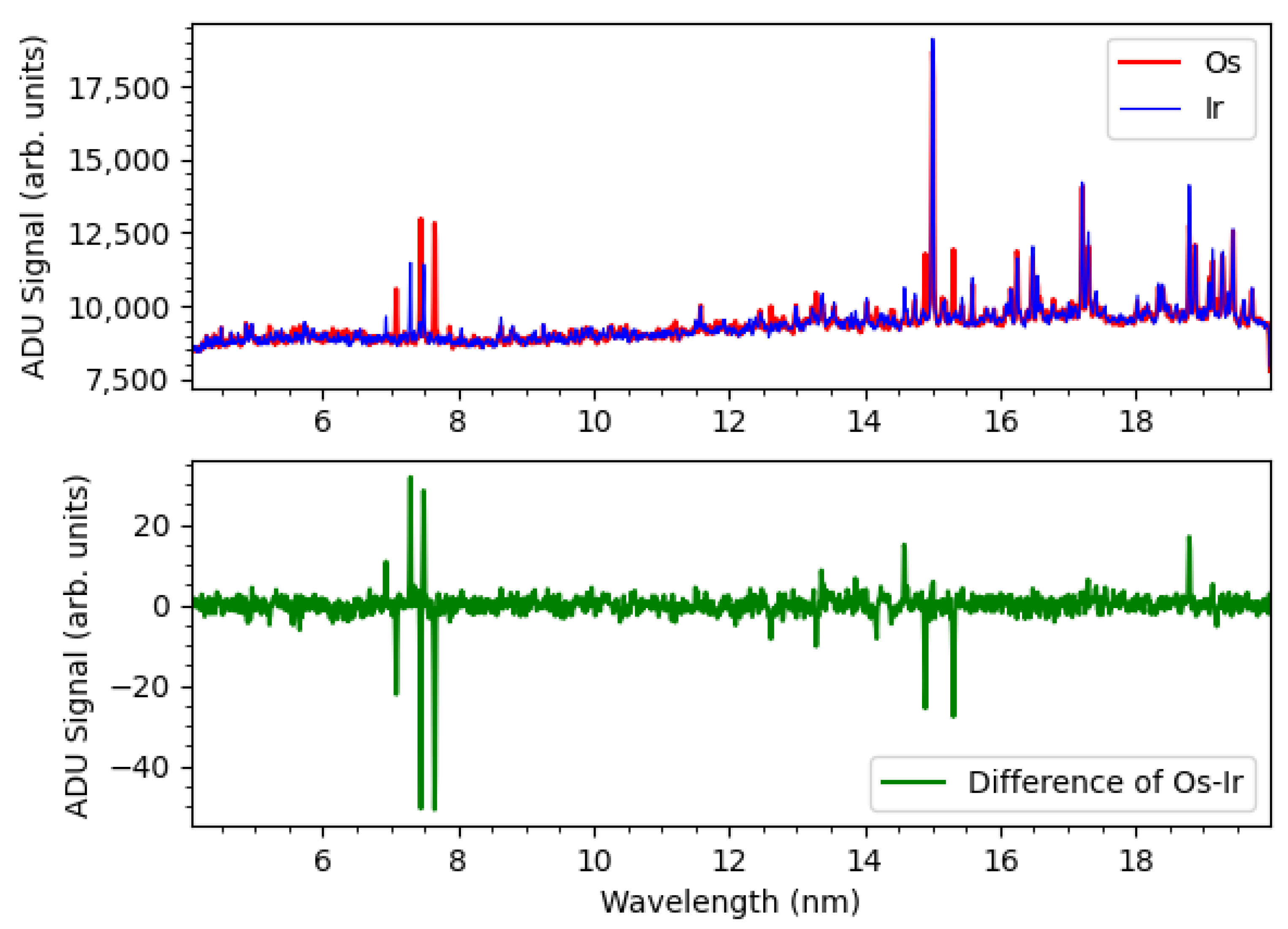
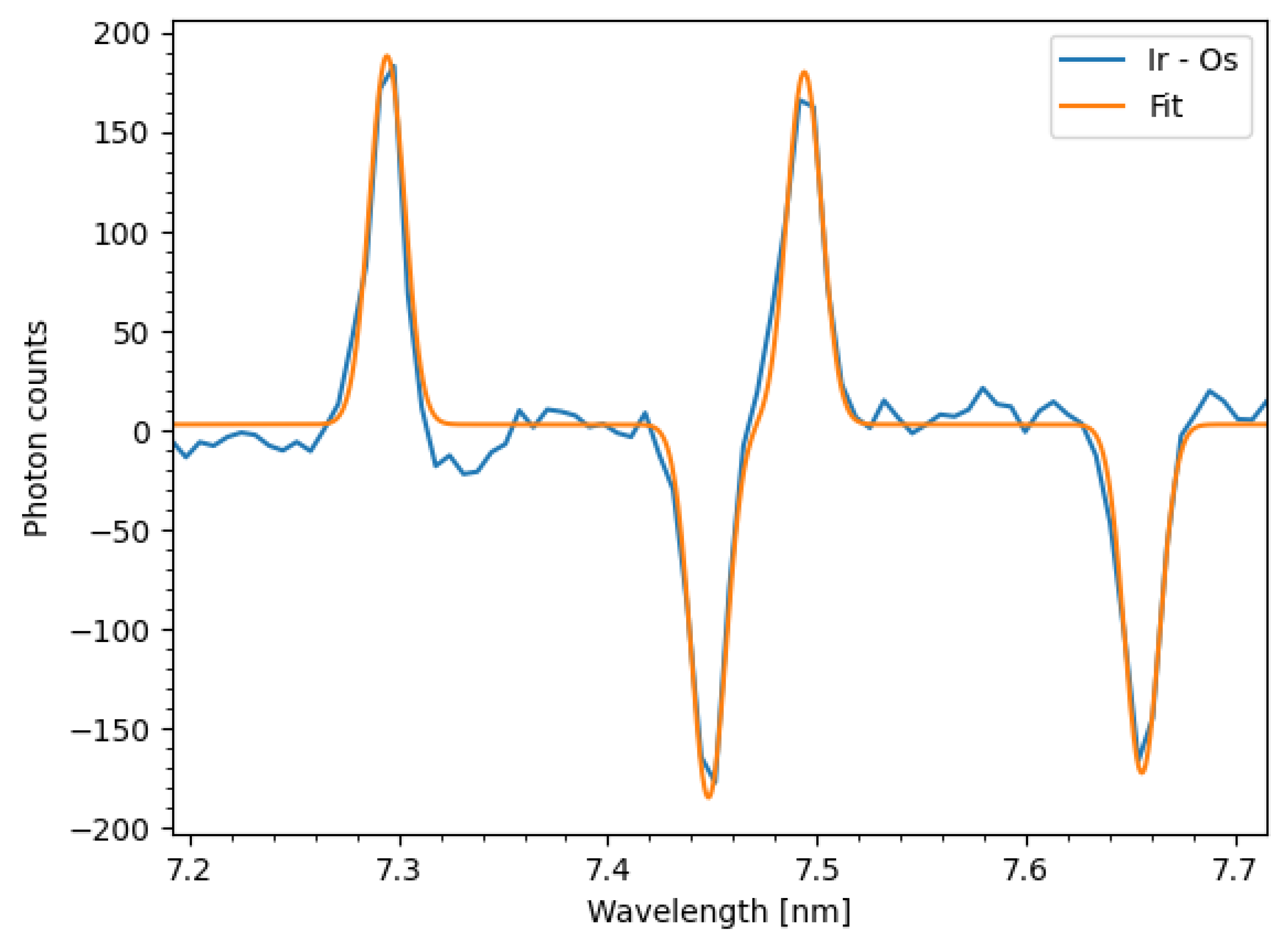
4. Removal of Blended Spectral Lines
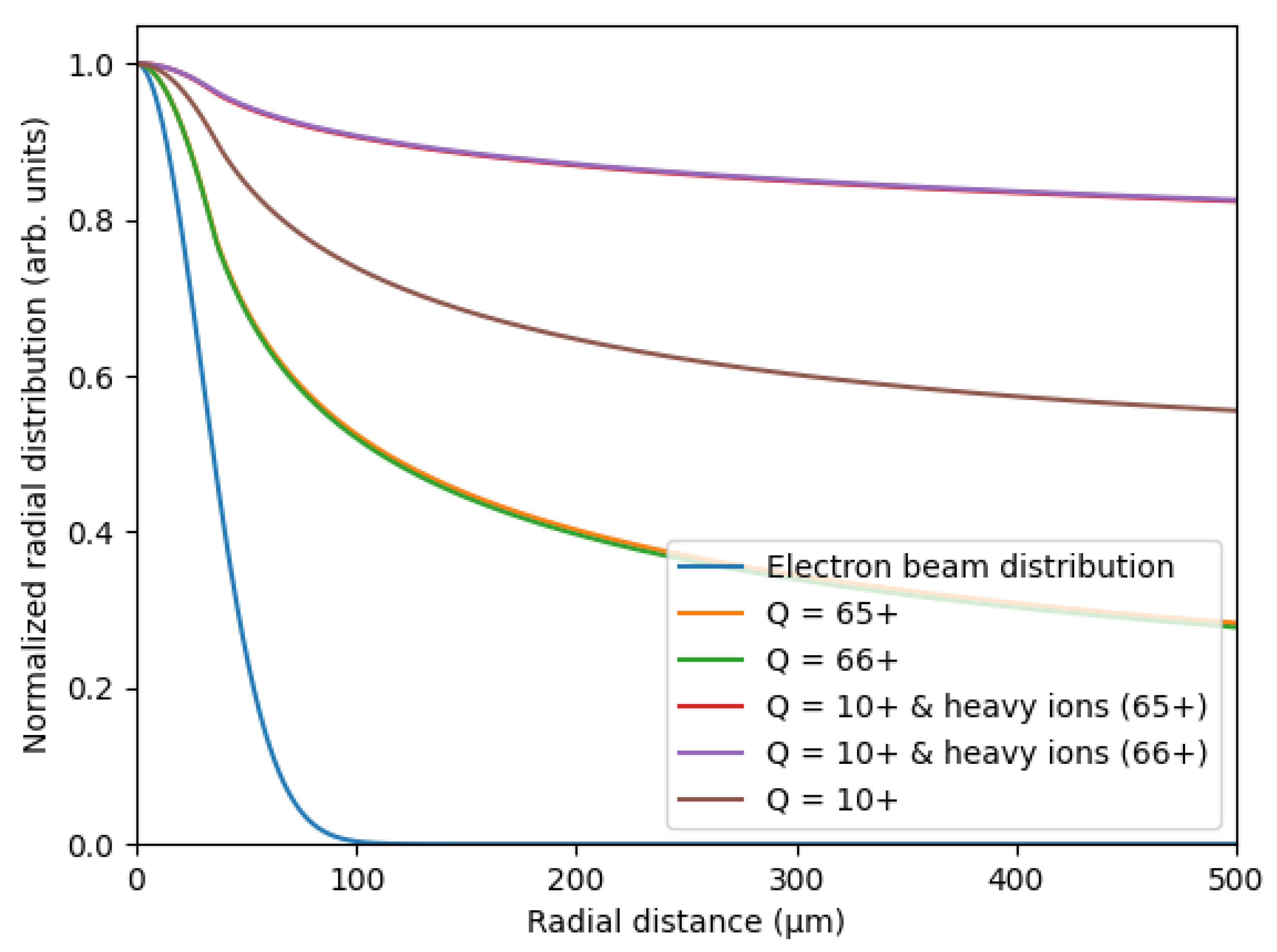
5. Ion Distributions
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Beiersdorfer, P. Testing QED and atomic-nuclear interactions with high- Z ions. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 074032. [Google Scholar] [CrossRef]
- Indelicato, P. QED tests with highly charged ions. J. Phys. At. Mol. Opt. Phys. 2019, 52, 232001. [Google Scholar] [CrossRef] [Green Version]
- Silwal, R.; Lapierre, A.; Gillaspy, J.D.; Dreiling, J.M.; Blundell, S.A.; Dipti; Borovik, A.; Gwinner, G.; Villari, A.C.C.; Ralchenko, Y.; et al. Determination of the isotopic change in nuclear charge radius from extreme-ultraviolet spectroscopy of highly charged ions of Xe. Phys. Rev. A 2020, 101, 062512. [Google Scholar] [CrossRef]
- Silwal, R.; Lapierre, A.; Gillaspy, J.D.; Dreiling, J.M.; Blundell, S.A.; Dipti; Borovik, A.; Gwinner, G.; Villari, A.C.C.; Ralchenko, Y.; et al. Measuring the difference in nuclear charge radius of Xe isotopes by EUV spectroscopy of highly charged Na-like ions. Phys. Rev. A 2018, 98, 052502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giacconi, R. Nobel Lecture: The dawn of X-ray astronomy. Rev. Mod. Phys. 2003, 75, 995–1010. [Google Scholar] [CrossRef] [Green Version]
- Szypryt, P.; O’Neil, G.C.; Takacs, E.; Tan, J.N.; Buechele, S.W.; Naing, A.S.; Bennett, D.A.; Doriese, W.B.; Durkin, M.; Fowler, J.W.; et al. A transition-edge sensor-based X-ray spectrometer for the study of highly charged ions at the National Institute of Standards and Technology electron beam ion trap. Rev. Sci. Instrum. 2019, 90, 123107. [Google Scholar] [CrossRef] [PubMed]
- Gillaspy, J.D. First results from the EBIT at NIST. Phys. Scr. 1997, T71, 99–103. [Google Scholar] [CrossRef]
- Ralchenko, Y.V.; Maron, Y. Accelerated recombination due to resonant deexcitation of metastable states. J. Quant. Spectrosc. Radiat. Transf. 2001, 71, 609–621. [Google Scholar] [CrossRef] [Green Version]
- Gu, M.F. The flexible atomic code. Can. J. Phys. 2008, 86, 675–689. [Google Scholar] [CrossRef]
- Jönsson, P.; Gaigalas, G.; Bieroń, J.; Fischer, C.F.; Grant, I.P. New version: Grasp2K relativistic atomic structure package. Comput. Phys. Commun. 2013, 184, 2197–2203. [Google Scholar] [CrossRef] [Green Version]
- Takács, E.; Meyer, E.S.; Gillaspy, J.D.; Roberts, J.R.; Chantler, C.T.; Hudson, L.T.; Deslattes, R.D.; Brown, C.M.; Laming, J.M.; Dubau, J.; et al. Polarization measurements on a magnetic quadrupole line in Ne-like barium. Phys. Rev. A 1996, 54, 1342–1350. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Currell, F.; Fussmann, G. Physics of electron beam ion traps and sources. IEEE Trans. Plasma Sci. 2005, 33, 1763–1777. [Google Scholar] [CrossRef]
- Penetrante, B.M.; Bardsley, J.N.; DeWitt, D.; Clark, M.; Schneider, D. Evolution of ion-charge-state distributions in an electron-beam ion trap. Phys. Rev. A 1991, 43, 4861–4872. [Google Scholar] [CrossRef] [PubMed]
- Porto, J.V.; Kink, I.; Gillaspy, J.D. Direct imaging of highly charged ions in an electron beam ion trap. Rev. Sci. Instrum. 2000, 71, 3050–3058. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Electron Beam Current | 10 mA to 150 mA |
| Electron Beam Energy | 1.0 kV to 30.0 kV |
| Dump Cycle | few s |
| Pressure of Gas Injector | 3 × 10 Pa |
| Visible Trap Length | 2 cm |
| Magnetic Field | 2.7 T |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosier, A.; Dipti; Yang, Y.; Szypryt, P.; Mondeel, G.P.; Naing, A.; Tan, J.N.; Silwal, R.; O’Neil, G.; Lapierre, A.; et al. Background and Blended Spectral Line Reduction in Precision Spectroscopy of EUV and X-ray Transitions in Highly Charged Ions. Atoms 2023, 11, 48. https://doi.org/10.3390/atoms11030048
Hosier A, Dipti, Yang Y, Szypryt P, Mondeel GP, Naing A, Tan JN, Silwal R, O’Neil G, Lapierre A, et al. Background and Blended Spectral Line Reduction in Precision Spectroscopy of EUV and X-ray Transitions in Highly Charged Ions. Atoms. 2023; 11(3):48. https://doi.org/10.3390/atoms11030048
Chicago/Turabian StyleHosier, Adam, Dipti, Yang Yang, Paul Szypryt, Grant P. Mondeel, Aung Naing, Joseph N. Tan, Roshani Silwal, Galen O’Neil, Alain Lapierre, and et al. 2023. "Background and Blended Spectral Line Reduction in Precision Spectroscopy of EUV and X-ray Transitions in Highly Charged Ions" Atoms 11, no. 3: 48. https://doi.org/10.3390/atoms11030048
APA StyleHosier, A., Dipti, Yang, Y., Szypryt, P., Mondeel, G. P., Naing, A., Tan, J. N., Silwal, R., O’Neil, G., Lapierre, A., Blundell, S. A., Gillaspy, J. D., Gwinner, G., Villari, A. C. C., Ralchenko, Y., & Takacs, E. (2023). Background and Blended Spectral Line Reduction in Precision Spectroscopy of EUV and X-ray Transitions in Highly Charged Ions. Atoms, 11(3), 48. https://doi.org/10.3390/atoms11030048






