Radiative Recombination Plasma Rate Coefficients for Multiply Charged Ions
Abstract
:1. Introduction
2. Theory Furthermore, Computations
2.1. Radiative Recombination Cross Sections
2.2. Temperature-Dependent Plasma Rate Coefficients
2.3. Radiative Recombination Cascades
2.4. Implementation of Plasma Rate Coefficients into the Jac Toolbox
2.5. Data Types for Radiative Recombination Cascades
3. Radiative Reombination Plasma Rate Coefficients for Multiply Charged Ions
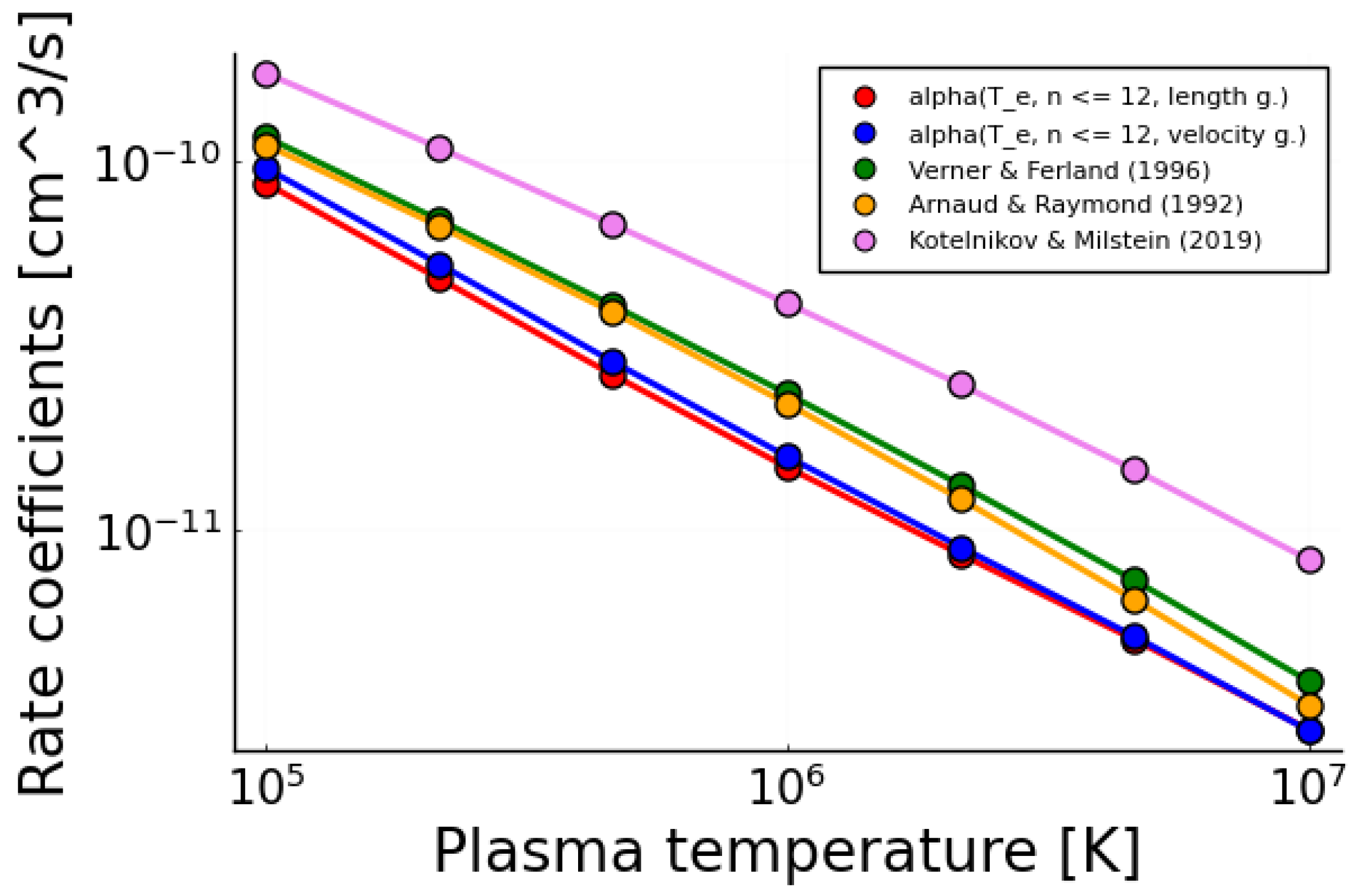
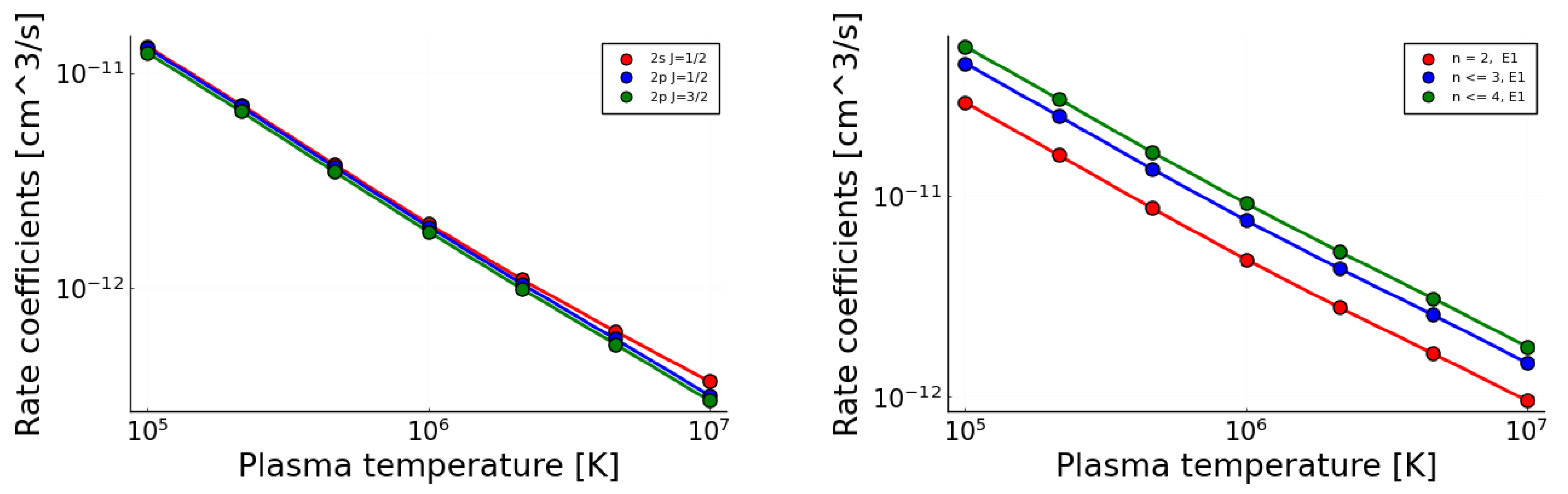
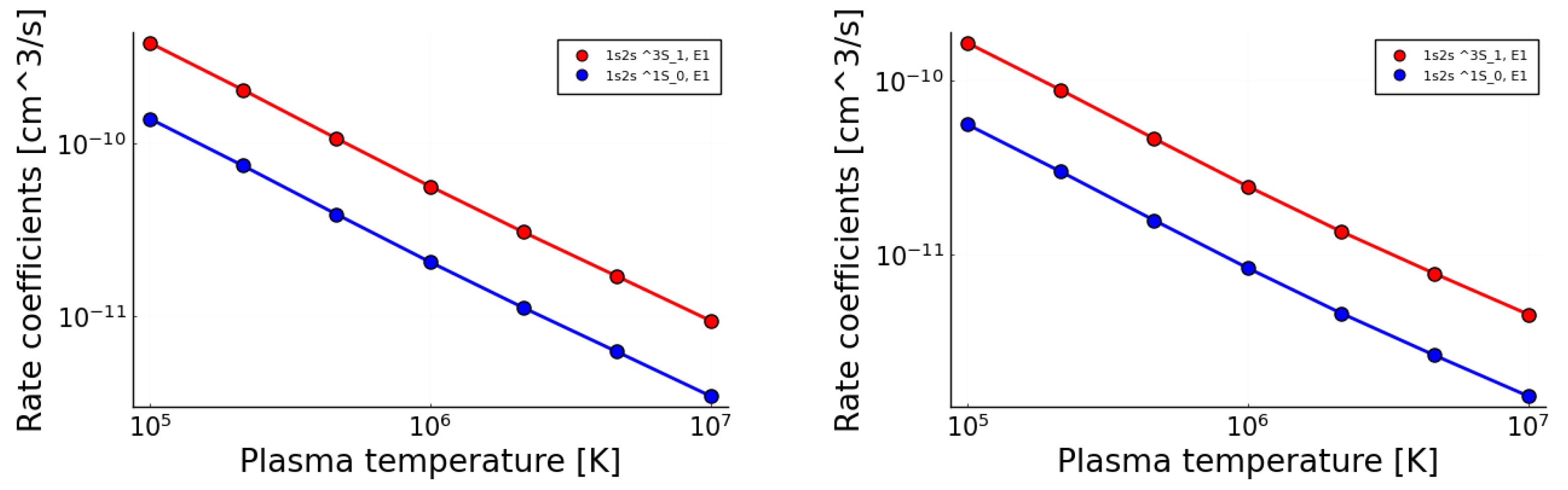
3.1. Plasma Rate Coefficients for Initially Fe Ions
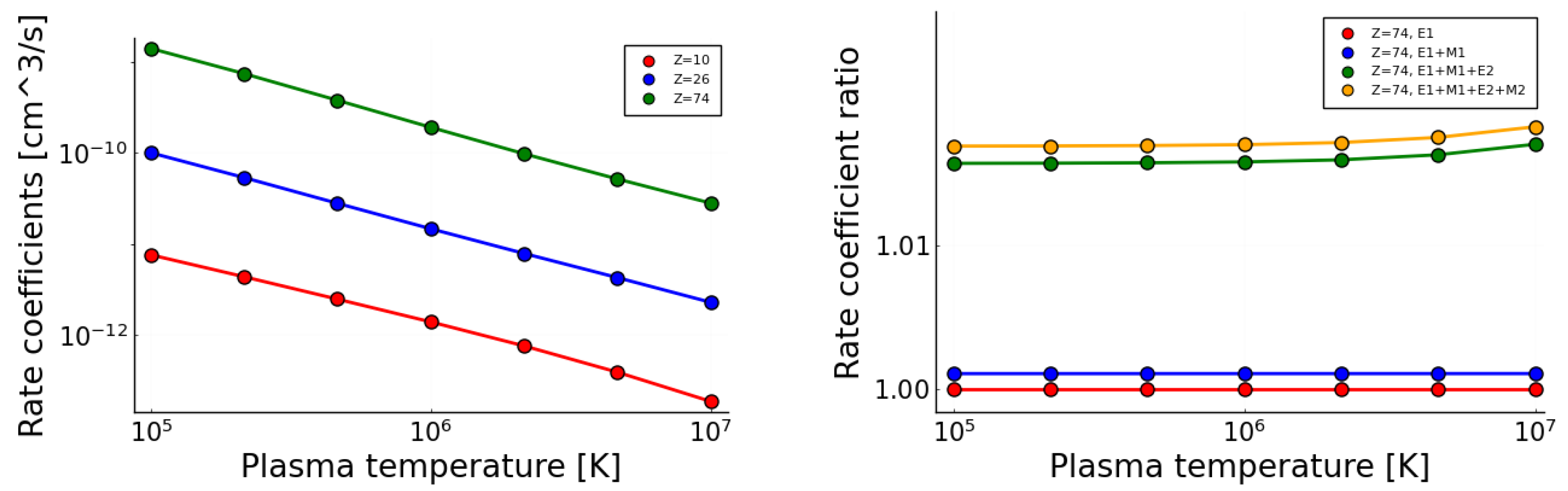
3.2. Trends for Multiply and Highly Charged Ions
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Seaton, M.J. Radiative Recombination of Hydrogenic Ions. Mon. Not. R. Astron. Soc. 1959, 119, 81. [Google Scholar] [CrossRef] [Green Version]
- Pequignot, D.; Petitjean, P.; Boisson, C. Total and effective radiative recombination coefficients. Astron. Astrophys. 1991, 251, 680. [Google Scholar]
- Nahar, S.N. Electron-ion recombination rate coefficients and photoionization cross sections for astrophysically abundant elements. XI. N v–vi and F vii–viii for ultraviolet and x-ray modeling. Astrophys. J. Suppl. 2006, 164, 280. [Google Scholar] [CrossRef] [Green Version]
- Surzhykov, A.; Fritzsche, S.; Stöhlker, T.; Tachenov, S. Polarization studies on the radiative recombination of highly charged bare ions. Phys. Rev. A 2003, 68, 022710. [Google Scholar] [CrossRef] [Green Version]
- Mazzotta, P.; Mazzitelli, G.; Colafrancesco, S.; Vittorio, N. Ionization balance for optically thin plasmas: Rate coefficients for all atoms and ions of the elements H to NI. Astr. Astrophys. Suppl. Ser. 1998, 133, 403. [Google Scholar] [CrossRef] [Green Version]
- Trzhaskovskaya, M.B.; Nikulin, V.K. Radiative recombination and photoionization data for tungsten ions. Electron structure of ions in plasmas. Atoms 2015, 3, 86. [Google Scholar] [CrossRef] [Green Version]
- Badnell, N.R. Radiative recombination data for modeling dynamic finite-density plasmas. Astr. Astrophys. Suppl. Ser. 2006, 167, 334. [Google Scholar] [CrossRef] [Green Version]
- Raymond, J.C.; Cox, D.P.; Smith, B.W. Radiative cooling of a low-density plasma. Astrophys. J. 1976, 204, 290. [Google Scholar] [CrossRef]
- Aldrovandi, S.M.V.; Pequignot, D. Radiative and dielectronic recombination coefficients for complex ions. Astron. Astrophys. 1973, 25, 137. [Google Scholar]
- Arnaud, M.; Rothenflug, R. An updated evaluation of recombination and ionization rates. Astron. Astrophys. Suppl. Ser. 1985, 60, 425. [Google Scholar]
- Landini, M.; Monsignori Fossi, B.C. Ion equilibrium for minor components in a thin plasma. Astron. Astrophys. 1991, 91, 183. [Google Scholar]
- Arnaud, M.; Raymond, J. Iron ionization and recombination rates and ionization equilibrium. Astrophys. J. 1992, 398, 394. [Google Scholar] [CrossRef]
- Verner, D.A.; Ferland, G.J. Atomic data for astrophysics. I.Radiative recombination rates for H-like, He-like, Li-like and Na-like ions over a broad range of temperature. Astrophys. J. Suppl. Ser. 1996, 103, 467. [Google Scholar] [CrossRef]
- Summers, H.P. The ADAS User Manual, Version 2.6. Unpublished. 1996. Available online: http://www.adas.ac.uk (accessed on 18 February 2023).
- Kim, Y.S.; Pratt, R.H. Direct radiative recombination of electrons with atomic ions: Cross sections and rate coefficients. Phys. Rev. A 1983, 27, 2913. [Google Scholar] [CrossRef]
- Zhang, H.L.; Pradhan, A.K. Photoionization and recombination of Fe XIX. Mon. Not. R. Astron. Soc. 2000, 313, 13–20. [Google Scholar] [CrossRef] [Green Version]
- Zatsarinny, O.; Gorcyca, T.; Fu, J.; Korista, K.T.; Badnell, N.R.; Savin, D.W. Dielectronic recombination data for dynamic finite-density plasmas. IX. The fluorine isoelectronic sequence. Astron. Astrophys. 2006, 447, 379. [Google Scholar] [CrossRef] [Green Version]
- Ralchenko, Y. Modern Methods in Collisional-Radiative Modeling of Plasma; Springer: New York, NY, USA, 2016. [Google Scholar]
- Ferland, G.J. The ionization balance of a non-equilibrium plasma. Astron. Astrophys. 2009, 500, 299. [Google Scholar] [CrossRef]
- Rodriguez, R.; Espinosa, G.; Gil, J.M. Radiative properties for astrophysical plasma mixtures in nonlocal thermodynamic equilibrium. Phys. Rev. E 2018, 98, 033213. [Google Scholar] [CrossRef] [Green Version]
- Fritzsche, S. A fresh computational approach to atomic structures, processes and cascades. Comp. Phys. Commun. 2019, 240, 1. [Google Scholar] [CrossRef]
- Zatsarinny, O.; Gorczyca, T.W.; Korista, K.; Badnell, N.R.; Savin, D.W. Dielectronic recombination data for dynamic finite-density plasmas. VII. The neon isoelectronic sequence. Astron. Astrophys. 2004, 426, 699. [Google Scholar] [CrossRef]
- Fritzsche, S. Dielectronic recombination strengths and plasma rate coefficients of multiply-charged ions. Astron. Astrophys. 2021, 656, A163. [Google Scholar] [CrossRef]
- Fritzsche, S. The Ratip program for relativistic calculations of atomic transition, ionization and recombination properties. Comp. Phys. Commun. 2012, 183, 1525. [Google Scholar] [CrossRef]
- Fritzsche, S. JAC: User Guide, Compendium & Theoretical Background. Unpublished. Available online: https://github.com/OpenJAC/JAC.jl (accessed on 10 December 2022).
- Grant, I.P. Relativistic Quantum Theory of Atoms and Molecules: Theory and Computation; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Fritzsche, S. Large-scale accurate structure calculations for open-shell atoms and ions. Phys. Scr. 2002, T100, 37. [Google Scholar] [CrossRef]
- Eliav, E.; Fritzsche, S.; Kaldor, U. Electronic structure theory of the superheavy elements. Nucl. Phys. A 2015, 944, 518. [Google Scholar] [CrossRef]
- Grant, I.P. Relativistic effects in atoms and molecules. In Methods in Computational Chemistry; Wilson, S., Ed.; Plenum: New York, NY, USA, 1988; Volume 2, p. 1. [Google Scholar]
- Kabachnik, N.M.; Fritzsche, S.; Grum-Grzhimailo, A.N.; Meyer, M.; Ueda, K. Coherence and correlations in photoinduced Auger and fluorescence cascades in atoms. Phys. Rep. 2007, 451, 155. [Google Scholar] [CrossRef]
- Fritzsche, S.; Fricke, B.; Sepp, W.D. Reduced L1 level-width and Coster-Kronig yields by relaxation and continuum interactions in atomic zinc. Phys. Rev. A 1992, 45, 1465. [Google Scholar] [CrossRef] [Green Version]
- Nahar, S.N. Electron-ion recombination rate coefficients and photoionization cross sections for astrophysically abundant elements. VIII. Ar XIII with new features. Astrophys. J. Suppl. Ser. 2005, 156, 93. [Google Scholar] [CrossRef]
- Trzhaskovskaya, M.B.; Nikulin, V.K.; Clark, R.E.H. Multipole and relativistic effects in radiative recombination process in hot plasmas. Phys. Rev. 2008, E78, 035401(R). [Google Scholar] [CrossRef] [Green Version]
- Fritzsche, S.; Palmeri, P.; Schippers, S. Atomic cascade computations. Symmetry 2021, 13, 520. [Google Scholar] [CrossRef]
- Schippers, S.; Martins, M.; Beerwerth, R.; Bari, S.; Holste, K.; Schubert, K.; Viefhaus, J.; Savin, D.W.; Fritzsche, S.; Müller, A. Near L-edge single and multiple photoionization of singly charged iron ions. Astrophys. J. 2017, 849, 5. [Google Scholar] [CrossRef] [Green Version]
- Beerwerth, R.; Buhr, T.; Perry-Sassmannshausen, A.; Stock, S.O.; Bari, S.; Holste, K.; Kilcoyne, A.L.D.; Reinwardt, S.; Ricz, S.; Savin, D.W.; et al. Near L-edge single and multiple photoionization of triply charged iron ions. Astrophys. J. 2019, 887, 189. [Google Scholar] [CrossRef] [Green Version]
- Schippers, S.; Beerwerth, R.; Bari, S.; Buhr, T.; Holste, K.; Kilcoyne, A.L.D.; Perry-Sassmannshausen, A.; Phaneuf, R.A.; Reinwardt, S.; Savin, D.W.; et al. Near L-edge single and multiple photoionization of doubly charged iron ions. Astrophys. J. 2021, 908, 52. [Google Scholar] [CrossRef]
- Schippers, S.; Beerwerth, R.; Abrok, L.; Bari, S.; Buhr, T.; Martins, M.; Ricz, S.; Viefhaus, J.; Fritzsche, S.; Müller, A.; et al. Prominent role of multielectron processes in K-shell double and triple photodetachment of oxygen anions. Phys. Rev. A 2016, 94, 041401(R). [Google Scholar] [CrossRef] [Green Version]
- Fritzsche, S. Photon emission from hollow ions near surfaces. Atoms 2022, 10, 37. [Google Scholar] [CrossRef]
- Hitomi Collaboration; Aharonian, F.; Akamatsu, H.; Akimoto, F.; Allen, S.W.; Angelini, L.; Audard, M.; Awaki, H.; Axelsson, M.; Bamba, A.; et al. Atomic data and spectral modeling constraints from high-resolution X-ray observations of the Perseus cluster with Hitomi. Public. Astron. Soc. Japan 2018, 70, 12. [Google Scholar] [CrossRef]
- Kramers, H. On the theory of X-ray absorption and of continuous X-ray spectrum. Phil. Mag. 1923, 46, 836. [Google Scholar] [CrossRef]
- Kotelnikov, I.A.; Milstein, A.I. Electron radiative recombination with a hydrogen-like ion. Phys. Scr. 2019, 94, 055403. [Google Scholar] [CrossRef] [Green Version]
- Perry-Sassmannshausen, A.; Buhr, T.; Borovik, A., Jr.; Martins, M.; Reinwardt, S.; Ricz, S.; Stock, S.; Trinter, F.; Müller, A.; Fritzsche, S.; et al. Multiple photodetachment of carbon anions via single and double core-hole creation. Phys. Rev. Lett. 2020, 124, 083203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schippers, S.; Hamann, A.; Perry-Sassmannshausen, A.; Buhr, T.; Müller, A.; Martins, M.; Reinwardt, S.; Trinter, F.; Fritzsche, S. Multiple photodetachment of oxygen anions via K-shell excitation and ionization: Direct double-detachment processes and subsequent deexcitation cascades. Phys. Rev. A 2022, 106, 013114. [Google Scholar] [CrossRef]
- Fritzsche, S.; Surzhykov, A. Approximate atomic Green functions. Molecules 2021, 26, 2660. [Google Scholar] [CrossRef]
- Julia 1.8 Documentation. Available online: https://docs.julialang.org/ (accessed on 10 December 2021).
- Bezanson, J.; Chen, J.; Chung, B.; Karpinski, S.; Shah, V.B.; Vitek, J.; Zoubritzky, L. Julia: Dynamism and performance reconciled by design. Proc. Acm Program. Lang. 2018, 2, 120. [Google Scholar] [CrossRef] [Green Version]
- McLaughlin, D.J.; Hahn, Y. Scaling behavior of radiative recombination cross sections and rate coefficients. Phys. Rev. A 1991, 43, 1313. [Google Scholar] [CrossRef] [PubMed]
- Saha, B.; Fritzsche, S. Influence of dense plasma on the low-lying transitions in Be-like ions: Relativistic multiconfiguration Dirac-Fock calculations. J. Phys. B 2007, 40, 259. [Google Scholar] [CrossRef]
- Mao, J.; Kaastra, J. Parameterization of the level-resolved radiative recombination rate coefficients for the SPEX code. Astron. Astrophys. 2016, 587, A84. [Google Scholar] [CrossRef] [Green Version]
- Ralchenko, Y. Collisional-Radiative Modeling for Highly-Charged Ions of Tungsten. Plasma Fusion Res. 2013, 8, 2503024. [Google Scholar] [CrossRef] [Green Version]
- Barfield, W.D. Partial photoionization cross sections and radiative recombination rate coefficients for lithium-like ions. Astrophys. J. 1979, 29, 856. [Google Scholar] [CrossRef]
- Pradhan, A.K. Radiative recombination of the ground state of lithium-like ions. Astrophys. J. 1983, 270, 339. [Google Scholar] [CrossRef]
- Fritzsche, S.; Surzhykov, A.; Stöhlker, T. Radiative recombination into high–Z few–electron ions: Cross sections and angular distributions. Phys. Rev. A 2005, 72, 012704. [Google Scholar] [CrossRef]
- Fritzsche, S. Level structure and properties of open f-shell elements. Atoms 2022, 10, 7. [Google Scholar] [CrossRef]
- Rose, M.E. Multipole Fields; John Wiley & Sons: New York, NY, USA, 1955. [Google Scholar]
- Jitrik, O.; Bunge, C.F. Transition probabilities for hydrogen-like atoms. J. Phys. Chem. Ref. Data 2004, 33, 1059. [Google Scholar] [CrossRef] [Green Version]
- Eichler, J.; Meyerhof, W.E. Relativistic Atomic Collisions; Academic Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Piron, R.; Gilleron, F.; Aglitskiy, Y.; Chung, H.-K.; Fontes, C.J.; Hansen, S.B.; Marchuk, O.; Scott, H.A.; Stambulchik, E.; Ralchenko, Y. Review of the 9th NLTE code comparison workshop. High Energy Density Phys. 2017, 23, 38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deprince, J.; Bautista, M.A.; Fritzsche, S.; García, J.A.; Kallman, T.R.; Mendoza, C.; Palmeri, P.; Quinet, P. Plasma environment effects on K lines of astrophysical interest. I. Atomic structure, radiative rates, and Auger widths of oxygen ions. Astron. Astrophys. 2019, 624, A74. [Google Scholar] [CrossRef] [Green Version]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fritzsche, S.; Maiorova, A.V.; Wu, Z. Radiative Recombination Plasma Rate Coefficients for Multiply Charged Ions. Atoms 2023, 11, 50. https://doi.org/10.3390/atoms11030050
Fritzsche S, Maiorova AV, Wu Z. Radiative Recombination Plasma Rate Coefficients for Multiply Charged Ions. Atoms. 2023; 11(3):50. https://doi.org/10.3390/atoms11030050
Chicago/Turabian StyleFritzsche, Stephan, Anna V. Maiorova, and Zhongwen Wu. 2023. "Radiative Recombination Plasma Rate Coefficients for Multiply Charged Ions" Atoms 11, no. 3: 50. https://doi.org/10.3390/atoms11030050
APA StyleFritzsche, S., Maiorova, A. V., & Wu, Z. (2023). Radiative Recombination Plasma Rate Coefficients for Multiply Charged Ions. Atoms, 11(3), 50. https://doi.org/10.3390/atoms11030050






