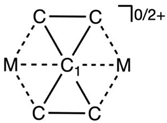
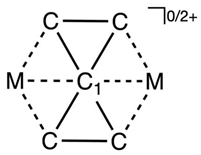
Abstract
Here, we present evidence that the D2h M2C50/2+ (M = Li-K, Be-Ca, Al-In, and Zn) species comprises planar hexacoordinate carbon (phC) structures that exhibit four covalent and two electrostatic interactions. These findings have been made possible using evolutionary methods for exploring the potential energy surface (AUTOMATON program) and the Interacting Quantum Atoms (IQA) methodology, which support the observed bonding interactions. It is worth noting, however, that these structures are not the global minimum. Nonetheless, incorporating two cyclopentadienyl anion ligands (Cp) into the CaC52+ system has enhanced the relative stability of the phC isomer. Moreover, cycloparaphenylene ([8]CPP) provides system protection and kinetic stability. These results indicate that using appropriate ligands presents a promising approach for expanding the chemistry of phC species.
1. Introduction
Chemists are fascinated by new chemical entities with exotic, non-classical structures, so they seek to rationalize these new systems based on known rules (concepts) or propose exceptions, and new methods, to achieve this goal. Molecules with planar hypercoordinate carbon atoms, which violate the well-established rule of Van ’t Hoff and Le Bel (regarding tetrahedral four-coordinate carbon), are particularly puzzling. Although these species, in the beginning, were considered experimentally inaccessible, in 1968, Monkhorst evaluated in silicon methane stereomutation through a planar tetracoordinate carbon (ptC) transition state [1]. Subsequently, in 1970, Hoffmann and co-workers proposed different approaches to stabilize a ptC to achieve a thermally accessible transition state for a racemization process [2]. These studies inspired other chemists who finally allowed the identification of viable ptC compounds [3,4,5,6,7].
In the last 50 years many ptC compounds have been reported, some synthesized or identified in the gas phase, and others designed in silicon [3,4,5,8,9,10,11]. In more recent years, the chemistry of the family has been extended to species in which the carbon coordination number is greater than four (penta [12,13,14,15,16,17,18,19,20,21] and hexacoordinated [22,23,24,25]). The examples for each group decrease according to the coordination, with only 15 structures reported as global minima with a hexacoordinated carbon in the plane.
In 2004, Merino et al. reported that their exploration of the potential energy surface of C52− revealed the existence of a local minimum with a planar tetracoordinate carbon for this dianionic cluster [26,27]. However, the ptC C42− isomer is 48.4 kcal·mol−1 above the global minimum (GM), which is an angular C2v structure (at the B3LYP/6-311++G(2d) level). In addition, these authors also found that adding metal cations (Mn+) to the C52− structure generates species with the targeted planar tetracoordinate carbon, which is stabilized exclusively by electronic factors. They tested cations from groups 1, 2, 11, and 13 of the periodic table. They concluded that the lithium salt C5Li2 is the most plausible candidate for experimental detection based on its energetic profile of the isomerization reaction. To our knowledge, none of these species have been detected experimentally. However, this study has inspired the identification of other viable gas-phase ptC systems (global minima).
In this work, we have raised some questions regarding the systems mentioned in the previous paragraph (results and discussion, Section 3). The first question is related to the proper coordination of the putative ptC (Section 3.1); since the natural population analysis (NPA) charge on the ptC is negative and that of the counterions is positive, and the ptC-M distance is smaller than the sum of the Van der Waals radii, an attractive ptC-M electrostatic interaction is to be expected. Therefore, this would genuinely be a planar hexacoordinated carbon (phC). The second question is related to the viability of any of these species. For this, we have explored the PES of some candidates (Section 3.2), showing that they do not correspond to global minima. In addition, we have explored the alternative of using ligands (cyclopentadienyl anion and 8-ring cycloparaphenylene) to provide thermodynamic and kinetic stability to the phC system (Section 3.3). Our results reveal that these systems are indeed phCs, with four covalent and two ionic interactions. Additionally, ligands provide relative energetic and kinetic stability to some systems, especially Ca2C52+. Therefore, we expect this study to open a pathway in the design of phCs with synthetic feasibility.
2. Computational Details
The PES of the Li2C5 system was explored using the AUTOMATON program [28,29]; in the search process, optimizations were performed at the PBE0 [30] /SDDAll [31,32,33,34,35] level. Then, the lowest energy minima were reoptimized at the ωb97XD [36] /def2-TZVP [37] level (both in singlet and triplet states). For the other systems C5M2 (M = Na, K, Al-In) and C5M2+2 (Be-Ca, Zn), the lowest energy minima obtained for C5Li2, were used as starting structures, then optimized at the PBE0/SDDAll level and reoptimized at the ωb97XD/def2-TZVP level, the latter being the level considered for the discussion of relative energies. The lowest energy isomers confined between aromatic ligands, benzene (C6H6) and cyclopentadienyl anion (C5H5−) were also optimized for the neutral and dicationic cases, respectively. Finally, the phC isomer of Ca2C52+ was optimized inside an 8-ring cycloparaphenylene, where two C5H5− have substituted two benzenes. The vibrational frequencies were checked to verify the structures as true minima on the PES. DFT computations were performed with Gaussian 16 software (Rev. B.01) [38]. The dynamic behavior of [(C5H5−)]2[Ca2C5]2+ and [8-CPP]2−[Ca2C5]2+ were assessed through Born Oppenheimer molecular dynamics (BOMD) simulations [39] on Gaussian 16 software at the PBE0-D3/SDDAll level. The BOMD simulations involve 20 ps at 500 K and within the NVT ensemble.
To gain insights about chemical bonding, we used different methods: Wiberg bond indices (WBI) [40], natural population analysis (NPA) [41], and the adaptive natural density partitioning (AdNDP) method [42,43]. These approaches are based on the natural bonding orbital (NBO) method and were performed at the ωb97XD/Def2-TZVP level. The WBI and NPA were computed with the NBO 6.0 code [44], and the AdNDP analysis was performed using Multiwfn 3.8 [45]. The molecular structure and AdNDP results were visualized using CYLview 2.0 [46] and VMD 1.9.3 [47], respectively.
3. Results and Discussion
3.1. Defining Whether the Systems Are ptC or phC
Table 1 shows the NPA charges, WBI values, and bond distances for the D2h structure for the combinations considered in this study. The charges are negative in carbons ranging from −0.35 to −0.23 |e| for the hypercoordinate one. The WBI values indicate a strong covalent connection between the C atoms and no or very weak C m covalent interaction, especially of the peripheral Cs, in agreement with its smaller C-C and larger M-C distances. Given that the charges on the hypercoordinate C and the metals have an opposite sign, one may inquire about a meaningful attractive electrostatic interaction between them that would contribute to the stability of this structure. Moreover, if attractive, these interactions would qualify them as phC species. The M-C distances are slightly greater than those of a single bond, according to the Pyykkö covalent radii [48]. However, they are much shorter than the sum of their van der Waals radii [49] (see Table 1). Therefore, it seems that, in these structures, the C is hexacoordinate.

Table 1.
Bond lengths (r, Å), natural charges (q, |e|) and Wiberg bond indices (WBI) of the M2C50/2+ (M = Li-K, Be-Ca, Al-In and Zn) computed at the ωb97XD/Def2-TZVP level [a].
All the above background points to the central carbon’s ionic bonding interactions with the M counterions. Hence, using an appropriate methodology to describe ionic interactions is mandatory. The IQA methodology is an accurate and chemically intuitive energy partitioning scheme that allows the analysis of chemical bonding in terms of covalent or ionic interactions [50,51,52,53]. This methodology has been used recently to gain insights into the bonding of the NaBH3− system [54], a system that has been a challenge for the theoretical community dedicated to the analysis of chemical bonding [55,56,57,58,59,60]. IQA was fundamental to introducing collective interactions in organometallic systems [61]. It also supports the hexacoordination of C in the global minima M3CE3+ (M = Li-Cs and E = S-Te) [24], with three covalent C-E and three ionic M-C interactions, becoming an indispensable method to rationalize coordination where there is a mixture of ionic and covalent interactions [21,62].
What is the interpretation of the chemical bond, according to IQA, of D2h M2C50/2+ (M = Li-K, Be-Ca, Al-In, and Zn) species? As shown in Table 2, the most important stabilizing interactions are between C-C bonds, mainly covalent (: −283.2 to −301.0 kcal·mol–1) with a relatively weaker electrostatic destabilizing C-C interaction (: 50.0 to 54.2 kcal·mol−1). Additionally, the delocalization index (δ) predicts C-C bond orders like those indicated by the WBI values. Therefore, IQA supports the coordination of the peripheral carbons with the central carbon by significant covalent C-C interactions. How about the interaction between the metallic counterions and the central C? IQA reveals that there is a stabilizing interaction (bonding), primarily electrostatic, and the ranges from −36.3 (M = K) to −175.4 kcal·mol–1 (M = Be). Therefore, IQA supports the hexacoordination of C in all these structures, four C-phC (covalent) and two M-phC (ionic).

Table 2.
Energy components (in kcal·mol−1) of IQA for the M2C50/2+ (M = Li-K, Be-Ca, Al-In, and Zn) computed at the ωb97XD/Def2-TZVP level. , , and are interatomic IQA interaction energy and their coulombic and exchange-correlation energy components, respectively. is the total integration error in IQA energies, and the delocalization indices are represented by δ.
We have also analyzed the bonding with the AdNDP method (see Figure 1 and Figures S1–S3). It predicts that the covalent bonds are distributed on the C5 fragment, with four lone pairs (one on each peripheral C), six single C-C bonds, two linking the peripheral Cs in pairs, and four linking these with the central C. Finally, AdNDP also recovers a delocalized π-bond throughout the C5 fragment, confirming that these systems consist of the C52− dianion interacting with the metal counterions. AdNDP also retrieves the non-bonding electron pairs on the Al, Ga, In, and Zn counterions (Figures S1–S3).
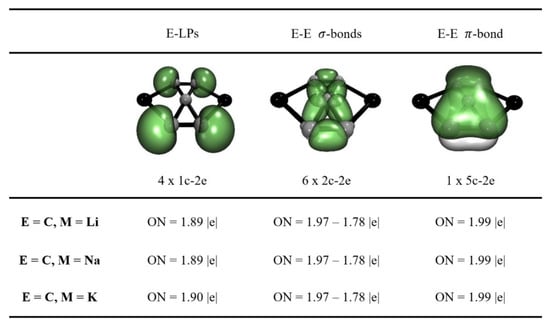
Figure 1.
Adaptive Natural Density Partitioning bonding pattern of the M2C5 (M=Li, Na, K) at the ωb97XD/Def2-TZVP level.
3.2. Are phC Systems Global Minima Structures?
To answer this question, we have explored the potential energy surface of the combinations of interest using the constraints specified in the computational details. The putative global minima and other relevant minima are shown in Figure 2. It should be noted that the lowest energy structure for neutral systems is in a singlet state, not for ionic systems where the D∞h triplet is more stable. However, the phC is only minimal in the singlet state. As can be seen, the phC structure does not correspond to the putative global minimum in any of the cases, being the closest isomer to the putative global minimum in the M2C5 combinations (M = Li-K; Al-In). The Li2C5 and Na2C5 phC structures have the closest energy to their corresponding putative global minimum, located above 9.0 and 11.4 kcal·mol–1, respectively. This agrees with previous claims that the D2h Li2C5 cluster would be the most viable for experimental identification [63].
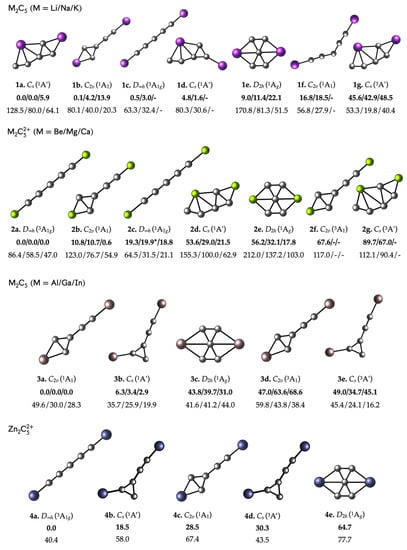
Figure 2.
Putative global minimum and low-lying isomers of M2C50/2+ (M = Li-K, Be-Ca, Al-In, and Zn) clusters with their point group symmetries. Relative energies, including zero-point energy (ZPE) corrections in kcal·mol−1 (in bold) and their lowest harmonic vibrational frequency in cm−1 (below) at ωb97XD/Def2-TZVP level, are also shown. Cartesian coordinates of phC structures are depicted in Table S1. * The 2c structure for M = Mg is slightly bent in the center; therefore, it has a C2v symmetry.
3.3. Exploring Strategies to Stabilize phC Systems
Using ligands to protect is a common technique to provide stability and viability to atomic clusters [19,64,65]. Thus, computational studies on clusters that include protection models have also been increasing, including some clusters with hypercoordinate atoms [66,67,68]. However, these studies do not analyze the relative stability of the different lower-energy isomers confined within these protective ligands. Here, we have evaluated how the relative stability of the sandwich complexes of the more stable isomers changes. We have employed as ligands the aromatic rings benzene (C6H6) and cyclopentadienyl anion (C5H5−). The former forms a sandwich with the neutral species, and the latter with the dicationic species, to have neutral complexes in all cases. The results are reported in Figures S4–S14. The use of ligands affects the relative energies; however, in no case is the phC structure preferred. The most striking case is the [(C5H5−)]2[Ca2C5]2+ system, where the complex containing the phC (Figure 3) is now within 8.0 kcal·mol–1 of the one that includes the putative global minimum. The barrier is reduced by half (relative to the isolated clusters, Figure 2) because of the C5H5− effect. This indicates that ligands should be explored in their protective role and in providing thermodynamic stability to the systems, as well.
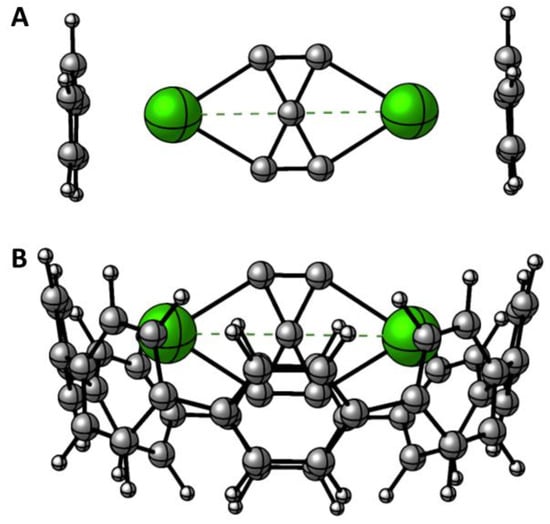
Figure 3.
Low-lying isomers of (A)[(C5H5−)]2[Ca2C5]2+ and (B) [8-CPP]2−[Ca2C5]2+.
Finally, we have studied the kinetic stability of the [(C5H5−)]2[Ca2C5]2+ complex (Figure 3A) to explore viable phC species, knowing that the isolated phC cluster is a high-energy isomer on the PES but the [(C5H5−)]2[Ca2C5]2+ is the closest energy isomer. Additionally, to provide more rigidity to the host ligand, we have placed the C5H5− rings inside a nanobelt (the 8-ring cycloparaphenylene, [8]CPP) to evaluate the dynamics of the [8-CPP]2−[Ca2C5]2+ complex (Figure 3B). Figure 4 shows results from ab initio BOMD simulations at 500 K for 20 ps. The structural fluctuations are plotted by the root mean square deviations curve (RMSD, in Å) versus simulation time. As Figure 4 shows, the RMSD has sharp changes, but the phC structure persists throughout the simulation. Additionally, two short movies extracted from the BOMD simulations are presented in the Supporting Information. Interestingly, structural fluctuations are approximately halved when using the [8-CPP]2− ligand (median RMSD ≈ 0.8 Å) relative to free C5H5− ligands (median RMSD ≈ 1.5 Å).
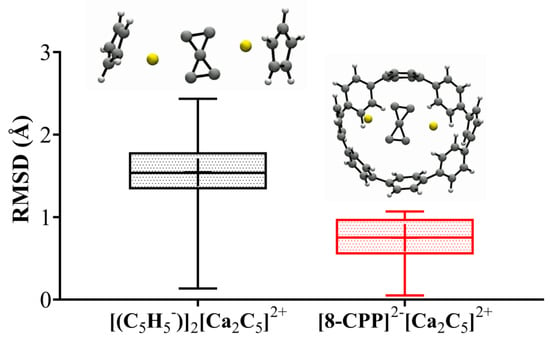
Figure 4.
Boxplot of RMSD fluctuation of ab initio BOMD simulations for [(C5H5−)]2[Ca2C5]2+ and [8-CPP]2−[Ca2C5]2+ systems.
4. Conclusions
It is shown that the D2h M2C50/2+ (M = Li-K, Be-Ca, Al-In, and Zn) clusters are planar hexacoordinate carbon species with four covalent and two electrostatic interactions. These assignments are supported by charges and chemical bonding analysis, where the interacting quantum atoms (IQA) method plays a fundamental role, identifying that central carbon sustains stabilizing interactions with the six surrounding atoms. However, our exploration of the potential energy surface reveals that these are not the global minimum structures. Nevertheless, the complexation of the Ca2C52+ system with two cyclopentadienyl anion ligands enhances the relative stability of the phC isomer. Moreover, when we harbor this structure within the cyclopentadienylene ([8]CPP) nano-ring, it provides protection and kinetic stability to the phC species. These results demonstrate that using suitable ligands is a promising strategy that deserves more systematic study in the search for new viable phC systems.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/atoms11030056/s1, Figures S1–S3: Adaptive Natural Density Partitioning bonding pattern of the M2C50/2+ (M = Be-Ca, Al-In, and Zn) at the ωb97XD/Def2-TZVP level, Figures S4–S9: Putative global minimum and low-lying isomers of (C6H6)2-M2C5 (M = Li-K and Al-In), Figures S10–S13: Putative global minimum and low-lying isomers of (C5H5−)2-M2C52+ (M = Be-Ca and Zn), Figure S14: Putative global minimum and low-lying isomers of [8-CPP]2−[Ca2C5]2+, Table S1: Cartesian coordinates of the M2C50/2+ (M = Li-K, Be-Ca, Al-In, and Zn) phC minima optimized structures at the ωb97XD/def2-TZVP level and Table S2: Cartesian coordinates of the [8-CPP]2−[Ca2C5]2+ optimized structures at the ωb97XD/def2-TZVP level. Video S1: Video-Ca-CPP[8]. Video S2: Video-Ca-Cp2
Author Contributions
Conceptualization, W.T., D.I. and O.Y.; methodology, D.I., O.Y., L.L.-P., J.S.-E. and A.V.-E.; software, D.I., O.Y., L.L.-P., J.S.-E. and A.V.-E.; validation, W.T., O.Y., D.I. and M.L.V.; formal analysis, W.T., O.Y. and D.I.; investigation, W.T., D.I. and O.Y.; resources, W.T. and M.L.V.; data curation, D.I., A.V.-E. and J.S.-E.; writing—original draft preparation, W.T., D.I. and O.Y.; writing—review and editing, all authors.; visualization, W.T., O.Y. and J.S.-E.; supervision, W.T. and M.L.V.; project administration, W.T.; funding acquisition, W.T. and M.L.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Agency for Research and Development (ANID) through FONDECYT projects 1211128 (W.T.) and 1221019 (A.V.-E.).
Data Availability Statement
The data presented in this study are available in the Supplementary Materials.
Acknowledgments
We thank the National Agency for Research and Development (ANID)/Scholarship Program/BECAS DOCTORADO NACIONAL/2019-21190427 (D.I.). National Agency for Research and Development (ANID)/Scholarship Program/BECAS DOCTORADO NACIONAL/2020-21201177 (L.L-P.). Scholarship Program/BECAS DOCTORADO UNAB (J.S.-E). Powered@NLHPC: This research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Monkhorst, H. Activation energy for interconversion of enantiomers containing an asymmetric carbon atom without breaking bonds. Chem. Commun. 1968, 18, 1111–1112. [Google Scholar] [CrossRef]
- Hoffmann, R.; Alder, R.W.; Wilcox, C.F. Planar Tetracoordinate Carbon. J. Am. Chem. Soc. 1970, 92, 4992–4993. [Google Scholar] [CrossRef]
- Siebert, W.; Gunale, A. Compounds containing a planar-tetracoordinate carbon atom as analogues of planar methane. Chem. Soc. Rev. 1999, 28, 367–371. [Google Scholar] [CrossRef]
- Keese, R. Carbon flatland: Planar tetracoordinate carbon and fenestranes. Chem. Rev. 2006, 106, 4787–4808. [Google Scholar] [CrossRef]
- Merino, G.; Méndez-Rojas, M.A.; Vela, A.; Heine, T. Recent advances in planar tetracoordinate carbon chemistry. J. Comput. Chem. 2007, 28, 362–372. [Google Scholar] [CrossRef]
- Yañez, O.; Vásquez-Espinal, A.; Pino-Rios, R.; Ferraro, F.; Pan, S.; Osorio, E.; Merino, G.; Tiznado, W. Exploiting electronic strategies to stabilize a planar tetracoordinate carbon in cyclic aromatic hydrocarbons. Chem. Commun. 2017, 53, 12112–12115. [Google Scholar] [CrossRef] [PubMed]
- Yañez, O.; Vásquez-Espinal, A.; Báez-Grez, R.; Rabanal-León, W.A.; Osorio, E.; Ruiz, L.; Tiznado, W. Carbon rings decorated with group 14 elements: New aromatic clusters containing planar tetracoordinate carbon. New J. Chem. 2019, 43, 6781–6785. [Google Scholar] [CrossRef]
- Erker, G. Planar-Tetracoordinate Carbon: Making Stable Anti-van’t Hoff/LeBel Compounds. Comments Inorg. Chem. 1992, 13, 111–131. [Google Scholar] [CrossRef]
- Rottger, D.; Erker, G. Compounds containing planar-tetracoordinate carbon. Angew. Chem. Int. Edit. 1997, 36, 813–827. [Google Scholar] [CrossRef]
- Zhang, X.-y.; Ding, Y.-h. Computational prediction of a global planar penta-coordinate carbon structure CAl4Ga+. Comput. Theor. Chem. 2014, 1048, 18–24. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.F.; Wang, L.S.; Geske, G.D.; Boldyrev, A.I. Pentaatomic tetracoordinate planar carbon, [CAl4]2−: A new structural unit and its salt complexes. Angew. Chem. 2000, 112, 3776–3778. [Google Scholar] [CrossRef]
- Wang, Z.-X.; Schleyer, P.v.R. Construction principles of “hyparenes”: Families of molecules with planar pentacoordinate carbons. Science 2001, 292, 2465–2469. [Google Scholar] [CrossRef]
- Wang, Y.; Li, F.; Li, Y.; Chen, Z. Semi-metallic Be5C2 monolayer global minimum with quasi-planar pentacoordinate carbons and negative Poisson’s ratio. Nat. Commun. 2016, 7, 11488. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Cabellos, J.L.; Orozco-Ic, M.; Chattaraj, P.K.; Zhao, L.; Merino, G. Planar pentacoordinate carbon in CGa 5+ derivatives. Phys. Chem. Chem. Phys. 2018, 20, 12350–12355. [Google Scholar] [CrossRef]
- Pei, Y.; An, W.; Ito, K.; Schleyer, P.V.R.; Zeng, X.C. Planar pentacoordinate carbon in CAl5+: A global minimum. J. Am. Chem. Soc. 2008, 130, 10394–10400. [Google Scholar] [CrossRef]
- Vassilev-Galindo, V.; Pan, S.; Donald, K.J.; Merino, G. Planar pentacoordinate carbons. Nat. Rev. Chem. 2018, 2, 0114. [Google Scholar] [CrossRef]
- Grande-Aztatzi, R.; Cabellos, J.L.; Islas, R.; Infante, I.; Mercero, J.M.; Restrepo, A.; Merino, G. Planar pentacoordinate carbons in CBe54− derivatives. Phys. Chem. Chem. Phys. 2015, 17, 4620–4624. [Google Scholar] [CrossRef]
- Zhao, X.-F.; Bian, J.-H.; Huang, F.; Yuan, C.; Wang, Q.; Liu, P.; Li, D.; Wang, X.; Wu, Y.-B. Stabilization of beryllium-containing planar pentacoordinate carbon species through attaching hydrogen atoms. RSC Adv. 2018, 8, 36521–36526. [Google Scholar] [CrossRef]
- Cui, Z.-h.; Vassilev-Galindo, V.; Cabellos, J.L.; Osorio, E.; Orozco, M.; Pan, S.; Ding, Y.-h.; Merino, G. Planar pentacoordinate carbon atoms embedded in a metallocene framework. Chem. Commun. 2017, 53, 138–141. [Google Scholar] [CrossRef] [PubMed]
- Yañez, O.; Báez-Grez, R.; Garza, J.; Pan, S.; Barroso, J.; Vásquez-Espinal, A.; Merino, G.; Tiznado, W. Embedding a Planar Hypercoordinate Carbon Atom into a [4n+ 2] π-System. ChemPhysChem 2020, 21, 145–148. [Google Scholar] [CrossRef]
- Leyva-Parra, L.; Diego, L.; Inostroza, D.; Yañez, O.; Pumachagua-Huertas, R.; Barroso, J.; Vásquez-Espinal, A.; Merino, G.; Tiznado, W. Planar Hypercoordinate Carbons in Alkali Metal Decorated CE32− and CE22− Dianions. Chem.—Eur. J. 2021, 27, 16701–16706. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.-B.; Duan, Y.; Lu, G.; Lu, H.-G.; Yang, P.; von Rague Schleyer, P.; Merino, G.; Islas, R.; Wang, Z.-X. D3h CN3Be3+ and CO 3 Li 3+: Viable planar hexacoordinate carbon prototypes. Phys. Chem. Chem. Phys. 2012, 14, 14760–14763. [Google Scholar] [CrossRef] [PubMed]
- Exner, K.; Schleyer, P.v.R. Planar hexacoordinate carbon: A viable possibility. Science 2000, 290, 1937–1940. [Google Scholar] [CrossRef]
- Leyva-Parra, L.; Diego, L.; Yañez, O.; Inostroza, D.; Barroso, J.; Vásquez-Espinal, A.; Merino, G.; Tiznado, W. Planar hexacoordinate carbons: Half covalent, half ionic. Angew. Chem. Int. Edit. 2021, 60, 8700–8704. [Google Scholar] [CrossRef]
- Li, Y.; Liao, Y.; Chen, Z. Be2C monolayer with quasi-planar hexacoordinate carbons: A global minimum structure. Angew. Chem. Int. Edit. 2014, 53, 7248–7252. [Google Scholar] [CrossRef]
- Merino, G.; Méndez-Rojas, M.A.; Beltrán, H.I.; Corminboeuf, C.; Heine, T.; Vela, A. Theoretical Analysis of the Smallest Carbon Cluster Containing a Planar Tetracoordinate Carbon. J. Am. Chem. Soc. 2004, 126, 16160–16169. [Google Scholar] [CrossRef]
- Pancharatna, P.D.; Méndez-Rojas, M.A.; Merino, G.; Vela, A.; Hoffmann, R. Planar Tetracoordinate Carbon in Extended Systems. J. Am. Chem. Soc. 2004, 126, 15309–15315. [Google Scholar] [CrossRef]
- Yanez, O.; Báez-Grez, R.; Inostroza, D.; Rabanal-León, W.A.; Pino-Rios, R.; Garza, J.; Tiznado, W. AUTOMATON: A program that combines a probabilistic cellular automata and a genetic algorithm for global minimum search of clusters and molecules. J. Chem. Theory Comput. 2018, 15, 1463–1475. [Google Scholar] [CrossRef] [PubMed]
- Yañez, O.; Inostroza, D.; Usuga-Acevedo, B.; Vásquez-Espinal, A.; Pino-Rios, R.; Tabilo-Sepulveda, M.; Garza, J.; Barroso, J.; Merino, G.; Tiznado, W. Evaluation of restricted probabilistic cellular automata on the exploration of the potential energy surface of Be6B11−. Theor. Chem. Acc. 2020, 139, 41. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Fuentealba, P.; Von Szentpaly, L.; Preuss, H.; Stoll, H. Pseudopotential calculations for alkaline-earth atoms. J. Phys. B At. Mol. 1985, 18, 1287. [Google Scholar] [CrossRef]
- Fuentealba, P.; Preuss, H.; Stoll, H.; Von Szentpály, L. A proper account of core-polarization with pseudopotentials: Single valence-electron alkali compounds. Chem. Phys. Lett. 1982, 89, 418–422. [Google Scholar] [CrossRef]
- Bergner, A.; Dolg, M.; Küchle, W.; Stoll, H.; Preuß, H. Ab initio energy-adjusted pseudopotentials for elements of groups 13–17. Mol. Phys. 1993, 80, 1431–1441. [Google Scholar] [CrossRef]
- Küchle, W.; Dolg, M.; Stoll, H.; Preuss, H. Energy-adjusted pseudopotentials for the actinides. Parameter sets and test calculations for thorium and thorium monoxide. J. Chem. Phys. 1994, 100, 7535–7542. [Google Scholar] [CrossRef]
- Küchle, W.; Dolg, M.; Stoll, H.; Preuss, H. Ab initio pseudopotentials for Hg through Rn: I. Parameter sets and atomic calculations. Mol. Phys. 1991, 74, 1245–1263. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Millam, J.M.; Bakken, V.r.; Chen, W.; Hase, W.L.; Schlegel, H.B. Ab initio classical trajectories on the Born–Oppenheimer surface: Hessian-based integrators using fifth-order polynomial and rational function fits. J. Chem. Phys. 1999, 111, 3800–3805. [Google Scholar] [CrossRef]
- Wiberg, K.B. Application of the pople-santry-segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane. Tetrahedron 1968, 24, 1083–1096. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural population analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
- Zubarev, D.Y.; Boldyrev, A.I. Developing paradigms of chemical bonding: Adaptive natural density partitioning. Phys. Chem. Chem. Phys. 2008, 10, 5207–5217. [Google Scholar] [CrossRef]
- Zubarev, D.Y.; Boldyrev, A.I. Revealing intuitively assessable chemical bonding patterns in organic aromatic molecules via adaptive natural density partitioning. J. Org. Chem. 2008, 73, 9251–9258. [Google Scholar] [CrossRef]
- Glendening, E.; Badenhoop, J.; Reed, A.; Carpenter, J.; Bohmann, J.; Morales, C.; Landis, C.; Weinhold, F. Natural Bond Orbital Analysis Program: NBO 6.0; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, USA, 2013. [Google Scholar]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Legault, C.Y. CYLview20; Université de Sherbrooke: Sherbrooke, QC, Canada, 2020. [Google Scholar]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Pyykkö, P. Additive covalent radii for single-, double-, and triple-bonded molecules and tetrahedrally bonded crystals: A summary. J. Phys. Chem. A 2015, 119, 2326–2337. [Google Scholar] [CrossRef]
- Alvarez, S. A cartography of the van der Waals territories. Dalton Trans. 2013, 42, 8617–8636. [Google Scholar] [CrossRef]
- Pendás, A.M.; Blanco, M.; Francisco, E. Two-electron integrations in the quantum theory of atoms in molecules. J. Chem. Phys. 2004, 120, 4581–4592. [Google Scholar] [CrossRef]
- Blanco, M.; Martín Pendás, A.; Francisco, E. Interacting quantum atoms: A correlated energy decomposition scheme based on the quantum theory of atoms in molecules. J. Chem. Theory Comput. 2005, 1, 1096–1109. [Google Scholar] [CrossRef]
- Pendás, A.M.; Blanco, M.A.; Francisco, E. Chemical fragments in real space: Definitions, properties, and energetic decompositions. J. Comput. Chem. 2007, 28, 161–184. [Google Scholar] [CrossRef]
- Pendás, A.M.; Francisco, E.; Blanco, M. Two-electron integrations in the Quantum Theory of Atoms in Molecules with correlated wave functions. J. Comput. Chem. 2005, 26, 344–351. [Google Scholar] [CrossRef]
- Foroutan-Nejad, C. The Na⋅⋅⋅ B Bond in NaBH3−: A Different Type of Bond. Angew. Chem. Int. Edit. 2020, 59, 20900–20903. [Google Scholar] [CrossRef]
- Liu, G.; Fedik, N.; Martinez-Martinez, C.; Ciborowski, S.M.; Zhang, X.; Boldyrev, A.I.; Bowen, K.H. Realization of Lewis Basic Sodium Anion in the NaBH3− Cluster. Angew. Chem. Int. Edit. 2019, 58, 13789–13793. [Google Scholar] [CrossRef]
- Liu, G.; Fedik, N.; Martinez-Martinez, C.; Ciborowski, S.M.; Zhang, X.; Boldyrev, A.I.; Bowen, K.H. Reply to the Comment on “Realization of Lewis Basic Sodium Anion in the NaBH3− Cluster”. Angew. Chem. Int. Edit. 2020, 59, 8760–8764. [Google Scholar] [CrossRef]
- Pan, S.; Frenking, G. Comment on “Realization of Lewis Basic Sodium Anion in the NaBH3− Cluster”. Amgew. Chem. 2020, 132, 8836–8839. [Google Scholar]
- Pino-Rios, R.; Inostroza, D.; Tiznado, W. Neither too Classic nor too Exotic: One-Electron Na⋅ B Bond in NaBH3− Cluster. Amgew. Chem. 2021, 133, 12857–12863. [Google Scholar] [CrossRef]
- Pino-Rios, R.; Inostroza, D.; Tiznado, W. Neither too Classic nor too Exotic: One-Electron Na⋅B Bond in NaBH3− Cluster. Angew. Chem. Int. Edit. 2021, 60, 12747–12753. [Google Scholar] [CrossRef]
- Radenković, S.; Shaik, S.S.; Braïda, B. Na⋅⋅⋅ B Bond in NaBH3−: Solving the Conundrum. Amgew. Chem. 2021, 133, 12833–12836. [Google Scholar]
- Sowlati-Hashjin, S.; Šadek, V.; Sadjadi, S.; Karttunen, M.; Martín-Pendás, A.; Foroutan-Nejad, C. Collective interactions among organometallics are exotic bonds hidden on lab shelves. Nat. Commun. 2022, 13, 2069. [Google Scholar] [CrossRef]
- Wang, M.-h.; Orozco-Ic, M.; Leyva-Parra, L.; Tiznado, W.; Barroso, J.; Ding, Y.-h.; Cui, Z.-h.; Merino, G. Planar Tetracoordinate Carbons in Allene-Type Structures. J. Phys. Chem. A 2021, 125, 3009–3014. [Google Scholar] [CrossRef]
- Vela, A.; Méndez-Rojas, M.A.; Merino, G. Theoretical design of electronically stabilized molecules containing planar tetracoordinate carbons. In Theoretical and Computational Chemistry; Elsevier: Amsterdam, The Netherlands, 2007; Volume 19, pp. 251–267. [Google Scholar]
- Zhang, M.-M.; Dong, X.-Y.; Wang, Y.-J.; Zang, S.-Q.; Mak, T.C. Recent progress in functional atom-precise coinage metal clusters protected by alkynyl ligands. Coord. Chem. Rev. 2022, 453, 214315. [Google Scholar] [CrossRef]
- Walter, M.; Akola, J.; Lopez-Acevedo, O.; Jadzinsky, P.D.; Calero, G.; Ackerson, C.J.; Whetten, R.L.; Grönbeck, H.; Häkkinen, H. A unified view of ligand-protected gold clusters as superatom complexes. Proc. Natl. Acad. Sci. USA 2008, 105, 9157–9162. [Google Scholar]
- Orellana, W.; Pino-Rios, R.; Yañez, O.; Vásquez-Espinal, A.; Peccati, F.; Contreras-García, J.; Cardenas, C.; Tiznado, W. Cluster Assembled Silicon-Lithium Nanostructures: A Nanowire Confined Inside a Carbon Nanotube. Front. Chem. 2021, 9, 884. [Google Scholar] [CrossRef]
- Chen, C.; Wang, M.-h.; Feng, L.-Y.; Zhao, L.-Q.; Guo, J.-C.; Zhai, H.-J.; Cui, Z.-h.; Pan, S.; Merino, G. Bare and ligand protected planar hexacoordinate silicon in SiSb 3 M 3+(M= Ca, Sr, Ba) clusters. Chem. Sci. 2022, 13, 8045–8051. [Google Scholar] [CrossRef]
- Inostroza, D.; Leyva-Parra, L.; Vásquez-Espinal, A.; Contreras-García, J.; Cui, Z.-H.; Pan, S.; Thimmakondu, V.S.; Tiznado, W. E 6 C 15 (E= Si–Pb): Polycyclic aromatic compounds with three planar tetracoordinate carbons. Chem. Commun. 2022, 58, 13075–13078. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).