Variational Approaches to Two-Dimensionally Symmetry-Broken Dipolar Bose–Einstein Condensates
Abstract
:1. Introduction
2. Theoretical Model
3. Variational Ansatz
3.1. Small-Amplitude Expansion
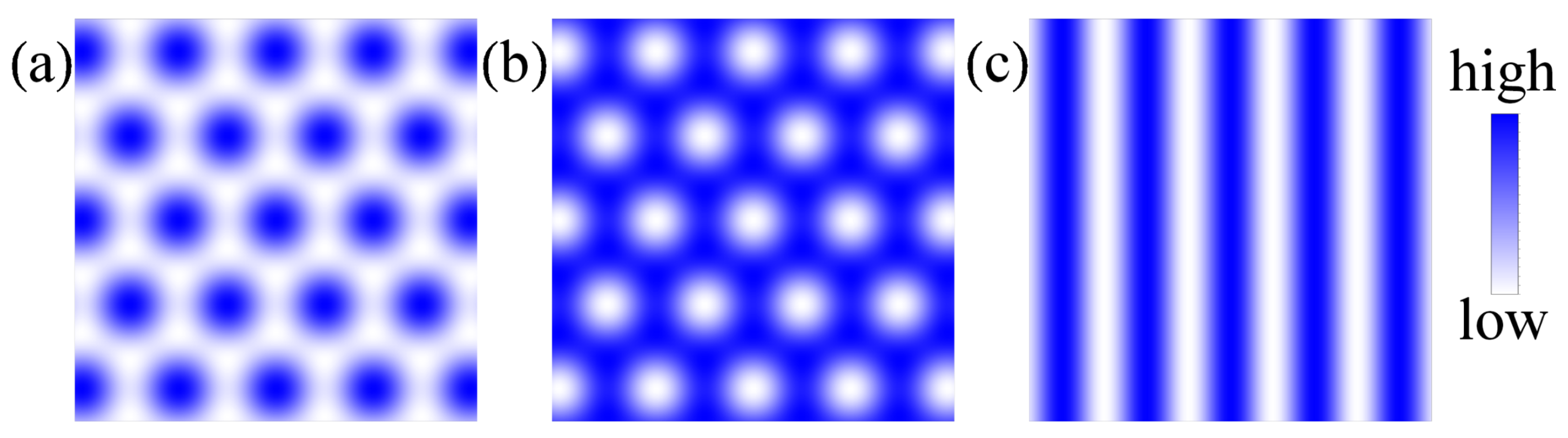
3.2. Hexagonal and Honeycomb Lattices
3.3. Square and Stripe Lattices
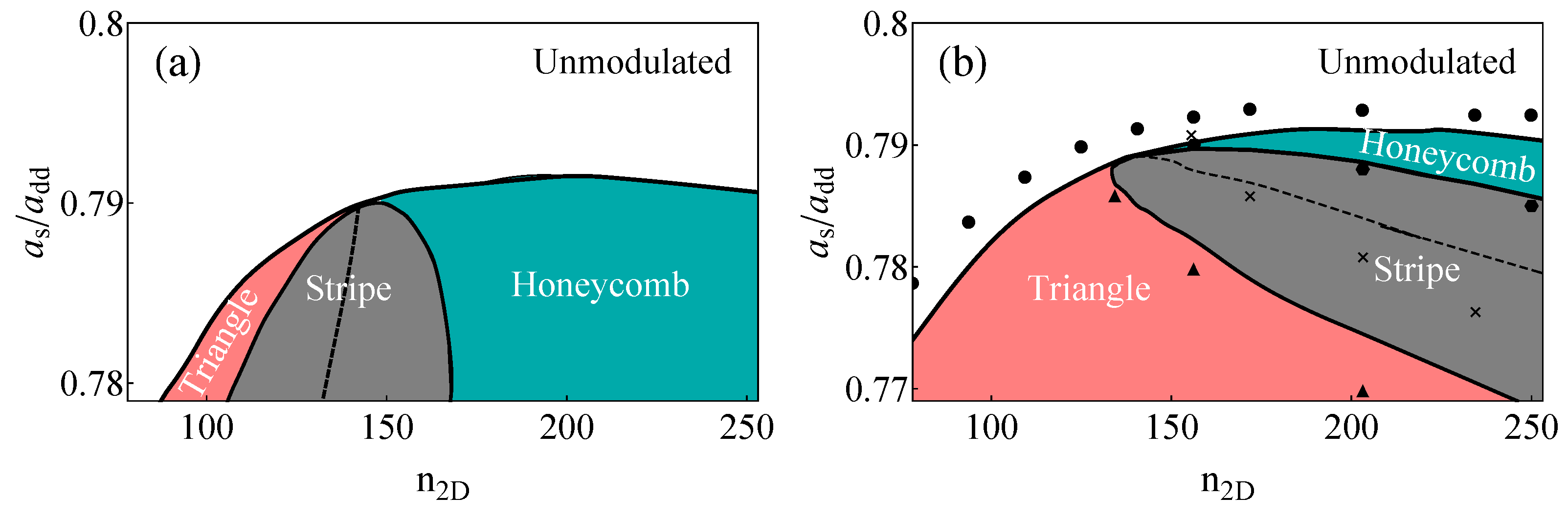
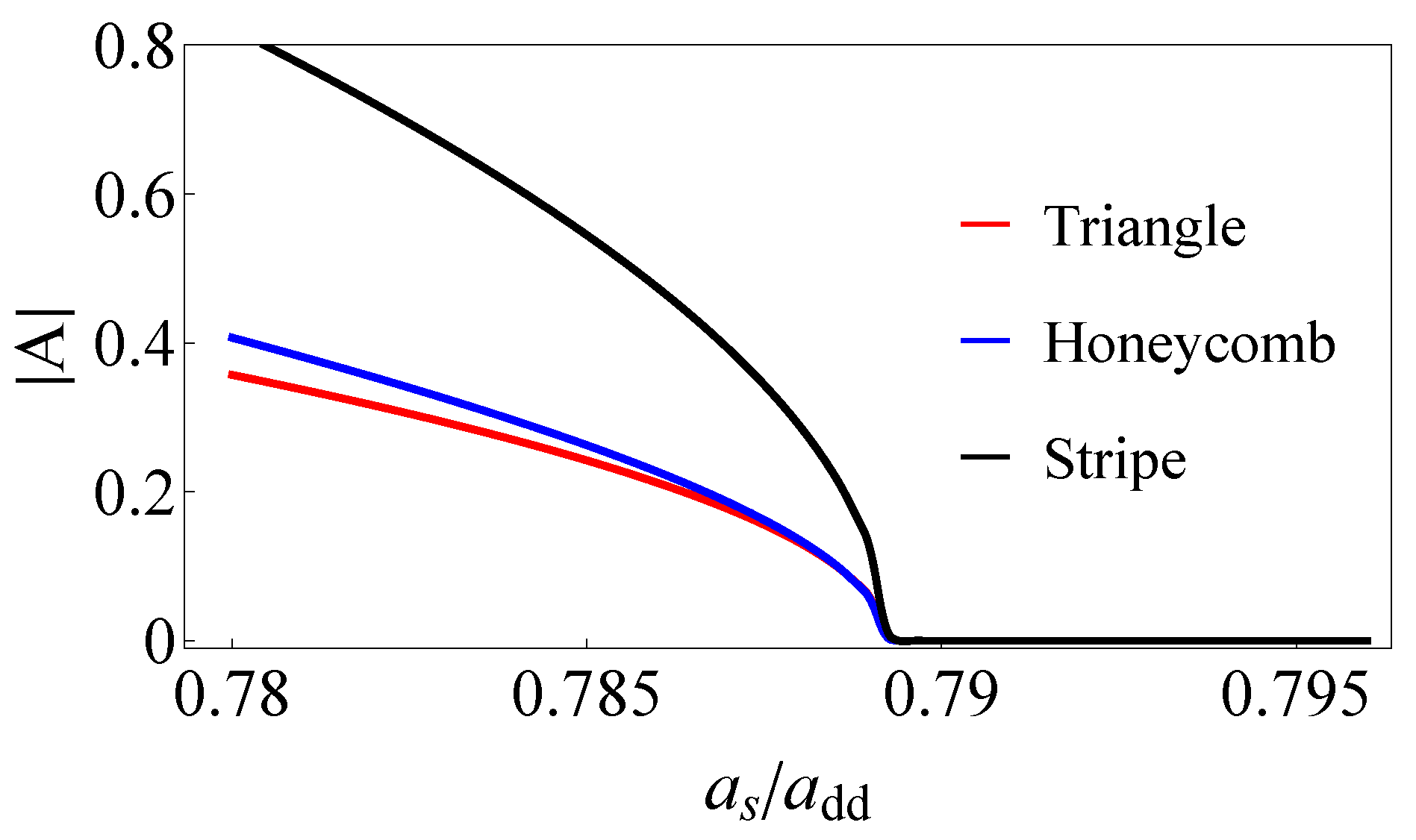
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Turing, A.M. The Chemical Basis of Morphogenesis. Philos. Trans. R. Soc. Lond. Ser. B-Biol. Sci. 1952, 23, 237. [Google Scholar] [CrossRef]
- Pismen, L.M. Patterns and Interfaces in Dissipative Dynamics, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef] [Green Version]
- Cross, M.C.; Hohenberg, P.C. Pattern formation outside of equilibrium. Rev. Mod. Phys. 1993, 65, 851–1112. [Google Scholar] [CrossRef] [Green Version]
- Andreev, A.F.; Lifshitz, I.M. Quantum theory of defects in crystals. Sov. Phys. JETP 1969, 29, 1107–1113. [Google Scholar] [CrossRef]
- Leggett, A.J. Can a solid be “superfluid”? Phys. Rev. Lett. 1970, 25, 1543–1546. [Google Scholar] [CrossRef] [Green Version]
- Chester, G.V. Speculations on Bose-Einstein condensation and quantum crystals. Phys. Rev. A 1970, 2, 256–258. [Google Scholar] [CrossRef]
- O’Dell, D.; Giovanazzi, S.; Kurizki, G.; Akulin, V.M. Bose-Einstein Condensates with 1/r Interatomic Attraction: Electromagnetically Induced “Gravity”. Phys. Rev. Lett. 2000, 84, 5687–5690. [Google Scholar] [CrossRef] [Green Version]
- Maucher, F.; Henkel, N.; Saffman, M.; Królikowski, W.; Skupin, S.; Pohl, T. Rydberg-Induced Solitons: Three-Dimensional Self-Trapping of Matter Waves. Phys. Rev. Lett. 2011, 106, 170401. [Google Scholar] [CrossRef]
- Petrov, D.S. Quantum Mechanical Stabilization of a Collapsing Bose-Bose Mixture. Phys. Rev. Lett. 2015, 115, 155302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Macia, A.; Sánchez-Baena, J.; Boronat, J.; Mazzanti, F. Droplets of Trapped Quantum Dipolar Bosons. Phys. Rev. Lett. 2016, 117, 205301. [Google Scholar] [CrossRef] [Green Version]
- Cabrera, C.R.; Tanzi, L.; Sanz, J.; Naylor, B.; Thomas, P.; Cheiney, P.; Tarruell, L. Quantum liquid droplets in a mixture of Bose-Einstein condensates. Science 2018, 359, 301–304. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ferioli, G.; Semeghini, G.; Masi, L.; Giusti, G.; Modugno, G.; Inguscio, M.; Gallemí, A.; Recati, A.; Fattori, M. Collisions of Self-Bound Quantum Droplets. Phys. Rev. Lett. 2019, 122, 090401. [Google Scholar] [CrossRef] [Green Version]
- Santos, L.; Shlyapnikov, G.V.; Lewenstein, M. Roton-Maxon Spectrum and Stability of Trapped Dipolar Bose-Einstein Condensates. Phys. Rev. Lett. 2003, 90, 250403. [Google Scholar] [CrossRef] [Green Version]
- Henkel, N.; Nath, R.; Pohl, T. Three-Dimensional Roton Excitations and Supersolid Formation in Rydberg-Excited Bose-Einstein Condensates. Phys. Rev. Lett. 2010, 104, 195302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Macrì, T.; Maucher, F.; Cinti, F.; Pohl, T. Elementary excitations of ultracold soft-core Bosons across the superfluid-supersolid phase transition. Phys. Rev. A 2013, 87, 061602. [Google Scholar] [CrossRef] [Green Version]
- Cinti, F.; Macrì, T.; Lechner, W.; Pupillo, G.; Pohl, T. Defect-induced supersolidity with soft-core Bosons. Nat. Commun. 2014, 5, 3235. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mottl, R.; Brennecke, F.; Baumann, K.; Landig, R.; Donner, T.; Esslinger, T. Roton-Type Mode Softening in a Quantum Gas with Cavity-Mediated Long-Range Interactions. Science 2012, 336, 1570–1573. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Landau, L. On the Theory of Superfluidity. Phys. Rev. 1949, 75, 884–885. [Google Scholar] [CrossRef]
- Kadau, H.; Schmitt, M.; Wenzel, M.; Wink, C.; Maier, T.; Ferrier-Barbut, I.; Pfau, T. Observing the Rosenzweig instability of a quantum ferrofluid. Nature 2016, 530, 194–197. [Google Scholar] [CrossRef] [Green Version]
- Schmitt, M.; Wenzel, M.; Böttcher, F.; Ferrier-Barbut, I.; Pfau, T. Self-bound droplets of a dilute magnetic quantum liquid. Nature 2016, 539, 259–262. [Google Scholar] [CrossRef] [Green Version]
- Ferrier-Barbut, I.; Kadau, H.; Schmitt, M.; Wenzel, M.; Pfau, T. Observation of Quantum Droplets in a Strongly Dipolar Bose Gas. Phys. Rev. Lett. 2016, 116, 215301. [Google Scholar] [CrossRef] [Green Version]
- Chomaz, L.; Baier, S.; Petter, D.; Mark, M.J.; Wächtler, F.; Santos, L.; Ferlaino, F. Quantum-Fluctuation-Driven Crossover from a Dilute Bose-Einstein Condensate to a Macrodroplet in a Dipolar Quantum Fluid. Phys. Rev. X 2016, 6, 041039. [Google Scholar] [CrossRef] [Green Version]
- Tanzi, L.; Lucioni, E.; Famà, F.; Catani, J.; Fioretti, A.; Gabbanini, C.; Bisset, R.N.; Santos, L.; Modugno, G. Observation of a Dipolar Quantum Gas with Metastable Supersolid Properties. Phys. Rev. Lett. 2019, 122, 130405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Böttcher, F.; Schmidt, J.N.; Wenzel, M.; Hertkorn, J.; Guo, M.; Langen, T.; Pfau, T. Transient Supersolid Properties in an Array of Dipolar Quantum Droplets. Phys. Rev. X 2019, 9, 011051. [Google Scholar] [CrossRef] [Green Version]
- Chomaz, L.; Petter, D.; Ilzhöfer, P.; Natale, G.; Trautmann, A.; Politi, C.; Durastante, G.; van Bijnen, R.M.W.; Patscheider, A.; Sohmen, M.; et al. Long-Lived and Transient Supersolid Behaviors in Dipolar Quantum Gases. Phys. Rev. X 2019, 9, 021012. [Google Scholar] [CrossRef] [Green Version]
- Tanzi, L.; Roccuzzo, S.M.; Lucioni, E.; Famà, F.; Fioretti, A.; Gabbanini, C.; Modugno, G.; Recati, A.; Stringari, S. Supersolid symmetry breaking from compressional oscillations in a dipolar quantum gas. Nature 2019, 574, 382–385. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hertkorn, J.; Schmidt, J.N.; Böttcher, F.; Guo, M.; Schmidt, M.; Ng, K.S.H.; Graham, S.D.; Büchler, H.P.; Langen, T.; Zwierlein, M.; et al. Density Fluctuations across the Superfluid-Supersolid Phase Transition in a Dipolar Quantum Gas. Phys. Rev. X 2021, 11, 011037. [Google Scholar] [CrossRef]
- Ilzhöfer, P.; Sohmen, M.; Durastante, G.; Politi, C.; Trautmann, A.; Natale, G.; Morpurgo, G.; Giamarchi, T.; Chomaz, L.; Mark, M.J.; et al. Phase coherence in out-of-equilibrium supersolid states of ultracold dipolar atoms. Nat. Phys. 2021. [Google Scholar] [CrossRef]
- Guo, M.; Böttcher, F.; Hertkorn, J.; Schmidt, J.N.; Wenzel, M.; Büchler, H.P.; Langen, T.; Pfau, T. The low-energy Goldstone mode in a trapped dipolar supersolid. Nature 2019, 574, 386–389. [Google Scholar] [CrossRef] [Green Version]
- Natale, G.; van Bijnen, R.M.W.; Patscheider, A.; Petter, D.; Mark, M.J.; Chomaz, L.; Ferlaino, F. Excitation Spectrum of a Trapped Dipolar Supersolid and Its Experimental Evidence. Phys. Rev. Lett. 2019, 123, 050402. [Google Scholar] [CrossRef] [Green Version]
- Tanzi, L.; Maloberti, J.G.; Biagioni, G.; Fioretti, A.; Gabbanini, C.; Modugno, G. Evidence of superfluidity in a dipolar supersolid from nonclassical rotational inertia. Science 2021, 371, 1162–1165. [Google Scholar] [CrossRef]
- Sohmen, M.; Politi, C.; Klaus, L.; Chomaz, L.; Mark, M.J.; Norcia, M.A.; Ferlaino, F. Birth, Life, and Death of a Dipolar Supersolid. Phys. Rev. Lett. 2021, 126, 233401. [Google Scholar] [CrossRef]
- Bortolotti, D.C.E.; Ronen, S.; Bohn, J.L.; Blume, D. Scattering Length Instability in Dipolar Bose-Einstein Condensates. Phys. Rev. Lett. 2006, 97, 160402. [Google Scholar] [CrossRef] [Green Version]
- Lahaye, T.; Metz, J.; Fröhlich, B.; Koch, T.; Meister, M.; Griesmaier, A.; Pfau, T.; Saito, H.; Kawaguchi, Y.; Ueda, M. d-Wave Collapse and Explosion of a Dipolar Bose-Einstein Condensate. Phys. Rev. Lett. 2008, 101, 080401. [Google Scholar] [CrossRef] [Green Version]
- Wächtler, F.; Santos, L. Quantum filaments in dipolar Bose-Einstein condensates. Phys. Rev. A 2016, 93, 061603. [Google Scholar] [CrossRef] [Green Version]
- Bisset, R.N.; Wilson, R.M.; Baillie, D.; Blakie, P.B. Ground-state phase diagram of a dipolar condensate with quantum fluctuations. Phys. Rev. A 2016, 94, 033619. [Google Scholar] [CrossRef] [Green Version]
- Baillie, D.; Wilson, R.M.; Bisset, R.N.; Blakie, P.B. Self-bound dipolar droplet: A localized matter wave in free space. Phys. Rev. A 2016, 94, 021602. [Google Scholar] [CrossRef] [Green Version]
- Saito, H. Path-Integral Monte Carlo Study on a Droplet of a Dipolar Bose–Einstein Condensate Stabilized by Quantum Fluctuation. J. Phys. Soc. Jpn. 2016, 85, 053001. [Google Scholar] [CrossRef]
- Wächtler, F.; Santos, L. Ground-state properties and elementary excitations of quantum droplets in dipolar Bose-Einstein condensates. Phys. Rev. A 2016, 94, 043618. [Google Scholar] [CrossRef] [Green Version]
- Baillie, D.; Blakie, P.B. Droplet Crystal Ground States of a Dipolar Bose Gas. Phys. Rev. Lett. 2018, 121, 195301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lima, A.R.P.; Pelster, A. Quantum fluctuations in dipolar Bose gases. Phys. Rev. A 2011, 84, 041604(R). [Google Scholar] [CrossRef] [Green Version]
- Lima, A.R.P.; Pelster, A. Beyond mean-field low-lying excitations of dipolar Bose gases. Phys. Rev. A 2012, 86, 063609. [Google Scholar] [CrossRef] [Green Version]
- Sánchez-Baena, J.; Politi, C.; Maucher, F.; Ferlaino, F.; Pohl, T. Heating a dipolar quantum fluid into a solid. Nat. Commun. 2023, 14, 1868. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Maucher, F.; Pohl, T. Supersolidity around a Critical Point in Dipolar Bose-Einstein Condensates. Phys. Rev. Lett. 2019, 123, 015301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.C.; Pohl, T.; Maucher, F. Phases of supersolids in confined dipolar Bose-Einstein condensates. Phys. Rev. A 2021, 104, 013310. [Google Scholar] [CrossRef]
- Hertkorn, J.; Schmidt, J.N.; Guo, M.; Böttcher, F.; Ng, K.S.H.; Graham, S.D.; Uerlings, P.; Langen, T.; Zwierlein, M.; Pfau, T. Pattern formation in quantum ferrofluids: From supersolids to superglasses. Phys. Rev. Res. 2021, 3, 033125. [Google Scholar] [CrossRef]
- Young-S., L.E.; Adhikari, S.K. Supersolid-like square- and honeycomb-lattice crystallization of droplets in a dipolar condensate. Phys. Rev. A 2022, 105, 033311. [Google Scholar] [CrossRef]
- Gallemí, A.; Santos, L. Superfluid properties of a honeycomb dipolar supersolid. Phys. Rev. A 2022, 106, 063301. [Google Scholar] [CrossRef]
- Norcia, M.A.; Politi, C.; Klaus, L.; Poli, E.; Sohmen, M.; Mark, M.J.; Bisset, R.N.; Santos, L.; Ferlaino, F. Two-dimensional supersolidity in a dipolar quantum gas. Nature 2021, 596, 357–361. [Google Scholar] [CrossRef]
- Schmidt, J.N.; Hertkorn, J.; Guo, M.; Böttcher, F.; Schmidt, M.; Ng, K.S.H.; Graham, S.D.; Langen, T.; Zwierlein, M.; Pfau, T. Roton Excitations in an Oblate Dipolar Quantum Gas. Phys. Rev. Lett. 2021, 126, 193002. [Google Scholar] [CrossRef]
- Biagioni, G.; Antolini, N.; Alaña, A.; Modugno, M.; Fioretti, A.; Gabbanini, C.; Tanzi, L.; Modugno, G. Dimensional Crossover in the Superfluid-Supersolid Quantum Phase Transition. Phys. Rev. X 2022, 12, 021019. [Google Scholar] [CrossRef]
- Klaus, L.; Bland, T.; Poli, E.; Politi, C.; Lamporesi, G.; Casotti, E.; Bisset, R.N.; Mark, M.J.; Ferlaino, F. Observation of vortices and vortex stripes in a dipolar condensate. Nat. Phys. 2022, 18, 1453–1458. [Google Scholar] [CrossRef] [PubMed]
- Lahaye, T.; Menotti, C.; Santos, L.; Lewenstein, M.; Pfau, T. The physics of dipolar Bosonic quantum gases. Rep. Prog. Phys. 2009, 72, 126401. [Google Scholar] [CrossRef]
- Lee, T.D.; Yang, C.N. Many-Body Problem in Quantum Mechanics and Quantum Statistical Mechanics. Phys. Rev. 1957, 105, 1119–1120. [Google Scholar] [CrossRef]
- Lee, T.D.; Huang, K.; Yang, C.N. Eigenvalues and Eigenfunctions of a Bose System of Hard Spheres and Its Low-Temperature Properties. Phys. Rev. 1957, 106, 1135–1145. [Google Scholar] [CrossRef]
- Sachdev, S. Quantum Phase Transitions, 2nd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef] [Green Version]
- Bisset, R.N.; Ardila, L.A.P.; Santos, L. Quantum Droplets of Dipolar Mixtures. Phys. Rev. Lett. 2021, 126, 025301. [Google Scholar] [CrossRef]
- Smith, J.C.; Baillie, D.; Blakie, P.B. Quantum Droplet States of a Binary Magnetic Gas. Phys. Rev. Lett. 2021, 126, 025302. [Google Scholar] [CrossRef]
- Han, W.; Zhang, X.F.; Wang, D.S.; Jiang, H.F.; Zhang, W.; Zhang, S.G. Chiral Supersolid in Spin-Orbit-Coupled Bose Gases with Soft-Core Long-Range Interactions. Phys. Rev. Lett. 2018, 121, 030404. [Google Scholar] [CrossRef] [Green Version]
- Mivehvar, F.; Piazza, F.; Donner, T.; Ritsch, H. Cavity QED with quantum gases: New paradigms in many-body physics. Adv. Phys. 2021, 70, 1–153. [Google Scholar] [CrossRef]
- Steinberg, A.B.; Maucher, F.; Gurevich, S.V.; Thiele, U. Exploring bifurcations in Bose–Einstein condensates via phase field crystal models. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 113112. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.-C.; Maucher, F. Variational Approaches to Two-Dimensionally Symmetry-Broken Dipolar Bose–Einstein Condensates. Atoms 2023, 11, 102. https://doi.org/10.3390/atoms11070102
Zhang Y-C, Maucher F. Variational Approaches to Two-Dimensionally Symmetry-Broken Dipolar Bose–Einstein Condensates. Atoms. 2023; 11(7):102. https://doi.org/10.3390/atoms11070102
Chicago/Turabian StyleZhang, Yong-Chang, and Fabian Maucher. 2023. "Variational Approaches to Two-Dimensionally Symmetry-Broken Dipolar Bose–Einstein Condensates" Atoms 11, no. 7: 102. https://doi.org/10.3390/atoms11070102
APA StyleZhang, Y.-C., & Maucher, F. (2023). Variational Approaches to Two-Dimensionally Symmetry-Broken Dipolar Bose–Einstein Condensates. Atoms, 11(7), 102. https://doi.org/10.3390/atoms11070102






