Tunability of Half Cycle Cutoff Harmonics with Inhomogeneously Enhanced Laser Pulse
Abstract
:1. Introduction
2. Theoretical Methods
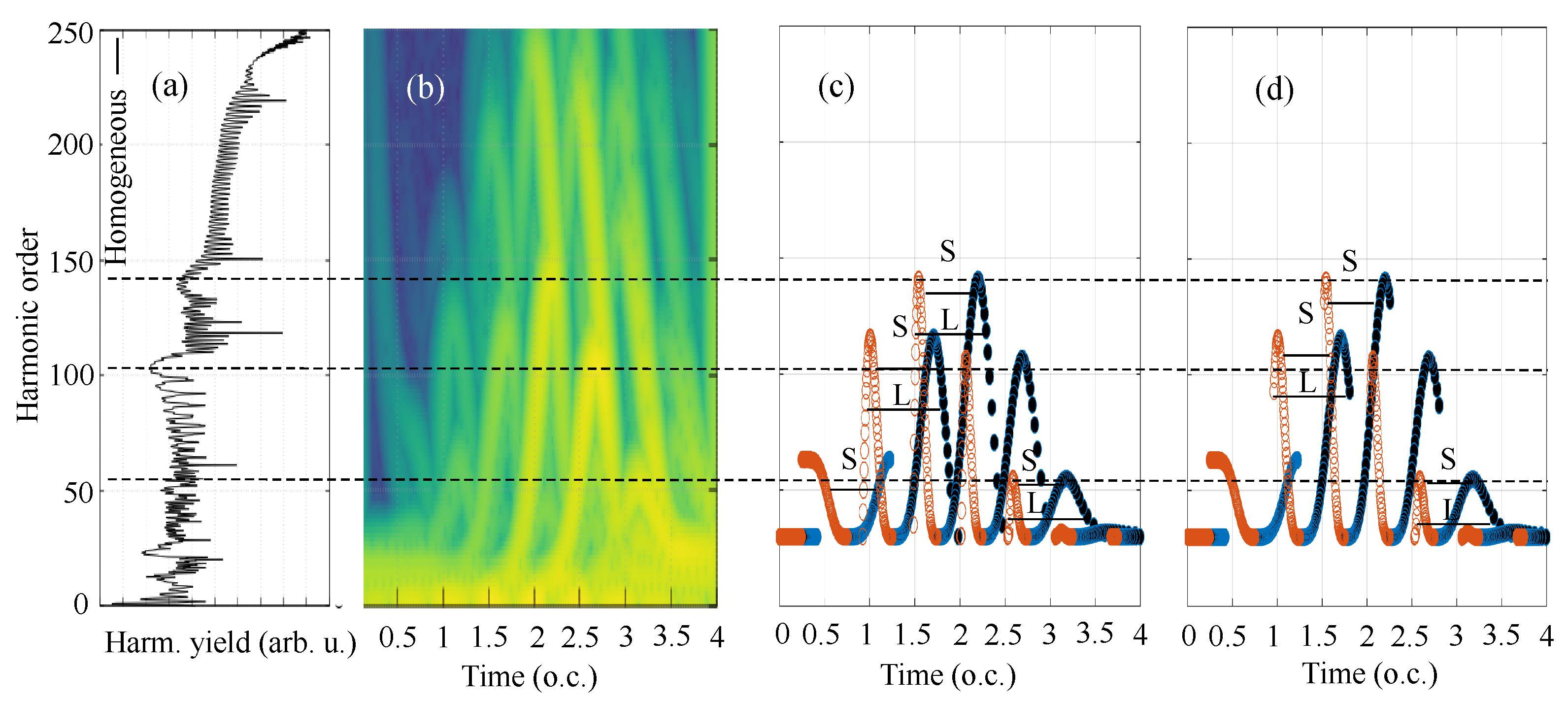
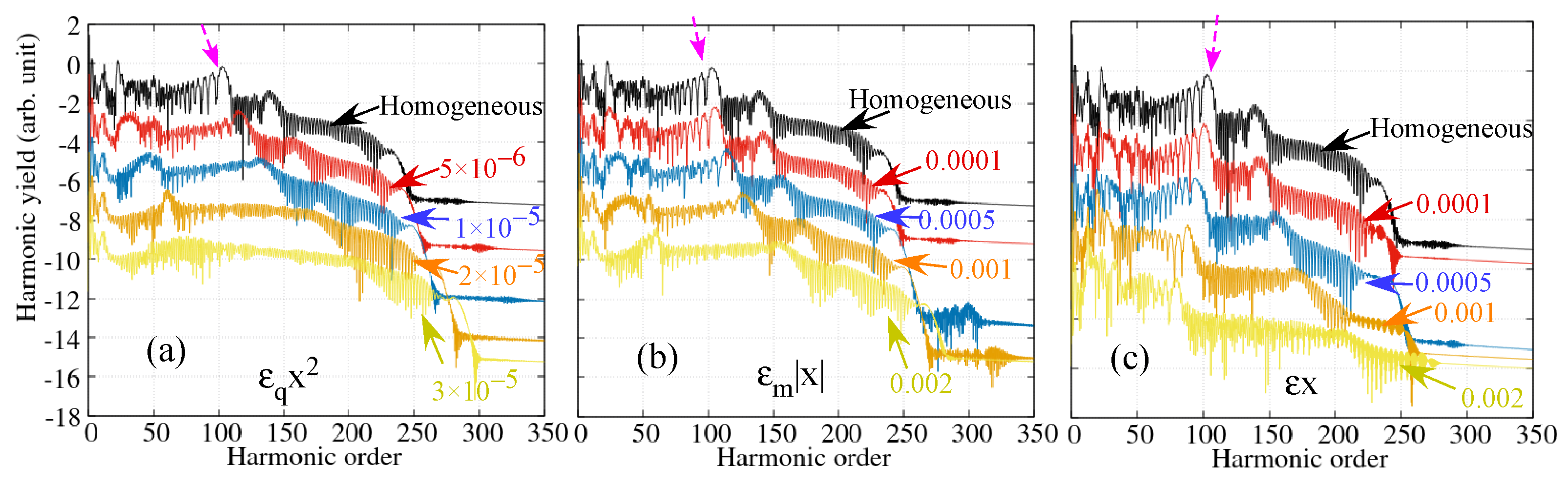
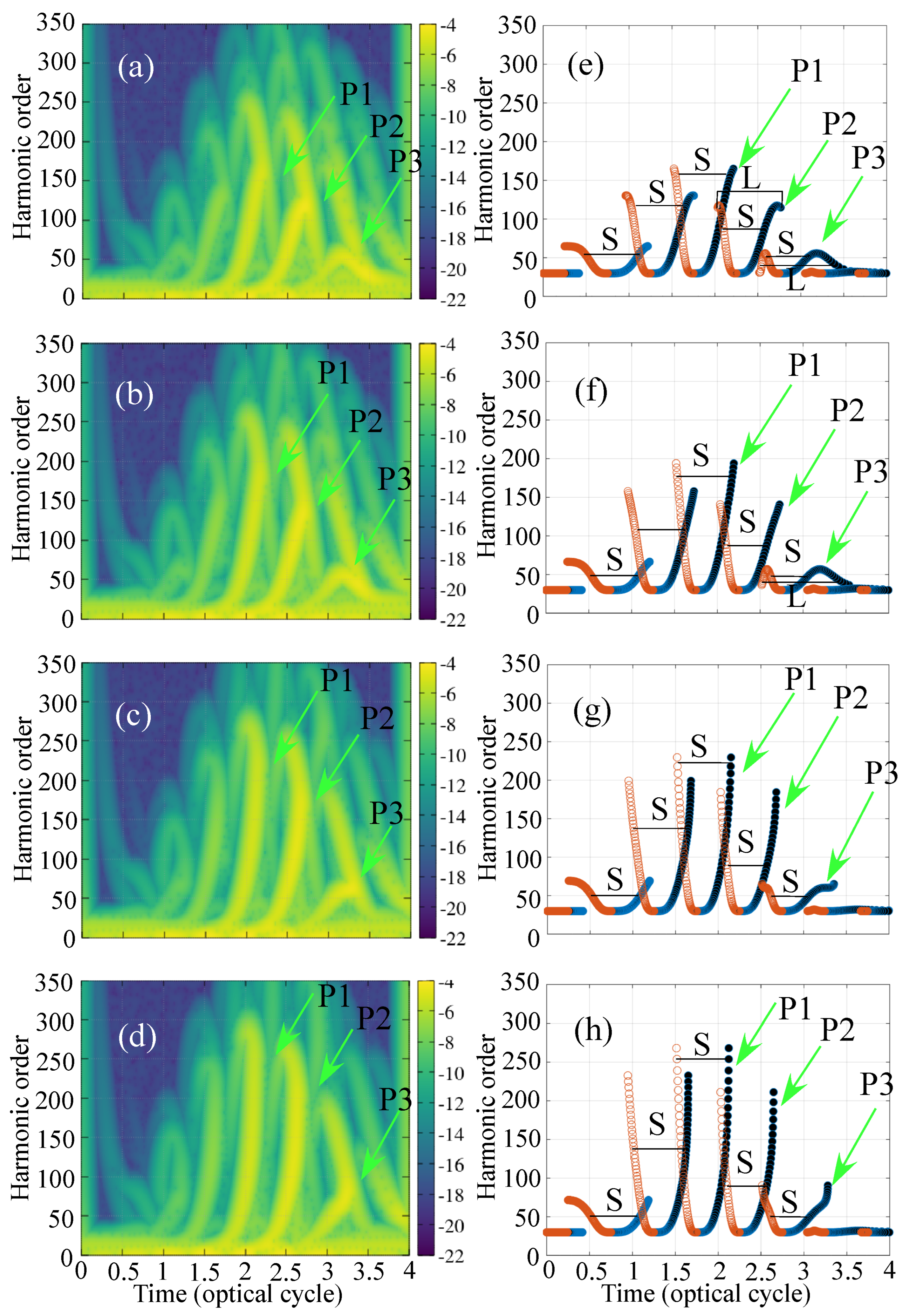
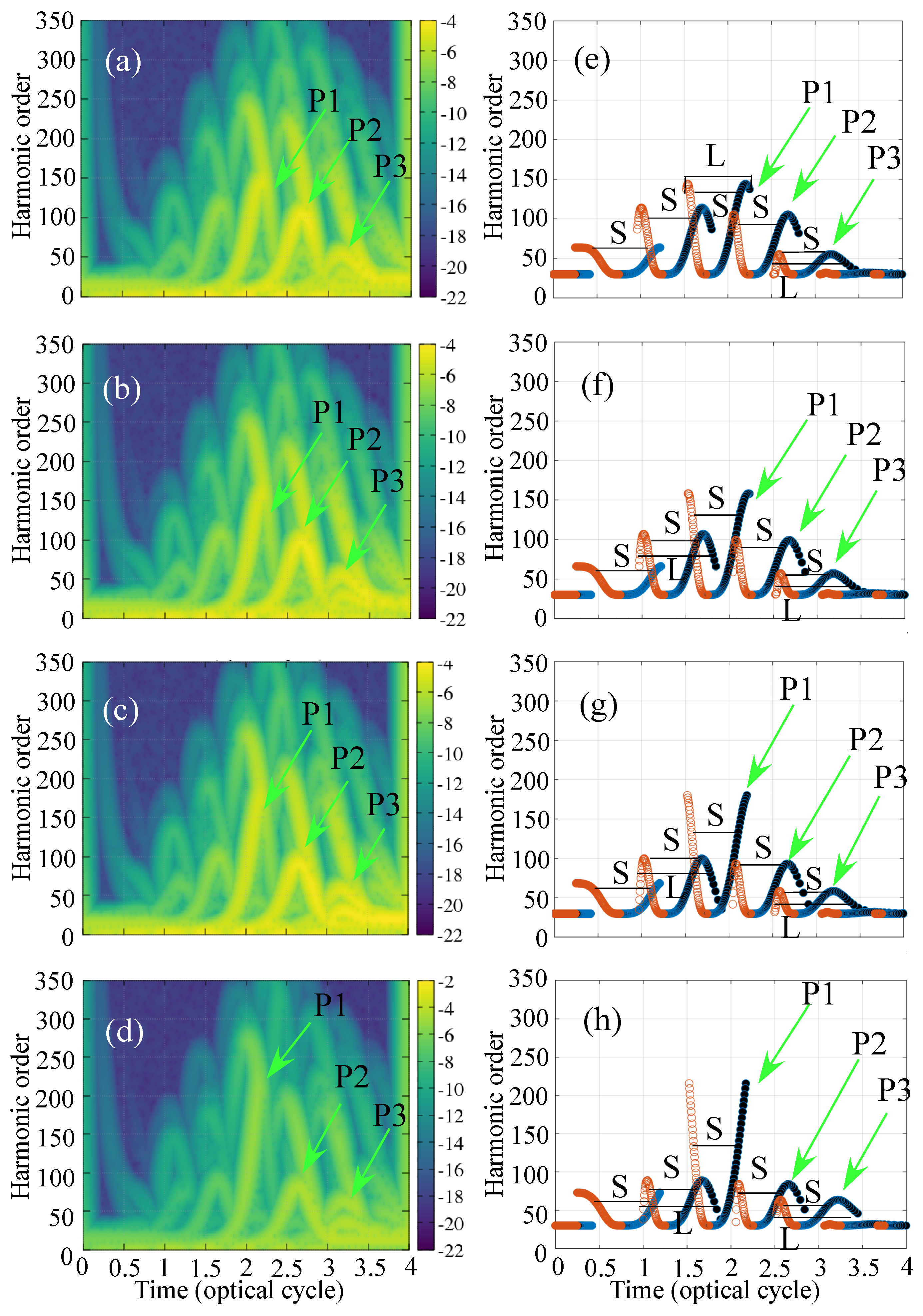
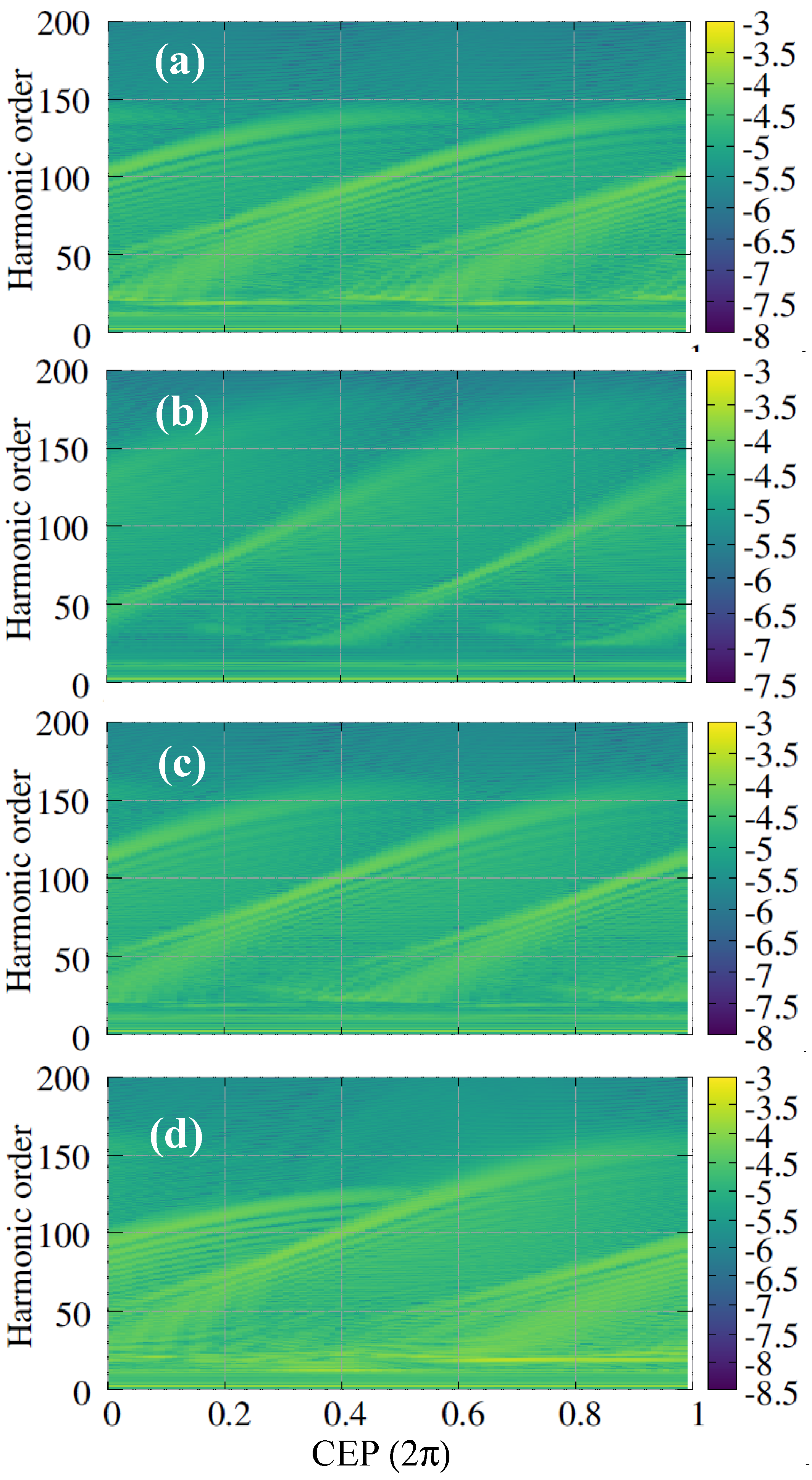
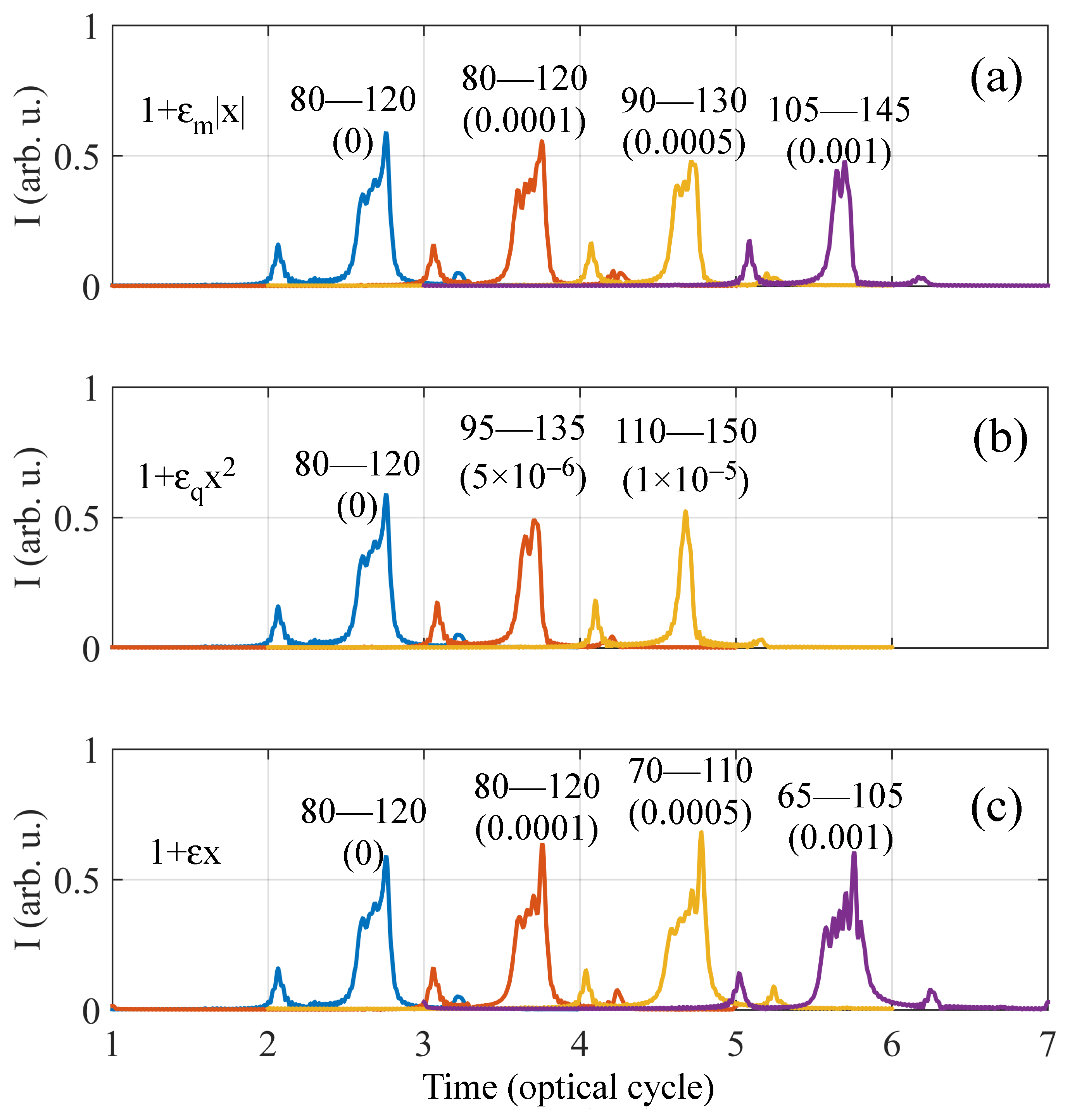
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HHG | High harmonic generation |
| CEP | Carrier envelope phase |
| HCO | Half cycle cutoff |
| XUV | Extreme-ultraviolet |
References
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163. [Google Scholar] [CrossRef]
- Baltuška, A.; Udem, T.; Uiberacker, M.; Hentschel, M.; Goulielmakis, E.; Gohle, C.; Holzwarth, R.; Yakovlev, V.; Scrinzi, A.; Hänsch, T.; et al. Attosecond control of electronic processes by intense light fields. Nature 2003, 421, 611–615. [Google Scholar] [CrossRef] [PubMed]
- Frolov, M.; Manakov, N.; Silaev, A.; Vvedenskii, N.; Starace, A.F. High-order harmonic generation by atoms in a few-cycle laser pulse: Carrier-envelope phase and many-electron effects. Phys. Rev. A 2011, 83, 021405. [Google Scholar] [CrossRef]
- Frolov, M.; Manakov, N.; Silaev, A.; Vvedenskii, N. Analytic description of high-order harmonic generation by atoms in a two-color laser field. Phys. Rev. A 2010, 81, 063407. [Google Scholar] [CrossRef]
- Peng, D.; Frolov, M.; Pi, L.W.; Starace, A.F. Enhancing high-order harmonic generation by sculpting waveforms with chirp. Phys. Rev. A 2018, 97, 053414. [Google Scholar] [CrossRef]
- Taoutioui, A.; Agueny, H. Femtosecond single cycle pulses enhanced the efficiency of high order harmonic generation. Micromachines 2021, 12, 610. [Google Scholar] [CrossRef]
- Yakovlev, V.S.; Scrinzi, A. High harmonic imaging of few-cycle laser pulses. Phys. Rev. Lett. 2003, 91, 153901. [Google Scholar] [CrossRef]
- Haworth, C.; Chipperfield, L.; Robinson, J.; Knight, P.; Marangos, J.; Tisch, J. Half-cycle cutoffs in harmonic spectra and robust carrier-envelope phase retrieval. Nat. Phys. 2007, 3, 52–57. [Google Scholar] [CrossRef]
- Cundiff, S.T. Better by half. Nat. Phys. 2007, 3, 16–18. [Google Scholar] [CrossRef]
- Xiong, W.H.; Geng, J.W.; Gong, Q.; Peng, L.Y. Half-cycle cutoff in near-threshold harmonic generation. New J. Phys. 2015, 17, 123020. [Google Scholar] [CrossRef]
- Pfeifer, T.; Jullien, A.; Abel, M.J.; Nagel, P.M.; Gallmann, L.; Neumark, D.M.; Leone, S.R. Generating coherent broadband continuum soft-x-ray radiation by attosecond ionization gating. Opt. Express 2007, 15, 17120–17128. [Google Scholar] [CrossRef] [PubMed]
- Abel, M.J.; Pfeifer, T.; Nagel, P.M.; Boutu, W.; Bell, M.J.; Steiner, C.P.; Neumark, D.M.; Leone, S.R. Isolated attosecond pulses from ionization gating of high-harmonic emission. Chem. Phys. 2009, 366, 9–14. [Google Scholar] [CrossRef]
- Cavalieri, A.L.; Goulielmakis, E.; Horvath, B.; Helml, W.; Schultze, M.; Fieß, M.; Pervak, V.; Veisz, L.; Yakovlev, V.; Uiberacker, M.; et al. Intense 1.5-cycle near infrared laser waveforms and their use for the generation of ultra-broadband soft-x-ray harmonic continua. New J. Phys. 2007, 9, 242. [Google Scholar] [CrossRef]
- Guo, Y.H.; Lu, R.F.; Han, K.L.; He, G.Z. Generation of an isolated sub-100 attosecond pulse in a two-color laser field. Int. J. Quantum Chem. 2009, 109, 3410–3415. [Google Scholar] [CrossRef]
- Zeng, Z.; Cheng, Y.; Song, X.; Li, R.; Xu, Z. Generation of an extreme ultraviolet supercontinuum in a two-color laser field. Phys. Rev. Lett. 2007, 98, 203901. [Google Scholar] [CrossRef]
- Lan, P.; Lu, P.; Cao, W.; Li, Y.; Wang, X. Carrier-envelope phase-stabilized attosecond pulses from asymmetric molecules. Phys. Rev. A 2007, 76, 021801. [Google Scholar] [CrossRef]
- Song, X.; Zeng, Z.; Fu, Y.; Cai, B.; Li, R.; Cheng, Y.; Xu, Z. Quantum path control in few-optical-cycle regime. Phys. Rev. A 2007, 76, 043830. [Google Scholar] [CrossRef]
- Ye, P.; He, X.; Teng, H.; Zhan, M.; Zhang, W.; Wang, L.; Zhong, S.; Wei, Z. Extraction of the in situ temporal information of few-cycle laser pulse from carrier-envelope phase-dependent high order harmonic spectrum. JOSA B 2014, 31, 1355–1359. [Google Scholar] [CrossRef]
- Geiseler, H.; Ishii, N.; Kaneshima, K.; Kitano, K.; Kanai, T.; Itatani, J. High-energy half-cycle cutoffs in high harmonic and rescattered electron spectra using waveform-controlled few-cycle infrared pulses. J. Phys. At. Mol. Opt. Phys. 2014, 47, 204011. [Google Scholar] [CrossRef]
- Teichmann, S.M.; Silva, F.; Cousin, S.L.; Biegert, J. Importance of intensity-to-phase coupling for water-window high-order-harmonic generation with few-cycle pulses. Phys. Rev. A 2015, 91, 063817. [Google Scholar] [CrossRef]
- Kim, S.; Jin, J.; Kim, Y.J.; Park, I.Y.; Kim, Y.; Kim, S.W. High-harmonic generation by resonant plasmon field enhancement. Nature 2008, 453, 757–760. [Google Scholar] [CrossRef] [PubMed]
- Husakou, A.; Im, S.J.; Herrmann, J. Theory of plasmon-enhanced high-order harmonic generation in the vicinity of metal nanostructures in noble gases. Phys. Rev. A 2011, 83, 043839. [Google Scholar] [CrossRef]
- Ciappina, M.; Pérez-Hernández, J.; Shaaran, T.; Biegert, J.; Quidant, R.; Lewenstein, M. Above-threshold ionization by few-cycle spatially inhomogeneous fields. Phys. Rev. A 2012, 86, 023413. [Google Scholar] [CrossRef]
- Ciappina, M.; Biegert, J.; Quidant, R.; Lewenstein, M. High-order-harmonic generation from inhomogeneous fields. Phys. Rev. A 2012, 85, 033828. [Google Scholar] [CrossRef]
- Du, T.Y.; Guan, Z.; Zhou, X.X.; Bian, X.B. Enhanced high-order harmonic generation from periodic potentials in inhomogeneous laser fields. Phys. Rev. A 2016, 94, 023419. [Google Scholar] [CrossRef]
- Blanco, M.; Hernández-García, C.; Chacón, A.; Lewenstein, M.; Flores-Arias, M.T.; Plaja, L. Phase matching effects in high harmonic generation at the nanometer scale. Opt. Express 2017, 25, 14974–14985. [Google Scholar] [CrossRef]
- Ansari, I.N.; Hofmann, C.; Medišauskas, L.; Lewenstein, M.; Ciappina, M.F.; Dixit, G. Controlling polarization of attosecond pulses with plasmonic-enhanced bichromatic counter-rotating circularly polarized fields. Phys. Rev. A 2021, 103, 013104. [Google Scholar] [CrossRef]
- Piglosiewicz, B.; Schmidt, S.; Park, D.J.; Vogelsang, J.; Groß, P.; Manzoni, C.; Farinello, P.; Cerullo, G.; Lienau, C. Carrier-envelope phase effects on the strong-field photoemission of electrons from metallic nanostructures. Nat. Photonics 2014, 8, 37–42. [Google Scholar] [CrossRef]
- Adnani, Y.; Taoutioui, A.; Makhoute, A.; Tőkési, K.; Agueny, H. Generation of superintense isolated attosecond pulses from trapped electrons in metal surfaces. Phys. Rev. A 2022, 105, 043104. [Google Scholar] [CrossRef]
- Mandal, A.; Singh, K.P. High harmonic generation near a bow-tie nanostructure: Sensitivity to carrier envelope phase and plasmonic inhomogeneity. Laser Phys. 2022, 33, 015301. [Google Scholar] [CrossRef]
- Protopapas, M.; Keitel, C.H.; Knight, P.L. Atomic physics with super-high intensity lasers. Rep. Prog. Phys. 1997, 60, 389. [Google Scholar] [CrossRef]
- Ciappina, M.F.; Aćimović, S.S.; Shaaran, T.; Biegert, J.; Quidant, R.; Lewenstein, M. Enhancement of high harmonic generation by confining electron motion in plasmonic nanostrutures. Opt. Express 2012, 20, 26261–26274. [Google Scholar] [CrossRef] [PubMed]
- Zagoya, C.; Bonner, M.; Chomet, H.; Slade, E.; de Morisson Faria, C.F. Different time scales in plasmonically enhanced high-order-harmonic generation. Phys. Rev. A 2016, 93, 053419. [Google Scholar] [CrossRef]
- Ansari, I.N.; Mrudul, M.; Ciappina, M.F.; Lewenstein, M.; Dixit, G. Simultaneous control of harmonic yield and energy cutoff of high-order harmonic generation using seeded plasmonically enhanced fields. Phys. Rev. A 2018, 98, 063406. [Google Scholar] [CrossRef]
- de Morisson Faria, C.F.; Dörr, M.; Becker, W.; Sandner, W. Time-frequency analysis of two-color high-harmonic generation. Phys. Rev. A 1999, 60, 1377. [Google Scholar] [CrossRef]
- Kohler, M.C.; Ott, C.; Raith, P.; Heck, R.; Schlegel, I.; Keitel, C.H.; Pfeifer, T. High harmonic generation via continuum wave-packet interference. Physical Rev. Lett. 2010, 105, 203902. [Google Scholar] [CrossRef]
- Chirilă, C.; Dreissigacker, I.; van der Zwan, E.V.; Lein, M. Emission times in high-order harmonic generation. Phys. Rev. A 2010, 81, 033412. [Google Scholar] [CrossRef]
- Sarantseva, T.; Silaev, A.; Romanov, A.; Vvedenskii, N.; Frolov, M. Time-frequency analysis of high harmonic generation using a probe XUV pulse. Opt. Express 2021, 29, 1428–1440. [Google Scholar] [CrossRef]
- de Morisson Faria, C.F.; Du, M. Enhancement of bichromatic high-order-harmonic generation with a high-frequency field. Phys. Rev. A 2001, 64, 023415. [Google Scholar] [CrossRef]
- Su, Q.; Eberly, J. Model atom for multiphoton physics. Phys. Rev. A 1991, 44, 5997. [Google Scholar] [CrossRef]
- Yu, C.; Wang, Y.; Cao, X.; Jiang, S.; Lu, R. Isolated few-attosecond emission in a multi-cycle asymmetrically nonhomogeneous two-color laser field. J. Phys. At. Mol. Opt. Phys. 2014, 47, 225602. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, A.; Wang, J.; Liu, X. Atomic even-harmonic generation due to symmetry-breaking effects induced by spatially inhomogeneous field. Chin. Phys. 2019, 28, 094212. [Google Scholar] [CrossRef]
- Manolopoulos, D.E. Derivation and reflection properties of a transmission-free absorbing potential. J. Chem. Phys. 2002, 117, 9552–9559. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mandal, A. Tunability of Half Cycle Cutoff Harmonics with Inhomogeneously Enhanced Laser Pulse. Atoms 2023, 11, 113. https://doi.org/10.3390/atoms11080113
Mandal A. Tunability of Half Cycle Cutoff Harmonics with Inhomogeneously Enhanced Laser Pulse. Atoms. 2023; 11(8):113. https://doi.org/10.3390/atoms11080113
Chicago/Turabian StyleMandal, Ankur. 2023. "Tunability of Half Cycle Cutoff Harmonics with Inhomogeneously Enhanced Laser Pulse" Atoms 11, no. 8: 113. https://doi.org/10.3390/atoms11080113
APA StyleMandal, A. (2023). Tunability of Half Cycle Cutoff Harmonics with Inhomogeneously Enhanced Laser Pulse. Atoms, 11(8), 113. https://doi.org/10.3390/atoms11080113





