Solving Time-Dependent Schödinger Equation for Some PT-Symmetric Quantum Mechanical Problems
Abstract
1. Introduction
2. Method of Calculation
2.1. The Eigenstates
2.2. Time-Dependent Schrödinger Equation, TDSE
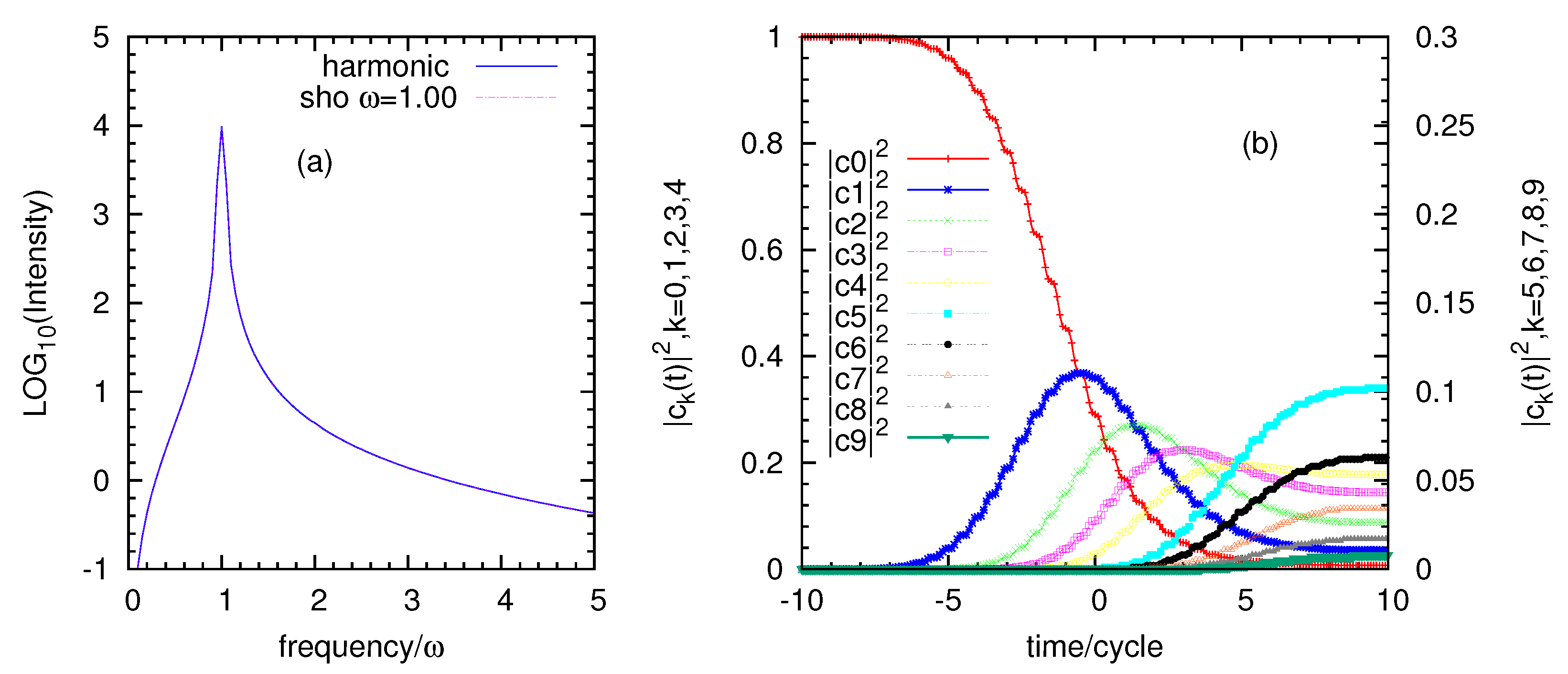
2.3. Driven Harmonic Oscillator
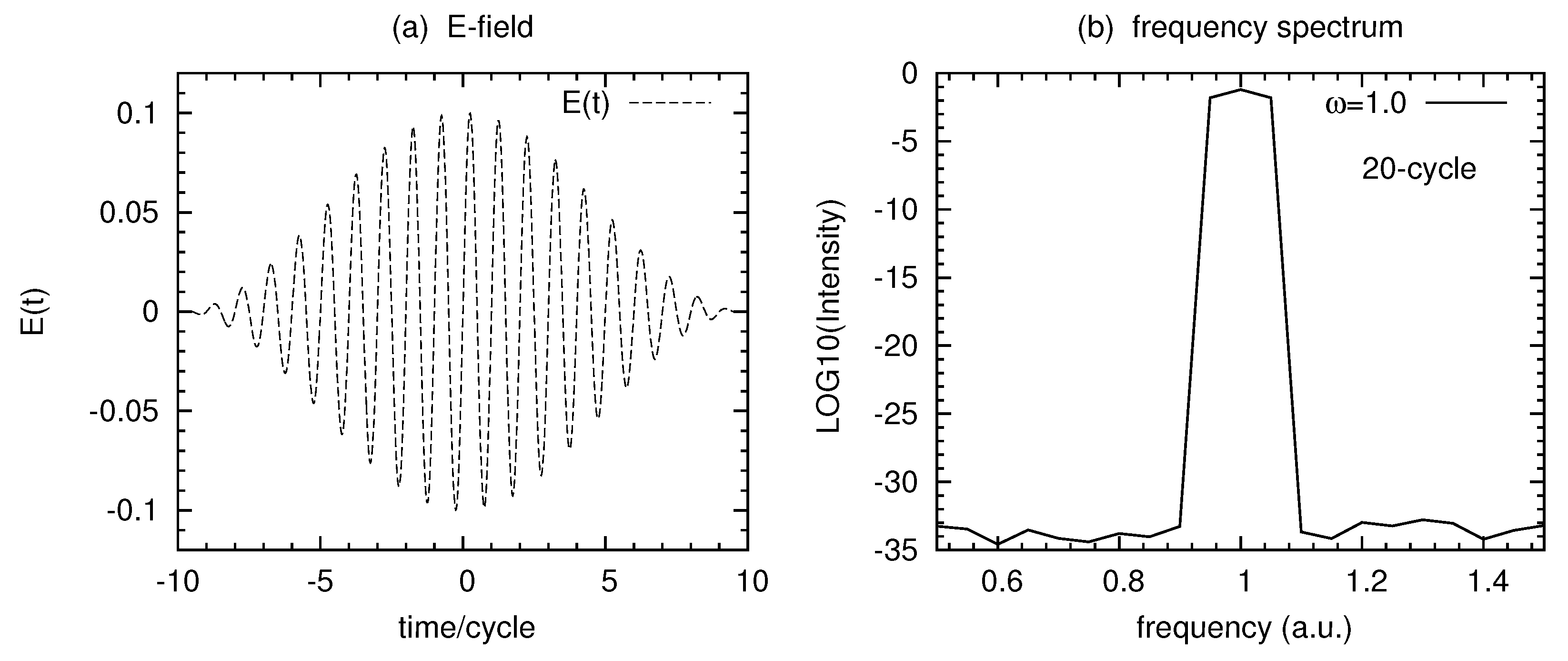
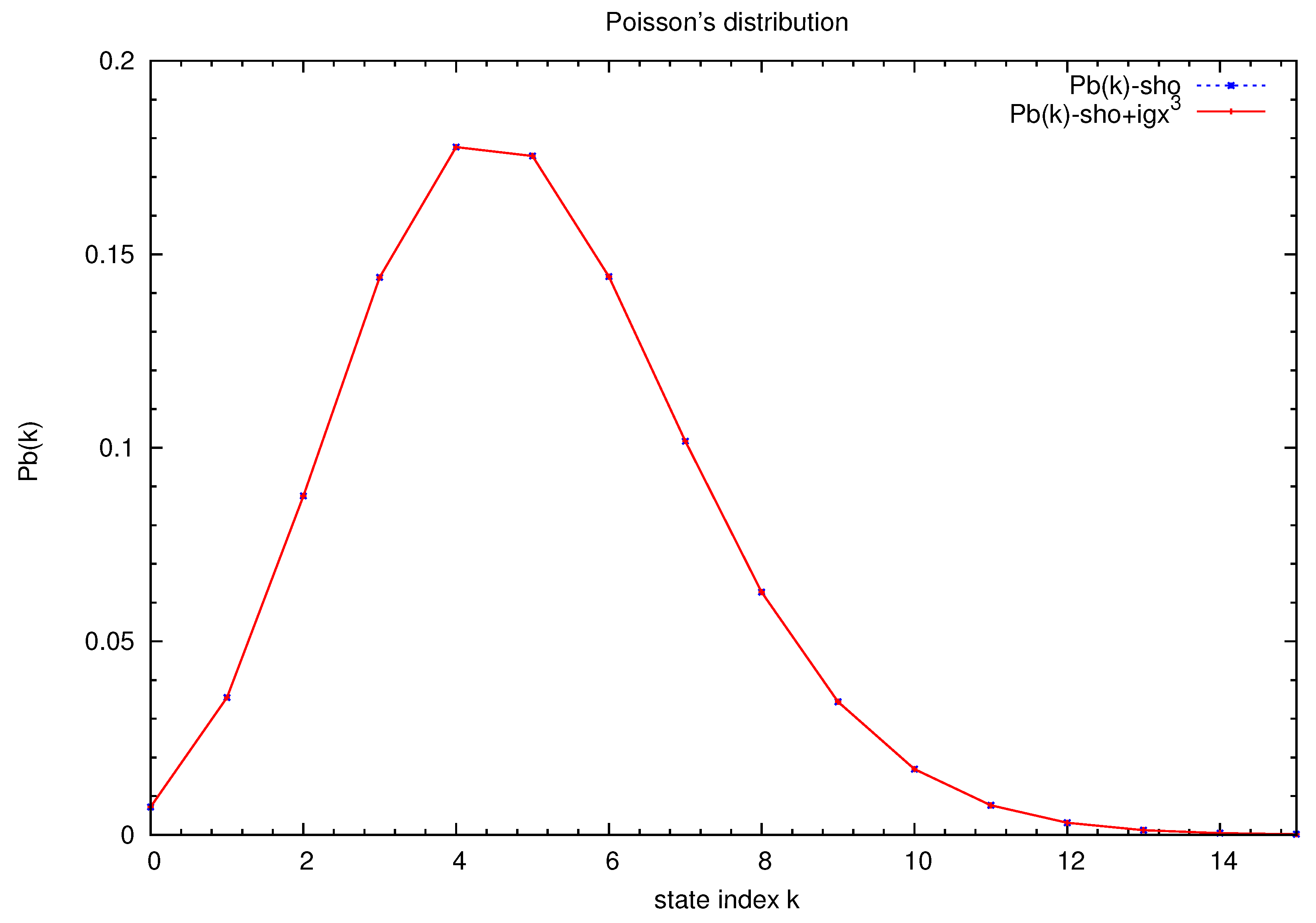
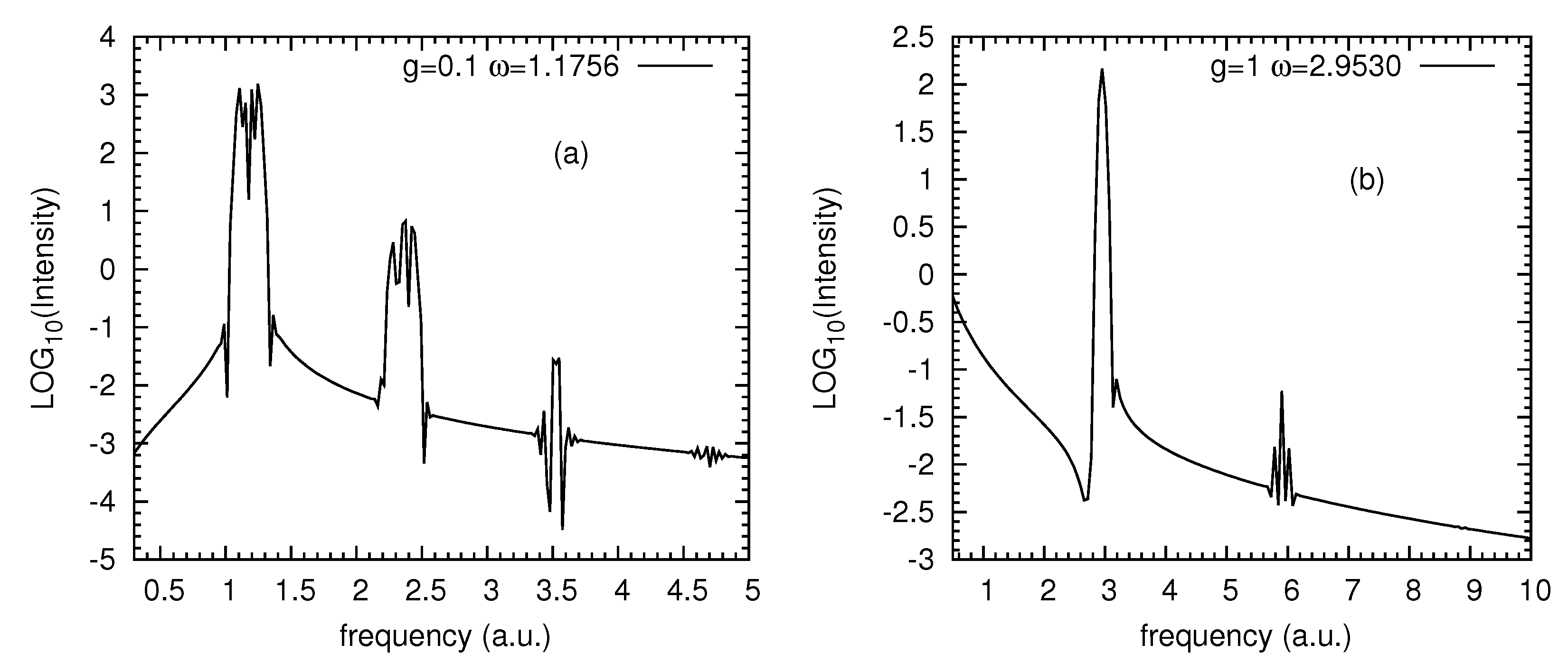
3. Results and Discussions
3.1.
3.2. and
3.3. and
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bender, C.M.; Boettcher, S. Real Spectra in Non-Hermitian Hamiltonians Having PT Symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef]
- Bender, C.M. PT Symmetry in Quantum and Classical Physics; World Science: London, UK, 2019. [Google Scholar]
- El-Ganainy, R.; Makris, K.; Christodoulides, D.; Musslimani, Z. Theory of coupled optical PT-symmetric structures. Opt. Lett. 2007, 32, 2632–2634. [Google Scholar] [CrossRef] [PubMed]
- Zyablovsky, A.A.; Vinogradov, A.P.; Dorofeenko, A.V.; Pukhov, A.A.; Lisyansky, A.A. Causality and phase transitions in PT-symmetric optical systems. Phys. Rev. A 2014, 89, 033808. [Google Scholar] [CrossRef]
- Makris, K.; El-Ganainy, R.; Christodoulides, D.; Musslimani, Z. Beam Dynamics in PT-Symmetric Optical Lattices. Phys. Rev. Lett. 2008, 100, 103904. [Google Scholar] [CrossRef] [PubMed]
- Graefe, E.M.; Jones, H.F. PT-symmetric sinusoidal optical lattices at the symmetry-breaking threshold. Phys. Rev. A 2011, 84, 013818. [Google Scholar] [CrossRef]
- Burckhardt, C.B. Diffraction of a plane wave at a sinusoidally stratified dilectric grating. J. Opt. Soc. Am. 1966, 56, 1502–1509. [Google Scholar] [CrossRef]
- Noble, J.H.; Lubasch, M.; Stevens, J.; Jentschura, U.D. Diagonalization of complex symmetric matrices: Generalized Householder reflections, iterative deflation and implicit shifts. Comp. Phys. Commun. 2017, 221, 304–316. [Google Scholar] [CrossRef]
- Anderson, E.; Bai, Z.; Bischof, C.; Blackford, S.; Demmel, J.; Dongarra, J.; Du Croz, J.; Greenbaum, A.; Hammarling, S.; McKenney, A.; et al. LAPACK Users’ Guide, 3rd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1999. [Google Scholar]
- Bender, C.M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 2007, 70, 947–1018. [Google Scholar] [CrossRef]
- Brabec, T.; Krausz, F. Intense few-cycle laser fields: Frontiers of nonlinear optics. Rev. Mod. Phys. 2000, 72, 545–591. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef]
- Lin, C.D.; Le, A.T.; Jin, C.; Wei, H. Attosecond and Strong-Field Physics; Cambridge University Press: New York, NY, USA, 2018; Section 5.2.2. [Google Scholar]
- Cohen-Tannoudji, C.; Dupont-Roc, J.; Fabre, C.; Grynberg, G. Comment on the Momentum-Translation Approximation. Phys. Rev. A 1973, 8, 2747–2751. [Google Scholar] [CrossRef]
- Ter Haar, D. (Ed.) Problems in Quantum Mechanics, 3rd ed.; Chapman and Hall: New York, NY, USA, 1975; Problem 3.41. [Google Scholar]
- Jiang, T.F. High-frequency stabilization and high-order harmonic generation of an excited Morse oscillator under Intense Fields. Phys. Rev. A 1993, 48, 3995–3998. [Google Scholar] [CrossRef] [PubMed]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 1994, 49, 2117–2132. [Google Scholar] [CrossRef] [PubMed]
- Jiang, T.F.; Chu, S.I. High-order harmonic generation in atomic hydrogen at 248 nm: Dipole-moment versus acceleration spectrum. Phys. Rev. A 1992, 46, 7322–7324. [Google Scholar] [CrossRef] [PubMed]
- Jentschura, U.D.; Surzhykov, A.; Lubasch, M.; Zinn-Justin, J. Structure, time propagation and dissipative terms for resonances. J. Phys. A Math. Theor. 2008, 41, 095302. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Consistent Treatment of Quantum Systems with a Time-Dependent Hilbert Space. Entropy 2024, 26, 314. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Pseudo-Hermitian representation of quantum mechanics. Int. J. Geom. Methods Mod. Phys. 2010, 7, 1191. [Google Scholar] [CrossRef]
- Matzkin, A. Non-Hermitian quantum mechanics: The case of bound state scattering theory. J. Phys. A Math. Gen. 2006, 39, 10859. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in Fortran, 2nd ed.; Cambridge University Press: New York, NY, USA, 1992; Chapter 12. [Google Scholar]
- NAG Fortran Library Mark 17; The Numerical Algorithms Group Inc.: Oxford, UK, 1995.
- Sakurai, J.J. Modern Quantum Mechanics, Revised ed.; Addison-Wesley: New York, USA, 1994; Eq.2.3.25. [Google Scholar]
- Chen, Z.; Le, A.T.; Morishita, T.; Lin, C.D. Quantitative rescattering theory for laser-induced high-energy plateau photoelectron spectra. Phys. Rev. A 2009, 79, 033409. [Google Scholar] [CrossRef]
- Chu, S.I.; Cooper, J. Threshold shift and above-threshold multiphoton ionization of atomic hydrogen in intense laser fields. Phys. Rev. A 1985, 32, 2769–2775. [Google Scholar] [CrossRef]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef] [PubMed]

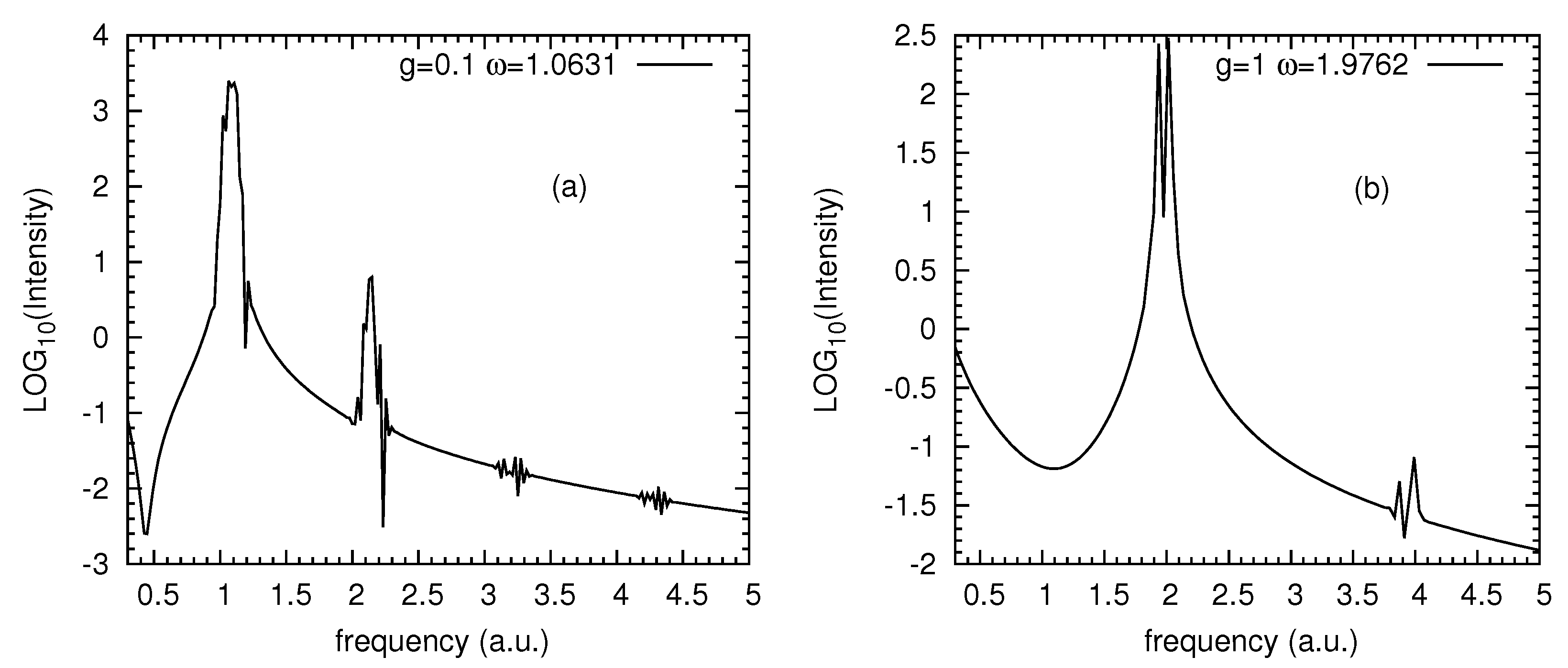
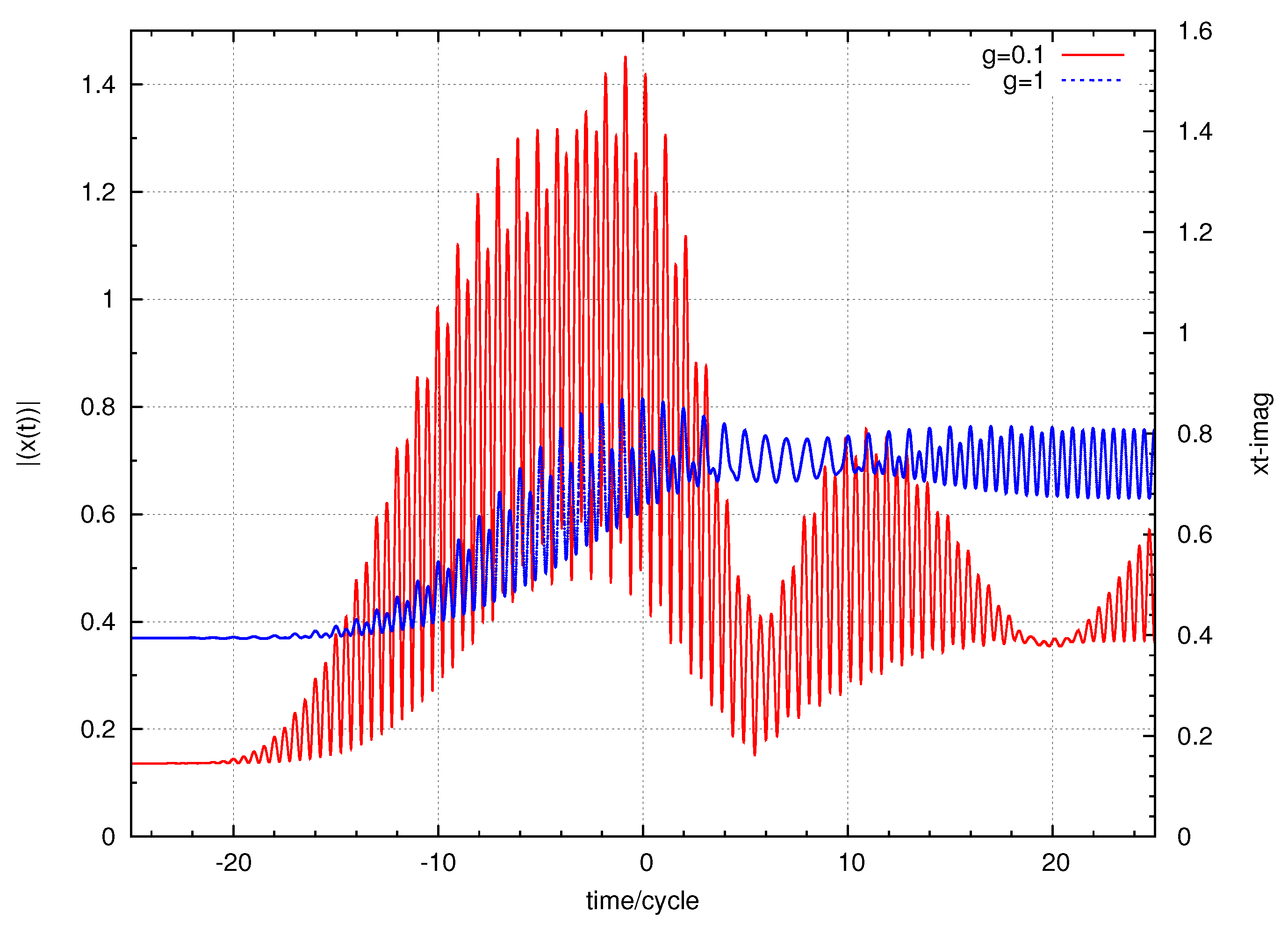
| g | ||||||
|---|---|---|---|---|---|---|
| 0.18326 | 0.65127 | 1.19854 | 1.79321 | 2.42355 | 3.08284 | |
| 0.34886 | 1.23979 | 2.28160 | 3.41366 | 4.61360 | 5.86870 | |
| 0.46032 | 1.63591 | 3.01059 | 4.50435 | 6.08768 | 7.74379 | |
| 0.87629 | 3.11421 | 5.73113 | 8.57473 | 11.58883 | 14.74150 | |
| 1.15627 | 4.10923 | 7.56227 | 11.31442 | 15.29155 | 19.45153 |
| g | ||||||
|---|---|---|---|---|---|---|
| 0.50000 | 1.50000 | 2.50000 | 3.50000 | 4.50000 | 5.50000 | |
| 0.50000 | 1.50000 | 2.50002 | 3.50005 | 4.50008 | 5.50011 | |
| 0.50014 | 1.50088 | 2.50238 | 3.50462 | 4.50760 | 5.51131 | |
| 0.50335 | 1.52118 | 2.55564 | 3.60558 | 4.67002 | 5.74811 | |
| 0.51254 | 1.57560 | 2.68971 | 3.84603 | 5.03863 | 6.26325 | |
| 0.64588 | 2.18448 | 3.94769 | 5.85246 | 7.86517 | 9.96627 | |
| 0.79734 | 2.77352 | 5.06782 | 7.55590 | 10.19040 | 12.94420 |
| g = 0.1 | g = 1 | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0.9462 | −0.1449 i | −0.0157 | 0.0015 i | −0.5970 | 0.0915 i | 0.0099 | −0.0009 i |
| 1 | −1.2486 | 0.1792 i | 0.0188 | 0.0017 i | −0.7878 | 0.1131 i | 0.0119 | −0.0011 i |
| 2 | −1.4677 | 0.2057 i | −0.0213 | 0.0019 i | −0.9260 | 0.1298 i | 0.0134 | −0.0012 i |
| 3 | −1.6464 | −0.2277 i | −0.0234 | 0.0021 i | −1.0388 | 0.1437 i | 0.0147 | 0.0013 i |
| g = 0.1 | g = 1 | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 | −0.6904 | 0.0559 i | 0.0038 | 0.0002 i | −0.5154 | −0.0770 i | −0.0082 | −0.0008 i |
| 1 | −0.9585 | 0.0862 i | −0.0062 | −0.0004 i | 0.6825 | −0.0964 i | 0.0100 | 0.0009 i |
| 2 | −1.1560 | −0.1108 i | 0.0083 | 0.0006 i | −0.8033 | −0.1112 i | 0.0114 | 0.0010 i |
| 3 | 1.3175 | 0.1319 i | −0.0102 | −0.0007 i | 0.9018 | 0.1235 i | −0.0126 | 0.0011 i |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, T.-F. Solving Time-Dependent Schödinger Equation for Some PT-Symmetric Quantum Mechanical Problems. Atoms 2024, 12, 46. https://doi.org/10.3390/atoms12090046
Jiang T-F. Solving Time-Dependent Schödinger Equation for Some PT-Symmetric Quantum Mechanical Problems. Atoms. 2024; 12(9):46. https://doi.org/10.3390/atoms12090046
Chicago/Turabian StyleJiang, Tsin-Fu. 2024. "Solving Time-Dependent Schödinger Equation for Some PT-Symmetric Quantum Mechanical Problems" Atoms 12, no. 9: 46. https://doi.org/10.3390/atoms12090046
APA StyleJiang, T.-F. (2024). Solving Time-Dependent Schödinger Equation for Some PT-Symmetric Quantum Mechanical Problems. Atoms, 12(9), 46. https://doi.org/10.3390/atoms12090046






