Relativistic Atomic Structure Calculations for the Study of Electron Dynamics of Sr+ Ion Confined Inside Fullerene
Abstract
:1. Introduction
2. Theoretical Methodology and Computational Details
2.1. MCDHF Formalism
2.2. GASW Model
3. Results and Discussion
3.1. Energy Levels, Probability Distributions, and Transition Data
| Energy (au) | = 0.000 | = 0.259 | = 0.280 | = 0.300 |
|---|---|---|---|---|

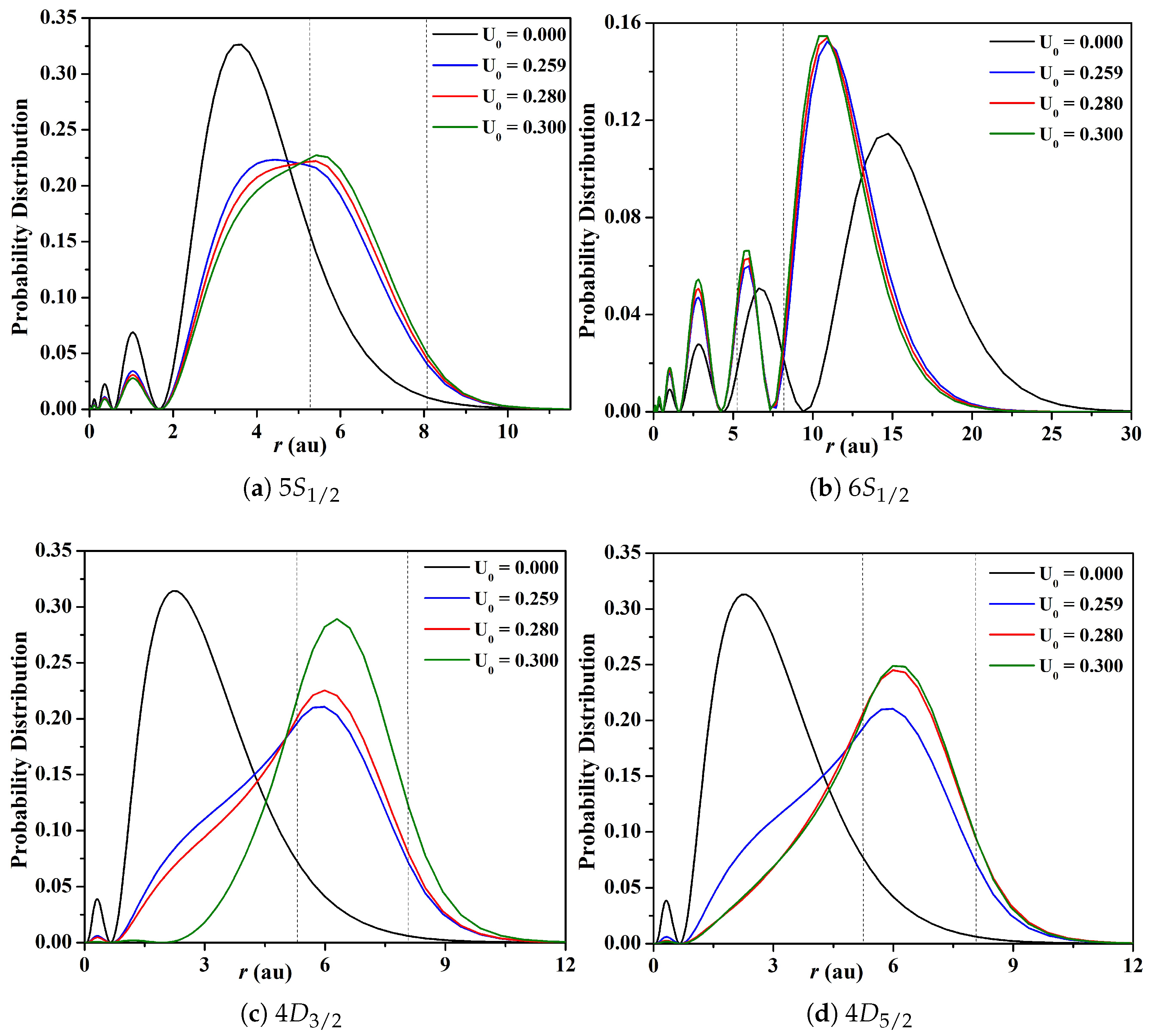
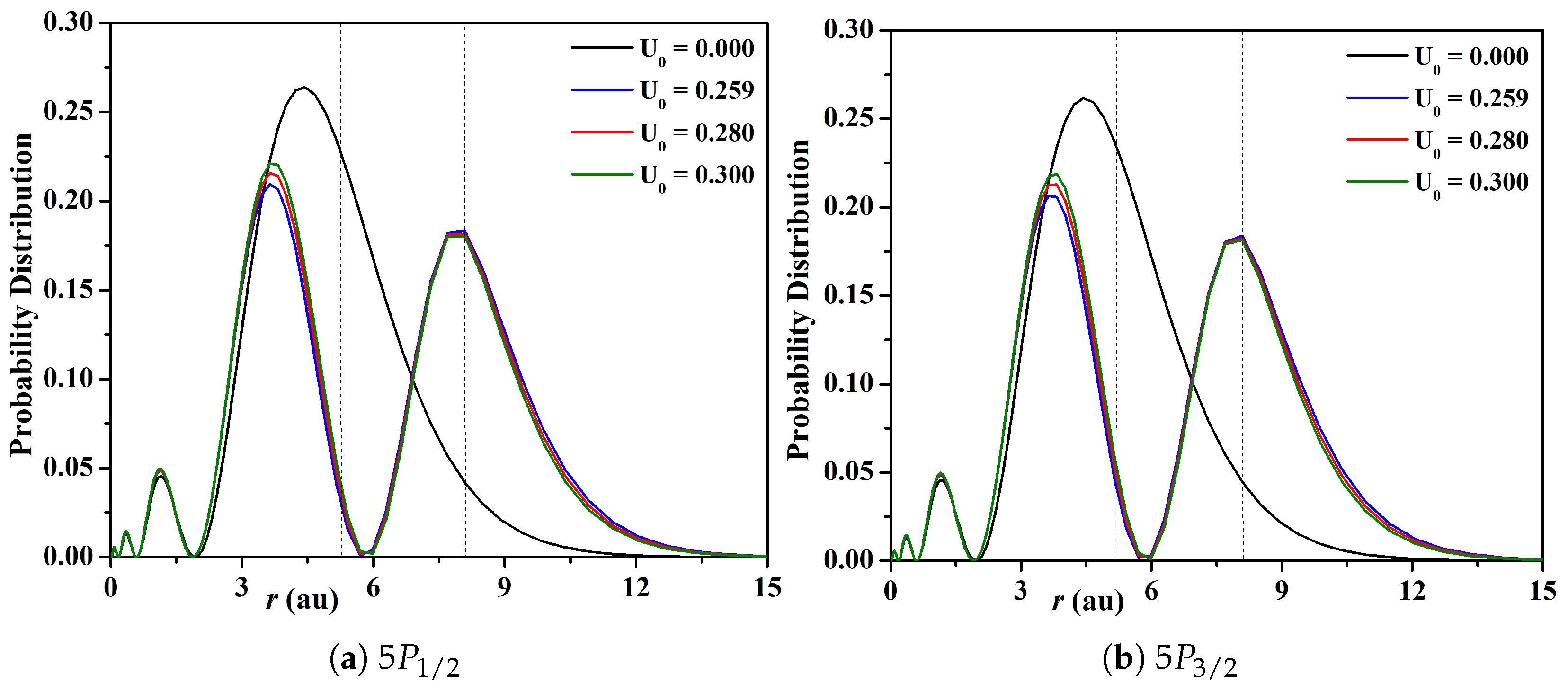
| Depth (au) | ||||||
|---|---|---|---|---|---|---|
| Transition Data | = 0.000 | = 0.259 | = 0.280 | = 0.300 |
|---|---|---|---|---|
| 21,834 | 62,039 | 62,648 | 63,335 | |
| 22,519 | 62,914 | 63,543 | 64,244 | |
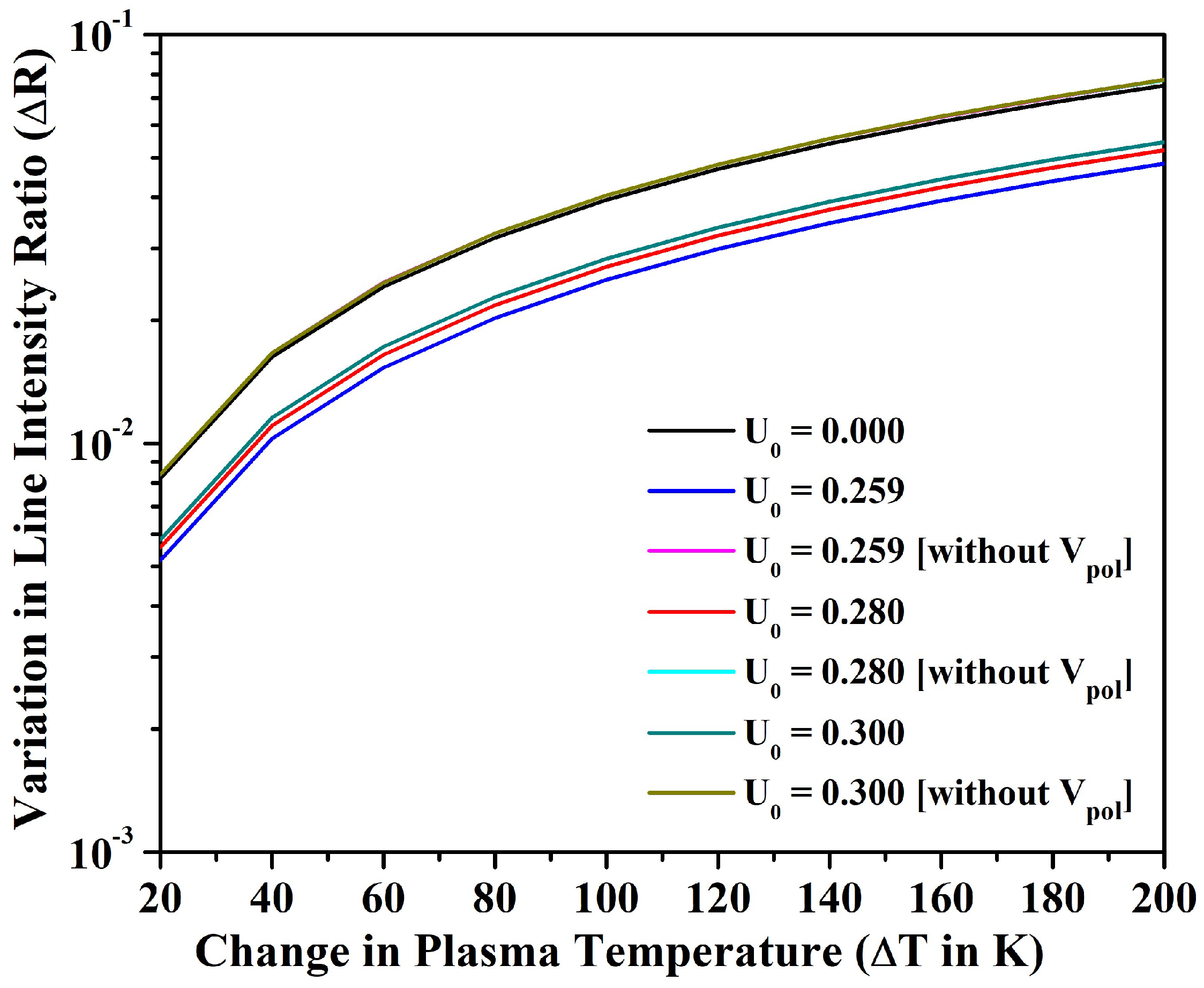
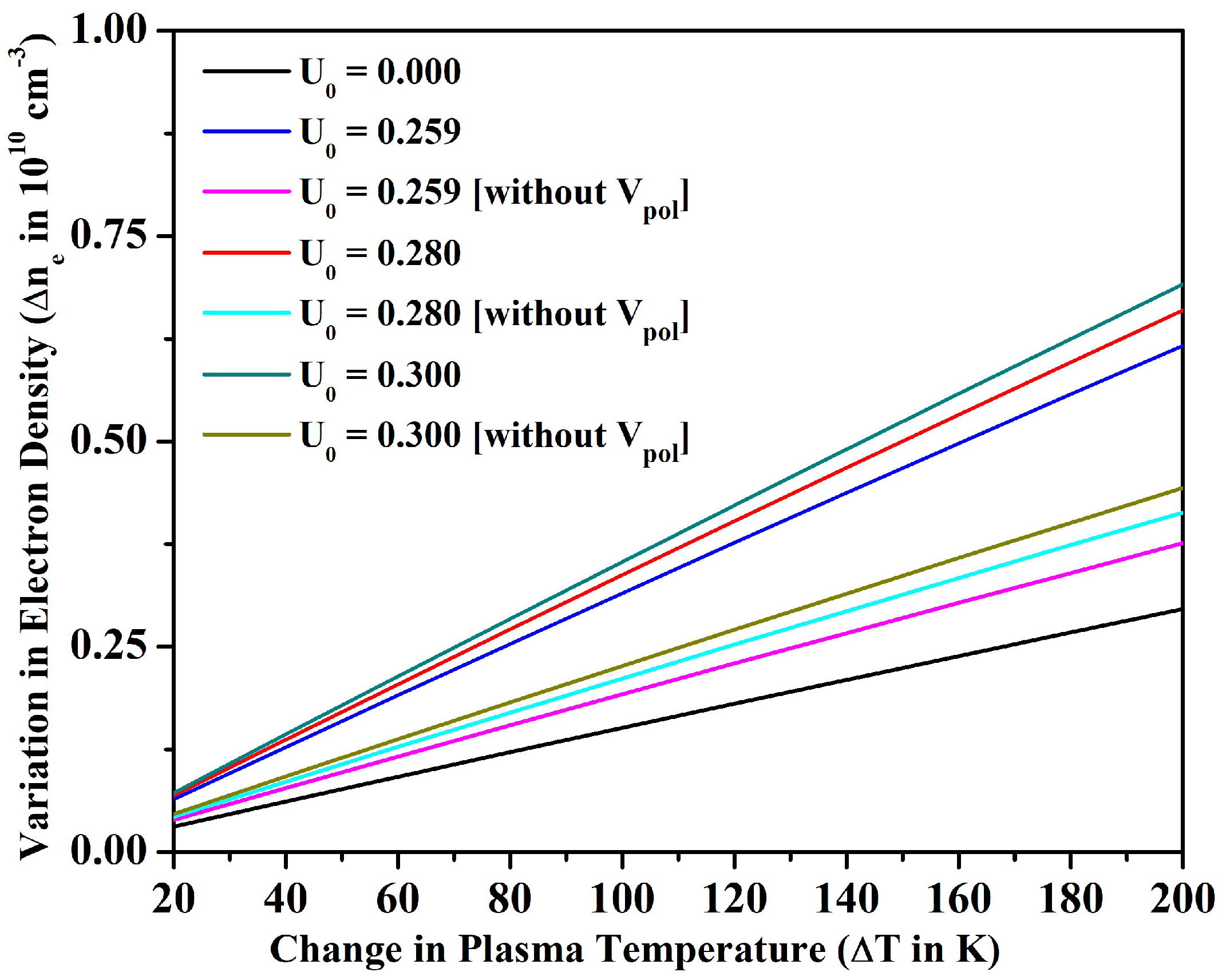
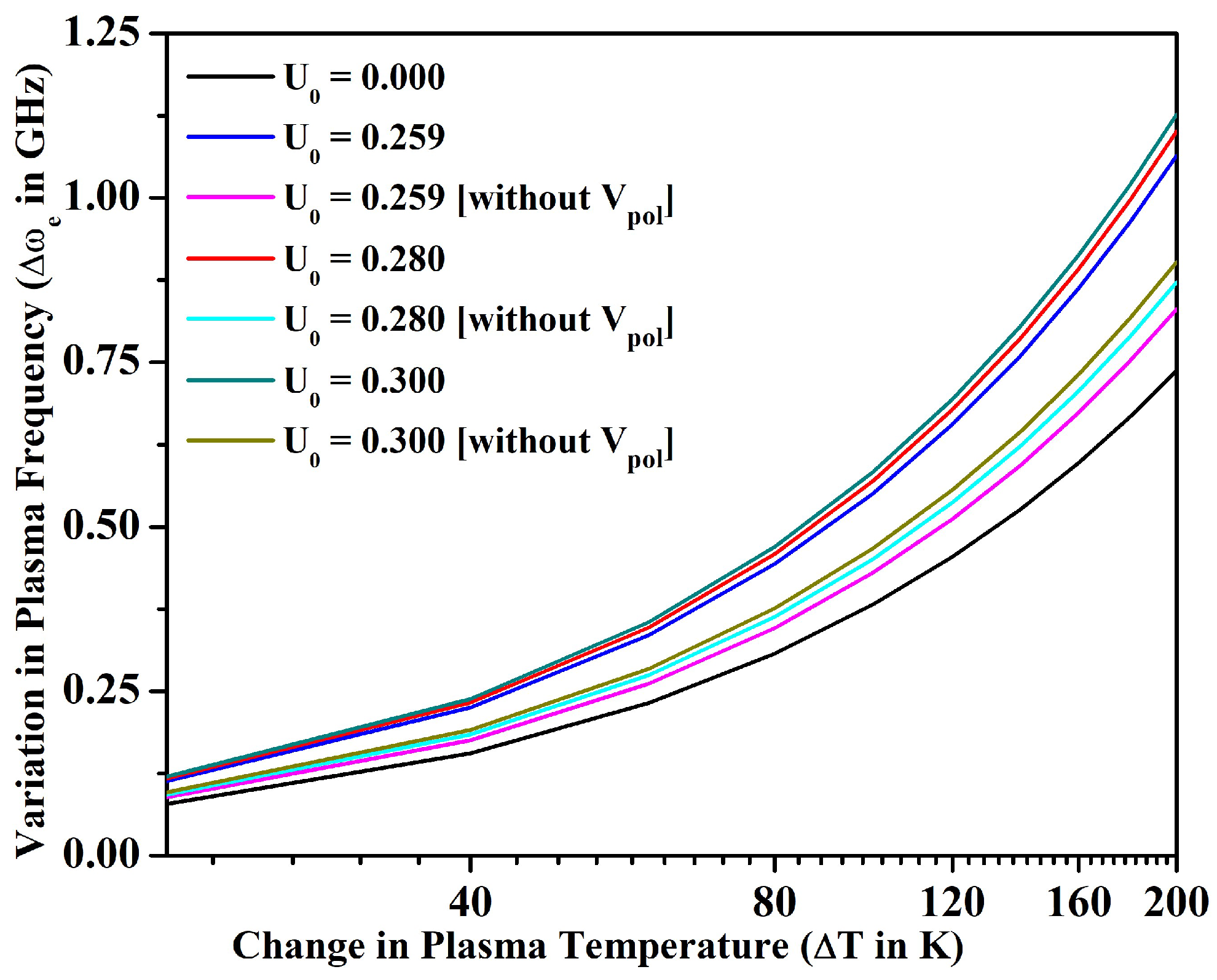
3.2. Line Intensity Ratio and Plasma Parameters
| = 0.000 au | |||||
|---|---|---|---|---|---|
| (In K) | (In 1010 cm−3) | (In 1010 Hz) | (In cm) | (In ) | |
| 1000 | |||||
| 1020 | |||||
| 1040 | |||||
| 1060 | |||||
| 1080 | |||||
| 1100 | |||||
| 1120 | |||||
| 1140 | |||||
| 1160 | |||||
| 1180 | |||||
| 1200 | |||||
| = 0.259 au | |||||
| (In K) | (In cm−3) | (In Hz) | (In cm) | (In ) | |
| 1000 | |||||
| 1020 | |||||
| 1040 | |||||
| 1060 | |||||
| 1080 | |||||
| 1100 | |||||
| 1120 | |||||
| 1140 | |||||
| 1160 | |||||
| 1180 | |||||
| 1200 | |||||
| = 0.280 au | |||||
| (In K) | (In cm−3) | (In Hz) | (In cm) | (In ) | |
| 1000 | |||||
| 1020 | |||||
| 1040 | |||||
| 1060 | |||||
| 1080 | |||||
| 1100 | |||||
| 1120 | |||||
| 1140 | |||||
| 1160 | |||||
| 1180 | |||||
| 1200 | |||||
| = 0.300 au | |||||
| (In K) | (In cm−3) | (In Hz) | (In cm) | (In ) | |
| 1000 | |||||
| 1020 | |||||
| 1040 | |||||
| 1060 | |||||
| 1080 | |||||
| 1100 | |||||
| 1120 | |||||
| 1140 | |||||
| 1160 | |||||
| 1180 | |||||
| 1200 |
4. Conclusions
- The MCDHF and GASW formalisms overall provided consistent and reliable results for the electronic properties of the Sr+ ion confined inside fullerene. The calculated orbital energies were a valuable component to study the electron impact ionization process using the BEB method.
- We performed two separate calculations: one with electrostatic and GASW potentials, and another by further adding the polarization potential. We found that inclusion of the polarization effect was very important in order to accurately determine the energy levels and transition data of the confined ion.
- We also investigated the merit of the fullerene in the alteration of line intensity ratio, electron density, plasma frequency, and skin depth with the variation in temperature for an optically thin plasma in LTE. In particular, the electron density could be increased only around 9% for the bare ion case by increasing the temperature up to 1200 K; however, could be increased around 50% by incorporating the effect of encapsulation within the fullerene. The electron density and other parameters of plasma could be further tuned by changing the potential depth of the fullerene.
- We noticed that the size of the plasmon could also be tuned by varying the confinement depth of the fullerene. Finally, we were able to conclude by calculating that the average kinetic energy of electrons in Sr+ ion is significantly higher than the average potential energy due to Coulomb interaction, and, therefore, these are weakly coupled in nature confined inside C60.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Acquah, S.F.A.; Penkova, A.V.; Markelov, D.A.; Semisalova, A.S.; Leonhardt, B.E.; Magi, J.M. Review—The beautiful molecule: 30 Years of C60 and its derivatives. ECS J. Solid State Sci. Technol. 2017, 6, M3155–M3162. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; ÓBrien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Harneit, W. Fullerene-based electron-spin quantum computer. Phys. Rev. B 2002, 65, 032322. [Google Scholar] [CrossRef]
- Jönsson, P.; Gaigalas, G.; Rynkun, P.; Radžiūtė, L.; Ekman, J.; Gustafsson, S.; Hartman, H.; Wang, K.; Godefroid, M.; Charlotte, F.F.; et al. Multiconfiguration Dirac-Hartree-Fock calculations with spectroscopic accuracy: Applications to astrophysics. Atoms 2017, 5, 16. [Google Scholar] [CrossRef]
- Watson, D.; Hansen, C.J.; Selsing, J.; Koch, A.; Malesani, D.B.; Andersen, A.C.; Fynbo, J.P.U.; Arcones, A.; Bauswein, A.; Covino, S.; et al. Identification of strontium in the merger of two neutron stars. Nature 2019, 574, 497–500. [Google Scholar] [CrossRef]
- Cowan, J.J.; Sneden, C.; Burles, S.; Ivans, I.I.; Beers, T.C.; Truran, J.W.; Lawler, J.E.; Primas, F.; Fuller, G.M.; Pfeiffer, B.; et al. The chemical composition and age of the metal-poor halo star BD +17°3248. Astrophys. J. 2002, 572, 861–879. [Google Scholar] [CrossRef]
- Barklem, P.S.; O’Mara, B.J. Broadening of lines of Be II, Sr II and Ba II by collisions with hydrogen atoms and the solar abundance of strontium. Mon. Not. R. Astron. Soc. 2000, 311, 535–540. [Google Scholar] [CrossRef]
- Zethson, T.; Gull, T.R.; Hartman, H.; Johansson, S.; Davidson, K.; Ishibashi, K. Sr II and [Sr II] emission in the ejecta of η Carinae. Astron. J. 2001, 122, 322–326. [Google Scholar] [CrossRef]
- Simien, C.E.; Chen, Y.C.; Gupta, P.; Laha, S.; Martinez, Y.N.; Mickelson, P.G.; Nagel, S.B.; Killian, T.C. Using absorption imaging to study ion dynamics in an ultracold neutral plasma. Phys. Rev. Lett. 2004, 92, 143001. [Google Scholar] [CrossRef]
- Cami, J.; Bernard-Salas, J.; Peeters, E.; Malek, S.E. Detection of C60 and C70 in a young planetary nebula. Science 2010, 329, 1180–1182. [Google Scholar] [CrossRef]
- Berné, O.; Tielens, A.G.G.M. Formation of buckminsterfullerene (C60) in interstellar space. Proc. Natl. Acad. Sci. USA 2011, 109, 401–406. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, M.; Jose, J.; Goswami, B.; Easwaran, R.K. Theoretical exploration of atomic structure calculation of sodium atom confined in the fullerene cage: A primer investigation for EIT applications. J. Phys. B At. Mol. Opt. Phys. 2024, 57, 155001. [Google Scholar] [CrossRef]
- Shen, Y.; Cui, M.; Takaishi, S.; Kawasoko, H.; Sugimoto, K.; Tsumuraya, T.; Otsuka, A.; Kwon, E.; Yoshida, T.; Hoshino, N.; et al. Heterospin frustration in a metal-fullerene-bonded semiconductive antiferromagnet. Nat. Commun. 2022, 13, 495. [Google Scholar] [CrossRef]
- Aoyagi, S.; Miwa, K.; Ueno, H.; Okada, H.; Matsuo, Y.; Kokubo, K. Structure of [60]fullerene with a mobile lithium cation inside. R. Soc. Open Sci. 2018, 5, 180337. [Google Scholar] [CrossRef]
- Cioslowski, J.; Nanayakkara, A. Endohedral effect in inclusion complexes of the C6 cluster. J. Chem. Phys. 1992, 96, 8354–8362. [Google Scholar] [CrossRef]
- Ravinder, P.; Subramanian, V. Studies on the encapsulation of various anions in different fullerenes using Density Functional Theory calculations and Born–Oppenheimer molecular dynamics simulation. J. Phys. Chem. A 2011, 115, 11723–11733. [Google Scholar] [CrossRef]
- Fischer, C.F.; Godefroid, M.; Brage, T.; Jönsson, P.; Gaigalas, G. Advanced multiconfiguration methods for complex atoms: I. Energies and wave functions. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 182004. [Google Scholar] [CrossRef]
- Nascimento, E.M.; Prudente, F.V.; Guimarães, M.N.; Maniero, A.M. A study of the electron structure of endohedrally confined atoms using a model potential. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 015003. [Google Scholar] [CrossRef]
- Saha, S.; Thuppilakkadan, A.; Varma, H.R.; Jose, J. Photoionization dynamics of endohedrally confined atomic H and Ar: A contrasting study between compact versus diffused model potential. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 145001. [Google Scholar] [CrossRef]
- Grant, I.P. Relativistic Quantum Theory of Atoms and Molecules: Theory and Computation; Springer: New York, NY, USA, 2007. [Google Scholar]
- Johnson, W.R. Atomic Structure Theory: Lectures on Atomic Physics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Bransden, B.H.; Joachain, C.J. Physics of Atoms and Molecules; Pearson Education: Bengaluru, India, 2003. [Google Scholar]
- Patel, A.B.; Chakraborty, H.S. Fourier photospectroscopy of Xe@C60 through a Xe 4d resonance window: Theory versus recent experiment. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 191001. [Google Scholar] [CrossRef]
- Dolmatov, V.K.; Baltenkov, A.S.; Connerade, J.-P.; Manson, S.T. Structure and photoionization of confined atoms. Radiat. Phys. Chem. 2004, 70, 417–433. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Chernysheva, L.V.; Dolmatov, V.K. Confinement and correlation effects in the Xe@C60 generalized oscillator strengths. Phys. Rev. A 2011, 84, 063201. [Google Scholar] [CrossRef]
- Dolmatov, V.K.; King, J.L.; Oglesby, J.C. Diffuse versus square-well confining potentials in modelling A@C60 atoms. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 105102, Erratum in J. Phys. B At. Mol. Opt. Phys. 2015, 48, 069501. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, Y.; Li, B.; Chen, X. Ab initio calculation of electrostatic potentials for C60 and C80. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 035102. [Google Scholar] [CrossRef]
- Puska, M.J.; Nieminen, R.M. Photoabsorption of atoms inside C60. Phys. Rev. A 1993, 47, 1181–1186. [Google Scholar] [CrossRef]
- Dubey, K.A.; Agrawal, S.; Rao, T.R.; Jose, J. A theoretical investigation of elastic scattering of H atom by C60 and Kr@C60. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 035203. [Google Scholar] [CrossRef]
- Lin, C.Y.; Ho, Y.K. Photoionization of atoms encapsulated by cages using the power-exponential potential. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 145001. [Google Scholar] [CrossRef]
- Dubey, K.A.; Jose, J. Effect of charge transfer on elastic scattering of electron from Ar@C60: Dirac partial wave calculation. Eur. Phys. J. Plus 2021, 136, 713. [Google Scholar] [CrossRef]
- Saha, S.; Jose, J. Shannon entropy as a predictor of avoided crossing in confined atoms. Int. J. Quantum Chem. 2020, 120, e26374. [Google Scholar] [CrossRef]
- Dolmatov, V.K.; Amusia, M.Y.; Chernysheva, L.V. Effects of target polarization in electron elastic scattering off endohedral A@C60. Phys. Rev. A 2017, 95, 012709. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Chernysheva, L.V. On the behavior of scattering phases in collisions of electrons with multiatomic objects. JETP Lett. 2015, 101, 503–506. [Google Scholar] [CrossRef]
- Drukarev, G.F. Collisions of Electrons with Atoms and Molecules; Springer: New York, NY, USA, 1987. [Google Scholar]
- Sabirov, D.S. Polarizability as a landmark property for fullerene chemistry and materials science. RSC Adv. 2014, 4, 44996–45028. [Google Scholar] [CrossRef]
- Stenholm, S. Foundations of Laser Spectroscopy; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Allen, L.; Eberly, J.H. Optical Resonance and Two Level Atoms; Courier Corporation: North Chelmsford, MA, USA, 1987. [Google Scholar]
- Fischer, C.F.; Gaigalas, G.; Jönsson, P.; Bieroń, J. GRASP 2018—A Fortran 95 version of the General Relativistic Atomic Structure Package. Comput. Phys. Commun. 2019, 237, 184–187. [Google Scholar] [CrossRef]
- Grant, I.P. Gauge invariance and relativistic radiative transitions. J. Phys. B At. Mol. Opt. Phys. 1974, 7, 1458–1475. [Google Scholar] [CrossRef]
- Jönsson, P.; Godefroid, M.; Gaigalas, G.; Ekman, J.; Grumer, J.; Li, W.; Li, J.; Brage, T.; Grant, I.P.; Bieroń, J.; et al. An introduction to relativistic theory as implemented in GRASP. Atoms 2023, 11, 7. [Google Scholar] [CrossRef]
- Olsen, J.; Godefroid, M.R.; Jönsson, P.; Malmqvist, P.Å.; Fischer, C.F. Transition probability calculations for atoms using nonorthogonal orbitals. Phys. Rev. E 1995, 52, 4499–4508. [Google Scholar] [CrossRef]
- Kumar, N.; Shivankar; Jha, A.K.S.; Dimri, M.; Dawra, D.; Mohan, M. Relativistic atomic structure calculations, plasma and thermodynamic parameters for Ca X. Eur. Phys. J. Plus 2023, 138, 1155. [Google Scholar] [CrossRef]
- Paijwar, R.; Sharma, R.; Jha, A.K.S. Relativistic atomic structure calculations of KIX with plasma parameters. Phys. Plasmas 2022, 29, 092702. [Google Scholar] [CrossRef]
- Goyal, A.; Khatri, I.; Singh, A.; Mohan, M.; Sharma, R.; Singh, N. Atomic structure calculations and study of plasma parameters of Al-like ions. Atoms 2016, 4, 22. [Google Scholar] [CrossRef]
- Deshmukh, P.C.; Jose, J.; Varma, H.R.; Manson, S.T. Electronic structure and dynamics of confined atoms. Eur. Phys. J. D 2021, 75, 166. [Google Scholar] [CrossRef]
- Madjet, M.E.; Chakraborty, H.S.; Manson, S.T. Giant enhancement in low energy photoemission of Ar confined in C60. Phys. Rev. Lett. 2007, 99, 243003. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.-K.; Rudd, M.E. Binary-encounter-dipole model for electron-impact ionization. Phys. Rev. A 1994, 50, 3954–3967. [Google Scholar] [CrossRef] [PubMed]
- Hwang, W.; Kim, Y.-K.; Rudd, M.E. New model for electron-impact ionization cross sections of molecules. J. Chem. Phys. 1996, 104, 2956–2966. [Google Scholar] [CrossRef]
- Gupta, D.; Choi, H.; Song, M.-Y.; Karwasz, G.P.; Yoon, J.-S. Electron impact ionization cross section studies of C2Fx (x = 1–6) and C3Fx (x = 1–8) fluorocarbon species. Eur. Phys. J. D 2017, 71, 88. [Google Scholar] [CrossRef]
- Suriyaprasanth, S.; Choi, H.; Gupta, D. Electron and positron impact ionization of SF6−nHn(n = 0–6); (SCln, SFn−1Cl(n = 1–6)) and SF5X(X = CN, CFO). Atoms 2023, 11, 137. [Google Scholar] [CrossRef]
- Wu, D.; He, X.T.; Yu, W.; Fritzsche, S. Monte Carlo approach to calculate ionization dynamics of hot solid-density plasmas within particle-in-cell simulations. Phys. Rev. E 2017, 95, 023208. [Google Scholar] [CrossRef]
- Pooser, R.C.; Marino, A.M.; Boyer, V.; Jones, K.M.; Lett, P.D. Quantum correlated light beams from non-degenerate four-wave mixing in an atomic vapor: The D1 and D2 lines of 85Rb and 87Rb. Opt. Express 2009, 17, 16722–16730. [Google Scholar] [CrossRef]
- Herrnstein, J.R.; Moran, J.M.; Greenhill, L.J.; Diamond, P.J.; Inoue, M.; Nakai, N.; Miyoshi, M.; Henkel, C.; Riess, A. A geometric distance to the galaxy NGC4258 from orbital motions in a nuclear gas disk. Nature 1999, 400, 539–541. [Google Scholar] [CrossRef]
- Nikonova, R.M.; Lad’yanov, V.I.; Rekhviashvili, S.S.; Pskhu, A.V. Thermal stability of C60 and C70 fullerites. High Temp. 2021, 59, 179–183. [Google Scholar] [CrossRef]
- Borodin, V.I.; Trukhacheva, V.A. Thermal stability of fullerenes. Tech. Phys. Lett. 2004, 30, 598–599. [Google Scholar] [CrossRef]
- McWhirter, R.W.P. Plasma Diagnostic Techniques; Huddleston, R.H., Leonard, S.L., Eds.; Academic Press: New York, NY, USA, 1965. [Google Scholar]
- Desch, S.J.; Mouschovias, T.C. The magnetic decoupling stage of star formation. Astrophys. J. 2001, 550, 314–333. [Google Scholar] [CrossRef]

| Configurations | States | Parity |
|---|---|---|
| ing | even | |
| even | ||
| even | ||
| odd | ||
| odd | ||
| even | ||
| even | ||
| even | ||
| odd | ||
| odd | ||
| even | ||
| even |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goswami, B.; Ahmad, M.; Jose, J.; Easwaran, R.K. Relativistic Atomic Structure Calculations for the Study of Electron Dynamics of Sr+ Ion Confined Inside Fullerene. Atoms 2025, 13, 36. https://doi.org/10.3390/atoms13040036
Goswami B, Ahmad M, Jose J, Easwaran RK. Relativistic Atomic Structure Calculations for the Study of Electron Dynamics of Sr+ Ion Confined Inside Fullerene. Atoms. 2025; 13(4):36. https://doi.org/10.3390/atoms13040036
Chicago/Turabian StyleGoswami, Biplab, Mobassir Ahmad, Jobin Jose, and Raghavan K. Easwaran. 2025. "Relativistic Atomic Structure Calculations for the Study of Electron Dynamics of Sr+ Ion Confined Inside Fullerene" Atoms 13, no. 4: 36. https://doi.org/10.3390/atoms13040036
APA StyleGoswami, B., Ahmad, M., Jose, J., & Easwaran, R. K. (2025). Relativistic Atomic Structure Calculations for the Study of Electron Dynamics of Sr+ Ion Confined Inside Fullerene. Atoms, 13(4), 36. https://doi.org/10.3390/atoms13040036






