A New Implementation of the STA Method for the Calculation of Opacities of Local Thermodynamic Equilibrium Plasmas
Abstract
:1. Introduction
2. The Model
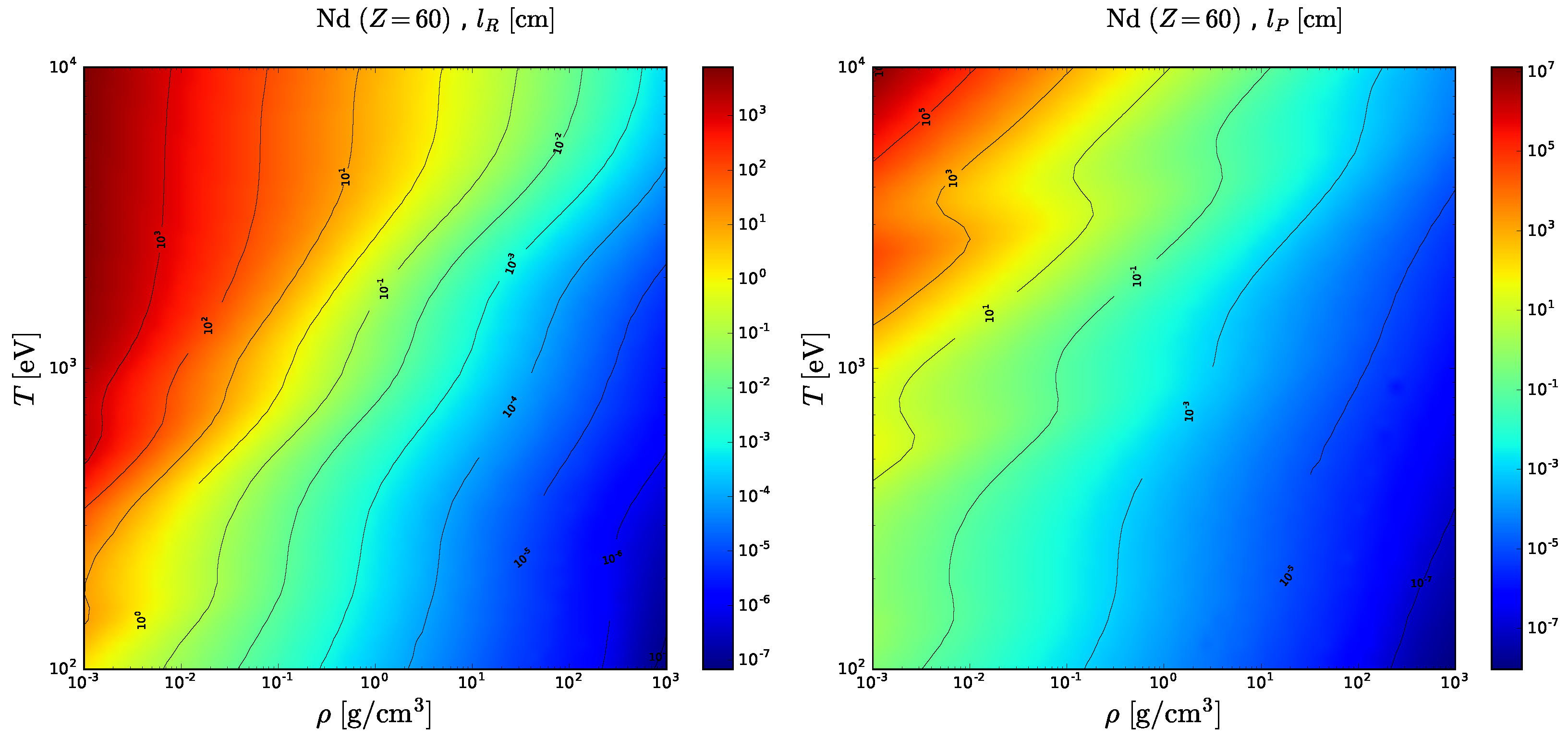
3. Opacity Calculations
4. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Bahcall, J.N.; Basu, S.; Pinsonneault, M.; Serenelli, A.M. Helioseismological implications of recent solar abundance determinations. Astrophys. J. 2005, 618, 1049. [Google Scholar] [CrossRef]
- Bergemann, M.; Serenelli, A. Solar abundance problem. In Determination of Atmospheric Parameters of B-, A-, F- and G-Type Stars; Springer: Cham, Switzerland, 2014; pp. 245–258. [Google Scholar]
- Asplund, M.; Grevesse, N.; Sauval, A.J.; Scott, P. The chemical composition of the sun. arXiv, 2009; arXiv:0909.0948. [Google Scholar] [CrossRef]
- Christensen-Dalsgaard, J.; di Mauro, M.P.; Houdek, G.; Pijpers, F. On the opacity change required to compensate for the revised solar composition. Astron. Astrophys. 2009, 494, 205–208. [Google Scholar] [CrossRef]
- Villante, F.L.; Serenelli, A.M. A quantitative analysis of the solar composition problem. Phys. Procedia 2015, 61, 366–375. [Google Scholar] [CrossRef]
- Krief, M.; Feigel, A.; Gazit, D. Line broadening and the solar opacity problem. Astrophys. J. 2016, 824, 98. [Google Scholar] [CrossRef]
- Krief, M.; Kurzweil, Y.; Feigel, A.; Gazit, D. The effect of ionic correlations on radiative properties in the solar interior and terrestrial experiments. Astrophys. J. 2018, 856, 135. [Google Scholar] [CrossRef]
- Krief, M.; Feigel, A. The effect of first order superconfiguration energies on the opacity of hot dense matter. High Energy Density Phys. 2015, 15, 59–66. [Google Scholar] [CrossRef]
- Krief, M.; Feigel, A. Variance and shift of transition arrays for electric and magnetic multipole transitions. High Energy Density Phys. 2015, 17 (Pt B), 254–262. [Google Scholar] [CrossRef]
- Krief, M.; Feigel, A.; Gazit, D. Solar opacity calculations using the super-transition-array method. Astrophys. J. 2016, 821, 45. [Google Scholar] [CrossRef]
- Bar-Shalom, A.; Oreg, J.; Goldstein, W.H.; Shvarts, D.; Zigler, A. Super-transition-arrays: A model for the spectral analysis of hot, dense plasma. Phys. Rev. A 1989, 40, 3183. [Google Scholar] [CrossRef]
- Huebner, W.F.; Barfield, W.D. Opacity; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Van Hoof, P.A.M.; Williams, R.J.R.; Volk, K.; Chatzikos, M.; Ferland, G.J.; Lykins, M.; Porter, R.L.; Wang, Y. Accurate determination of the free–free gaunt factor–i. non-relativistic gaunt factors. Mon. Not. R. Astron. Soc. 2014, 444, 420–428. [Google Scholar] [CrossRef]
- Gilleron, F.; Pain, J.-C. Efficient methods for calculating the number of states, levels and lines in atomic configurations. High Energy Density Phys. 2009, 5, 320–327. [Google Scholar] [CrossRef]
- Scott, H.A.; Hansen, S.B. Advances in NLTE modeling for integrated simulations. High Energy Density Phys. 2010, 6, 39–47. [Google Scholar] [CrossRef] [Green Version]
- Seaton, M.J.; Yan, Y.; Mihalas, D.; Pradhan, A.K. Opacities for stellar envelopes. Mon. Not. R. Astron. Soc. 1994, 266, 805–828. [Google Scholar] [CrossRef] [Green Version]
- Iglesias, C.A.; Rogers, F.J. Updated OPAL opacities. Astrophys. J. 1996, 464, 943. [Google Scholar] [CrossRef]
- Bar-Shalom, A.; Klapisch, M.; Oreg, J. HULLAC, an integrated computer package for atomic processes in plasmas. J. Quant. Spectrosc. Radiat. Transf. 2001, 71, 169–188. [Google Scholar] [CrossRef]
- Gu, M.F. The flexible atomic code. Can. J. Phys. 2008, 86, 675–689. [Google Scholar] [CrossRef]
- Fontes, C.J.; Zhang, H.L.; Abdallah, J., Jr.; Clark, R.E.H.; Kilcrease, D.P.; Colgan, J.; Cunningham, R.T.; Hakel, P.; Magee, N.H.; Sherrill, M.E. The Los Alamos suite of relativistic atomic physics codes. J. Phys. B: Atom. Mol. Opt. Phys. 2015, 48, 144014. [Google Scholar] [CrossRef]
- Moszkowski, S.A. On the energy distribution of terms and line arrays in atomic spectra. Prog. Theor. Phys. 1962, 28, 1–23. [Google Scholar] [CrossRef]
- Bauche-Arnoult, C.; Bauche, J.; Klapisch, M. Variance of the distributions of energy levels and of the transition arrays in atomic spectra. Phys. Rev. A 1979, 20, 2424. [Google Scholar] [CrossRef]
- Bauche-Arnoult, C.; Bauche, J.; Klapisch, M. Variance of the distributions of energy levels and of the transition arrays in atomic spectra. II. configurations with more than two open subshells. Phys. Rev. A 1982, 25, 2641. [Google Scholar] [CrossRef]
- Bauche-Arnoult, C.; Bauche, J.; Klapisch, M. Variance of the distributions of energy levels and of the transition arrays in atomic spectra. III. case of spin-orbit-split arrays. Phys. Rev. A 1985, 31, 2248. [Google Scholar] [CrossRef]
- Bauche-Arnoult, C.; Bauche, J. Statistical approach to the spectra of plasmas. Phys. Scr. 1992, 1992, 58. [Google Scholar] [CrossRef]
- Nikiforov, A.F.; Novikov, V.G.; Uvarov, V.B. Quantum-Statistical Models of Hot Dense Matter: Methods for Computation Opacity and Equation of State; Springer Science & Business Media: Basel, Switzerland, 2006; Volume 37. [Google Scholar]
- Liberman, D.A. Self-consistent field model for condensed matter. Phys. Rev. B 1979, 20, 4981. [Google Scholar] [CrossRef]
- Wilson, B.; Sonnad, V.; Sterne, P.; Isaacs, W. Purgatorio a new implementation of the Inferno algorithm. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 658–679. [Google Scholar] [CrossRef]
- Pénicaud, M. An average atom code for warm matter: application to aluminum and uranium. J. Phys. Condens. Matter 2009, 21, 095409. [Google Scholar] [CrossRef] [PubMed]
- Ovechkin, A.A.; Loboda, P.A.; Novikov, V.G.; Grushin, A.S.; Solomyannaya, A.D. RESEOS—A model of thermodynamic and optical properties of hot and warm dense matter. High Energy Density Phys. 2014, 13, 20–33. [Google Scholar] [CrossRef]
- Rozsnyai, B.F. Relativistic Hartree-Fock-Slater calculations for arbitrary temperature and matter density. Phys. Rev. A 1972, 5, 1137–1149. [Google Scholar] [CrossRef]
- Rozsnyai, B.F. Photoabsorption in hot plasmas based on the ion-sphere and ion-correlation models. Phys. Rev. A 1991, 43, 3035. [Google Scholar] [CrossRef] [PubMed]
- Starrett, C.E.; Saumon, D.; Daligault, J.; Hamel, S. Integral equation model for warm and hot dense mixtures. Phys. Rev. E 2014, 90, 033110. [Google Scholar] [CrossRef] [PubMed]
- Blenski, T.; Piron, R. Free-energy functional of the debye–hückel model of two-component plasmas. High Energy Density Phys. 2017, 24, 28–32. [Google Scholar] [CrossRef]
- Wilson, B.G.; Liberman, D.A.; Springer, P.T. A deficiency of local density functionals for the calculation of self-consistent field atomic data in plasmas. J. Quant. Spectrosc. Radiat. Transf. 1995, 54, 857–878. [Google Scholar] [CrossRef]
- Wilson, B.G.; Gilleron, F.; Pain, J.-C. Further stable methods for the calculation of partition functions in the superconfiguration approach. Phys. Rev. E 2007, 76, 032103. [Google Scholar] [CrossRef] [PubMed]
- Gilleron, F.; Pain, J.-C. Stable method for the calculation of partition functions in the superconfiguration approach. Phys. Rev. E 2004, 69, 056117. [Google Scholar] [CrossRef] [PubMed]
- Blancard, C.; Cossé, P.; Faussurier, G. Solar Mixture Opacity Calculations Using Detailed Configuration and Level Accounting Treatments. Astrophys. J. 2012, 745, 10. [Google Scholar] [CrossRef]







© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krief, M.; Feigel, A.; Gazit, D. A New Implementation of the STA Method for the Calculation of Opacities of Local Thermodynamic Equilibrium Plasmas. Atoms 2018, 6, 35. https://doi.org/10.3390/atoms6030035
Krief M, Feigel A, Gazit D. A New Implementation of the STA Method for the Calculation of Opacities of Local Thermodynamic Equilibrium Plasmas. Atoms. 2018; 6(3):35. https://doi.org/10.3390/atoms6030035
Chicago/Turabian StyleKrief, Menahem, Alexander Feigel, and Doron Gazit. 2018. "A New Implementation of the STA Method for the Calculation of Opacities of Local Thermodynamic Equilibrium Plasmas" Atoms 6, no. 3: 35. https://doi.org/10.3390/atoms6030035
APA StyleKrief, M., Feigel, A., & Gazit, D. (2018). A New Implementation of the STA Method for the Calculation of Opacities of Local Thermodynamic Equilibrium Plasmas. Atoms, 6(3), 35. https://doi.org/10.3390/atoms6030035




