Doubly-Excited States of Beryllium-Like Ions with Screened Coulomb Potentials
Abstract
:1. Introduction
2. Method and Calculations
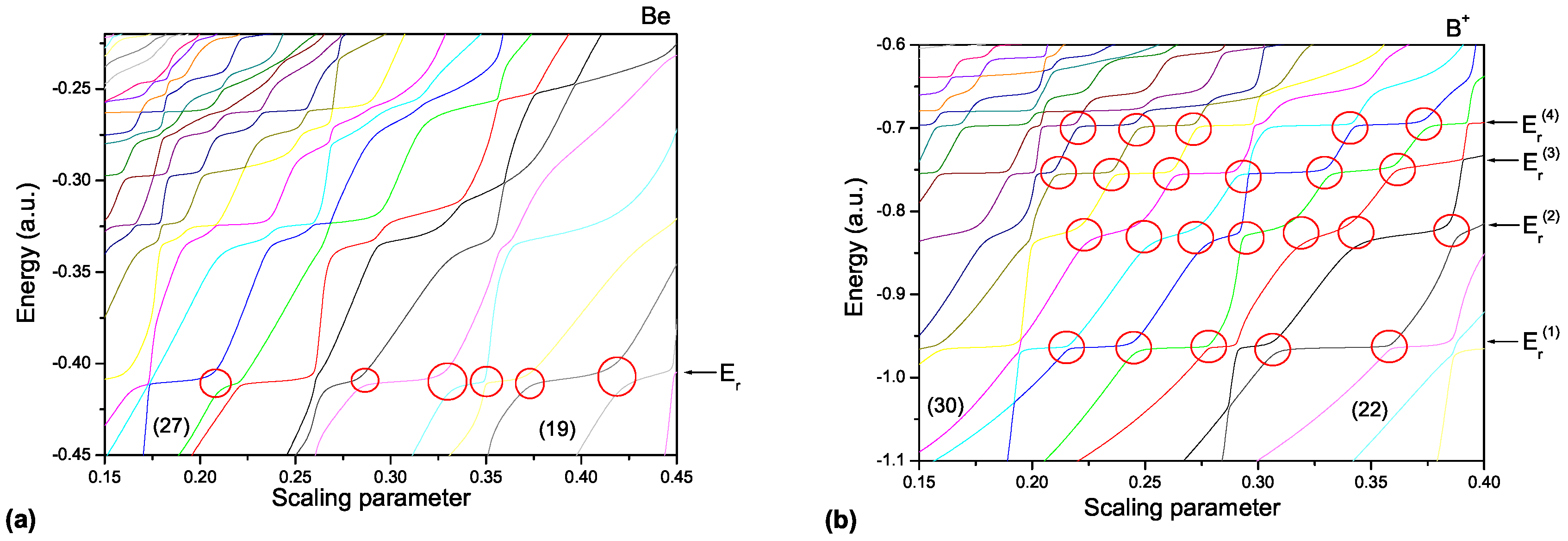
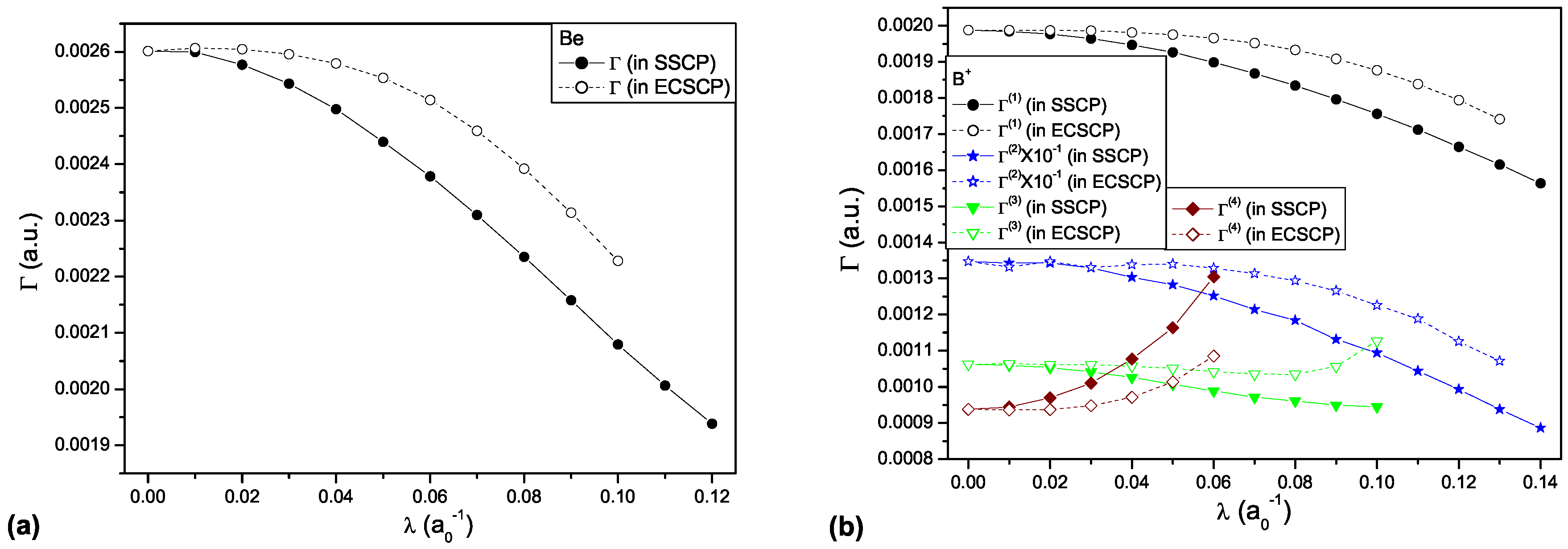
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ghoshal, A.; Ho, Y.K. Resonances below the Ps(n = 2) excitation threshold of the e+ − He(1s2s 3Se) system interacting with screened potentials. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 075001. [Google Scholar] [CrossRef]
- Janev, R.K.; Zhang, S.; Wang, J. Review of quantum collision dynamics in Debye plasmas. Matter Radiat. Extremes 2016, 1, 237–248. [Google Scholar] [CrossRef]
- Saha, J.K.; Mukherjee, T.K.; Mukherjee, P.K.; Fricke, B. Effect of strongly coupled plasma on the doubly excited states of heliumlike ions. Eur. Phys. J. D 2012, 66, 43. [Google Scholar] [CrossRef]
- Murillo, M.S.; Weisheit, J.C. Dense plasmas, screened interactions, and atomic ionization. Phys. Rep. 1998, 302, 1–65. [Google Scholar] [CrossRef]
- Weisheit, J.C. Atomic excitation in dense plasmas. Adv. At. Mol. Phys. 1989, 25, 101–131. [Google Scholar]
- Salzmann, D. Atomic Physics in Hot Plasmas; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Scheibner, K.; Weisheit, J.C.; Lane, N.F. Plasma screening effects on proton-impact excitation of positive ions. Phys. Rev. A 1987, 35, 1252. [Google Scholar] [CrossRef]
- Nguyen, H.; Koenig, M.; Benredjem, D.; Caby, M.; Coulaud, G. Atomic structure and polarization line shift in dense and hot plasmas. Phys. Rev. A 1986, 33, 1279. [Google Scholar] [CrossRef]
- Whitten, B.L.; Lane, N.F.; Weisheit, J.C. Plasma-screening effects on electron-impact excitation of hydrogenic ions in dense plasmas. Phys. Rev. A 1984, 29, 945. [Google Scholar] [CrossRef]
- Ichimaru, S. Strongly coupled plasmas: High-density classical plasmas and degenerate electron liquids. Rev. Mod. Phys. 1982, 54, 1017. [Google Scholar] [CrossRef]
- Margenau, H.; Lewis, M. Structure of Spectral Lines from Plasmas. Rev. Mod. Phys. 1959, 31, 569. [Google Scholar] [CrossRef]
- Shukla, P.K.; Eliasson, B. Screening and wake potentials of a test charge in quantum plasmas. Phys. Lett. A 2008, 372, 2897–2899. [Google Scholar] [CrossRef]
- Ghoshal, A.; Ho, Y.K. Ground states of helium in exponential-cosine-screened Coulomb potentials. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 075002. [Google Scholar] [CrossRef]
- Hall, R.L. The Yukawa and Hulthen potentials in quantum mechanics. J. Phys. A Math. Gen. 1992, 25, 1373. [Google Scholar] [CrossRef]
- Li, K.; Zhuo, L.; Gou, B. Energies, radiative rates, and Auger widths of the doubly-excited 1s2 3l3l′ states of the Be isoelectronic sequence. J. Quant. Spectrosc. Radiat. Transf. 2016, 182, 94–101. [Google Scholar] [CrossRef]
- Zajac, T.; Simulik, V.; Tymchyk, R. The Beryllium Atom Lowest Autoionizing States in the Method of Interacting Configurations in the Complex Number Representation. Int. J. Theor. Math. Phys. 2016, 6, 111–116. [Google Scholar]
- Cardona, J.C.; Sanz-Vicario, J.L. Autoionizing states in beryllium-like atomic systems using explicitly correlated coordinates. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 055003. [Google Scholar] [CrossRef]
- Roy, U.; Ho, Y.K. Computation of doubly-excited 1s2 3l3l′ 1P0 1F0 states in beryllium-like ions. Indian J. Phys. 2008, 82, 387. [Google Scholar]
- Murakami, I.; Safronova, U.I.; Kato, T. Dielectronic recombination rate coefficients to excited states of Be-like oxygen and dielectronic satellite lines. Can. J. Phys. 2002, 80, 1525–1542. [Google Scholar] [CrossRef]
- Pong, W.J.; Ho, Y.K. Doubly-excited states of beryllium-like ions. Phys. Scr. 2000, 61, 690. [Google Scholar] [CrossRef]
- Murakami, I.; Safronova, U.I.; Kato, T. Dielectronic recombination rate coefficients to excited states of Ne VII from Ne VIII. J. Phys. B At. Mol. Opt. Phys. 1999, 32, 5331. [Google Scholar] [CrossRef]
- Pong, W.J.; Ho, Y.K. Calculations of doubly excited states of beryllium-like ions using the stabilization method. J. Phys. B At. Mol. Opt. Phys. 1998, 31, 2177. [Google Scholar] [CrossRef]
- Safronova, U.; Kato, T.; Ohira, M. Dielectronic recombination rate coefficients to the excited states of CIII from CIV. J. Quant. Spectrosc. Radiat. Transf. 1997, 58, 193. [Google Scholar] [CrossRef]
- Van der Hart, H.W.; Hansen, J.E. Competition between radiative and non-radiative decay for the doubly-excited ls2 3lnl′ states in O4+. J. Phys. B At. Mol. Opt. Phys. 1993, 26, 3297. [Google Scholar] [CrossRef]
- Van der Hart, H.W.; Hansen, J.E. Calculations of doubly-excited states in He, N5+ and N3+ using B-splines. J. Phys. B At. Mol. Opt. Phys. 1992, 25, 41. [Google Scholar] [CrossRef]
- Lengyel, V.I.; Navrotsky, V.T.; Sabad, E.P. Resonant scattering of low-energy electrons by Be+ and Mg+ ions. J. Phys. B At. Mol. Opt. Phys. 1990, 23, 2847. [Google Scholar] [CrossRef]
- Bachau, H.; Galan, P. Resonance parameters and properties of Beryllium-like Doubly excited states: 4 ≤ Z ≤ 10. At. Data Nucl. Data Tables 1990, 44, 305–348. [Google Scholar] [CrossRef]
- Bachau, H.; Galan, P.; Martin, F. Feshbach-model potential approach for the study of resonant and bound states of Be-like ions. Phys. Rev. A 1990, 41, 3534. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Lin, C.D. Calculations of energies of intrashell doubly excited states of beryllium-like ions. J. Phys. B At. Mol. Opt. Phys. 1989, 22, 2875. [Google Scholar] [CrossRef]
- Vaeck, N.; Hansen, J.E. Calculations for 1s2 3l3l′ states in C2+, N3+, O4+, Ne6+ and Xe50+. J. Phys. B At. Mol. Opt. Phys. 1989, 22, 3137. [Google Scholar] [CrossRef]
- Bordenave-Montesquieu, A.; Moretto-Capelle, P.; Bordenave-Montesquieu, D. An accurate test of calculated positions and lifetimes for Ne6+ (1s2 3lnl′) 1L states (n = 3 and 4) using a high-resolution electron spectroscopy. Nucl. Instrum. Meth. Phys. Res. B 2003, 205, 74–77. [Google Scholar] [CrossRef]
- Bordenave-Montesquieu, A.; Moretto-Capelle, P.; Bordenave-Montesquieu, D. High-resolution electron spectroscopy of the 1s2 3lnl′ Be-like series in oxygen and neon. Test of theoretical data: I. Experimental method and theoretical background. J. Phys. B At. Mol. Opt. Phys. 2003, 36, 47. [Google Scholar] [CrossRef]
- Bordenave-Montesquieu, A.; Moretto-Capelle, P.; Bordenave-Montesquieu, D. High-resolution electron spectroscopy of the 1s2 3lnl′ Be-like series in oxygen and neon. Test of theoretical data: II. Experimental results. J. Phys. B At. Mol. Opt. Phys. 2003, 36, 65. [Google Scholar] [CrossRef]
- Bordenave-Montesquieu, A.; Moretto-Capelle, P.; Bordenave-Montesquieu, D. Experimental positions and lifetimes of Be-like 1s2 3lnl′ (n = 3 to 5) states of O4+ and Ne6+ ions investigated by high resolution electron spectroscopy: Test of calculations. Phys. Scr. 1999, 80, 372. [Google Scholar] [CrossRef]
- Kitazawa, S.; Tanabe, K.; Machida, S.; Matsui, Y.; Ida, H.; Takayanagi, T.; Wakiya, K.; Iemura, K.; Currell, F.; Ohtani, S.; et al. Electron spectra from singlet and triplet states of N3+ (1s2 3l3l′ and 1s2 3l4l′) produced by low-energy N5+ + He, Ne and Ar collisions. J. Phys. B At. Mol. Opt. Phys. 1998, 31, 3233. [Google Scholar] [CrossRef]
- Nakamura, N.; Ida, H.; Matsui, Y.; Wakiya, K.; Takayanagi, T.; Koide, M.; Currell, F.J.; Kitazawa, S.; Suzuki, H.; Ohtani, S.; et al. Electron spectra from singlet and triplet states of O4+ (1s2 3l3l′, 1s2 3l4l′) produced by 60 and 120 keV O6+ + He, Ne, Ar collisions. J. Phys. B At. Mol. Opt. Phys. 1995, 28, 4743. [Google Scholar] [CrossRef]
- Nakamura, N.; Nabeshima, T.; Currell, F.J.; Kanai, Y.; Kitazawa, S.; Koide, M.; Sakaue, H.A.; Ida, H.; Matsui, Y.; Wakiya, K.; et al. Ejected-electron spectra from the triplet states of O4+ (1s2 3l3l′) produced by O6 + O2 collisions. J. Phys. B At. Mol. Opt. Phys. 1994, 27, L785. [Google Scholar] [CrossRef]
- Clark, C.W.; Fassett, J.D.; Lucatorto, T.B.; Moore, L.J. Observation of autoionizing states of beryllium by resonance-ionizationmass spectrometry. J. Opt. Soc. Am. B 1985, 2, 891–896. [Google Scholar] [CrossRef]
- Cavaliere, P.; Ferrante, G. Model-Potential Theory of Positron-Alkali-Atom Bound States. I: Ground-State Energy and Atomic Properties. Nuovo Cimento 1973, 14, 127–146. [Google Scholar] [CrossRef]
- Hilbert, A. Model potentials in atomic structure. Adv. At. Mol. Phys. 1982, 18, 309–340. [Google Scholar]
- Laughlin, C.; Victor, G.A. Model-Potential methods. Adv. At. Mol. Phys. 1988, 25, 163–194. [Google Scholar]
- Schweizer, W.; Fabbinder, P. Model potentials for alkali metal atoms and li-like ions. At. Data Nucl. Data Tables 1999, 72, 33–55. [Google Scholar] [CrossRef]
- Ghoshal, A.; Ho, Y.K. Autoionization states of the positronium negative ion in exponential cosine-screened Coulomb potentials. Eur. Phys. J. D 2010, 56, 151–156. [Google Scholar] [CrossRef]
- Ghoshal, A.; Ho, Y.K. Doubly excited resonance states of helium in exponential cosine-screened Coulomb potentials. Phys. Rev. A. 2009, 79, 062514. [Google Scholar] [CrossRef]
- Ghoshal, A.; Ho, Y.K. Properties of the Positronium Negative Ion Interacting with Exponential Cosine-Screened Coulomb Potentials. Few-Body Syst. 2009, 46, 249–256. [Google Scholar] [CrossRef]
- Fang, T.K.; Ho, Y.K. Determination of resonance energies and widths of Mg 3pnl 1De and 1F0 doubly excited states by the stabilization method with the B-spline-based configuration interaction approach. J. Phys. B At. Mol. Opt. Phys. 1999, 32, 3863. [Google Scholar] [CrossRef]
- Tan, S.S.; Ho, Y.K. Determination of Resonance Energy and Width by Calculation of the Density of Reesonance States Using the Stabilisation Method. Chin. J. Phys. 1997, 35, 701–707. [Google Scholar]
- Bowman, J.M. Collision lifetime approach to recombination and a new derivation of RRKM theory. J. Phys. Chem. 1986, 90, 3492–3495. [Google Scholar] [CrossRef]
- Bashkin, S.; Stoner, J.O. Atomic Energy Levels and Gotrian Diagrams; North-Holland: Amsterdam, The Netherlands, 1975; Volume 1. [Google Scholar]
- Chung, K.T. Ionization potential of the lithiumlike 1s2 2s states from lithium to neon. Phys. Rev. A 1991, 44, 5421. [Google Scholar] [CrossRef] [PubMed]
- Kelly, R.L. Atomic and Ionic Spectrum Lines below 2000 Angstrom: Hydrogen through Krypton Part I (H-Cr). J. Phys. Chem. Ref. Data 1987, 16, 1. [Google Scholar]


| (in | nl | |||||
|---|---|---|---|---|---|---|
| A | B | A | B | |||
| 0.0 | 2s | 0.66964102 | 0.66964102 | 1.39474181 | 1.39474181 | |
| 0.669246 | 0.669246 | 1.3936211 | 1.3936211 | |||
| 1.394522 | 1.394522 | |||||
| 2p | 0.52430329 | 0.52430329 | 1.17584781 | 1.17584781 | ||
| 0.523768 | 0.523768 | |||||
| 3s | 0.26775134 | 0.26775134 | 0.57384421 | 0.57384421 | ||
| 0.267233 | 0.267233 | |||||
| 3p | 0.22998134 | 0.22998134 | 0.51587898 | 0.51587898 | ||
| 0.229582 | 0.229582 | |||||
| 3d | 0.22240325 | 0.22240325 | 0.50052384 | 0.50052384 | ||
| 0.222478 | 0.222478 | |||||
| 4s | 0.14340301 | 0.14340301 | 0.31137200 | 0.31137200 | ||
| 0.143153 | 0.143153 | |||||
| 4p | 0.12833340 | 0.12833340 | 0.28803005 | 0.28803005 | ||
| 0.128134 | 0.128134 | |||||
| 4d | 0.12510394 | 0.12510394 | 0.28154683 | 0.28154683 | ||
| 0.125124 | 0.125124 | |||||
| 0.02 | 2s | 0.62984556 | 0.62898469 | 1.33486968 | 1.33392802 | |
| 2p | 0.48484262 | 0.48395393 | 1.11620861 | 1.11529802 | ||
| 3s | 0.22974020 | 0.22776016 | 0.51592131 | 0.51376335 | ||
| 3p | 0.19217000 | 0.19007265 | 0.45805733 | 0.45585483 | ||
| 3d | 0.18441982 | 0.18255588 | 0.44255868 | 0.44062172 | ||
| 4s | 0.10723572 | 0.10391841 | 0.25541166 | 0.25171891 | ||
| 4p | 0.09242998 | 0.08894775 | 0.23221675 | 0.22842460 | ||
| 4d | 0.08900850 | 0.08569234 | 0.22553449 | 0.22195201 | ||
| 0.05 | 2s | 0.57337057 | 0.56838958 | 1.24858165 | 1.24301496 | |
| 2p | 0.42898087 | 0.42386046 | 1.03015901 | 1.02477217 | ||
| 3s | 0.18011693 | 0.16985931 | 0.43708142 | 0.42525691 | ||
| 3p | 0.14331425 | 0.13260204 | 0.37954810 | 0.36752946 | ||
| 3d | 0.13444727 | 0.12462687 | 0.36285344 | 0.35206529 | ||
| 4s | 0.06551481 | 0.05095356 | 0.18528180 | 0.16713958 | ||
| 4p | 0.05183304 | 0.03695721 | 0.16272235 | 0.14425590 | ||
| 4d | 0.04755823 | 0.03299501 | 0.15499158 | 0.13723551 | ||
| 0.07 | 2s | 0.53775806 | 0.52848185 | 1.19331404 | 1.18279881 | |
| 2p | 0.39384940 | 0.38433489 | 0.97498406 | 0.96480121 | ||
| 3s | 0.15142686 | 0.13370041 | 0.38944296 | 0.36820744 | ||
| 3p | 0.11541419 | 0.09707969 | 0.33224471 | 0.31071264 | ||
| 3d | 0.10539851 | 0.08820589 | 0.31422331 | 0.29461566 | ||
| 4s | 0.04461574 | 0.02256958 | 0.14651563 | 0.11634361 | ||
| 4p | 0.03210162 | 0.01027558 | 0.12463246 | 0.09412611 | ||
| 4d | 0.02717185 | 0.00537842 | 0.11590575 | 0.08618019 | ||
| Energy | Width | ||||||
|---|---|---|---|---|---|---|---|
| Be | −0.40998 | −0.40989 | −0.40990 | 0.0027581 | 0.0026238 | 0.002602 | |
| −0.96376 | −0.96379 | −0.96374 | 0.0019519 | 0.0019713 | 0.001988 | ||
| Be | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Present | 0.40990 | 0.00260 | 0.96374 | 0.00199 | 0.82887 | 0.01347 | 0.75457 | 0.00106 | 0.69710 | 0.00094 | |
| (a) | 0.40817 | 0.00295 | |||||||||
| (b) | 0.40891 | 0.00301 | |||||||||
| (c) | 0.4105 | 0.00365 | 0.9638 | 0.00312 | 0.8246 | 0.01301 | 0.7541 | 0.00156 | 0.6974 | 0.00119 | |
| Be | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.40990 | 0.00260 | 0.96374 | 0.00199 | 0.82887 | 0.01347 | 0.75457 | 0.00106 | 0.69710 | 0.00094 | |
| 0.01 | 0.38051 | 0.00260 | 0.91447 | 0.00198 | 0.77974 | 0.01343 | 0.70576 | 0.00106 | 0.64822 | 0.00094 | |
| 0.01 | 0.37981 | 0.00261 | 0.91359 | 0.00199 | 0.77879 | 0.01332 | 0.70449 | 0.00106 | 0.64711 | 0.00094 | |
| 0.03 | 0.32589 | 0.00254 | 0.82117 | 0.00196 | 0.68692 | 0.01330 | 0.61566 | 0.00104 | 0.55710 | 0.00101 | |
| 0.03 | 0.32008 | 0.00260 | 0.81380 | 0.00199 | 0.67926 | 0.01330 | 0.60561 | 0.00106 | 0.54811 | 0.00095 | |
| 0.05 | 0.27654 | 0.00244 | 0.73450 | 0.00193 | 0.60107 | 0.01283 | 0.53475 | 0.00101 | 0.47432 | 0.00116 | |
| 0.05 | 0.26181 | 0.00255 | 0.71549 | 0.00198 | 0.58136 | 0.01340 | 0.51017 | 0.00105 | 0.45181 | 0.00101 | |
| 0.07 | 0.23215 | 0.00231 | 0.65407 | 0.00187 | 0.52183 | 0.01214 | 0.46226 | 0.00097 | |||
| 0.07 | 0.20596 | 0.00246 | 0.61954 | 0.00195 | 0.48611 | 0.01314 | 0.41994 | 0.00104 | |||
| 0.09 | 0.19242 | 0.00216 | 0.57956 | 0.00180 | 0.44878 | 0.01131 | 0.39751 | 0.00095 | |||
| 0.09 | 0.15347 | 0.00231 | 0.52673 | 0.00191 | 0.39440 | 0.01266 | 0.33657 | 0.00106 | |||
| 0.10 | 0.17422 | 0.00208 | 0.54444 | 0.00176 | 0.41453 | 0.01094 | 0.36787 | 0.00095 | |||
| 0.10 | 0.12876 | 0.00223 | 0.48172 | 0.00188 | 0.35014 | 0.01226 | 0.29793 | 0.00113 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghoshal, A.; Ho, Y.K. Doubly-Excited States of Beryllium-Like Ions with Screened Coulomb Potentials. Atoms 2018, 6, 41. https://doi.org/10.3390/atoms6030041
Ghoshal A, Ho YK. Doubly-Excited States of Beryllium-Like Ions with Screened Coulomb Potentials. Atoms. 2018; 6(3):41. https://doi.org/10.3390/atoms6030041
Chicago/Turabian StyleGhoshal, Arijit, and Yew Kam Ho. 2018. "Doubly-Excited States of Beryllium-Like Ions with Screened Coulomb Potentials" Atoms 6, no. 3: 41. https://doi.org/10.3390/atoms6030041
APA StyleGhoshal, A., & Ho, Y. K. (2018). Doubly-Excited States of Beryllium-Like Ions with Screened Coulomb Potentials. Atoms, 6(3), 41. https://doi.org/10.3390/atoms6030041






