Atomic and Molecular Processes in a Strong Bicircular Laser Field
Abstract
:1. Introduction: Three-Step Model and Bicircular Laser Field
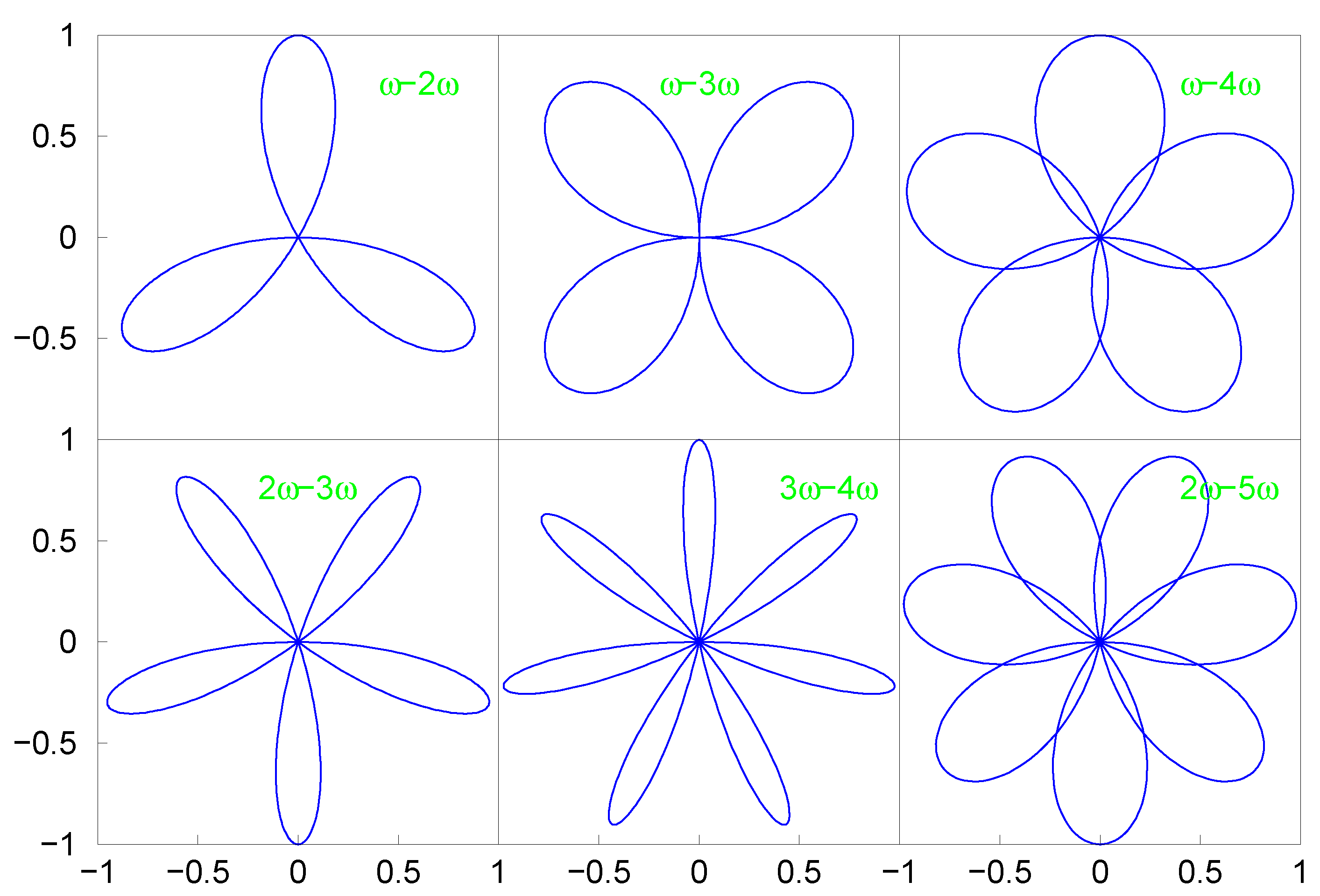
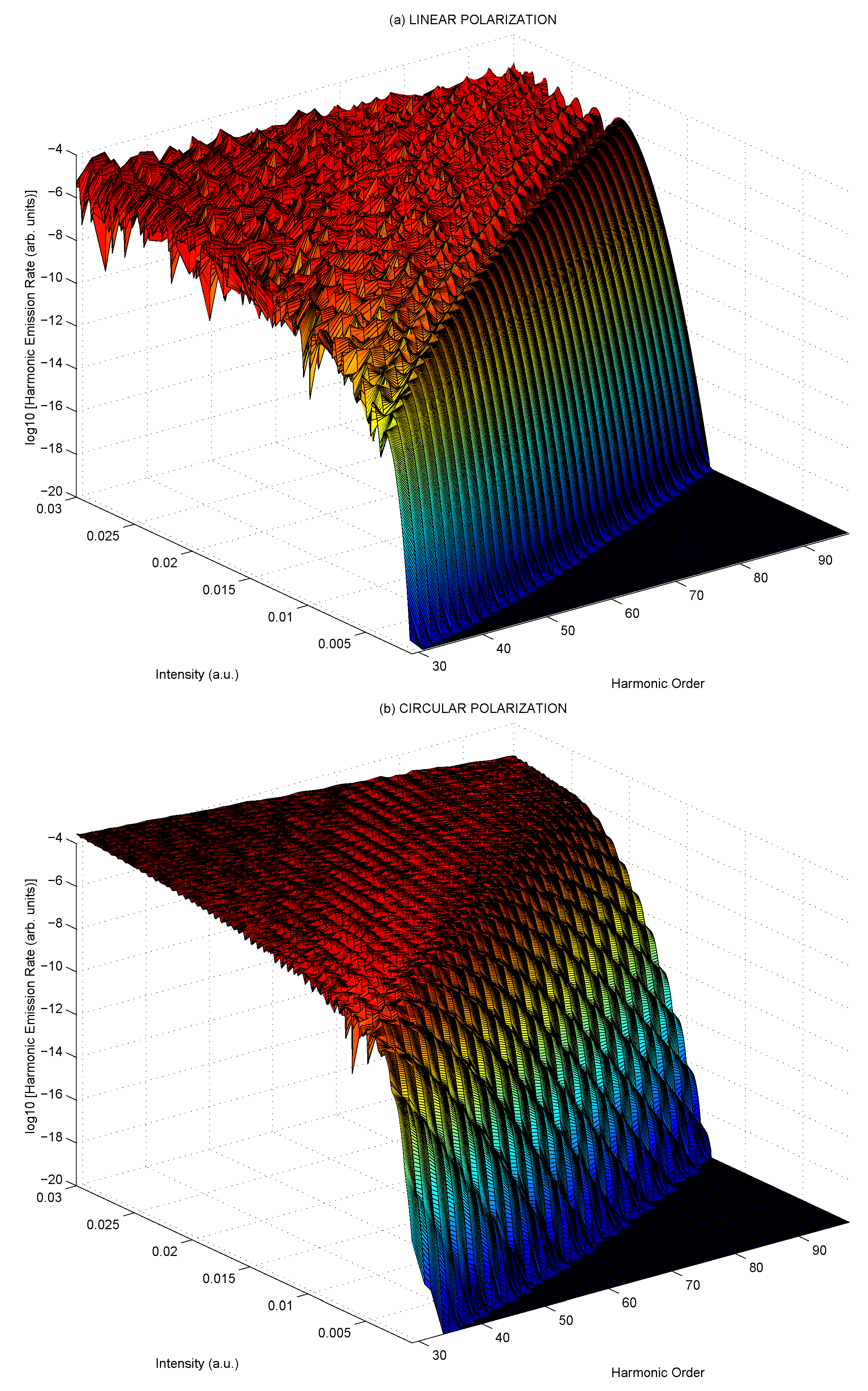
2. Results for High-Order Harmonic Generation by Bicircular Field
3. Spin Asymmetry in Above-Threshold Ionization by Bicircular Field
4. Conclusions
Funding
Conflicts of Interest
References
- Kohler, M.; Pfeifer, T.; Hatsagortsyan, K.; Keitel, C. Frontiers of Atomic High-Harmonic Generation. Adv. At. Mol. Opt. Phys. 2012, 61, 159–208. [Google Scholar] [CrossRef]
- Becker, W.; Goreslavski, S.P.; Milošević, D.B.; Paulus, G.G. The plateau in above-threshold ionization: The keystone of rescattering physics. J. Phys. B 2018, 51, 162002. [Google Scholar] [CrossRef]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schafer, K.J.; Yang, B.; DiMauro, L.F.; Kulander, K.C. Above threshold ionization beyond the high harmonic cutoff. Phys. Rev. Lett. 1993, 70, 1599–1602. [Google Scholar] [CrossRef] [PubMed]
- Paulus, G.G.; Becker, W.; Nicklich, W.; Walther, H. Rescattering effects in above-threshold ionization: A classical model. J. Phys. B 1994, 27, L703–L708. [Google Scholar] [CrossRef]
- Becker, W.; Grasbon, F.; Kopold, R.; Milošević, D.B.; Paulus, G.G.; Walther, H. Above-threshold ionization: From classical features to quantum effects. Adv. At. Mol. Opt. Phys. 2002, 48, 35–98. [Google Scholar]
- Scrinzi, A.; Ivanov, M.Y.; Kienberger, R.; Villeneuve, D.M. Attosecond physics. J. Phys. B 2006, 39, R1–R37. [Google Scholar] [CrossRef]
- Milošević, D.B.; Paulus, G.G.; Bauer, D.; Becker, W. Above-threshold ionization by few-cycle pulses. J. Phys. B 2006, 39, R203–R262. [Google Scholar] [CrossRef]
- Kling, M.F.; Vrakking, M.J.J. Attosecond electron dynamics. Annu. Rev. Phys. Chem. 2008, 59, 463–492. [Google Scholar] [CrossRef] [PubMed]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef]
- Ueda, K.; Ishikawa, K.L. Attosecond science: Attoclocks play devil’s advocate. Nat. Phys. 2011, 7, 371–372. [Google Scholar] [CrossRef]
- Calegari, F.; Sansone, G.; Stagira, S.; Vozzi, C.; Nisoli, M. Advances in attosecond science. J. Phys. B 2016, 49, 062001. [Google Scholar] [CrossRef] [Green Version]
- Eichmann, H.; Egbert, A.; Nolte, S.; Momma, C.; Wellegehausen, B.; Becker, W.; Long, S.; McIver, J.K. Polarization-dependent high-order two-color mixing. Phys. Rev. A 1995, 51, R3414–R3417. [Google Scholar] [CrossRef] [PubMed]
- Long, S.; Becker, W.; McIver, J.K. Model calculations of polarization-dependent two-color high-harmonic generation. Phys. Rev. A 1995, 52, 2262–2278. [Google Scholar] [CrossRef] [PubMed]
- Odžak, S.; Hasović, E.; Becker, W.; Milošević, D.B. Atomic processes in bicircular fields. J. Mod. Opt. 2017, 64, 971–980. [Google Scholar] [CrossRef]
- Milošević, D.B. Quantum-orbit analysis of high-order harmonic generation by bicircular field. J. Mod. Opt. 2018, 66, 47–58. [Google Scholar] [CrossRef]
- Kramo, A.; Hasović, E.; Milošević, D.B.; Becker, W. Above-threshold detachment by a two-color bicircular laser field. Laser Phys. Lett. 2007, 4, 279–286. [Google Scholar] [CrossRef]
- Hasović, E.; Kramo, A.; Milošević, D.B. Energy- and angle-resolved photoelectron spectra of above-threshold ionizationand detachment. Eur. Phys. J. Spec. Top. 2008, 160, 205–216. [Google Scholar] [CrossRef]
- Hasović, E.; Milošević, D.B.; Becker, W. A method of carrier-envelope phase control for few-cycle laser pulses. Laser Phys. Lett. 2006, 3, 200–204. [Google Scholar] [CrossRef]
- Mancuso, C.A.; Hickstein, D.D.; Grychtol, P.; Knut, R.; Kfir, O.; Tong, X.M.; Dollar, F.; Zusin, D.; Gopalakrishnan, M.; Gentry, C.; et al. Strong-field ionization with two-color circularly polarized laser fields. Phys. Rev. A 2015, 91, 031402. [Google Scholar] [CrossRef] [Green Version]
- Hasović, E.; Becker, W.; Milošević, D.B. Electron rescattering in a bicircular laser field. Opt. Express 2016, 24, 6413–6424. [Google Scholar] [CrossRef] [PubMed]
- Milošević, D.B.; Becker, W. Improved strong-field approximation and quantum-orbit theory: Application to ionization by a bicircular laser field. Phys. Rev. A 2016, 93, 063418. [Google Scholar] [CrossRef]
- Hoang, V.-H.; Le, V.-H.; Lin, C.D.; Le, A.-T. Retrieval of target structure information from laser-induced photoelectrons by few-cycle bicircular laser fields. Phys. Rev. A 2017, 95, 031402. [Google Scholar] [CrossRef]
- Mancuso, C.A.; Hickstein, D.D.; Dorney, K.M.; Ellis, J.L.; Hasović, E.; Knut, R.; Grychtol, P.; Gentry, C.; Gopalakrishnan, M.; Zusin, D.; et al. Controlling electron-ion rescattering in two-color circularly polarized femtosecond laser fields. Phys. Rev. A 2016, 93, 053406. [Google Scholar] [CrossRef] [Green Version]
- Mancuso, C.A.; Dorney, K.M.; Hickstein, D.D.; Chaloupka, J.I.; Tong, X.-M.; Ellis, J.L.; Kapteyn, H.C.; Murnane, M.M. Observation of ionization enhancement in two-color circularly polarized laser fields. Phys. Rev. A 2017, 96, 023402. [Google Scholar] [CrossRef] [Green Version]
- Milošević, D.B.; Becker, W.; Kopold, R. Generation of circularly polarized high-order harmonics by two-color coplanar field mixing. Phys. Rev. A 2000, 61, 063403. [Google Scholar] [CrossRef]
- Milošević, D.B.; Bauer, D.; Becker, W. Quantum-orbit theory of high-order atomic processes in intense laser fields. J. Mod. Opt. 2006, 53, 125–134. [Google Scholar] [CrossRef]
- Fleischer, A.; Kfir, O.; Diskin, T.; Sidorenko, P.; Cohen, O. Spin angular momentum and tunable polarization in high-harmonic generation. Nat. Photonics 2014, 8, 543–549. [Google Scholar] [CrossRef]
- Cireasa, R.; Boguslavskiy, A.E.; Pons, B.; Wong, M.C.H.; Descamps, D.; Petit, S.; Ruf, H.; Thiré, N.; Ferré, A.; Suarez, J.; et al. Probing molecular chirality on a sub-femtosecond timescale. Nat. Phys. 2015, 11, 654–658. [Google Scholar] [CrossRef]
- Nahon, L.; Nag, L.; Garcia, G.A.; Myrgorodska, I.; Meierhenrich, U.; Beaulieu, S.; Wanie, V.; Blanchet, V.; Geneaux, R.; Powis, I. Determination of accurate electron chiral asymmetries in fenchone and camphor in the VUV range: Sensitivity to isomerism and enantiomeric purity. Phys. Chem. Chem. Phys. 2016, 18, 12696–12706. [Google Scholar] [CrossRef] [PubMed]
- Fan, T.; Grychtol, P.; Knut, R.; Hernández-García, C.; Hickstein, D.D.; Zusin, D.; Gentry, C.; Dollar, F.J.; Mancuso, C.A.; Hogle, C.; et al. Bright circularly polarized soft X-ray high harmonics for X-ray magnetic circular dichroism. Proc. Natl. Acad. Sci. USA 2015, 112, 14206–14211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kfir, O.; Zayko, S.; Nolte, C.; Sivis, M.; Möller, M.; Hebler, B.; Arekapudi, S.S.P.K.; Steil, D.; Schäfer, S.; Albrecht, M.; et al. Nanoscale magnetic imaging using circularly polarized high-harmonic radiation. Sci. Adv. 2017, 3, eaao4641. [Google Scholar] [CrossRef] [PubMed]
- Milošević, D.B.; Becker, W. Attosecond pulse trains with unusual nonlinear polarization. Phys. Rev. A 2000, 62, 011403. [Google Scholar] [CrossRef]
- Chen, C.; Tao, Z.; Hernández-García, C.; Matyba, P.; Carr, A.; Knut, R.; Kfir, O.; Zusin, D.; Gentry, C.; Grychtol, P.; et al. Tomographic reconstruction of circularly polarized high-harmonic fields: 3D attosecond metrology. Sci. Adv. 2016, 2, e1501333. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Milošević, D.B.; Becker, W.; Kopold, R.; Sandner, W. High-Harmonic Generation by a Bichromatic Bicircular Laser Field. Laser Phys. 2001, 11, 165–168. [Google Scholar]
- Milošević, D.B. Generation of elliptically polarized attosecond pulse trains. Opt. Lett. 2015, 40, 2381–2384. [Google Scholar] [CrossRef] [PubMed]
- Medišauskas, L.; Wragg, J.; van der Hart, H.; Ivanov, M.Y. Generating isolated elliptically polarized attosecond pulses using bichromatic counterrotating circularly polarized laser fields. Phys. Rev. Lett. 2015, 115, 153001. [Google Scholar] [CrossRef] [PubMed]
- Milošević, D.B. Circularly polarized high harmonics generated by a bicircular field from inert atomic gases in the p state: A tool for exploring chirality-sensitive processes. Phys. Rev. A 2015, 92, 043827. [Google Scholar] [CrossRef]
- Odžak, S.; Milošević, D.B. Bicircular-laser-field-assisted electron-ion radiative recombination. Phys. Rev. A 2015, 92, 053416. [Google Scholar] [CrossRef]
- Milošević, D.B.; Becker, W. Role of long quantum orbits in high-order harmonic generation. Phys. Rev. A 2002, 66, 063417. [Google Scholar] [CrossRef]
- Milošević, D.B.; Ehlotzky, F. Scattering and reaction processes in powerful laser field. Adv. At. Mol. Opt. Phys. 2003, 49, 373–532. [Google Scholar]
- Milošević, D.B. Control of the helicity of high-order harmonics generated by bicircular laser fields. Phys. Rev. A 2018, 98, 033405. [Google Scholar] [CrossRef]
- Milošević, D.B. Possibility of introducing spin into attoscience with spin-polarized electrons produced by a bichromatic circularly polarized laser field. Phys. Rev. A 2016, 93, 051402. [Google Scholar] [CrossRef]
- Milošević, D.B. Spin-dependent effects in high-order above-threshold ionization: Spin-orbit interaction and exchange effects. J. Phys. B 2017, 50, 164003. [Google Scholar] [CrossRef]
- Ayuso, D.; Jiménez-Galán, A.; Morales, F.; Ivanov, M.; Smirnova, O. Attosecond control of spin polarization in electron-ion recollision driven by intense tailored fields. New J. Phys. 2017, 19, 073007. [Google Scholar] [CrossRef]
- Hasović, E.; Busuladžić, M.; Gazibegović-Busuladžić, A.; Milošević, D.B.; Becker, W. Simulation of Above-Threshold Ionization Experiments Using the Strong-Field Approximation. Laser Phys. 2007, 17, 376–389. [Google Scholar] [CrossRef]
- Milošević, D.B.; Becker, W.; Okunishi, M.; Prümper, G.; Shimada, K.; Ueda, K. Strong-field electron spectra of rare-gas atoms in the rescattering regime: Enhanced spectral regions and a simulation of the experiment. J. Phys. B 2010, 43, 015401. [Google Scholar] [CrossRef]
- Baykusheva, D.; Ahsan, M.S.; Lin, N.; Wörner, H.J. Bicircular High-Harmonic Spectroscopy Reveals Dynamical Symmetries of Atoms and Molecules. Phys. Rev. Lett. 2016, 116, 123001. [Google Scholar] [CrossRef] [PubMed]
- Mauger, F.; Bandrauk, A.D.; Uzer, T. Circularly polarized molecular high harmonic generation using a bicircular laser. J. Phys. B 2016, 49, 10LT01. [Google Scholar] [CrossRef]
- Reich, D.M.; Madsen, L.B. Illuminating Molecular Symmetries with Bicircular High-Order-Harmonic Generation. Phys. Rev. Lett. 2016, 117, 133902. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhu, X.; Li, L.; Li, Y.; Zhang, Q.; Lan, P.; Lu, P. Selection rules of high-order-harmonic generation: Symmetries of molecules and laser fields. Phys. Rev. A 2016, 94, 033410. [Google Scholar] [CrossRef]
- Odžak, S.; Hasović, E.; Milošević, D.B. High-order harmonic generation in polyatomic molecules induced by a bicircular laser field. Phys. Rev. A 2016, 94, 033419. [Google Scholar] [CrossRef]
- Hasović, E.; Odžak, S.; Becker, W.; Milošević, D.B. High-order harmonic generation in non-planar molecules driven by a bicircular field. Mol. Phys. 2017, 115, 1750–1757. [Google Scholar] [CrossRef]
- Gay, T.J. Physics and technology of polarized electron scattering from atoms and molecules. Adv. At. Mol. Opt. Phys. 2009, 57, 157–247. [Google Scholar] [CrossRef]
- Žutić, I.; Fabian, J.; Das Sarma, S. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 2004, 76, 323–410. [Google Scholar] [CrossRef] [Green Version]
- Barth, I.; Smirnova, O. Spin-polarized electrons produced by strong-field ionization. Phys. Rev. A 2013, 88, 013401. [Google Scholar] [CrossRef]
- Herath, T.; Yan, L.; Lee, S.K.; Li, W. Strong-field ionization rate depends on the sign of the magnetic quantum number. Phys. Rev. Lett. 2012, 109, 043004. [Google Scholar] [CrossRef] [PubMed]
- Barth, I.; Smirnova, O. Comparison of theory and experiment for nonadiabatic tunneling in circularly polarized fields. Phys. Rev. A 2013, 87, 065401. [Google Scholar] [CrossRef]
- Hartung, A.; Morales, F.; Kunitski, M.; Henrichs, K.; Laucke, A.; Richter, M.; Jahnke, T.; Kalinin, A.; Schöffler, M.; Schmidt, L.P.H.; et al. Electron spin polarization in strong-field ionization of xenon atoms. Nat. Photonics 2016, 10, 526–528. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.-M.; Shao, Y.; Han, M.; Ge, P.; Deng, Y.; Wu, C.; Gong, Q.; Liu, Y. Energy- and Momentum-Resolved Photoelectron Spin Polarization in Multiphoton Ionization of Xe by Circularly Polarized Fields. Phys. Rev. Lett. 2018, 120, 043201. [Google Scholar] [CrossRef] [PubMed]
- Trabert, D.; Hartung, A.; Eckart, S.; Trinter, F.; Kalinin, A.; Schöffler, M.; Schmidt, L.P.H.; Jahnke, T.; Kunitski, M.; Dörner, R. Spin and Angular Momentum in Strong-Field Ionization. Phys. Rev. Lett. 2018, 120, 043202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Milošević, D.B.; Becker, W. Channel-closing effects in strong-field ionization by a bicircular field. J. Phys. B 2018, 51, 054001. [Google Scholar] [CrossRef] [Green Version]
- Busuladžić, M.; Gazibegović-Busuladžić, A.; Milošević, D.B.; Becker, W. Angle-Resolved High-Order Above-Threshold Ionization of a Molecule: Sensitive Tool for Molecular Characterization. Phys. Rev. Lett. 2008, 100, 203003. [Google Scholar] [CrossRef] [PubMed]
- Okunishi, M.; Itaya, R.; Shimada, K.; Prümper, G.; Ueda, K.; Busuladžić, M.; Gazibegović-Busuladžić, A.; Milošević, D.B.; Becker, W. Two-Source Double-Slit Interference in Angle-Resolved High-Energy Above-Threshold Ionization Spectra of Diatoms. Phys. Rev. Lett. 2009, 103, 043001. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milošević, D.B. Atomic and Molecular Processes in a Strong Bicircular Laser Field. Atoms 2018, 6, 61. https://doi.org/10.3390/atoms6040061
Milošević DB. Atomic and Molecular Processes in a Strong Bicircular Laser Field. Atoms. 2018; 6(4):61. https://doi.org/10.3390/atoms6040061
Chicago/Turabian StyleMilošević, Dejan B. 2018. "Atomic and Molecular Processes in a Strong Bicircular Laser Field" Atoms 6, no. 4: 61. https://doi.org/10.3390/atoms6040061
APA StyleMilošević, D. B. (2018). Atomic and Molecular Processes in a Strong Bicircular Laser Field. Atoms, 6(4), 61. https://doi.org/10.3390/atoms6040061




