Optical Rotation Approach to Search for the Electric Dipole Moment of the Electron
Abstract
:1. Introduction
2. Theory of the ,-Odd Faraday Effect
3. Application to Transitions in Different Atomic Species
3.1. Ra Atom ()
3.2. Pb Atom ()
- (1)
- The first one is the E1 with the transition wavelength nm. We employ the value for the eEDM enhancement factor of the state from [18]: . Assuming K and employing s, according to Equation (19) s. The natural line width for the chosen transition is s [49]. For V/cm, e cm and from Equation (28) it followsThe necessary column density appears to be cm. This result shows that the best possible estimate for the eEDM with the maximum modern sensitivity achievement ( rad [40]) would be still an order of magnitude above the value quoted in [13].
- (2)
- Now we consider the M1 transition with nm. Here we also employ the value for the eEDM enhancement factor of the state from [18]: . Assuming K and employing s, according to Equation (19) s. The natural line width for the chosen transition (for the metastable state) is s according to [49]. Let us estimate the value of the collisional broadening according to Equation (4). The characteristic value for the collisional cross-section is cm [41]. Then in terms of density we obtain s. So in this case the dimensionless . It appears that for cm the collisional broadening mechanism dominates over the natural broadening one. Since now the maximum rotation angle (Equation (28)) (optimal for the experiment) depends on () and the column density according to Equation (26) is not fixed (the fixed quantity is , i.e., ) then let us employ the maximum feasible value for the optical path lengths in our estimates. In [39] path length of 70,000 km for the cavity of the same size as in [38] was reported. If such a large electric field ( V/cm) can be implemented in the cavity in a volume of a several centimetres size then the optical path length appears to be cm. It corresponds to the optimal number density, according to Equation (26), cm. Then, for e cm and from Equation (28) it followsThus, if to assume the record sensitivity [40] and the record optical path length [39], then the lead atom appears to be a good candidate for improving the eEDM bound by 2 orders of magnitude.
3.3. Tl Atom ()
3.4. Hg Atom ()
- (1)
- The first one is from the metastable state to the excited state with nm. The population of the lower metastable level can be obtained with the laser pumping [38]. The eEDM enhancement factors were calculated in [42] and . In [42] factors are presented for definite hyperfine levels. Here these values are recalculated for the levels and . The natural line width for the chosen transition is s [49]. Assuming the room temperature K and employing the transition frequency value s, according to Equation (19) we obtain the value for the Doppler width s. For V/cm, e cm and from Equation (28) it followsThe necessary column density appears to be cm. This result shows that the best possible estimate for the eEDM with the maximum modern sensitivity achievement (∼ rad [40]) would be still 2 orders of magnitude above the value quoted in [13].
- (2)
- The second transition of E1 type is from the ground to the metastable state with nm. According to [42], . Employing s, according to Equation (19), s. The natural line width for the chosen transition is s. For V/cm, e cm and from Equation (28) it followsThe necessary column density appears to be cm. This result shows that the best possible estimate for the eEDM with the maximum modern sensitivity achievement (∼ rad [40]) could give the same upper bound for eEDM as already quoted in [13].
3.5. Cs Atom ()
3.6. Xe Atom ()
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pospelov, M.; Khriplovich, I. Electric dipole moment of the W boson and the electron in the Kobayashi-Maskawa model. Sov. Nucl. Phys. 1991, 53, 638. [Google Scholar]
- Salpeter, E.E. Some atomic effects of an electronic electric dipole moment. Phys. Rev. 1958, 112, 1642. [Google Scholar] [CrossRef]
- Sandars, P.G.H. The electric dipole moment of an atom. Phys. Lett. 1965, 14, 194. [Google Scholar] [CrossRef]
- Sandars, P.G.H. The search for violation of P or T invariance in atoms or molecules. At. Phys. 1975, 4, 71. [Google Scholar]
- Gorshkov, V.G.; Labzowsky, L.N.; Moskalev, A.N. Space and time parity nonconservation effects in the diatomic molecule spectra. Sov. Phys. JETP 1979, 49, 209. [Google Scholar]
- Pospelov, M.; Ritz, A. CKM benchmarks for electron electric dipole moment experiments. Phys. Rev. D 2014, 89, 056006. [Google Scholar] [CrossRef]
- Chubukov, D.V.; Labzowsky, L.N. P, T-odd electron-nucleus interaction in atomic systems as an exchange by Higgs bosons. Phys. Rev. A 2016, 93, 062503. [Google Scholar] [CrossRef]
- Bondarevskaya, A.A.; Chubukov, D.V.; Andreev, O.Y.; Mistonova, E.A.; Labzowsky, L.N.; Plunien, G.; Liesen, D.; Bosch, F. On the electric dipole moment of the electron and the P, T-odd electron-nucleus interaction in highly-charged heavy ions. J. Phys. B 2015, 48, 144007. [Google Scholar] [CrossRef]
- Ginges, J.S.; Flambaum, V.V. Violations of fundamental symmetries in atoms and tests of unification theories of elementary particles. Phys. Rep. 2004, 397, 63–154. [Google Scholar] [CrossRef]
- Regan, B.C.; Commins, E.D.; Schmidt, C.J.; DeMille, D. New limit on the electron electric dipole moment. Phys. Rev. Lett. 2002, 88, 071805. [Google Scholar] [CrossRef]
- Hudson, J.J.; Kara, D.M.; Smallman, I.J.; Sauer, B.E.; Tarbutt, M.R.; Hinds, E.A. Improved measurement of the shape of the electron. Nature 2011, 473, 493. [Google Scholar] [CrossRef] [PubMed]
- Baron, J.; Campbell, W.C.; DeMille, D.; Doyle, J.M.; Gabrielse, G.; Gurevich, Y.V.; Hess, P.W.; Hutzler, N.R.; Kirilov, E.; Kozyryev, I.; et al. Order of magnitude smaller limit on the electric dipole moment of the electron. Science 2014, 343, 269–272. [Google Scholar]
- Andreev, V.; Hutzler, N.R. Improved limit on the electric dipole moment of the electron. Nature 2018, 562, 355–360. [Google Scholar]
- Cairncross, W.B.; Gresh, D.N.; Grau, M.; Cossel, K.C.; Roussy, T.S.; Ni, Y.; Zhou, Y.; Ye, J.; Cornell, E.A. Precision measurement of the electron’s electric dipole moment using trapped molecular ions. Phys. Rev. Lett. 2017, 119, 153001. [Google Scholar] [CrossRef]
- Liu, Z.W.; Kelly, H.P. Analysis of atomic electric dipole moment in thallium by all-order calculations in many-body perturbation theory. Phys. Rev. A 1992, 45, R4210(R). [Google Scholar] [CrossRef]
- Dzuba, V.A.; Flambaum, V.V. Calculation of the (T,P)-odd electric dipole moment of thallium and cesium. Phys. Rev. A 2009, 80, 062509. [Google Scholar] [CrossRef]
- Porsev, S.G.; Safronova, M.S.; Kozlov, M.G. Electric dipole moment enhancement factor of thallium. Phys. Rev. Lett. 2012, 108, 173001. [Google Scholar] [CrossRef]
- Chubukov, D.V.; Skripnikov, L.V.; Labzowsky, L.N. P,T-odd Faraday rotation in heavy neutral atoms. Phys. Rev. A 2018, 97, 062512. [Google Scholar] [CrossRef]
- Quiney, H.M.; Skaane, H.; Grant, I.P. Hyperfine and PT-odd effects in YbF. J. Phys. B 1998, 31, 85. [Google Scholar] [CrossRef]
- Parpia, F. Ab initio calculation of the enhancement of the electric dipole moment of an electron in the YbF molecule. J. Phys. B 1998, 31, 1409. [Google Scholar] [CrossRef]
- Mosyagin, N.S.; Kozlov, M.G.; Titov, A.V. Electric dipole moment of the electron in the YbF molecule. J. Phys. B At. Mol. Opt. Phys. 1998, 31, L763. [Google Scholar] [CrossRef]
- Abe, M.; Gopakumar, G.; Hada, M.; Das, B.P.; Tatewaki, H.; Mukherjee, D. Application of relativistic coupled-cluster theory to the effective electric field in YbF. Phys. Rev. A 2014, 90, 022501. [Google Scholar] [CrossRef]
- Skripnikov, L.V.; Petrov, A.N.; Titov, A.V. Communication: Theoretical study of ThO for the electron electric dipole moment search. J. Chem. Phys. 2013, 139, 221103. [Google Scholar] [CrossRef] [Green Version]
- Skripnikov, L.V.; Titov, A.V. Theoretical study of thorium monoxide for the electron electric dipole moment search: Electronic properties of H3Δ1 in ThO. J. Chem. Phys. 2015, 142, 024301. [Google Scholar] [CrossRef] [PubMed]
- Skripnikov, L.V. Combined 4-component and relativistic pseudopotential study of ThO for the electron electric dipole moment search. J. Chem. Phys. 2016, 145, 214301. [Google Scholar] [CrossRef] [PubMed]
- Denis, M.; Fleig, T. In search of discrete symmetry violations beyond the standard model: Thorium monoxide reloaded. J. Chem. Phys. 2016, 145, 214307. [Google Scholar] [CrossRef] [PubMed]
- Petrov, A.N.; Mosyagin, N.S.; Isaev, T.A.; Titov, A.V. Theoretical study of HfF+ in search of the electron electric dipole moment. Phys.Rev. A 2007, 76, 030501(R). [Google Scholar] [CrossRef]
- Skripnikov, L.V. Communication: Theoretical study of HfF+ cation to search for the T,P-odd interactions. J. Chem. Phys. 2017, 147, 021101. [Google Scholar] [CrossRef] [PubMed]
- Fleig, T. P,T-odd and magnetic hyperfine-interaction constants and excited-state lifetime for HfF+. Phys. Rev. A 2017, 96, 040502. [Google Scholar] [CrossRef]
- Petrov, A.N.; Skripnikov, L.V.; Titov, A.V.; Flambaum, V.V. Evaluation of C P violation in HfF+. Phys. Rev. A 2018, 98, 042502. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B. Parity nonconservation in the first Order in the weak-interaction constant in electron scattering and other Effects. Sov. Phys. JETP 1959, 9, 682. [Google Scholar]
- Khriplovich, I.B. Feasibility of observing parity nonconservation in atomic transitions. Sov. Phys. JETP Letters 1974, 20, 315. [Google Scholar]
- Barkov, L.M.; Zolotorev, M.S. Observation of parity non-conservation in atomic transitions. Sov. Phys. 1978, 27, 357. [Google Scholar]
- Baranova, N.B.; Bogdanov, Y.V.; Zel’dovich, B.Y. New electro-optical and magneto-optical effects in liquids. Sov.Phys.Usp 1977, 20, 870. [Google Scholar] [CrossRef]
- Sushkov, O.P.; Flambaum, V.V. Parity breaking effects in diatomic molecules. Sov. Phys. JETP 1978, 48, 608. [Google Scholar]
- Budker, D.; Gawlik, W.; Kimball, D.; Rochester, S.M.; Yashchuk, V.; Weis, A. Resonant nonlinear magneto-optical effects in atoms. Rev. Mod. Phys. 2002, 74, 1153. [Google Scholar] [CrossRef]
- Chubukov, D.V.; Labzowsky, L.N. P,T-odd Faraday effect in intracavity absorption spectroscopy. Phys. Rev. A 2017, 96, 052105. [Google Scholar] [CrossRef]
- Bougas, L.; Katsoprinakis, G.E.; von Klitzing, W.; Rakitzis, T.P. Fundamentals of cavity-enhanced polarimetry for parity-nonconserving optical rotation measurements: Application to Xe, Hg, and I. Phys. Rev. A 2014, 89, 052127. [Google Scholar] [CrossRef]
- Baev, V.M.; Latz, T.; Toschek, P.E. Laser intracavity absorption spectroscopy. Appl. Phys. B 1999, 69, 171–202. [Google Scholar] [CrossRef]
- Durand, M.; Morville, J.; Romanini, D. Shot-noise-limited measurement of sub-parts-per-trillion birefringence phase shift in a high-finesse cavity. Phys. Rev. A 2010, 82, 031803. [Google Scholar] [CrossRef]
- Khriplovich, I.B. Parity Nonconservation in Atomic Phenomena; Gordon and Breach: London, UK, 1991. [Google Scholar]
- Chubukov, D.V.; Skripnikov, L.V.; Labzowsky, L.N.; Kutuzov, V.N.; Chekhovskoi, S.D. Evaluation of the P,T-odd Faraday effect in Xe and Hg atoms. Phys. Rev. A 2019, 99, 052515. [Google Scholar] [CrossRef]
- Johnson, W.R.; Guo, D.S.; Idrees, M.; Sapirstein, J. Weak-interaction effects in heavy atomic systems. II. Phys.Rev. A 1986, 34, 1043. [Google Scholar] [CrossRef]
- Lindroth, E.; Lynn, B.W.; Sandars, P.G.H. Order α2 theory of the atomic electric dipole moment due to an electric dipole moment on the electron. J. Phys. B 1989, 22, 559. [Google Scholar] [CrossRef]
- Skripnikov, L.V.; Titov, A.V.; Petrov, A.N.; Mosyagin, N.S.; Sushkov, O.P. Enhancement of the electron electric dipole moment in Eu2+. Phys. Rev. A 2011, 84, 022505. [Google Scholar] [CrossRef]
- Skripnikov, L.V.; Maison, D.E.; Mosyagin, N.S. Scalar-pseudoscalar interaction in the francium atom. Phys. Rev. A 2017, 95, 022507. [Google Scholar] [CrossRef] [Green Version]
- Roberts, G.J.; Baird, P.E.G.; Brimicombe, M.W.S.M.; Sandars, P.G.H.; Selby, D.R.; Stacey, D.N. The Faraday effect and magnetic circular dichroism in atomic bismuth. J. Phys. B At. Mol. Phys. 1980, 13, 1389. [Google Scholar] [CrossRef]
- Scielzo, N.D.; Guest, J.R.; Schulte, E.C.; Ahmad, I.; Bailey, K.; Bowers, D.L.; Holt, R.J.; Lu, Z.-T.; O’Connor, T.P.; Potterveld, D.H. Measurement of the lifetimes of the lowest 3P1 state of neutral Ba and Ra. Phys. Rev. A 2006, 73, 010501(R). [Google Scholar] [CrossRef]
- Radzig, A.A.; Smirnov, B.M. Reference Data on Atoms, Molecules, and Ions; Springer: Berlin, Germany, 1985. [Google Scholar]

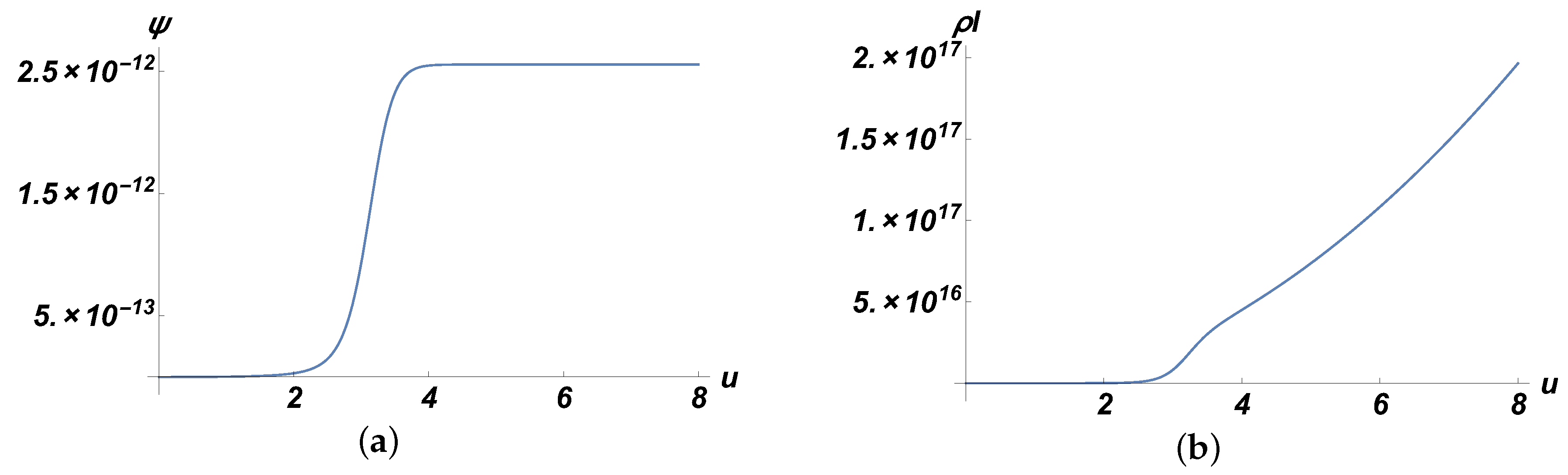
| Atom | Transition | Wavelength | Linewidth | Column Density | Rotation Angle |
|---|---|---|---|---|---|
| , nm | , s | , cm | , rad | ||
| Ra | (M1) | 714 | |||
| Pb | (E1) | 283 | |||
| Pb | (M1) | 1279 | 7 | ||
| Tl | (M1) | 1283 | 4 | ||
| Hg | (E1) | 436 | |||
| Hg | (E1) | 254 | |||
| Cs | (E1) | 895 | |||
| Xe | (E1) | 980 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chubukov, D.V.; Skripnikov, L.V.; Kutuzov, V.N.; Chekhovskoi, S.D.; Labzowsky, L.N. Optical Rotation Approach to Search for the Electric Dipole Moment of the Electron. Atoms 2019, 7, 56. https://doi.org/10.3390/atoms7020056
Chubukov DV, Skripnikov LV, Kutuzov VN, Chekhovskoi SD, Labzowsky LN. Optical Rotation Approach to Search for the Electric Dipole Moment of the Electron. Atoms. 2019; 7(2):56. https://doi.org/10.3390/atoms7020056
Chicago/Turabian StyleChubukov, Dmitry V., Leonid V. Skripnikov, Vasily N. Kutuzov, Sergey D. Chekhovskoi, and Leonti N. Labzowsky. 2019. "Optical Rotation Approach to Search for the Electric Dipole Moment of the Electron" Atoms 7, no. 2: 56. https://doi.org/10.3390/atoms7020056
APA StyleChubukov, D. V., Skripnikov, L. V., Kutuzov, V. N., Chekhovskoi, S. D., & Labzowsky, L. N. (2019). Optical Rotation Approach to Search for the Electric Dipole Moment of the Electron. Atoms, 7(2), 56. https://doi.org/10.3390/atoms7020056





