Laboratory Courses on Laser Spectroscopy and Atom Trapping
Abstract
:1. Introduction
2. Course Format
3. Description of Experiments
3.1. Emission and Absorption Spectroscopy and the Electro-Optic Phase Modulator
3.2. Zeeman Shift
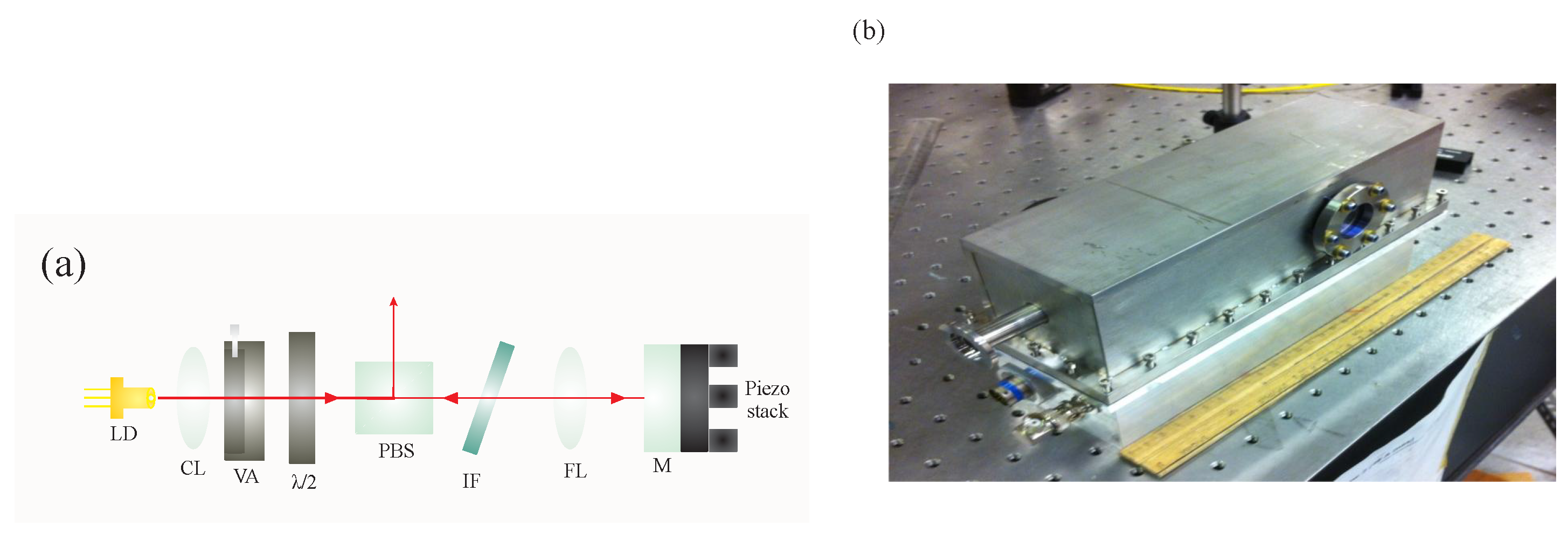
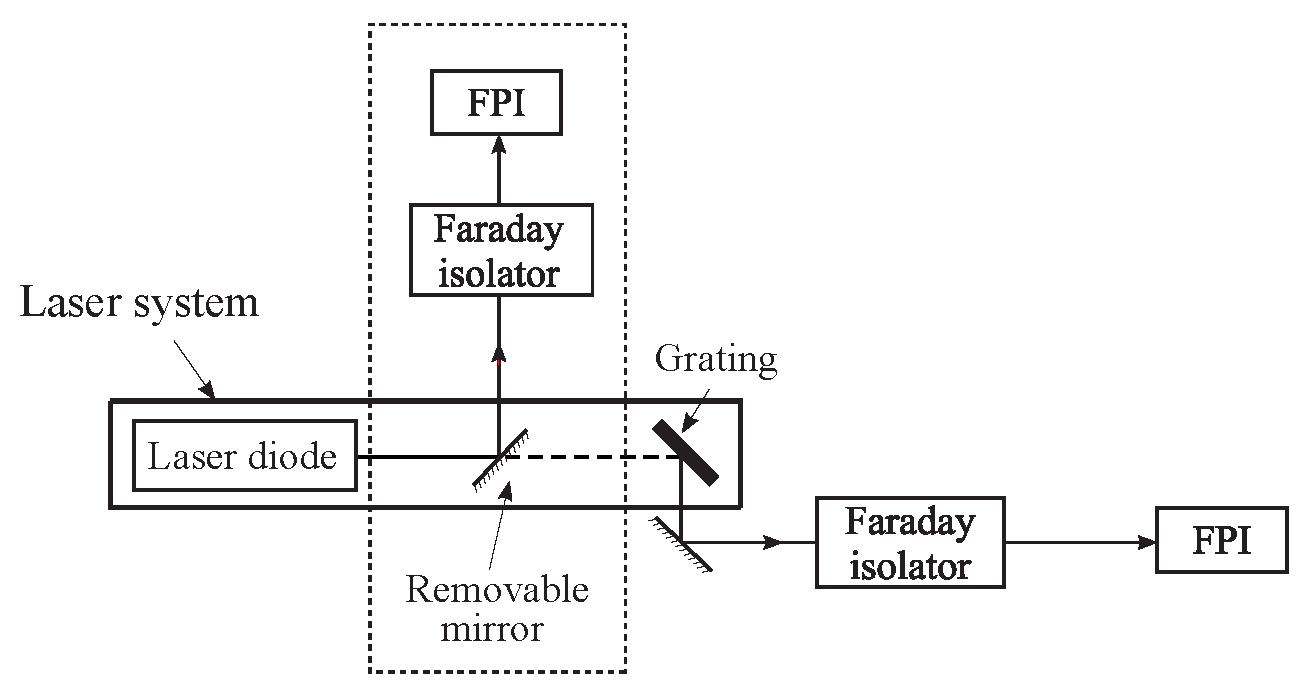
3.3. Faraday Isolator and Fabry-Pérot Interferometry
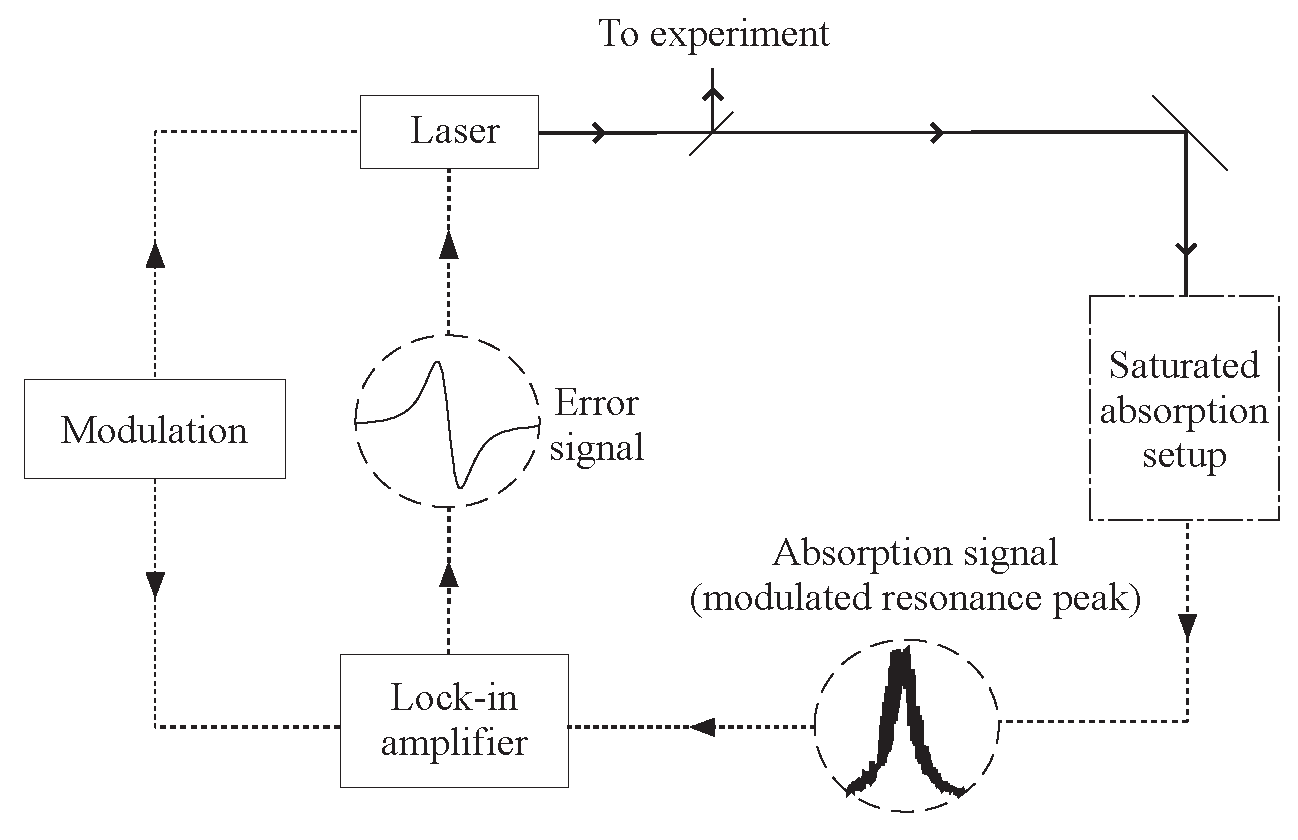
3.4. Laser Frequency Stabilization and the Lock-In Amplifier
3.5. Radio Frequency Components and Optical Heterodyne Detection
3.6. Optical Detectors
3.7. Gaussian Beam Propagation and Optical Fiber Coupling
3.8. Vacuum Components and Pumping Techniques
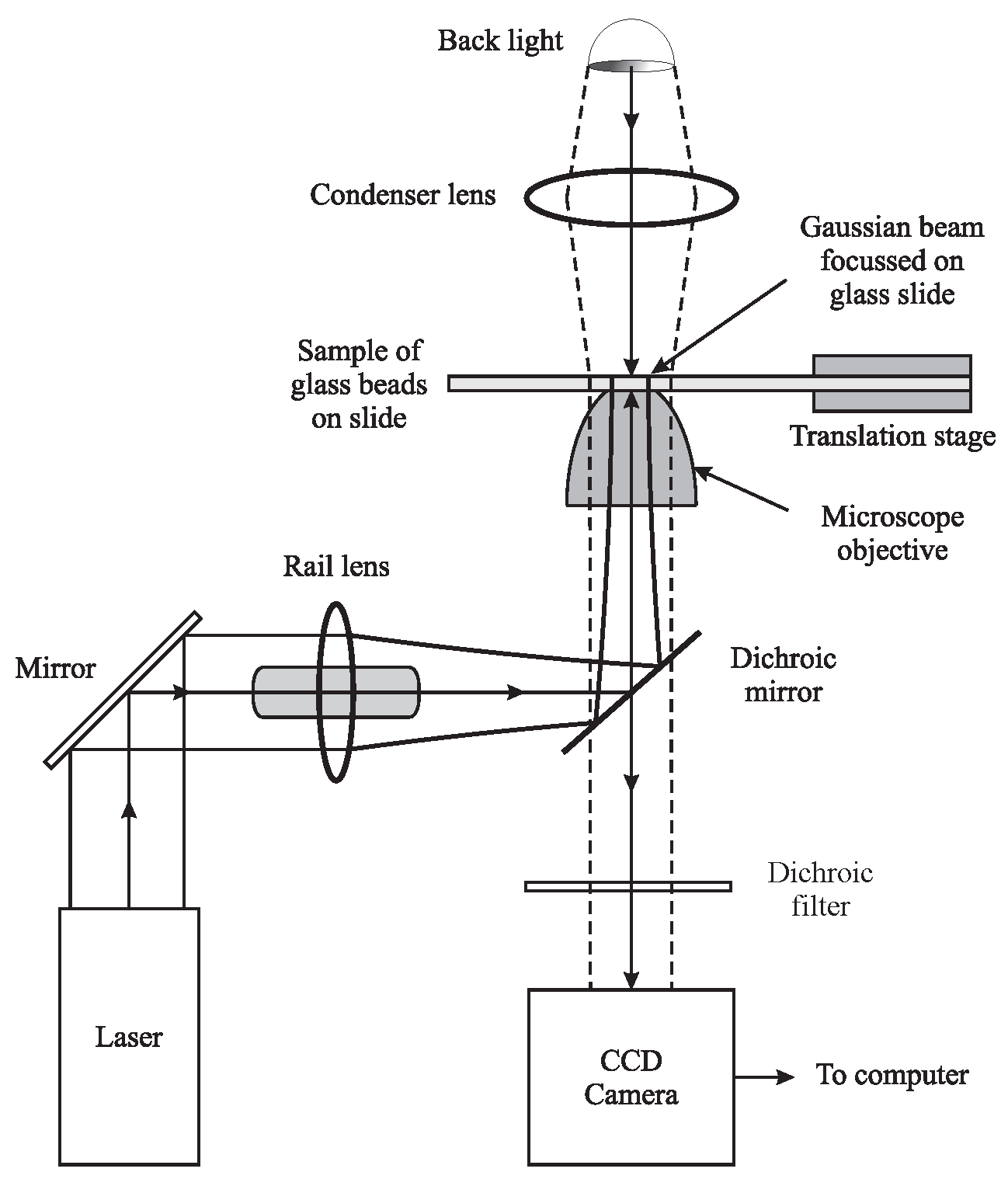
3.9. Optical Tweezers
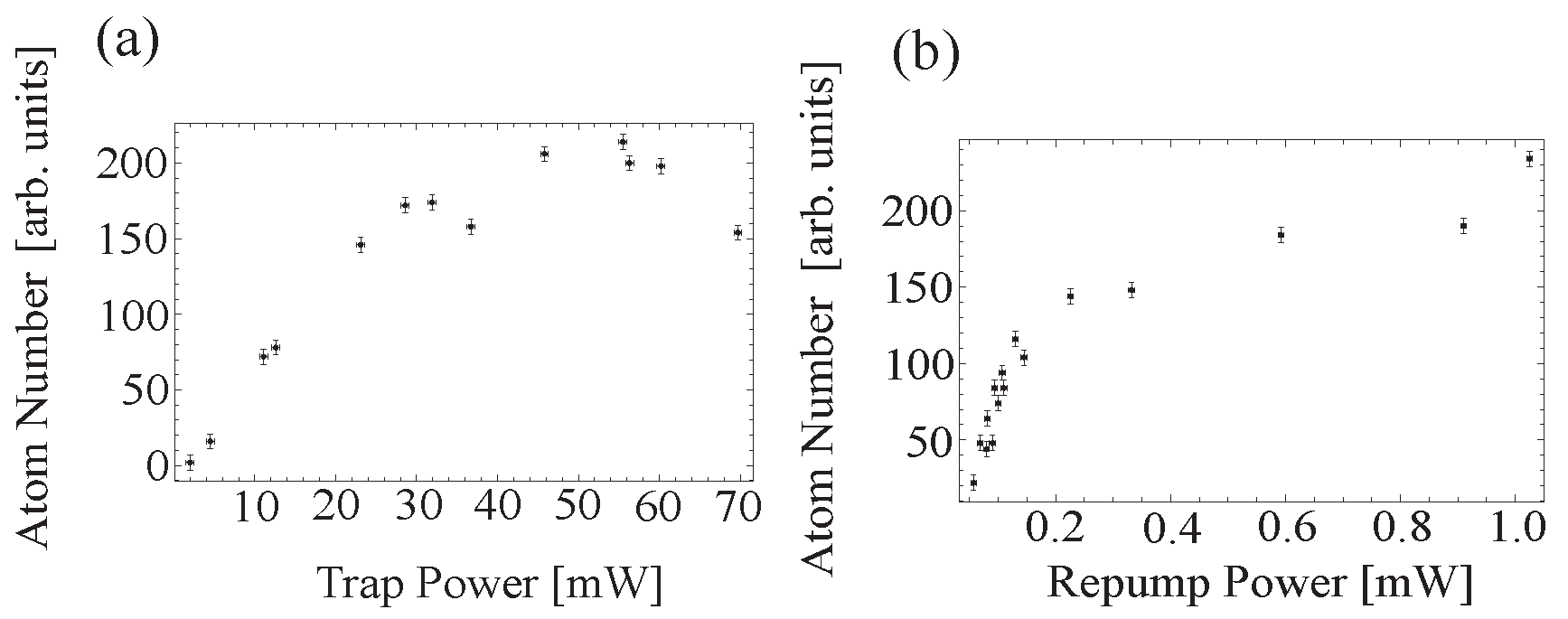
3.10. Atom Trapping in a MOT
3.11. Experiments with Laser Cooled Atoms
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Monroe, C.; Swann, W.; Robinson, H.; Wieman, C. Very cold trapped atoms in a vapor cell. Phys. Rev. Lett. 1990, 65, 1571. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raab, E.L.; Prentiss, M.; Cable, A.; Chu, S.; Pritchard, D.E. Trapping of neutral sodium atoms with radiation pressure. Phys. Rev. Lett. 1987, 59, 2631. [Google Scholar] [CrossRef] [Green Version]
- Ricci, L.; Weidemuller, M.; Esslinger, T.; Hemmerich, A.; Zimmermann, C.; Vuletic, V.; Konig, W.; Hänsch, T.W. A compact grating-stabilized diode laser system for atomic physics. Opt. Commun. 1995, 117, 541. [Google Scholar] [CrossRef] [Green Version]
- MacAdam, K.; Steinbach, A.; Wieman, C. A narrow-band tunable diode laser system with grating feedback, and a saturated absorption spectrometer for Cs and Rb. Am. J. Phys. 1992, 60, 1098. [Google Scholar] [CrossRef] [Green Version]
- Weiman, C.; Hollberg, L. Using diode lasers for atomic physics. Rev. Sci. Instrum. 1991, 62, 1. [Google Scholar] [CrossRef] [Green Version]
- Libbecht, K.G.; Boyd, R.A.; Williams, P.A.; Gustavson, T.L.; Kim, D.K. Teaching physics with 670 nm diode lasers—construction of stabilized lasers and lithium cells. Am. J. Phys. 1995, 63, 729. [Google Scholar] [CrossRef]
- Carr, A.V.; Sechrest, Y.H.; Waitukaitis, S.R.; Perreaulta, J.D.; Lonij, V.P.A.; Cronin, A.D. Cover slip external cavity diode laser. Rev. Sci. Instrum. 2007, 78, 106108. [Google Scholar] [CrossRef] [Green Version]
- Baillard, X.; Gauguet, A.; Bize, S.; Lemonde, P.; Laurent, P.; Clairon, A.; Rosenbusch, P. Interference-filter-stabilized external-cavity diode lasers. Opt. Commun. 2006, 266, 609. [Google Scholar] [CrossRef] [Green Version]
- Gilowski, M.; Schubert, C.; Zaiser, M.; Herr, W.; Wubbena, T.; Wendrich, T.; Muller, T.; Rasel, E.M.; Ertmer, W. Narrow bandwidth interference filter-stabilized diode laser systems for the manipulation of neutral atoms. Opt. Commun. 2007, 280, 443. [Google Scholar] [CrossRef] [Green Version]
- Phillips, W.D. Nobel Lecture: Laser cooling and trapping of neutral atoms. Rev. Mod. Phys. 1998, 70, 721. [Google Scholar] [CrossRef] [Green Version]
- Cohen-Tannoudji, C.N. Nobel Lecture: Manipulating atoms with photons. Rev. Mod. Phys. 1998, 70, 707. [Google Scholar] [CrossRef] [Green Version]
- Chu, S. Nobel Lecture: The manipulation of neutral particles. Rev. Mod. Phys. 1998, 70, 685. [Google Scholar] [CrossRef]
- Ketterle, W. Nobel lecture: When atoms behave as waves: Bose-Einstein condensation and the atom laser. Rev. Mod. Phys. 2002, 74, 1131. [Google Scholar] [CrossRef] [Green Version]
- Cornell, E.A.; Wieman, C.E. Nobel Lecture: Bose-Einstein condensation in a dilute gas, the first 70 years and some recent experiments. Rev. Mod. Phys. 2002, 74, 875. [Google Scholar] [CrossRef] [Green Version]
- Hänsch, T.W. Nobel lecture: Passion for precision. Rev. Mod. Phys. 2006, 78, 1297. [Google Scholar] [CrossRef] [Green Version]
- Hall, J.L. Nobel Lecture: Defining and measuring optical frequencies. Rev. Mod. Phys. 2006, 78, 1279. [Google Scholar] [CrossRef] [Green Version]
- Glauber, R.J. Nobel Lecture: One hundred years of light quanta. Rev. Mod. Phys. 2006, 78, 1267. [Google Scholar] [CrossRef] [Green Version]
- Haroche, S. Nobel Lecture: Controlling photons in a box and exploring the quantum to classical boundary. Rev. Mod. Phys. 2013, 85, 1083. [Google Scholar] [CrossRef] [Green Version]
- Wineland, D.J. Nobel Lecture: Superposition, entanglement, and raising Schrödinger’s cat. Rev. Mod. Phys. 2013, 91, 1103. [Google Scholar] [CrossRef]
- Ashkin, A. NobelPrize.org. Nobel Media AB. 2019. Available online: https://www.nobelprize.org/prizes/physics/2018/ashkin/lecture/ (accessed on 16 March 2019).
- Mourou, G. Nobel Lecture: Extreme light physics and application. Rev. Mod. Phys. 2019, 85, 1103. [Google Scholar] [CrossRef]
- Strickland, D. Nobel Lecture: Generating high-intensity ultrashort optical pulses. Rev. Mod. Phys. 2019, 91, 030502. [Google Scholar] [CrossRef]
- Peters, A.; Chung, K.; Chu, S. Measurement of gravitational acceleration by dropping atoms. Nature 1999, 400, 849. [Google Scholar] [CrossRef]
- Kasevich, M.; Chu, S. Atomic interferometry using stimulated Raman transitions. Phys. Rev. Lett. 1991, 67, 181. [Google Scholar] [CrossRef]
- McGuirk, J.M.; Foster, G.T.; Fixler, J.B.; Snadden, M.J.; Kasevich, M.A. Sensitive absolute-gravity gradiometry using atom interferometry. Phys. Rev. A 2002, 65, 033608. [Google Scholar] [CrossRef] [Green Version]
- Gustavson, T.L.; Bouyer, P.; Kasevich, M.A. Precision rotation measurements with an atom interferometer gyroscope. Phys. Rev. Lett. 1997, 78, 2046. [Google Scholar] [CrossRef] [Green Version]
- Kohel, N.Y.J.M.; Kellogg, J.R.; Maleki, L. Development of an atom-interferometer gravity gradiometer for gravity measurement from space. Appl. Phys. B 2006, 84, 647. [Google Scholar]
- Gouet, J.L.; Mehlstaubler, T.E.; Kim, J.; Merlet, S.; Clairon, A.; Landragin, A.; Santos, F.P.D. Limits to the sensitivity of a low noise compact atomic gravimeter. Appl. Phys. B 2008, 92, 133. [Google Scholar] [CrossRef] [Green Version]
- Young, B.; Bonomi, D.S.; Patterson, T.; Roller, F.; Tran, T.; Vitouchkine, A.; Gustavson, T.; Kasevich, M. Atom Optic Inertial and Gravitational Sensors; Laser Science XXIII, OSA Technical Digest, Paper LTuH1; Optical Society of America: California, CA, USA, 2007. [Google Scholar]
- Weiss, D.; Young, B.; Chu, S. Precision measurement of the photon recoil of an atom using atomic interferometry. Phys. Rev. Lett. 1993, 70, 2706. [Google Scholar] [CrossRef] [PubMed]
- Wicht, A.; Hensley, J.M.; Sarajlic, E.; Chu, S. A preliminary measurement of the fine structure constant based on atom interferometry. Phys. Scr. 2002, T102, 82. [Google Scholar] [CrossRef]
- Cladé, P.; de Mirandes, E.; Cadoret, M.; Guellati-Khxexlifa, S.; Schwob, C.; Nez, F.; Julien, L.; Biraben, F. Determination of the fine structure constant based on Bloch oscillations of ultracold atoms in a vertical optical lattice. Phys. Rev. Lett. 2006, 96, 033001. [Google Scholar] [CrossRef] [Green Version]
- Cadoret, M.; de Mirandes, E.; Cladé, P.; Guellati-Khxexlifa, S.; Schwob, C.; Nez, F.; Julien, L.; Biraben, F. Combination of Bloch oscillations with a Ramsey-Bordé interferometer: new determination of the fine structure constant. Phys. Rev. Lett. 2008, 101, 230801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fray, S.; Diez, C.A.; Hänsch, T.W.; Weitz, M. Atomic interferometer with amplitude gratings of light and its applications to atom based tests of the equivalence principle. Phys. Rev. Lett. 2004, 93, 240404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Müller, H.; Peters, A.; Chu, S. A precision measurement of the gravitational redshift by the interference of matter waves. Nature 2010, 463, 926. [Google Scholar] [CrossRef] [PubMed]
- Chou, C.; Hume, D.; Rosenband, T.; Wineland, D. Optical clocks and relativity. Science 2010, 329, 1630. [Google Scholar] [CrossRef] [Green Version]
- Wood, C.S.; Bennett, S.C.; Cho, D.; Masterson, B.P.; Roberts, J.L.; Tanner, C.E.; Wieman, C.E. Measurement of parity nonconservation and an anapole moment in cesium. Science 1997, 275, 1759. [Google Scholar] [CrossRef] [Green Version]
- Santarelli, G.; Laurent, P.; Lemonde, P.; Clairon, A.; Mann, A.G.; Chang, S.; Luiten, A.N.; Salomon, C. Quantum projection noise in an atomic fountain: A high stability cesium frequency standard. Phys. Rev. Lett. 1999, 82, 4619. [Google Scholar] [CrossRef] [Green Version]
- Gibble, K.; Chu, S. Laser-cooled Cs frequency standard and a measurement of the frequency shift due to ultracold collisions. Phys. Rev. Lett. 1993, 70, 1771. [Google Scholar] [CrossRef]
- Udem, T.; Reichert, J.; Holzwarth, R.; Hänsch, T.W. Absolute Optical Frequency Measurement of the Cesium Line with a Mode-Locked Laser. Phys. Rev. Lett. 1999, 82, 3568. [Google Scholar] [CrossRef] [Green Version]
- Udem, T.; Huber, A.; Gross, B.; Reichert, J.; Prevedelli, M.; Weitz, M.; Hänsch, T.W. Phase-Coherent Measurement of the Hydrogen 1S-2S Transition Frequency with an Optical Frequency Interval Divider Chain. Phys. Rev. Lett. 1997, 79, 2646. [Google Scholar] [CrossRef]
- Anderson, M.H.; Ensher, J.R.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. Observation of Bose-Einstein condensation in a dilute atomic vapor. Science 1995, 269, 198. [Google Scholar] [CrossRef] [Green Version]
- Davis, K.B.; Mewes, M.O.; Andrews, M.R.; van Druten, N.J.; Durfee, D.S.; Kurn, D.M.; Ketterle, W. Bose-Einstein condensation in a gas of sodium atoms. Phys. Rev. Lett. 1995, 75, 3969. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ovchinnikov, Y.B.; Müller, J.H.; Doery, M.R.; Vredenbregt, E.J.D.; Helmerson, K.; Rolston, S.L.; Phillips, W.D. Diffraction of a released Bose-Einstein condensate by a pulsed standing light wave. Phys. Rev. Lett. 1999, 83, 284. [Google Scholar] [CrossRef] [Green Version]
- Andrews, M.R.; Townsend, C.G.; Miesner, H.-J.; Durfee, D.S.; Kurn, D.M.; Ketterle, W. Observation of Interference Between Two Bose Condensates. Science 1997, 31, 275637. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schneble, D.; Torii, Y.; Boyd, M.; Streed, E.W.; Pritchard, D.E.; Ketterle, W. The onset of matter-wave amplification in a superradiant Bose-Einstein condensate. Science 2003, 300, 475. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Greiner, M.; Mandel, O.; Esslinger, T.; Hänsch, T.; Bloch, I. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 2002, 415, 39. [Google Scholar] [CrossRef]
- Zoest, T.V.; Gaaloul, N.; Singh, Y.; Ahlers, H.; Herr, W.; Seidel, S.T.; Ertmer, W.; Rasel, E.; Eckart, M.; Kajari, E.; et al. Bose-Einstein condensation in microgravity. Science 2010, 328, 1540. [Google Scholar] [CrossRef] [Green Version]
- Weel, M.; Kumarakrishnan, A. Laser-frequency stabilization using a lock-in amplifier. Can. J. Phys. 2002, 80, 1449. [Google Scholar] [CrossRef]
- Yavin, I.; Weel, M.; Andreyuk, A.; Kumarakrishnan, A. A calculation of the time-of-flight distribution of trapped atoms. Am. J. Phys. 2002, 70, 149. [Google Scholar] [CrossRef] [Green Version]
- Spirou, G.; Yavin, I.; Weel, M.; Vorozcovs, A.; Kumarakrishnan, A.; Battle, P.R.; Swanson, R.C. A high-speed-modulated retro-reflector for lasers using an acousto-optic modulator. Can. J. Phys. 2003, 81, 625. [Google Scholar] [CrossRef]
- Mikaelian, T.; Weel, M.; Kumarakrishnan, A.; Battle, P.R.; Swanson, R.C. A high-speed retro-reflector for free-space communication based on electro-optic phase modulation. Can. J. Phys. 2003, 81, 639. [Google Scholar] [CrossRef]
- Yavin, I.; Mikaelian, T.; Kumarakrishnan, A. Calculation of the transfer efficiency between dual magneto-optical traps and simulation of a Ioffe trap for Bose Einstein condensation. Can. J. Phys. 2003, 81, 651. [Google Scholar] [CrossRef]
- Cauchi, S.; Vorozcovs, A.; Weel, M.; Beattie, S.; Gagnon, O.; Kumarakrishnan, A. Absorption spectroscopy of trapped rubidium atoms. Can. J. Phys. 2004, 82, 905. [Google Scholar] [CrossRef]
- Sowka, K.; Weel, M.; Cauchi, S.; Cockins, L.; Kumarakrishnan, A. Laser-frequency stabilization using a lock-in amplifier. Can. J. Phys. 2005, 83, 907. [Google Scholar] [CrossRef]
- Vorozcovs, A.; Weel, M.; Beattie, S.; Cauchi, S.; Kumarakrishnan, A. Measurements of temperature scaling laws in an optically dense magneto-optical trap. J. Opt. Soc. Am. B 2005, 22, 943. [Google Scholar] [CrossRef] [Green Version]
- Mok, C.; Weel, M.; Rotberg, E.; Kumarakrishnan, A. Design and construction of an efficient electro-optic modulator for laser spectroscopy. Can. J. Phys. 2006, 84, 775. [Google Scholar] [CrossRef] [Green Version]
- Winter, S.; Mok, C.; Kumarakrishnan, A. Tools for laser spectroscopy: The design and construction of a Faraday isolator. Can. J. Phys. 2006, 84, 845. [Google Scholar] [CrossRef]
- Wolfram, S. wolfram.com 2020. Available online: https://reference.wolfram.com/language/guide/HelpMenu.html (accessed on 25 April 2020).
- Barrett, B.; Carew, A.; Beica, H.C.; Carlse, G.; Kumarakrishnan, A. (Eds.) Laboratory Manual for PHYS 4061 and PHYS 4062; York University: Toronto, ON, Canada, 2018. [Google Scholar]
- Nyman, R.A.; Varoquaux, G.; Villier, B.; Sacchet, D.; Moron, F.; Coq, Y.L.; Aspect, A.; Bouyer, P. Tapered-amplified antireflection-coated laser diodes for potassium and rubidium atomic-physics experiments. Rev. Sci. Instrum. 2006, 77, 033105. [Google Scholar] [CrossRef] [Green Version]
- Beica, H.C.; Carew, A.; Vorozcovs, A.; Dowling, P.; Pouliot, A.; Barron, B.; Kumarakrishnan, Ȧ. Characterization and applications of auto-locked vacuum-sealed diode lasers for precision metrology. Proc. SPIE 2017, 101910K, 6. [Google Scholar]
- Beica, H.C.; Pouliot, A.; Carew, A.; Vorozcovs, A.; Afkhami-Jeddi, N.; Vacheresse, T.; Carlse, G.; Dowling, P.; Barron, B.; Kumarakrishnan, A. Characterization and applications of auto-locked vacuum-sealed diode lasers for precision metrology. Rev. Sci. Instrum. 2019, 90, 085113. [Google Scholar] [CrossRef]
- Barrett, B.; Carew, A.; Beica, H.C.; Vorozcovs, A.; Pouliot, A.; Kumarakrishnan, A. Prospects for precise measurements with echo atom interferometry. Atoms 2016, 4, 19. [Google Scholar] [CrossRef] [Green Version]
- Pouliot, A.; Beica, H.C.; Carew, A.; Vorozcovs, A.; Carlse, G.; Kumarakrishnan, A. Auto-locking waveguide amplifier system for lidar and magnetometric applications. Proc. SPIE 2018, 10514, 105140S. [Google Scholar]
- Gibble, K.E.; Kasapi, S.; Chu, S. Improved magneto-optic trapping in a vapor cell. Opt. Lett. 1992, 17, 526. [Google Scholar] [CrossRef] [PubMed]
- Dinneen, T.; Wallace, C.; Gould, P. Narrow linewidth, highly stable, tunable diode laser system. Opt. Commun. 1992, 92, 277. [Google Scholar] [CrossRef]
- Bechhoefer, J.; Wilson, S. Faster, cheaper, safer optical tweezers for the undergraduate laboratory. Am. J. Phys. 2002, 70, 393. [Google Scholar] [CrossRef]
- Perkins, T.; Smith, D.E.; Chu, S. Direct observation of tube-like motion of a single polymer chain. Science 1994, 64, 819. [Google Scholar] [CrossRef] [Green Version]
- Henon, S.; Lenormand, G.; Richert, A.; Gallet, F. A new determination of the shear modulus of the human erythrocyte membrane using optical tweezers. Biophys. J. 1999, 76, 1145. [Google Scholar] [CrossRef] [Green Version]
- Lindquist, K.; Stephens, M.; Wieman, C. Experimental and theoretical study of the vapor-cell Zeeman optical trap. Phys. Rev. A 1992, 46, 4082. [Google Scholar] [CrossRef]
- Metcalf, H.J.; Straten, P.V. Laser Cooling and Trapping; Springer: New York, NY, USA, 1999. [Google Scholar]
- Mellish, A.S.; Wilson, A.C. A simple laser cooling and trapping apparatus for undergraduate laboratories. Am. J. Phys. 2002, 70, 965. [Google Scholar] [CrossRef]
- Wieman, C.; Flowers, G.; Gilbert, S. Inexpensive laser cooling and trapping experiment for undergraduate laboratories. Am. J. Phys. 1995, 63, 317. [Google Scholar] [CrossRef]
- Walker, T.; Sesko, D.; Wieman, C. Collective behavior of optically trapped neutral atoms. Phys. Rev. Lett. 1990, 64, 408. [Google Scholar] [CrossRef] [Green Version]
- Lett, P.D.; Phillips, W.D.; Rolston, S.L.; Tanner, C.E.; Watts, R.N.; Westbrook, C.I. Optical molasses. J. Opt. Soc. Am. B 1989, 6, 2084. [Google Scholar] [CrossRef] [Green Version]
- Chu, S.; Wieman, C. Atom cooling, trapping, and quantum manipulation. Laser Cooling and Trapping. J. Opt. Soc. Am. B 1989, 60, 2020. [Google Scholar]
- Ketterle, W.; Davis, K.B.; Joffe, M.A.; Martin, A.; Pritchard, D.E. High densities of cold atoms in a dark spontaneous-force optical trap. Phys. Rev. Lett. 1993, 70, 2253. [Google Scholar] [CrossRef] [PubMed]
- Wallace, C.D.; Dinneen, T.P.; Tan, K.Y.N.; Kumarakrishnan, A.; Gould, P.L.; Javanainen, J. Measurements of temperature and spring constant in a magneto-optical trap. J. Opt. Soc. Am. B 1994, 11, 703. [Google Scholar] [CrossRef]
- Chu, S.; Hollberg, L.; Bjorkholm, J.E.; Cable, A.; Ashkin, A. Three-dimensional viscous confinement and cooling of atoms by resonance radiation pressure. Phys. Rev. Lett. 1985, 55, 48. [Google Scholar] [CrossRef] [Green Version]
- Grove, T.T. A low-cost scanning Fabry–Perot cavity for laser experiments. Am. J. Phys. 2003, 71, 184. [Google Scholar] [CrossRef]
- Barrett, B.; Chan, I.; Mok, C.; Carew, A.; Yavin, I.; Kumarakrishnan, A.; Cahn, S.B.; Sleator, T. Advances in Atomic, Molecular and Optical Physics; Berman, P.R., Arimondo, E., Lin, C.C., Eds.; Elsevier: New York, NY, USA, 2011; Volume 60, Chapter 3. [Google Scholar]






















© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beica, H.C.; Winter, S.; Mok, C.; Barrett, B.; Berthiaume, R.; Vorozcovs, A.; Yachoua, F.; Afkhami-Jeddi, N.; Aggarwal, M.; Carlse, G.; et al. Laboratory Courses on Laser Spectroscopy and Atom Trapping. Atoms 2020, 8, 25. https://doi.org/10.3390/atoms8020025
Beica HC, Winter S, Mok C, Barrett B, Berthiaume R, Vorozcovs A, Yachoua F, Afkhami-Jeddi N, Aggarwal M, Carlse G, et al. Laboratory Courses on Laser Spectroscopy and Atom Trapping. Atoms. 2020; 8(2):25. https://doi.org/10.3390/atoms8020025
Chicago/Turabian StyleBeica, Hermina C., Shoshana Winter, Carson Mok, Brynle Barrett, Rob Berthiaume, Andrejs Vorozcovs, Fadi Yachoua, Nima Afkhami-Jeddi, Monika Aggarwal, Gehrig Carlse, and et al. 2020. "Laboratory Courses on Laser Spectroscopy and Atom Trapping" Atoms 8, no. 2: 25. https://doi.org/10.3390/atoms8020025
APA StyleBeica, H. C., Winter, S., Mok, C., Barrett, B., Berthiaume, R., Vorozcovs, A., Yachoua, F., Afkhami-Jeddi, N., Aggarwal, M., Carlse, G., Pouliot, A., Borsos, K. B., Vacheresse, T., Marants, R., & Kumarakrishnan, A. (2020). Laboratory Courses on Laser Spectroscopy and Atom Trapping. Atoms, 8(2), 25. https://doi.org/10.3390/atoms8020025




