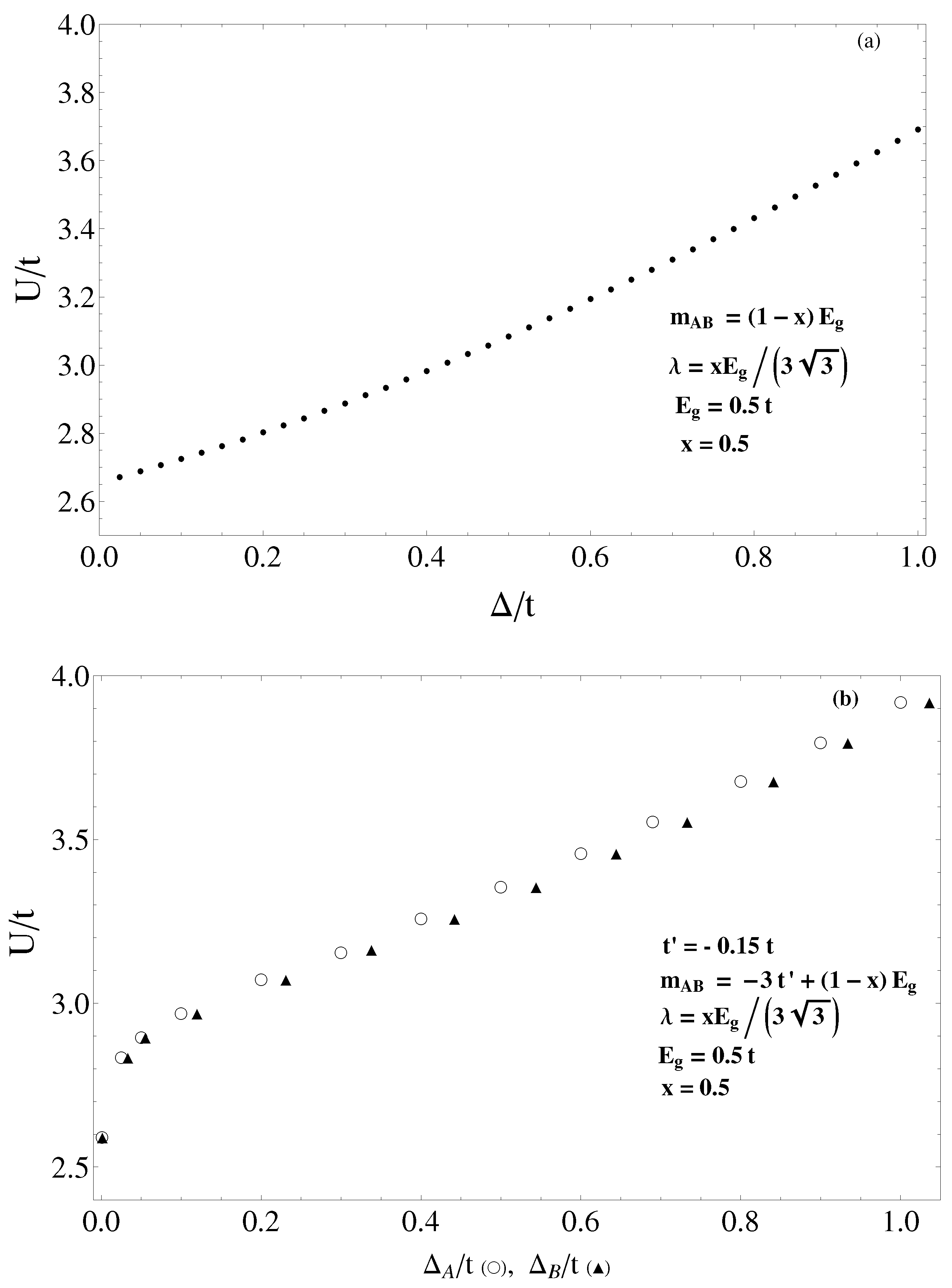Phase Diagram of the Attractive Kane-Mele-Hubbard Model at Half Filling

Abstract

Motivated by recent developments in the experimental study of ultracold atoms in graphene-like honeycomb optical lattices, we investigate superconductivity of the attractive Kane-Mele-Habbard (KMH) model with the next-nearest-neighbor (NNN) hoping at half filling. The mean-field approximation is used to study the phase diagram which interpolates the trivial and the non-trivial topological states. It is shown that: (a) when the NNN hoping is taken into account, one has to introduce two mean-field gap equations for the two sublattices, instead of a single gap when the NNN hopping is neglected, and (b) in the non-trivial topological region the phase diagram with the NNN hopping is significantly different compared to the phase diagram calculated previously, but without the NNN term. We also discuss the superconducting instability of the attractive KMH model that is driven by condensation of Cooperons.

1. Introduction

The present-day experiments with ultracold atoms in optical lattices allow for us to simulate both the Haldane’s model [1] and the situation [2,3] considered by Kane and Mele (KM). The Haldane’s model [4,5] is a tight-binding representation of electron motion on a honeycomb lattice in the presence of a magnetic field, where vector potential has the full symmetry of the lattice and generates a magnetic field with zero total flux through the unit cell. It was pointed out by Haldane that in two-dimensional (2D) honeycomb lattice the topological ordering requires time reversal symmetry breaking. Because of the zero magnetic flux through each unit cell, the phase accumulated through a nearest neighbor hopping vanishes, whereas the phase accumulated through NNN hopping is nonzero. This extra phase breaks the time-reversal symmetry. The Haldane model has been experimentally realized with ultracold atoms [6,7]. However, the electron spin is not included in the Haldane’s model.

It is known that the spin-orbit coupling preserves the time-reversal symmetry, but the spin-orbit effects can be used to obtain topological insulators. The first example was the KM Hamiltonian for the electrons in a graphene [8,9], which consists of two copies of the Haldane’s model, one for spin-up electrons and one for spin-down electrons. In the KM model, each spin component breaks time-reversal symmetry, but the time reversal symmetry is restored when taking two copies with different signs for the spin together.

The KM Hamiltonian can be generalized by including: (a) the Rashba interaction [10,11,12,13]; (b) on-site Hubbard interaction [14,15,16,17]; and, (c) both the Rashba and the Hubbard interactions [18,19].

In a recent paper [20], the phase diagram of the attractive Kane–Mele–Hubbard (KMH) model at half filling has been obtained as a function of a tuning parameter $x=3\sqrt{3}\lambda /(m_{AB}+3\sqrt{3}\lambda )$. Here, $\lambda$ is the strength of intrinsic spin-orbit (ISO) coupling and $m_{AB}$ is sublattice potential. However, the NNN hopping term has been neglected, although it is several orders of magnitude stronger than the ISO coupling.

In this paper, we have presented the phase diagram of the attractive KMH model with NNN hoping at half filling as a function of a tuning parameter $x=3\sqrt{3}\lambda /(3\sqrt{3}\lambda +3t^{\prime }+m_{AB})$, where $t^{\prime }$ is the NNN hoping amplitude. It is shown that, in the mean-field approximation, we have two gap equations for ${\Delta }_A$ and ${\Delta }_B$, instead of a single gap $\Delta$ when NNN hopping is neglected.

We shall discuss the case of Fermi (spin-$1/2$) atoms loaded into honeycomb optical lattice, but the results are also valid for the tight-binding description of electrons in a graphene as well. Our tight-binding Hamiltonian $H=H_{KM}+H_{NNN}+H_U$ includes the KM terms, as well as the NNN hopping and the onsite attractive Hubbard interaction, where

$$\begin{array}{cc}& H_{KM}=-t{\displaystyle \sum _{<\mathbf{i},\mathbf{j}>}}\left[{\mathsf{\Psi }}_{\mathbf{i}+\mathbf{j}}^{†}{\mathsf{\Psi }}_{\mathbf{i}}+H.c.\right]+\hfill \\ \hfill & H_{ISO}-m_{AB}{\displaystyle \sum _{\mathbf{i}}}\left({\mathsf{\Psi }}_{{\mathbf{i}}_A}^{†}{\mathsf{\Psi }}_{{\mathbf{i}}_A}-{\mathsf{\Psi }}_{{\mathbf{i}}_B}^{†}{\mathsf{\Psi }}_{{\mathbf{i}}_B}\right).\hfill \end{array}$$

(1)

The first term in (1) takes into account the possibility for nearest-neighbor hopping. $H_{ISO}$ represents the ISO interaction, which originates from the hybridization of the higher angular momentum orbit and exerts opposite magnetic fields upon electrons with opposite spin polarizations. The third term in (1) describes the possible energy offset between sites of A and B sublattices. t is the nearest-neighbor hopping amplitudes, $m_{AB}$ is the energy offset parameter, and ${\mathsf{\Psi }}_{\mathbf{i}}^{†}=({\psi }_{\mathbf{i},\uparrow }^{†},{\psi }_{\mathbf{i},\downarrow }^{†})$ is the creation operator for spin-up and spin-down fermions at site $\mathbf{i}$. Throughout this paper, we have assumed the lattice constant $a=1$. The hopping to the nearest neighbor sites the vectors $\mathbf{j}$ are: ${\delta }_1=(1/2,\sqrt{3}/2)$, ${\delta }_2=(1/2,-\sqrt{3}/2)$, ${\delta }_3=(-1,0)$ (see Figure 1a). The NNN hopping term is $H_{NNN}=-t^{\prime }{\sum }_{<<{\mathbf{i},\mathbf{j}}^{\prime }>>}\left[{\mathsf{\Psi }}_{\mathbf{i}+{\mathbf{j}}^{\prime }}^{†}{\mathsf{\Psi }}_{\mathbf{i}}+H.c.\right]$. For hopping to the next nearest neighbor sites the vectors ${\mathbf{j}}^{\prime }$ are $d_{1,2}=\pm (3/2,\sqrt{3}/2)$, $d_{3,4}=\pm (3/2,-\sqrt{3}/2)$, and $d_{5,6}=\pm (0,\sqrt{3})$. The attractive Hubbard interaction is described by $H_U=-U{\sum }_{\mathbf{i}}{\widehat{n}}_{\mathbf{i},\uparrow }{\widehat{n}}_{\mathbf{i},\downarrow }$, where $U>0$.

The KM Hamiltonian along with the NNN hopping term are represented by the following $4\times 4$ matrix in the momentum space on the basis of the four-component wave function ${\mathsf{\Psi }}^{†}=({\psi }_{A,\mathbf{k},\uparrow }^{†},{\psi }_{A,\mathbf{k},\downarrow }^{†},{\psi }_{B,\mathbf{k},\uparrow }^{†},{\psi }_{B,\mathbf{k},\downarrow }^{†})$:

$$\widehat{H}\left(\mathbf{k}\right)=\left(\begin{array}{cccc}Z\left(\mathbf{k}\right)+h_1\left(\mathbf{k}\right)-m_{AB}& 0& h\left(\mathbf{k}\right)& 0\\ 0& -Z\left(\mathbf{k}\right)+h_1\left(\mathbf{k}\right)-m_{AB}& 0& h\left(\mathbf{k}\right)\\ h^{*}\left(\mathbf{k}\right)& 0& -Z\left(\mathbf{k}\right)+h_1\left(\mathbf{k}\right)+m_{AB}& 0\\ 0& h^{*}\left(\mathbf{k}\right)& 0& Z\left(\mathbf{k}\right)+h_1\left(\mathbf{k}\right)+m_{AB}\end{array}\right),$$

(2)

where $h\left(\mathbf{k}\right)=-t\left[cos\left(k_x\right)+2cos\left(\frac{k_x}{2}\right)cos\left(\frac{\sqrt{3}{k}_y}{2}\right)\right]+𝚤t\left[sin\left(k_x\right)-2sin\left(\frac{k_x}{2}\right)cos\left(\frac{\sqrt{3}{k}_y}{2}\right)\right]$, $h_1\left(\mathbf{k}\right)=-2t^{\prime }\left[cos\left(\sqrt{3}{k}_y\right)+2cos\left(\frac{3}{2}{k}_x\right)cos\left(\frac{\sqrt{3}}{2}{k}_y\right)\right]$, $Z\left(\mathbf{k}\right)=-2\lambda \left[sin\left(\sqrt{3}{k}_y\right)-2cos\left(\frac{3k_x}{2}\right)sin\left(\frac{\sqrt{3}{k}_y}{2}\right)\right]$, and $\lambda$ is the strength of the ISO interaction. The eigenvalues of the Hamiltonian (2) are ${\mathsf{\Omega }}_{1,2}\left(\mathbf{k}\right)=h_1\left(\mathbf{k}\right)\pm \sqrt{{\left[m_{AB}-Z\left(\mathbf{k}\right)\right]}^2+{\left|h\left(\mathbf{k}\right)\right|}^2}$, and ${\mathsf{\Omega }}_{3,4}\left(\mathbf{k}\right)=h_1\left(\mathbf{k}\right)\pm \sqrt{{\left[m_{AB}+Z\left(\mathbf{k}\right)\right]}^2+{\left|h\left(\mathbf{k}\right)\right|}^2}$.

The authors of Ref. [20] pointed out that, depending on the value of the parameter $0\le x\le 1$, the system can be taken across the topological phase transition. For $x<1/2$, we have a topological trivial insulator, while, for $x>1/2$, the system is in topological non-trivial insulator state. The phase diagram of the KMH model, as reported in Ref. [20], was calculated within the self-consistent Bogoliubov- de Gennes theory while using a supercell with six sites. The corresponding system parameters are $\mathsf{\Lambda }=(1-x)E_g$, $3\sqrt{3}\lambda =x{E}_g$, and $E_g=t/2$.

In what follows, we apply the mean-field approximation to obtain the matrix elements of the single-particle Green’s functions of the KMH model with NNN hopping term at half filling. The above-mentioned supercell approach is more complicated than the mean-field approximation, but, as can be seen from Figure 2a, in this paper, our approach reproduces the corresponding phase diagram (Figure 2a in Ref. [20]). If the NNN term is taken into account, then the matrix elements of the mean-field single-particle Green’s function in the momentum space, proportional to $<{\mathsf{\Psi }}_{A\mathbf{k}\downarrow }{\mathsf{\Psi }}_{A-\mathbf{k}\uparrow }>$ and $<{\mathsf{\Psi }}_{B\mathbf{k}\downarrow }{\mathsf{\Psi }}_{B-\mathbf{k}\uparrow }>$, are different ands, therefore, we have to introduce two gaps, ${\Delta }_A$, and ${\Delta }_B$. If the NNN hopping is neglected, we have ${\Delta }_A={\Delta }_B=\Delta$. When the NNN hopping is included, we have $m_{AB}=-3t^{\prime }+(1-x)E_g$, and $3\sqrt{3}\lambda =x{E}_g$. At $3t^{\prime }+m_{AB}=3\sqrt{3}\lambda$ the the single-particle gap does close at $K=\left(\frac{2\pi }{3a},\frac{2\pi }{3\sqrt{3}a}\right)$, while the mass of the other bands at $K^{\prime }=\left(\frac{2\pi }{3a},-\frac{2\pi }{3\sqrt{3}a}\right)$ remains constant throughout the transition for all values of x, and viceversa. As in Ref. [20], the ground state of the KM Hamiltonian with NNN hopping is topological nontrivial (or topological trivial), when the parameter $x=3\sqrt{3}\lambda /(3\sqrt{3}\lambda +3t^{\prime }+m_{AB})$ is $x>1/2$ (or $x<1/2$).

2. Single-Particle Dispersion in the Mean-Field Approximation

In the presence of an onsite attractive interaction between the fermions, the fermion atoms form bound (Cooper) pairs. As a result, the system becomes unstable against the formation of a s-wave spin-singlet superfluid ground state. At low energies, the system admits an effective description in terms of massless Dirac fermions; therefore, in a honeycomb optical lattice we have a possibility to observe a superfluidity of Fermi atoms with the Dirac spectrum. We restricted our calculations to half-filling (the chemical potential $\mu =0$), where the particle-hole symmetry takes place. We further assume that the BCS mean-field order parameters ${\Delta }_{A\left(B\right)}=U<{\psi }_{A\left(B\right),-\mathbf{k},\downarrow }{\psi }_{A\left(B\right),\mathbf{k},\uparrow }>$ are real constants. When the attractive Hubbard interaction is taken into account, the KM basis of the four-component wave function ${\mathsf{\Psi }}^{†}=({\psi }_{A,\mathbf{k},\uparrow }^{†},{\psi }_{A,\mathbf{k},\downarrow }^{†},{\psi }_{B,\mathbf{k},\uparrow }^{†},{\psi }_{B,\mathbf{k},\downarrow }^{†})$ becomes a basis of the eight-component wave function ${\mathsf{\Psi }}^{†}=({\psi }_{A,\mathbf{k},\uparrow }^{†},{\psi }_{B,\mathbf{k},\uparrow }^{†},{\psi }_{B,-\mathbf{k},\downarrow },{\psi }_{A,-\mathbf{k},\downarrow },{\psi }_{A,\mathbf{k},\downarrow }^{†},{\psi }_{B,\mathbf{k},\downarrow }^{†},{\psi }_{B,-\mathbf{k},\uparrow },$${\psi }_{A,-\mathbf{k},\uparrow })$. Thus, the generalized Hamiltonian $H=H_{KM}+H_{NNN}+H_U$ in the mean-field approximation in the momentum space on the basis of the eight-component wave function is represented by the following $8\times 8$ block-diagonal matrix

$${\widehat{H}}_{MF}\left(\mathbf{k}\right)=\left(\begin{array}{cc}{\widehat{H}}_1\left(\mathbf{k}\right)& 0\\ 0& {\widehat{H}}_2\left(\mathbf{k}\right)\end{array}\right),$$

(3)

where the corresponding $4\times 4$ blocks are defined in the Appendix A.

We define the Matsubara single-particle Green’s functions:

$$\widehat{G}(\mathbf{k},𝚤{\omega }_m)={\left(𝚤{\omega }_m\widehat{1}-{\widehat{H}}_{MF}\left(\mathbf{k}\right)\right)}^{-1}$$

$$=\left(\begin{array}{cc}{G}^{\left(1\right)}(\mathbf{k},𝚤{\omega }_m)& 0\\ 0& G^{\left(2\right)}(\mathbf{k},𝚤{\omega }_m)\end{array}\right).$$

Here, the Matsubara fermion energies are ${\omega }_m=(2\pi /\beta )(m+1/2),m=0,1,2,\dots$, $\beta =1/\left(k_{B}T\right)$, and $k_B$ is the Boltzmann constant (throughout this paper we have assumed $\hslash =k_B=1$). The single-particle excitations ${\omega }_i\left(\mathbf{k}\right),i=1,2,3,4$ in the mean-field approximation are defined in the Appendix A. They manifest themselves as poles of the Green’s function $\widehat{G}(\mathbf{k},𝚤{\omega }_m)$. The corresponding zero-temperature Green’s function $\widehat{G}(\mathbf{k},\omega )$ is an $8\times 8$ matrix with elements $G_{n_1,n_2}^{(1,2)}(\mathbf{k},\omega )\{n_1,n_2\}=1,2,\dots ,8$ written in the following forms:

$$\begin{array}{cc}\hfill & G_{n_1,n_2}^{\left(1\right)}(\mathbf{k},\omega )=\frac{A_{n_1,n_2}^{\left(1\right)}\left(\mathbf{k}\right)}{\omega -{\omega }_1\left(\mathbf{k}\right)+𝚤0^{+}}+\frac{B_{n_1,n_2}^{\left(1\right)}\left(\mathbf{k}\right)}{\omega +{\omega }_2\left(\mathbf{k}\right)-𝚤0^{+}}+\frac{C_{n_1,n_2}^{\left(1\right)}\left(\mathbf{k}\right)}{\omega -{\omega }_2\left(\mathbf{k}\right)+𝚤0^{+}}+\frac{D_{n_1,n_2}^{\left(1\right)}\left(\mathbf{k}\right)}{\omega +{\omega }_2\left(\mathbf{k}\right)+𝚤0^{+}},\hfill \\ \hfill & G_{n_1,n_2}^{\left(2\right)}(\mathbf{k},\omega )=\frac{A_{n_1,n_2}^{\left(2\right)}\left(\mathbf{k}\right)}{\omega -{\omega }_3\left(\mathbf{k}\right)+𝚤0^{+}}+\frac{B_{n_1,n_2}^{\left(2\right)}\left(\mathbf{k}\right)}{\omega +{\omega }_3\left(\mathbf{k}\right)-𝚤0^{+}}+\frac{C_{n_1,n_2}^{\left(3\right)}\left(\mathbf{k}\right)}{\omega -{\omega }_4\left(\mathbf{k}\right)+𝚤0^{+}}+\frac{D_{n_1,n_2}^{\left(2\right)}\left(\mathbf{k}\right)}{\omega +{\omega }_4\left(\mathbf{k}\right)+𝚤0^{+}}.\hfill \end{array}$$

(4)

The functions $A_{n_1,n_2}^{(1,2)}\left(\mathbf{k}\right),B_{n_1,n_2}^{(1,2)}\left(\mathbf{k}\right),C_{n_1,n_2}^{(1,2)}\left(\mathbf{k}\right)$, and $D_{n_1,n_2}^{(1,2)}\left(\mathbf{k}\right)$ can be numerically calculated by inverting the matrix $\left(𝚤{\omega }_m\widehat{1}-{\widehat{H}}_{MF}\left(\mathbf{k}\right)\right)$.

The momentum distribution for the spin components $n_{\uparrow (\downarrow )}\left(\mathbf{k}\right)$ can be evaluated using the corresponding elements of the $8\times 8$ Green’s function matrix:

$$n_{\uparrow }\left(\mathbf{k}\right)=<{\psi }_{A,\mathbf{k},\uparrow }^{†}{\psi }_{A,\mathbf{k},\uparrow }>+<{\psi }_{B,\mathbf{k},\uparrow }^{†}{\psi }_{B,\mathbf{k},\uparrow }>={\beta }^{-1}\sum _{𝚤{\omega }_m}\left[G_{11}(\mathbf{k},𝚤{\omega }_m)+G_{22}(\mathbf{k},𝚤{\omega }_m)\right],$$

$$n_{\downarrow }\left(\mathbf{k}\right)=<{\psi }_{A,\mathbf{k},\downarrow }^{†}{\psi }_{A,\mathbf{k},\downarrow }>+<{\psi }_{B,\mathbf{k},\downarrow }^{†}{\psi }_{B,\mathbf{k},\downarrow }>={\beta }^{-1}\sum _{𝚤{\omega }_m}\left[G_{55}(\mathbf{k},𝚤{\omega }_m)+G_{66}(\mathbf{k},𝚤{\omega }_m)\right].$$

Very similarly, one can derive a set of two gap equations ${\Delta }_A=U<{\psi }_{A,-\mathbf{k},\downarrow }{\psi }_{A,\mathbf{k},\uparrow }>=U{\beta }^{-1}{\sum }_{𝚤{\omega }_m}{G}_{58}^{\left(2\right)}(\mathbf{k},𝚤{\omega }_m)$, ${\Delta }_B=U<{\psi }_{B,-\mathbf{k},\downarrow }{\psi }_{B,\mathbf{k},\uparrow }>=U{\beta }^{-1}{\sum }_{𝚤{\omega }_m}{G}_{67}^{\left(2\right)}(\mathbf{k},𝚤{\omega }_m)$, which at a zero temperature assume the form:

$${\Delta }_A=U\sum _{\mathbf{k}\in BZ}\left[B_{58}^{\left(2\right)}\left(\mathbf{k}\right)+D_{58}^{\left(2\right)}\left(\mathbf{k}\right)\right],{\Delta }_B=U\sum _{\mathbf{k}\in BZ}\left[B_{67}^{\left(2\right)}\left(\mathbf{k}\right)+D_{67}^{\left(2\right)}\left(\mathbf{k}\right)\right].$$

(5)

Our next step is to solve the gap Equations (5) assuming $t^{\prime }=-0.15t$ (the same value has been used previously in [21]). At $x=1/2$, i.e., $3t^{\prime }+m_{AB}=3\sqrt{3}\lambda$, the band structure is at a topological phase transition, because the Dirac bands at points $K=(2\pi /\left(3a\right),2\pi /\left(3\sqrt{3}a\right)$ or $K^{\prime }=(2\pi /\left(3a\right),-2\pi /\left(3\sqrt{3}a\right)$) being massless (at $x=1/2$, we have ${\omega }_4\left({\mathbf{k}}_K\right)=0$ and ${\omega }_2\left({\mathbf{k}}_{K^{\prime }}\right)=0$. Let us assume that ${\Delta }_B=\alpha {\Delta }_A$, so we use Equations (5) to obtain an equation, $\alpha =f(\alpha ,{\Delta }_A)$, for $\alpha$ and ${\Delta }_A$ with

$$f(\alpha ,{\Delta }_A)=\frac{{\sum }_{\mathbf{k}\in BZ}\left[B_{67}^{\left(2\right)}\left(\mathbf{k}\right)+D_{67}^{\left(2\right)}\left(\mathbf{k}\right)\right]}{{\sum }_{\mathbf{k}\in BZ}\left[B_{58}^{\left(2\right)}\left(\mathbf{k}\right)+D_{58}^{\left(2\right)}\left(\mathbf{k}\right)\right]}$$

(6)

Next, we fixed the value of ${\Delta }_A$, and solve iteratively our equation for $\alpha$. Having $\alpha$ and ${\Delta }_A$, we used Equation (5) to obtain the corresponding value of U. The results of our numerical calculations for $x=1/2$ are presented in Figure 3. The minimum value of the Hubbard interaction that creates non-zero superfluid gaps is almost the same with and without the NNN hopping term, as can be seen. The difference between the two gaps becomes important for higher values of U. The fact that the minimum value $U_c\approx 2.6$ that can produce non-zero gap (or a Cooperon bound state, particularly in the vicinity of the Gamma point at which the dispersion has its minimum) has been observed previously in Ref. [22]. Our numerical results that $U_c$ does not change significantly with and without NNN hopping term tells us that on-site attractive interaction, rather than the NNN term, boosts the formation of the a Cooperon bound state.

3. Discussion

To summarize, we use the mean-field approximation to numerically calculate the phase diagram of the attractive KMH model with NNN hoping at half filling, which interpolates the trivial and the non-trivial topological states. It is shown that, as soon as the NNN hoping is included, we have to solve two mean-field gap equations for ${\Delta }_A$ and ${\Delta }_B$, instead of a single gap equation for $\Delta$ in the case when NNN hopping is neglected.

Recently, the possibility to have superconducting instability in the attractive KMH model has been analyzed within the T-matrix approximation [22]. The question that naturally arises here is about the contributions due to the bubble diagrams, which are included in the Bethe–Salpeter (BS) equation, but neglected by the T-matrix approximation. In Ref. [23], we apply the BS formalism to calculate the slope of the Goldstone mode and the corresponding sound velocity. We found $8\%$ difference between the values of the sound velocity provided by the T-matrix approximation and the BS equation.

It is known that the Gaussian approximation also neglects the bubble diagrams, but, in a square lattice, the difference between the speeds of the sound calculated in the Gaussian and in the BS approximations is about $25\%$ (see Figure 10 in Ref. [24]). To explain the difference of $8\%$ in our numerical calculations, we refer to the system parameters: $x=1$, $\lambda =0.1t$, $U=2.69t$, and $\Delta =0.151t$. From the value of $\lambda$ follows that $E_g\approx 0.52t$, and, therefore, the phase diagram is very close to that presented in Figure 2. From another point of view, the value of $U=2.69t$ tells us that the system is very close to the topological phase transition line at $x=1$. The fact that close to the phase transition boundary the speed of sound calculated with in the Gaussian and the BS approaches is essentially the same as has been previously found in a square lattice [25]. Thus, it is natural to expect that away from the phase transition boundary contributions due to the bubble diagrams will be more important.