Spin-Polarized Photoelectron Fluxes from Fullerene Anions
Abstract
:1. Introduction
2. Review of Theory
2.1. Cherepkov’S Theory of Spin-Polarized Photoelectron Fluxes from Atoms
2.2. Modeling Fullerene Anion Photodetachment
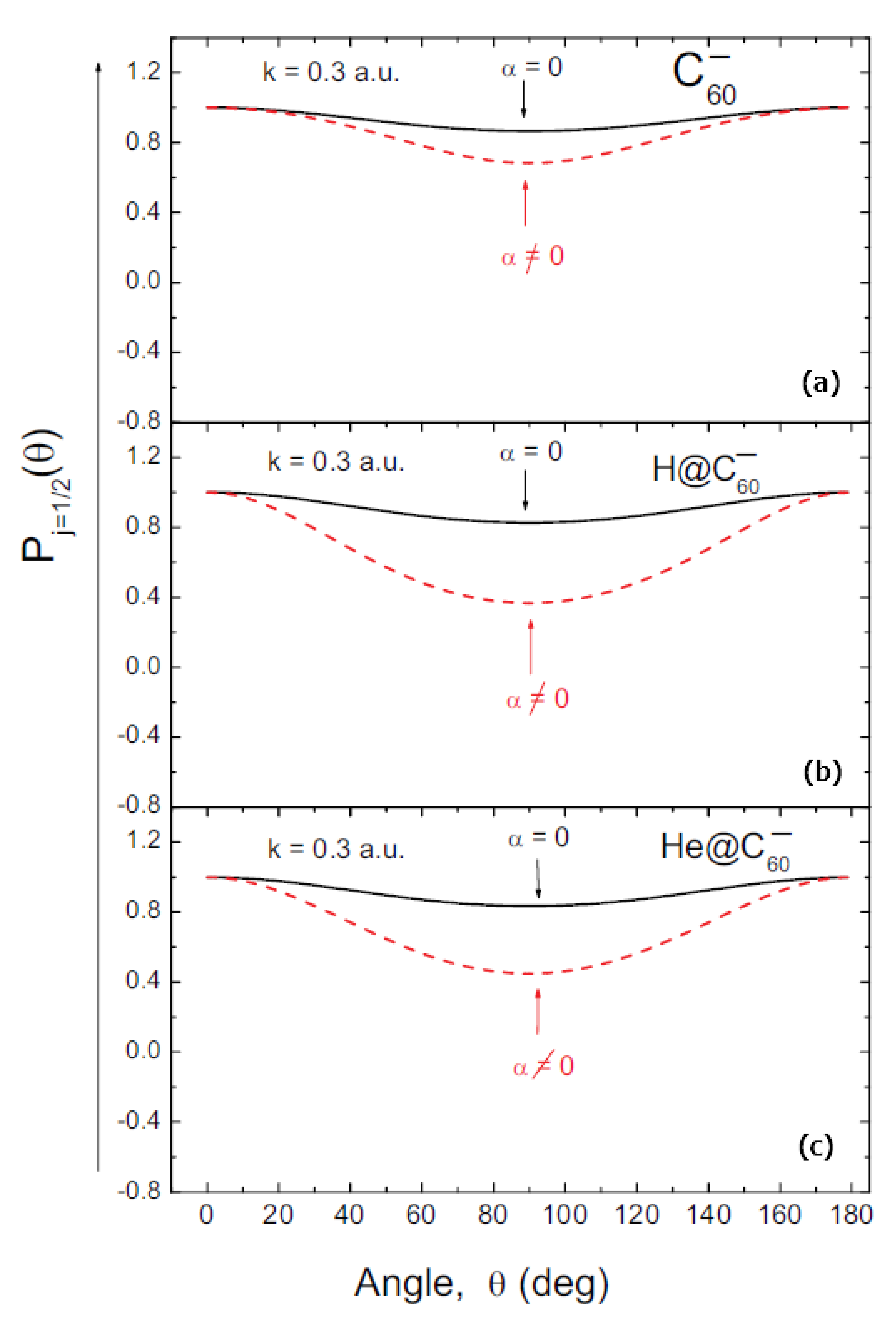
3. Results and Discussion
4. Conclusions
Funding
Conflicts of Interest
Appendix A. Comparison of Calculated Data Obtained with the Use of U0 = 0.302 and 0.347 a.u.

References
- Kato, T. Absorption and emission spectra for C60. Laser Chem. 1994, 52, 155. [Google Scholar] [CrossRef] [Green Version]
- Bilodeau, R.C.; Gibson, N.D.; Walter, C.W.; Esteves-Macaluso, D.A.; Schippers, S.; Mü ller, A.; Phaneuf, R.A.; Aguilar, A.; Hoener, M.; Rost, J.M.; et al. Single-Photon Multiple Detachment in Fullerene Negative Ions: Absolute Ionization Cross Sections and the Role of the Extra Electron. Phys. Rev. Lett. 2013, 111, 043003. [Google Scholar] [CrossRef]
- Müller, A.; Martins, M.; Kilcoyne, A.L.D.; Phaneuf, R.A.; Hellhund, J.; Borovik, A.; Holste, K.; Bari, S.; Buhr, T.; Klumpp, S.; et al. Photoionization and photofragmentation of singly charged positive and negative Sc3N@C80 endohedral fullerene ions. Phys. Rev. A 2019, 99, 063401. [Google Scholar] [CrossRef] [Green Version]
- Lohr, L.L.; Blinder, S.M. Electron photodetachment from a Dirac bubble potential. A model for the fullerene negative ion C. Chem. Phys. Lett. 1992, 198, 100. [Google Scholar] [CrossRef] [Green Version]
- Amusia, M.Y.; Baltenkov, A.S.; Krakov, B.G. Photodetachment of negative C ions. Phys. Lett. A 1998, 243, 99. [Google Scholar] [CrossRef]
- Korol, A.V.; Solov’yov, A.V. Vacancy decay in endohedral atoms: The role of an atom’s non-central position. J. Phys. B 2011, 44, 085001. [Google Scholar] [CrossRef] [Green Version]
- Baltenkov, A.S.; Msezane, A.Z. Doubly-charged Negative Ion of C Molecule. Proc. Dyn. Syst. Appl. 2016, 7, 239. [Google Scholar]
- Kumar, A.; Varma, H.R.; Deshmukh, P.C.; Manson, S.T.; Dolmatov, V.K.; Kheifets, A.S. Wigner photoemission time delay from endohedral anions. Phys. Rev. A 2016, 94, 043401. [Google Scholar] [CrossRef] [Green Version]
- Chaudhuri, S.K.; Mukherjee, P.K.; Fricke, B. Spectroscopy of low lying transitions of He confined in a fullerene cage. Eur. Phys. J. D 2016, 70, 196. [Google Scholar] [CrossRef]
- Dolmatov, V.K. Impact of fullerene polarizability on Wigner time delay in photodetachment of fullerene anions C. J. Phys. Conf. Ser. 2017, 875, 022013. [Google Scholar] [CrossRef]
- Puska, M.J.; Nieminen, R.M. Photoabsorption of atoms inside C60. Phys. Rev. A 1993, 47, 1181. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baltenkov, A.S. Resonances in photoionization cross sections of inner subshells of atoms inside the fullerene cage. J. Phys. B 1999, 32, 2745. [Google Scholar] [CrossRef]
- Scully, S.W.J.; Emmons, E.D.; Gharaibeh, M.F.; Phaneuf, R.A.; Kilcoyne, A.L.D.; Schlachter, A.S.; Schippers, S.; Müller, A.; Chakraborty, H.S.; Madjet, M.E.; et al. Photoexcitation of a volume plasmon in C60 ions. Phys. Rev. Lett. 2005, 94, 065503. [Google Scholar] [CrossRef] [PubMed]
- Shields, D.; De, R.; Madjet, M.E.; Manson, S.T.; Chakraborty, H.S. Photoemission from hybrid states of Cl@C60 before and after a stabilizing charge transfer. J. Phys. B 2020, 53, 125101. [Google Scholar] [CrossRef] [Green Version]
- McCune, M.A.; De, R.; Madjet, M.E.; Chakraborty, H.S. First prediction of the direct effect of a confined atom on photoionization of the confining fullerene. J. Phys. B 2010, 43, 181001. [Google Scholar] [CrossRef]
- McCune, M.A.; Madjet, M.E.; Chakraborty, H.S. Reflective and collateral photoionization of an atom inside a fullerene: Confinement geometry from reciprocal spectra. Phys. Rev. A 2009, 80, 011201(R). [Google Scholar] [CrossRef]
- McCune, M.A.; Madjet, M.E.; Chakraborty, H.S. Unique role of orbital angular momentum in subshell-resolved photoionization of C60. J. Phys. B 2008, 41, 201003. [Google Scholar] [CrossRef]
- Dolmatov, V.K.; Edwards, A. Role of polarizability of a CN fullerene cage in A@CN photoionization and e--CN scattering: The size effect. J. Phys. B 2019, 52, 105001. [Google Scholar] [CrossRef]
- Baltenkov, A.S.; Manson, S.T.; Msezane, A.Z. Jellium model potentials for the C60 molecule and the photoionization of endohedral atoms, A@C60. J. Phys. B 2015, 48, 185103. [Google Scholar] [CrossRef]
- Phaneuf, R.A.; Kilcoyne, A.L.D.; Aryal, N.B.; Baral, K.K.; Esteves-Macaluso, D.A.; Thomas, C.M.; Hellhund, J.; Lomsadze, R.; Gorczyca, T.W.; Ballance, C.P.; et al. Probing confinement resonances by photoionizing Xe inside a C molecular cage. Phys. Rev. A 2013, 88, 053402. [Google Scholar] [CrossRef]
- Gorczyca, T.W.; Hasoglu, M.F.; Manson, S.T. Photoionization of endohedral atoms using R-matrix methods: Application to Xe@C60. Phys. Rev. A 2012, 86, 033204. [Google Scholar] [CrossRef]
- Li, B.; O’Sullivan, G.; Dong, C. Relativistic R-matrix calculation photoionization cross section of Xe and Xe@C60. J. Phys. B 2013, 46, 155203. [Google Scholar] [CrossRef]
- Korol, A.V.; Solov’yov, A.V. Confinement resonances in the photoionization of endohedral atoms: Myth or reality? J. Phys. B 2010, 43, 201004. [Google Scholar] [CrossRef] [Green Version]
- Amusia, M.Y.; Baltenkov, A.S.; Chernysheva, L.V.; Felfli, Z.; Msezane, A.Z. Dramatic distortion of the 4d giant resonance by the C60 fullerene shell. J. Phys. B 2005, 38, L169. [Google Scholar] [CrossRef] [Green Version]
- Dolmatov, V. On fullerene anions as sources of spin-polarized electrons. In Proceedings of the 12th European Conference on Atoms Molecules and Photons: Extended Abstracts (ECAMP 2016), Frankfurt am Main, Germany, 5–9 September 2016; p. 8. [Google Scholar]
- Edwards, A.C.; Lane, C.G.; Dolmatov, V.K. Spin-polarized electrons upon nondipole photodetachment of fullerene anions. J. Phys. Conf. Ser. 2017, 875, 032032. [Google Scholar] [CrossRef] [Green Version]
- Heinzmann, U.; Dil, J.H. Spin-orbit-induced photoelectron spin polarization in angle-resolved photoemission from both atomic and condensed matter targets. J. Phys. B 2012, 24, 173001. [Google Scholar] [CrossRef]
- Dolmatov, V.K.; Amusia, M.Y.; Chernysheva, L.V. On the e--C60 elastic angle-differential scattering cross section. J. Phys. Conf. Ser. 2020, 1412, 182011. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Chernysheva, L.V.; Dolmatov, V.K. Angle-differential elastic-electron scattering off C60: A simple semi-empirical theory versus experiment. J. Phys. B 2019, 52, 085201. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, H.; Boesten, L.; Onda, K.; Ohashi, O. Cross-beam experiment for the scattering of low-energy electron grom gas phase C60. J. Phys. Soc. Jpn. 1994, 63, 485. [Google Scholar] [CrossRef]
- Winstead, C.; McKoy, V. Elastic electron scattering by fullerene, C60. Phys. Rev. A 2006, 73, 012711. [Google Scholar] [CrossRef] [Green Version]
- Cherepkov, N.A. Angular distribution of photoelectrons with a given spin orientation. Sov. Phys. JETP 1974, 38, 463. [Google Scholar]
- Cherepkov, N.A. Spin polarization of photoelectrons ejected from unpolarized atoms. J. Phys. B 1983, 12, 1279. [Google Scholar] [CrossRef]
- Jaskólski, W. Confined many-electron systems. Phys. Rep. 1996, 271, 1. [Google Scholar] [CrossRef]
- Buchachenko, A.L. Compressed atoms. J. Phys. Chem. B 2001, 105, 5839. [Google Scholar] [CrossRef]
- Sabin, J.R.; Brändas, E.; Cruz, S.A. (Eds.) Advances in Quantum Chemistry: Theory of Confined Quantum Systems. Part 1; Academic: New York, NY, USA, 2009; Volume 57, pp. 1–334. [Google Scholar]
- Sabin, J.R.; Brändas, E.; Cruz, S.A. (Eds.) Advances in Quantum Chemistry: Theory of Confined Quantum Systems. Part 2; Academic: New York, NY, USA, 2009; Volume 58, pp. 1–297. [Google Scholar]
- Connerade, J.-P.; Kengkanb, P.; Semaounea, R. Confined Atoms in Clusters, Bubbles, Dots and Fullerenes. J. Chin. Chem. Soc. 2001, 48, 265. [Google Scholar] [CrossRef]
- Connerade, J.-P. 2013 From Pauli’s birthday to “Confinement Resonances” —A potted history of Quantum Confinement. J. Phys. Conf. Ser. 2013, 438, 012001. [Google Scholar] [CrossRef]
- Sen, K.D. (Ed.) Electronic Structure of Quantum Confined Atoms and Molecules; Springer: New York, NY, USA, 2014; pp. 1–253. [Google Scholar]
- Ley-Koo, E. Recent progress in confined atoms and molecules: Superintegrability and symmetry breakings. Rev. Mex. Fis. 2018, 64, 326. [Google Scholar] [CrossRef] [Green Version]
- Chakraborty, H.S.; Deshmukh, P.C.; Manson, S.T. Interchannel-coupling effects in the spin polarization of energetic photoelectrons. Phys. Rev. A 2003, 67, 052701. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, V.K. Theoretical studies of photodetachment. Radiat. Phys. Chem. 2004, 70, 345. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Baltenkov, A.S. On the possibility of considering the fullerene shell C60 as a conducting sphere. Phys. Lett. A 2006, 360, 294. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.-S.; Conceicao, J.; Jin, C.; Smalley, R.E. Threshold photodetachment of cold C. Chem. Phys. Lett. 1991, 182, 5. [Google Scholar] [CrossRef]
- Connerade, J.-P.; Dolmatov, V.K.; Manson, S.T. On the nature and origin of confinement resonances. J. Phys. B 2000, 33, 2279. [Google Scholar] [CrossRef]





© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dolmatov, V.K. Spin-Polarized Photoelectron Fluxes from Fullerene Anions. Atoms 2020, 8, 65. https://doi.org/10.3390/atoms8040065
Dolmatov VK. Spin-Polarized Photoelectron Fluxes from Fullerene Anions. Atoms. 2020; 8(4):65. https://doi.org/10.3390/atoms8040065
Chicago/Turabian StyleDolmatov, Valeriy K. 2020. "Spin-Polarized Photoelectron Fluxes from Fullerene Anions" Atoms 8, no. 4: 65. https://doi.org/10.3390/atoms8040065
APA StyleDolmatov, V. K. (2020). Spin-Polarized Photoelectron Fluxes from Fullerene Anions. Atoms, 8(4), 65. https://doi.org/10.3390/atoms8040065



