Calculation of Electron Impact Single Ionization TDCS of Tungsten Atoms at 200, 500 and 1000 eV
Abstract
:1. Introduction
2. Theory
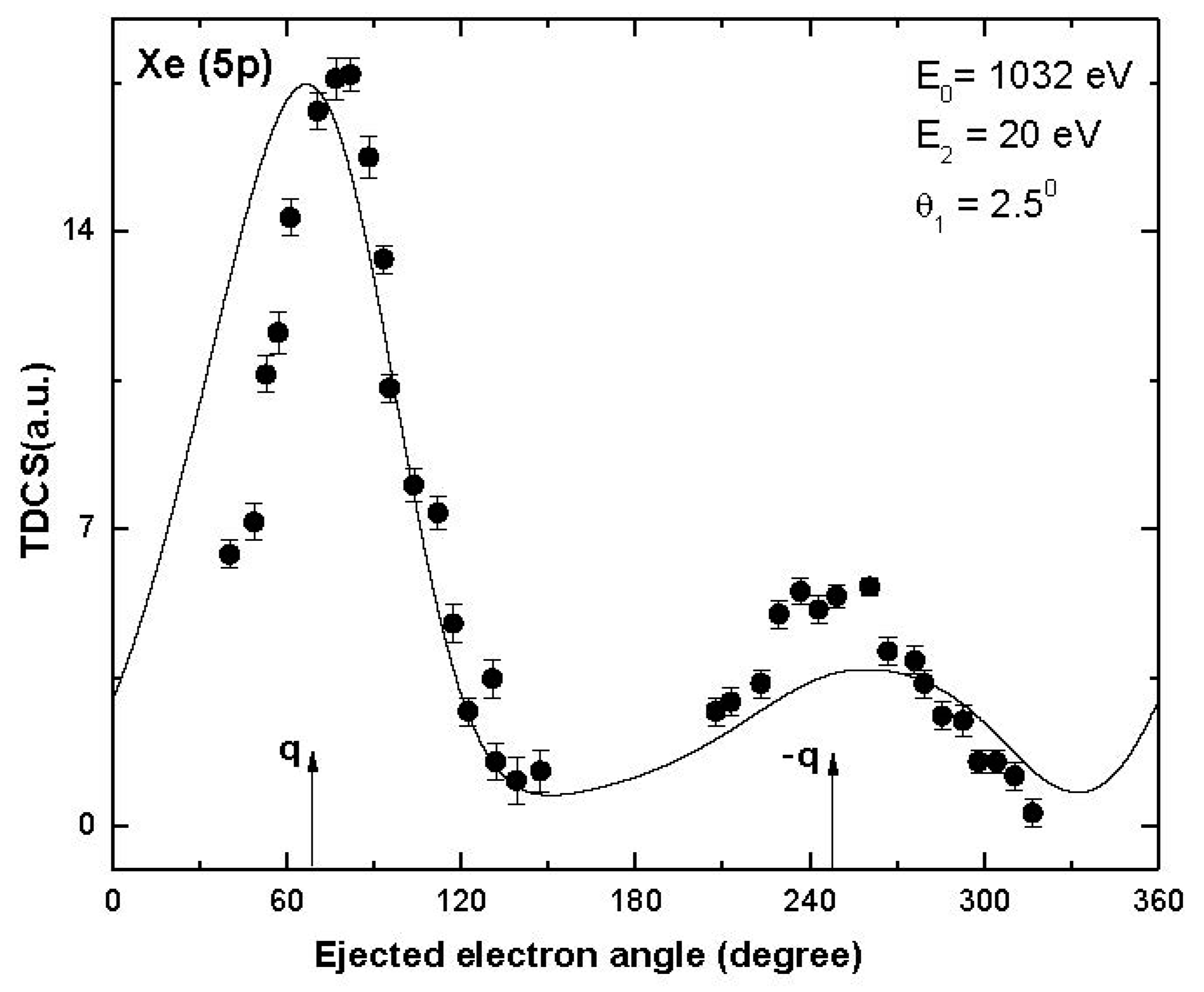
3. Results and Discussion
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Ehrhardt, H.; Hesselbacher, K.H.; Jung, K.; Willmann, K. Collisional Ionization of Helium by Slow Electrons. J. Phys. B 1972, 5, 1559. [Google Scholar] [CrossRef]
- Madison, D.H. Full Second-Order Distorted Wave Calculation Without Approximations for Atomic Excitation by Electron Impact. Phys. Rev. Lett. 1984, 53, 42. [Google Scholar] [CrossRef]
- Lahmam-Bennani, A. Recent developments and New Trends in (e, 2e) and (e, 3e) Studies. J. Phys. B At. Mol. Opt. Phys. 1991, 24, 2401. [Google Scholar] [CrossRef]
- Rescigno, T.N.; Baertschy, M.W.; Isaacs, A.; McCurdy, C.W. Collisional Breakup in a Quantum System of Three Charged Particles. Science 1999, 286, 2474. [Google Scholar] [CrossRef] [PubMed]
- Nakel, W.; Whelan, C.T. Relativistic (e, 2e) Processes. Phys. Rep. 1999, 315, 409. [Google Scholar] [CrossRef]
- Bray, I.; Fursa, D.V.; Kheifets, A.S.; Stelbovics, A.T. Electtrons and Photons Colliding With Atoms: Development and Application of the Convergent Close-Coupling Method. J. Phys. B 2002, 35, R117. [Google Scholar] [CrossRef]
- Bartschat, K.; Vorov, O. Channel-coupling, Target-structure and Second-order Effects in Electron-impact Ionization of Ar (3p) and Ar (3s). Phys. Rev. A 2005, 72, 022728. [Google Scholar] [CrossRef]
- Purohit, G.; Patidar, V.; Sud, K.K. Triple Differential Cross Section of Potassium for Doubly Symmetric Ionization. Phys. Lett. A. 2010, 374, 2654. [Google Scholar] [CrossRef]
- Purohit, G.; Singh, P.; Patidar, V.; Azuma, Y.; Sud, K.K. Effect of Target Polarization and Post Collision Interaction on the Electron Impact Single Ionization of Ne (2p), Ar (3p) and Na (3s) atoms. Phys. Rev. A. 2012, 85, 022714. [Google Scholar] [CrossRef]
- Madison, D.H.; Al-Hagan, O. The Distorted-Wave Born Approach for Calculating Electron-Impact Ionization of Molecules. J. At. Mol. Opt. Phys. 2010, 2010, 367180. [Google Scholar] [CrossRef]
- Purohit, G.; Kato, D. Calculation for Electron Impact Ionization of Be atoms and its charged states Be+ and Be+2. J. Phys. B At. Mol.Opt. Phys. 2018, 51, 135201. [Google Scholar] [CrossRef]
- Purohit, G.; Kato, D. Projectile Charge Effects on the Differential Cross Sections for the Ionization of Molecular Nitrogen by Positrons and Electrons. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 135202. [Google Scholar] [CrossRef]
- de Mars, C.M.; Ward, S.J.; Colgan, J.; Amami, S.; Madison, D.H. Deep Minima in the Triply Differential Cross Section for Ionization of Atomic Hydrogen by Electron and Positron Impact. Atoms 2020, 8, 26. [Google Scholar] [CrossRef]
- Pitts, R.A.; Carpentier, S.; Escourbiac, F.; Hirai, T.; Komarov, V.; Kukushkin, A.S.; Lisgo, S.; Loarte, A.; Merola, M.; Mitteau, R.; et al. Physics Basis and Design of the ITER Plasma-Facing Components. J. Nucl. Mater. 2011, 415, 5957. [Google Scholar] [CrossRef]
- Federici, G. Plasma Wall Interactions in ITER. Phys. Scr. 2006, T124, 1. [Google Scholar] [CrossRef]
- Neu, R.; Bobkov, V.; Dux, R.; Kallenbach, A.; Pütterich, T.; Greuner, H.; Gruber, O.; Herrmann, A.; Hopf, C.; Krieger, K.; et al. Final Steps to an All Tungsten Divertor Tokamak. J. Nucl. Mater. 2007, 52, 363–365. [Google Scholar]
- Balance, C.P.; Loch, S.D.; Pinzola, M.S.; Griffin, D.C. Electron Impact Excitation and Ionization of W3+ for the determination of tungsten influx in a fusion plasma. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 055202. [Google Scholar] [CrossRef]
- Spruck, K.; Becker, A.; Borovik, A., Jr.; Gharaibeh, M.F.; Rausch, J.; Schippers, S.; Muller, A. Electron-Impact Ionization of Multiply Charged Tungsten Ions. J. Phys. Conf. Ser. 2014, 488, 062026. [Google Scholar] [CrossRef] [Green Version]
- Muller, A. Fusion-Related Ionization and Recombination Data for Tungsten Ions in Low to Moderately High Charge States. Atoms 2015, 3, 120. [Google Scholar] [CrossRef] [Green Version]
- Pindzola, M.S.; Griffin, D.C. Electron-Impact Ionization of the Tungsten Atoms. Phys. Rev. A 1992, 46, 2486. [Google Scholar] [CrossRef]
- Deutsch, H.; Hilpert, K.; Becker, K.; Probst, M.; Märk, T.D. Calculated Absolute Electron-Impact Ionization Cross Sections for AlO, Al2O, and WOx (x = 1-3). J. Appl. Phys. 2001, 89, 1915. [Google Scholar] [CrossRef]
- Kwon, D.H.; Rhee, Y.J.; Kim, Y.K. Ionization of W and W+ by Electron Impact. Int. J. Mass Spectrom. 2006, 252, 213. [Google Scholar] [CrossRef]
- Vainshtein, L.; Beigman, I.; Mertens, P.; Brezinse, S.; Pospieszczykand, A.; Borodin, D. Ionization of W atoms and W+ ions by Electrons. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 125201. [Google Scholar] [CrossRef]
- Goswami, B.; Naghma, R.; Antony, B. Calculation of Electron Impact Total Ionization Cross sections for tungsten, uranium and their oxide radicals. Int. J. Mass Spectrom. 2014, 372, 8. [Google Scholar] [CrossRef]
- Pindzola, M.S.; Loch and, S.D.; Foster, A.R. Electron Impact Single and Double Ionization of W. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 095201. [Google Scholar] [CrossRef]
- Blanco, F.; Ferreira da Silva, F.; Limão-Vieiraand, P.; García, G. Electron Scattering Cross Section Data for Tungsten and Beryllium atoms from 0.1 to 5000 eV. Plasma Sources Sci. Technol. 2017, 26, 085004. [Google Scholar] [CrossRef] [Green Version]
- Purohit, G.; Kato, D.; Murakami, I. Electron Impact Ionization Cross Sections of Tungsten Atoms and Tungsten Ions. Plasma Fusion Res. 2018, 13, 3401026. [Google Scholar] [CrossRef]
- Purohit, G.; Kato, D.; Murakami, I.; Gupta, S.; Sinha, P. Calculation of Electron Induced Ionization Cross Sections of Fusion Plasma Relevant Material: W atoms. Eur. Phys. J. D. 2021, 75, 9. [Google Scholar] [CrossRef]
- Purohit, G. Electron Impact Single Ionization Differential Cross Sections of W(6s), W(5d), W(5p) and W(4f). J. Phys. B At. Mol. Opt. Phys. 2021, 54, 065203. [Google Scholar] [CrossRef]
- Purohit, G.; Kato, D. Dependence of Electron Impact Differential Cross Sections on the Ionic Charge to Mass Ratio for the A/3+(2p) and Be2+(1s) ions. J. Chem. Phys. 2018, 148, 084307. [Google Scholar] [CrossRef]
- Vahedi, V.; Surendra, M. A Monte Carlo Collision Model for the Particle-in-Cell Method: Applications to Argon and Oxygen Discharges. Comput. Phys. Commun. 1995, 87, 179. [Google Scholar] [CrossRef] [Green Version]
- Mclean, A.D.; Mclean, R.S. Roothaan-Hartree-Fock Atomic Wave Functions Slater Basis-Set Expansions for Z = 55-92. At. Data Nucl. Data Tab. 1981, 26, 287. [Google Scholar] [CrossRef]
- Furness, J.B.; McCarthy, I.E. Semiphenomenological Optical Model for Electron Scattering on Atoms. J. Phys. B. 1973, 6, 2280. [Google Scholar] [CrossRef]
- Riley, M.E.; Truhlar, D.G. Approximations for the Exchange Potential in Electron Scattering. J. Chem. Phys. 1975, 63, 2182. [Google Scholar] [CrossRef]
- McCarthy, I.E. Distorted-Wave Born and Impulse Approximations for Electron-Atom Ionisation. Aust. J. Phys. 1995, 48, 1. [Google Scholar] [CrossRef]
- Rasch, J.; Zitnik, M.; Avaldi, L.; Colm, T.; Whelan, G.; Stefani, R.; Camilloni, R.; Allan, J.; Walters, H.R.J. Theoretical and Experimental Investigation of the Triple-Differential Cross Sections for Electron-Impact Ionization of Kr(4p) and Xe(5p) at 1-keV Impact Energy. Phys. Rev. A. 1997, 56, 4644. [Google Scholar] [CrossRef]
- Purohit, G.; Singh, P.; Patidar, V. Fully Differential Cross Sections for Low to Intermediate Energy Perpendicular Plane Ionization of Xenon Atoms. J. Elec. Spec. Rel. Phenom. 2014, 197, 50. [Google Scholar] [CrossRef]
- Purohit, G.; Patidar, V.; Sud, K.K. Importance of Polarization Effects in Electron Impact Single Ionization of Argon Atom. J. Elec. Spec. Rel. Phenom. 2009, 175, 1. [Google Scholar] [CrossRef]

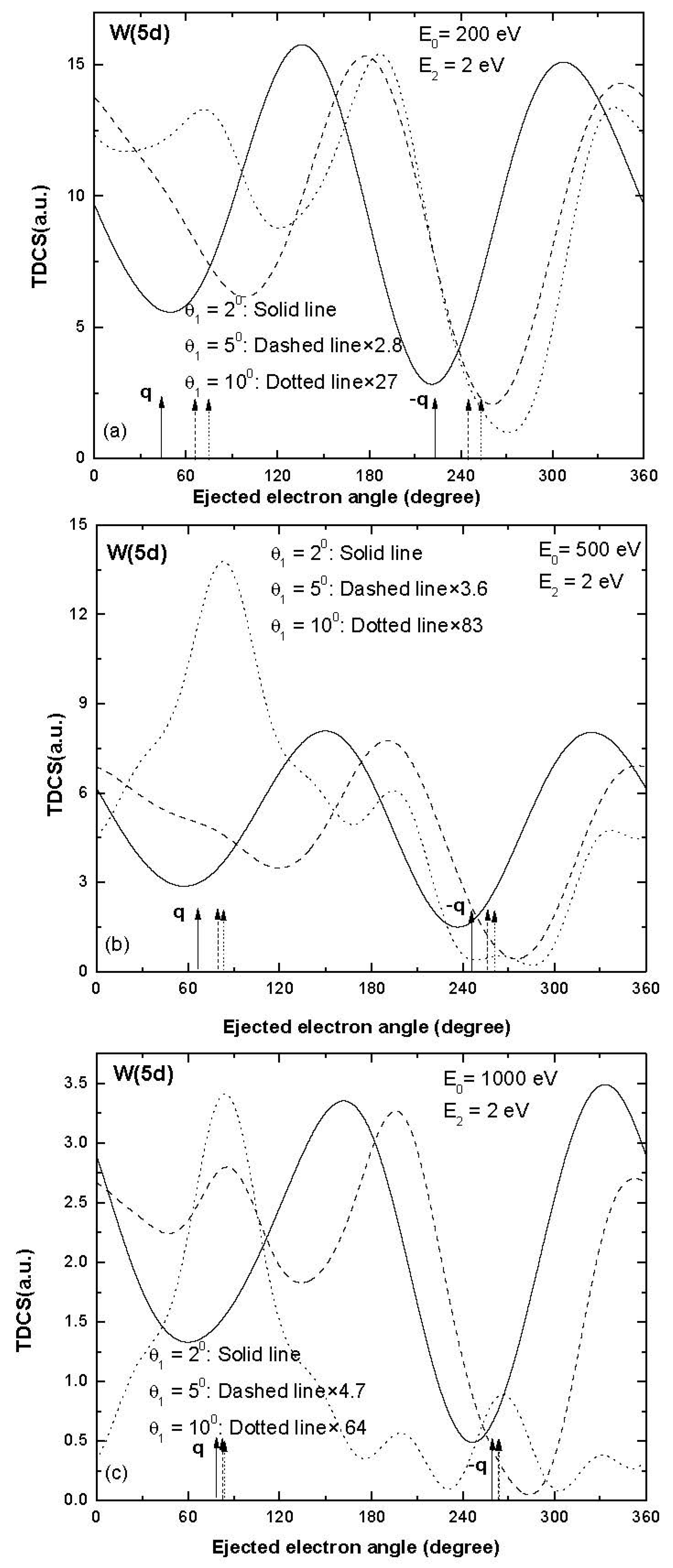
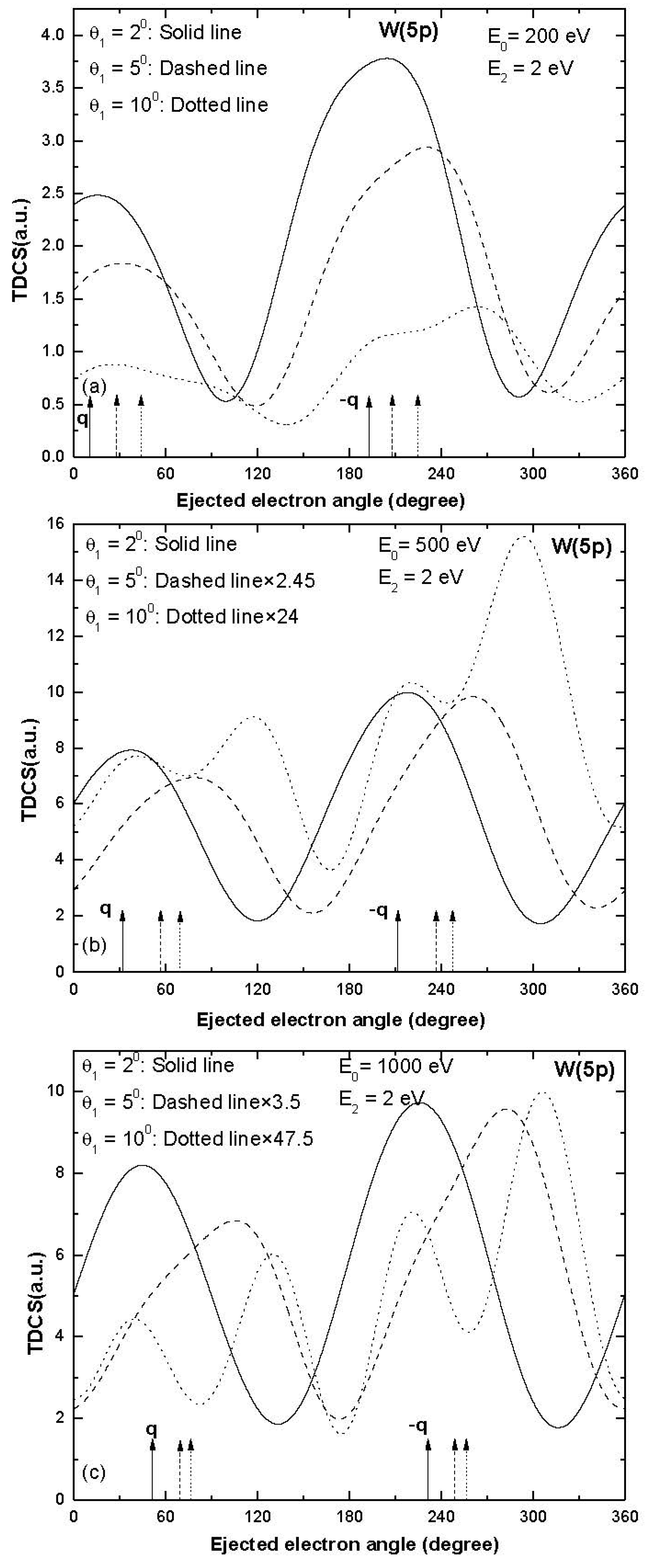
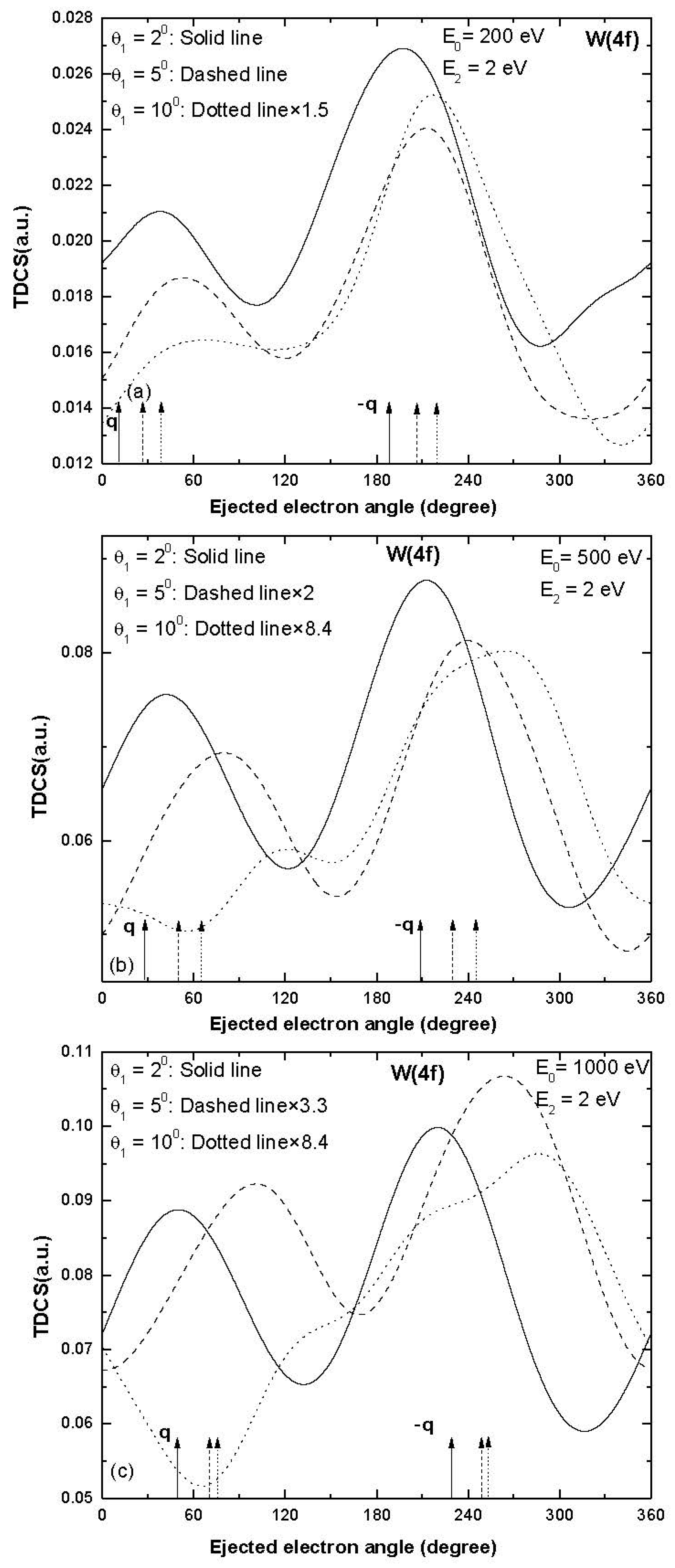
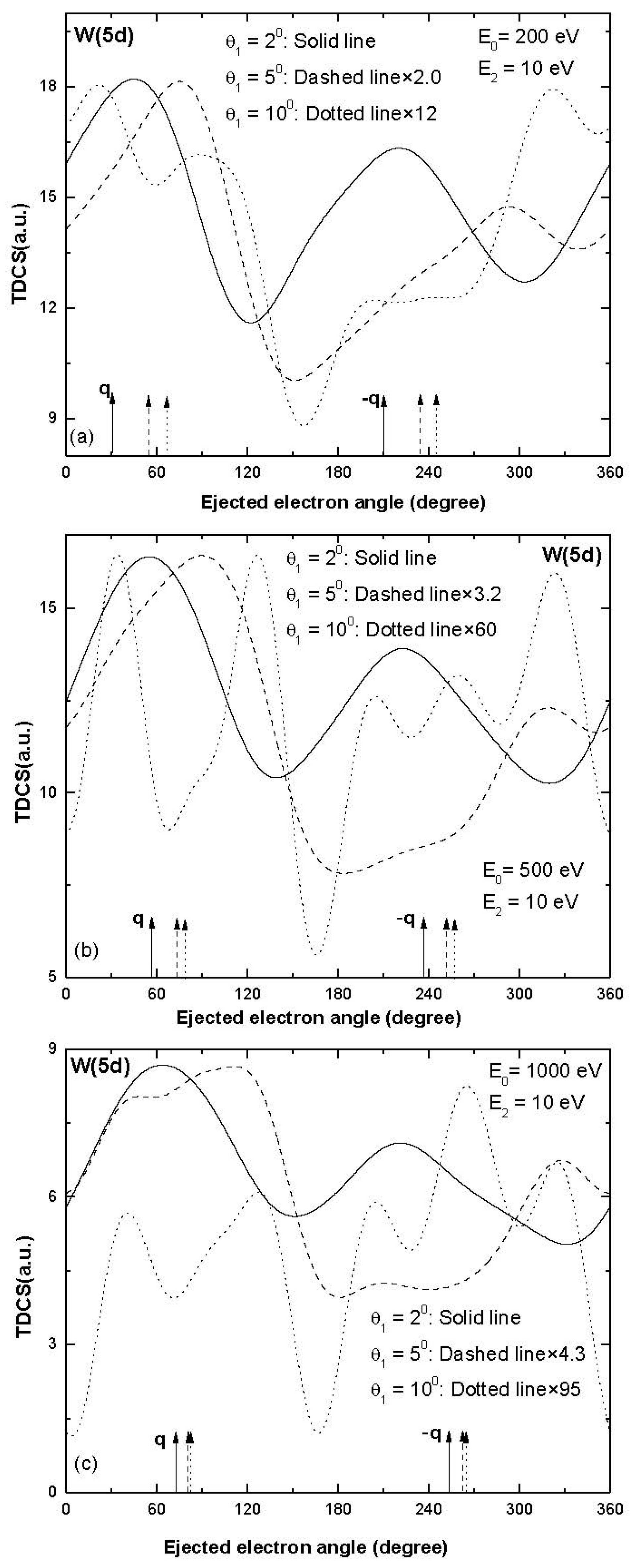
| Sub-Shell | Incident Electron Energy (eV), Ejected Electron Energy (eV) | Scattered Electron Angle (Degree) | Momentum Transfer Value (a.u.) | Momentum Transfer Direction (Degree) |
|---|---|---|---|---|
| W(6s) | 200, 2 | 2° | 0.15 | 59 |
| 5° | 0.34 | 74 | ||
| 10° | 0.67 | 78 | ||
| 500, 2 | 2° | 0.22 | 76 | |
| 5° | 0.53 | 82 | ||
| 10° | 1.1 | 82 | ||
| 1000, 2 | 2° | 0.3 | 82 | |
| 5° | 0.75 | 85 | ||
| 10° | 1.5 | 84 | ||
| W(5d) | 200, 2 | 2° | 0.19 | 44 |
| 5° | 0.35 | 65 | ||
| 10° | 0.67 | 74 | ||
| 500, 2 | 2° | 0.23 | 67 | |
| 5° | 0.53 | 79 | ||
| 10° | 1.1 | 81 | ||
| 1000, 2 | 2° | 0.30 | 78 | |
| 5° | 0.75 | 83 | ||
| 10° | 1.5 | 83 | ||
| W(5p) | 200, 2 | 2° | 0.54 | 12 |
| 5° | 0.61 | 28 | ||
| 10° | 0.81 | 45 | ||
| 500, 2 | 2° | 0.38 | 32 | |
| 5° | 0.60 | 56 | ||
| 10° | 1.07 | 68 | ||
| 1000, 2 | 2° | 0.37 | 52 | |
| 5° | 0.77 | 71 | ||
| 10° | 1.5 | 77 | ||
| W(4f) | 200, 2 | 2° | 0.62 | 11 |
| 5° | 0.68 | 25 | ||
| 10° | 0.86 | 41 | ||
| 500, 2 | 2° | 0.42 | 29 | |
| 5° | 0.63 | 52 | ||
| 10° | 1.1 | 66 | ||
| 1000, 2 | 2° | 0.39 | 48 | |
| 5° | 0.78 | 69 | ||
| 10° | 1.5 | 73 | ||
| W(5d) | 200, 10 | 2° | 0.25 | 30 |
| 5° | 0.39 | 54 | ||
| 10° | 0.68 | 67 | ||
| 500, 10 | 2° | 0.25 | 57 | |
| 5° | 0.54 | 73 | ||
| 10° | 1.05 | 77 | ||
| 1000, 10 | 2° | 0.31 | 72 | |
| 5° | 0.75 | 80 | ||
| 10° | 1.5 | 81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Purohit, G. Calculation of Electron Impact Single Ionization TDCS of Tungsten Atoms at 200, 500 and 1000 eV. Atoms 2021, 9, 31. https://doi.org/10.3390/atoms9020031
Purohit G. Calculation of Electron Impact Single Ionization TDCS of Tungsten Atoms at 200, 500 and 1000 eV. Atoms. 2021; 9(2):31. https://doi.org/10.3390/atoms9020031
Chicago/Turabian StylePurohit, Ghanshyam. 2021. "Calculation of Electron Impact Single Ionization TDCS of Tungsten Atoms at 200, 500 and 1000 eV" Atoms 9, no. 2: 31. https://doi.org/10.3390/atoms9020031
APA StylePurohit, G. (2021). Calculation of Electron Impact Single Ionization TDCS of Tungsten Atoms at 200, 500 and 1000 eV. Atoms, 9(2), 31. https://doi.org/10.3390/atoms9020031





