Few Body Effects in the Electron and Positron Impact Ionization of Atoms
Abstract
:1. Introduction
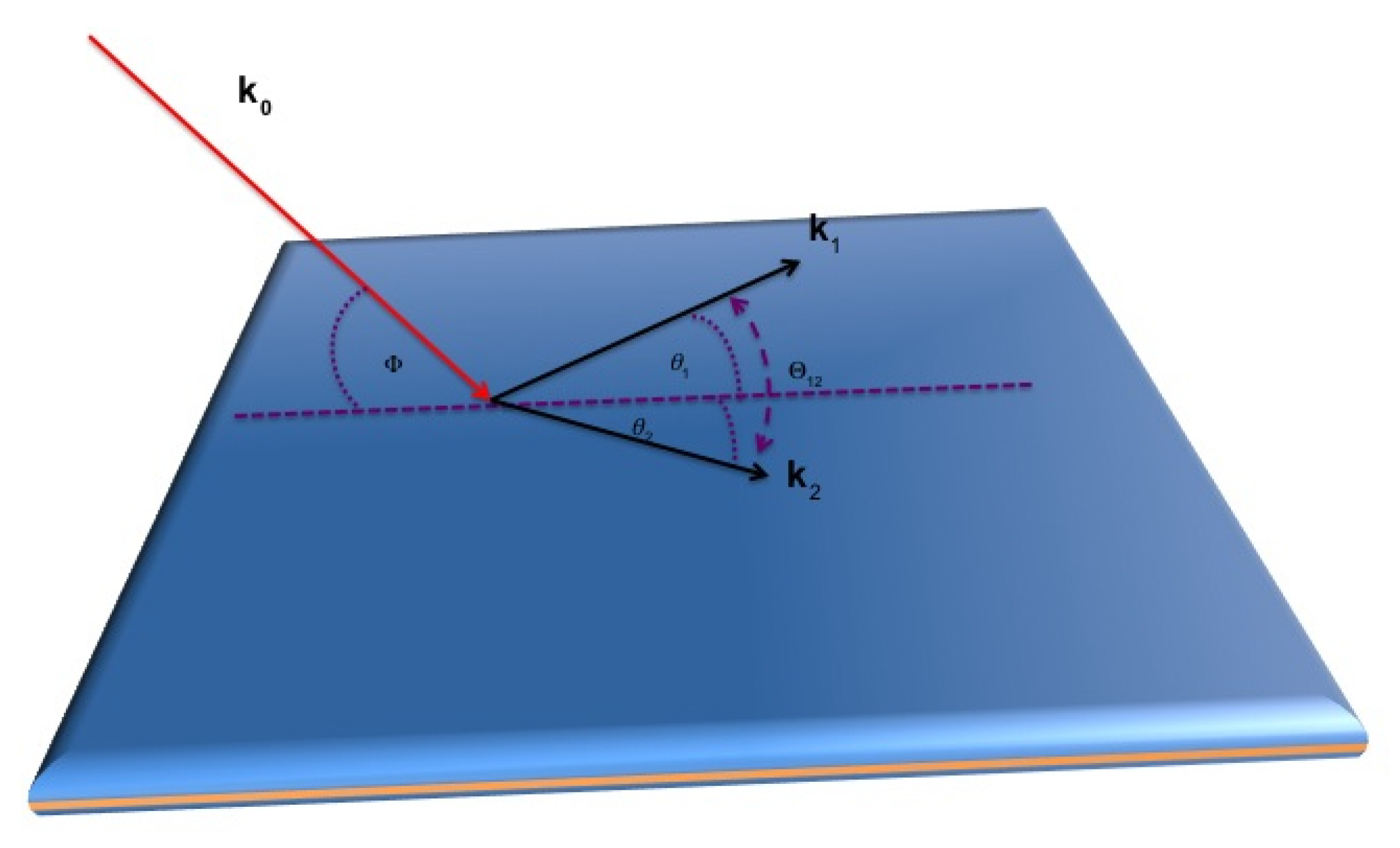
2. Scattering Approximations
2.1. Electron Impact
2.2. Positron Scattering
3. Results
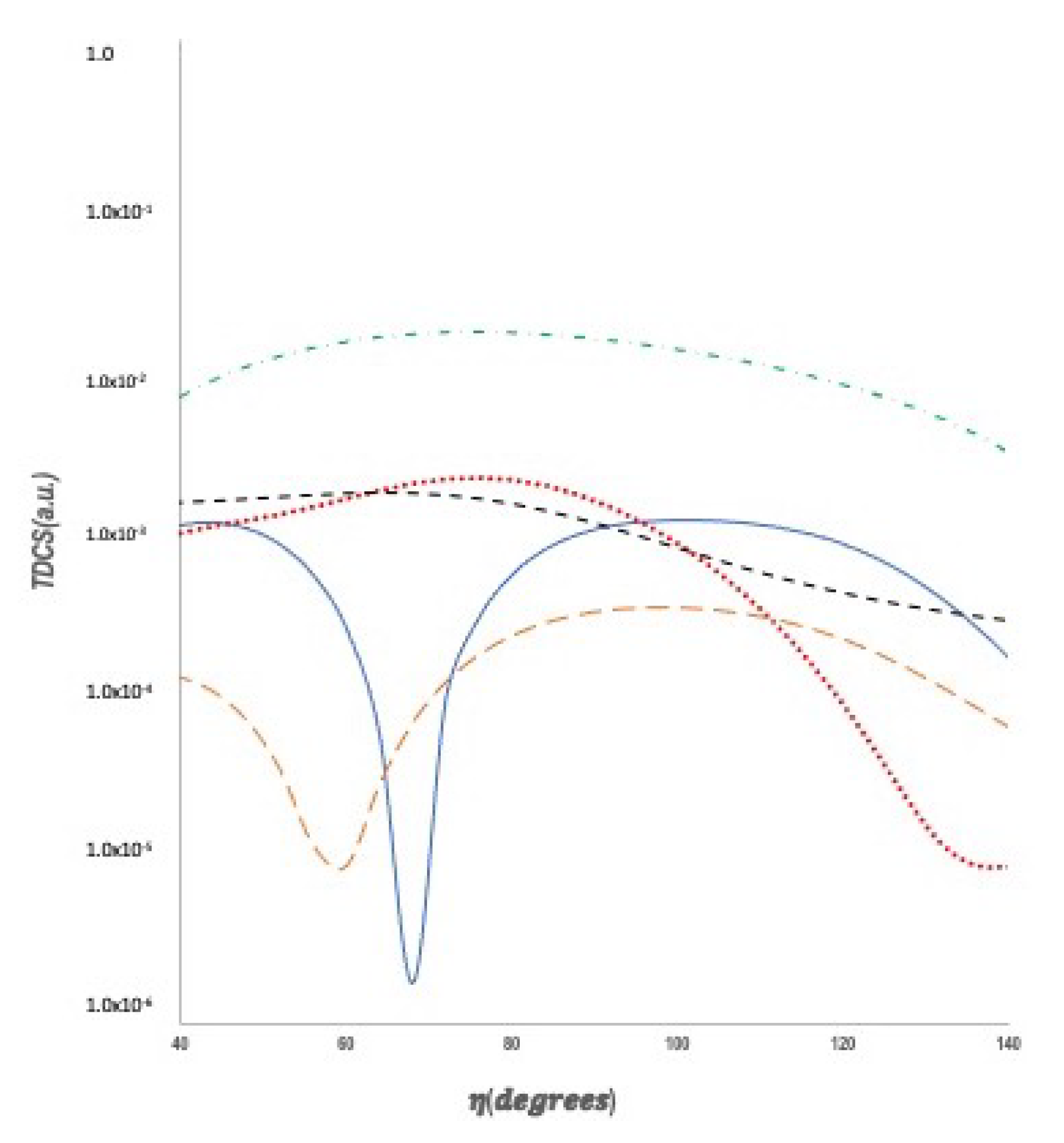
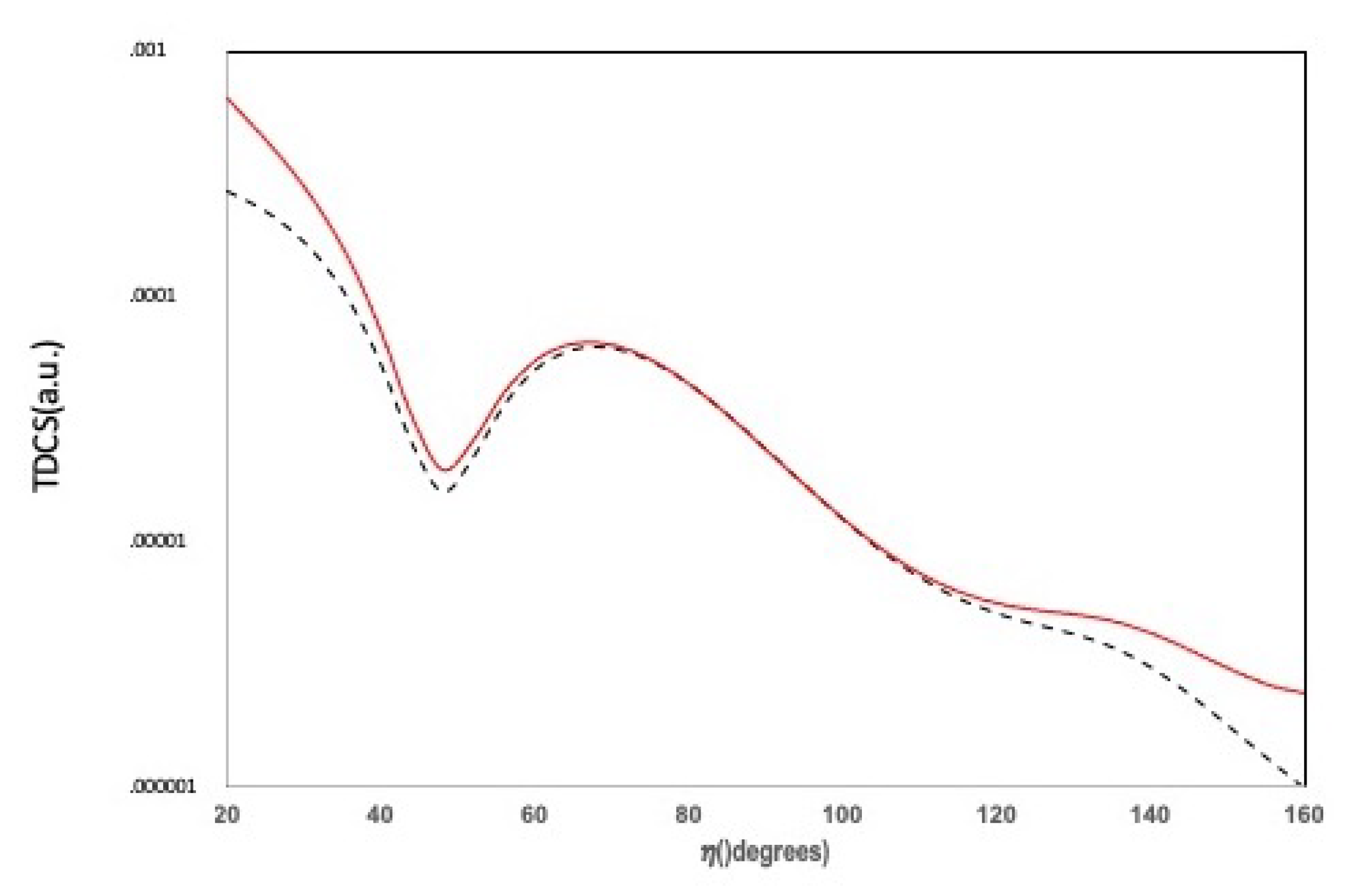
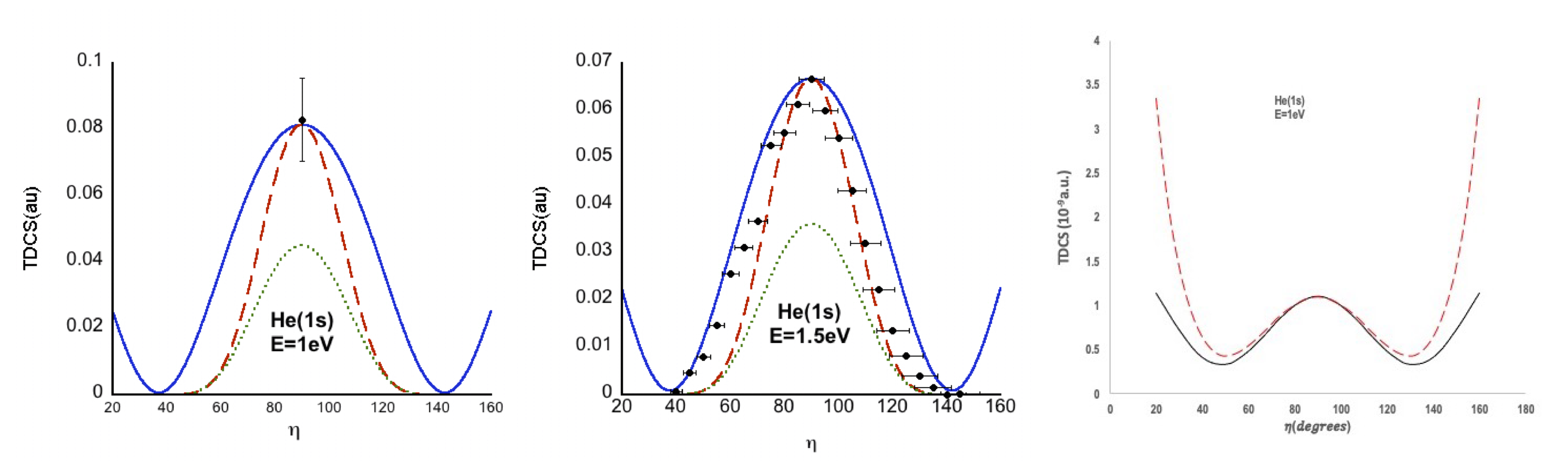
3.1. Coplanar Symmetric Geometry
3.2. Non Coplanar Energy Sharing Geometries
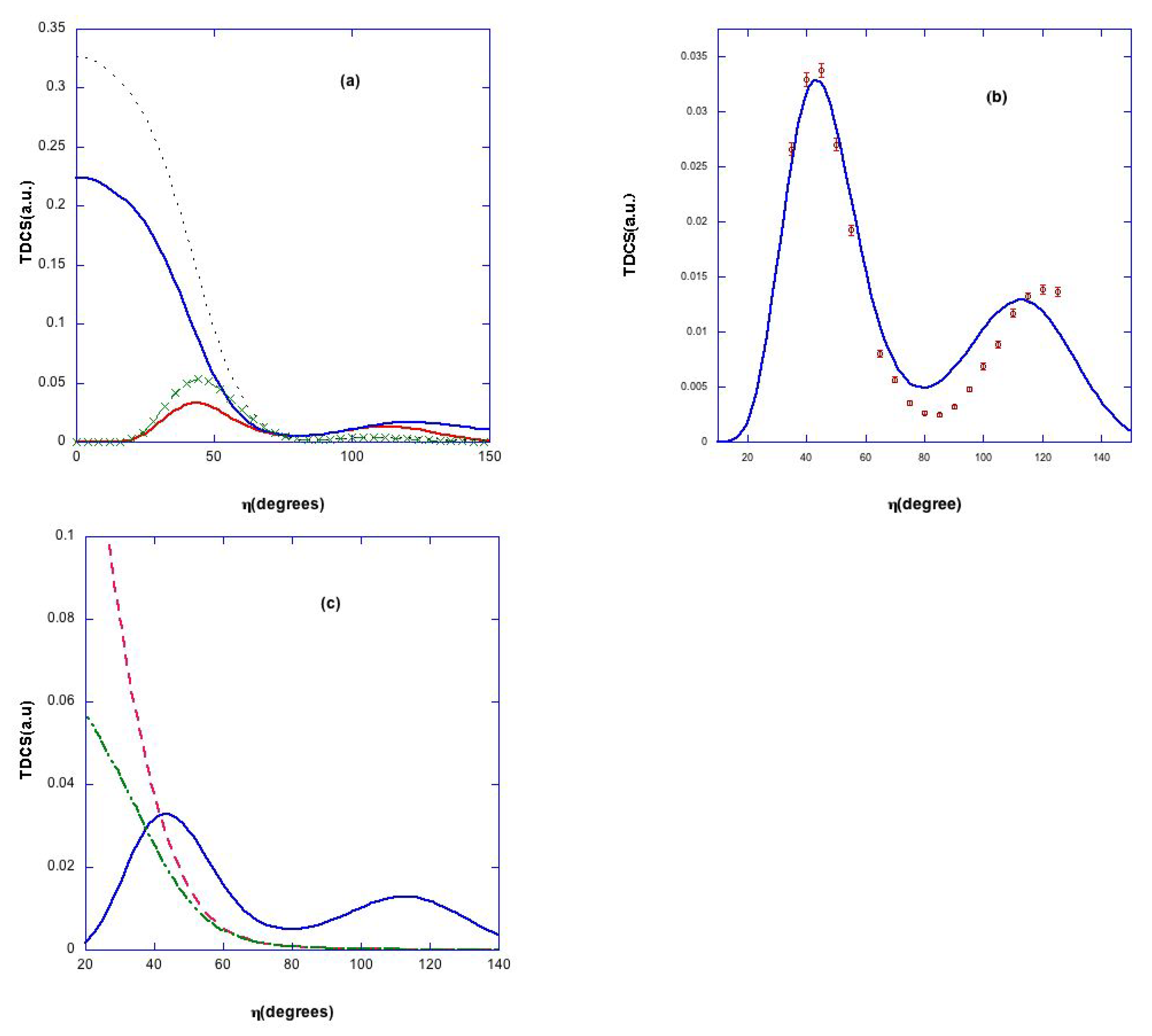
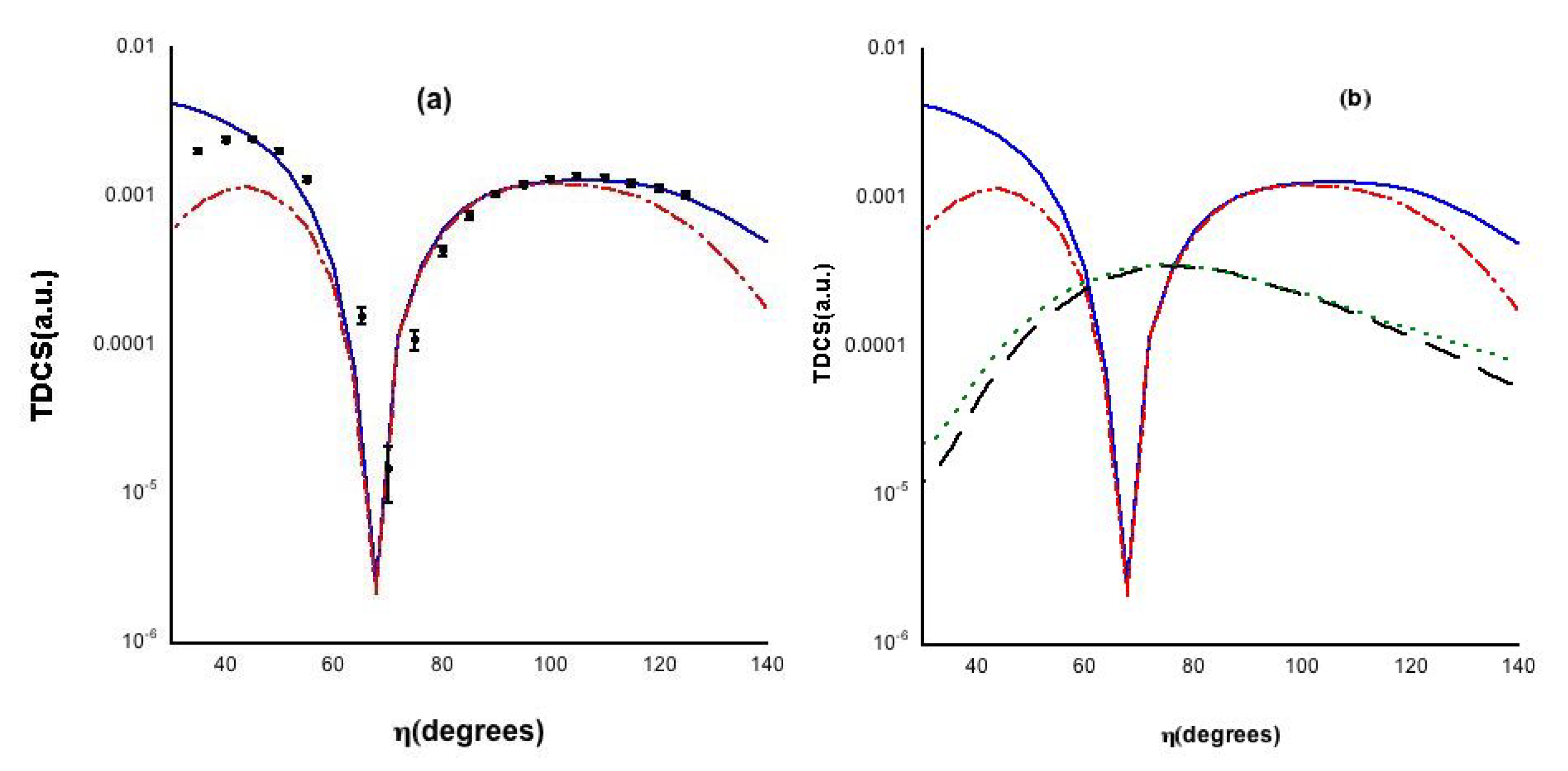
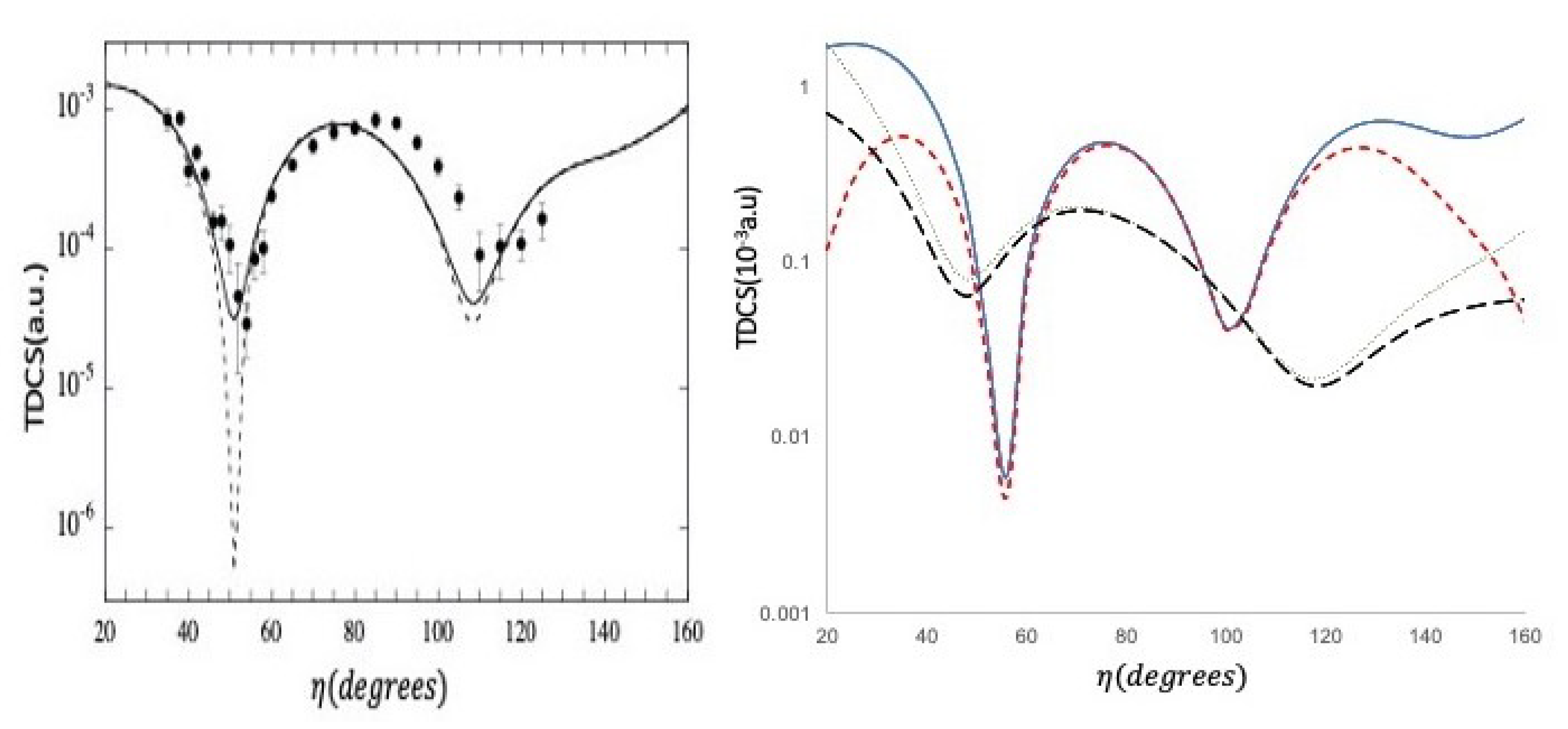
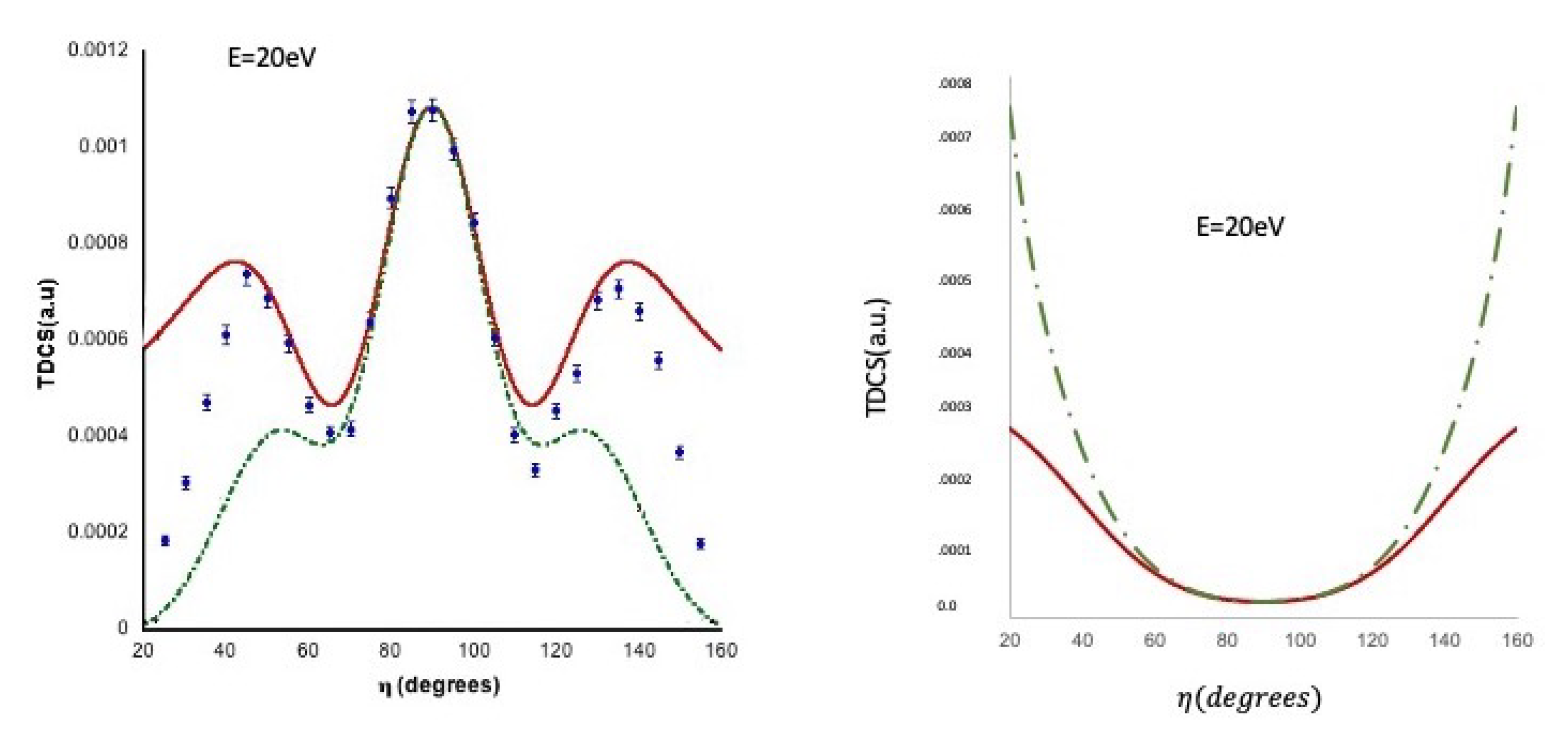
3.3. Energy Sharing Perpendicular Plane Geometry
- Single scattering: For a free collision between an incident and a stationary electron resulting in two outgoing electrons of equal energy, conservation of energy and momentum requires all three vectors to lie in the same plane with . Now, the atomic electron is not free but rather in a bound state with a momentum distribution, for both electrons to end up in the perpendicular plane as the result of a single collision, the incoming electron would have to collide with a bound electron that had momentumwhere , thus both electrons will emerge in the perpendicular plane with momentum . Since the electron distribution in the helium atom is sharply peaked to zero, the most probable value will beThus, for single scattering, one would expect a single peak at . This is purely a wavefunction effect, and it would be misleading to interpret the back to back emission as being in some way related to the Wannier mechanism [37], since the peak is seen in the DWBA without pci.
- Double scattering: here, the incoming electron is first elastically scattered into the plane perpendicular to the incoming beam and then in a second collision ionizes the atom with both final state electrons coming out at roughly to each other.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Du Bois, R.D.; Gavin, J.; de Lucio, O.G. Differential cross sections for ionization of argon by 1 keV positron and electron impact. J. Phys. Conf. Ser. 2014, 488, 072004. [Google Scholar] [CrossRef] [Green Version]
- Gavin, J.; de Lucio, O.G.; DuBois, R.D. Triply differential measurements of single ionization of argon by 1-keV positron and electron impact. Phys. Rev. A 2017, 95, 062703. [Google Scholar] [CrossRef] [Green Version]
- Campeanu, R.I.; Walters, H.R.J.; Whelan, C.T. The electron and positron impact ionization of inert gases. Phys. Rev. A 2018, 97, 062702. [Google Scholar] [CrossRef] [Green Version]
- Miller, F.K.; Whelan, C.T.; Walters, H.R.J. Energy sharing (e,2e) collisions-ionization of the inert gases in the perpendicular plane. Phys. Rev. A 2015, 91, 012706. [Google Scholar] [CrossRef]
- Curran, E.P.; Whelan, C.T.; Walters, H.R.J. On the electron impact ionisation of H(1s) in coplanar asymmetric geometry. J. Phys. B At. Mol. Opt. Phys. 1991, 24, L19. [Google Scholar] [CrossRef]
- Lucey, S.P.; Rasch, J.; Whelan, C.T. On the use of analytic ansatz wavefunctions in the study of (e,2e) processes. Proc. R. Soc. A 1999, 455, 349. [Google Scholar] [CrossRef]
- Rasch, J.; Whelan, C.T.; Allan, R.J.; Walters, H.R.J. The normalization of the experimental triple differential cross section of noble gas atoms in extreme asymmetric geometry. In Electron and Photon Impact Ionization; Whelan, C.T., Walters, H.R.J., Eds.; Plenum: New York, NY, USA, 1997; pp. 305–318. [Google Scholar]
- Walters, H.R.J. Perturbative methods in electron- and positron-atom scattering. Phys. Rep. 1984, 116, 1. [Google Scholar] [CrossRef]
- Curran, E.P.; Walters, H.R.J. Triple differential cross sections for electron impact ionisation of atomic hydrogen—A coupled pseudostate calculation. J. Phys. B At. Mol. Opt. Phys. 1987, 20, 333. [Google Scholar] [CrossRef]
- Bartlett, P.L.; Stelbovics, A.T. The application of propagating exterior complex scaling in atomic collisions. In Fragmentation Processes: Topics in Atomic and Molecular Physics; Whelan, C.T., Ed.; Cambridge University Press: Cambridge, UK, 2013; pp. 48–71. [Google Scholar]
- Madision, D.H.; Calhoun, R.V.; Shelton, W.N. Triple-differential cross sections for electron-impact ionization of helium. Phys. Rev. A 1977, 16, 552. [Google Scholar] [CrossRef]
- Whelan, C.T.; Allan, R.J.; Walters, H.R.J.; Zhang, X. (e,2e), effective charges, distorted waves and all that ! In (e, 2e) & Related Processes; Whelan, C.T., Walters, H.R.J., Lahmam-Bennani, A., Ehrhardt, H., Eds.; Kluwer: Dordrecht, The Netherlands, 1993; pp. 33–74. [Google Scholar]
- Rasch, J. (e,2e) Processes with Neutral Atom Targets. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 1996. [Google Scholar]
- Clementi, E.; Roetti, C. Roothan-Hartree-Fock atomic wavefunctions. At. Data Nucl. Data Tables 1974, 14, 177. [Google Scholar] [CrossRef]
- Furness, J.B.; Carthy, I.E.M. Semi phenomenological optical model for electron scattering. J. Phys. B At. Mol. Opt. Phys. 1973, 6, 2280. [Google Scholar] [CrossRef]
- Riley, M.E.; Truhlar, D.G. Approximations for exchange potentials in electron scattering. J. Chem. Phys. 1975, 63, 2182. [Google Scholar] [CrossRef]
- Martinez, J.M.; Walters, H.R.J.; Whelan, C.T. The electron impact ionization of one and two electron atoms and ions close to the ionization threshold. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 065202. [Google Scholar] [CrossRef]
- Bransden, B.H.; McDowell, M.R.C.; Noble, C.J.; Scott, T. Equivalent exchange potentials in electron scattering. J. Phys. B At. Mol. Opt. Phys. 1976, 9, 1301. [Google Scholar] [CrossRef]
- Zhang, X.; Whelan, C.T.; Walters, H.R.J. (e,2e) cross sections for the ionisation of helium in coplanar symmetric geometry. J. Phys. B At. Mol. Opt. Phys. 1990, 23, L509. [Google Scholar] [CrossRef]
- Rasch, J.; Whelan, C.T.; Allan, R.J.; Lucey, S.P.; Walters, H.R.J. Strong interference effects in the triple differential cross section of neutral atom targets. Phys. Rev. A 1997, 56, 1379. [Google Scholar] [CrossRef]
- Botero, J.; Macek, J.H. Threshold angular distributions of(e,2e) cross sections of helium atoms. Phys. Rev. Lett. 1992, 68, 576. [Google Scholar] [CrossRef]
- Ward, S.J.; Macek, J.H. Wave functions for continuum states of charged fragments. Phys. Rev. A 1994, 49, 1049. [Google Scholar] [CrossRef]
- Pochat, A.; Tweed, R.J.; Peresses, J.; Joachain, J.; Piraux, C.B.; Byron, F.W., Jr. Second-order effects in large-angle coplanar symmetric (e, 2e) processes. J. Phys. B At. Mol. Opt. Phys. 1983, 16, L755. [Google Scholar] [CrossRef]
- Rösel, T.; Dupré, C.; Röder, J.; Duguet, A.; Jung, K.; Lahmam-Bennani, A.; Ehrhardt, H. Coplanar symmetric(e,2e) cross sections on helium and neon. J. Phys. B At. Mol. Opt. Phys. 1991, 24, 3059. [Google Scholar] [CrossRef]
- Frost, L.; Freienstein, P.; Wagner, M. 200 eV coplanar symmetric (e,2e) on helium: A sensitive test of reaction models. J. Phys. B At. Mol. Opt. Phys. 1990, 23, L715. [Google Scholar] [CrossRef]
- Zhang, X.; Whelan, C.T.; Walters, H.R.J. Energy sharing (e,2e) collisions-ionisation of Helium in the perpendicular plane. J. Phys. B At. Mol. Opt. Phys. 1990, 23, L173. [Google Scholar] [CrossRef]
- Murray, A.J. Electron impact ionization using (e,2e) coincidence techniques from threshold to intermediate energies. In Fragmentation Processes: Topics in Atomic and Molecular Physics; Whelan, C.T., Ed.; Cambridge University Press: Cambridge, UK, 2013; pp. 164–206. [Google Scholar]
- Whelan, C.T.; Allan, R.J.; Walters, H.R.J. PCI, polarisation and exchange effects in (e,2e) collisions. J. Phys. IV 1993, 3, C6. [Google Scholar] [CrossRef]
- Röder, J.; Rasch, J.; Jung, K.; Whelan, C.T.; Ehrhardt, H.; Allan, J.R.; Walters, H.R.J. Coulomb 3 body effects in low energy electron impact ionization of H(1s). Phys. Rev. A 1994, 53, 225. [Google Scholar] [CrossRef]
- Whelan, C.T.; Allan, R.J.; Rasch, J.; Walters, H.R.J.; Zhang, X.; Röder, J.; Jung, K.; Walters, H.R.J.; Ehrhardt, H. Coulomb 3-body effects in (e,2e) Collisions: The ionisation of H in coplanar symmetric geometry. Phys. Rev. A 1994, 50, 4394. [Google Scholar] [CrossRef]
- Murray, A.J. Electron impact ionization using (e,2e) coincidence techniques from threshold to intermediate energies. In (e, 2e) & Related Processes; Whelan, C.T., Walters, H.R.J., Lahmam-Bennani, A., Ehrhardt, H., Eds.; Kluwer: Dordrecht, The Netherlands, 1993; pp. 327–340. [Google Scholar]
- Rasch, J.; Whelan, C.T.; Allan, R.J.; Walters, H.R.J. An explanation of the structure observed in out of plane symmetric measurements on helium. In Electron and Photon Impact Ionization; Whelan, C.T., Walters, H.R.J., Eds.; Plenum: New York, NY, USA, 1997; pp. 185–193. [Google Scholar]
- Murray, A.J.; Read, F.H. Deep interference minima in experimental ionization differential cross sections. Phys. Rev. A 2000, 63, 012714. [Google Scholar] [CrossRef] [Green Version]
- DeMars, C.M.; Kent, J.B.; Ward, S.J. Deep minima in the Coulomb-Born triply differential cross sections for ionization of helium by electron and positron impact. Eur. Phys. J. D 2020, 74, 48. [Google Scholar] [CrossRef]
- DeMars, C.M.; Ward, S.J.; Colgan, J.; Amari, S.; Madison, D.H. Deep Minima in the Triply Differential Cross Section for Ionization of Atomic Hydrogen by Electron and Positron Impact. Atoms 2020, 8, 26. [Google Scholar] [CrossRef]
- Woolf, M.B.J. (e,2e) Measurements in the Perpendicular Plane. Ph.D. Thesis, University of Manchester, Manchester, UK, 1996. [Google Scholar]
- Wannier, G.H. The threshold law for single ionization of atoms or ions by electrons. Phys. Rev. 1953, 90, 817. [Google Scholar] [CrossRef]
- Ehrhardt, H.; Rösel, T. Near threshold (e,2e) ionisation of helium and atomic hydrogen. In (e, 2e) & Related Processes; Whelan, C.T., Walters, H.R.J., Lahmam-Bennani, A., Ehrhardt, H., Eds.; Kluwer: Dordrecht, The Netherlands, 1993; pp. 76–82. [Google Scholar]
- Rösel, T.; Röder, J.; Frost, L.; Jung, K.; Ehrhardt, H.; Jones, S.; Madison, D.H. Absolute triple differential cross section for ionization of helium near threshold. Phys. Rev. A 1992, 46, 2539. [Google Scholar] [CrossRef] [PubMed]
- Nixon, K.L.; Murray, A.J.; Kaiser, C. Low energy (e,2e) studies of the noble gases in the perpendicular plane. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 085202. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campeanu, R.I.; Whelan, C.T. Few Body Effects in the Electron and Positron Impact Ionization of Atoms. Atoms 2021, 9, 33. https://doi.org/10.3390/atoms9020033
Campeanu RI, Whelan CT. Few Body Effects in the Electron and Positron Impact Ionization of Atoms. Atoms. 2021; 9(2):33. https://doi.org/10.3390/atoms9020033
Chicago/Turabian StyleCampeanu, R.I., and Colm T. Whelan. 2021. "Few Body Effects in the Electron and Positron Impact Ionization of Atoms" Atoms 9, no. 2: 33. https://doi.org/10.3390/atoms9020033
APA StyleCampeanu, R. I., & Whelan, C. T. (2021). Few Body Effects in the Electron and Positron Impact Ionization of Atoms. Atoms, 9(2), 33. https://doi.org/10.3390/atoms9020033





