Asymmetric Lineshapes of Efimov Resonances in Mass-Imbalanced Ultracold Gases
Abstract
1. Introduction
2. General Considerations and Methods
2.1. The Adiabatic Hyperspherical Representation and the Semi-Classical Approach
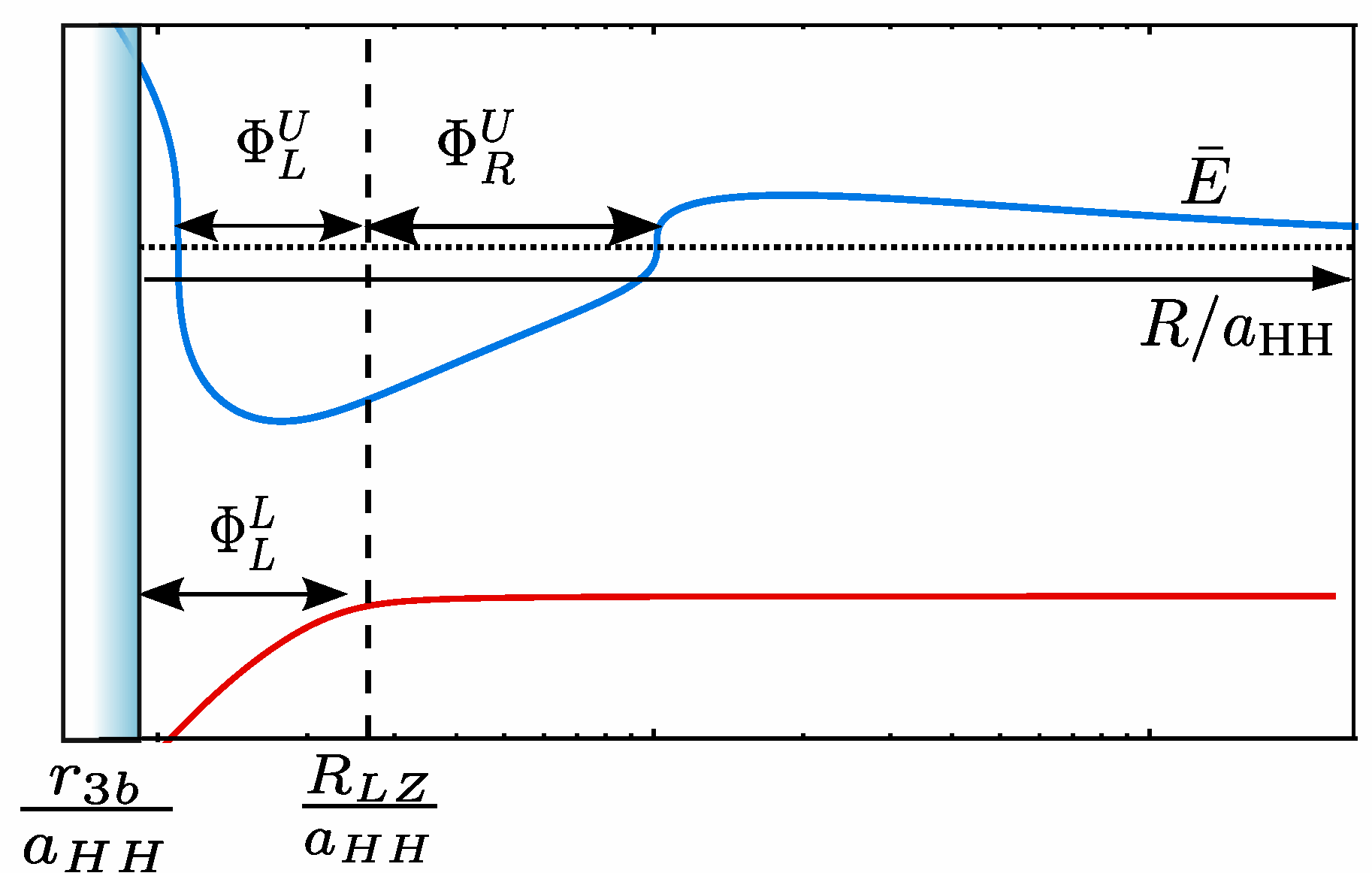
2.2. A Simplified Semi-Classical Model
3. Asymmetric Lineshapes in Three-Body Recombination Coefficients
4. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nielsen, E.; Fedorov, D.V.; Jensen, A.S.; Garrido, E. The three-body problem with short-range interactions. Phys. Rep. 2001, 347, 373–459. [Google Scholar] [CrossRef]
- Greene, C.H.; Giannakeas, P.; Pérez-Ríos, J. Universal few-body physics and cluster formation. Rev. Mod. Phys. 2017, 89, 035006. [Google Scholar] [CrossRef]
- Naidon, P.; Endo, S. Efimov Physics: A Review. Rep. Prog. Phys. 2017, 80, 056001. [Google Scholar] [CrossRef] [PubMed]
- D’Incao, J.P. Few-Body Physics in Resonantly Interacting Ultracold Quantum Gases. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 043001. [Google Scholar] [CrossRef]
- Efimov, V. Hard-core interaction and the three-nucleon problem. Sov. J. Nucl. Phys. 1970, 10, 62. [Google Scholar]
- Kraemer, T.; Mark, M.; Waldburger, P.; Danzl, J.G.; Chin, C.; Engeser, B.; Lange, A.D.; Pilch, K.; Jaakkola, A.; Nägerl, H.C.; et al. Evidence for Efimov quantum states in an ultracold gas of caesium atoms. Nature 2006, 440, 315–318. [Google Scholar] [CrossRef]
- Riisager, K. Nuclear halo states. Rev. Mod. Phys. 1994, 66, 1105–1116. [Google Scholar] [CrossRef]
- Braaten, E.; Hammer, H.W. Universality in few-body systems with large scattering length. Phys. Rep. 2006, 428, 259–390. [Google Scholar] [CrossRef]
- Rittenhouse, S.T.; von Stecher, J.; D’Incao, J.; Mehta, N.; Greene, C.H. The hyperspherical four-fermion problem. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 172001. [Google Scholar] [CrossRef]
- Blume, D. Few-body physics with ultracold atomic and molecular systems in traps. Rep. Prog. Phys. 2012, 75, 046401. [Google Scholar] [CrossRef]
- Wang, Y.; D’Incao, J.P.; Esry, B.D. Chapter 1—Ultracold Few-Body Systems. In Advances in Atomic, Molecular, and Optical Physics; Ennio Arimondo, P.R.B., Lin, C.C., Eds.; Academic Press: Berlin/Heidelberg, Germany, 2013; Volume 62, 115p. [Google Scholar]
- Wang, Y.; Julienne, P.; Greene, C.H. Few-body physics of ultracold atoms and molecules with long-range interactions. In Annual Review of Cold Atoms and Molecules; Madison, K.W., Bongs, K., Carr, L.D., Rey, A.M., Zhai, H., Eds.; World Scientific Press: Singapore, 2015; Volume 3, pp. 77–134. [Google Scholar]
- Huang, B.; Sidorenkov, L.A.; Grimm, R.; Hutson, J.M. Observation of the second triatomic resonance in Efimov’s scenario. Phys. Rev. Lett. 2014, 112, 190401. [Google Scholar] [CrossRef] [PubMed]
- Thomas, L.H. The interaction between a neutron and a proton and the structure of H3$. Phys. Rev. 1935, 47, 903–909. [Google Scholar] [CrossRef]
- Wang, Y.; Julienne, P.S. Universal van der Waals physics for three cold atoms near Feshbach resonances. Nat. Phys. 2014, 10, 768–773. [Google Scholar] [CrossRef]
- Roy, S.; Landini, M.; Trenkwalder, A.; Semeghini, G.; Spagnolli, G.; Simoni, A.; Fattori, M.; Inguscio, M.; Modugno, G. Test of the Universality of the Three-Body Efimov Parameter at Narrow Feshbach Resonances. Phys. Rev. Lett. 2013, 111, 053202. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; D’Incao, J.; Esry, B.; Greene, C.H. Origin of the three-body parameter universality in Efimov physics. Phys. Rev. Lett. 2012, 108, 263001. [Google Scholar] [CrossRef]
- Gross, N.; Shotan, Z.; Kokkelmans, S.; Khaykovich, L. Observation of universality in ultracold 7Li three-body recombination. Phys. Rev. Lett. 2009, 103, 163202. [Google Scholar] [CrossRef] [PubMed]
- Naidon, P.; Endo, S.; Ueda, M. Microscopic Origin and Universality Classes of the Efimov Three-Body Parameter. Phys. Rev. Lett. 2014, 112, 105301. [Google Scholar] [CrossRef]
- Naidon, P.; Endo, S.; Ueda, M. Physical origin of the universal three-body parameter in atomic Efimov physics. Phys. Rev. A 2014, 90, 022106. [Google Scholar] [CrossRef]
- Ferlaino, F.; Grimm, R. Forty years of Efimov physics: How a bizarre prediction turned into a hot topic. Physics 2010, 3, 9. [Google Scholar] [CrossRef]
- Giannakeas, P.; Greene, C.H. Van Der Waals Universality in Homonuclear Atom-Dimer Elastic Collisions. Few-Body Syst. 2017, 58, 20. [Google Scholar] [CrossRef]
- Mestrom, P.M.A.; Wang, J.; Greene, C.H.; D’Incao, J.P. Efimov–van Der Waals Universality for Ultracold Atoms with Positive Scattering Lengths. Phys. Rev. A 2017, 95, 032707. [Google Scholar] [CrossRef]
- Mestrom, P.M.A.; Colussi, V.E.; Secker, T.; Groeneveld, G.P.; Kokkelmans, S.J.J.M.F. Van Der Waals Universality near a Quantum Tricritical Point. Phys. Rev. Lett. 2020, 124, 143401. [Google Scholar] [CrossRef] [PubMed]
- Kunitski, M.; Zeller, S.; Voigtsberger, J.; Kalinin, A.; Schmidt, L.P.H.; Schoeffler, M.; Czasch, A.; Schoellkopf, W.; Grisenti, R.E.; Jahnke, T.; et al. Observation of the Efimov state of the helium trimer. Science 2015, 348, 551–555. [Google Scholar] [CrossRef] [PubMed]
- Pires, R.; Ulmanis, J.; Häfner, S.; Repp, M.; Arias, A.; Kuhnle, E.D.; Weidemüller, M. Observation of Efimov Resonances in a Mixture with Extreme Mass Imbalance. Phys. Rev. Lett. 2014, 112, 250404. [Google Scholar] [CrossRef] [PubMed]
- Ulmanis, J.; Häfner, S.; Pires, R.; Kuhnle, E.D.; Weidemüller, M.; Tiemann, E. Universality of weakly bound dimers and Efimov trimers close to Li–Cs Feshbach resonances. New J. Phys. 2015, 17, 055009. [Google Scholar] [CrossRef][Green Version]
- Tung, S.K.; Jiménez-García, K.; Johansen, J.; Parker, C.V.; Chin, C. Geometric Scaling of Efimov States in a 6Li-133$Cs. Phys. Rev. Lett. 2014, 113, 240402. [Google Scholar] [CrossRef]
- Häfner, S.; Ulmanis, J.; Kuhnle, E.D.; Wang, Y.; Greene, C.H.; Weidemüller, M. Role of the intraspecies scattering length in the Efimov scenario with large mass difference. Phys. Rev. A 2017, 95, 062708. [Google Scholar] [CrossRef]
- Petrov, D.S.; Werner, F. Three-body recombination in heteronuclear mixtures at finite temperature. Phys. Rev. A 2015, 92, 022704. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Han, H.L.; Wu, M.S.; Shi, T.Y. Universal three-body parameter of heavy-heavy-light systems with a negative intraspecies scattering length. Phys. Rev. A 2019, 100, 052702. [Google Scholar] [CrossRef]
- Sun, M.; Liu, C.; Shi, Z.Y. Efimov physics in the complex plane. arXiv 2021, arXiv:2109.11206. [Google Scholar]
- Ulmanis, J.; Häfner, S.; Pires, R.; Kuhnle, E.D.; Wang, Y.; Greene, C.H.; Weidemüller, M. Heteronuclear Efimov Scenario with Positive Intraspecies Scattering Length. Phys. Rev. Lett. 2016, 117, 153201. [Google Scholar] [CrossRef] [PubMed]
- Chin, C.; Grimm, R.; Julienne, P.; Tiesinga, E. Feshbach resonances in ultracold gases. Rev. Mod. Phys. 2010, 82, 1225. [Google Scholar] [CrossRef]
- Johansen, J.; DeSalvo, B.J.; Patel, K.; Chin, C. Testing universality of Efimov physics across broad and narrow Feshbach resonances. Nat. Phys. 2017, 13, 731–735. [Google Scholar] [CrossRef]
- Giannakeas, P.; Greene, C.H. Ultracold Heteronuclear Three-Body Systems: How Diabaticity Limits the Universality of Recombination into Shallow Dimers. Phys. Rev. Lett. 2018, 120, 023401. [Google Scholar] [CrossRef] [PubMed]
- D’Incao, J.P.; Esry, B.D. Scattering Length Scaling Laws for Ultracold Three-Body Collisions. Phys. Rev. Lett. 2005, 94, 213201. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound States in the Continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef]
- Rittenhouse, S.T.; Mehta, N.P.; Greene, C.H. Green’s functions and the adiabatic hyperspherical method. Phys. Rev. A 2010, 82, 022706. [Google Scholar] [CrossRef]
- Avery, J. Hyperspherical Harmonics: Applications in Quantum Theory; Kluwer Academic Publishers: Norwell, MA, USA, 1989. [Google Scholar]
- Smirnov, Y.F.; Shitikova, K.V. Method of K harmonics and the shell model. Sov. J. Part. Nucl. 1977, 8, 44. [Google Scholar]
- Kartavtsev, O.I.; Malykh, A.V. Low-energy three-body dynamics in binary quantum gases. J. Phys. B 2007, 40, 1429–1441. [Google Scholar] [CrossRef]
- Kartavtsev, O.I.; Malykh, A.V. Universal low-energy properties of three two-dimensional bosons. Phys. Rev. A 2006, 74, 042506. [Google Scholar] [CrossRef]
- Aymar, M.; Greene, C.H.; Luc-Koenig, E. Multichannel Rydberg spectroscopy of complex atoms. Rev. Mod. Phys. 1996, 68, 1015. [Google Scholar] [CrossRef]
- Mehta, N.; Esry, B.; Greene, C.H. Three-body recombination in one dimension. Phys. Rev. A 2007, 76, 022711. [Google Scholar] [CrossRef]
- Burke, J.P., Jr. Theoretical Investigation of Cold Alkali Atom Collisions. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 1999. [Google Scholar]
- Nielsen, E.; Macek, J. Low-energy recombination of identical bosons by three-body collisions. Phys. Rev. Lett. 1999, 83, 1566. [Google Scholar] [CrossRef]
- Clark, C.W. Calculation of Non-adiabatic Transition Probabilities. Phys. Lett. A 1979, 70, 295. [Google Scholar] [CrossRef]
- Child, M. Semiclassical theory of tunneling and curve-crossing problems: A diagrammatic approach. J. Mol. Spectrosc. 1974, 53, 280–301. [Google Scholar] [CrossRef]
- Zhu, C.; Nakamura, H. Theory of nonadiabatic transition for general two-state curve crossing problems. I. Nonadiabatic tunneling case. J. Chem. Phys. 1994, 101, 10630–10647. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; D’Incao, J.P.; Greene, C.H. Universal Three-Body Parameter in Heteronuclear Atomic Systems. Phys. Rev. Lett. 2012, 109, 243201. [Google Scholar] [CrossRef]
- Fano, U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys. Rev. 1961, 124, 1866–1878. [Google Scholar] [CrossRef]







| HHL System | |||||
|---|---|---|---|---|---|
| -- | 1.983 | 2.003 | 4.42 | 0.46 | 0.13 |
| -- | 1.633 | 1.682 | 3.13 | 0.8 | 0.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giannakeas, P.; Greene, C.H. Asymmetric Lineshapes of Efimov Resonances in Mass-Imbalanced Ultracold Gases. Atoms 2021, 9, 110. https://doi.org/10.3390/atoms9040110
Giannakeas P, Greene CH. Asymmetric Lineshapes of Efimov Resonances in Mass-Imbalanced Ultracold Gases. Atoms. 2021; 9(4):110. https://doi.org/10.3390/atoms9040110
Chicago/Turabian StyleGiannakeas, Panagiotis, and Chris H. Greene. 2021. "Asymmetric Lineshapes of Efimov Resonances in Mass-Imbalanced Ultracold Gases" Atoms 9, no. 4: 110. https://doi.org/10.3390/atoms9040110
APA StyleGiannakeas, P., & Greene, C. H. (2021). Asymmetric Lineshapes of Efimov Resonances in Mass-Imbalanced Ultracold Gases. Atoms, 9(4), 110. https://doi.org/10.3390/atoms9040110






