Benchmark PhotoIonization Cross-Sections of Neutral Scandium from the Ground and Excited States

Abstract

The B-spline R-matrix method has been used to investigate cross-sections for photoionization of neutral scandium from the ground and excited states in the energy region from the 3d and 4s valence electron ionization thresholds to 25 eV. The initial bound states of Sc and the final residual Sc${}^{+}$ ionic states have been accurately calculated by combining the multiconfiguration Hartree-Fock method with the frozen-core close-coupling approach. The lowest 20 bound states of Sc I belonging to the ground $3d4s^2$ and excited $3d^{2}4s$, $3d^{2}4p$, $3d4s4p$, $4s^{2}4p$, and $3d^3$ configurations have been considered as initial states. The 81 $LS$ final ionic states of Sc${}^{+}$ belonging to the terms of $3p^{6}3d^2$, $3p^{6}3d4l$ (l = 0–3), $3p^{6}3d5l$ (l = 0–3), $3p^{6}3d6s$, $3p^{6}4s^2$, $3p^{6}4s4l$ (l = 0–3), $3p^{6}4s5l$ (l = 0–1), and $3p^{6}4p^2$ configurations have been included in the final-state close-coupling expansion. The cross-sections are dominated by complicated resonance structures in the low energy region converging to several Sc${}^{+}$ ionic thresholds. The inclusion of all these final ionic states has been noted to significantly impact the near-threshold resonance structures and background cross-sections. The important scattering channels for leaving the residual ion in various final states have been identified, and the $3d$ electron ionization channels have been noted to dominate the cross-sections at higher photon energies.

1. Introduction

The iron-group elements (Z = 21–28) have a high abundance in many astronomical objects, including metal-poor stars, HII regions, and gaseous nebulae. Highly accurate atomic data are important for the analysis of stellar and nebular spectra to determine physical conditions and elemental abundances. Atomic data such as transition probabilities, electron excitation collision strengths, and photoionization cross-sections are needed to develop a reliable non-local thermodynamical equilibrium (NLTE) model of stellar atmospheres. A comprehensive atomic model is required, for NLTE modeling calculations, that includes atomic and ionic states of the elements under consideration. Under NLTE conditions, the atomic populations are described by a set of statistical equilibrium equations by taking into account radiative and collisional processes. The partial photoionization cross-sections from the ground and excited states are normally needed for detailed NLTE modeling. Over the last few decades, reliable transition probabilities have been measured by several experimental groups for the important transitions in iron-group elements, but there is a lack of experimental studies on the cross-sections due to collisions of electrons and photons. The majority of atomic data of increasing accuracy have been produced through theoretical and computational efforts. Recently we have provided improved computational transition probabilities, electron impact excitation collision strengths, and photoionization cross-sections for Fe I and Fe II [1,2], Cr I and Cr II [3,4], and Ti II [5] for a wide array of transitions to fulfill some of the atomic data needs for the modeling of astrophysical plasmas.

Scandium, with the ground state $3d4s^2{}^{2}D$, is the simplest $3d$ element of the iron-group. There is an intrinsic physical interest in the iron-group elements because of the competition between $4s$ and $3d$ orbitals and because the $3d$ orbitals are the first to be subjected to a collapse phenomenon. When collapse occurs, the 3d electrons become inner electrons, located inside the 4s electrons. This leads to a very strong interaction with core orbitals making the theoretical calculations complicated, and provides a good understanding of many-electron dynamics. Most studies are devoted to the inner shell $3p$ photoionization, which leads to a series of strong resonances in the photon energy region from 29 to 40 eV (for references, see review of Martins et al. [6]). Scandium did not receive much attention from both theory and experiment compared to other iron-group elements for the valence electron photoionization. The low-energy photoionization of the $3d$ and $4s$ valence electrons is of particular importance in the 3-dimensional NLTE modeling of stellar atmospheres. Several Sc I (Z = 21) spectral lines have been observed in stellar and nebular objects [7,8]. Significant discrepancies for the abundance of scandium have been found between the meteoritic abundance and solar photospheric value [9,10].

The valence shell excitation of Sc I was first analysed by Robicheaux and Greene [11,12]. They described the Sc I photoabsorption in the wavelength range from 170 to 190 nm (6–7 eV) using the eigenchannel R-matrix method [13]. These studies provide details of the positions and widths of several autoionizing states, however, they do not provide total or partial cross-sections for use in the plasma modelling. Altun and Manson [14] performed photoionization calculations of the ground state of Sc I in the photon energy region from threshold to 60 eV using the many-body perturbation theory (MBPT) based on the close-coupling approximation for final state channels and the multi-configuration Hartree–Fock (MCHF) approach for energies. Their close-coupling expansion for the final ionic states of Sc II contain only three $3d4s{}^{3}D,{}^{1}D$, and $4s^2{}^{1}S$ terms describing the valence $3d$ and $4s$ excitation in single-electron approximation. It represents only a small part of the Sc I spectrum and raises concerns about the convergence of the results. The use of approximate empirical formulae to generate atomic data may introduce significant uncertainties. The available atomic-structure computer codes and modern computational facilities allow one to generate atomic data sets routinely with sufficient accuracy. The collections of photoionzation cross-sections can be found in several on-line atomic databases, e.g., TOPbase (http://cdsweb.u-strasbg.fr/topbase/topbase.html (accessed on 14 July 2019)) or NORAD-Atomic-Data (https://norad.astronomy.osu.edu/#intro (accessed on 14 July 2019)). Absence of the Sc I photoionization cross-section data in these popular databases calls for further calculations. The purpose of the present work is to provide a new set of sufficiently accurate computational partial and total photoionization cross-sections of Sc I from both the ground and excited states for NLTE modeling of the astrophysical objects.

Our work is based on the B-spline R-matrix (BSR) method [15] in $LS$ approximation. The reliable photoionization calculation needs an accurate description of Sc I bound states as well as that of the final continuum states and Sc II ionic states. A variety of correlation and relaxation effects need to be included for an accurate description of all these states. The target wave functions were improved by using flexible nonorthogonal orbitals for accounting for the term dependence of valence orbitals and for representing correlation and relaxation effects. The multiconfiguration Hartree-Fock method [16], together with the B-spline box-based multichannel approach [17,18], were used to accurately determine correlation corrections. The B-spline basis was used for the description of continuum functions and we did not impose any orthogonality constraint between continuum functions, and the valence spectroscopic and correlation orbitals. Thus, the possible inconsistencies between the continuum and bound parts of the close-coupling plus correlation expansions were avoided. This allowed us to improve the correct positions and magnitudes of near-threshold resonances.

We have investigated photoionization of valence $3d$, $4s$, and $4p$ electrons from the atomic scandium initial bound terms of the $3d4s^2$, $3d^{2}4s$, $3d4s4p$, $3d^{2}4p$, $4s^{2}4p$, and $3d^3$ configurations giving rise to various final states of singly-ionized scandium. We have included the first 81 $LS$ final ionic states up to $4s6s$ in the close-coupling expansion to calculate the likely converged photoionization cross-sections. Our calculation includes many Rydberg series of resonances converging to these ionic thresholds. We have included electron correlation effects both in the initial bound and final continuum states in a consistent manner to ensure accurate representation of resonances. Our calculation includes the important photoionization process in which the photoelectron is ejected and a second electron is allowed to be excited. We have found that the inclusion of all these final Sc II states has considerable impact on the resonance structures. They also have significant influence on the energy dependence of the photoionization cross-sections from the excited states.

2. Computational Methods

2.1. Calculation of Target States Wave Functions

The low-energy spectrum of Sc I can be considered as a three-electron system outside the $1s^{2}2s^{2}2p^{6}3s^{2}3p^6$ closed core. The correlation between valence electrons is expected to be important. However, there is another complication due to proximity of the $3d$ orbital to the core orbitals. It is supposed to produce strong interaction with the core orbitals as well as strong correlation effects for the $3d$ wave function. Therefore, we can not restrict the atomic state expansions to configurations with a closed core, and should introduce the configurations with excited core orbitals. The present calculations of the Sc I atomic wave functions have been performed using the MCHF code of Froese Fischer et al. [16], together with the configuration-interaction code [17]. Our initial configuration expansions for Sc I contain all one, two, and three valence $3d$, $4s$, and $4p$ electrons excitations to the $5l$ and $6l$ (l = 0–4) correlated orbitals, along with the one and two electron excitations of the $3s$ and $3p$ core orbitals to the spectroscopic $3d$, $4s$, and $4p$ orbitals. Each atomic state has been considered in separate MCHF calculations, with individual term-dependent sets of the valence and correlation nonorthogonal orbitals. This speeds up the convergence of atomic state expansions, however, this procedure still leads to the extremely large expansions with tens of thousands of individual configurations. Our strategy has been to include significant electron correlation effects by properly choosing important configurations. All initial atomic expansions were restricted by the cut-off parameters in the range from 0.010 to 0.025 for the various states due to different convergence rates for individual states. As a result, the final configuration expansions included all significant correlation effects and have been found to be of manageable size in the photoionization calculations. The $LS$ initial states of Sc I in the present work were represented by configuration expansions of sizes between 400 and 1200.

We compare our calculated $LS$ excitation energies for the 20 bound states of neutral scandium considered in the present photoionization calculations with the experimental excitation energies from the NIST compilation [19] in

Table 1. The Sc I target state excitation energies (in eV).

Index	Configuration	Term	NIST	Present	Diff.	Index	Configuration	Term	NIST	Present	Diff.
1	$3d4s^2$	${}^{2}D$	$0.00000$	$0.00000$	$0.000$	11	$3d^2{(}^{1}G)4s$	${}^{2}G$	$2.49669$	$2.49141$	$-0.005$
2	$3d^2{(}^{3}F)4s$	${}^{4}F$	$1.42694$	$1.43557$	$0.009$	12	$3d^2{(}^{3}P)4s$	${}^{2}P$	$2.55482$	$2.55626$	$0.001$
3	$3d^2{(}^{3}F)4s$	${}^{2}F$	$1.84628$	$1.85528$	$0.009$	13	$3d4s{(}^{1}D)4p$	${}^2{F}^o$	$2.59897$	$2.56998$	$-0.029$
4	$3d4s{(}^{3}D)4p$	${}^4{F}^o$	$1.95594$	$1.96443$	$0.008$	14	$3d4s{(}^{1}D)4p$	${}^2{P}^o$	$3.04454$	$3.04465$	$0.000$
5	$3d4s{(}^{3}D)4p$	${}^4{D}^o$	$1.98759$	$2.02268$	$0.035$	15	$3d4s{(}^{3}D)4p$	${}^2{D}^o$	$3.08150$	$3.07788$	$-0.004$
6	$3d4s{(}^{1}D)4p$	${}^2{D}^o$	$1.97772$	$1.97608$	$-0.002$	16	$3d4s{(}^{3}D)4p$	${}^2{F}^o$	$3.16949$	$3.17757$	$0.008$
7	$3d^2{(}^{1}D)4s$	${}^{2}D$	$2.09741$	$2.09541$	$-0.002$	17	$3d^2{(}^{1}S)4s$	${}^{2}S$	$3.32724$	$3.31765$	$-0.010$
8	$3d^2{(}^{3}P)4s$	${}^{4}P$	$2.12946$	$2.11840$	$-0.011$	18	$3d^2{(}^{3}F)4p$	${}^4{G}^o$	$3.60522$	$3.62726$	$0.022$
9	$3d4s{(}^{3}D)4p$	${}^4{P}^o$	$2.28634$	$2.27636$	$0.010$	19	$3d^2{(}^{3}F)4p$	${}^2{G}^o$	$4.09246$	$4.09617$	$0.004$
10	$4s^{2}4p$	${}^2{P}^o$	$2.31931$	$2.29476$	$-0.025$	20	$3d^3$	${}^{4}F$	$4.18382$	$4.19027$	$0.006$

. It is clear from the comparison that our approach described above gives very accurate theoretical energies. The agreement with the observed $LS$ energies is better than 35 meV for all 20 bound states. However, we have used experimental binding energies for the scandium states in our photoionization calculations to further improve the positions of close-to-threshold resonances.

The final ionic states of Sc II in the present calculations were produced by combining the multi-configuration Hartree-Fock and the B-spline box-based close-coupling methods [17]. Specifically, the structure of the multi-channel target expansion was chosen as:

$$\begin{array}{ccc}\hfill {\Phi }^{LS\pi }& =& \sum _{nl}{\left\{\varphi (3p^{6}3d)P(nl)\right\}}^{LS\pi }+\sum _{nl}{\left\{\varphi (3p^{6}4s)P(nl)\right\}}^{LS\pi }\hfill \\ & +& \sum _{nl}{\left\{\varphi (3p^{6}4p)P(nl)\right\}}^{LS\pi }+a\phi {(3p^{6}3d^2)}^{LS\pi }\hfill \\ & +& b\phi {(3p^{6}3d4s)}^{LS\pi }+c\phi {(3p^{6}3d4p)}^{LS\pi }\hfill \\ & +& d\phi {(3p^{6}4s^2)}^{LS\pi }+e\phi {(3p^{6}4p^2)}^{LS\pi }.\hfill \end{array}$$

(1)

In the above equation, the orbital of the outer valence electron is denoted by $P\left(nl\right)$. The configuration interaction (CI) expansions of the corresponding ionic Sc III or specific atomic Sc II states are denoted by the $\varphi$ and $\phi$ functions, respectively. The CI expansions for each state have been produced in separate MCHF calculations. Equation (1) represents the entire $3dnl$, $4snl$, and $4pnl$ Rydberg series in singly ionized scandium. We employed separate CI expansions for the $3d^2$ or $4s^2$ states with equivalent electrons and included relaxation and term-dependence by generating state-specific nonorthogonal one-electron orbitals. The same procedure has also been adopted for the low-lying $3d4s$ and $3d4p$ states. The core-valence correlation is determined by the CI expansion of the ionic $3s^{2}3p^{5}3d,4s,4p$ states. These expansions include all one electron and two electrons promotions from the $3s$ and $3p$ spectroscopic orbitals to the $4l$ and $5l$ (l = 0–3) correlation orbitals. We have kept the CI expansions to a reasonable size by imposing a cut-off parameter of 0.01 on the coefficients of configurations and obtained an agreement within 0.01 eV between the calculated and experimental [19] values of ionization potentials.

The outer valence electron functions $P\left(nl\right)$ have been expanded in a B-spline basis. These functions have been subjected to the condition that they become almost zero at the boundary. The R-matrix radius was set to $30a_0$, where $a_0$ denotes the Bohr radius. This radial range was spanned by 105 B-splines of order eight using a semi-exponential knot grid. The B-spline coefficients for the valence electron functions $P\left(nl\right)$ and that for the perturbers have been determined by diagonalization of the $LS$ Hamiltonian. All perturber states in the expansion (1) were generated through separate MCHF calculations, in the same way as the initial Sc I wave functions discussed above. We included the most important correlation effects for the target states by keeping the target expansions to a reasonable size. This was achieved by retaining only significant configurations in the CI expansions with coefficients in the range from 0.015 to 0.030, or larger. The semi-empirical corrections were then applied by adjusting the theoretical $LS$ energies to experimental values. The cut-off parameters have been varied to take a balanced account of correlation effects in the initial bound states of neutral scandium and the residual singly-ionized scandium. The balance in the correlation effects between the initial bound and final continuum states allowed us to determine the resonance structures accurately in the threshold regions. We were able to include from 200 to 400 configurations for each state in our computational calculations.

We included 81 $LS$ final ionic states of Sc${}^{+}$ belonging to the terms of the $3p^{6}3d^2$, $3p^{6}3d4l$ (l = 0–3), $3p^{6}3d5l$ (l = 0–3), $3p^{6}3d6s$, $3p^{6}4s^2$, $3p^{6}4s4l$ (l = 0–3), $3p^{6}4s5l$ (l = 0–1), and $3p^{6}4p^2$ configurations.

Table 2. The Sc II target state excitation energies (in eV).

Index	Configuration	Term	Present	NIST	Diff.	Index	Configuration	Term	Present	NIST	Diff.
1	$3d4s$	${}^{3}D$	0.00000	0.00000	0.000	42	$3d4f$	${}^1{H}^o$	9.39693	9.39977	−0.003
2	$3d4s$	${}^{1}D$	0.31767	0.30196	0.016	43	$3d4f$	${}^3{P}^o$	9.40402	9.40163	0.002
3	$3d2$	${}^{3}F$	0.59227	0.59556	−0.003	44	$3d4f$	${}^1{P}^o$	9.41875	9.41880	−0.000
4	$3d2$	${}^{1}D$	1.36353	1.34387	0.020	45	$4p2$	${}^{1}D$	9.46731	9.21547	0.252
5	$3d2$	${}^{3}P$	1.48190	1.49058	−0.009	46	$3d6s$	${}^{3}D$	9.60683	9.57157	0.035
6	$4s2$	${}^{1}S$	1.51860	1.44204	0.077	47	$3d6s$	${}^{1}D$	9.71856	9.63709	0.081
7	$3d2$	${}^{1}G$	1.77215	1.75510	0.017	48	$3d5d$	${}^{1}F$	9.72935	9.70654	0.023
8	$3d2$	${}^{1}S$	3.20710	3.20495	0.002	49	$3d5d$	${}^{3}D$	9.74595	9.72732	0.019
9	$3d4p$	${}^1{D}^o$	3.24791	3.22059	0.027	50	$3d5d$	${}^{1}P$	9.75389	9.75160	0.002
10	$3d4p$	${}^3{F}^o$	3.41384	3.41720	−0.003	51	$3d5d$	${}^{3}G$	9.76721	9.74943	0.018
11	$3d4p$	${}^3{D}^o$	3.49953	3.46664	0.033	52	$3d5d$	${}^{3}S$	9.78282	9.80326	−0.020
12	$3d4p$	${}^3{P}^o$	3.70783	3.68003	0.028	53	$4p2$	${}^{3}P$	9.78928	9.46857	0.321
13	$3d4p$	${}^1{P}^o$	3.79382	3.80758	−0.014	54	$4s5s$	${}^{3}S$	9.89716	9.69063	0.207
14	$3d4p$	${}^1{F}^o$	4.00081	3.99781	0.003	55	$3d5d$	${}^{3}F$	9.94269	9.89828	0.044
15	$4s4p$	${}^3{P}^o$	5.18174	4.85089	0.331	56	$3d5d$	${}^{1}D$	10.00266	9.95468	0.048
16	$4s4p$	${}^1{P}^o$	7.12477	6.89474	0.230	57	$3d5d$	${}^{1}G$	10.03374	9.99390	0.040
17	$3d5s$	${}^{3}D$	7.24090	7.13614	0.105	58	$3d6p$	${}^{1}D$	10.07017
18	$3d5s$	${}^{1}D$	7.31687	7.20926	0.108	59	$3d6p$	${}^{3}D$	10.09479
19	$3d4d$	${}^{1}F$	7.38925	7.36750	0.022	60	$3d6p$	${}^{3}F$	10.09940
20	$3d4d$	${}^{3}D$	7.43957	7.42007	0.020	61	$3d5d$	${}^{3}P$	10.12891	10.03810	0.091
21	$3d4d$	${}^{1}P$	7.46611	7.47562	−0.010	62	$3d5d$	${}^{1}S$	10.13816
22	$3d4d$	${}^{3}G$	7.49140	7.47205	0.019	63	$3d6p$	${}^{3}P$	10.14128
23	$3d4d$	${}^{3}S$	7.57644	7.55881	0.018	64	$3d6p$	${}^{1}F$	10.16611
24	$3d4d$	${}^{3}F$	8.00500	7.85547	0.150	65	$3d6p$	${}^{1}P$	10.17914
25	$3d4d$	${}^{1}D$	8.12623	7.96737	0.159	66	$4s5s$	${}^{1}S$	10.28326	10.04474	0.239
26	$3d4d$	${}^{3}P$	8.17583	8.00574	0.170	67	$4s4d$	${}^{3}D$	10.44663	10.25450	0.192
27	$3d4d$	${}^{1}G$	8.20799	8.07516	0.133	68	$3d5f$	${}^1{G}^o$	10.57951	10.56946	0.010
28	$3d5p$	${}^1{D}^o$	8.24316	8.17588	0.067	69	$3d5f$	${}^3{F}^o$	10.58667	10.59752	−0.011
29	$3d5p$	${}^3{D}^o$	8.30766	8.23368	0.074	70	$3d5f$	${}^3{G}^o$	10.59359	10.59578	−0.002
30	$3d5p$	${}^3{F}^o$	8.31475	8.24495	0.070	71	$3d5f$	${}^1{F}^o$	10.59850	10.60277	−0.004
31	$3d5p$	${}^3{P}^o$	8.40630	8.33671	0.070	72	$3d5f$	${}^1{D}^o$	10.60119	10.59479	0.006
32	$3d5p$	${}^1{F}^o$	8.47378	8.38607	0.088	73	$3d5f$	${}^3{H}^o$	10.60287	10.59402	0.009
33	$3d4d$	${}^{1}S$	8.52566	8.32071	0.205	74	$3d5f$	${}^3{D}^o$	10.60897	10.60811	0.001
34	$3d5p$	${}^1{P}^o$	8.56150	8.47960	0.082	75	$3d5f$	${}^3{P}^o$	10.62363	10.62377	−0.000
35	$3d4f$	${}^1{G}^o$	9.32220	9.31319	0.009	76	$3d5f$	${}^1{H}^o$	10.62470	10.62692	−0.002
36	$3d4f$	${}^3{F}^o$	9.33504	9.33524	−0.000	77	$3d5f$	${}^1{P}^o$	10.63105
37	$3d4f$	${}^3{G}^o$	9.34062	9.33560	0.005	78	$4s4d$	${}^{1}D$	11.36043	11.13809	0.222
38	$3d4f$	${}^1{F}^o$	9.35045	9.35423	−0.004	79	$4p2$	${}^{1}S$	12.08931
39	$3d4f$	${}^1{D}^o$	9.36291	9.35899	0.004	80	$4s6s$	${}^{3}S$	12.60138
40	$3d4f$	${}^3{H}^o$	9.36909	9.36413	0.005	81	$4s6s$	${}^{1}S$	12.77644
41	$3d4f$	${}^3{D}^o$	9.37282	9.37142	0.001

lists the calculated energies for the lowest 81 $LS$ terms of Sc${}^{+}$ and compares the predicted results with the experimental values. As seen from Table 2, the agreement between the predicted and observed $LS$ energies is better than 0.1 eV for most states, except for some $4p^2$ and $3d4d$ states where the convergence was found to be very slow. A reasonable agreement between the calculated and experimental values supports the good quality of final ionic state wave function expansions.

2.2. PhotoIonization Calculations

The present photoionization calculations have been performed using the parallelized version of the $BSR$ code [15] based on the R-matrix method to solve the close-coupling equations. An additional description of the $BSR$ method can be found in the review by Zatsarinny and Bartschat [20]. The continuum wave functions in the inner region, $r\le a$ have been described by the B-splines as a universal basis. The R-matrix expansion in the inner region is represented as:

$$\begin{array}{ccc}\hfill & & {\Psi }_k(x_1,\dots ,x_{N+1})=\hfill \\ & & \mathcal{A}\sum _{ij}{\overline{\Phi }}_i(x_1,\dots ,x_N;{\widehat{\mathbf{r}}}_{N+1}{\sigma }_{N+1})r_{N+1}^{-1}{B}_j\left(r_{N+1}\right)a_{ijk}\hfill \\ & & +\sum _i{\chi }_i(x_1,\dots ,x_{N+1})b_{ik}.\hfill \end{array}$$

(2)

In this equation $\mathcal{A}$ denotes the antisymmetrization operator, the channel functions and continuum wave functions are described by ${\overline{\Phi }}_i$ and the splines $B_j\left(r\right)$, respectively. The B-splines form a complete basis and the coefficient of the last spline provides the amplitudes of the wave functions at the boundary. Only limited orthogonality conditions are imposed between the bound and continuum wave functions. We imposed orthogonality of the continuum orbitals to the bound orbitals in the closed $1s$, $2s$, $2p$, $3s$, and $3p$ subshells in the present calculations. No orthogonality constraints were imposed between the continuum wave functions and other spectroscopic or correlated orbitals. Thus, we were able to avoid the $(N+1)$-electron configurations of ${\chi }_i$ in the second part of Equation (2), and were able to keep a balance between the scattering and bound parts of the close-coupling expansions. This allowed us to avoid the pseudo-resonance structure in the photoionization cross-sections.

In R-matrix theory, the photoionization cross-section is defined through the dipole matrix elements between the initial state ${\Psi }_0$ and the R-matrix basis states ${\Psi }_k$, provided that all radial orbitals of the initial state are well confined to the inner region. The total photoionization cross-section (in $a_0^2$) for a photon energy $\omega$ (in Rydberg) and an initial state with total orbital angular momentum $L_0$ is given by:

$$\begin{array}{c}\hfill \sigma \left(\omega \right)=\frac{8}{3}{\pi }^2\alpha {\omega }^{\pm 1}\frac{1}{(2L_0+1)}\sum _j\left|\right({\Psi }_j^{-}\parallel D\parallel {\Psi }_0{\left)\right|}^2,\end{array}$$

(3)

where $\alpha \approx 1/137$ is the fine-structure constant and D is the electric dipole operator. The powers of $\omega$ (+1 or −1) correspond to the length and velocity formulations of the photoionization cross-sections, respectively. The index j runs over the various open channels. The solutions ${\Psi }_j^{-}$ correspond to asymptotic conditions with a plane wave in the direction of the ejected electron momentum k and ingoing waves in all open channels. The radial wave function of the scattered electron has been generated by using the program ASYPCK [21].

3. Results and Discussion

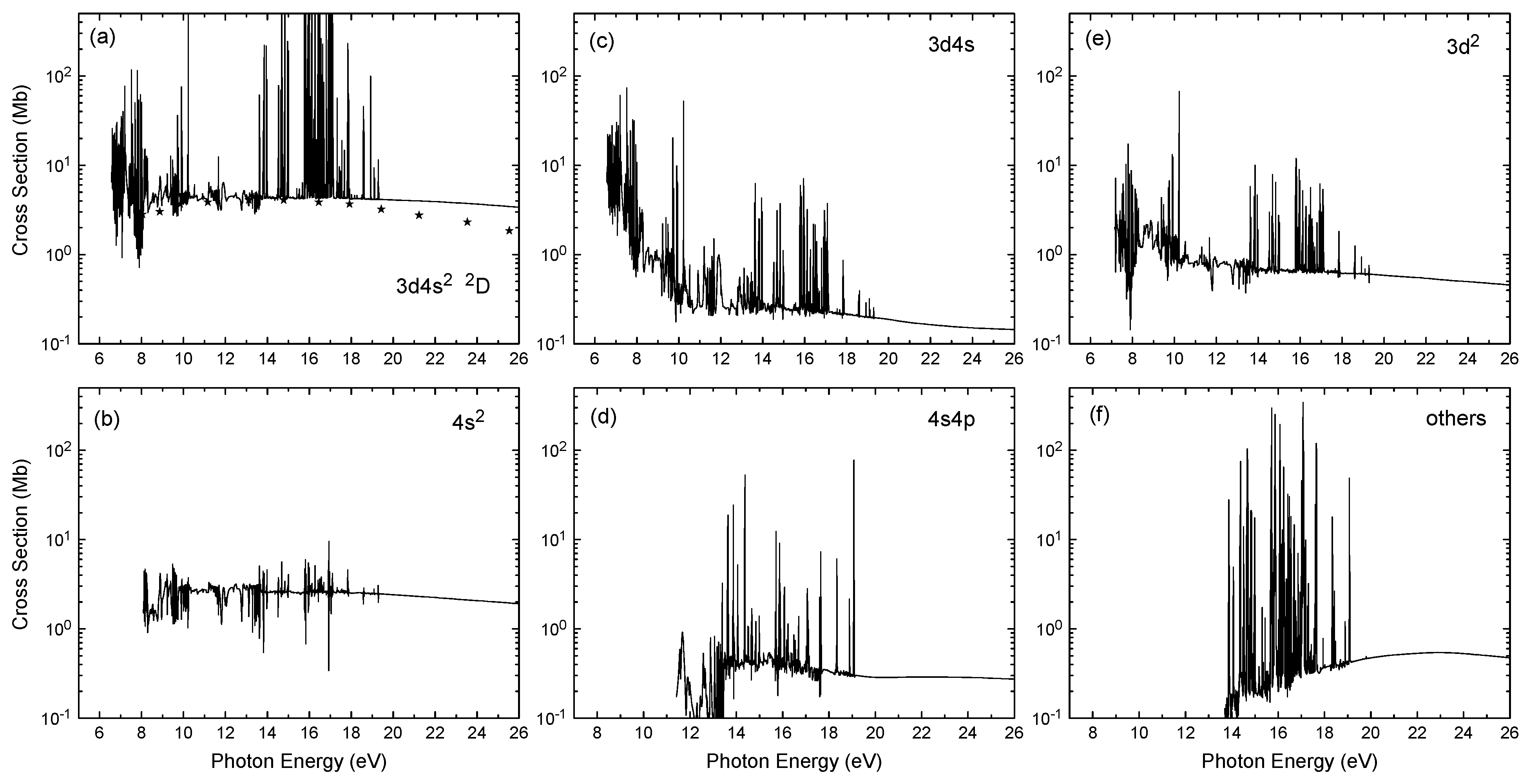
The total photoionization cross-sections from the ground $3d4s^2{}^{2}D$ state of scandium are shown in Figure 1a in the photon energy region from the Sc${}^{+}$ $3d4s{}^{3}D$ ionization threshold to 26 eV. It is clear from the figure that the resonance structures dominate total photoionization cross-sections, especially in the low energy region. A fine energy grid of $1.36\times {10}^{-3}$ eV has been employed from the Sc${}^{+}$ first ionization threshold at 6.56 eV to the highest ionization threshold around 19 eV to account for resonances. There are many narrow and strong resonance series converging to various residual Sc${}^{+}$ ionic thresholds. The nonlocal thermodynamic equilibrium modeling calculations require the partial photoionization cross-sections for leaving the residual ion in various states. The photoionization of Sc populates many residual final ionic states. Our calculations exhibit no dominant ionic channel in the photoionization of a given initial state. It is due to the complex Sc${}^{+}$ atomic structure. The partial photoionization cross-sections from the ground $3d4s^2{}^{2}D$ state, for leaving the residual Sc${}^{+}$ ion in the final states of the $4s^2$, $3d^2$, $3d4s$, and $4s4p$, are presented in Figure 1b–e, whereas Figure 1f presents thr contribution from all other states of Sc II. The summed partial cross-sections from various states of Sc${}^{+}$ belonging to a given configuration are presented in Figure 1, as there are a large number of final ionic states.

It is clear from Figure 1 that the dominant channels in the photoionization of the ground state $3d4s^2{}^{2}D$, in the near-threshold region are due to photoionization of the $4s$ electron leaving the Sc${}^{+}$ ion in the final states of $3d4s$ configuration. As seen from the figure, the cross-sections rapidly decrease with increasing photon energy. The $3d$ ionization channels become available above 8.08 eV and ionization to $4s^2$ final ionic states becomes dominant. These channels contribute about 50% to the magnitude of the total photoionization cross-sections at higher energies. As shown in the other panels, ionization with another electron excitation to the $3d^2$ and $4s4p$ final ionic states is also significant. This reflects strong close-coupling effects as well as strong configurations mixing in the atomic and ionic states. As seen from Figure 1f, the photoionization to the highly excited state, above 14 eV, is also important for the background cross-sections as well as for resonance structure. Their contribution is estimated to be about 25%.

The only comparison with previous calculations can be made with the available MBPT calculation of Altun & Manson [14]. The background cross-section for the photoionization of the ground state of Sc is shown in Figure 1a. We see very close agreement in a wide range of energies, except the higher energies above 20 eV. Their model includes only three final ionic states $3d4s{}^{3}D,{}^{1}D$ and $4s^2{}^{1}S$, and corresponds to the contribution of the $3d4s$ and $4s^2$ configurations from the present calculations shown in Figure 1b,c. This contribution is about 30% less than the MBPT results, indicating that the strong coupling between different channels results in a considerable redistribution of the total flux.

We now discuss the photoionization of the excited states in Sc with different shell occupations. The total and partial photoionization cross-sections of even-parity $3d^{2}4s{}^{2}F$ excited state are displayed in Figure 2. The background cross-section in this case decreases linearly from 12 Mb at threshold to 5 Mb at 25 ev. The resonance structures consist of a set of narrow resonances and only provide relatively small overall contribution to the cross-sections. The populations of the final ionic states change significantly compared to the $3d4s^2{}^{2}D$ ground state. Direct ionization of $4s$ electron leads to final ionic states with configuration $3d^2$, with average contribution to the total photoionization cross-sections of 10%. The $3d$ ionization leads to the $3d4s$ final ionic states and the photoionization cross-sections are shown in Figure 2c. These channels provide a dominant contribution in the near-threshold region and 65% at higher energies. As shown in the other panels, ionization with another electron excitation to the $3d4p$ and $3d5s$ final ionic states is also noticeable. The $3d4p$ channel shown in Figure 2d, are expected to be important due to the strong 3d-4p and 4s-4p transitions in the ionic states. Their overall contribution is about 10%. The $3d5s$ channels result from the $3d$ electron ionization plus shakeup of the $4s$ electron to $5s$. The individual contribution of all other channels are relatively small and do not exceed 1%. However, they add up to an overall contribution of about 12%. These examples of partial cross-sections once again confirm the strong close-coupling effects in the Sc photoionization process.

An example of photoionization for the odd-parity $3d4s4p{}^{4}D$ bound state is given in Figure 3. The $3d4s4p$ states have three main photoionization channels related to the ionization of the $3d$, $4s$, and $4p$ electrons. Ionization of the outer $4p$ electron leads mostly to the $3d4s$ final ionic states. It can be seen from Figure 3c that the corresponding partial cross-sections provide the main contribution in the near-threshold region, but these contributions rapidly decrease with increasing energy. The ionization of the $4s$ electron, Figure 3b, on the other hand, leads to the $3d4p$ ionic states. The background cross-sections for these ionic states change slowly with added energy. On average, the contribution from the $4s$ electron ionization to the total cross-section at higher energies is only ∼8%. The major contribution to the total cross-sections at higher energies comes from the $3d$ electron ionization leading to the $4s4p$ final ionic states, with an average contribution of ∼70%. The contribution of the other channels is relatively small. We have shown in Figure 3e an example for the $3d^2$ channels. Their overall contributions add up to 8% on average.

The total and partial photoionization cross-sections of odd-parity $3d^{2}4p{}^{4}G$ excited state are displayed in Figure 4. The total cross-sections are presented in Figure 4a, which displays three regions with different energy behaviors. In the near-threshold region, where the channels with direct $3d$ or $4p$ ionization are closed, the cross-section has almost zero background and consists of a set of strong resonances. After 3.61 eV, the cross-section is mainly defined by the $4p$ ionization leading to the $3d^2$ final ionic states. These cross-sections are shown in Figure 4c and gradually decrease from 18 Mb at threshold to 0.1 Mb at 26 eV photon energy. At 6.35 eV, the $3d$ ionization channels are opened, leading to $3d4p$ ionic states, shown in Figure 4b. These channels provide dominant contributions to the total cross-section and are responsible for the step-like structure at 6.35 eV. As seen from Figure 4d,e, other significant contributions are provided by the $3d4s$ and $3d4d$ channels due to close-coupling effects related to the $4s$-$4p$ and $4p$-$4d$ transitions in the ionic states. The contributions of highly excited states are shown in Figure 4f. They contribute up to 10% depending on photon energy. The main contribution here comes from the $3d5p$ channels, due to the $4p$-$5p$ shakeup transition.

An example of photoionization for the highly-excited $3d^3{}^{4}F$ bound state is given in Figure 5. As seen from the figure, the direct $3d$ electron ionization provides clearly dominant channels in this case, leaving the Sc${}^{+}$ in the $3d^2$ levels. The average contribution of these channels is 80%. Before the opening of $3d^2$ channels at 2.96 eV, the cross-sections have nearly zero background, and consist of a series of resonances. We also see the considerable contributions of the $3d4p$ and $3d4f$ channels due to close-coupling effects related to the strong $3d-4p$ and $3d-4f$ transitions in the ionic states. The shake-up process is also important, as indicated by relatively strong contributions of the $3d4d$ channels in Figure 5e. In this case we have $3d$ to $4d$ transitions. All other channels from highly excited ionic states contribute from 4 to 8%, depending on photon energies. A detailed inspection of partial cross-sections shows that the dominant contribution is provided by the $3d5f$ channels.

As can be seen from the above examples, the photoionization of scandium gives rise to many residual Sc${}^{+}$ ionic states. The relative population of the ionic states changes considerably with photon energy, and with the symmetry of the initial state. The background cross-sections for photoionization from the ground and excited states have similar shapes and magnitudes. The background cross-sections are mostly given by direct ionization of the $3d$ electron causing them to have similar values at higher energies.

4. Summary

We have studied low energy total and partial photoionization cross-sections of Scandium. We considered many final Sc${}^{+}$ ionic states corresponding to the ejection of $3d$, $4s$, and $4p$ photoelectrons. We also included the important process of photoionization where one electron is excited and another electron is ejected. We calculated total and partial photoionization cross-sections for the first 20 bound states of Sc in the $3d4s^2$, $3d^{2}4s$, $3d^{2}4p$, $3d4s4p$, $4s^{2}4p$, and $3d^3$ configurations. The present calculations adopted a large set of 81 $LS$ Sc${}^{+}$ final ionic states to cover all of the main ionization channels. We employed the B-spline R-matrix code [15] to determine solutions in the $LS$ coupling scheme inside the R-matrix box. The initial bound and final ionic states have been described by extensive multiconfiguration expansions using term-dependent non-orthogonal orbitals. The predicted photoionization cross-sections for the ground state are in reasonable agreement with the other available theoretical calculations of Altun and Manson [14]. However, there are no other results available for photoionization from higher-lying excited states. We found that the background photoionization cross-sections for all Sc bound states are very similar due to the dominant $3d$ ionization channels at higher photon energies. The autoionizing resonance structures have been carefully delineated in our calculation. Our analysis of the various channels show significant changes in the relative population of the ionic states with photon energy.