Abstract
The accuracy of the most recent recommended cross sections dataset for electron scattering from gaseous H2O (J. Phys. Chem. Ref. Data 2021, 50, 023103) is probed in a joint experimental and computational study. Simulations of the magnetically confined electron transport through a gas cell containing H2O for different beam energies (3, 10 and 70 eV) and pressures (2.5 to 20.0 mTorr) have been performed by using a specifically designed Monte Carlo code. The simulated results have been compared with the corresponding experimental data as well as with simulations performed with Geant4DNA. The comparison made between the experiment and simulation provides insight into possible improvement of the recommended dataset.
1. Introduction
Water (H2O) is the main constituent of all living organisms, it is a key molecular compound in the interaction of primary radiation with biological systems, where radiolysis (photoelectric and Compton effects) dictates the type of prevalent local chemistry at the molecular level. Additionally, the outcome provided by event-by-event Monte Carlo simulations, which require reliable and consistent sets of cross sections as input data [1,2,3], has been widely used in modelling radiation protocols in hospitals and/or clinical units devoted to radiotherapy treatment planning. Water has been attracting the attention of the international scientific community for several decades. In particular, in the last 20 years, we note widespread interest across the globe in cross sections for electron scattering from water at both the experimental and theoretical levels [4,5,6,7,8,9,10,11,12,13,14,15,16,17] (see also references therein). However, there is still no consensus on a recommended set of cross sections for electron scattering from H2O, particularly regarding dipole driven cross sections where important discrepancies are found. In fact, rotational excitations play a significant role in those discrepancies, as they are either not properly accounted or even not resolved in experimental setups at electron scattering angles close to 0 degrees, making the computation of the total cross section (TCS) [18] or the momentum transfer cross sections (MTCSs) required for deriving swarm transport coefficients [7,11] more difficult. Therefore, it is of major interest to evaluate the reliability of the proposed datasets.
In the Madrid laboratory, we have successfully implemented a well-proven methodology capable of delivering the most accurate dataset [19,20,21] through a procedure combining experimental and simulation methods. In this study we aim at evaluating the reliability and applicability of the most recent recommended cross sections dataset for electron scattering from gaseous H2O [22]. For this purpose, we have used those cross sections as input data for our novel event-by-event Monte Carlo code. The simulated results are then compared with the experimental data for the transmitted intensity of magnetically confined electrons [23] at different energies in the range of 3 to 70 eV, through a gas cell at different sample pressures (2.5 to 20.0 mTorr). Finally, we compare those results with simulations performed with the Geant4DNA [24,25,26,27] code for the same conditions.
2. Results and Discussion
In this section we present the cross sections for electron scattering from H2O recommended by Song et al. [22], together with a brief description of their origin. Next, we probe these cross sections as input data for our Monte Carlo simulation. A comparison with the results obtained using Geant4DNA relative to the experimental data is then thoroughly discussed.
2.1. Recommended Cross Sections
The most recent compilation from the literature (up to the end of 2019) on electron scattering cross sections data from water has been reported by Song and collaborators [22]. Their recommended TCSs are based on the elastic + rotational excitation R-matrix calculations of Tennyson and co-workers from 0.01 up to 7 eV [28,29,30], the experimental data of Szmytkowski and Mozejko [31] together with those from Kadokura et al. [32] between 7 and 50 eV, and those from Muñoz et al. [18] from 1 up to 10,000 eV. For the elastic integral cross sections (ICSs), Song et al. [22] followed the previously recommendation of Itikawa and Mason [10] adding the theoretical values of Faure et al. [29] for energies between 0.1 and 7 eV. For the electron energy range between 7 and 50 eV, Song et al. interpolated the theoretical values of Faure et al. [29] and used the experimental data recommended by Itikawa and Mason [10] above 50 eV. As far as elastic differential cross sections (DCSs) are concerned, the most recent measurements of Matsui et al. [33] were recommended in the incident energy range of 2−100 eV [22].
Regarding inelastic processes, the vibrational excitation integral cross sections recommended are those from Khakoo et al. [34] for incident energies of 10–100 eV, whereas the data of Seng and Linder [35] is used from threshold up to 10 eV. Concerning electronic excitation cross section, Song et al. [22] recommend Ralphs et al. [36] for energies below 17 eV and the BE f-scaled data for energies above 17 eV [37,38]. For the excitation of the state, the data of Matsui et al. [33] for energies above 12 eV and Ralphs’s for energies below 12 eV are recommended. It is relevant to note that excitation cross sections for 3A2, 1A2, 3A1, and 1A1 electronic states were also reported by Ralphs et al. [36], yet these were not recommended by Song et al. [22] based on the disagreement found between that data and the previous experimental results of Thorn et al. [37], the latter thoroughly discussed in ref. [39]. For rotational excitations, Song et al. [22] recommend the previous cross sections from J′′(000) to J′ = 0–3, [10], together with the calculated data of Machado et al. [40] up to 100 eV electron impact energy. The recommended data for water neutral dissociation yielding •OH radical formation in the ground and first excited states and O (1S), are from Harb et al. [41] and Kedzierski et al. [42], respectively. Finally, the recommended electron-impact ionization cross sections are those from Lindsay and Mangan [43] based on previous measurements of Straub et al. [44].
2.2. Input Data for Our Simulation
The required input data for electron transport simulation based on event-by-event Monte Carlo methods are the total cross sections, the partial integral cross sections, the angular distribution functions, and the energy loss distribution functions of all the relevant physical processes (both elastic and inelastic). For the present simulations we have used those cross sections, with complementary data for both elastic and inelastic DCSs.
We note that Song et al. [22] recommended elastic ICSs and DCSs, which are rotationally unresolved. Therefore, in our simulation we have not explicitly included rotational excitations but rather considered both elastic and rotational excitation processes as a single rotationally unresolved elastic process (see Section 3.2 for further details). Moreover, Song et al. [22] recommended DCSs values are reported between 10–20° and 130° scattering angles, based on the R-matrix calculation of Faure et al. [29] to complement the experimental DCSs from Matsui et al. [33]. However, not all of the data required to either extend the available DCS values to all the scattering angles or to interpolate to all the required energies are available from ref. [29]. For this reason, we have repeated the calculation of elastic electron scattering cross sections for a larger number of scattering energies employing exactly the same model used by Faure et al. (see Section 3.3).
With these additional results (available online1), we have extrapolated, after appropriate scaling, the recommended DCSs to 0° and 180° covering thus the whole angular range for electron impact energies below 15 eV. Above this energy, we followed a similar procedure by using the sum of our elastic IAM-SCAR+I [45,46,47] calculation and the rotational excitation cross sections calculated within the first Born approximation [48,49]. In Figure 1 we show the results of our calculated DCSs and the recommended experimental values for some selected incident energies.
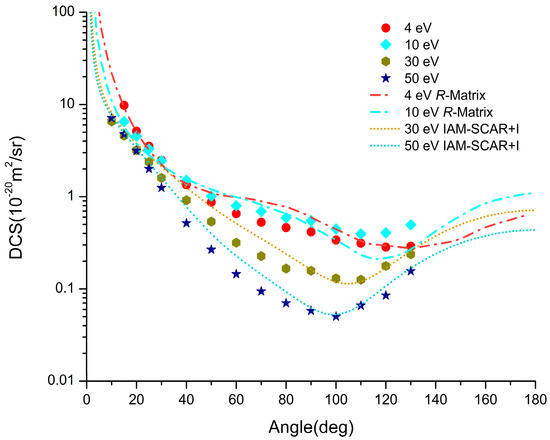
Figure 1.
Rotationally summed differential cross sections calculated with the R-matrix method for energies below 15 eV and differential elastic IAM-SCAR+I plus rotational (Born) cross sections for higher energies, compared to the recommended experimental values at 4, 10, 30, and 50 eV [33].
A very important input dataset which was not considered at all in the recent review [22] pertains to DCSs for the inelastic processes, from which the inelastic angular distribution function can be derived. As it is required for our simulations, and in order to show the relevance of these data for the shape and magnitude of the transmission spectra, we have considered two different cases. In case A, we assumed that all inelastic processes lead to isotropic scattering, whereas in case B, the inelastic angular distribution is assumed to be the same as that of the elastic scattering. In the latter case, we have used the ‘uncorrected’ (see Section 3.3 R-matrix DCSs for electron energies below 15 eV and the IAM-SCAR+I (pure elastic) DCSs for energies above 15 eV (see Figure 2).
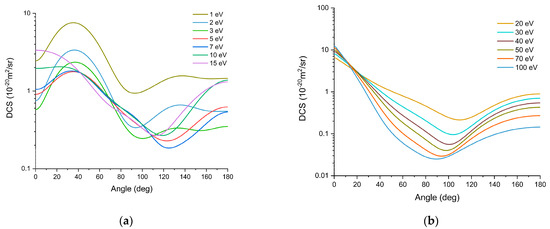
Figure 2.
Theoretical elastic differential cross sections for H2O. (a) Uncorrected (see text) R-matrix results in the electron energy range 1–15 eV. (b) IAM-SCAR+I results in the electron energy range 20–100 eV.
Another requirement for the input of our simulation code is an energy loss distribution function for each inelastic process considered (see Figure 3). We have used the experimental averaged energy loss spectrum from Muñoz et al. [18] for the ionization energy loss distribution, as well as for the electronic excitation and neutral dissociation processes. For vibrational excitations, we have used the electron energy loss spectrum from El-Zein et al. [50] following the same procedure as noted by Blanco and co-workers [51].
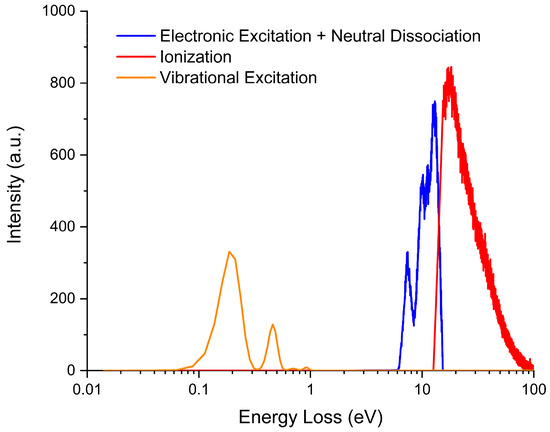
Figure 3.
Proposed electron energy loss distribution function associated to each inelastic process in the energy range 1–100 eV. See legend for the different processes depicted.
Finally, it is also important to note that the present TCSs are given by the sum of the partial ICS for each of the physical processes considered in the simulation. Therefore, our TCSs do not exactly match those recommended by Song et al. [22], although these values lie in the 7% range of reasonable uncertainty which can be generally attributed to obtaining TCS data. Table 1 summarizes the ICS and TCS used as input data for our simulation.

Table 1.
Integral cross sections (ICS) for each considered physical process and total cross section (TCS), used as input data for the present Monte Carlo simulation of electron transport through gaseous H2O together with TCS recommended values of ref. [22]. Energy in eV and cross sections in units of 10−20 m2.
2.3. Experiment vs. Simulation
The main goal of this study is to evaluate the reliability of a recently recommended dataset of cross sections for electron scattering from H2O to be used for modelling purposes. A well-proven procedure to validate the accuracy of a given cross sections dataset is via event-by-event Monte Carlo simulations of the magnetically confined electron transport through a gas cell, as proven in previous studies [19,20,21]. As described in Section 3.1, under these conditions, after any collision event the expected scattering angle is transformed into an energy loss in the axial direction. Therefore, the results given by the simulations are very sensitive to both the integral and the differential cross sections used as input data. As the cross sections for elastic processes have only been recommended up to 100 eV [22], we focused our analysis in the low-energy range to make a comparison between the results from the simulation and the experiment for three different electron energies (viz. 3, 10, and 70 eV). Moreover, for each incident energy, we considered two different cases for the pressure in the gas cell, except for the lowest energy (see below). This methodology provides some insight into the effect of increasing the number of multiple collisions, which is relevant for the accuracy and reliability of the input data dependent simulation results.
In Figure 4, Figure 5 and Figure 6 we depict the integrated transmission curves obtained from our simulations and from Geant4DNA for electron beam incident energies of 3, 10, and 70 eV, respectively. The experimental distributions obtained with the magnetically confined electron beam system are also plotted in these figures for comparison. For 3 eV, we restrict the transmitted spectrum to a gas pressure of 2.5 mTorr given that at higher pressures we have encountered reasonable instabilities; for 10 eV, the electron transmission was obtained at 5.0 and 10.0 mTorr; and for 70 eV, at 10.0 and 20.0 mTorr.
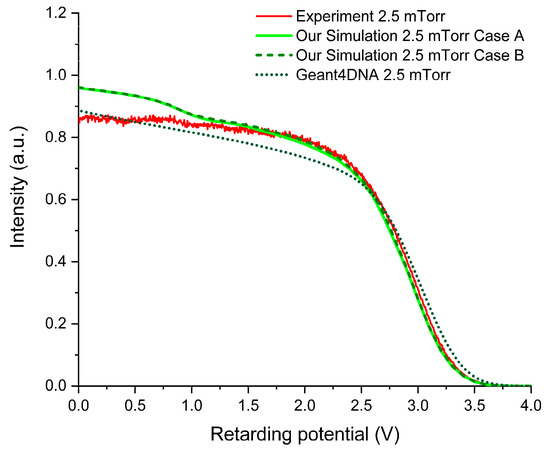
Figure 4.
Experimental and simulated transmission spectra (i.e., the intensity of the electrons with a corresponding axial kinetic energy above the retarding potential barrier) of a 3 eV electron beam through 2.5 mTorr of gaseous .
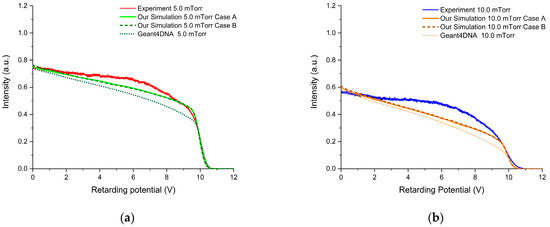
Figure 5.
Experimental and simulated transmission spectra (i.e., the intensity of the electrons with a corresponding axial kinetic energy above the retarding potential barrier) of a 10 eV electron beam through (a) 5.0 and (b) 10.0 mTorr of gaseous .
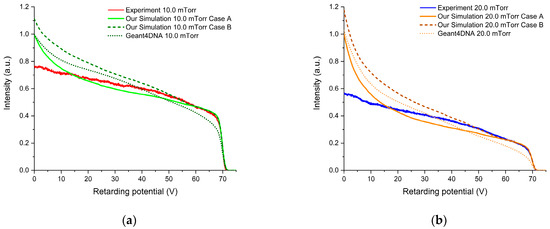
Figure 6.
Experimental and simulated transmission spectra (i.e., the intensity of the electrons with a corresponding axial kinetic energy above the retarding potential barrier) of a 70 eV electron beam through (a) 10.0 and (b) 20.0 mTorr of gaseous .
For each incident energy we obtained, in general, a good agreement between the simulations and the experimental results for the lowest pressure values considered, while significant discrepancies were found for the highest-pressure values. The results obtained from the simulations performed with Geant4DNA are qualitatively similar to ours but with some systematic discrepancies, which can be attributed to the differences between our input cross sections and those derived from the models considered by Geant4DNA at low energies (see Section 3.2 for further details).
With respect to the results at 3 eV, the main discrepancy appears in the low retarding potential region of the spectra, particularly below 1 V (i.e., where electrons with axial kinetic energies below 1 eV are incorporated to the integral transmission curve), where our simulation shows a significant enhancement which is not visible in the Geant4DNA results and is just slightly appreciable in the experimental data. This suggests that the recommended rotationally unresolved DCSs are overestimating the high angle contribution. However, as we mentioned in a previous study dealing with a larger polyatomic molecule, para-benzoquinone [20], a lower probability of the low-energy electrons reaching the detector would also contribute to such discrepancy.
At 10 eV we notice that both our simulation and the Geant4DNA results remain systematically below the experimental transmission curve. At this energy, elastic processes are still predominant, such that the observed systematic underestimation suggests a substantial overestimation of the recommended integral elastic cross sections. In addition, at this energy both electronic excitation and neutral dissociation channels are becoming more significant, so perhaps the overestimation of the elastic cross section at 10 eV is accompanied by an underestimation of the cross section of one of these inelastic processes. Hence, a more accurate cross sections dataset of these processes might significantly improve the agreement between simulations and experiment.
For an incident energy of 70 eV, all inelastic channels are now open, and their influence in the transmission spectra becomes at least as important as that of the elastic one. Our simulations reproduce the experimental results with excellent agreement for retarding potentials above 60 V, suggesting reasonably accurate integral cross sections. However, some discrepancies appear below that energy, which can be attributed to the contribution of the DCSs. As we mentioned in Section 2.1, a set of DCSs for the inelastic processes was absent from the recommended dataset [22], which we are using as input for our simulation. When comparing the present simulations using the two limit assumptions for the inelastic angular distributions (Case A, isotropic; and Case B, the same as that for pure elastic processes) with the experimental results, we observe a significant discrepancy in the slope of the transmission spectrum in the 20–60 V retarding potential range for both cases. In fact, the experimental results seem to lie somewhere in-between these two cases. Moreover, the results obtained with Geant4DNA, in no better agreement with the experimental data than ours, also show a transmission slope which lies in-between our two simulation cases. The discrepancies below 20 V (i.e., where electrons with axial kinetic energies below 20 eV are incorporated to the integral transmission curve) can again be mainly explained by the lower probability of low-energy electrons reaching the detector. Therefore, the results at this incident energy suggest that the inelastic angular distributions play a major role in shaping the transmission spectra. Taking this into account, the incorporation of inelastic DCSs to the cross section compilation of H2O should lead to a major improvement in the simulation of electron tracks through gaseous water.
Finally, in order to better illustrate the magnitude of the discrepancies found between the present simulated and experimental results as a function of pressure, Table 2 shows the number of processes and the total deposited energy per incident electron for different electron energies and gas pressures. A close inspection of this table reveals that the number of total interactions notably increase with pressure (by a factor of 3 or 4, at 10 and 70 eV, respectively). As the number of total interactions per incident electron increases, the discrepancies between the simulation and experiment are magnified due to the higher number of times that the cross sections data, with their respective uncertainties, are used. At 70 eV incident energy, ionization processes are significant and, accordingly, a high number of secondary electrons are produced, thus making the simulation more challenging. In addition, at the highest pressure considered (20.0 mTorr), the formation of water clusters, which are not considered in our simulations, might be playing a non-negligible role. It is important to note that despite the simulation including all inelastic processes, electronic excitations and electron attachment have such a low rate in the considered experimental conditions that their influence in the shape of the transmission curve is too small to enable evaluation of the accuracy of the associated recommended cross sections from this study.

Table 2.
Average number of interactions for each physical process and total energy deposited (bottom row) per initial electron at different incident energy and gas pressure conditions. Simulations were performed for case A (isotropic inelastic scattering assumption).
3. Materials and Methods
In this study we have combined the use of experimental and computational methods in a powerful procedure to validate the accuracy of a given cross sections dataset for electron scattering from gaseous water molecules. Such procedure has previously been applied with success to other molecules of biological interest, such as furfural [19], para-benzoquinone [20], and pyridine [21]. In the following subsections, we briefly describe the experimental setup used, as well as the simulation and computational procedures.
3.1. Magnetically Confined Electron Beam Experiment
The experimental results of the transmitted electron intensity spectra through gaseous H2O have been performed in a state-of the art magnetically confined electron beam experiment (see Figure 7) which has been described in detail elsewhere [23]. Some recent improvements in the performance of this experimental setup have been achieved after introducing small modifications consisting mainly on the replacement of the grids by collimators with apertures of 1.5 mm in diameter, which are depicted in Figure 7 as Ci (i = 1–7). This modification allows one to apply the potentials along the electrons’ path avoiding the formation of secondary electrons and it does not affect the working principle of this setup, which consists of the axial magnetic confinement of the electron beam (around 0.1 T) inside both the nitrogen gas trap and the scattering chamber (see Figure 7). As reported before [23], under these conditions, any collision event converts the expected scattering angle into an energy loss in the axial direction. A hairpin filament generates the electron beam which is guided through a nitrogen gas trap where it can be cooled, thereby reducing its initial energy spread of 500 meV down to about 100–200 meV in the optimal working conditions. Subsequently, before entering the scattering chamber, where a constant pressure of gaseous H2O is introduced through a leak valve, the electron beam is pulsed. Using a retarding potential analyzer (RPA), at the exit of the scattering chamber, the integrated transmission for electrons up to a given axial kinetic energy is recorded and, by performing an energy scan, the integrated transmission curves can be obtained.
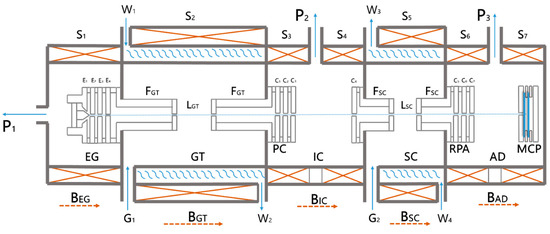
Figure 7.
Schematic representation of the magnetically confined electron beam experiment: EG, electron gun; GT, gas trap; IC, interphase chamber; PC, pulse-controlling system; SC, scattering chamber; RPA, retarding potential analyzer; AD, detection area; MCP, microchannel plate detector; C1–C7 various transmission collimators; P1, P2, P3, differential pumping system; BEG, BGT, BIC, BSC, BAD, axial magnetic fields of the different chambers generated by the corresponding solenoids (S1–S7); W1–W4, water cooling system; G1, G2, gas inlet to the GT and SC, respectively. (See also text and ref. [23] for further explanation).
3.2. Simulation Procedure
A specifically designed and developed event-by-event Monte Carlo code, fully built and implemented in Python, has been used to simulate the transmitted intensity of magnetically confined electrons through gaseous H2O.
This code has a modular structure that allows one to easily implement, revise, and modify each of the physical processes involved in a specific simulation. When simulating charged particles tracks, the code considers the different physical processes by sampling the step length between collisions, the interaction type, the energy loss, and the angular deflection of the scattered particles. This sampling procedure is performed from the probability distributions derived from the input dataset consisting of the total cross sections, the partial integral cross sections, the energy loss spectra, and the differential cross sections. Special attention is needed for sampling the scattering angle of the rotational excitations as their DCS are very strongly peaked in the forward scattering direction and a double logarithmic fitting for the interpolation at low angles is required in order to perform an accurate sampling. This is especially important in the present simulations, where rotational excitations and pure elastic collisions are merged into one single quasi-elastic process.
In the present study, we generated 104 incident electrons with an initial energy distribution obtained from the experimental transmission measurements with no gas (0 mTorr) in the collision chamber for each specific condition (incident energy and gas pressure) investigated. Although we could have achieved an electron beam energy resolution of around 100–200 meV, for the present study we have worked with suboptimal conditions (see Supplementary Information in Supplementary Materials for the precise energy resolution determination) in order to make even more challenging for the simulation to reproduc the transmitted energy spectra. This number of electrons was found to be enough to ensure that statistical uncertainties on the simulated transmitted intensities are less than 1%. It is also important to note that the RPA only affects the axial component of the emerging electrons’ momentum. Therefore, the simulated transmitted intensity is obtained by measuring only the kinetic energy associated with such component.
We have also performed simulations using the Geant4DNA [2,26] code, which is an extension of the well-known multipurpose Monte Carlo simulation toolkit Geant4 [52]. This extension includes models for processes relevant to the simulation of biological damage induced by ionizing radiation at the DNA scale. These processes mainly account for low-energy electron collisions with water and other DNA analogue molecules such as tetrahydrofuran (THF) and pyrimidine. The Geant4DNA simulation procedure has been thoroughly described by the Geant4DNA collaboration [2,3] so no further details will be given here. Among the available models for low-energy electron transport through water, we have selected those which have the lowest energy limit in their applicability. For elastic processes, we have used the Screened Rutherford model; for electronic excitations and ionizations we have selected the Emfietzoglou model; and for vibrational excitations and electron attachment we have applied the Sanche Excitation model and the Melton Attachment model, respectively.
3.3. Theoretical Calculation of Elastic and Rotational Cross Sections
The electronically elastic cross sections below 15 eV were calculated using the R-matrix method, as implemented in the UKRmol1 suite [53], within the fixed-nuclei approximation. As mentioned above, the model used in these calculations is identical to that employed by Faure et al. [29]. The model can be briefly summarized as follows (see [54] for more details): the molecular geometry corresponds to rOH = 1.81a0 and an angle between the OH bonds α = 104.5°. The Dunning DZP basis set was used for O and the TZP for H, this latter augmented with one diffuse s and two p functions, to generate pseudonatural orbitals that best describe (within this basis) the ground state and lowest six excited states of H2O. Seven target states were included in the close-coupling expansion: a complete active space configuration interaction model was used to expand the electronic state wavefunctions, in which the 1s orbitals of O were kept frozen and the eight remaining electrons were allowed to occupy the orbitals in the active space (2a1, 3a1, 4a1, 5a1, 1b1, 2b1, 1b2). This model produces a good description of the target states [54]: the ground state dipole moment (a critical quantity when describing electron scattering from a polar molecule) obtained is μ = 0.7334 a.u. (the experimental value is μ = 0.7295 a.u.). An R-matrix radius of 10 a0 was sufficient to ensure the electronic density associated to these states was negligible outside the R-matrix sphere. Gaussian type orbitals with angular momentum l ≤ 4 were used to describe the continuum. Using this model, K- and T-matrices were generated and used as input to a modified version of POLYDCS [55]. This modification enables the use of T-matrices and therefore the accurate calculation of elastic DCS above the first electronic excitation threshold. K-matrices were used to calculate DCS below the first excitation threshold (as done by Faure et al.) and T-matrices were employed to perform the calculations above it.
The DCS are determined (by POLYDCS) using a closure formula which compensates for the truncation of the partial wave expansion of the continuum and, at the same time, removes the divergence of this expansion in the fixed-nuclei approximation [56]. The dipolar Born approximation is used to calculate the contribution of partial waves not included in the R-matrix calculation: the cross sections thus determined are said to be ‘Born-corrected’. The cross sections thus obtained are not rotationally elastic: they are rotationally summed over a number of final states (the initial rotational state was assumed to be the one corresponding to J = 0 in our calculations). The ‘uncorrected’ cross sections for energies ≤7 eV presented in Figure 2. Correspond to performing a POLYDCS calculation assuming the molecule is non-polar, i.e., no Born-approximation based terms are added to the differential cross sections, but the frame transformation is performed. The uncorrected results for 7 eV < E ≤ 15 eV were calculated using the T-matrices and a different program that implements a similar approach, DCS [57].
4. Conclusions
The accuracy of the cross sections dataset for electron collisions with H2O recommended by Song et al. [22] has been critically evaluated by simulating the transmission of magnetically confined electrons with 3, 10, and 70 eV kinetic energy through different pressures of water vapor using their data as input. Also, simulations using Geant4DNA have been performed and compared with the experimental results and those from our own Monte Carlo simulation code.
The recommended dataset from ref. [22] presents two main deficiencies to serve as input for our simulation code: (a) the elastic DCSs recommended are experimental values and do not extend either to angles below 10–20° or above 130°. Thus, we had to extrapolate these by using an extended R-matrix dataset for incident energies up to 15 eV and a dataset calculated with the IAM-SCAR+I method for electron energies in the range of 15–100 eV; (b) angular DCSs for the inelastic processes are absent in the recommended dataset, so we have performed simulations considering two limit cases (A and B) in order to gain a better understanding of the role played by the inelastic angular distributions in shaping the transmission curves. Case A considered that all inelastic processes yielded an isotropic scattering distribution, while case B assumed that the inelastic angular distribution contributes equally as the pure elastic scattering.
In general, a good agreement in the transmission spectra, although with some discrepancies, has been obtained for all incident energies at the lowest pressures considered here. Nonetheless, some insight as to how to improve the cross section dataset has been gained by considering the observed discrepancies. Some inaccuracy in the rotationally unresolved elastic DCSs at 3 eV is suggested by the disagreement found in the low energy region of the transmission spectra. At 10 eV, the results suggest an overestimation of the integral elastic cross sections. The results obtained at 70 eV with our two simulations assuming different angular distributions for the inelastic processes revealed the importance of these DCSs for an accurate simulation of the electron transport process. Therefore, the present results clearly show the need to incorporate recommended data for those inelastic DCSs in order to improve the simulations of electron transport through gaseous H2O.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/atoms9040098/s1. Table S1: IAM-SCAR+I elastic DCS H2O; Table S2: FBA rotational DCS H2O; Table S3: Simulation input elastic+rotational DCS H2O, SI: Transmitted Spectra No Gas. The elastic DCS and integral cross section calculated with the R-matrix method are available for download here: https://doi.org/10.5281/zenodo.5566537.
Author Contributions
Formal analysis, A.G.-A., A.I.L. and J.D.G.; investigation, A.G.-A. and A.I.L.; methodology, J.C.O., F.B., J.D.G., P.L.-V. and G.G.; software, A.G.-A., J.C.O., F.B. and J.D.G.; writing—original draft, A.G.-A. and A.I.L.; writing—review and editing, J.D.G., P.L.-V. and G.G. All authors have read and agreed to the published version of the manuscript.
Funding
This study has been partially funded by the Spanish Ministerio de Ciencia e Innovación (Project PID2019-104727RB-C21) and CSIC (Project LINKA20085).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in the Supplementary Materials section and in https://doi.org/10.5281/zenodo.5566537.
Acknowledgments
A.G.-A. thank MICIU for his grant within the “Garantía Juvenil” programme. A.I.L., P.L.-V. acknowledge the Portuguese National Funding Agency (FCT) through research grants CEFITEC (UIDB/00068/2020) and PTDC/FIS-AQM/31281/2017. J.D.G. acknowledges support of the UK-AMOR consortium funded by EPSRC (EP/R029342/1).
Conflicts of Interest
The authors declare no conflict of interest.
Note
| 1 | The suite can be downloaded from: https://doi.org/10.5281/zenodo.2630454 and https://doi.org/10.5281/zenodo.2630474 (accessed on 1 November 2021). |
References
- Verkhovtsev, A.; Traore, A.; Muñoz, A.; Blanco, F.; García, G. Modeling secondary particle tracks generated by intermediate- and low-energy protons in water with the Low-Energy Particle Track Simulation code. Radiat. Phys. Chem. 2017, 130, 371–378. [Google Scholar] [CrossRef]
- Incerti, S.; Baldacchino, G.; Bernal, M.; Capra, R.; Champion, C.; Francis, Z.; Guèye, P.; Mantero, A.; Mascialino, B.; Moretto, P.; et al. THE GEANT4-DNA PROJECT. Int. J. Model. Simul. Sci. Comput. 2010, 01, 157–178. [Google Scholar] [CrossRef]
- Bernal, M.A.; Bordage, M.C.; Brown, J.M.C.; Davídková, M.; Delage, E.; El Bitar, Z.; Enger, S.A.; Francis, Z.; Guatelli, S.; Ivanchenko, V.N.; et al. Track structure modeling in liquid water: A review of the Geant4-DNA very low energy extension of the Geant4 Monte Carlo simulation toolkit. Phys. Med. 2015, 31, 861–874. [Google Scholar] [CrossRef]
- Yousfi, M.; Benabdessadok, M.D. Boltzmann equation analysis of electron-molecule collision cross sections in water vapor and ammonia. J. Appl. Phys. 1998, 80, 6619. [Google Scholar] [CrossRef]
- Karwasz, G.P.; Brusa, R.S.; Zecca, A. One century of experiments on electron-atom and molecule scattering: A critical review of integral cross-sections. La Riv. del Nuovo Cim. 2001, 24, 1–101. [Google Scholar] [CrossRef]
- Robson, R.E.; White, R.D.; Ness, K.F. Transport coefficients for electrons in water vapor: Definition, measurement, and calculation. J. Chem. Phys. 2011, 134, 064319. [Google Scholar] [CrossRef]
- Ness, K.F.; Robson, R.E.; Brunger, M.J.; White, R.D. Transport coefficients and cross sections for electrons in water vapour: Comparison of cross section sets using an improved Boltzmann equation solution. J. Chem. Phys. 2012, 136, 024318. [Google Scholar] [CrossRef] [PubMed]
- Shirai, T.; Tabata, T.; Tawara, H. Analytic cross sections for electron collisions with CO, CO2, and H2O relevant to edge plasma impurities. At. Data Nucl. Data Tables 2001, 79, 143–184. [Google Scholar] [CrossRef]
- Blanco, F.; Muñoz, A.; Almeida, D.; Ferreira da Silva, F.; Limão-Vieira, P.; Fuss, M.C.; Sanz, A.G.; García, G. Modelling low energy electron and positron tracks in biologically relevant media. Eur. Phys. J. D 2013, 67, 199. [Google Scholar] [CrossRef]
- Itikawa, Y.; Mason, N. Cross Sections for Electron Collisions with Water Molecules. J. Phys. Chem. Ref. Data 2005, 34, 1–22. [Google Scholar] [CrossRef]
- Song, M.-Y.; Yoon, J.-S.; Cho, H.; Karwasz, G.P.; Kokoouline, V.; Nakamura, Y.; Tennyson, J. “Recommended” cross sections for electron collisions with molecules. Eur. Phys. J. D 2020, 74, 60. [Google Scholar] [CrossRef]
- De Urquijo, J.; Basurto, E.; Juárez, A.M.; Ness, K.F.; Robson, R.E.; Brunger, M.J.; White, R.D. Electron drift velocities in He and water mixtures: Measurements and an assessment of the water vapour cross-section sets. J. Chem. Phys. 2014, 141, 014308. [Google Scholar] [CrossRef]
- Fuss, M.C.; Ellis-Gibbings, L.; Jones, D.B.; Brunger, M.J.; Blanco, F.; Muñoz, A.; Limão-Vieira, P.; García, G. The role of pyrimidine and water as underlying molecular constituents for describing radiation damage in living tissue: A comparative study. J. Appl. Phys. 2015, 117, 214701. [Google Scholar] [CrossRef]
- Muñoz, A.; Blanco, F.; Garcia, G.; Thorn, P.A.; Brunger, M.J.; Sullivan, J.P.; Buckman, S.J. Single electron tracks in water vapour for energies below 100 eV. Int. J. Mass Spectrom. 2008, 277, 175–179. [Google Scholar] [CrossRef]
- Anzai, K.; Kato, H.; Hoshino, M.; Tanaka, H.; Itikawa, Y.; Campbell, L.; Brunger, M.J.; Buckman, S.J.; Cho, H.; Blanco, F.; et al. Cross section data sets for electron collisions with H2, O2, CO, CO2, N2O and H2O. Eur. Phys. J. D 2012, 66, 36. [Google Scholar] [CrossRef]
- Ruíz-Vargas, G.; Yousfi, M.; Urquijo, J. de Electron transport coefficients in the mixtures of H2O with N2, O2, CO2 and dry air for the optimization of non-thermal atmospheric pressure plasmas. J. Phys. D. Appl. Phys. 2010, 43, 455201. [Google Scholar] [CrossRef]
- White, R.D.; Cocks, D.; Boyle, G.; Casey, M.; Garland, N.; Konovalov, D.; Philippa, B.; Stokes, P.; De Urquijo, J.; González-Magaña, O.; et al. Electron transport in biomolecular gaseous and liquid systems: Theory, experiment and self-consistent cross-sections. Plasma Sources Sci. Technol. 2018, 053001. [Google Scholar] [CrossRef]
- Muñoz, A.; Oller, J.C.; Blanco, F.; Gorfinkiel, J.D.; Limão-Vieira, P.; García, G. Electron-scattering cross sections and stopping powers in H2O. Phys. Rev. A 2007, 76, 052707. [Google Scholar] [CrossRef]
- Lozano, A.I.; Krupa, K.; Ferreira da Silva, F.; Limão-Vieira, P.; Blanco, F.; Muñoz, A.; Jones, D.B.; Brunger, M.J.; García, G. Low energy electron transport in furfural. Eur. Phys. J. D 2017, 71, 226. [Google Scholar] [CrossRef]
- Lozano, A.I.; Oller, J.C.; Jones, D.B.; da Costa, R.F.; Varella, M.T.d.N.; Bettega, M.H.F.; Ferreira da Silva, F.; Limão-Vieira, P.; Lima, M.A.P.; White, R.D.; et al. Total electron scattering cross sections from para -benzoquinone in the energy range 1–200 eV. Phys. Chem. Chem. Phys. 2018, 20, 22368–22378. [Google Scholar] [CrossRef] [PubMed]
- Costa, F.; Traoré-Dubuis, A.; Álvarez, L.; Lozano, A.I.; Ren, X.; Dorn, A.; Limão-Vieira, P.; Blanco, F.; Oller, J.C.; Muñoz, A.; et al. A Complete Cross Section Data Set for Electron Scattering by Pyridine: Modelling Electron Transport in the Energy Range 0–100 eV. Int. J. Mol. Sci. 2020, 21, 6947. [Google Scholar] [CrossRef]
- Song, M.-Y.; Cho, H.; Karwasz, G.P.; Kokoouline, V.; Nakamura, Y.; Tennyson, J.; Faure, A.; Mason, N.J.; Itikawa, Y. Cross Sections for Electron Collisions with H2O. J. Phys. Chem. Ref. Data 2021, 50, 023103. [Google Scholar] [CrossRef]
- Lozano, A.I.; Oller, J.C.; Krupa, K.; Ferreira da Silva, F.; Limão-Vieira, P.; Blanco, F.; Muñoz, A.; Colmenares, R.; García, G. Magnetically confined electron beam system for high resolution electron transmission-beam experiments. Rev. Sci. Instrum. 2018, 89, 063105. [Google Scholar] [CrossRef]
- Incerti, S.; Ivanchenko, A.; Karamitros, M.; Mantero, A.; Moretto, P.; Tran, H.N.; Mascialino, B.; Champion, C.; Ivanchenko, V.N.; Bernal, M.A.; et al. Comparison of GEANT4 very low energy cross section models with experimental data in water. Med. Phys. 2010, 37, 4692–4708. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; et al. Recent developments in GEANT4. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Incerti, S.; Kyriakou, I.; Bernal, M.A.; Bordage, M.C.; Francis, Z.; Guatelli, S.; Ivanchenko, V.; Karamitros, M.; Lampe, N.; Lee, S.B.; et al. Geant4-DNA example applications for track structure simulations in liquid water: A report from the Geant4-DNA Project. Med. Phys. 2018, 45, e722–e739. [Google Scholar] [CrossRef] [PubMed]
- Incerti, S.; Douglass, M.; Penfold, S.; Guatelli, S.; Bezak, E. Review of Geant4-DNA applications for micro and nanoscale simulations. Phys. Med. 2016, 32, 1187–1200. [Google Scholar] [CrossRef]
- Zhang, R.; Faure, A.; Tennyson, J. Electron and positron collisions with polar molecules: Studies with the benchmark water molecule. Phys. Scr. 2009, 80, 015301. [Google Scholar] [CrossRef]
- Faure, A.; Gorfinkiel, J.D.; Tennyson, J. Low-energy electron collisions with water: Elastic and rotationally inelastic scattering. J. Phys. B At. Mol. Opt. Phys. 2004, 37, 801. [Google Scholar] [CrossRef][Green Version]
- Faure, A.; Gorfinkiel, J.D.; Tennyson, J. Electron-impact rotational excitation of water. Mon. Not. R. Astron. Soc. 2004, 347, 323–333. [Google Scholar] [CrossRef]
- Szmytkowski, C.; Możejko, P. Electron-scattering total cross sections for triatomic molecules: NO2 and H2O. Opt. Appl. 2006, 36, 543–550. [Google Scholar]
- Kadokura, R.; Loreti, A.; Kövér, Á.; Faure, A.; Tennyson, J.; Laricchia, G. Angle-Resolved Electron Scattering from H2O near 0°. Phys. Rev. Lett. 2019, 123. [Google Scholar] [CrossRef]
- Matsui, M.; Hoshino, M.; Kato, H.; da Silva, F.F.; Limão-Vieira, P.; Tanaka, H. Measuring electron-impact cross sections of water: Elastic scattering and electronic excitation of the ã3B1 and Ã1B1 states. Eur. Phys. J. D 2016, 70, 77. [Google Scholar] [CrossRef]
- Khakoo, M.A.; Winstead, C.; McKoy, V. Vibrational excitation of water by electron impact. Phys. Rev. A 2009, 79, 052711. [Google Scholar] [CrossRef]
- Seng, G.; Linder, F. Vibrational excitation of polar molecules by electron impact. II. Direct and resonant excitation in H2O. J. Phys. B At. Mol. Phys. 1976, 9, 2539. [Google Scholar] [CrossRef]
- Ralphs, K.; Serna, G.; Hargreaves, L.R.; Khakoo, M.A.; Winstead, C.; McKoy, V. Excitation of the six lowest electronic transitions in water by 9–20 eV electrons. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 125201. [Google Scholar] [CrossRef]
- Thorn, P.A.; Brunger, M.J.; Teubner, P.J.O.; Diakomichalis, N.; Maddern, T.; Bolorizadeh, M.A.; Newell, W.R.; Kato, H.; Hoshino, M.; Tanaka, H.; et al. Cross sections and oscillator strengths for electron-impact excitation of the ÃB11 electronic state of water. J. Chem. Phys. 2007, 126, 064306. [Google Scholar] [CrossRef]
- Kim, Y.-K. Scaled Born cross sections for excitations of H2 by electron impact. J. Chem. Phys. 2007, 126, 064305. [Google Scholar] [CrossRef]
- Brunger, M.J. Electron scattering and transport in biofuels, biomolecules and biomass fragments. Int. Rev. Phys. Chem. 2017, 36, 333–376. [Google Scholar] [CrossRef]
- Machado, L.E.; Brescansin, L.M.; Iga, I.; Lee, M.-T. Elastic and rotational excitation cross-sections for electron-water collisions in the low- and intermediate-energy ranges. Eur. Phys. J. D-At. Mol. Opt. Plasma Phys. 2005, 33, 193–199. [Google Scholar] [CrossRef]
- Harb, T.; Kedzierski, W.; McConkey, J.W. Production of ground state OH following electron impact on H2O. J. Chem. Phys. 2001, 115, 5507. [Google Scholar] [CrossRef]
- Kedzierski, W.; Derbyshire, J.; Malone, C.; McConkey, J.W. Isotope effects in the electron impact break-up of water. J. Phys. B At. Mol. Opt. Phys. 1998, 31, 5361. [Google Scholar] [CrossRef]
- Lindsay, B.G.; Mangan, M.A. 5.1 Ionization. Interact. Photons Electrons Mol. 2005, 5001–5077. [Google Scholar] [CrossRef]
- Straub, H.C.; Lindsay, B.G.; Smith, K.A.; Stebbings, R.F. Absolute partial cross sections for electron-impact ionization of H2O and D2O from threshold to 1000 eV. J. Chem. Phys. 1998, 108, 109–116. [Google Scholar] [CrossRef]
- Blanco, F.; García, G. Screening corrections for calculation of electron scattering from polyatomic molecules. Phys. Lett. A 2003, 317, 458–462. [Google Scholar] [CrossRef]
- Blanco, F.; Ellis-Gibbings, L.; García, G. Screening corrections for the interference contributions to the electron and positron scattering cross sections from polyatomic molecules. Chem. Phys. Lett. 2016, 645, 71–75. [Google Scholar] [CrossRef]
- Dubuis, A.T.; Costa, F.; da Silva, F.F.; Limão-Vieira, P.; Oller, J.C.; Blanco, F.; García, G. Total electron scattering cross section from pyridine molecules in the energy range 10–1000 eV. Chem. Phys. Lett. 2018, 699, 182–187. [Google Scholar] [CrossRef]
- Jain, A. Theoretical study of the total (elastic+inelastic) cross sections for electron -H2O (NH3) scattering at 10-3000 eV. J. Phys. B At. Mol. Opt. Phys. 1988, 21, 905–924. [Google Scholar] [CrossRef]
- Álvarez, L.; Costa, F.; Lozano, A.I.; Oller, J.C.; Muñoz, A.; Blanco, F.; Limão-Vieira, P.; White, R.D.; Brunger, M.J.; García, G. Electron scattering cross sections from nitrobenzene in the energy range 0.4–1000 eV: The role of dipole interactions in measurements and calculations. Phys. Chem. Chem. Phys. 2020, 22, 13505–13515. [Google Scholar] [CrossRef]
- El-Zein, A.A.A.; Brunger, M.J.; Newell, W.R. Excitation of vibrational quanta in water by electron impact. J. Phys. B At. Mol. Opt. Phys. 2000, 33, 5033. [Google Scholar] [CrossRef]
- Blanco, F.; Roldán, A.M.; Krupa, K.; McEachran, R.P.; White, R.D.; Marjanović, S.; Petrović, Z.L.; Brunger, M.J.; Machacek, J.R.; Buckman, S.J.; et al. Scattering data for modelling positron tracks in gaseous and liquid water. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 145001. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Carr, J.M.; Galiatsatos, P.G.; Gorfinkiel, J.D.; Harvey, A.G.; Lysaght, M.A.; Madden, D.; Mašín, Z.; Plummer, M.; Tennyson, J.; Varambhia, H.N. UKRmol: A low-energy electron-and positron-molecule scattering suite. Eur. Phys. J. D 2012, 66, 58. [Google Scholar] [CrossRef]
- Gorfinkiel, J.D.; Morgan, L.A.; Tennyson, J. Electron impact dissociative excitation of water within the adiabatic nuclei approximation. J. Phys. B At. Mol. Opt. Phys. 2002, 35, 543–555. [Google Scholar] [CrossRef]
- Sanna, N.; Gianturco, F.A. Differential cross sections for electron/positron scattering from polyatomic molecules. Comput. Phys. Commun. 1998, 114, 142–167. [Google Scholar] [CrossRef]
- Gianturco, F.A.; Jain, A. The theory of electron scattering from polyatomic molecules. Phys. Rep. 1986, 143, 347–425. [Google Scholar] [CrossRef]
- Mašín, Z. DCS: A Program to Generate Orientation-Averaged DCS for Electronically Elastic and Inelastic Collsions. Available online: https://gitlab.com/Masin/DCS (accessed on 1 May 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).