Next Article in Journal
Zika and Flavivirus Shell Disorder: Virulence and Fetal Morbidity
Next Article in Special Issue
Molecular Dynamics Simulations Suggest a Non-Doublet Decoding Model of −1 Frameshifting by tRNASer3
Previous Article in Journal
Algae: Critical Sources of Very Long-Chain Polyunsaturated Fatty Acids
Previous Article in Special Issue
MS-Based Approaches Enable the Structural Characterization of Transcription Factor/DNA Response Element Complex
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Biomolecules
Volume 9
Issue 11
10.3390/biom9110709
biomolecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Dynamic DNA Energy Landscapes and Substrate Complexity in Triplet Repeat Expansion and DNA Repair

by
Jens Völker
1,
G. Eric Plum
2,
Vera Gindikin
1 and
Kenneth J. Breslauer
1,3,*
1
Department of Chemistry and Chemical Biology, Rutgers University, Piscataway, NJ 08854, USA
2
IBET Inc, Columbus, OH 43220, USA
3
The Rutgers Cancer Institute of New Jersey, New Brunswick, NJ 08901, USA
*
Author to whom correspondence should be addressed.
Biomolecules 2019, 9(11), 709; https://doi.org/10.3390/biom9110709
Submission received: 2 October 2019 / Revised: 29 October 2019 / Accepted: 31 October 2019 / Published: 6 November 2019
(This article belongs to the Special Issue Nucleic Acids, Structure and Modeling)
Browse Figures
Versions Notes

Abstract

:
DNA repeat domains implicated in DNA expansion diseases exhibit complex conformational and energy landscapes that impact biological outcomes. These landscapes include ensembles of entropically driven positional interchanges between isoenergetic, isomeric looped states referred to as rollamers. Here, we present evidence for the position-dependent impact on repeat DNA energy landscapes of an oxidative lesion (8oxodG) and of an abasic site analogue (tetrahydrofuran, F), the universal intermediate in base excision repair (BER). We demonstrate that these lesions modulate repeat bulge loop distributions within the wider dynamic rollamer triplet repeat landscapes. We showed that the presence of a lesion disrupts the energy degeneracy of the rollameric positional isomers. This lesion-induced disruption leads to the redistribution of loop isomers within the repeat loop rollamer ensemble, favoring those rollameric isomers where the lesion is positioned to be energetically least disruptive. These dynamic ensembles create a highly complex energy/conformational landscape of potential BER enzyme substrates to select for processing or to inhibit processing. We discuss the implications of such lesion-induced alterations in repeat DNA energy landscapes in the context of potential BER repair outcomes, thereby providing a biophysical basis for the intriguing in vivo observation of a linkage between pathogenic triplet repeat expansion and DNA repair.

Graphical Abstract

1. Introduction

Sequence repeat DNA domains exhibit enhanced propensities to undergo expansion and deletion events in vivo, frequently with deleterious outcomes for the affected organism [1,2,3,4,5,6,7,8]. Such expansion or deletion events often correlate with complex repeat DNA conformational landscapes that can cause dysregulation of common DNA metabolic processes [9,10,11,12,13,14,15,16,17]. In particular, expansion of CNG (N = A,T,C or G) triplet repeat DNA domains in response to DNA replication [13,18,19,20], recombination [21,22], or repair processes [14,23,24,25,26] has been linked to the propensities of these repeats to adopt stable and metastable bulge loop self-structures in competition with the Watson-Crick duplex [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41]. Triplet repeats also exhibit a threshold phenomenon whereby the presence of a stretch of more than 35 or so CNG repeats inevitably leads to pathogenic DNA expansion events [42,43]. We have shown that a bulge loop structure comprised of a part of a larger repeat sequence domain can exist as several isoenergetic loop isomers called rollamers in dynamic equilibrium with each other [44]. Such loop formation and migration results in a complex dynamic energy landscape, illustrated schematically by the red curve in Figure 1A. The three isoenergetic local minima relative to the global minimum of the corresponding fully bonded duplex state reflect each of the three rollameric positional isomers shown schematically in the absence of a lesion in Figure 1A, which creates substrate complexity for the processing of such rollamer domains. This degenerate distribution of isoenergetic rollameric states potentially provides an entropic explanation for the observed threshold phenomenon for DNA expansion [43,44]. In short, rollamers are fleeting/transient dynamic substrates for DNA processing machineries that are optimized to process double helical substrates [26,45,46], thereby potentially explaining why triplet repeat DNAs are prone to undergo expansion and deletion events in vivo.
This substrate complexity becomes even more challenging when the triplet repeat domain contains DNA lesions that require processing within this dynamic landscape by different repair pathways. We have shown that a particular lesion almost always destabilizes the duplex state [47,48,49], but it can either stabilize, remain neutral, or destabilize the static repeat bulge loop state depending on the position of the lesion with respect to the loop domain [50]. Such position-dependent differential impact of lesions on static repeat bulge loops is also expected to significantly influence the properties of dynamic bulge loop rollamer substrates. This next level of lesion-induced substrate complexity is illustrated schematically by the green curve in Figure 1B. Note that the presence of a lesion (indicated by a green dot) can differentially disrupt the isoenergetic degeneracy of the rollameric isomers in a position-dependent manner, as reflected by the example of different well depths for each rollamer shown in Figure 1B.
Below, we experimentally map the impact of DNA lesions embedded within and modulating the complex, dynamic triplet repeat landscape. One goal of these studies is to establish a better appreciation for the dynamic complexities of the repeat DNA substrates encountered by DNA repair pathways during lesion repair, which is part of our broader goal of correlating biophysical properties with biological mechanisms and outcomes. Specifically, we focused on the role of 8oxodG and abasic site lesions as the most common oxidative DNA damage and universal intermediate in base excision repair (BER) of oxidative DNA damage [51,52,53], respectively. Such constructs are biologically relevant since it has been estimated that between 10,000 and 30,000 incidences of oxidative damage to DNA occur in each cell per day [54,55]. Moreover, CAG repeat secondary structures are hotspots for oxidative DNA damage [28,56], while base excision repair (BER) of oxidative DNA lesions within or near CAG repeats leads to DNA expansion in mouse models of Huntington’s disease [57,58]. Here, we present the first experimental evidence in support of such coupling of repair and expansion by mapping the complex, dynamic energy landscapes of potential substrates for DNA processing within dynamic rollamer repeat domains. Specifically, we demonstrate that DNA lesions within or proximal to triplet repeat domains can bias dynamic rearrangement and redistribution of loop isomers in favor of those rollamers where the lesion is positioned to be energetically least disruptive. Our results provide an intriguing biophysical basis for the in vivo observation of the coupling of DNA repair and DNA triplet repeat expansion.

2. Materials and Methods

2.1. Materials

Oligonucleotides were synthesized in our lab on a 10 µmole scale by standard phosphoramidite chemistry using an Äkta DNA synthesizer or were purchased from IDT (Coralville, IA, USA). Oligonucleotides were purified by Dimethoxytrityl –on (DMT-on) and subsequent repeated DMT-off reverse phase high performance liquid chromatography (HPLC), as previously described [32,34,44,50,60]. The purities of the oligonucleotides were assessed by analytical HPLC and ion spray mass spectroscopy, and were found to be pure by analytical HPLC and better than 98% pure by mass spectroscopy. Purified oligonucleotides were dialyzed using dispo-dialyzers with MWCO 500 Da (Spectrum, CA) against at least two changes of pH 6.8 buffer containing 10 mM cacodylic acid/Na-cacodylate, and 0.1 mM Na2 EDTA and sufficient NaCl to yield a final concentration of 100 mM in Na+ ions. Molar extinction coefficients of the parent DNA oligomers lacking repeats ([CAG]0, [CTG]0) were determined by phosphate assay under denaturing conditions (90 °C) [61,62] and were found to be: ε[CAG]0 (260 nm, 90 °C) = 190,400 M−1 cm−1; ε[CTG]0 (260 nm, 90 °C) = 186,200 M−1 cm−1. For all other oligonucleotides, extinction coefficients were determined from continuous variation titrations (Job plots) [63] with the complementary parent oligonucleotide, and were found to be: ε[CTG]2 (260 nm, 90 °C) = 221,700 M−1 cm−1; ε[CTG]4 (260 nm, 90 °C) = 271,100 M−1 cm−1. For the abasic site and 8oxodG lesion containing oligonucleotides extinction coefficients were found to be: ε[CAG]6-F(n) (260 nm, 90 °C) = 368,400 M−1 cm−1; and ε[CAG]6-O(n) (260 nm, 90 °C) = 368,400 M−1 cm−1 regardless of lesion positions. As expected, for the 40-mers, the impact of a single abasic site or 8oxodG lesion in place of guanine is independent of lesion position and too small to result in a measurable change in extinction coefficient when compared to the [CAG]6 parent 40-mer.

2.2. Differential Scanning Calorimetry (DSC) Studies

Differential Scanning Calorimetry (DSC) studies were conducted as previously described using a NanoDSC II differential scanning calorimeter (Calorimetry Science Corporation, Provo, UT, USA) with a nominal cell volume of 0.3 mL [64,65]. Oligonucleotides, at a concentration of 50 µM in strand, were repeatedly scanned between 0 °C and 90 or 95 °C with a constant heating rate of 1 °C /min, while continuously recording the excess power required to maintain sample and reference cells at the same temperature. After conversion of the measured excess power values to heat capacity units (cal/K) and subtractions of buffer vs. buffer scans, the raw DSC traces were normalized for DNA concentration and analyzed using Origin software. The calorimetric enthalpy change (ΔHcal) was derived by the integration of the excess heat capacity curve, and ΔCp was derived from the difference in the linearly extrapolated pre- and post-transition baselines at Tm. ΔS was derived by ΔH/Tm, assuming “pseudomonomolecular” dissociation behavior in which propagation dominates initiation [66]. The Tm is defined as the temperature at the midpoint of the integrated excess heat capacity curve for a given conformational transition, which corresponds to half the sample being denatured for a process that exhibits pseudomonomolecularity.

2.3. Modeling of DSC Curves

For our model, we defined six accessible states: the three rollamer isomers (Loop Upstream, Loop MidStream, and Loop Downstream), two states wherein only the non-repetitive terminal upstream or downstream segments and the two proximate CAG triplets are base paired, and the fully denatured reference state. We assume that each triplet acts as a unit and that all unmodified triplets are thermodynamically indistinguishable. A segment containing a lesion within it is independently parameterized. The heat capacity change associated with each segment’s disruption is assumed to be zero.
We derived a partition function for this system parameterized in terms of temperature dependent and temperature independent contributions to each segment’s equilibrium constant [67,68]. A term accounting for the contribution of loop formation is also included. Using the partition function, the change in population of each state is calculated as a function of temperature. The contribution of the population changes to the excess heat capacity is calculated at each temperature to produce a calculated DSC curve. The parameters are adjusted to minimize the difference between the measured and calculated DSC curves. To this aim, we wrote a program in Labview using the Levenberg-Marquardt algorithm for the function minimization.

2.4. Ultraviolet Absorption Studies

Ultraviolet (UV) spectra and temperature dependent changes in UV absorbance were measured using an AVIV model 400 UV/VIS spectrophotometer (Aviv Biomedical, Lakewood, NJ, USA). Temperature dependent changes in absorbance at 260 nm with a 1 nm bandwidth were recorded with an averaging time of 5 s while the temperature was raised in steps of 0.5 °C with 1 min equilibration time. Oligonucleotide concentrations were 1.5 or 2 µM in strand.

3. Results and Discussion

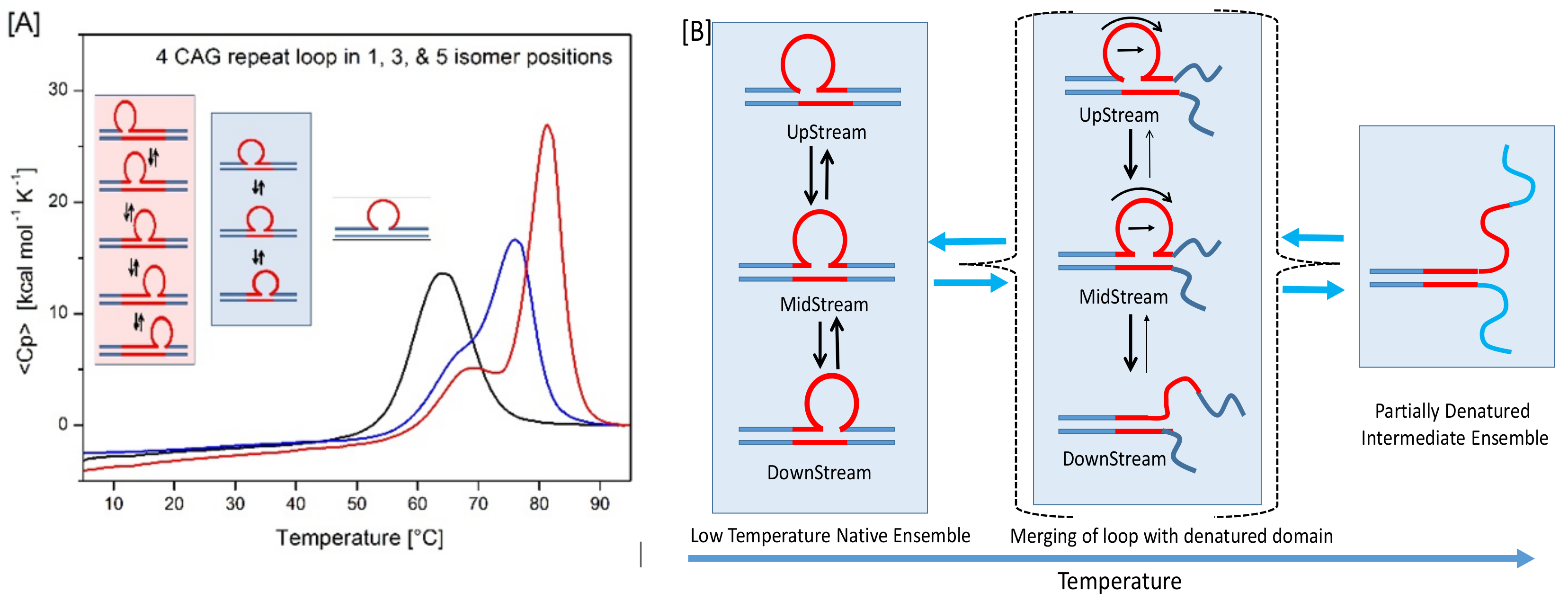
3.1. The Systems Studied

We designed a family of rollamer constructs containing a (CAG)4 repeat bulge loop that can exist in three possible isoenergetic loop positions by combining a [CAG]6 oligonucleotide with a partially complementary [CTG]2 oligonucleotide, as per the rules we previously described [44]. As illustrated in Scheme 1, such a construct exhibits a dynamic landscape of 3 interchanging, rollamer bulged loops. This dynamic behavior of (CAG)4 repeat loop rollamers contrasts with the static landscape of the corresponding single, fixed loop structure [32,33,44]. In panel A of Figure 2, note the characteristic changes in the excess heat capacity profiles of a static (CAG)4 repeat bulge loop (black) compared to the same (CAG)4 bulge loops existing as three (blue) or five (red) rollamer isomers. The consequences of such static versus dynamic loop properties are manifest in the differential DSC profiles shown in Figure 2, as described in the figure legend, and elaborated on below.

3.1.1. The Shape of the Rollamer Heat Capacity Curve Reflects the Coupling and Merging of Duplex Arm Melting and Loop Migration

The shape of the excess heat capacity profile of the three isomer rollamer construct shown in Figure 2 is primarily determined by the two additional base paired CAG·CTG triplets not present in the static repeat bulge loop. As shown in Scheme 1, these additional triplet base pairs are dynamically redistributed between the upstream and downstream duplex domains in the three isomers depending on loop position. Due to the relative positions occupied by the loop, we defined each of the three rollamers as loop MidStream with the designation of 1:1, reflective of the two additional triplet base pairs partitioning equally between the upstream and downstream duplex domains; loop UpStream with the designation of 0:2, reflective of both additional triplet base pairs partitioning in the downstream duplex domain; and, loop DownStream with the designation of 2:0, reflective of both additional triplet base pairs partitioning in the upstream duplex domain.
As we previously have shown in the absence of lesions [44], in our construct, denaturation of the rollamer in Figure 2A is initiated by melting of the less stable downstream duplex arm, resulting in a partially denatured complex (the initial transition seen in Figure 2A and the schematic shown in Figure 2B). Denaturation of this downstream domain induces loop migration to merge the loop with the denatured domain in those isomers where the loop is located away from the denatured arm. This process disrupts existing CAG·CTG pairs ahead of the migrating loop while regenerating an equivalent number of CAG·CTG pairs behind the migrating loop. Thus, loop migration is energetically neutral, but kinetically relatively slow on the timescale of our experiments, thereby impacting the shape of the DSC pre-transition peak. As a consequence, the two additional base paired CAG·CTG triplets partition into and stabilize the upstream duplex arm, giving rise to the main transition seen at higher temperature in the excess heat capacity profile. The presence of the free ends (“end effects”) in these oligonucleotides enhances the difference in the melting temperature of the two stable duplex domains, thereby allowing a clear differentiation of the sequential melting steps. The increase in enthalpy and melting temperature in the rollamers compared to the static structure reflects the additional base pairs in rollamers as well as the gain in entropy due to the degeneracy in the loop positions [44].
To summarize, denaturation initiates at the more unstable duplex domain coupled with the enthalpically neutral, but kinetically relatively slow migration of the loop from its three possible positions to merge with the denatured domain. As a consequence, loop migration adds base pairs to the more stable (upstream) duplex domain, thereby resulting in the thermal and thermodynamic stabilization of the upstream domain. Subsequent denaturation of the upstream domain at higher temperatures conforms to conventional oligonucleotide duplex behavior.

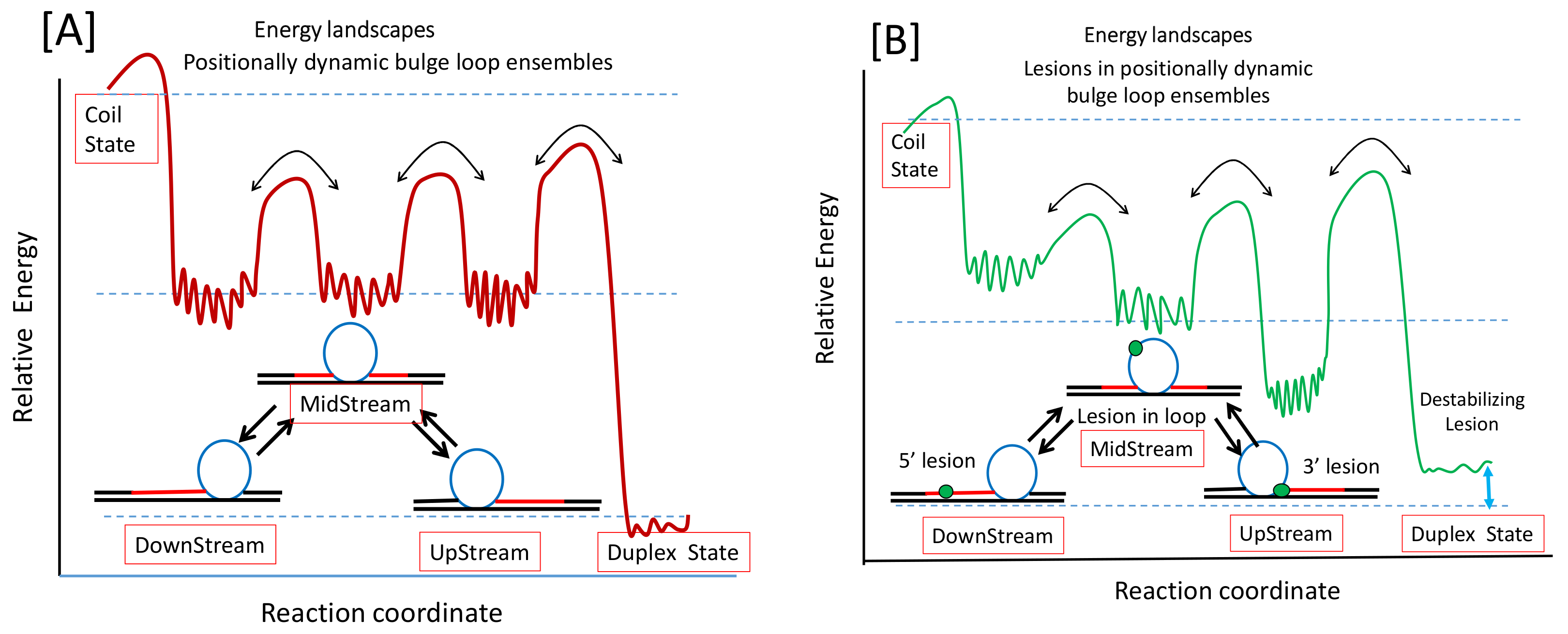
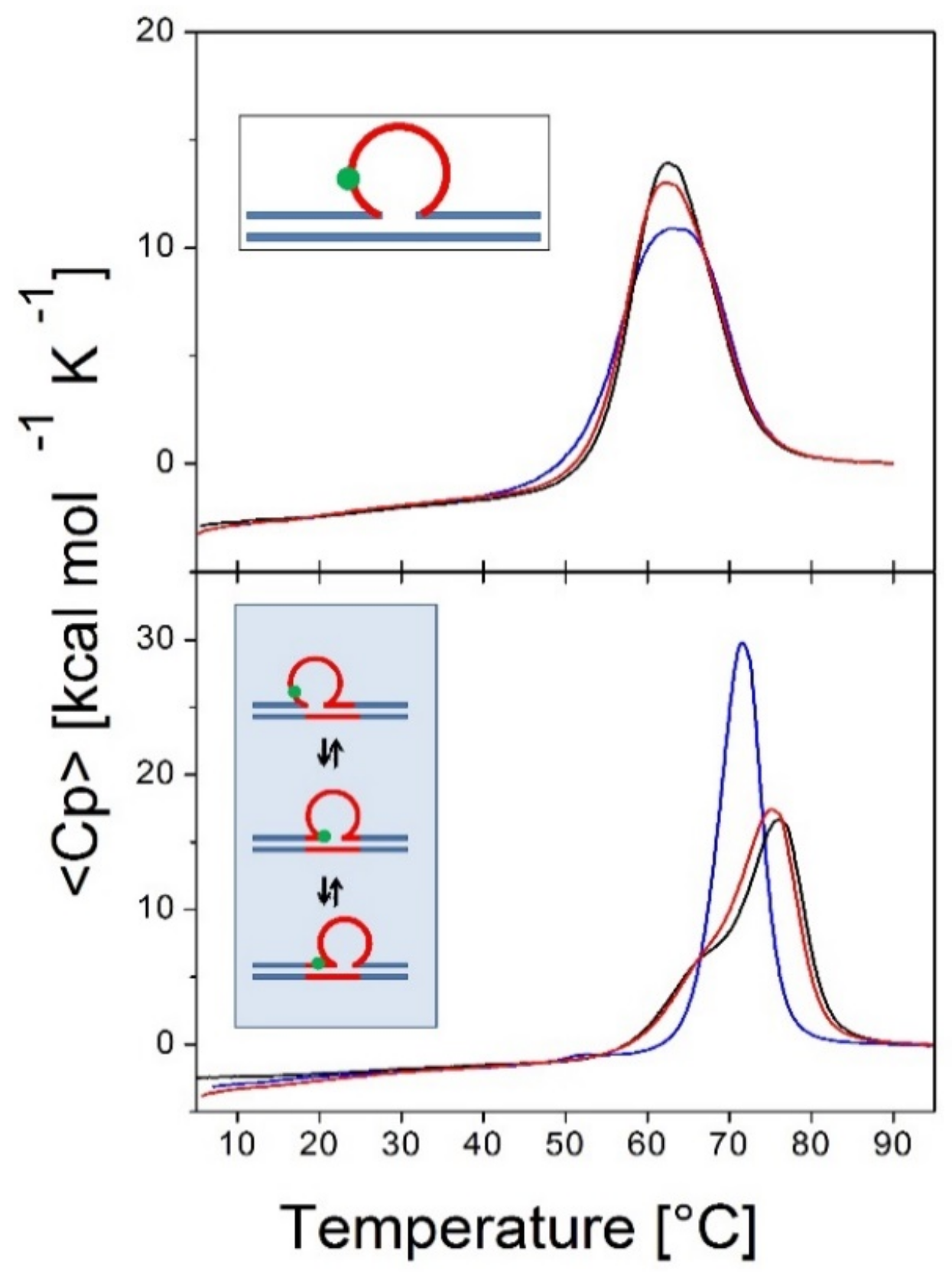
3.1.2. Differential Impact of Lesions on Static Versus Dynamic Loop Landscapes

To probe lesion-induced alterations in the triplet repeat dynamic energy landscape, we systematically introduced a single oxidative lesion (8oxodG or abasic site analogue) in place of dG at select positions within the CAG strand (shown schematically in Figure 1) such that multiple possible lesion positions are represented relative to the three rollamer loop isomers (see inserts in Figure 3 and Figure 4 and Table 1). Changes in loop distribution caused by the presence of a lesion in a particular repeat are expected to be reflected in corresponding changes in the excess heat capacity profile during melting. These changes would be due to the altered distribution of base paired CAG·CTG triplets between the upstream and downstream duplex domains, in addition to the position-dependent differential enthalpy effect of the lesion itself. These expectations are borne out by the experimental data. For example, as shown in Figure 3, and noted in the legend, if a lesion is located in the first CAG repeat, we observed that the presence of the lesion within the repeat significantly altered the characteristic shape of the rollamer heat capacity profile relative to the lesion-free parent rollamer, while barely altering the excess heat capacity curve of the static repeat loop construct.
Specifically, whereas the abasic site lesion (blue curve in Figure 3) in the static bulge loop is associated with a slight broadening of the melting transition, but no net enthalpy change [50], it results in the exact opposite melting behavior in the dynamic rollamer construct. In the dynamic rollamer, the lesion causes the apparent loss of the pre-transition and a significant apparent increase in cooperative melting transition relative to the lesion free rollamer, reflecting primarily lesion-induced changes in loop isomer distribution.
The excess heat capacity curves therefore provide a good window into the impact of lesions on dynamic loop distributions. In contrast, the impact of 8oxodG lesions (red curve in Figure 3) in either static bulge loop or dynamic rollamer is minor, with only a small decrease in Tm of the main transition in the rollamer construct as the main lesion impact. The differential impact of 8oxodG versus the abasic site lesion is reflective of the differential impact of these two lesions on DNA stability [69,70,71]. Based on these observations, we concluded that the repeat bulge loop distribution and redistribution as a function of lesion presence and position can be detected and monitored by differential heat capacity signatures, as measured by scanning calorimetry.

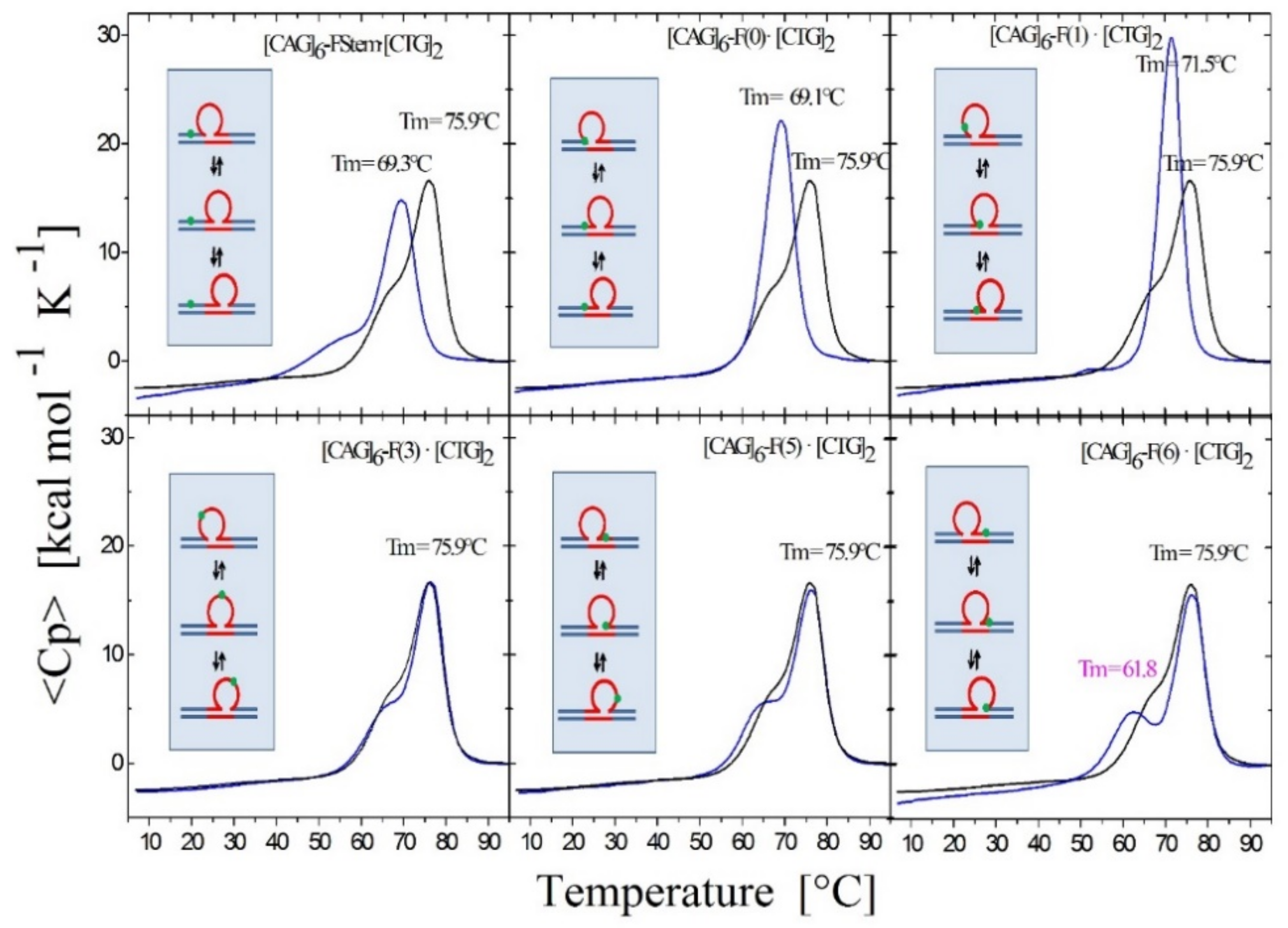
3.1.3. Lesion Impact Is Position Dependent

As shown in Figure 4, for all lesion-containing rollamers investigated, and as elaborated in the figure legend, we found characteristic changes in the shape of the excess heat capacity curves relative to that of the control, lesion-free, set of parent rollamers. Significantly, these characteristic changes were specific for the position of the lesion within the repeat sequence. These position-dependent, lesion-induced changes occurred despite the lesions being located in the same nearest neighbor context in all but one of the constructs. Consequently, our observations reflect lesion-induced alterations in loop isomer distribution and occupancy as well as any coupled events. Importantly, we found the same general trends for 8oxodG (not shown).
Figure 4 shows and Table 1 and Table S2 (Supplementary Material) summarizes the data for all of the lesion-containing constructs studied herein. Note that by strategically locating a lesion within a specific repeat within the three dynamic loop constructs, we were able to define features of and extract data from the DSC profiles that allow us to examine the differential distribution of the lesion into different structural domains accessible to the rollamers (5′ or 3′ stem duplex domain; 5′ or 3′ stem/loop junction; or loop domain). Collectively, these results are characteristic of position-dependent, lesion-induced redistribution of dynamic loop structures; a feature that generates a highly complex landscape of dynamic substrates for DNA processing systems.

3.1.4. Position-Dependent Lesion Impact on Rollamer Distribution

To further define the impact of the lesion positions within the dynamic landscape of rollamers, we compared the results reported here with our previous studies on 8oxodG and abasic site lesions in fixed positions within the corresponding, static, single isomer repeat bulge loop [50] (Supplementary Materials). Such comparisons between our datasets on dynamic and static repeat bulge loop constructs allowed us to define a general hierarchy of position-dependent lesion impacts on bulge loop properties. Specifically, relative to the lesion-free, parent bulge loop structure, we found that in static repeat bulge loop constructs, lesions in the duplex portion of the bulge loop structure were strongly enthalpically destabilizing (--); lesions at the 5′ loop-duplex junction were marginally enthalpically destabilizing (-); lesions within the repeat loop domain had no net effect on the enthalpy change (0); whereas lesions at the 3′ junction were overall enthalpically stabilizing (+). Within the bulge loop domain, lesions in the center of a repeat loop may exert a small positive/stabilizing enthalpy contribution. These position-dependent lesion effects are summarized pictorially in Scheme 2.
Direct comparisons of these position-dependent, differential, enthalpic impacts of lesions within the CAG triplet repeat bulge loops, absent error-prone heat capacity adjustments, were justified by the overall similarities in Tm and transition widths for all constructs studied. Significantly, the relative enthalpy trends noted remained unaltered when the heat capacity term was considered. In the constructs studied here, with one exception, the abasic site or the 8oxodG lesion always replaced a Guanine as its redox potential makes guanine the most readily oxidized and therefore most frequently damaged of the DNA bases [72,73]. The single exception in our constructs occurred at the 5′ junction, where F replaced a C instead of a G in the static loops to disrupt the repeat sequence and prevent loop migration. Due to the initial steps of BER repair of 8oxodG lesions [74,75] as well as spontaneous loss of guanines [54], an abasic site results in place of dG. As a consequence of the 5′-3′ directionality and the repeat sequence, the lesion at the 5′ junction occurs in place of the last “formal” base pair of the upstream duplex domain, whereas the lesion at the 3′ junction is the last “formally unpaired” base within the loop domain prior to the beginning of the downstream duplex domain. The relative differences in the enthalpic impact of the lesion at 5′ and 3′ duplex junctions may in part be due to these sequence-induced constraints. The relative differences in enthalpy between lesions at the 5′ and 3 junction may also reflect topological constraints imparted by the three dimensional nature of the bulge loop construct.
Applying these position-dependent criteria to the calorimetric data for the lesion-containing, dynamic rollamers reported here allowed us to assess the lesion impact on rollamer distribution. This information on the impact of lesions on alterations in rollamer distribution is summarized in Table 1. For example, in the construct [CAG]6-F(1)·[CTG]2, (Figure 3 and Figure 4, panel 3) the lesion is located in the first CAG repeat in sequence space, while simultaneously, the lesion may partition into the upstream duplex domain (enthalpically destabilizing), the 5′ loop duplex junction (slightly enthalpically destabilizing), or into the loop (neutral) in conformational space. The observed lack of any enthalpy change relative to the parent construct is consistent with the lesion primarily partitioning into the loop domain; in other words, the population of the rollamer with the lesion located within the loop is enriched relative to the occupancy of the other rollamer conformations. This enthalpy-based conclusion is also consistent with the observed shape of the excess heat capacity curve, as partitioning of a lesion in the first CAG repeat primarily into the loop domain implies that the extra paired CAG base triplets are part of the downstream duplex arm. The resulting increase in melting temperature and enthalpy of the downstream duplex arm causes its melting transition to overlap with that of the upstream domain, thereby resulting in the observed shape of the melting curve.

3.1.5. Lesions Cause Preferential Occupancy of the Enthalpically Most Stabilizing of the Three Possible Loop Isomer States

In the aggregate, our data show that the lesion causes enriched occupancy of the enthalpically most stabilizing of the three possible loop isomer states; a feature emphasized in Table 1 via yellow highlighting. For example, for the construct [CAG]6-F(6)·[CTG]2 (Figure 4, panel 6), the lesion in the sixth CAG repeat in sequence space may partition in conformational space either into the 3′ loop/duplex junction (enthalpically stabilizing) or the downstream duplex domain (enthalpically destabilizing). The calorimetrically observed more favorable enthalpy relative to the parent rollamer construct is consistent with the lesion preferentially enriching the population of the 3′ loop/duplex junction rollamer. This enthalpy based deduction is also reflected in the shape of the excess heat capacity curve. A partition of the lesion in the last (sixth) CAG repeat into the 3′ loop/duplex junction implies that the two extra base paired CAG·CTG triplets are part of the upstream duplex arm; thereby resulting in an increase in thermal stability and enthalpy of this arm relative to the downstream arm and clearly separated melting transitions. Moreover, if the loop exclusively partitions into the 3′ loop /junction, as implied by the enthalpy gain of this loop position, then denaturation of the downstream arm and loop occur simultaneously in all molecules and no loop migration into the denatured domain occurs. Indeed, the heat capacity curve for [CAG]6-F(6)·[CTG]2 is the only one of those displayed in Figure 4, where both observed melting transitions approximate two- state-like behavior, and where the shape of the pre-transition does not show any distortions due to kinetically controlled loop migration. In summary, our data show that the lesion induces rollamer migration/redistribution to cause preferential occupancy of the enthalpically most stabilizing of the three possible loop isomers, as highlighted in Table 1.
Continuing this straight forward analysis for each of the lesion positions reveals that the presence of the lesion indeed alters the distribution of rollamer isomers in a position-dependent manner through loop migration, as summarized in Table 1. Note that this migration-induced differential distribution of rollamers is defined by partitioning of the lesion into different structural domains (3′ stem/loop junction > loop domains > 5′ stem/loop junction >> 5′ or 3′ stem duplexes), so as to favor those rollamer isomers where the lesion is least energetically disruptive.

3.2. Semi-Empirical Modeling Yields Rollamer Distributions Consistent with Our Experimental Results

To gain further insights into our observations of lesion induced alterations in rollamer distribution, we modeled the measured rollamer excess heat capacity curves. Our model considers the simultaneous presence of three initial states with different fractional occupancies corresponding to the three different rollamer isomers that can be adopted by the [CAG]6-X(n)·[CTG]2 complex. The model includes two melting intermediates corresponding to partially denatured states with either the upstream or the downstream duplex arm and the two proximate CAG·CTG triplets remaining base paired, while the other arm and remaining repeat loop triplets are denatured. This model allows for introduction of a position dependent perturbation to account for the lesions. Many of the initial estimates for the thermodynamic parameters needed to fit our model to the experimental DSC thermograms were extracted from our prior experimental data on the large number of related bulge loop structures that we have studied [32,44,50,60,76]. The values of the fitted parameters, while not necessarily determinative, are plausible within the context of established DNA thermodynamics. A more detailed description of the model will be published elsewhere. Despite its simplicity, the model captures all salient features of the measured excess heat capacity curves for all constructs studied. Importantly, our model allows us to predict fractional occupancies of the individual rollamer loop isomers as a function of lesion position, as depicted in Figure 5. The results shown in this figure complement and reinforce the conclusions derived by our enthalpy analysis described above. To be specific, our model predicts that the presence of the lesion results in a fractional enrichment of those initial loop isomer states that accommodate the lesion with the least energetic perturbation. Less favorable loop isomer states do remain populated, but with significantly reduced fractional occupancies relative to the favorable loop isomer. These modeling results support our hypothesis that the presence of the lesion leads to rearrangement and redistribution of loop isomers within the repeat loop rollamer ensemble, in favor of those rollamer isomers where the lesion impact is least disruptive.
In summary, our experimental and computational results reveal that the formation of a lesion within a triplet repeat domain significantly alters the already complex energy landscape by creating a hierarchy of additional local energy minima within the larger repeat energy landscape (Figure 1). In short, our results demonstrate that lesions can induce second-order alterations in the global, dynamic repeat DNA energy landscape through favorable (lower local energy minima) and unfavorable (higher local energy minima) contributions that influence the ensemble of states that BER enzymes encounter during repair processes; thereby adding an additional level of substrate complexity that likely impacts repair outcomes. Moreover, our most recent results (unpublished data) revealed that such lesion-induced alterations in rollamer landscape and loop distribution extends to systems with more potential rollamer isomers than the three bulge loop isomers described here, consistent with the generality of our conclusions.

3.3. Implications of Dynamic Energy Landscapes on DNA Repair

Although oxidative lesion formation can generally be considered as a stochastic process, it has been found that repeat domains are ‘hot spots’ where lesion formation is enhanced relative to other DNA sequences. It has also been suggested that the propensity of triplet repeat domains to adopt, even if only transiently, altered, non-B DNA structures such as bulge loops is one potential reason for enhanced rates of oxidative damage in trinucleotide repeat DNAs.[56] Numerous pathways by which repeat bulge loops might form transiently during replication recombination or repair processes have been proposed [24,77,78,79]. Our in vitro observations reveal that the presence of lesions, even within relatively simple short repeat bulge loop constructs, yield complex dynamic energy landscapes. This result suggests that lesions within larger rollameric repeat bulge ensembles may generate significant challenges for DNA processing machineries in terms of substrate selection. The complexity of the substrate landscape we detected for our relatively simple, well controlled oligonucleotide constructs suggests that within repetitive DNA domains, DNA processing machineries are not only challenged by a multitude of potential substrate conformations, but also by their differential thermodynamic recognition profiles and kinetic availabilities. Our results show that within such rollameric repeat ensembles, a particular lesion, even within the same sequence/ nearest neighbor context and/or sequence position, can adopt multiple conformational states with different occupancy rates; a feature which undoubtedly will impact how effectively DNA processing machineries interact with such substrates.
Consistent with this expectation, Delaney and coworkers have shown reduced OGG1 activity to cleave 8oxodG lesions within CAG repeat structures [56] whereas we have previously shown that APE1 processing is much reduced or completely absent when the abasic site lesion is located within static repeat self-structures [80]. Base excision repair depends on an intricate, tightly controlled handoff of repair intermediates between a group of core proteins, aided by a number of associated helper proteins. [81] Loop redistribution to partition a lesion/repair intermediate into an altered structural domain, and/or the transient occupancy of preferred or inexpedient substrate conformations, would quite likely disrupt the intricate balance of sequential BER repair steps [52,74,75,82,83] necessary for successful repair outcomes, thereby potentially contributing to aberrant expansion events. Intriguingly, the dynamic nature of lesion-induced rollamer distribution may result in either beneficial or detrimental repair outcomes, depending on the context. Our results reported here provide a basis for future testing of the extent to which complex substrate dynamics inhibit or enhance various critical BER steps. For example, we have shown partial recognition and processing/cleavage of abasic sites by the crucial BER enzyme APE1 in rollamer constructs where the abasic site lesion can partition into the 5′ duplex domain (a thermodynamically unfavorable isomer) or the bulge loop (a thermodynamically favorable isomer), whereas the same lesion in a static repeat bulge loop is barely processed [80].The latter observation, not surprisingly, also suggests that APE1 binding/processing can alter loop distribution through its interactions with an unfavorable loop isomer. APE1, however, appears to not be able to process abasic sites where loop rearrangement results in partitioning of the lesion into the loop or 3′ junction domain, both of which are thermodynamically favored lesion positions. In other words, the same lesion within a larger repeat domain can be a suitable substrate for BER repair enzymes or not, depending on the dynamic distribution of repeat bulge loop rollamers and the as yet unknown impact of repair protein binding on loop distribution. We are in the process of evaluating to what extent binding by the repair protein further influences rollamer distributions and thereby repair outcomes.

4. Conclusions

We have shown that lesion-induced alterations in the energy landscape of repeat DNAs result in dynamic redistributions of repeat bulge loops so as to minimize the energetic impact of the DNA damage. This dynamic ensemble of potential substrates creates an additional level of complexity with which the DNA processing machinery is confronted. It is not unreasonable to expect that such challenging dynamic substrates contribute to the observed DNA expansion phenomenon upon BER lesion repair. We propose that such conformational fluidity influences repair efficiencies and outcomes and contributes to the processes that lead to DNA expansion.

Supplementary Materials

The following are available online at https://www.mdpi.com/2218-273X/9/11/709/s1, Figure S1: Differential Scanning Calorimetry (DSC) thermograms of static CAG repeat bulge loops containing either an abasic site or a 8oxodG lesion in different sequence positions; Table S1: The impact of the position of the abasic site lesion on static CAG repeat bulge loop transition enthalpy changes; Table S2: The impact of the position of the abasic site lesion on the transition enthalpy changes of the three isomeric, dynamic CAG repeat bulge loop rollamer ensembles.

Author Contributions

Conceptualization, J.V.; Methodology, J.V., G.E.P., and V.G.; Software, G.E.P.; Formal analysis, J.V., G.E.P., and K.J.B.; Investigation, J.V. and V.G.; Writing—original draft preparation, J.V.; Writing—review and editing, J.V., G.E.P., and K.J.B.; Visualization, J.V., G.E.P., and K.J.B.; Supervision, K.J.B.; Project administration, K.J.B.; Funding acquisition, K.J.B.

Funding

This research was funded by the National Institutes of Health, grant numbers GM23509, GM34469, and CA47995 (all to K.J.B.).

Acknowledgments

The authors wish to thank Barbara Gaffney and Roger Jones (Rutgers University) for their help with DNA synthesis and purification, and Craig A. Gelfand for helpful discussions.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Bagshaw, A.T.M. Functional Mechanisms of Microsatellite DNA in Eukaryotic Genomes. Genome Biol. Evol. 2017, 9, 2428–2443. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  2. Ellegren, H. Microsatellites: Simple sequences with complex evolution. Nat. Rev. Genet. 2004, 5, 435–445. [Google Scholar] [CrossRef] [PubMed]
  3. Lander, E.S.; Linton, L.M.; Birren, B.; Nusbaum, C.; Zody, M.C.; Baldwin, J.; Devon, K.; Dewar, K.; Doyle, M.; FitzHugh, W.; et al. International Human Genome Sequencing Consortium Initial sequencing and analysis of the human genome. Nature 2001, 409, 860–921. [Google Scholar] [CrossRef] [PubMed]
  4. Subramanian, S.; Mishra, R.K.; Singh, L. Genome-Wide analysis of microsatellite repeats in humans: Their abundance and density in specific genomic regions. Genome Biol. 2003, 4, R13. [Google Scholar] [CrossRef] [PubMed]
  5. Sutherland, G.R.; Richards, R.I. Simple Tandem DNA Repeats and Human Genetic Disease. Proc. Natl. Acad. Sci. USA 1995, 92, 3636–3641. [Google Scholar] [CrossRef] [PubMed]
  6. Cummings, C.J.; Zoghbi, H.Y. Trinucleotide repeats: Mechanisms and pathophysiology. Annu. Rev. Genom. Hum. Genet. 2000, 1, 281–328. [Google Scholar] [CrossRef] [PubMed]
  7. Orr, H.T.; Zoghbi, H.Y. Trinucleotide repeat disorders. Annu. Rev. Neurosci. 2007, 30, 575–621. [Google Scholar] [CrossRef] [PubMed]
  8. Ashley, C.T.; Warren, S.T. Trinucleotide repeat expansion and human disease. Annu. Rev. Genet. 1995, 29, 703–728. [Google Scholar] [CrossRef] [PubMed]
  9. Bacolla, A.; Wells, R.D. Non-B DNA conformations as determinants of mutagenesis and human disease. Mol. Carcinog. 2009, 48, 273–285. [Google Scholar] [CrossRef]
  10. Wells, R.D.; Dere, R.; Hebert, M.L.; Napierala, M.; Son, L.S. Advances in mechanisms of genetic instability related to hereditary neurological diseases. Nucl. Acids Res. 2005, 33, 3785–3798. [Google Scholar] [CrossRef] [Green Version]
  11. Wells, R.D. Non-B DNA conformations, mutagenesis and disease. Trends Biochem. Sci. 2007, 32, 271–278. [Google Scholar] [CrossRef] [PubMed]
  12. Zhao, J.; Bacolla, A.; Wang, G.; Vasquez, K.M. Non-B DNA structure-induced genetic instability and evolution. Cell. Mol. Life Sci. 2009, 67, 43–62. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  13. Gadgil, R.; Barthelemy, J.; Lewis, T.; Leffak, M. Replication stalling and DNA microsatellite instability. Biophys. Chem. 2017, 225, 38–48. [Google Scholar] [CrossRef] [PubMed]
  14. McMurray, C.T. DNA secondary structure: A common and causative factor for expansion in human disease. Proc. Natl. Acad. Sci. USA 1999, 96, 1823–1825. [Google Scholar] [CrossRef] [Green Version]
  15. Bacolla, A.; Larson, J.E.; Collins, J.R.; Li, J.; Milosavljevic, A.; Stenson, P.D.; Cooper, D.N.; Wells, R.D. Abundance and length of simple repeats in vertebrate genomes are determined by their structural properties. Genome Res. 2008, 18, 1545–1553. [Google Scholar] [CrossRef] [Green Version]
  16. Wells, R.D. Discovery of the role of non-B DNA structures in mutagenesis and human genomic disorders. J. Biol. Chem. 2009, 284, 8997–9009. [Google Scholar] [CrossRef]
  17. Bacolla, A.; Wojciechowska, M.; Kosmider, B.; Larson, J.E.; Wells, R.D. The involvement of non-B DNA structures in gross chromosomal rearrangements. DNA Repair (Amst.) 2006, 5, 1161–1170. [Google Scholar] [CrossRef]
  18. Liu, G.; Chen, X.; Bissler, J.J.; Sinden, R.R.; Leffak, M. Replication-Dependent instability at (CTG) x (CAG) repeat hairpins in human cells. Nat. Chem. Biol. 2010, 6, 652–659. [Google Scholar] [CrossRef]
  19. Liu, G.; Chen, X.; Gao, Y.; Lewis, T.; Barthelemy, J.; Leffak, M. Altered replication in human cells promotes DMPK (CTG)(n) (CAG)(n) repeat instability. Mol. Cell. Biol. 2012, 32, 1618–1632. [Google Scholar] [CrossRef]
  20. Liu, G.; Leffak, M. Instability of (CTG)n*(CAG)n trinucleotide repeats and DNA synthesis. Cell Biosci. 2012, 2, 7. [Google Scholar] [CrossRef]
  21. Jakupciak, J.P.; Wells, R.D. Gene conversion (recombination) mediates expansions of CTG[middle dot]CAG repeats. J. Biol. Chem. 2000, 275, 40003–40013. [Google Scholar] [CrossRef] [PubMed]
  22. Jakupciak, J.P.; Wells, R.D. Genetic instabilities of triplet repeat sequences by recombination. IUBMB Life 2000, 50, 355–359. [Google Scholar] [CrossRef] [PubMed]
  23. Usdin, K.; House, N.C.; Freudenreich, C.H. Repeat instability during DNA repair: Insights from model systems. Crit. Rev. Biochem. Mol. Biol. 2015, 50, 142–167. [Google Scholar] [CrossRef] [PubMed]
  24. Panigrahi, G.B.; Lau, R.; Montgomery, S.E.; Leonard, M.R.; Pearson, C.E. Slipped (CTG)*(CAG) repeats can be correctly repaired, escape repair or undergo error-prone repair. Nat. Struct. Mol. Biol. 2005, 12, 654–662. [Google Scholar] [CrossRef]
  25. Budworth, H.; McMurray, C.T. Bidirectional transcription of trinucleotide repeats: Roles for excision repair. DNA Repair (Amst.) 2013, 12, 672–684. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  26. McMurray, C.T. Hijacking of the mismatch repair system to cause CAG expansion and cell death in neurodegenerative disease. DNA Repair (Amst.) 2008, 7, 1121–1134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  27. Avila Figueroa, A.; Delaney, S. Mechanistic studies of hairpin to duplex conversion for trinucleotide repeat sequences. J. Biol. Chem. 2010, 285, 14648–14657. [Google Scholar] [CrossRef]
  28. Volle, C.B.; Jarem, D.A.; Delaney, S. Trinucleotide Repeat DNA Alters Structure To Minimize the Thermodynamic Impact of 8-Oxo-7,8-dihydroguanine. Biochemistry (N. Y.) 2011, 51, 52–62. [Google Scholar] [CrossRef] [Green Version]
  29. Polyzos, A.A.; McMurray, C.T. Close encounters: Moving along bumps, breaks, and bubbles on expanded trinucleotide tracts. DNA Repair (Amst.) 2017, 56, 144–155. [Google Scholar] [CrossRef] [Green Version]
  30. Avila-Figueroa, A.; Cattie, D.; Delaney, S. A small unstructured nucleic acid disrupts a trinucleotide repeat hairpin. Biochem. Biophys. Res. Commun. 2011, 413, 532–536. [Google Scholar] [CrossRef] [Green Version]
  31. Figueroa, A.A.; Cattie, D.; Delaney, S. Structure of even/odd trinucleotide repeat sequences modulates persistence of non-B conformations and conversion to duplex. Biochemistry 2011, 50, 4441–4450. [Google Scholar] [CrossRef] [PubMed]
  32. Völker, J.; Klump, H.H.; Breslauer, K.J. DNA metastability and biological regulation: Conformational dynamics of metastable omega-DNA bulge loops. J. Am. Chem. Soc. 2007, 129, 5272–5280. [Google Scholar] [CrossRef] [PubMed]
  33. Völker, J.; Plum, G.E.; Gindikin, V.; Klump, H.H.; Breslauer, K.J. Impact of bulge loop size on DNA triplet repeat domains: Implications for DNA repair and expansion. Biopolymers 2014, 101, 1–12. [Google Scholar] [CrossRef] [PubMed]
  34. Völker, J.; Makube, N.; Plum, G.E.; Klump, H.H.; Breslauer, K.J. Conformational energetics of stable and metastable states formed by DNA triplet repeat oligonucleotides: Implications for triplet expansion diseases. Proc. Natl. Acad. Sci. USA 2002, 99, 14700–14705. [Google Scholar] [CrossRef] [Green Version]
  35. Degtyareva, N.N.; Reddish, M.J.; Sengupta, B.; Petty, J.T. Structural studies of a trinucleotide repeat sequence using 2-aminopurine. Biochemistry (N. Y.) 2009, 48, 2340–2346. [Google Scholar] [CrossRef]
  36. Degtyareva, N.N.; Barber, C.A.; Sengupta, B.; Petty, J.T. Context dependence of trinucleotide repeat structures. Biochemistry (N. Y.) 2010, 49, 3024–3030. [Google Scholar] [CrossRef]
  37. Degtyareva, N.N.; Barber, C.A.; Reddish, M.J.; Petty, J.T. Sequence length dictates repeated CAG folding in three-way junctions. Biochemistry (N. Y.) 2011, 50, 458–465. [Google Scholar] [CrossRef]
  38. Mitchell, M.L.; Leveille, M.P.; Solecki, R.S.; Tran, T.; Cannon, B. Sequence-Dependent Effects of Monovalent Cations on the Structural Dynamics of Trinucleotide-Repeat DNA Hairpins. J. Phys. Chem. B 2018. [Google Scholar] [CrossRef]
  39. Slean, M.M.; Reddy, K.; Wu, B.; Nichol Edamura, K.; Kekis, M.; Nelissen, F.H.; Aspers, R.L.; Tessari, M.; Scharer, O.D.; Wijmenga, S.S.; et al. Interconverting conformations of slipped-DNA junctions formed by trinucleotide repeats affect repair outcome. Biochemistry 2013, 52, 773–785. [Google Scholar] [CrossRef]
  40. Gacy, A.M.; McMurray, C.T. Influence of hairpins on template reannealing at trinucleotide repeat duplexes: A model for slipped DNA. Biochemistry 1998, 37, 9426–9434. [Google Scholar] [CrossRef]
  41. Gacy, A.M.; Goellner, G.; Juranic, N.; Macura, S.; McMurray, C.T. Trinucleotide repeats that expand in human disease form hairpin structures in vitro. Cell 1995, 81, 533–540. [Google Scholar] [CrossRef] [Green Version]
  42. Lee, D.Y.; McMurray, C.T. Trinucleotide expansion in disease: Why is there a length threshold? Curr. Opin. Genet. Dev. 2014, 26, 131–140. [Google Scholar] [CrossRef] [PubMed]
  43. Harvey, S.C. Slipped Structures in DNA Triplet Repeat Sequences:  Entropic Contributions to Genetic Instabilities. Biochemistry 1997, 36, 3047–3049. [Google Scholar] [CrossRef] [PubMed]
  44. Völker, J.; Gindikin, V.; Klump, H.H.; Plum, G.E.; Breslauer, K.J. Energy landscapes of dynamic ensembles of rolling triplet repeat bulge loops: Implications for DNA expansion associated with disease states. J. Am. Chem. Soc. 2012, 134, 6033–6044. [Google Scholar] [CrossRef] [PubMed]
  45. Lai, Y.; Budworth, H.; Beaver, J.M.; Chan, N.L.; Zhang, Z.; McMurray, C.T.; Liu, Y. Crosstalk between MSH2-MSH3 and polbeta promotes trinucleotide repeat expansion during base excision repair. Nat. Commun. 2016, 7, 12465. [Google Scholar] [CrossRef]
  46. Liu, Y.; Prasad, R.; Beard, W.A.; Hou, E.W.; Horton, J.K.; McMurray, C.T.; Wilson, S.H. Coordination between polymerase beta and FEN1 can modulate CAG repeat expansion. J. Biol. Chem. 2009, 284, 28352–28366. [Google Scholar] [CrossRef]
  47. Gelfand, C.A.; Plum, G.E.; Grollman, A.P.; Johnson, F.; Breslauer, K.J. The impact of a bistrand abasic lesion on DNA duplex properties. Biopolymers 1996, 38, 439–445. [Google Scholar] [CrossRef]
  48. Gelfand, C.A.; Plum, G.E.; Grollman, A.P.; Johnson, F.; Breslauer, K.J. Thermodynamic consequences of an abasic lesion in duplex DNA are strongly dependent on base sequence. Biochemistry (N. Y.) 1998, 37, 7321–7327. [Google Scholar] [CrossRef]
  49. Minetti, C.A.; Remeta, D.P.; Zharkov, D.O.; Plum, G.E.; Johnson, F.; Grollman, A.P.; Breslauer, K.J. Energetics of lesion recognition by a DNA repair protein: Thermodynamic characterization of formamidopyrimidine-glycosylase (Fpg) interactions with damaged DNA duplexes. J. Mol. Biol. 2003, 328, 1047–1060. [Google Scholar] [CrossRef]
  50. Völker, J.; Plum, G.E.; Klump, H.H.; Breslauer, K.J. DNA repair and DNA triplet repeat expansion: The impact of abasic lesions on triplet repeat DNA energetics. J. Am. Chem. Soc. 2009, 131, 9354–9360. [Google Scholar] [CrossRef]
  51. David, S.S.; O’Shea, V.L.; Kundu, S. Base-Excision repair of oxidative DNA damage. Nature 2007, 447, 941–950. [Google Scholar] [CrossRef] [PubMed]
  52. Sung, J.S.; Demple, B. Roles of base excision repair subpathways in correcting oxidized abasic sites in DNA. FEBS J. 2006, 273, 1620–1629. [Google Scholar] [CrossRef] [PubMed]
  53. Kim, Y.J.; Wilson, D.M. Overview of base excision repair biochemistry. Curr. Mol. Pharmacol. 2012, 5, 3–13. [Google Scholar] [CrossRef] [PubMed]
  54. Lindahl, T.; Nyberg, B. Rate of depurination of native deoxyribonucleic acid. Biochemistry 1972, 11, 3610–3618. [Google Scholar] [CrossRef]
  55. Loeb, L.A.; Preston, B.D. Mutagenesis by apurinic/apyrimidinic sites. Annu. Rev. Genet. 1986, 20, 201–230. [Google Scholar] [CrossRef]
  56. Jarem, D.A.; Wilson, N.R.; Delaney, S. Structure-Dependent DNA Damage and Repair in a Trinucleotide Repeat Sequence. Biochemistry (N. Y.) 2009, 48, 6655–6663. [Google Scholar] [CrossRef]
  57. Kovtun, I.V.; McMurray, C.T. Features of trinucleotide repeat instability in vivo. Cell Res. 2008, 18, 198–213. [Google Scholar] [CrossRef] [Green Version]
  58. Kovtun, I.V.; Liu, Y.; Bjoras, M.; Klungland, A.; Wilson, S.H.; McMurray, C.T. OGG1 initiates age-dependent CAG trinucleotide expansion in somatic cells. Nature 2007, 447, 447–452. [Google Scholar] [CrossRef] [Green Version]
  59. Völker, J.; Klump, H.H.; Breslauer, K.J. DNA energy landscapes via calorimetric detection of microstate ensembles of metastable macrostates and triplet repeat diseases. Proc. Natl. Acad. Sci. USA 2008, 105. [Google Scholar] [CrossRef]
  60. Völker, J.; Plum, G.E.; Klump, H.H.; Breslauer, K.J. Energetic coupling between clustered lesions modulated by intervening triplet repeat bulge loops: Allosteric implications for DNA repair and triplet repeat expansion. Biopolymers 2010, 93, 355–369. [Google Scholar] [CrossRef]
  61. Snell, F.D.; Snell, C.T. Colorimetric Methods of Analysis, including Some Turbidimetric and Nephelometric Methods; R. E. Krieger Pub. Co.: Malabar, FL, USA, 1972. [Google Scholar]
  62. Plum, G.E. Optical Methods; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000; pp. 7.3.1–7.3.17. [Google Scholar]
  63. Job, P. Job’s method of continuous variation. Ann. Chim. 1928, 9, 113–203. [Google Scholar]
  64. Völker, J.; Blake, R.; Delcourt, S.G.; Breslauer, K.J. High-Resolution calorimetric and optical melting profiles of DNA plasmids: Resolving contributions from intrinsic melting domains and specifically designed inserts. Biopolymers 1999, 50, 303–318. [Google Scholar] [CrossRef]
  65. Privalov, G.; Kavina, V.; Freire, E.; Privalov, P.L. Precise scanning calorimeter for studying thermal properties of biological macromolecules in dilute solution. Anal. Biochem. 1995, 232, 79–85. [Google Scholar] [CrossRef] [PubMed]
  66. Marky, L.A.; Breslauer, K.J. Calculating thermodynamic data for transitions of any molecularity from equilibrium melting curves. Biopolymers 1987, 26, 1601–1620. [Google Scholar] [CrossRef]
  67. Wyman, J.; Gill, S.J. Binding and Linkage. Functional Chemistry of Biological Macromolecules; University Science Books: Mill Valley, CA, USA, 1990. [Google Scholar]
  68. Gill, S.J.; Richey, B.; Bishop, G.; Wyman, J. Generalized binding phenomena in an allosteric macromolecule. Biophys. Chem. 1985, 21, 1–14. [Google Scholar] [CrossRef]
  69. Plum, G.E.; Grollman, A.P.; Johnson, F.; Breslauer, K.J. Influence of the oxidatively damaged adduct 8-oxodeoxyguanosine on the conformation, energetics, and thermodynamic stability of a DNA duplex. Biochemistry (N. Y.) 1995, 34, 16148–16160. [Google Scholar] [CrossRef]
  70. Plum, G.E.; Grollman, A.P.; Johnson, F.; Breslauer, K.J. Influence of an exocyclic guanine adduct on the thermal stability, conformation, and melting thermodynamics of a DNA duplex. Biochemistry 1992, 31, 12096–12102. [Google Scholar] [CrossRef]
  71. Crenshaw, C.M.; Wade, J.E.; Arthanari, H.; Frueh, D.; Lane, B.F.; Nunez, M.E. Hidden in plain sight: Subtle effects of the 8-oxoguanine lesion on the structure, dynamics, and thermodynamics of a 15-base pair oligodeoxynucleotide duplex. Biochemistry 2011, 50, 8463–8477. [Google Scholar] [CrossRef]
  72. Steenken, S.; Jovanovic, S.V. How Easily Oxidizable Is DNA? One-Electron Reduction Potentials of Adenosine and Guanosine Radicals in Aqueous Solution. J. Am. Chem. Soc. 1997, 119, 617. [Google Scholar] [CrossRef]
  73. Yennie, C.J.; Delaney, S. Thermodynamic consequences of the hyperoxidized guanine lesion guanidinohydantoin in duplex DNA. Chem. Res. Toxicol. 2012, 25, 1732–1739. [Google Scholar] [CrossRef]
  74. Wilson, D.M., III; Bohr, V.A. The mechanics of base excision repair, and its relationship to aging and disease. DNA Repair (Amst.) 2007, 6, 544–559. [Google Scholar] [CrossRef] [PubMed]
  75. Zharkov, D.O. Base excision DNA repair. Cell. Mol. Life Sci. 2008, 65, 1544–1565. [Google Scholar] [CrossRef] [PubMed]
  76. Völker, J.; Plum, G.E.; Klump, H.H.; Breslauer, K.J. Energy crosstalk between DNA lesions: Implications for allosteric coupling of DNA repair and triplet repeat expansion pathways. J. Am. Chem. Soc. 2010, 132, 4095–4097. [Google Scholar] [CrossRef] [PubMed]
  77. McMurray, C.T. Mechanisms of trinucleotide repeat instability during human development. Nat. Rev. Genet. 2010, 11, 786–799. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  78. Lenzmeier, B.A.; Freudenreich, C.H. Trinucleotide repeat instability: A hairpin curve at the crossroads of replication, recombination, and repair. Cytogenet. Genome Res. 2003, 100, 7–24. [Google Scholar] [CrossRef] [PubMed]
  79. Pearson, C.E.; Tam, M.; Wang, Y.H.; Montgomery, S.E.; Dar, A.C.; Cleary, J.D.; Nichol, K. Slipped-Strand DNAs formed by long (CAG)*(CTG) repeats: Slipped-Out repeats and slip-out junctions. Nucleic Acids Res. 2002, 30, 4534–4547. [Google Scholar] [CrossRef]
  80. Li, M.; Völker, J.; Breslauer, K.J.; Wilson, D.M. APE1 incision activity at abasic sites in tandem repeat sequences. J. Mol. Biol. 2014, 426, 2183–2198. [Google Scholar] [CrossRef]
  81. Wilson, S.H.; Kunkel, T.A. Passing the baton in base excision repair. Nat. Struct. Biol. 2000, 7, 176–178. [Google Scholar] [CrossRef]
  82. Goula, A.V.; Pearson, C.E.; Della Maria, J.; Trottier, Y.; Tomkinson, A.E.; Wilson, D.M.; Merienne, K. The nucleotide sequence, DNA damage location, and protein stoichiometry influence the base excision repair outcome at CAG/CTG repeats. Biochemistry 2012, 51, 3919–3932. [Google Scholar] [CrossRef]
  83. Prasad, R.; Batra, V.K.; Yang, X.; Krahn, J.M.; Pedersen, L.C.; Beard, W.A.; Wilson, S.H. Structural insight into the DNA polymerase beta deoxyribose phosphate lyase mechanism. DNA Repair 2005, 4, 1347–1357. [Google Scholar] [CrossRef]
Biomolecules 09 00709 g001 550
Figure 1. A schematic representation of the dynamic triplet repeat energy landscape in the absence (A) and presence (B) of a DNA lesion. The fine structure indicated by the squiggly lines within the wells of the rollamers reflects that each bulge loop positional isomer is itself comprised of ensembles of microstates, as we have previously demonstrated [59].
Figure 1. A schematic representation of the dynamic triplet repeat energy landscape in the absence (A) and presence (B) of a DNA lesion. The fine structure indicated by the squiggly lines within the wells of the rollamers reflects that each bulge loop positional isomer is itself comprised of ensembles of microstates, as we have previously demonstrated [59].
Biomolecules 09 00709 g001
Biomolecules 09 00709 g002 550
Figure 2. (A) Characteristic changes in the excess heat capacity profiles of a static (CAG)4 repeat bulge loop (black) compared to the same (CAG)4 bulge loops existing as three (blue) or five (red) rollamer isomers. The excess heat capacity profile of the five isomer rollamer (red curve), where four additional base pair CAG·CTG triplets can partition between the upstream and downstream duplex domain [44], is included in Figure 2A to demonstrate that the characteristic changes in the shape of the melting curve are general features due to the dynamic nature of the rollamer relative to the static bulge loop construct. (B) Schematic presentation of the initial steps in the denaturation pathway for the three isomer (CAG)4 rollamer that is the focus of this paper, reflecting the impact of the dynamic rollamers on the excess heat capacity curves shown in Figure 2A. Denaturation of the residual duplex (the main transition in the DSC thermogram) that is formed as the result of the initial melting step is not shown and conforms to conventional duplex melting behavior.
Figure 2. (A) Characteristic changes in the excess heat capacity profiles of a static (CAG)4 repeat bulge loop (black) compared to the same (CAG)4 bulge loops existing as three (blue) or five (red) rollamer isomers. The excess heat capacity profile of the five isomer rollamer (red curve), where four additional base pair CAG·CTG triplets can partition between the upstream and downstream duplex domain [44], is included in Figure 2A to demonstrate that the characteristic changes in the shape of the melting curve are general features due to the dynamic nature of the rollamer relative to the static bulge loop construct. (B) Schematic presentation of the initial steps in the denaturation pathway for the three isomer (CAG)4 rollamer that is the focus of this paper, reflecting the impact of the dynamic rollamers on the excess heat capacity curves shown in Figure 2A. Denaturation of the residual duplex (the main transition in the DSC thermogram) that is formed as the result of the initial melting step is not shown and conforms to conventional duplex melting behavior.
Biomolecules 09 00709 g002
Biomolecules 09 00709 sch001 550
Scheme 1. Schematic representation of the three loop isomers (Upstream, MidStream, and Downstream) of our rollamer construct highlighting in color the partitioning of the extra triplets in the upstream (yellow) and downstream (red) domain due to the loop position in each of the isomers. In the UpStream isomer, both additional triplets partition in the downstream duplex domain (0:2); in the MidStream isomer, the additional triplets partition one each in the upstream and downstream duplex domain (1:1); and in the DownStream isomer, both additional triplets partition in the upstream duplex domain (2:0).
Scheme 1. Schematic representation of the three loop isomers (Upstream, MidStream, and Downstream) of our rollamer construct highlighting in color the partitioning of the extra triplets in the upstream (yellow) and downstream (red) domain due to the loop position in each of the isomers. In the UpStream isomer, both additional triplets partition in the downstream duplex domain (0:2); in the MidStream isomer, the additional triplets partition one each in the upstream and downstream duplex domain (1:1); and in the DownStream isomer, both additional triplets partition in the upstream duplex domain (2:0).
Biomolecules 09 00709 sch001
Biomolecules 09 00709 g003 550
Figure 3. Figure 3 shows the excess heat capacity curves measured for a static (CAG)6 repeat bulge loop (top panel) [50] and dynamic (CAG)4 repeat bulge loop (bottom panel) in the absence (black curve) and presence of either 8oxodG (red curve) or an abasic site lesion (blue curve) in place of dG in the first CAG repeat. Note that whereas the abasic site lesion in the static bulge loop is associated with a slight broadening of the melting transition, but no net change in enthalpy change, it results in the exact opposite melting behavior in the dynamic rollamer construct. In the dynamic rollamer, the abasic site lesion causes the loss of the pre-transition and a significant apparent increase in cooperative melting transition relative to the lesion free rollamer, reflecting lesion induced changes in loop isomer distribution. The excess heat capacity curves therefore provide a good window into the impact of lesions on dynamic loop distributions. As reported for duplex DNA [69,70,71], the impact of 8oxodG lesions in either the static bulge loop or dynamic rollamer is minor.
Figure 3. Figure 3 shows the excess heat capacity curves measured for a static (CAG)6 repeat bulge loop (top panel) [50] and dynamic (CAG)4 repeat bulge loop (bottom panel) in the absence (black curve) and presence of either 8oxodG (red curve) or an abasic site lesion (blue curve) in place of dG in the first CAG repeat. Note that whereas the abasic site lesion in the static bulge loop is associated with a slight broadening of the melting transition, but no net change in enthalpy change, it results in the exact opposite melting behavior in the dynamic rollamer construct. In the dynamic rollamer, the abasic site lesion causes the loss of the pre-transition and a significant apparent increase in cooperative melting transition relative to the lesion free rollamer, reflecting lesion induced changes in loop isomer distribution. The excess heat capacity curves therefore provide a good window into the impact of lesions on dynamic loop distributions. As reported for duplex DNA [69,70,71], the impact of 8oxodG lesions in either the static bulge loop or dynamic rollamer is minor.
Biomolecules 09 00709 g003
Biomolecules 09 00709 g004 550
Figure 4. Excess heat capacity curves measured for the [CAG]6-F(n)·[CTG]2 constructs (F = Tetrahydro Furan abasic site analogue) for different lesion positions within the repeat domain F(n), where F replaces the dG in the nth CAG repeat counting from the 5′ end. The lesion free parent construct (black) is the same in all panels, blue curves correspond to abasic site (F) lesions in the CAG strand. A schematic representation of the different lesion position relative to the three possible loop isomers (green dot) is shown as the insert in each panel.
Figure 4. Excess heat capacity curves measured for the [CAG]6-F(n)·[CTG]2 constructs (F = Tetrahydro Furan abasic site analogue) for different lesion positions within the repeat domain F(n), where F replaces the dG in the nth CAG repeat counting from the 5′ end. The lesion free parent construct (black) is the same in all panels, blue curves correspond to abasic site (F) lesions in the CAG strand. A schematic representation of the different lesion position relative to the three possible loop isomers (green dot) is shown as the insert in each panel.
Biomolecules 09 00709 g004
Biomolecules 09 00709 sch002 550
Scheme 2. Pictorial map summarizing the position-dependent, differential, enthalpic impacts of lesions within the CAG triplet repeat bulge loops as derived from data on static bulge loops.
Scheme 2. Pictorial map summarizing the position-dependent, differential, enthalpic impacts of lesions within the CAG triplet repeat bulge loops as derived from data on static bulge loops.
Biomolecules 09 00709 sch002
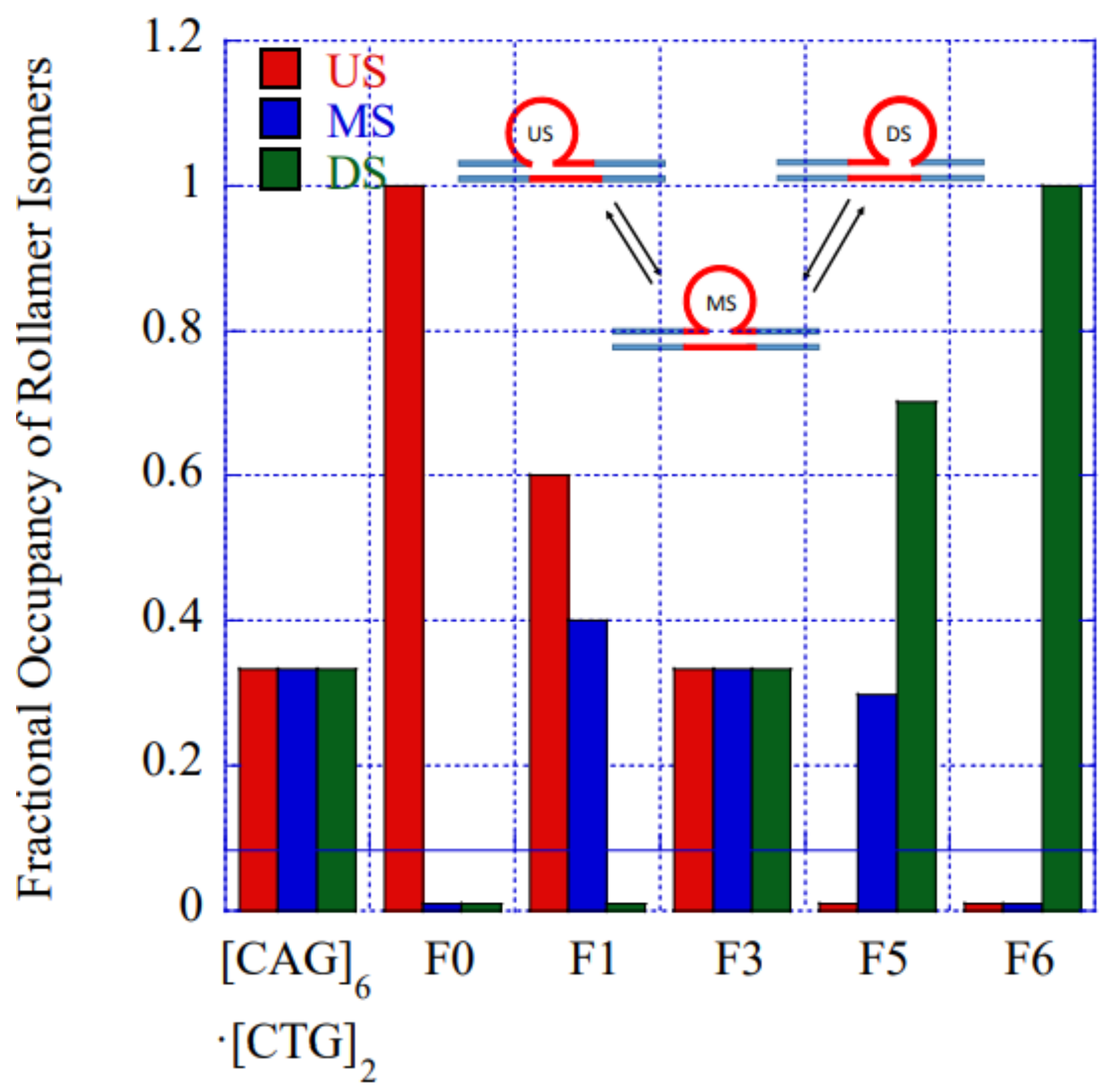
Biomolecules 09 00709 g005 550
Figure 5. Impact of lesion position on the fractional occupancy of loop isomers at 25 °C derived by fitting to our semi-empirical model. In the absence of lesion induced local changes in the rollamer energy landscape (e.g., in the [CAG]6·[CTG]2 parent or in [CAG]6-F(3)·[CTG]2) all three loop isomers are occupied equally (=0.33). (US = UpStream, MS = MidStream, and DS = DownStream).
Figure 5. Impact of lesion position on the fractional occupancy of loop isomers at 25 °C derived by fitting to our semi-empirical model. In the absence of lesion induced local changes in the rollamer energy landscape (e.g., in the [CAG]6·[CTG]2 parent or in [CAG]6-F(3)·[CTG]2) all three loop isomers are occupied equally (=0.33). (US = UpStream, MS = MidStream, and DS = DownStream).
Biomolecules 09 00709 g005
Table
Table 1. Position-dependent, lesion (X)-induced impact on rollamer distributions in [CAG]6-X(n)·[CTG]2*.
Table 1. Position-dependent, lesion (X)-induced impact on rollamer distributions in [CAG]6-X(n)·[CTG]2*.
Rollamer ConstructsLesion (x) Position in SequenceLesion Positions in Each of the Three RollamersPredicted Impacts from Static Loop StudiesObserved Impact on Rollamer Loop Distributions Assessed Calorimetrically and Computationally
UpstreamMidstream Downstream
[CAG]6·[CTG]2
Lesion-free control		N/AN/A Biomolecules 09 00709 i001 Biomolecules 09 00709 i002 Biomolecules 09 00709 i003N/A
[CAG]6-X(Stem) ·[CTG]2Upstream Stem5 b. upstream
8 b. upstream
11 b. upstream		s. destabilizing -
Biomolecules 09 00709 i004		s. destabilizing –
Biomolecules 09 00709 i005		s. destabilizing -
Biomolecules 09 00709 i006		No impact on loop distribution
[CAG]6-F(0) ·[CTG]2Last base before 1st repeat5′ junction
3b. upstream
6 b. upstream		m. Destabilizing -
Biomolecules 09 00709 i007		s. Destabilizing -
Biomolecules 09 00709 i008		s. Destabilizing -
Biomolecules 09 00709 i009		Populates rollamer with lesion at 5′ duplex/loop junction
[CAG]6-X(1) ·[CTG]2G in 1st repeat1 repeat loop
5′ junction
3 b. upstream		Neutral 0
Biomolecules 09 00709 i010		m. Destabilizing -
Biomolecules 09 00709 i011		s. Destabilizing --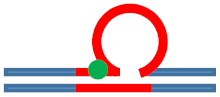
Biomolecules 09 00709 i012		Populates rollamer with lesion within loop
[CAG]6-X(3) ·[CTG]2G in 3rd repeat5′ of loop apex
Loop apex
3′ of loop apex		Neutral 0
Biomolecules 09 00709 i013		m. Stabilizing +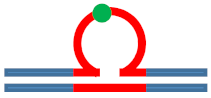
Biomolecules 09 00709 i014		neutral 0
Biomolecules 09 00709 i015		Populates rollamer with lesion within loop
[CAG]6-X(5) ·[CTG]2G in 5th repeat3 b. downstream
3′ junction
3 b. into loop		Destabilizing -
Biomolecules 09 00709 i016		s. Stabilizing ++
Biomolec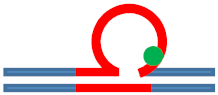ules 09 00709 i017		Neutral 0
Biomolecules 09 00709 i018		Populates rollamer with lesion at 3/loop/duplex junction
[CAG]6-F(6) ·[CTG]2G in 6th repeat6 b. downstream
3 b. downstream
3′ junction		s. Destabilizing -
Biomolecules 09 00709 i019		s. Destabilizing -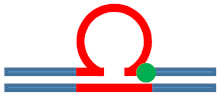
Biomolecules 09 00709 i020		s. Stabilizing ++
Biomolecules 09 00709 i021		Populates rollamer with lesion at 3/loop/duplex junction
Abbreviations used in table: X—generic placeholder for X = tetrahydrofuran abasic site analogue (F), or X = 8oxodG lesion (O); 3b, 5b number of bases separating lesion position and bulge loop junction; s.—strongly (stabilizing/destabilizing); m.—moderately (stabilizing/destabilizing).

Share and Cite

MDPI and ACS Style

Völker, J.; Plum, G.E.; Gindikin, V.; Breslauer, K.J. Dynamic DNA Energy Landscapes and Substrate Complexity in Triplet Repeat Expansion and DNA Repair. Biomolecules 2019, 9, 709. https://doi.org/10.3390/biom9110709

AMA Style

Völker J, Plum GE, Gindikin V, Breslauer KJ. Dynamic DNA Energy Landscapes and Substrate Complexity in Triplet Repeat Expansion and DNA Repair. Biomolecules. 2019; 9(11):709. https://doi.org/10.3390/biom9110709

Chicago/Turabian Style

Völker, Jens, G. Eric Plum, Vera Gindikin, and Kenneth J. Breslauer. 2019. "Dynamic DNA Energy Landscapes and Substrate Complexity in Triplet Repeat Expansion and DNA Repair" Biomolecules 9, no. 11: 709. https://doi.org/10.3390/biom9110709

APA Style

Völker, J., Plum, G. E., Gindikin, V., & Breslauer, K. J. (2019). Dynamic DNA Energy Landscapes and Substrate Complexity in Triplet Repeat Expansion and DNA Repair. Biomolecules, 9(11), 709. https://doi.org/10.3390/biom9110709

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop