Nonlinear Model Predictive Horizon for Optimal Trajectory Generation

Abstract

This paper presents a trajectory generation method for a nonlinear system under closed-loop control (here a quadrotor drone) motivated by the Nonlinear Model Predictive Control (NMPC) method. Unlike NMPC, the proposed method employs a closed-loop system dynamics model within the optimization problem to efficiently generate reference trajectories in real time. We call this approach the Nonlinear Model Predictive Horizon (NMPH). The closed-loop model used within NMPH employs a feedback linearization control law design to decrease the nonconvexity of the optimization problem and thus achieve faster convergence. For robust trajectory planning in a dynamically changing environment, static and dynamic obstacle constraints are supported within the NMPH algorithm. Our algorithm is applied to a quadrotor system to generate optimal reference trajectories in 3D, and several simulation scenarios are provided to validate the features and evaluate the performance of the proposed methodology.

1. Introduction

For autonomous vehicle systems, the ability to generate and track collision-free trajectories in unknown environments is a crucial task that is attracting both researchers’ and companies’ attention in a world witnessing steep advancements in this area. The need to generate real-time trajectories for highly nonlinear systems puts an emphasis on finding ways to efficiently predict trajectories which respect the system dynamics as well as internal and external constraints. One methodology which meets these requirements is nonlinear model predictive control.

Nonlinear Model Predictive Control (NMPC) is the nonlinear variant of Model Predictive Control (MPC), which was originally developed for process control applications and can be traced back to the late 1970s [1,2]. MPC, sometimes called moving horizon or receding horizon optimal control, involves using a system dynamics model to predict a sequence of control inputs over a time interval known as the prediction horizon. For nonlinear systems, NMPC can be used as an optimization-based feedback control technique [3], and it has been viewed as one of the few control strategies which can account for state and input constraints and respect the nonlinearities and coupling of the system dynamics.

NMPC is employed in applications including setpoint stabilization, trajectory tracking, and path following. In setpoint stabilization, the system is controlled to converge to a specified setpoint within a terminal region. NMPC for setpoint stabilization has been used in many applications, such as fluid level and temperature control [4,5]. In trajectory tracking, the system must track a time-varying reference, which is a more challenging problem. Some examples of this taken from the fields of aerial vehicles and medicine are presented in [6,7]. Meanwhile, the path following problem considers time-invariant reference trajectories, where the goal is to achieve the best possible tracking of the geometric path regardless of the time taken. A common example of a path following problem is controlling the end-effector of a robot manipulator to follow a prescribed path within its workspace, which is treated using MPC in [8,9]. Ref. [10] provides a comprehensive overview of the setpoint stabilization, trajectory tracking, and path following problems and their relevant features and challenges.

Within the model predictive control approach, the optimization problem solves for both the input and the state of the system over a finite time horizon. These local plans can then be combined online to generate a prediction of the state trajectory, which is used for motion planning [11]. The work in [12] considers the problem of point-to-point trajectory generation using linear MPC, while NMPC is used for trajectory optimization and tracking control in [13], where it solves the nonlinear problem using an iterative sequential linear quadratic algorithm to obtain the optimal feedforward and feedback control inputs to a hexacopter vehicle.

In the present work, we focus on the reference trajectory generation problem for a nonlinear system (in our case a drone) under closed-loop control by an existing control law design, which may be linear (e.g., a PID-based design) or nonlinear (e.g., the geometric tracking controller in [14]). Our paper presents the development of an algorithm which allows the generation of optimal trajectories based on the NMPC approach, but using a closed-loop system model consisting of the nonlinear plant connected to a state feedback linearization (FBL) control law. This proposed formulation is called Nonlinear Model Predictive Horizon (NMPH). The purpose of employing FBL within the NMPH is to reduce or eliminate the nonconvexity of the optimization problem relative to working directly with the nonlinear plant dynamics as in standard NMPC.

Please note that while NMPC provides an input to a nonlinear plant, our proposed NMPH computes a reference trajectory to be tracked by a closed-loop system consisting of a nonlinear plant connected to a feedback control law. This makes NMPH ideally suited for drones, which run a closed-loop control law in their onboard firmware to obtain a stable hover for the vehicle. Employing an NMPC design thus requires bypassing the onboard control system, which can lead to a loss of the drone in scenarios where the computer running the NMPC code has an operating system crash or timeout. An alternative is to include a model of the onboard control law into the plant model used by the NMPC, but the full details of this control law are often kept proprietary (as seen in [15], for instance), which in turn requires employing system identification techniques and their resulting uncertain models.

To understand the differences between the proposed method and approaches based on model predictive control,

Table 1. Comparison between nonlinear model predictive control-based approaches.

	NMPC	NMHE	NMPH (Ours)
Objective	Predicts future control inputs and states of the system	Estimates the system states from previous measurements over the estimation horizon	Plans an optimal reference trajectory for the system under an existing feedback control design
Optimization Problem (OP)	Dynamic OP is solved iteratively for the optimal control inputs over the prediction horizon	OP is solved for state estimates and model parameters	Dynamic OP is solved iteratively for the optimal trajectory over the given prediction horizon
Cost/Objective Function	In general, a quadratic function which penalizes deviations of the predicted system states and control inputs. Composed of a stage cost and a terminal cost	In general, a quadratic function which penalizes deviations of the estimated outputs from the measured outputs. Composed of an arrival cost and a stage cost	Quadratic function which penalizes the deviation of the predicted system states and reference trajectory. Composed of a stage cost and a terminal cost
Optimization Variables	System inputs (states might be considered in some implementations)	System states and parameters	System states and prediction of the reference trajectory
Optimization Problem Convexity	Nonconvex	Nonconvex	Reduced nonconvexity or convex
Optimization Problem Constraints	Initial state; Nonlinear system model; Limits on states and control inputs	Nonlinear system model; Limits on states and parameter values	Initial state; Nonlinear system model; Limits on trajectories, states, controls; Obstacles
Optimization Performance	Depends on the accuracy of the system model and initial state estimate	Sensitive to the accuracy of the system model. Process noise may affect the solution, leading to inaccurate or unstable results	Relies on the accuracy of the system model, stability of closed-loop system, and accuracy of the initial state estimate

shows a comparison between NMPC, NMPH and NMHE (Nonlinear Moving Horizon Estimation). NMHE is an optimization-based technique that inputs measurements, which may contain noise and other uncertainties, and outputs estimates of the nonlinear system state or parameters. Further information about NMHE is given in [16].

The research contributions of this paper are:

• Formulating a novel motion planning approach (named NMPH), which employs a model of a closed-loop system under feedback linearization to efficiently solve for the optimal reference trajectory of the target closed-loop system;
• Designing a feedback linearization control law for a model augmented with integral states to achieve a more robust performance in the presence of modeling uncertainties.
• Implementing support for static and dynamic obstacles within the NMPH, enabling collision-free reference trajectory generation in unknown, dynamic environments;
• Validating the ability of the system to generate optimal trajectories for the quadrotor vehicle in real time using realistic flight environment simulation scenarios.

The remainder of this paper is structured as follows. Section 2 presents the formulation of NMPH and the design of its state feedback linearization control law. The application of the algorithm to a quadrotor vehicle is presented in Section 3. Section 4 presents different simulation scenarios to evaluate and validate the proposed approach. Concluding remarks are given in Section 5.

2. Nonlinear Model Predictive Horizon

Our proposed Nonlinear Model Predictive Horizon (NMPH) is an optimization-based trajectory generation method based on Nonlinear Model Predictive Control (NMPC). Unlike NMPC, which yields an optimal feedback control law for a nonlinear system, the objective of NMPH is to generate optimal reference trajectories that a closed-loop system can follow.

The goal of NMPH is to generate a smooth trajectory which is continuously updated by solving an Optimal Control Problem (OCP) in real time while respecting the state and input constraints of the closed-loop system. The resulting optimization problem will be referred to as an Optimal Trajectory Problem (OTP).

An overview of the NMPH architecture is depicted in Figure 1. The Nonlinear System Model and the Nonlinear Control Law, representing the model of the plant and the upcoming feedback linearization control law design, are both involved in the solution of the optimization problem. The NMPH inputs the current system state and a desired setpoint stabilization and outputs an optimal reference trajectory by solving the OTP at each time instant $t_n$.

Our proposed NMPH method:

• Predicts the trajectory of a nonlinear closed-loop system;
• Works in real-time using a specified time horizon;
• Uses a feedback linearization control law to reduce the nonconvexity of the optimization problem;
• Supports state and input constraints of the closed-loop system, and is able to account for environmental constraints such as dynamic obstacles;
• Assumes that a stable terminal point is specified, and the state vector of the closed-loop system is available (measured or estimated), and
• provides a combination of stabilization and tracking functionality:

  –

  Stabilization: provides a solution which guides the closed-loop system to a specified setpoint or terminal condition;

  –

  Tracking: generates a smooth reference trajectory for the closed-loop system to track or follow.

The NMPH provides a dynamic parameterization of the reference trajectory. This provides a continually evolving optimal reference trajectory from the current state of the closed-loop system to the terminal setpoint, which respects the system dynamics and environmental constraints such as dynamic obstacles.

In the following subsections, a formulation of the NMPH using a state feedback linearization control law is presented which produces optimal reference trajectories. First, the proposed NMPH algorithm structure and its constraints are discussed, then the design of the state feedback linearization control law is performed.

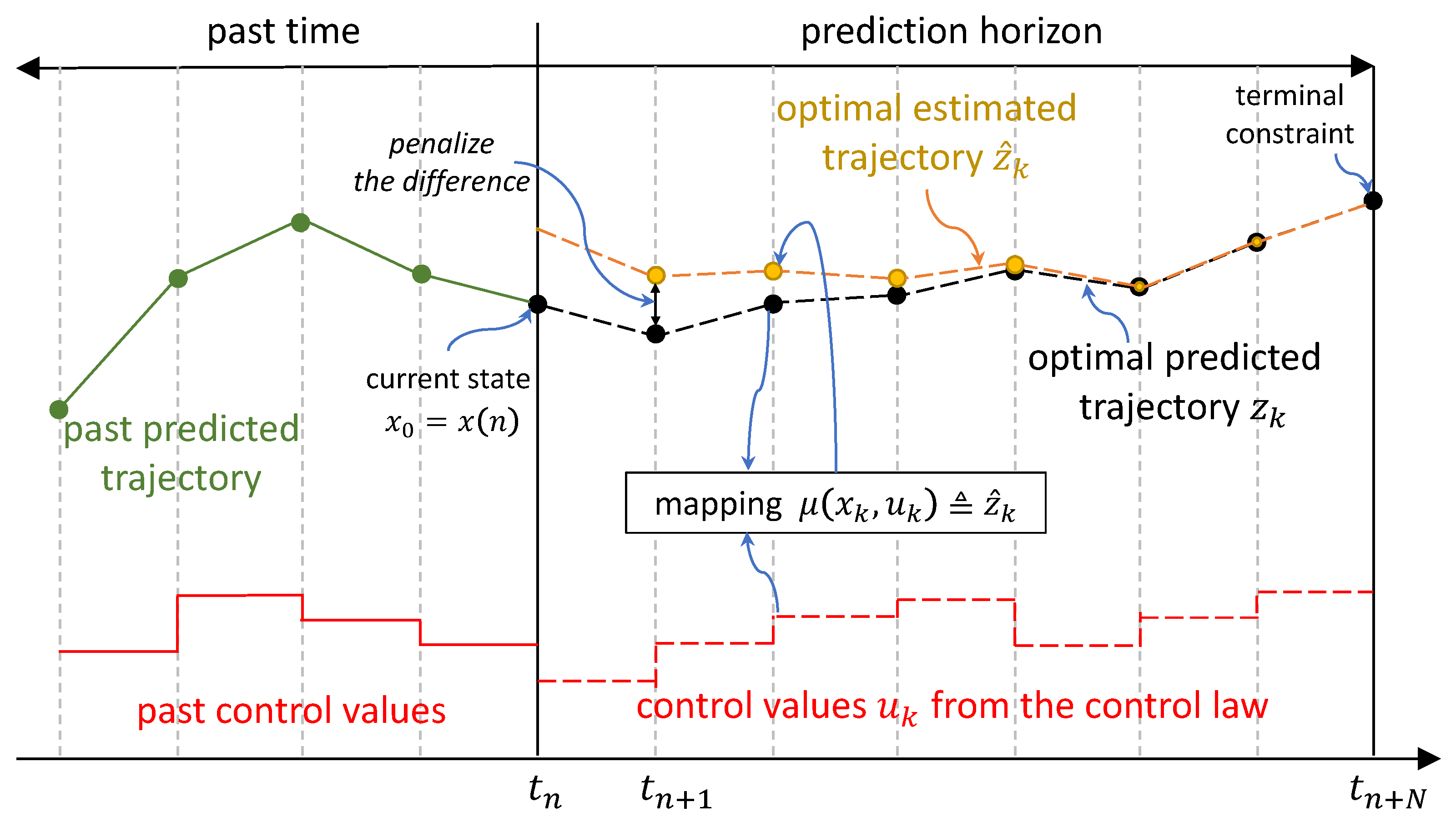
2.1. NMPH Algorithm

Consider a discrete-time model of the nonlinear closed-loop system at time instant $t_n$,

$$\begin{array}{}\hfill \mathrm{(1a)}& \hfill x\left(n+1\right)& =f\left(x\left(n\right),u\left(n\right)\right)\hfill \hfill \mathrm{(1b)}& \hfill z\left(n\right)& =h\left(x\left(n\right)\right)\hfill \hfill \mathrm{(1c)}& \hfill u\left(n\right)& =g(x\left(n\right),z_{ref}\left(n\right))\hfill \end{array}$$

where $x\left(n\right)\in X\subseteq {\mathbb{R}}^{n_x}$ are the system states, $z\left(n\right)\in Z\subseteq {\mathbb{R}}^{n_z}$ are the system outputs, $u\left(n\right)\in U\subseteq {\mathbb{R}}^{n_u}$ are the system inputs, and $z_{ref}\left(n\right)\in Z$ is the reference trajectory at time instant $t_n$. We assume that the system outputs are a subset of the system state vector, $Z\subseteq X$, in our case the drone’s position and yaw angle. The map $f:X\times U\to X$ represents the discrete-time plant dynamics and $x\left(n+1\right)$ are the states at the next sampling instant. $g:X\times Z\to U$ is the control law that is used to steer the system output to follow the reference trajectory.

A closer look at the NMPH structure is shown in Figure 2. The OTP solver uses the plant dynamics (1a), output (1b) and control law (1c) plus any applicable constraints (e.g., obstacles in the environment) to predict the sequence of future states and outputs of the closed-loop system model over the finite time horizon. In order to differentiate between the variables of the actual nonlinear system and its model within the NMPH, the latter uses subscripts as seen in Figure 2 and discussed below in Algorithm 1.

As shown in Figure 2, the sequence $x_k$ provides a prediction of the trajectory of the system (1) between its current state $x\left(n\right)$ and the setpoint stabilization $x_{ss}$, which is regenerated each time the OTP is solved. Meanwhile, the sequences $z_k$ and ${\widehat{z}}_k$ calculated by the OTP are defined as follows:

• $z_k$ is the predicted output trajectory sequence which represents a subset of the vector entries of the state sequence $x_k$ (in our case the quadrotor’s position and yaw angle). It is important to distinguish between $z\left(n\right)$, the current output of the actual closed-loop system, and $z_k$, the predicted output sequence produced by the OTP solution.
• ${\widehat{z}}_k$ is the estimated reference trajectory sequence which is calculated by solving an optimization problem inside the NMPH. Using ${\widehat{z}}_k$ as the reference trajectory for the actual closed-loop system yields smoother flight paths plus the ability to deal with constraints such as obstacles in the environment. In this way, $z_{ref}\left(n\right)$ in (1c) acquires its value from the first predicted point of the ${\widehat{z}}_k$ sequence.

As illustrated in Figure 3, the trajectory sequences $z_k$ and ${\widehat{z}}_k$ will converge to each other and towards the terminal point. Thus, either of them can be taken as the reference trajectory for the actual closed-loop system.

The predicted future of the closed-loop system’s behaviour is optimized at each sampling instant n and over a finite time horizon $k=0,1,\dots ,N-1$ of length $N\ge 2$. The system is assumed to follow the first j elements of the predicted optimal trajectory sequence until the next sampling instant, at which time the trajectory is recalculated, and so on. The predicted state $x_k$ and the control input $u_k$ sequences at each time instant n are calculated as

$$x_k\left(0\right)=x\left(n\right),x_{k+1}=f\left(x_k,u_k\right),u_k=g\left(x_k,{\widehat{z}}_k\right),k=n,\dots ,n+N-1$$

(2)

Now, consider $\mu \left(x_k,u_k\right):{\mathbb{R}}^{n_x}\times {\mathbb{R}}^{n_u}\to {\mathbb{R}}^{n_z}$ which is the mapping from the predicted state and control law sequences to the estimated trajectory sequence. This is written as

$${\widehat{z}}_k:=\mu \left(x_k,u_k\right),k=n,\dots ,n+N-1$$

(3)

Our objective is to use an optimization methodology to determine the estimated reference trajectory ${\widehat{z}}_k$ and the state $x_k$ (whose subset is $z_k$) sequences that both converge to the stabilization setpoint $x_{ss}=x_N^{ref}$. To do this, a cost function $J\left(x_k,{\widehat{z}}_k\right)$ is chosen to penalize the deviation of the system states from the reference, and the predicted output from the estimated reference trajectory, as shown below in Algorithm 1 and the cost function in (5).

Algorithm 1 NMPH algorithm with stabilizing terminal condition $x_{ss}$.

1: Let $n=0$; measure the initial state $x_0{\leftarrow x\left(n\right)|}_{n=0}$

2: while$\parallel x_{ss}-x_0\parallel \ge \delta$do

Solve the following Optimal Trajectory Problem, $$\underset{x_k,{\widehat{z}}_k}{min}\left(J\left(x_k,{\widehat{z}}_k\right):=\sum _{k=n}^{n+N-1}L\left(x_k,{\widehat{z}}_k\right)+E\left(x_{n+N}\right)\right)$$ (4) $$\begin{array}{}\hfill \mathrm{(4a)}& \hfill \mathrm{subject}\mathrm{to}& x_{k=0}=x\left(n\right)\hfill & \hfill & \hfill \hfill \mathrm{(4b)}& \hfill & x_{k+1}=f\left(x_k,u_k\right),\hfill & \hfill & k=n,\dots ,n+N-1,\hfill \hfill \mathrm{(4c)}& \hfill & u_k=g\left(x_k,{\widehat{z}}_k\right),\hfill & \hfill & k=n,\dots ,n+N-1,\hfill \hfill \mathrm{(4d)}& \hfill & x_k\in \mathcal{X},\hfill & \hfill & k=n,\dots ,n+N,\hfill \hfill \mathrm{(4e)}& \hfill & {\widehat{z}}_k\in \mathcal{Z},u_k\in \mathcal{U},\hfill & \hfill & k=n,\dots ,n+N-1,\hfill \hfill \mathrm{(4f)}& \hfill & {\mathcal{O}}_i\left(x_k\right)\le 0,\hfill & \hfill & i=1,2,\dots ,p\hfill & \hfill \end{array}$$

if $x_k\to x_{ss}$ then (estimated trajectory converging to terminal condition)

$n\leftarrow n+1$;

else

break;

end

end

In Algorithm 1, N is the prediction horizon, $x\left(n\right)$ is the current measured state at a time instant $t_n$, which represents the initial condition of the OTP, and $L\left(·,·\right)$ and $E\left(·\right)$ are the stage cost function and the terminal cost function, respectively. The constraint sets $\mathcal{X}$, $\mathcal{U}$, and $\mathcal{Z}$ will be defined in Section 2.2, and the inequality constraints ${\mathcal{O}}_i\left(x_k\right)\le 0$ allow modeling a set of p static and dynamic obstacles. The optimization process of Algorithm 1 is summarized as follows:

• Measure or estimate the actual closed-loop system’s current state $x\left(n\right)$;
• Obtain a prediction of the reference trajectory sequence ${\widehat{z}}_k$ for an admissible control input by minimizing the cost function over the prediction horizon subject to the dynamics of the closed-loop system plus state and input constraints;
• Send the predicted reference trajectory sequence to the closed-loop system for tracking;
• Repeat until the system reaches the desired terminal point or encounters an infeasible optimization solution.

Within NMPH, convergence can be achieved by proper choices of the stage cost $L\left(x,\widehat{z}\right)$ and the terminal cost $E\left(x\right)$ for a setpoint stabilization problem [10]. The requirements for these cost functions are summarized below in Assumption 1:

Assumption 1

(Cost Function). The stage cost $L\left(x,\widehat{z}\right):{\mathbb{R}}^{n_x}\times {\mathbb{R}}^{n_z}\to {\mathbb{R}}_0^{+}$ and terminal cost $E\left(x\right):{\mathbb{R}}^{n_x}\to {\mathbb{R}}_0^{+}$ functions introduced in (4) have the following properties:

• The stage cost is continuous and bounded from below, meaning that $L\left(x,\widehat{z}\right)\ge \alpha$ for all $\left(x,\widehat{z}\right)\in X\times Z\backslash \{0,0\}$ and $L\left(0,0\right)=0$.
• The terminal cost is a positive semi-definite function, which is continuously differentiable and satisfies

  $$\frac{\partial E}{\partial x}f\left(x,g\left(x,\widehat{z}\right)\right)+L\left(x,\widehat{z}\right)\le 0$$
• The terminal constraint set ${\mathcal{E}}_N$ is a subset of the state constraint set $\mathcal{X}$ and it is compact.
• For every $x_N\in {\mathcal{E}}_N$, there exists an estimate of the reference trajectory ${\widehat{z}}_k$ and predicted output trajectory $z_k$ sequences where both converge to the terminal setpoint and stay within the terminal region ${\mathcal{E}}_N$.

Our cost function is chosen to penalize the deviation of states from their reference values, and the deviation of the predicted output trajectory from the estimated reference trajectory, as follows:

$$J\left(x_k,{\widehat{z}}_k\right):=\sum _{k=n}^{n+N-1}\left(\parallel x_k-x_k^{ref}{\parallel }_{W_x}^2+{\parallel z_k-{\widehat{z}}_k\parallel }_{W_z}^2\right)+{\parallel x_N-x_N^{ref}\parallel }_{W_N}^2$$

(5)

where $x_k^{ref}\in X$ is the reference states sequence used in the optimization problem. The terminal cost $\parallel x_N-x_N^{ref}{\parallel }_{W_N}^2$ with its weighting matrix $W_N$ steers the system towards the stabilization setpoint $x_{ss}=x_N^{ref}$, while the stage cost function $L\left(x_k,{\widehat{z}}_k\right)$ uses the weighting matrices $W_x$ and $W_z$ to penalize deviations of the states and outputs, respectively. The entries of the weighting matrices are selected to adjust the relative importance of these three factors for the optimization problem.

A visual interpretation of the NMPH process can be seen in Figure 3, where the path planning task is to guide the closed-loop system described by (1) to follow a predicted trajectory from $x\left(n\right)$ (at time instant $t_n$) to $x_{ss}$ (at a future time $t_{n+N}$) while minimizing the cost function (5) and respecting the system’s state and input constraints.

Some of the features of the predicted trajectory sequences are:

• The first j elements of the reference trajectory sequence ${\widehat{z}}_k$ are passed to the closed-loop system, which is different from the NMPC control problem where only the first element of the predicted control sequence $u^{*}\left(n\right)$ is used. This provides some flexibility in choosing the rate at which the OTP is solved, which addresses the computation time issue of solving a Nonlinear Program (NLP).
• Thanks to recent advancements in computing, specifically graphics processing units (GPUs), the computations required for optimization problems can be performed very quickly, meaning solving the NLP problem for OTP or even OCP can be done in real-time. Irrespective of this, OTP has an advantage over OCP since the computational power requirement can be controlled by adjusting the rate of solving the optimization problem while allowing the vehicle to track the first j elements of the estimated reference trajectory.
• While the tailing $N-j$ elements of the reference trajectory sequence are discarded, the entire trajectory is still required to be calculated over the prediction horizon. The reason for this is that optimizing over the full horizon ensures a smooth trajectory from the initial state to the terminal setpoint.
• The optimization problem is solved iteratively using a reliable and accurate optimization approach based on the multiple shooting method and sequential quadratic programming.

The discrete-time representation (1) shown in Section 2.1 was presented to understand the problem formulation analysis and NMPH development, with the optimization being performed in the discrete-time domain as in sampled-data MPC [17]. Conversely, a continuous-time representation is important for NMPH implementation since our chosen optimization algorithm (ACADO [18]) has the ability to discretize the system equations.

Consider the continuous-time nonlinear closed-loop system

$$\begin{array}{ccc}\hfill \dot{x}\left(t\right)& =& f\left(x\left(t\right),u\left(t\right)\right)\hfill \\ \hfill z\left(t\right)& =& h\left(x\left(t\right)\right)\hfill \\ \hfill u\left(t\right)& =& g\left(x\left(t\right),z_{ref}\left(t\right)\right)\hfill \end{array}$$

(6)

where $x\left(t\right)\in {\mathbb{R}}^{n_x}$ are the system states and $u\left(t\right)\in {\mathbb{R}}^{n_u}$ are the system inputs. $z\left(t\right)\in {\mathbb{R}}^{n_z}$ are the system outputs, assumed to be a subset of the state vector $x\left(t\right)$. The maps f and g are the nonlinear system dynamics and control law, respectively.

The optimization problem presented in Algorithm 1 can be rewritten in the continuous-time domain as

$$\begin{array}{cc}\hfill & \underset{x\left(t\right),\widehat{z}\left(t\right)}{min}\left({\int }_{t_n}^{t_n+T}L\left(x\left(\tau \right),\widehat{z}\left(\tau \right)\right)d\tau +E\left(x\left(t_n+T\right)\right)\right)\hfill \\ \hfill & \underset{x\left(t\right),\widehat{z}\left(t\right)}{min}({\int }_{t_n}^{t_n+T}\left(\parallel x\left(\tau \right)-x{\left(\tau \right)}^{ref}{\parallel }_{W_x}^2+{\parallel z\left(\tau \right)-\widehat{z}\left(\tau \right)\parallel }_{W_z}^2\right)d\tau \hfill \\ \hfill & +\parallel x\left(t_n+T\right)-x{\left(t_n+T\right)}^{ref}{\parallel }_{W_N}^2)\hfill \end{array}$$

(7)

$$\begin{array}{cccc}\hfill \mathrm{subject}\mathrm{to}& x_0=x\left(t_n\right),\hfill & \hfill & \\ \hfill & \dot{x}\left(\tau \right)=f\left(x\left(\tau \right),u\left(\tau \right)\right),\hfill & \hfill & \\ \hfill & u\left(\tau \right)=g\left(x\left(\tau \right),\widehat{z}\left(\tau \right)\right),\hfill & \hfill & \\ \hfill & x\left(\tau \right)\in \mathcal{X},\widehat{z}\left(\tau \right)\in \mathcal{Z},u\left(\tau \right)\in \mathcal{U},\hfill & \hfill & \\ \hfill & {\mathcal{O}}_i\left(x\left(\tau \right)\right)\le 0,\hfill & \hfill & i=1,2,\dots ,p.\hfill \end{array}$$

The continuous-time optimization problem must be solved over the full time interval $\tau \in [t_n,t_n+T]$. As discussed above, the closed-loop system will be asked to track a portion of the resulting reference trajectory running from $t_n$ to $t_n+t_j$, where $t_j<T$ and where $t_j$ can be adjusted online to affect the trajectory generation and tracking performance and control the computational power required by the optimization.

2.2. NMPH Constraints

Support for constraints within the NMPH algorithm provides full control over the optimization problem. The constraints can apply to the state, input and output trajectories, and also model dynamic obstacles.

State constraints belong to the subset $\mathcal{X}\subseteq X$, while outputs, which are assumed to be a subset of the state vector entries, belong to the subset $\mathcal{Z}\subseteq \mathcal{X}$. $\mathcal{U}\left(x,\widehat{z}\right)\subseteq U$ is defined by physical input constraints in the system, for instance due to actuator limits.

The objective of introducing the constraint sets are to ensure that the optimized trajectories are bounded and lie within their allowable ranges. The following assumptions regarding the constraint sets are made [3,10]:

Assumption 2

(Closed and Bounded Sets). The constraint sets of the state $\mathcal{X}$ and the reference trajectory $\mathcal{Z}$ are closed, and the control constraint set $\mathcal{U}$ is compact.

Assumption 3

(Differentiability and Lipschitz). The system dynamics $f\left(x,u\right):{\mathbb{R}}^{n_x}\times {\mathbb{R}}^{n_u}\to {\mathbb{R}}^{n_x}$ is continuously differentiable for all $\left(x,u\right)\in \mathcal{X}\times \mathcal{U}$. Also, $f\left(x,u\right)$ and the reference trajectory mapping $\mu \left(x,u\right):{\mathbb{R}}^{n_x}\times {\mathbb{R}}^{n_u}\to {\mathbb{R}}^{n_z}$ are considered to be locally Lipschitz.

Assumption 4

(Uniqueness). For any element of the estimated reference trajectory $\widehat{z}$ resulting from a control input u and any possible initial states $x_0\in \mathcal{X}$, the system dynamics produce a unique and continuous solution.

Assumption 5

(Viability). For each state $x\in \mathcal{X}$ and estimated reference trajectory $\widehat{z}\in \mathcal{Z}$ there exists a control $u=g\left(x,\widehat{z}\right)\in \mathcal{U}$ such that $f\left(x,u\right)\in \mathcal{X}$.

Taking Assumptions 2–4, we can make the following definition:

Definition 1

(Admissibility). In the discrete-time OTP, consider the system dynamics $x_{k+1}=f\left(x_k,u_k\right)$ and the control law $u_k=g\left(x_k,{\widehat{z}}_k\right)$, which maps the state to the estimated trajectory as $\mu \left(x_k,u_k\right):={\widehat{z}}_k\in \mathcal{Z}$, with the constraint sets for state $\mathcal{X}\subseteq X$, control $\mathcal{U}\left(x,\widehat{z}\right)\subseteq U$, and reference trajectory $\mathcal{Z}\subseteq X$.

• The system states $x_k\in \mathcal{X}$ and the estimated reference trajectory ${\widehat{z}}_k\in \mathcal{Z}$ are called admissible states and trajectories, respectively, and the control $u_k=g\left(x_k,{\widehat{z}}_k\right)\in \mathcal{U}$ are called admissible control values for $x_k$ and ${\widehat{z}}_k$. Hence, the admissible set can be defined as

  $$\mathcal{Y}:=\left\{\left(x_k,{\widehat{z}}_k,u_k\right)\in X\times Z\times U|x_k\in \mathcal{X},{\widehat{z}}_k\in \mathcal{Z},u_k=g\left(x_k,{\widehat{z}}_k\right)\in \mathcal{U}\right\}$$

  (8)
• The control sequence $u_k$ and its associated estimated reference trajectory ${\widehat{z}}_k$ and state sequence $x_k$ from the time $t_0$ of the initial value $x_0\in \mathcal{X}$ up to time $t_N$ of the setpoint stabilization value $x_N$ are admissible if $\left(x_k,{\widehat{z}}_k,u_k\right)\in \mathcal{Y}$ for $k=0,\dots ,N-1$ and $x_N\in \mathcal{X}$.
• The control law is called admissible if $g\left(x_k,{\widehat{z}}_k\right)\in \mathcal{U}$ for all $x_k\in \mathcal{X}$ and ${\widehat{z}}_k\in \mathcal{Z}$.
• The estimated reference trajectory is called admissible if $\mu \left(x_k,u_k\right)\in \mathcal{Z}$ for all $x_k\in \mathcal{X}$ and $u_k\in \mathcal{U}$.

A feasible problem is defined as an optimization problem in which there exists at least one set of solutions that satisfies all the constraints [3]. Based on Assumptions 2–5 and the admissibility Definition 1, the feasibility of the OTP is determined by Theorem 1.

Theorem 1

(Feasibility). If the OTP is feasible for an initial condition $x_0$ and the cost function for a setpoint stabilization problem with associated constraint sets satisfy Assumptions 2–5, then the OTP is recursively feasible, meaning the state converges to the stabilizing terminal point $x_N$, and both the estimated reference trajectory ${\widehat{z}}_k$ and predicted output trajectory $z_k$ sequences converge toward the terminal stabilization setpoint under sampled-data NMPH.

Proof. 

The solution of the OTP is feasible for an initial value $x_0\in \mathcal{X}$ to a stabilizing terminal point $x_N\in \mathcal{X}$ if the sets over which we optimize are nonempty. The viability considered in Assumption 5 for $\mathcal{Z}$ and $\mathcal{X}$ implies that the OTP is feasible for each initial state $x_0$ and consequently ensures that the control $g\left(x_k,{\widehat{z}}_k\right)$ is properly defined for each $x\in \mathcal{X}$ and $\widehat{z}\in \mathcal{Z}$. Since the OTP is performed with respect to admissible predicted state trajectory and control law sequences (as stated in Definition 1), the future behavior of the system is consequently feasible. □

It is important to note that the solution of the OTP is viable in the case of a stabilizing terminal constraint, meaning the NMPH problem is confined to feasible subsets since the terminal constraint is viable. The closed-loop system embedded within NMPH satisfies the desired constraints, which will lead to a feasible solution in the OTP. The stability of a feasible solution is governed by Theorem 2.

Theorem 2

(Stability). Assume that the OTP within Algorithm 1 satisfies Assumption 1 and has a feasible solution as determined by Theorem 1. Then the optimized solution leads to a stable prediction of the system state $x_k$ and estimated reference trajectory ${\widehat{z}}_k$.

Proof. 

Assume that at any time instant $t_i$, $i\in [n,...,n+N-2]$, $x_i^{*}$ and ${\widehat{z}}_i^{*}$ are the optimal solutions of the OTP in Algorithm 1, with their associated control value $u_i^{*}$. A Lyapunov-like function is defined as

$$V\left(x_i,{\widehat{z}}_i\right)=\underset{x_i^{*},{\widehat{z}}_i^{*}}{min}J\left(x_i,{\widehat{z}}_i\right)=J\left(x_i^{*},{\widehat{z}}_i^{*}\right)$$

(9)

The cost function in (5) guarantees a positive semi-definite Lyapunov-like candidate [19], meaning that $0\le V\left(x_i,{\widehat{z}}_i\right)<\infty$, which can be written at time $t_i$ as

$$V\left(x_i,{\widehat{z}}_i\right)=E\left(x_{n+N}^{*}\right)+\sum _{i=n}^{n+N-1}L\left(x_i^{*},{\widehat{z}}_i^{*}\right)$$

(10)

Considering the solution at a subsequent time $t_{i+\delta }$, the feasible solution of the cost function is

$$J\left(x_{i+\delta },{\widehat{z}}_{i+\delta }\right)=E\left(x_{n+N+\delta }\right)+L\left(x_{n+N-1+\delta },{\widehat{z}}_{n+N-1+\delta }\right)+\sum _{i=n+\delta }^{n+N-1}L\left(x_i^{*},{\widehat{z}}_i^{*}\right)$$

(11)

Since $V\left(x_{i+\delta },{\widehat{z}}_{i+\delta }\right)\le J\left(x_{i+\delta },{\widehat{z}}_{i+\delta }\right)$, we have

$$\begin{array}{ccc}\hfill V\left(x_{i+\delta },{\widehat{z}}_{i+\delta }\right)-V\left(x_i,{\widehat{z}}_i\right)& \le & J\left(x_{i+\delta },{\widehat{z}}_{i+\delta }\right)-V\left(x_i,{\widehat{z}}_i\right)\hfill \\ & \le & E\left(x_{n+N+\delta }\right)+L\left(x_{n+N-1+\delta },{\widehat{z}}_{n+N-1+\delta }\right)\hfill \\ & & +{\Sigma }_{i=n+\delta }^{n+N-1}L\left(x_i^{*},{\widehat{z}}_i^{*}\right)-\left(E\left(x_{n+N}^{*}\right)+{\Sigma }_{i=n}^{n+N-1}L(x_i^{*},{\widehat{z}}_i^{*})\right)\hfill \\ & \le & L\left(x_{n+N-1+\delta },{\widehat{z}}_{n+N-1+\delta }\right)+E\left(x_{n+N+\delta }\right)\hfill \\ & & -L(x_n^{*},{\widehat{z}}_n^{*})-E\left(x_{n+N}^{*}\right)\hfill \end{array}$$

where $E\left(x_{n+N+\delta }\right)-E\left(x_{n+N}^{*}\right)+L\left(x_{n+N-1+\delta },{\widehat{z}}_{n+N-1+\delta }\right)\le 0$ based on the inequality considered in Assumption 1. Therefore,

$$V\left(x_{i+\delta },{\widehat{z}}_{i+\delta }\right)-V\left(x_i,{\widehat{z}}_i\right)\le -L\left(x_n^{*},{\widehat{z}}_n^{*}\right)$$

this implies that the rate of change in the Lyapunov-like function is decreasing with time. Hence, the solution of the OTP problem in Algorithm 1 converges asymptotically to the terminal setpoint. □

To perform safe navigation, it is necessary to include the obstacle constraints within the optimization problem. The inequality constraint presented in (4f) accounts for the space that the predicted trajectory should avoid. For instance, the obstacle constraints ${\mathcal{O}}_i\left(x_k\right)\le 0$ are defined as

$$\parallel x_k^{pos}-o_i\parallel -{ϵ}_i\ge 0,i=1,2,\dots ,p$$

where $x_k^{pos}\in {\mathbb{R}}^3$ is the predicted vehicle position over the prediction horizon, $o_i\in {\mathbb{R}}^3$ are the position of the obstacles centers, and ${ϵ}_i$ represents the safety distance between the $i^{th}$ obstacle and the vehicle, which accounts for the drone and obstacle sizes, including the safety tolerance.

2.3. NMPH Closed-Loop Form with Feedback Linearization Control Law

In this section, we cover the feedback linearization-based control law design within the NMPH. The nonlinear system studied in this work, a quadrotor drone, is a Multi-Input Multi-Output (MIMO) system. We thus start by reviewing the method of feedback linearization for a class of MIMO systems.

Consider a MIMO nonlinear control-affine system of the form

$$\dot{x}=f\left(x\right)+\sum _{i=1}^{n_u}{\mathfrak{g}}_i\left(x\right)u_i\triangleq f\left(x\right)+G\left(x\right)u$$

(12)

in which $x\in {\mathbb{R}}^{n_x}$, and f,${\mathfrak{g}}_1,\dots ,{\mathfrak{g}}_{n_u}$ are smooth vector fields in ${\mathbb{R}}^{n_x}$. $G\left(x\right)$ is an $n_x\times n_u$ matrix and its rank at $x=0$ is $\mathrm{rank}G\left(0\right)=n_u$. For notation simplicity in the following sections, take $n_x\equiv n$ and $n_u\equiv m$.

Prior to feedback linearization analysis, the following theorems and definitions are presented in the context of differential geometry.

Definition 2

(Diffeomorphism). A diffeomorphism is a differentiable map φ between two manifolds $\mathcal{M}$ and $\mathcal{N}$, such that $\phi :\mathcal{M}\to \mathcal{N}$ is one-to-one and onto (bijective), and its differentiable inverse map ${\phi }^{-1}:\mathcal{N}\to \mathcal{M}$ is bijective as well. φ is called a $C^{\omega }$ diffeomorphism if it is ω times continuously differentiable. If $\omega =\infty$, then φ is called a $C^{\infty }$ smooth map [20].

A change in coordinates can be defined globally or locally. A map $\xi :{\mathbb{R}}^n\to {\mathbb{R}}^n$ is called a global diffeomorphism between two coordinates if, and only if, the determinant $det\frac{\partial \xi }{\partial x}\ne 0$ for all $x\in {\mathbb{R}}^n$, and ${lim}_{\parallel x\parallel \to \infty }\parallel \xi \left(x\right)\parallel =\infty$ [21]. For a local change in coordinates, let $\mathcal{U}$ be an open subset of ${\mathbb{R}}^n$ with $\xi :\mathcal{U}\to {\mathbb{R}}^n$. If $det\frac{\partial \xi }{\partial x}\ne 0$ at some $x\in \mathcal{U}$, then there exists $\mathcal{V}\subset \mathcal{U}$, which is an open set that includes x such that the map $\xi :\mathcal{V}\to \mathcal{V}\left(\xi \right)$ is a diffeomorphism [20].

A specific class of nonlinear systems can be transformed into a linear state feedback controllable form by satisfying the conditions to be presented in Theorem 3. To facilitate our understanding of this process, we first define a nonsingular state feedback transformation and controllability indices in Definitions 3 and 4, respectively [20]:

Definition 3

(Nonsingular state feedback transformation). Consider ${\mathcal{V}}_0\subset {\mathcal{U}}_0$ which is a neighborhood of the origin. On the one hand, the nonsingular state feedback is defined as:

$$u=\beta \left(x\right)+D{\left(x\right)}^{-1}v$$

(13)

where the function $\beta \left(x\right)$ is smooth from ${\mathcal{V}}_0$ into ${\mathbb{R}}^n$ and $\beta \left(0\right)=0$. $D{\left(x\right)}^{-1}$ is the inverse of a nonsingular $m\times m$ matrix in ${\mathcal{V}}_0$.

On the other hand, a local diffeomorphism in ${\mathcal{V}}_0$, which is defined by $(\xi =T\left(x\right),T\left(0\right)=0)$, exists if, and only if, in ${\mathcal{U}}_0$ the distributions ${\mathcal{G}}_l=span\left\{a{d}_f^j{\mathfrak{g}}_i:1\le i\le m,0\le j\le l\right\}$ are involutive and of constant rank for $0\le l\le n-2$, and the rank of the distribution of $n-1$ is $rank{\mathcal{G}}_{n-1}=n$.

A transformation that contains a nonsingular state feedback and a local diffeomorphism is called a nonsingular state feedback transformation.

Definition 4

(Controllability Indices). The controllability indices $r_i$, $i=1,\dots ,m$ associated with control-affine systems of the form (12) are calculated as

$$r_i=card\left\{m_j\ge i:j\ge 0\right\}$$

(14)

with

$$\begin{array}{cc}\hfill m_0& =rank{\mathcal{G}}_0,\hfill \\ \hfill m_k& =rank{\mathcal{G}}_k-rank{\mathcal{G}}_{k-1},k=1,\dots ,n-1.\hfill \end{array}$$

Employing Definitions 3 and 4, the sufficient conditions for feedback linearization and the form of its feedback transformation are given in Theorem 3 [20].

Theorem 3

(MIMO Feedback Linearization). A system of the form (12) can be locally transformed by means of a nonsingular state feedback transformation as given in Definition 3 into a linear Brunovsky controller form in ${\mathcal{U}}_0$ if:

(i) 

The controllability indices satisfy the condition $r_1\ge \dots \ge r_m$;

(ii) 

The distributions ${\mathcal{G}}_{r_i-2}$ are involutive and of constant rank for $i=1,\dots ,m$;

(iii) 

The rank of the distribution ${\mathcal{G}}_{r_1-1}$ is $rank{\mathcal{G}}_{r_1-1}=n$.

In this case, there are smooth functions $\{{\phi }_i\left(x\right):\langle d{\phi }_i,{\mathcal{G}}_{r_i-2}\rangle =0,j\ge i,i=1,\dots ,m\}$ that form a nonsingular matrix $D\left(x\right)$ in ${\mathcal{V}}_0$,

$$D\left(x\right)=\left[\begin{array}{ccc}\langle d{\phi }_1,a{d}_f^{r_1-1}{\mathfrak{g}}_1\rangle & \cdots & \langle d{\phi }_1,a{d}_f^{r_1-1}{\mathfrak{g}}_m\rangle \\ ⋮& \ddots & ⋮\\ \langle d{\phi }_m,a{d}_f^{r_m-1}{\mathfrak{g}}_1\rangle & \cdots & \langle d{\phi }_m,a{d}_f^{r_m-1}{\mathfrak{g}}_m\rangle \end{array}\right],$$

(15)

and consequently the nonsingular state feedback transformation is

$$v=\left[\begin{array}{c}{L}_f^{r_1}{\phi }_1\\ ⋮\\ L_f^{r_m}{\phi }_m\end{array}\right]+\left[\begin{array}{ccc}{L}_{{\mathfrak{g}}_1}{L}_f^{r_1-1}{\phi }_1& \cdots & L_{{\mathfrak{g}}_m}{L}_f^{r_1-1}{\phi }_1\\ ⋮& \ddots & ⋮\\ L_{{\mathfrak{g}}_1}{L}_f^{r_m-1}{\phi }_m& \cdots & L_{{\mathfrak{g}}_m}{L}_f^{r_m-1}{\phi }_m\end{array}\right]u,\xi =\left[\begin{array}{c}{\phi }_1\\ ⋮\\ L_f^{r_1-1}{\phi }_1\\ ⋮\\ {\phi }_m\\ ⋮\\ L_f^{r_m-1}{\phi }_m\end{array}\right]$$

(16)

In Theorem 3, $L_f\phi =\langle d\phi ,f\rangle$ is the Lie derivative which can be realized as a directional derivative of the smooth function $\phi$ along the smooth vector field f, and $a{d}_f^r\mathfrak{g}=[f,a{d}_f^{r-1}\mathfrak{g}]$ is the iterated Lie bracket between the vector fields f and g.

Using the feedback linearization control law yields a locally stable closed-loop system model within the NMPH structure. One of the main motivations for choosing the feedback linearization approach in our work was to reduce nonlinearities. Since the NMPH works with a closed-loop system model, the optimization problem will have a reduced nonconvexity as compared to working directly with the nonlinear plant model as in NMPC. This will lead to better optimization performance in terms of computation time to find feasible solutions.

Modeling errors, system uncertainties, and external disturbances can affect the performance of the state feedback linearization control law. For instance, a constant wind gust applied to the drone while following a trajectory will lead to an offset in the corresponding position outputs. The baseline feedback linearization controller is unable to compensate for this type of offset, which will consequently degrade the accuracy of the predicted states and reference trajectories produced by the NMPH. To overcome this issue, an extension of the state feedback linearization can be achieved by augmenting the system model with integral states of the position vector and yaw angle of the drone. The validity of using this extension is demonstrated by using Theorem 3 in the feedback linearization design Section 3.2.

3. Application of NMPH to a Quadrotor Vehicle

3.1. System Model

In this section, the NMPH is developed for a quadrotor vehicle connected to a feedback linearization control law. A standard nonlinear rigid-body dynamics vehicle model is adopted in this work from [22]. This model is simplified by ignoring drag forces, rotor gyroscopic effects, and propeller dynamics. A more comprehensive nonlinear model that includes those assumptions can be considered in future work.

The rigid-body kinematics and dynamics are developed using two reference frames, which are the fixed navigation frame $\mathcal{N}$ and the moving body frame $\mathcal{B}$ (fixed to the quadrotor’s Center of Gravity, CG). The bases of both frames are selected based on the North, East, and Down (NED) directions in a local tangent plane as the orthonormal vector sets $\{n_1,n_2,n_3\}$ and $\{b_1,b_2,b_3\}$ for the navigation and body frames, respectively. The two basis are depicted in Figure 4.

In general, any configuration of a rigid body in space belongs to the Special Euclidean group SE(3), the product space of the rigid-body orientation and position $\left(R_{nb},p^n\right)\in \mathrm{SO}\left(3\right)\times {\mathbb{R}}^3=\mathrm{SE}\left(3\right)$, where the Special Orthogonal group SO(3) is defined as $\mathrm{SO}\left(3\right)=\{R\in {\mathbb{R}}^{3\times 3}|R{R}^T=R^{T}R=I,det\left(R\right)=+1\}$, and the rotation matrix of $\mathcal{B}$ with respect to $\mathcal{N}$ is denoted as $R_{nb}\in \mathrm{SO}\left(3\right)$. To represent the orientation, the ZYX Euler angle parameterization is employed. Based on the roll-pitch-yaw Euler angles $\eta ={[\varphi ,\theta ,\psi ]}^T$, the rotation matrix can be written as

$$R=R_{nb}=R_{\psi }{R}_{\theta }{R}_{\varphi }=\left[\begin{array}{ccc}{c}_{\theta }{c}_{\psi }& s_{\varphi }{s}_{\theta }{c}_{\psi }-c_{\varphi }{s}_{\psi }& c_{\varphi }{s}_{\theta }{c}_{\psi }+s_{\varphi }{s}_{\psi }\\ c_{\theta }{s}_{\psi }& s_{\varphi }{s}_{\theta }{s}_{\psi }+c_{\varphi }{c}_{\psi }& c_{\varphi }{s}_{\theta }{s}_{\psi }-s_{\varphi }{c}_{\psi }\\ -s_{\theta }& s_{\varphi }{c}_{\theta }& c_{\varphi }{c}_{\theta }\end{array}\right]$$

(17)

where $s_{(·)}=sin(·)$ and $c_{(·)}=cos(·)$. Note $t_{(·)}=tan(·)$ will be used in (20).

The most prominent issue of using Euler angles is the singularity when the parameterization loses injectivity at $\theta =\pi /2+k\pi$, $k\in \mathbb{Z}$. A recent work by [23] tackles this issue by using non-Euclidean rotation groups in the NMPC, but in this work the problem is addressed simply by adding state constraints within the NMPH optimization problem in (4d).

The rigid-body kinematics and dynamics are modeled as shown below

$$\begin{array}{ccc}\hfill {\dot{p}}^n& =& v^n\hfill \\ \hfill m{\dot{v}}^n& =& -\overline{u}R{n}_3+g{n}_3\hfill \\ \hfill \dot{R}& =& R\mathcal{S}\left({\omega }^b\right)\hfill \\ \hfill J{\dot{\omega }}^b& =& -\mathcal{S}\left({\omega }^b\right)J{\omega }^b+{\tau }^b\hfill \end{array}$$

(18)

where $p^n,v^n\in {\mathbb{R}}^3$ are the vehicle’s position and velocity with respect to the inertial frame $\mathcal{N}$, respectively. m is the mass of the quadrotor, g = 9.81 m/s² is the gravitational acceleration, and the vehicle’s mass moment of inertia matrix is assumed to be diagonal with $J=\mathrm{diag}\left([J_1,J_2,J_3]\right)$. The system input vector is ${[\overline{u},{\tau }^b]}^T$, where $\overline{u}={\sum }_{i=1}^4{f}_i>0$ is the total generated thrust in the direction of $-b_3$, and ${\tau }^b={[{\tau }^{b1},{\tau }^{b2},{\tau }^{b3}]}^T$ are the torques created by the rotors about the body frame axes. ${\omega }^b$ and $\dot{{\omega }^b}$ are the angular velocity and acceleration vectors, respectively. The operator $\mathcal{S}(·):{\mathbb{R}}^3\to \mathfrak{so}\left(3\right)$ maps a vector to a skew-symmetric matrix such that $\mathcal{S}\left(a\right)b=a\times b$ for $a,b\in {\mathbb{R}}^3$.

3.2. Quadrotor Feedback Linearization Control

The system represented in (18) has to be described in a nonlinear control-affine form as shown in (12). The state and input vectors are

$$\begin{array}{ccc}\hfill x& =& {\left[{\left(p^n\right)}^T,{\left(v^n\right)}^T,{\left(\eta \right)}^T,{\left({\omega }^b\right)}^T\right]}^T\in {\mathbb{R}}^{12}\hfill \\ \hfill u& =& {\left[\overline{u},{\left({\tau }^b\right)}^T\right]}^T\in {\mathbb{R}}^4\hfill \end{array}$$

(19)

The control-affine form is as described below

$$\dot{x}=f\left(x\right)+\sum _{i=1}^4{\mathfrak{g}}_i\left(x\right)u_i\triangleq f\left(x\right)+G\left(x\right)u$$

(20)

where

$$f\left(x\right)=\left[\begin{array}{c}{x}_4\\ x_5\\ x_6\\ 0\\ 0\\ g\\ x_{10}+s_{x_7}{t}_{x_8}{x}_{11}+c_{x_7}{t}_{x_8}{x}_{12}\\ c_{x_7}{x}_{11}-s_{x_7}{x}_{12}\\ \frac{s_{x_7}}{c_{x_8}}{x}_{11}+\frac{c_{x_7}}{c_{x_8}}{x}_{12}\\ \left(\frac{J_2-J_3}{J_1}\right)x_{11}{x}_{12}\\ \left(\frac{J_3-J_1}{J_2}\right)x_{10}{x}_{12}\\ \left(\frac{J_1-J_2}{J_3}\right)x_{10}{x}_{11}\end{array}\right],G\left(x\right)=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ -\frac{1}{m}\left(c_{x_7}{s}_{x_8}{c}_{x_9}+s_{x_7}{s}_{x_9}\right)& 0& 0& 0\\ -\frac{1}{m}\left(c_{x_7}{s}_{x_8}{s}_{x_9}-s_{x_7}{c}_{x_9}\right)& 0& 0& 0\\ -\frac{1}{m}{c}_{x_7}{c}_{x_8}& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& \frac{1}{J_1}& 0& 0\\ 0& 0& \frac{1}{J_2}& 0\\ 0& 0& 0& \frac{1}{J_3}\end{array}\right]$$

As stated in Theorem 3, the controllability indices $\{r_1,r_2,r_3,r_4\}$ of the system need to be found first to verify whether the system is state feedback linearizable or not. To find them, first $m_j,0\le j\le 4$ is computed based on the distributions ${\mathcal{G}}_l=\mathrm{span}\left\{a{d}_f^j{\mathfrak{g}}_i:1\le i\le 4,0\le j\le l\right\}$ for $l=0,...,10$. Therefore, the calculated controllability indices are $\{5,2,2,2\}$. These need to be checked against the conditions of Theorem 3. ${\mathcal{G}}_3$ is found to not be involutive and $dim{\mathcal{G}}_4=11\ne n$. Hence, the system is not state feedback linearizable as conditions $\left(ii\right)$ and $\left(iii\right)$ are not satisfied. It can also be noted that ${\sum }_{i=1}^4{r}_i=11\ne n$.

From the above, the system is not locally state feedback linearizable, meaning it cannot be transformed into a linear controllable system written in Brunovsky controller form. The system states and inputs are thus reformulated by augmenting the state vector with two additional states, which are the thrust $x_{13}=\overline{u}$ and its rate $x_{14}=\dot{\overline{u}}$, and replacing the thrust by $\ddot{\overline{u}}$ in the input vector. The same approach was successfully validated in [24,25,26]. Furthermore, the system is extended by including the integral states $\zeta$ defined by ${\dot{\zeta }}^p=p^n$, ${\dot{\zeta }}^{\psi }=\psi$, as shown below:

$$\begin{array}{ccc}\hfill x& =& {\left[{\left(p_{{}_{3\times 1}}^n\right)}^T,{\left(v_{{}_{3\times 1}}^n\right)}^T,{\left({\eta }_{3\times 1}\right)}^T,{\left({\omega }_{{}_{3\times 1}}^b\right)}^T,\overline{u},\dot{\overline{u}},{\left({\zeta }_{{}_{3\times 1}}^{p^n}\right)}^T,{\zeta }^{\psi }\right]}^T\in {\mathbb{R}}^{18}\hfill \\ \hfill u& =& {\left[\ddot{\overline{u}},{\left({\tau }_{{}_{3\times 1}}^b\right)}^T\right]}^T\in {\mathbb{R}}^4\hfill \end{array}$$

(21)

Based on the extended system’s vectors, the presented state space control-affine form in (21) can be written as follows

$$\dot{x}=\overline{f}\left(x\right)+\overline{G}\left(x\right)u$$

(22)

where

$$\overline{f}\left(x\right)=\left[\begin{array}{c}{x}_4\\ x_5\\ x_6\\ -\frac{1}{m}\left(c_{x_7}{s}_{x_8}{c}_{x_9}+s_{x_7}{s}_{x_9}\right)x_{13}\\ -\frac{1}{m}\left(c_{x_7}{s}_{x_8}{s}_{x_9}-s_{x_7}{c}_{x_9}\right)x_{13}\\ g-\frac{1}{m}{c}_{x_7}{c}_{x_8}{x}_{13}\\ x_{10}+s_{x_7}{t}_{x_8}{x}_{11}+c_{x_7}{t}_{x_8}{x}_{12}\\ c_{x_7}{x}_{11}-s_{x_7}{x}_{12}\\ \frac{s_{x_7}}{c_{x_8}}{x}_{11}+\frac{c_{x_7}}{c_{x_8}}{x}_{12}\\ \left(\frac{J_2-J_3}{J_1}\right)x_{11}{x}_{12}\\ \left(\frac{J_3-J_1}{J_2}\right)x_{10}{x}_{12}\\ \left(\frac{J_1-J_2}{J_3}\right)x_{10}{x}_{11}\\ x_{14}\\ 0\\ x_1\\ x_2\\ x_3\\ x_9\end{array}\right],\overline{G}\left(x\right)=\left[\begin{array}{c}{\mathbf{0}}_{{}_{9\times 4}}\\ \begin{array}{cccc}0& \frac{1}{J_1}& 0& 0\\ 0& 0& \frac{1}{J_2}& 0\\ 0& 0& 0& \frac{1}{J_3}\\ 0& 0& 0& 0\\ 1& 0& 0& 0\end{array}\\ {\mathbf{0}}_{{}_{4\times 4}}\end{array}\right]$$

The controllability indices of the extended system are $\{5,5,5,3\}$, where ${\sum }_{i=1}^4{r}_i=18=n$. With $r_1=5$, the distribution ${\mathcal{G}}_3$ is found to be involutive and $dim{\mathcal{G}}_4=18=n$, meaning all conditions of Theorem 3 are satisfied. Therefore, the system is state feedback linearizable, meaning it is locally transformable into a linear controllable system in Brunovsky controller form about the origin, as shown below in (23).

The existence of four smooth functions is guaranteed, representing the linearizing position and yaw outputs $\{{\phi }_1\left(x\right)=x_1,{\phi }_2\left(x\right)=x_2,{\phi }_3\left(x\right)=x_3,{\phi }_4\left(x\right)=x_9\}$, such that matrix $D\left(x\right)$ in (15) is nonsingular about the origin. The resulting linear system is written as

$$\begin{array}{ccc}\hfill \dot{\xi }& =& A_c\xi +B_{c}v,\xi \in {\mathbb{R}}^{18},v\in {\mathbb{R}}^4\hfill \\ \hfill z& =& C_c\xi ,z\in {\mathbb{R}}^4\hfill \end{array}$$

(23)

where

$$\begin{array}{ccc}\hfill \xi & =& {\left[{\phi }_1,\cdots ,L_f^{r_1-1}{\phi }_1,\cdots ,{\phi }_m,\cdots ,L_f^{r_m-1}{\phi }_m\right]}^T\hfill \\ & =& {\left[x_{15},x_1,x_4,{\dot{x}}_4,{\ddot{x}}_4,x_{16},x_2,x_5,{\dot{x}}_5,{\ddot{x}}_5,x_{17},x_3,x_6,{\dot{x}}_6,{\ddot{x}}_6,x_{18},x_9,{\dot{x}}_9\right]}^T\hfill \\ \\ \hfill \dot{\xi }& =& {\left[{\xi }_2,{\xi }_3,{\xi }_4,{\xi }_5,v_1,{\xi }_7,{\xi }_8,{\xi }_9,{\xi }_{10},v_2,{\xi }_{12},{\xi }_{13},{\xi }_{14},{\xi }_{15},v_3,{\xi }_{17},{\xi }_{18},v_4\right]}^T\hfill \end{array}$$

To determine the domain of the transformation, the determinant of the matrix $D\left(x\right)$ is calculated to be

$$detD\left(x\right)=-\frac{{\overline{u}}^{2}cos\left(\varphi \right)}{m^3{J}_1{J}_2{J}_{3}cos\left(\theta \right)}$$

Therefore, the domain for a nonsingular solution is $\{\overline{u}\ne 0,-\frac{\pi }{2}<\varphi <\frac{\pi }{2},-\frac{\pi }{2}<\theta <\frac{\pi }{2}\}$. As discussed earlier in Section 3.1, these constraints will be included within the NMPH optimization problem in (4d).

The actual control law is obtained using (16), giving

$$\begin{array}{cc}\hfill \ddot{\overline{u}}& =m{c}_{x_9}{s}_{x_7}{v}_2-m{s}_{x_7}{s}_{x_9}{v}_1-m{c}_{x_7}\left(s_{x_8}{c}_{x_9}{v}_1+s_{x_8}{s}_{x_9}{v}_2+c_{x_8}{v}_3\right)\hfill \\ \hfill & +x_{13}\left(x_{10}^2+x_{11}^2\right)\hfill \\ \hfill {\tau }^{b1}& =\frac{m{J}_1}{x_{13}}{s}_{x_7}\left(s_{x_8}{c}_{x_9}{v}_1+s_{x_8}{s}_{x_9}{v}_2+c_{x_8}{v}_3\right)+\frac{m{J}_1}{x_{13}}{c}_{x_7}\left(c_{x_9}{v}_2-s_{x_9}{v}_1\right)-\left(J_2-J_3\right)x_{12}{x}_{11}\hfill \\ \hfill & +\frac{J_1}{x_{13}}\left(x_{11}{x}_{12}{x}_{13}-2x_{10}{x}_{14}\right)\hfill \\ \hfill {\tau }^{b2}& =-\frac{m{J}_2}{x_{13}}{c}_{x_8}\left(c_{x_9}{v}_1+s_{x_9}{v}_2\right)+\frac{m{J}_2}{x_{13}}{s}_{x_8}{v}_3-\frac{J_2}{x_{13}}\left(x_{10}{x}_{12}{x}_{13}+2x_{11}{x}_{14}\right)\hfill \\ \hfill & +\left(J_1-J_3\right)x_{12}{x}_{10}\hfill \\ \hfill {\tau }^{b3}& =-\frac{1}{c_{x_7}{c}_{x_8}{x}_{13}}[2J_3\left(2x_{12}{x}_{11}{c}_{x_7}^2+s_{x_7}{x}_{11}^2-x_{12}^2{c}_{x_7}-x_{12}{x}_{11}\right)x_{13}{s}_{x_8}\hfill \\ \hfill & +\left(\left(J_1-J_2+J_3\right)x_{10}{x}_{11}{x}_{13}{c}_{x_7}+J_3{s}_{x_7}\left(m{s}_{x_8}{v}_3-2x_{10}{x}_{12}{x}_{13}-2x_{11}{x}_{14}\right)\right)c_{x_8}\hfill \\ \hfill & -J_3\left(m{s}_{x_7}\left(c_{x_9}{v}_1+s_{x_9}{v}_2\right)+x_{13}{v}_4\right)c_{x_8}^2]\hfill \end{array}$$

(24)

where $v_k$ are feedback inputs defined as

$$v_j=\sum _{i=5j-4}^{5j}{k}_i{e}_{{\xi }_i},j=1,2,3,v_4=\sum _{i=16}^{18}{k}_i{e}_{{\xi }_i}$$

(25)

where the error $e_{{\xi }_i}$ is defined as the difference between the desired and the actual feedback linearized system state $e_{{\xi }_i}={\xi }_i^d-{\xi }_{i}i=1,...,n$. The errors can be interpreted as the differences between the desired outputs ${\left[p_d^n,{\psi }_d\right]}^T$ with their rates and integrals, and the corresponding actual system outputs ${\left[p^n,\psi \right]}^T$ with their rates and integrals.

3.3. Trajectory Generation Using NMPH with Feedback Linearization

The optimization problem of NMPH uses the system dynamics (18) and state feedback linearization control law (24) to solve for an optimal reference trajectory for the resulting closed-loop system. The OTP, which is written in the continuous-time domain and presented in (7), is solved using an efficient direct multiple shooting technique [27]. The solver discretizes the system dynamics, control law, and state and input constraints over the prediction horizon into $k=n,\dots ,n+N$ at each time instant $t_n$, as discussed in (4). An overview of the process from the optimization problem formulation to the trajectory generation is given in Figure 5.

The optimization problem operates on the dynamics of a closed-loop system which may not be convex. Therefore, the optimization problem is solved iteratively using a Sequential Quadratic Programming (SQP [28]) approach of splitting the problem into a sequence of subproblems, each of which solves for a quadratic objective function subject to linearized constraints about their operating point using the qpOASES solver [29].

To ensure local convergence of the SQP, the quadratic function of the subproblem has to be bounded within a feasible region of the optimization problem sets. Starting from an initial condition $x_0$, the optimization variables should be sufficiently close to the terminal condition $x_{ss}$; then, the sequence $x_k$ generated by the NMPH converges to the terminal condition at a quadratic rate.

The purpose of using the feedback linearization-based control law within the NMPH is to reduce the nonconvexity of the optimization problem. Assuming a perfect system model, the closed-loop system contains the linear Brunovsky system form as shown in (23), leading to an optimization problem in which feasibility and stability of the optimized solution and the computational power required to solve the optimization problem are notably improved relative to working with a nonlinear open-loop system as in standard NMPC.

4. Simulation Results

In this section, several simulations are presented to validate the proposed NMPH approach to generating optimal trajectories for a quadrotor vehicle.

The Robot Operating System (ROS) [30] is the base environment used to implement our algorithm. It is a platform that integrates different software packages or frameworks by handling communication between them and the host hardware. The ACADO Toolkit [18] is used for dynamic optimization in this work. It allows users to write their code within a self-contained C++ environment and generates the nonlinear solver that can solve the optimization problems in real time. The compiled codes run within ROS to communicate with either a simulation model or the actual hardware [27]. For testing and validation of the proposed approaches on a quadrotor vehicle, we used the AirSim simulator [31], which is an open-source software that includes a physics engine and provides photo realistic images.

The NMPH optimization problem (7) was written in C++ code using ACADO and compiled into a highly efficient C code that is able to solve the optimization problem online. The AirSim simulator, ACADO optimization solver, and ROS environment run on a system with an Intel Core i7-10750H CPU @ 2.60–5.00 GHz equipped with the Nvidia GeForce RTX 2080 Super (Max-Q) GPU. The prediction horizon of the optimization problem was set to $N=40$ with a sampling period of 0.2 s, which was found to be sufficient for the purposes of trajectory generation. The cost function weights $W_x$, $W_z$, and $W_N$ were adjusted heuristically to ensure a balanced trajectory generation performance towards the terminal setpoint.

The initial state of the quadrotor is acquired from the AirSim simulator and sent to the NMPH solver. The solution of the optimization problem is sent back to AirSim as a reference trajectory for the vehicle. The 3D visualization tool for ROS (rviz) is used to monitor and visualize the simulation process. Figure 6 shows the network architecture of the nodes and topics employed for running the simulation.

In the following sections, various simulation scenarios are provided to verify the features and evaluate the performance of the proposed NMPH approach. Note the NED frame representation used within NMPH is converted to ENU (East, North, and Up) representation used by AirSim, and so the simulation results will be presented using the ENU convention as well.

4.1. Predicted Output and Estimated Reference Trajectories

The purpose of this simulation is to show the convergence of the estimated reference ${\widehat{z}}_k$ and predicted output $z_k$ trajectories toward the setpoint stabilization $x_{ss}$ while minimizing the difference between them. The quadrotor is assumed to start at position $p^n={[0,0,0.2]}^T\mathrm{m}$ and NMPH is used to generate a trajectory to the terminal setpoint $p_d={[6,-3,5]}^T\mathrm{m}$, as shown in Figure 7. The plots depict a sequence of the optimal predicted trajectory $z_k$, $k=0,...,N$ and the estimated reference trajectory ${\widehat{z}}_k$, $k=0,...,N-1$ produced by the NMPH. It is important to mention that the convergence of the estimated reference trajectory to the terminal point ensures that the closed-loop system is steered to the desired endpoint.

4.2. Trajectory Generation and Initial Conditions

In this simulation, the generated trajectory is investigated for different initial conditions. The initial conditions being tested are related to the quadrotor’s kinematics, where the vehicle is commanded to move in a straight path between ${[4,2,0]}^T$ and ${[8,8,8]}^T$ while changing its speed $\left|v\right|$ linearly from 0 to 1.5 m/s, as shown in Figure 8. Note the objective is not to track generated trajectories, but just to observe the behaviour of OTP solutions towards the stabilization setpoint $p_d={[5,10,5]}^T$.

The solution of the optimization problem for eight different trajectories are plotted in Figure 8 to show the effect of the initial conditions on them. The resulting solution of each one shows a trajectory which convergences smoothly to the stabilization setpoint while taking into consideration the initial position and velocity of the system. Commanding the quadrotor to track generated trajectories which account for its initial conditions will reduce jerky flight motions and therefore reduce flight power consumption, which is especially important for exploration missions.

Using the setup described in Section 4, our NMPH achieves a 250 Hz generation rate, meaning a reference trajectory is generated every $4\mathrm{ms}$. If running on lower-powered hardware, the computational power can be minimized by reducing the rate of trajectory generation, which still provides a smooth reference trajectory for the vehicle.

4.3. Trajectory Tracking

In this simulation, the quadrotor’s trajectory tracking and static obstacle avoidance performance are examined. First, the vehicle is commanded to track a continuously updated trajectory generated on the fly by the NMPH algorithm while avoiding static obstacles, as shown in Figure 9. Each static obstacle is considered to be a sphere of $1\mathrm{m}$ in diameter. A radial allowance of $1\mathrm{m}$ is considered for the obstacle to avoid crashing into it. Hence, the constraint of each obstacle represents a sphere with a diameter of $3\mathrm{m}$, which makes the safety distance $ϵ=1.5$. The smooth tracking performance while avoiding the obstacles can be seen in Figure 9, which shows the importance of using the NMPH in regenerating the trajectory while tracking it.

In the second study, the regeneration process of the predicted trajectory is limited to one regeneration in order to examine its effect on the tracking performance while avoiding the obstacles. The simulation result is depicted and explained in Figure 10.

The continuous regeneration of the reference trajectory provides optimal flight paths in real time based on the system’s state. This ability also enables handling dynamic obstacles, as shown next in Section 4.4.

4.4. Dynamic Obstacle Avoidance

Figure 11a–c depict the online regeneration of the predicted optimal trajectory when the obstacle moves in the direction of y-axis. The optimized trajectory starts at the hover position $p={[0,0,1.5]}^T\mathrm{m}$ and converges to the terminal setpoint $p_d={[4,0,0.5]}^T\mathrm{m}$ while the predicted reference trajectory is being continuously regenerated. An obstacle placed at the initial position $(3,0,0.5)\mathrm{m}$ with total diameter of $2\mathrm{m}$ moves at a velocity of $0.5\mathrm{m}/\mathrm{s}$ in the y-axis direction.

Selected predictions over 2 $\mathrm{s}$ are shown in Figure 11d, which illustrates the smooth regeneration of the trajectories while avoiding the dynamic obstacle. It is important to note that about 500 trajectories are generated in $2\mathrm{s}$.

5. Conclusions

This paper proposed a novel reference trajectory generation method for a nonlinear closed-loop system (in our case, a piloted quadrotor drone) based on the NMPC approach. The proposed formulation, called NMPH, applies a feedback linearization control law to the nonlinear plant model, resulting in a closed-loop dynamics model with decreased nonconvexity used by the online optimization problem to generate feasible and optimal reference trajectories for the actual closed-loop system. The feedback linearization design includes integral states to compensate for modeling uncertainties and external disturbances in the system. The proposed NMPH algorithm supports both static and dynamic obstacles, enabling trajectory generation in continuously changing environments.

The NMPH was implemented on a simulated quadrotor drone and validated to generate 3D optimal reference trajectories in real time. Four different simulation scenarios were carried out to evaluate the performance of the proposed method. Convergence of the predicted and estimated trajectories, trajectory generation under different initial conditions, trajectory tracking performance, and the ability to navigate around static and dynamic obstacles were validated through simulation results.

Future work will include testing the NMPH methodology with alternative nonlinear control law designs such as backstepping, using a more detailed dynamics model of the vehicle, and implementing and validating the proposed method onboard hardware drones, which has become feasible thanks to GPU-equipped single-board computers such as NVIDIA’s Jetson Xavier NX.