Mutli-Robot Cooperative Object Transportation with Guaranteed Safety and Convergence in Planar Obstacle Cluttered Workspaces via Configuration Space Decomposition
Abstract
:1. Introduction
1.1. Related Work
1.2. Contribution
- Completeness: We innovatively introduce appropriately designed under- and over-approximations of the free configuration space in order to guide the configuration space’s exploration by selecting the cells that need further subdivision, thus establishing the completeness of our approach (i.e., if there exists a feasible path to go to the goal configuration, our algorithm will discover it, otherwise it halts when the problem cannot be solved when the initial and the goal configurations belong to disconnected parts of the workspace).
- Safety and Convergence: We combine methodologies based on Reference Governors and Prescribed Performance Control with our recently proposed harmonic maps approach [37] in order to design a distributed control law that implements specified cell transitions with guaranteed invariance and convergence properties.
- Lean Communication: Contrary to majority of the related literature, the proposed low-level control law does not require continuous information exchange between the robots (e.g., via a local network), thus rendering the expected latency negligible, since it relies exclusively on measurements of the object’s current configuration and the state of the corresponding robot in order to compute the respective control inputs. Regarding potential delays in the local measurements since our approach is a feedback control approach certain levels of robustness against measurement delays are expected.
1.3. Outline
2. Preliminaries
3. Problem Formulation
3.1. Mobile Manipulator Kinematics
3.2. Mobile Manipulator Dynamics
4. Control Design
- (a)
- a high-level controller that given an initial configuration and a final configuration configuration, can compute a sequence of reachable intermediate goals for the robotic system, if a solution to the above problem exists, or determine its infeasibility otherwise (completeness), and
- (b)
- a low-level controller which utilizes appropriate workspace transformations in order to drive the object and the mobile manipulators from each goal to the next while avoiding collisions with the workspace boundary (safety and convergence).
4.1. Configuration Space Decomposition
- 1.
- If there exists a path of adjacent under-approximation cells for a given cover containing and , then a solution to our problem exists.
- 2.
- If there exists a path of adjacent over-approximation cells for a given cover containing and , then whether our problem has a solution is unknown and further expansion of is in order.
- 3.
- If there is no path of adjacent over-approximation cells for a given cover containing and , then our problem is infeasible.
| Algorithm 1 Configuration space exploration algorithm. |
functionConnectConfigs(, ) loop FindEnclosingCells(, ) FindEnclosingCells(, ) if is Nil or is Nil then return Nil end if ConnectUACells(, ) if is Nil then ConnectOACells(, ) if is empty then return Nil else Refine( , , , ) end if else return end if end loop end function |
| Algorithm 2 Heuristic choosing next simple slice for subdivision. |
functionRefine(, , , ) if then return Subdivide(, ) else if then else for all in do end for end if for all in do for all in do if then end if end for end for if then return Refine(, , , ) else return SubdivideLongest(, , ) end if end if end function |
4.2. Distributed Control Law
- ensure invariance of the current cell, i.e., , and , , until the transition is complete, and
- ensure converge to the system’s states to the corresponding goals sets , and .
4.2.1. Object’s Position
4.2.2. Object’s Orientation
4.2.3. Manipulators
5. Stability Analysis
6. Simulation Results
7. Conclusions and Future Directions
Author Contributions
Funding
Conflicts of Interest
References
- Gerkey, B.P.; Matarić, M.J. Pusher-watcher: An approach to fault-tolerant tightly-coupled robot coordination. In Proceedings of the IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002; Volume 1, pp. 464–469. [Google Scholar]
- Yamada, S.; Saito, J. Adaptive action selection without explicit communication for multi-robot box-pushing. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Phoenix, AZ, USA, 15–19 March 1999; Volume 3, pp. 1444–1449. [Google Scholar]
- Munoz Melendez, A.; Drogoul, A. Analyzing Multi-Robot Box-Pushing. Technical Report; Universidad de Colima: Colima, Mexico, 2004. [Google Scholar]
- Wang, Z.D.; Kumar, V. Object closure and manipulation by multiple cooperating mobile robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002; Volume 1, pp. 394–399. [Google Scholar]
- Fink, J.; Michael, N.; Kumar, V. Composition of vector fields for multi-robot manipulation via caging. In Proceedings of the International Conference on Robotics Science and Systems, Orlando, FL, USA, 7–10 July 2008; Volume 3, pp. 25–32. [Google Scholar]
- Eoh, G.; Lee, S.; Lee, T.H.; Lee, B. Distributed Object Transportation Using Virtual Object. J. Ind. Intell. Inf. 2014, 2, 20–25. [Google Scholar] [CrossRef]
- Dai, Y.; Kim, Y.; Wee, S.; Lee, D.; Lee, S. Symmetric caging formation for convex polygonal object transportation by multiple mobile robots based on fuzzy sliding mode control. ISA Trans. 2016, 60, 321–332. [Google Scholar] [CrossRef] [PubMed]
- Wan, W.; Shi, B.; Wang, Z.; Fukui, R. Multirobot Object Transport via Robust Caging. IEEE Trans. Syst. Man, Cybern. Syst. 2020, 50, 270–280. [Google Scholar] [CrossRef]
- Ferrante, E.; Brambilla, M.; Birattari, M.; Dorigo, M. Socially-mediated negotiation for obstacle avoidance in collective transport. In Distributed Autonomous Robotic Systems; Springer Tracts in Advanced Robotics; Springer: Berlin/Heidelberg, Germany, 2012; Volume 83, pp. 571–583. [Google Scholar]
- Habibi, G.; Kingston, Z.; Xie, W.; Jellins, M.; McLurkin, J. Distributed centroid estimation and motion controllers for collective transport by multi-robot systems. In Proceedings of the IEEE International Conference on Robotics and Automation, Seattle, WA, USA, 26–30 May 2015; pp. 1282–1288. [Google Scholar]
- Machado, T.; Malheiro, T.; Monteiro, S.; Erlhagen, W.; Bicho, E. Multi-constrained joint transportation tasks by teams of autonomous mobile robots using a dynamical systems approach. In Proceedings of the IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 16–21 May 2016; pp. 3111–3117. [Google Scholar]
- Wang, Z.; Schwager, M. Kinematic multi-robot manipulation with no communication using force feedback. In Proceedings of the PIEEE International Conference on Robotics and Automation, Stockholm, Sweden, 16–21 May 2016; pp. 427–432. [Google Scholar]
- Wang, Z.; Yang, G.; Su, X.; Schwager, M. OuijaBots: Omnidirectional Robots for Cooperative Object Transport with Rotation Control Using No Communication. In Distributed Autonomous Robotic Systems; Springer Proceedings in Advanced Robotics; Springer: Cham, Switzerland, 2018; Volume 6, pp. 117–131. [Google Scholar]
- Hekmatfar, T.; Masehian, E.; Mousavi, S.J. Cooperative object transportation by multiple mobile manipulators through a hierarchical planning architecture. In Proceedings of the 2014 2nd RSI/ISM International Conference on Robotics and Mechatronics, ICRoM 2014, Tehran, Iran, 15–17 October 2014; pp. 503–508. [Google Scholar]
- Wang, Y.; De Silva, C.W. Multi-robot box-pushing: Single-agent Q-learning vs. team Q-learning. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Beijing, China, 9–13 October 2006; pp. 3694–3699. [Google Scholar]
- Goldman, C.V.; Zilberstein, S. Decentralized control of cooperative systems: Categorization and complexity analysis. J. Artif. Intell. Res. 2004, 22, 143–174. [Google Scholar] [CrossRef]
- Haddadin, S.; De Luca, A.; Albu-Schäffer, A. Robot collisions: A survey on detection, isolation, and identification. IEEE Trans. Robot. 2017, 33, 1292–1312. [Google Scholar] [CrossRef] [Green Version]
- Haddadin, S.; Khoury, A.; Rokahr, T.; Parusel, S.; Burgkart, R.; Bicchi, A.; Albu-Schäffer, A. On making robots understand safety: Embedding injury knowledge into control. Int. J. Robot. Res. 2012, 31, 1578–1602. [Google Scholar] [CrossRef]
- Uchiyama, M.; Dauchez, P. A symmetric hybrid position/force control scheme for the coordination of two robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Philadelphia, PA, USA, 24–29 April 1988; pp. 350–356. [Google Scholar]
- Khatib, O. Object Manipulation in a Multi-effector Robot System. In Proceedings of the 4th International Symposium on Robotics Research; MIT Press: Cambridge, MA, USA, 1988; Volume 4, pp. 137–144. [Google Scholar]
- Tanner, H.; Loizou, S.; Kyriakopoulos, K. Nonholonomic navigation and control of cooperating mobile manipulators. IEEE Trans. Robot. Autom. 2003, 19, 53–64. [Google Scholar] [CrossRef]
- Erhart, S.; Hirche, S. Model and Analysis of the Interaction Dynamics in Cooperative Manipulation Tasks. IEEE Trans. Robot. 2016, 32, 672–683. [Google Scholar] [CrossRef]
- Khatib, O.; Yokoi, K.; Chang, K.; Ruspini, D.; Holmberg, R.; Casal, A. Vehicle/arm coordination and multiple mobile manipulator decentralized cooperation. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Osaka, Japan, 4–8 November 1996; Volume 2, pp. 546–553. [Google Scholar]
- Verginis, C.K.; Mastellaro, M.; Dimarogonas, D.V. Robust cooperative manipulation without force/torque measurements: Control design and experiments. IEEE Trans. Control Syst. Technol. 2020, 28, 713–729. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zou, M.; Xiao, H.; Wen, J.; Wang, Y. Cooperative-manipulation scheme of routh-hurwitz type for simultaneous repetitive motion planning of two-manipulator robotic systems. In Proceedings of the 28th Chinese Control and Decision Conference, CCDC 2016, Yinchuan, China, 28–30 May 2016; pp. 4409–4414. [Google Scholar]
- Petitti, A.; Franchi, A.; Di Paola, D.; Rizzo, A. Decentralized motion control for cooperative manipulation with a team of networked mobile manipulators. In Proceedings of the IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 16–21 May 2016; pp. 441–446. [Google Scholar]
- Noohi, E.; Zefran, M. Modeling the interaction force during a haptically-coupled cooperative manipulation. In Proceedings of the 25th IEEE International Symposium on Robot and Human Interactive Communication, RO-MAN 2016, New York, NY, USA, 26–31 August 2016; pp. 119–124. [Google Scholar]
- Pajak, I. Real-Time Trajectory Generation Methods for Cooperating Mobile Manipulators Subject to State and Control Constraints. J. Intell. Robot. Syst. Theory Appl. 2019, 93, 649–668. [Google Scholar] [CrossRef]
- He, Y.; Wu, M.; Liu, S. An optimisation-based distributed cooperative control for multi-robot manipulation with obstacle avoidance. IFAC-PapersOnLine 2020, 53, 9859–9864. [Google Scholar] [CrossRef]
- Kosuge, K.; Oosumi, T. Decentralized control of multiple robots handling an object. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Osaka, Japan, 4–8 November 1996; Volume 1, pp. 318–323. [Google Scholar]
- Stilwell, D.J.; Bay, J.S. Toward the development of a material transport system using swarms of ant-like robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 2–6 May 1993; Volume 1, pp. 766–771. [Google Scholar]
- Gross, R.; Dorigo, M. Evolution of solitary and group transport behaviors for autonomous robots capable of self-assembling. Adapt. Behav. 2008, 16, 285–305. [Google Scholar]
- Chen, J.; Gauci, M.; Gross, R. A strategy for transporting tall objects with a swarm of miniature mobile robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 863–869. [Google Scholar]
- Chen, J.; Gauci, M.; Li, W.; Kolling, A.; Gross, R. Occlusion-Based Cooperative Transport with a Swarm of Miniature Mobile Robots. IEEE Trans. Robot. 2015, 31, 307–321. [Google Scholar] [CrossRef]
- Wang, Z.; Schwager, M. Force-Amplifying N-robot Transport System (Force-ANTS) for cooperative planar manipulation without communication. Int. J. Robot. Res. 2016, 35, 1564–1586. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Kyriakopoulos, K.J. Collaborative multi-robot transportation in obstacle-cluttered environments via implicit communication. Front. Robot. AI 2018, 5, 90. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vlantis, P.; Vrohidis, C.; Bechlioulis, C.P.; Kyriakopoulos, K.J. Robot Navigation in Complex Workspaces Using Harmonic Maps. In Proceedings of the IEEE International Conference on Robotics and Automation, Brisbane, QLD, Australia, 21–25 May 2018; pp. 1726–1731. [Google Scholar]
- Vlantis, P.; Vrohidis, C.; Bechlioulis, C.P.; Kyriakopoulos, K.J. Orientation-Aware Motion Planning in Complex Workspaces using Adaptive Harmonic Potential Fields. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 8592–8598. [Google Scholar] [CrossRef]
- Loizou, S.G. The navigation transformation: Point worlds, time abstractions and towards tuning-free navigation. In Proceedings of the 2011 19th Mediterranean Conference on Control & Automation (MED), Corfu, Greece, 20–23 June 2011; pp. 303–308. [Google Scholar]
- Loizou, S.G. The Navigation Transformation. IEEE Trans. Robot. 2017, 33, 1516–1523. [Google Scholar] [CrossRef]
- Arslan, O.; Koditschek, D.E. Smooth extensions of feedback motion planners via reference governors. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 4414–4421. [Google Scholar] [CrossRef]
- Krstic, M.; Kokotovic, P.V.; Kanellakopoulos, I. Nonlinear and Adaptive Control Design, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1995. [Google Scholar]




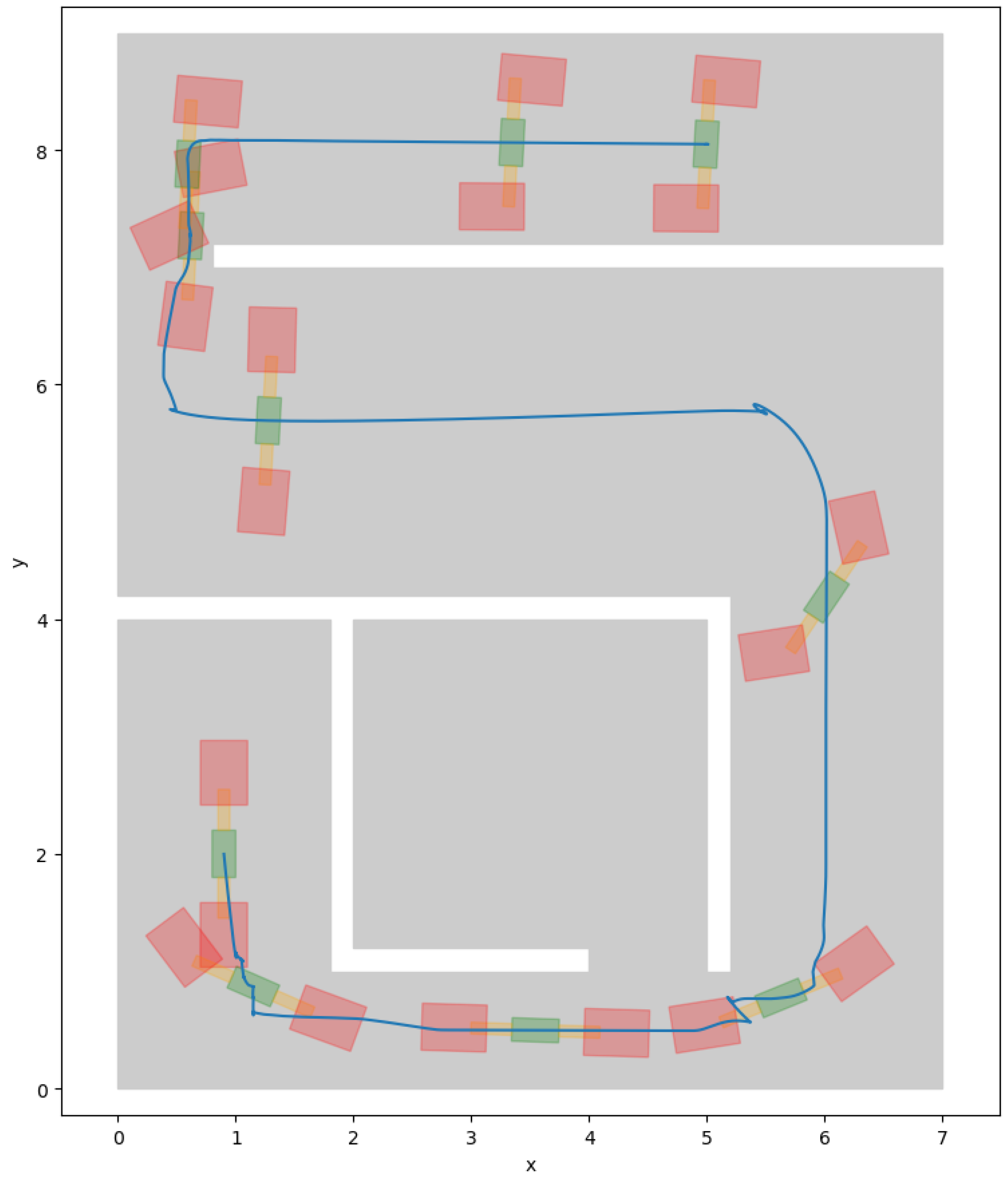


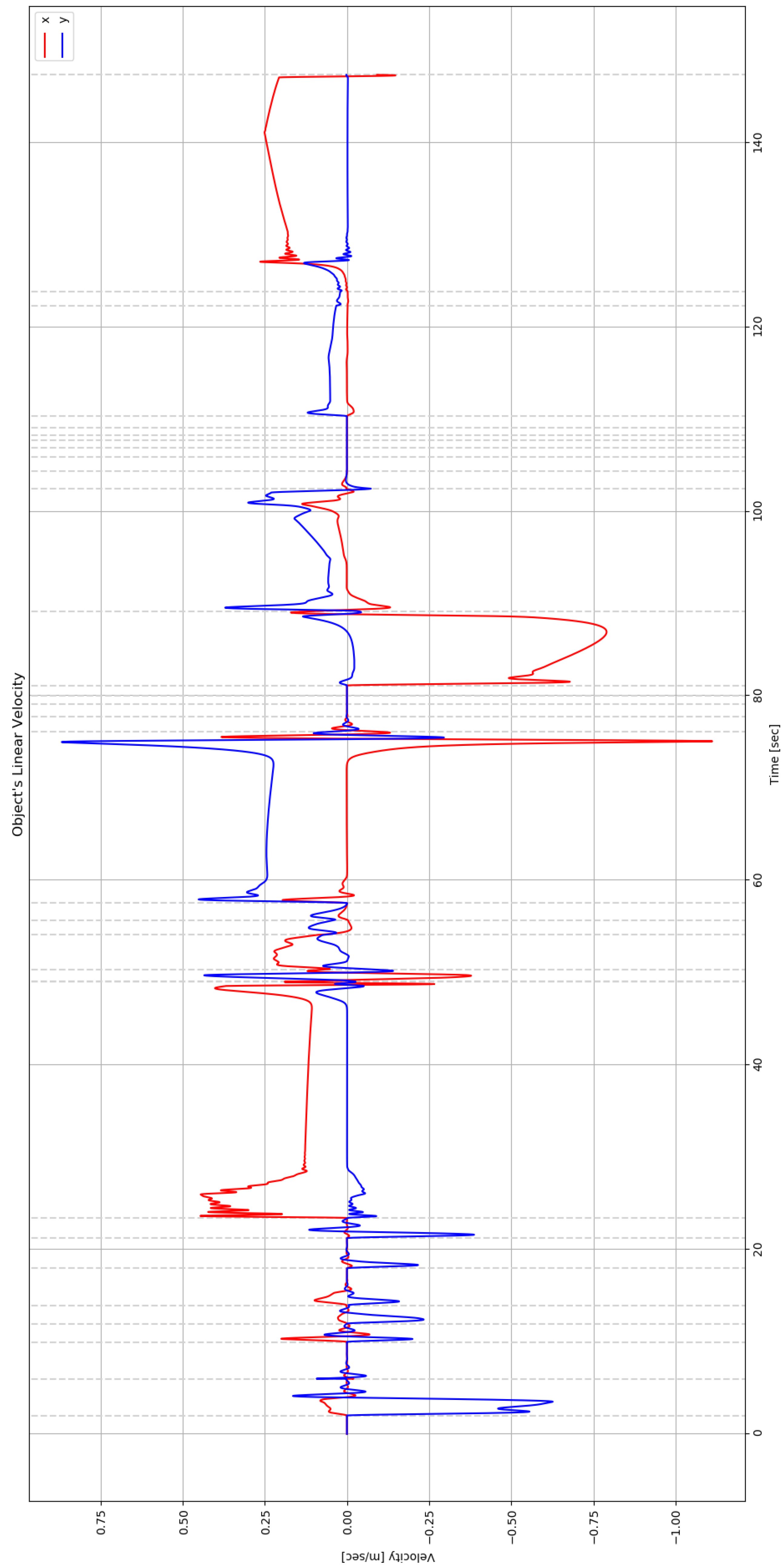
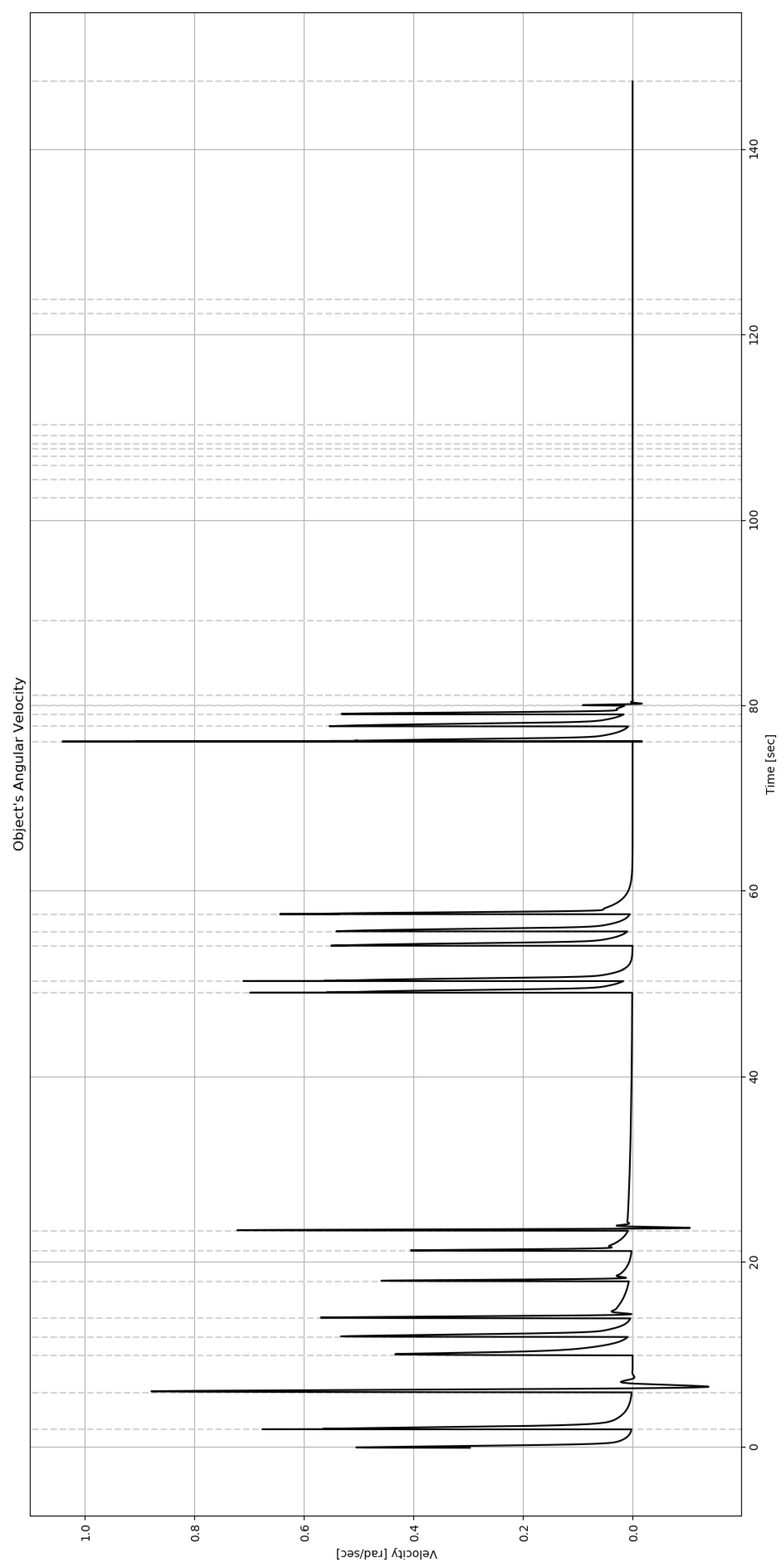

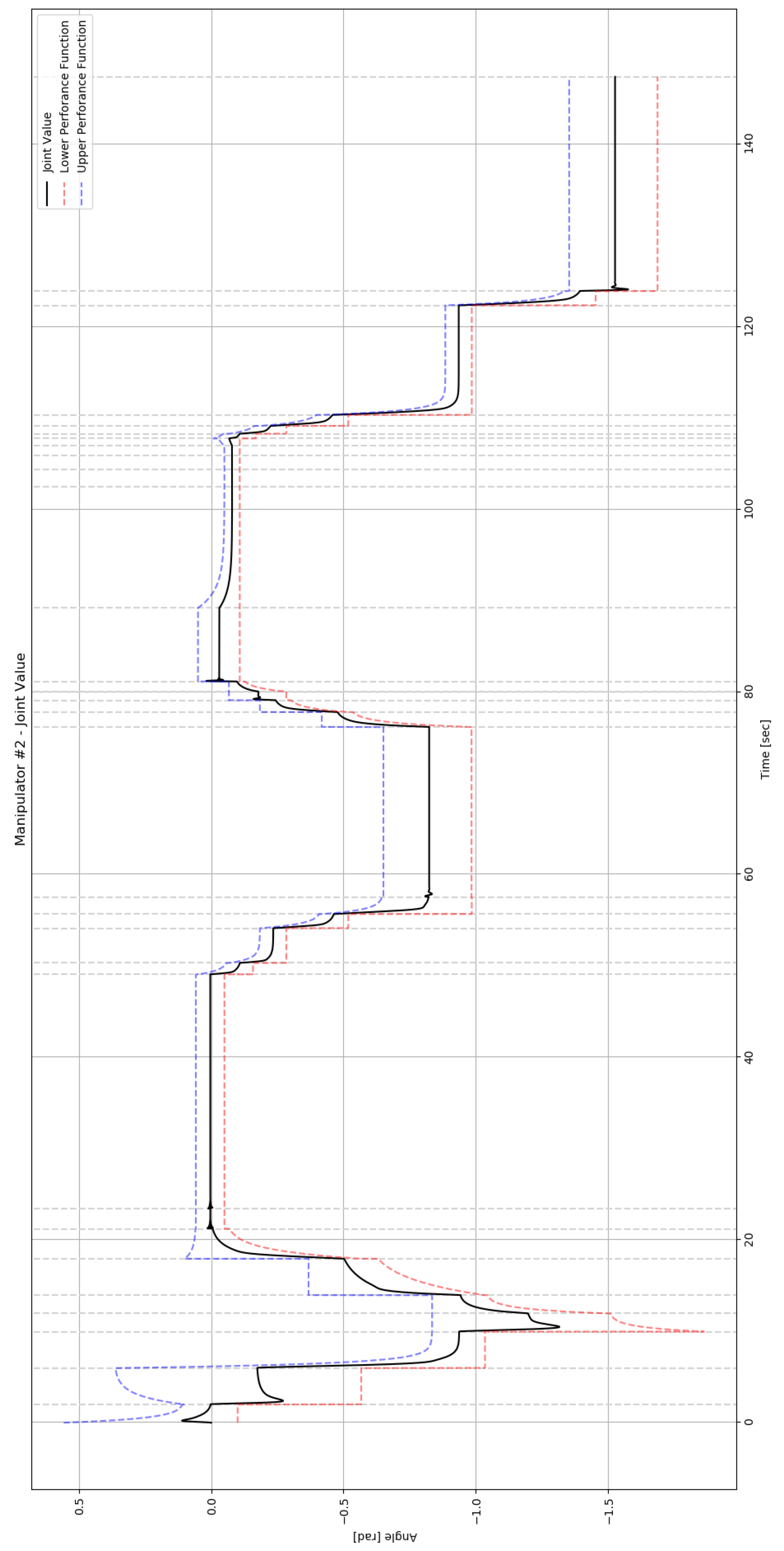
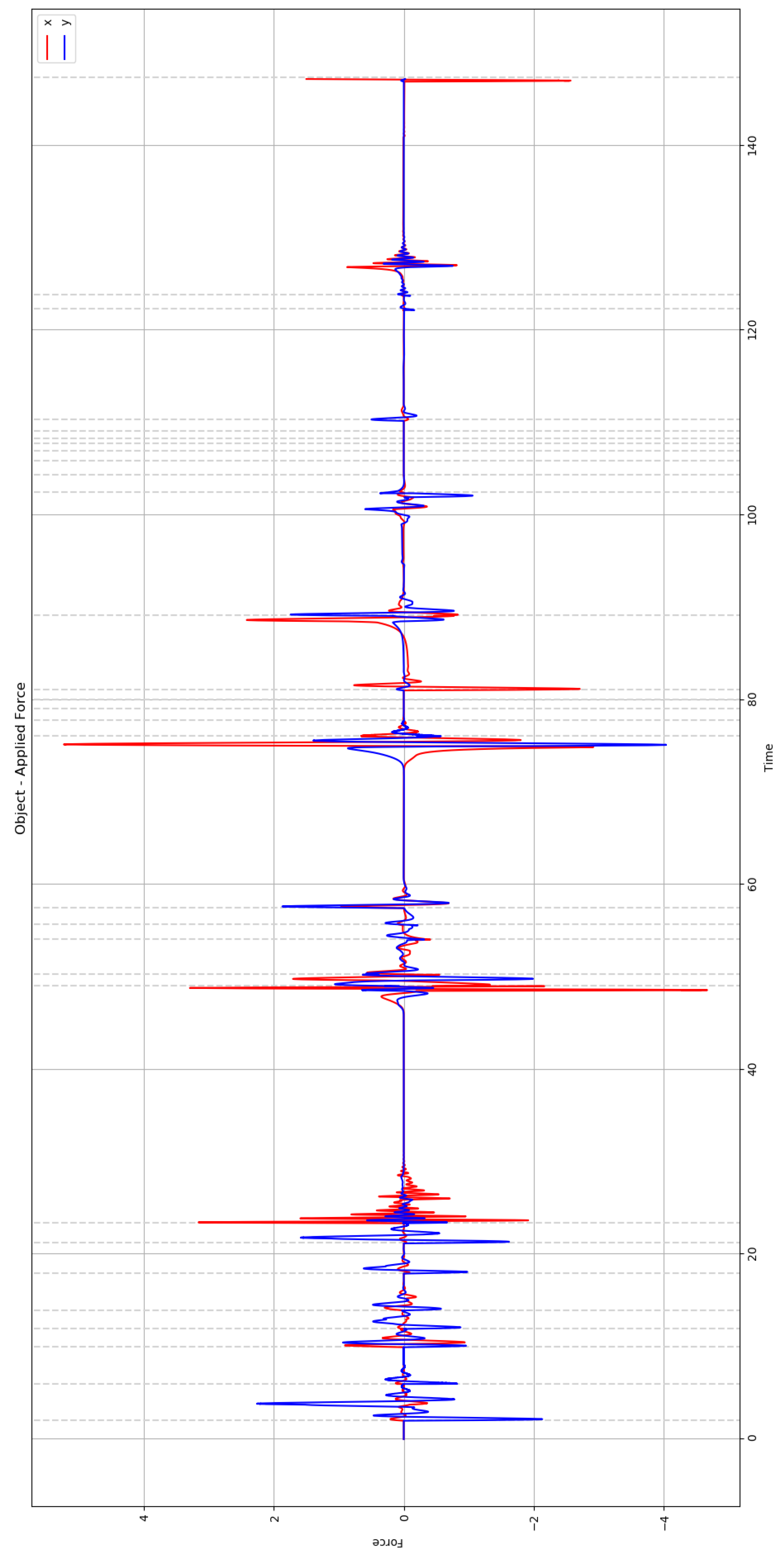
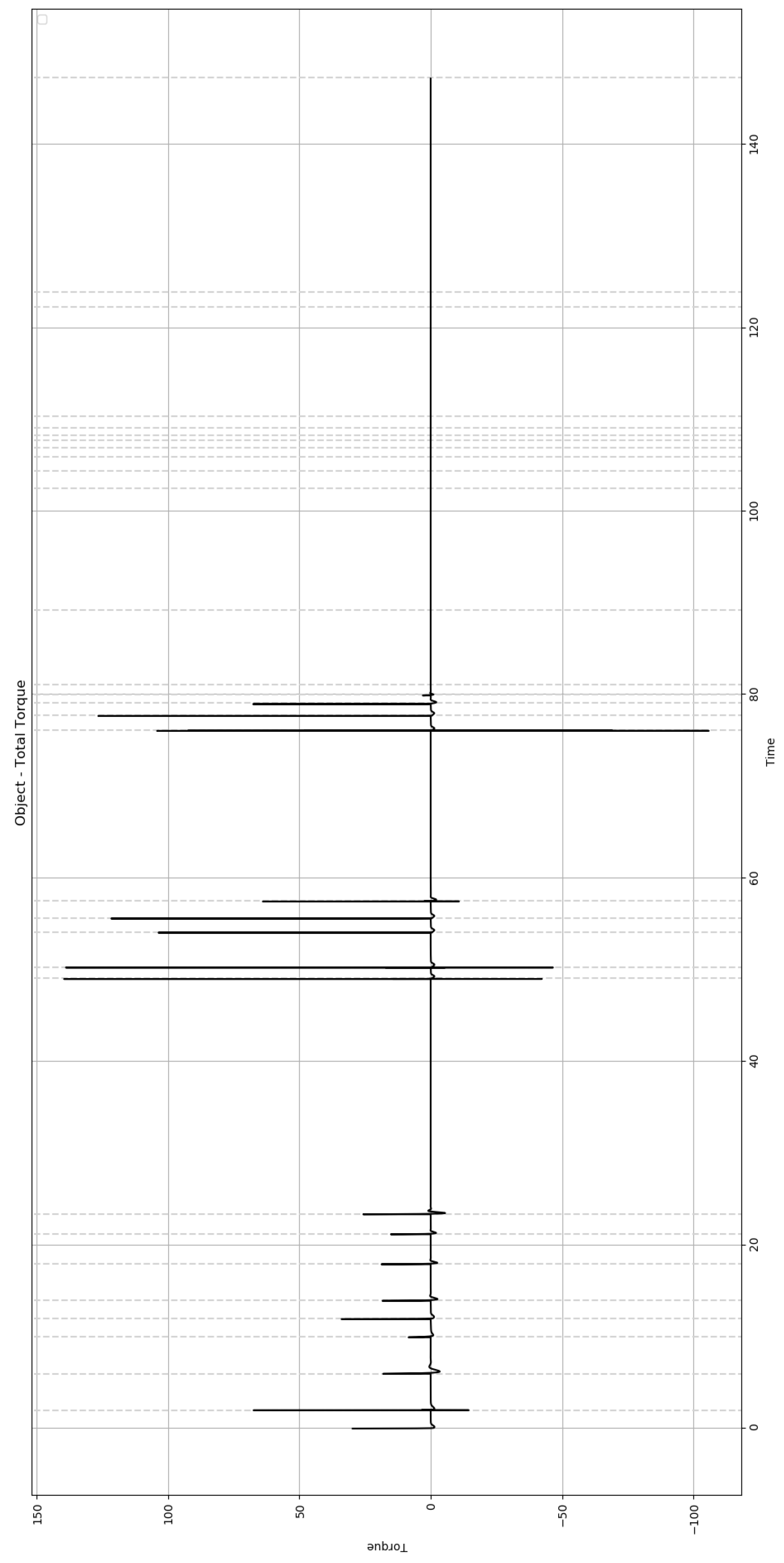
| Cell ID | ||||||
|---|---|---|---|---|---|---|
| 1 | 1.470 | 1.867 | −0.100 | 0.567 | −0.100 | 0.567 |
| 2 | 1.667 | 2.065 | −0.100 | 0.567 | −0.567 | 0.100 |
| 3 | 1.863 | 2.456 | −0.100 | 0.567 | −1.035 | 0.367 |
| 4 | 1.863 | 2.456 | −0.100 | 0.333 | −1.870 | −0.835 |
| 5 | 2.256 | 2.652 | −0.100 | 0.333 | −1.503 | −0.835 |
| 6 | 2.452 | 2.849 | −0.100 | 0.333 | −1.035 | −0.368 |
| 7 | 2.649 | 2.947 | −0.100 | 0.217 | −0.567 | 0.100 |
| 8 | 2.747 | 3.045 | −0.050 | 0.108 | −0.050 | 0.108 |
| 9 | 2.895 | 3.191 | −0.050 | 0.108 | −0.050 | 0.108 |
| 10 | 3.091 | 3.388 | −0.050 | 0.158 | −0.158 | 0.050 |
| 11 | 3.287 | 3.584 | 0.067 | 0.284 | −0.284 | −0.067 |
| 12 | 3.484 | 3.781 | 0.184 | 0.518 | −0.518 | −0.184 |
| 13 | 3.681 | 3.977 | 0.418 | 0.985 | −0.985 | −0.418 |
| 14 | 3.877 | 4.172 | 0.651 | 0.984 | −0.984 | −0.651 |
| 15 | 4.072 | 4.370 | 0.418 | 0.985 | −0.985 | −0.418 |
| 16 | 4.270 | 4.576 | 0.184 | 0.518 | −0.518 | −0.184 |
| 17 | 4.476 | 4.762 | 0.067 | 0.284 | −0.284 | −0.067 |
| 18 | 4.564 | 4.762 | 0.067 | 0.284 | −0.284 | −0.067 |
| 19 | 4.564 | 4.762 | −0.050 | 0.108 | −0.108 | 0.050 |
| 20 | 4.564 | 4.762 | −0.050 | 0.108 | −0.108 | 0.050 |
| 21 | 4.564 | 4.762 | −0.985 | 0.050 | −0.108 | 0.050 |
| 22 | 4.564 | 4.762 | −1.453 | −0.885 | −0.108 | 0.050 |
| 23 | 4.564 | 4.762 | −1.687 | −1.353 | −0.108 | 0.050 |
| 24 | 4.564 | 4.762 | −1.687 | −1.528 | −0.108 | −0.050 |
| 25 | 4.564 | 4.762 | −1.687 | −1.528 | −0.168 | −0.008 |
| 26 | 4.564 | 4.762 | −1.687 | −1.528 | −0.284 | −0.067 |
| 27 | 4.564 | 4.762 | −1.687 | −1.528 | −0.518 | −0.184 |
| 28 | 4.564 | 4.762 | −1.687 | −1.528 | −0.985 | −0.418 |
| 29 | 4.564 | 4.762 | −1.687 | −1.528 | −1.453 | −0.885 |
| 30 | 4.564 | 4.762 | −1.687 | −1.528 | −1.687 | −1.353 |
| Parameter | Value |
|---|---|
| 1 kg | |
| 1 kg m | |
| 50 | |
| 5 | |
| 5 | |
| 2 | |
| 1 | |
| 1 | |
| 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vlantis, P.; Bechlioulis, C.P.; Kyriakopoulos, K.J. Mutli-Robot Cooperative Object Transportation with Guaranteed Safety and Convergence in Planar Obstacle Cluttered Workspaces via Configuration Space Decomposition. Robotics 2022, 11, 148. https://doi.org/10.3390/robotics11060148
Vlantis P, Bechlioulis CP, Kyriakopoulos KJ. Mutli-Robot Cooperative Object Transportation with Guaranteed Safety and Convergence in Planar Obstacle Cluttered Workspaces via Configuration Space Decomposition. Robotics. 2022; 11(6):148. https://doi.org/10.3390/robotics11060148
Chicago/Turabian StyleVlantis, Panagiotis, Charalampos P. Bechlioulis, and Kostas J. Kyriakopoulos. 2022. "Mutli-Robot Cooperative Object Transportation with Guaranteed Safety and Convergence in Planar Obstacle Cluttered Workspaces via Configuration Space Decomposition" Robotics 11, no. 6: 148. https://doi.org/10.3390/robotics11060148
APA StyleVlantis, P., Bechlioulis, C. P., & Kyriakopoulos, K. J. (2022). Mutli-Robot Cooperative Object Transportation with Guaranteed Safety and Convergence in Planar Obstacle Cluttered Workspaces via Configuration Space Decomposition. Robotics, 11(6), 148. https://doi.org/10.3390/robotics11060148








