Static Modeling of a Class of Stiffness-Adjustable Snake-like Robots with Gravity Compensation

Abstract

Stiffness-adjustable snake-like robots have been proposed for various applications, including minimally invasive surgery. Based on a variable neutral-line mechanism, previous works proposed a class of snake-like robots that can adjust their stiffness by changing the driving cables’ tensions. A constant curvature hypothesis was used to formulate such robots’ kinematics and was further verified by our previous work via rigorous force analysis and ADAMS simulations. However, all these models and analyses have ignored the effect of the robot links’ gravity, resulting in significant errors in real systems. In this paper, a static model considering gravity compensation is proposed for the stiffness-adjustable snake-like robots. The proposed model adopts a nonlinear Gauss–Seidel iteration scheme and consists of two parts: gravity update and pose estimation. In each iteration, the former updates the payload of each link caused by gravity, and the latter estimates the pose of the robot by refreshing the angle and position values. This iteration stops when the change in the tip position is less than a pre-set error $ϵ$. During the above process, the only dependent information is each cable’s tension. Simulations and experiments are carried out to verify the effectiveness of the proposed model. The impact of gravity is found to increase with growing material densities in the simulations. The experimental results further indicate that compared with a model without gravity compensation, our model reduces the tip estimation error by 91.5% on average.

1. Introduction

Inspired by nature, snake-like robots [1,2] have been invented to provide higher flexibility compared with traditional rigid manipulators. Usually designed with high degrees of freedom in small sizes, snake-like robots are highly suitable for tasks requiring traversing through narrow and tortuous passages or dexterous manipulation in confined environments [3,4]. As such, they have been proposed for various applications, including industrial inspection [5], search and rescue [6], and robotic surgery [7,8,9,10].

The capability of adjusting the robot’s stiffness has been a desired property in many applications. For example, the robot may need to present low stiffness during compliant and safe deployment and high stiffness for high-force and precise operations once reaching target sites in minimally invasive surgery [11]. Different designs have been studied to address this need, such as using compliant joints [12,13], shape memory alloy [14], and phase change material alloy [15]. Among them, a cable-driven, curved-joint-based manipulator was proposed that is simple in design and fabrication [16]. The robot achieves adjustable stiffness by changing the driving cable’s tensions, which results in a varying neutral line between adjacent links during bending. A system using this design was developed for Single-Port Access Surgery, in which the main structure housing multiple instruments could adjust its stiffness during surgery [17]. For the same purpose, [18,19] designed a torsionally steerable flexible robot with an analysis of its dexterity and motion optimization. A similar mechanism has also been used in the SnakeRaven system for robotic arthroscopy based on patient-specific design [20,21].

Static modeling relating the robot’s shape and tip position to its cable forces is important for predicting the robot’s behaviors, as the stiffness is adjusted by changing the cables’ tensions. In our previous study [22], a static model for the stiffness-adjustable robot ignoring the robot’s gravity was developed, which can accurately estimate the robot’s bending angles and tip position given the cable tensions. The model also verified, through a rigorous force analysis, the constant curvature hypothesis commonly adopted in the kinematic modeling of such snake-like robots [16,23].

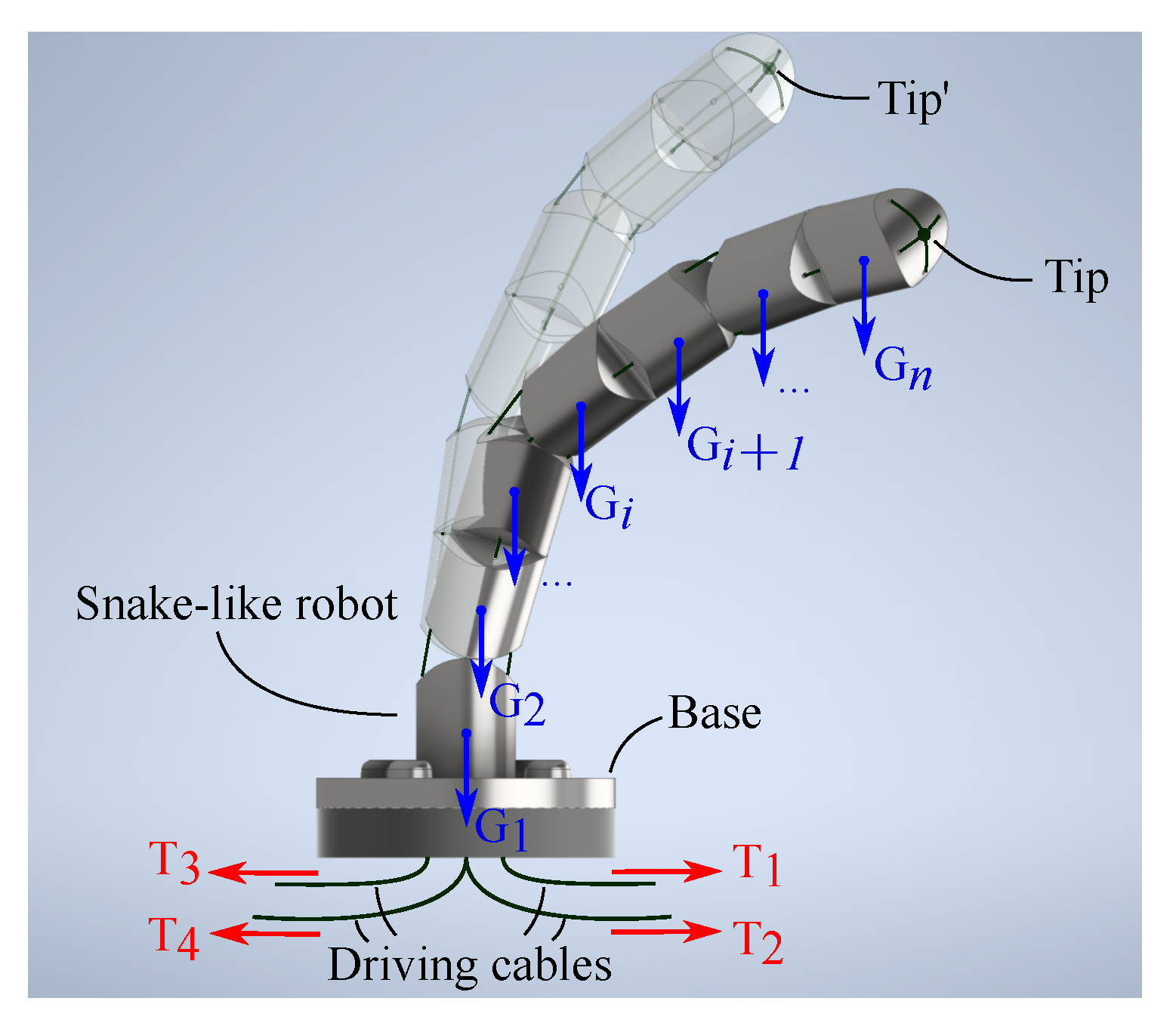
The hypothesis is valid when the robot is tiny in size and made of low-density material. However, when the robot’s size is considerably large (such as the main structure design in [16]) or the robot uses high-density material (such as metal), the effects of gravity may not be ignored. As shown in Figure 1, the robot’s real shape affected by gravity may deviate significantly from the one estimated from a constant curvature hypothesis. Therefore, it is necessary to investigate the effect of gravity in the static modeling of the stiffness-adjustable snake-like robot.

1.1. Related Works

1.1.1. Non-Static Modeling of Stiffness-Adjustable Rolling-Joint Snake-Like Robots

Early works on stiffness-adjustable rolling-joint snake-like robots have focused on the design and kinematic modeling of the robots. Yong-Jae Kim et al. [16] first introduced the rolling-joint snake-like robot capable of controlling stiffness by varying cable tensions. The approximate correspondence between the stiffness and tensions is obtained by the analysis of geometry and energy relying on the simplified geometric assumptions. In the same year, Jongwon Lee et al. [24] designed a teleoperation platform for this kind of robot and conducted a tension propagation analysis. In 2014, Jusuk Lee et al. [17] continued to perform kinematic modeling on the robot to estimate the workspace and control its tip pose through inverse kinematics.

Although the rough tip position and orientation of the robot could be achieved in these studies under the constant bending-angle assumption, the accurate mapping between the robot’s shape and the cable tensions still needs to be investigated.

1.1.2. Static Modeling of Stiffness-Adjustable Rolling-Joint Snake-Like Robots

In 2020, Jeongryul Kim et al. [25] first performed static modeling on a one-degree-of-freedom plastic robot to estimate its stiffness. Here, blocks were added between adjacent links to improve the performance of the stiffness for the rolling-joint snake-like robot described in Section 1.1.1. The key point of the algorithm proposed in the paper is to solve all the static equilibrium equations by optimization, i.e., by minimizing the sum of the absolute value of moments. In the same year, Jeongryul Kim et al. [26] extended the algorithm to the steel robot proposed by [16] to derive more accurate values of the shape. Independently from these two works, our group also achieved the shape of a similar robot with generalized orientation angles by conducting static analysis in our previous study [22]. The bending angle of each link is calculated quickly and iteratively from the tip to the bottom. However, the existence of friction and gravity has still been neglected in these studies.

In 2022, to enhance the accuracy of shape estimation, Jeongryul Kim et al. [27] continued to apply their previous algorithm to the modified steel snake-like robot by including the Coulomb friction model. Although the materials of the prototype vary from plastic to stainless steel, and the diameters of each link vary from 4.5 to 12 mm in the studies in this section, the effect of gravity has still not been discussed.

1.1.3. Gravity Compensation in Static Modeling

Models without gravity compensation may yield significant estimation error [28], especially when the robot is made of high-density material or is long or large in size. Various studies have assessed the effect of gravity in the field of continuum robots. For example, in 2009, Bryan A. Jones et al. [29] conducted a static analysis based on the Cosserat rod theory to evaluate the shape of the continuum robot. Gravity was included in the modeling and proved to be critical to the accuracy of the experiment by the comparison of accuracy between the proposed model with the analytical one without gravity. In 2016, Han Yuan, et al. [30] also performed static modeling incorporating gravity based on the Newton–Euler method on continuum robots. The accuracy of the model was validated by the simulations in ANSYS.

Despite these research efforts, gravity compensation is still absent in previous studies on the modeling of this kind of rolling-joint snake-like robot [16,22,25,26,27,31].

1.2. Contributions

In this paper, a static model with gravity compensation is established for the stiffness-adjustable snake-like robot. Given the forces of the driving cables, the proposed model can accurately estimate the overall shape of the robot and its tip position. This is achieved by conducting a static analysis of the force interaction between adjacent links and the driving cables, followed by developing an algorithm iteratively updating the effect of each link’s gravity and evaluating the bending angles between adjacent links. A group of simulations is carried out in the MSC ADAMS (Automated Dynamic Analysis of Mechanical Systems) to validate the model with various materials and robot configurations. The results show that the hypothesis of constant curvature taken in previous studies is violated when considering gravity’s effect. In particular, the disparity in the bending angles becomes dominant when the robot’s material density increases. The results are further confirmed in experiments with a real snake-like robot under ground- and ceiling-mounted setups. In all the simulations and experiments, the developed algorithm can precisely estimate the robot’s shape and tip position compared to the ground truth generated by ADAMS (simulation) and a camera/optical tracking system (experiment).

The contributions of this work lie in two parts: (1) We propose a static model with gravity compensation that can accurately predict the shape and tip position of a stiffness-adjustable robot given the actuating cable forces. The model sets a foundation for further development in stiffness control, external force estimation, and compliant motion control. (2) Using the developed static model, we reveal the impact of gravity on the constant curve hypothesis widely adopted in the modeling of such robots. It is found that the effect of gravity cannot be ignored when the robot’s size is considerably large or dense materials are used. Incorporating gravity compensation will significantly improve the accuracy of shape estimation in such cases.

2. Modeling

The snake-like robot studied in this paper is illustrated in Figure 2a. Before we study the relationship between the cable forces and the shape of the robot with gravity, each bending angle between adjacent links will be evaluated by a detailed analysis of the static model on a single link in this section.

2.1. Static Model of One Link

This robot is composed of n links with $n-1$ joints. They are connected in a staggered manner with four driving cables. To simplify the calculations, the robot is assumed to be stationary, rigid, and homogeneous without sliding motion between adjoining links. The elasticity, weight, friction, and backlash related to the cables are also neglected. In this paper, the length of each link is set as L, and the radii of both contact surfaces are R. The orientation is $\alpha$, where $\alpha \in \left[-\frac{\pi }{2},\frac{\pi }{2}\right]$. The bending angle of joint $\theta$ between two adjacent links are shown in Figure 2b. Each link has a top and a bottom cylindrical contact surface, as shown in Figure 2c. The index of each link is numbered from the base to the tip with $i\in \{1,2,\cdots ,n\}$, which is similar to that of each joint.

2.1.1. Coordinate System Definition

As shown in Figure 2a, there are two kinds of coordinate systems used in the paper: The local coordinate system (LCS) and the world coordinate system (WCS). In this section, the LCS (frame $\left\{i\right\}$) is adopted to estimate the bending angle ${\theta }_{i-1}$ between link-$(i-1)$ and link-i. The origin is located on the mass center of the link. The z-axis is co-linear with the center line of the link body and toward the base, whereas its y-axis is parallel to the center line of its curved contact surface that is closer to the base. The WCS (frame $\left\{w\right\}$) is used in the next section to determine the tip position of the robot. Its origin is fixed in the center of the base of the robot. Its z-axis is parallel with that of the LCS $\left\{1\right\}$ but toward the body of the robot. Its y-axis is also parallel with that of the LCS $\left\{1\right\}$.

2.1.2. Cable Tensions and Contact Forces

The variables in the LCS on link-i defined above are shown in Figure 2a. $T_{i,j}$ is the value of the tension applied on cable-j of link-i. ${\phi }_{i,j}$ is the phase angle of cable-j around the center line in link-i, which determines the locations of the cables. The tension applied to the bottom surface $\mathbf{T}$${}_b^{i,j}$ and its displacement vector ${\mathbf{l}}_b^{i,j}$ in the Euclidean space ${\mathbb{R}}^3$ are:

$${\mathbf{T}}_b^{i,j}\left({\theta }_i\right)={\left[-T_{i,j}sin\frac{{\theta }_i}{2}cos{\alpha }_i,T_{i,j}sin\frac{{\theta }_i}{2}sin{\alpha }_i,-T_{i,j}cos\frac{{\theta }_i}{2}\right]}^{\top },$$

(1)

$${\mathbf{l}}_b^{i,j}={\left[rcos{\phi }_{i,j},rsin{\phi }_{i,j},-\frac{L}{2}+R-\sqrt{R^2-{\left[rcos\left({\phi }_{i,j}+{\alpha }_i\right)\right]}^2}\right]}^{\top }.$$

(2)

The tension applied to the top surface ${\mathbf{T}}_t^{i,j}$ and its displacement vector ${\mathbf{l}}_t^{i,j}$ are:

$${\mathbf{T}}_t^{i,j}\left({\theta }_{i-1}\right)={\left[T_{i,j}sin\frac{{\theta }_{i-1}}{2},0,T_{i,j}cos\frac{{\theta }_{i-1}}{2}\right]}^{\top },$$

(3)

$${\mathbf{l}}_t^{i,j}={\left[rcos{\phi }_{i,j},rsin{\phi }_{i,j},\frac{L}{2}-R+\sqrt{R^2-{\left(rcos{\phi }_{i,j}\right)}^2}\right]}^{\top }.$$

(4)

The contact force applied to the bottom surface ${\mathbf{F}}_{cb}^i$, its displacement vector ${\mathbf{l}}_{cb}^i$, and corresponding torque ${\mathbf{M}}_{cb}^i$ are:

$${\mathbf{F}}_{cb}^i\left({\theta }_i,{\theta }_{i+1},\cdots ,{\theta }_{n-1}\right)={\left[F_{bx,i},F_{by,i},F_{bz,i}\right]}^{\top },$$

(5)

$${\mathbf{l}}_{cb}^i\left({\theta }_i\right)={\left[-Rsin\frac{{\theta }_i}{2}cos{\alpha }_i,Rsin\frac{{\theta }_i}{2}sin{\alpha }_i,-\frac{L}{2}+R-Rcos\frac{{\theta }_i}{2}\right]}^{\top },$$

(6)

$${\mathbf{M}}_{cb}^i\left({\theta }_i,{\theta }_{i+1},\cdots ,{\theta }_{n-1}\right)={\left[M_{bx,i},M_{by,i},M_{bz,i}\right]}^{\top }.$$

(7)

The contact force applied to the top surface ${\mathbf{F}}_{ct}^i$, its displacement vector ${\mathbf{l}}_{ct}^i$, and corresponding torque ${\mathbf{M}}_{ct}^i$ are:

$${\mathbf{F}}_{ct}^i\left({\theta }_{i-1},{\theta }_i,\cdots ,{\theta }_{n-1}\right)={\left[F_{tx,i},F_{ty,i},F_{tz,i}\right]}^{\top },$$

(8)

$${\mathbf{l}}_{ct}^i\left({\theta }_{i-1}\right)={\left[Rsin\frac{{\theta }_{i-1}}{2},0,\frac{L}{2}-R+Rcos\frac{{\theta }_{i-1}}{2}\right]}^{\top },$$

(9)

$${\mathbf{M}}_{ct}^i\left({\theta }_{i-1},{\theta }_i,\cdots ,{\theta }_{n-1}\right)={\left[M_{tx,i},M_{ty,i},M_{tz,i}\right]}^{\top }.$$

(10)

The gravity vector ${\mathbf{F}}_g^i$ in the LCS $\left\{i\right\}$ and its torque ${\mathbf{M}}_g^i$ applied on the mass center of link-i are:

$${\mathbf{F}}_g^i\left({\theta }_1,{\theta }_2,\cdots ,{\theta }_{i-1}\right)\triangleq {\mathbf{G}}_i={\left[G_{x,i},G_{y,i},G_{z,i}\right]}^{\top },$$

(11)

$${\mathbf{M}}_g^i\left({\theta }_1,{\theta }_2,\cdots ,{\theta }_{i-1}\right)=\mathbf{0}.$$

(12)

2.1.3. Constraint Equations

Since the robot is static, it should satisfy the constraints of static equilibrium. The equilibrium equations of link-i are:

$$\sum {\mathbf{F}}^i=\sum _{j=1}^4\left({\mathbf{T}}_b^{i,j}+{\mathbf{T}}_t^{i,j}\right)+{\mathbf{F}}_{cb}^i+{\mathbf{F}}_{ct}^i+{\mathbf{F}}_g^i=\mathbf{0},$$

(13)

$$\begin{array}{cc}\hfill \sum {\mathbf{M}}^i=& \sum _{j=1}^4\left({\mathbf{l}}_b^{i,j}\times {\mathbf{T}}_b^{i,j}+{\mathbf{l}}_t^{i,j}\times {\mathbf{T}}_t^{i,j}\right)+{\mathbf{l}}_{cb}^i\times {\mathbf{F}}_{cb}^i+{\mathbf{l}}_{ct}^i\times {\mathbf{F}}_{ct}^i\hfill \\ & +{\mathbf{M}}_{cb}^i+{\mathbf{M}}_{ct}^i+{\mathbf{M}}_g^i=\mathbf{0}.\hfill \end{array}$$

(14)

For the distal link, we have ${\mathbf{T}}_b^{n,j}=\mathbf{0}$, ${\mathbf{F}}_{cb}^n=\mathbf{0}$, and ${\mathbf{M}}_{cb}^n=\mathbf{0}$, since its bottom in the LCS $\left\{n\right\}$ is free.

3. Shape Estimation

To explore the relationship between the tension and the shape of the robot considering gravity, an iterative method is developed in this paper. The proposed method consists of two parts: gravity update and pose estimation. This section introduces these two components followed by the tip position calculation and the integral algorithm.

3.1. Update of Gravity Vectors

The gravity of link-i in the LCS $\left\{i\right\}$ should be obtained before performing the static analysis on link-i. Its coordinate ${{}^w\mathbf{G}}_i^{}$ in the WCS is already known at the beginning of each iteration according to the installation form. Assuming that the mass of each link analyzed is identical (except for the base link, which is not included in the calculation), the gravity of link-i in the WCS is the same for $i=2,3,\cdots ,n$. Let ${\mathbf{G}}_i\left(u\right)$ be the gravity of link-i in the LCS $\left\{u\right\}$, where $u=1,2,\cdots ,i$. As shown Algorithm 1, to achieve ${\mathbf{G}}_i\left(i\right)$, its coordinate should be first transformed from WCS $\left\{w\right\}$ to LCS $\left\{1\right\}$, i.e., ${\mathbf{G}}_i\left(1\right)={\mathbf{R}}_z\left(\pi -{\alpha }_1\right){\mathbf{R}}_y\left(\pi \right){{}^w\mathbf{G}}_i^{}$. Later, it requires iterations to transform the coordinate from LCS $\left\{1\right\}$ to LCS $\left\{i\right\}$. The iteration function of u is:

$$\begin{array}{c}\hfill {\mathbf{G}}_i^{}\left(u\right)={\mathbf{R}}_y\left({\theta }_{u-1}\right){\mathbf{R}}_z\left(-{\alpha }_u\right){\mathbf{G}}_i^{}(u-1)\end{array},$$

(15)

where ${\mathbf{R}}_x\left(\theta \right)$, ${\mathbf{R}}_y\left(\varphi \right)$, and ${\mathbf{R}}_z\left(\psi \right)$ are $SO\left(3\right)$ rotation matrices about the x, y, z-axes, respectively.

Algorithm 1: Update of gravity vectors.

3.2. Evaluation of Bending Angles

After the update of the gravity vectors, a backward iterative process is performed to calculate the bending angles. The calculation starts from the angle between the distal link and its adjacent link. Then it continues to calculate the angles between intermediate links iteratively. The complete evaluation process is presented in Algorithm 2.

Algorithm 2: Evaluation of bending angles.

3.2.1. Single Bending-Angle Computation

Take the calculation of bending angle ${\theta }_{i-1}$ as an example. The expressions of forces are derived from Equation (13). As illustrated in Figure 1, we have $M_{ty,i}=0$ since the contact force passes through the contact point on the top contact surface in the x–z plane, and ${\mathbf{M}}_g^i=\mathbf{0}$ since the gravity force passes through the origin (mass center). Thus, ${\theta }_{i-1}$ can be obtained from the y-axis component of the torque-balance equation; Equation (14):

$$asin\frac{{\theta }_{i-1}}{2}+bcos\frac{{\theta }_{i-1}}{2}+c=0,$$

(16)

where:

$$\left\{\begin{array}{c}a=R\left(cos\frac{{\theta }_i}{2}{\displaystyle \sum _{j=1}^4}{T}_{i,j}-F_{bz,i}-G_{z,i}\right)-{\displaystyle \sum _{j=1}^4}\left[T_{i,j}\sqrt{R^2-{\left(rcos{\phi }_{i,j}\right)}^2}\right]\hfill \\ b=r{\displaystyle \sum _{j=1}^4}\left(T_{i,j}cos{\phi }_{i,j}\right)+R\left(-sin\frac{{\theta }_i}{2}cos{\alpha }_i{\displaystyle \sum _{j=1}^4}{T}_{i,j}+F_{bx,i}+G_{x,i}\right)\hfill \\ c=cos\frac{{\theta }_i}{2}\left[R{F}_{bx,i}-r{\displaystyle \sum _{j=1}^4}\left(T_{i,j}cos{\phi }_{i,j}\right)\right]-sin\frac{{\theta }_i}{2}cos{\alpha }_i\{2\left(\frac{L}{2}-R\right){\displaystyle \sum _{j=1}^4}{T}_{i,j}\hfill \\ +{\displaystyle \sum _{j=1}^4}\left(T_{i,j}\sqrt{R^2-{\left[rcos\left({\phi }_{i,j}+{\alpha }_i\right)\right]}^2}\right)+R{F}_{bz,i}\}+2\left(\frac{L}{2}-R\right)F_{bx,i}+\left(\frac{L}{2}-R\right)G_{x,i}-M_{by,i}\hfill \end{array}\right.$$

Equation (16) can be solved analytically or by applying the modified Anderson–Björck–King method [32]. The value of ${\theta }_{i-1}$, which is both within the range $\left(-\frac{\pi }{2},\frac{\pi }{2}\right)$ and close to the previous value is selected to be the answer. The remaining components of the torque acting on the top contact surface are derived from Equation (14).

3.2.2. Transformation of Coordinates between Adjacent Links

During the iterative processes, coordinate transformations are needed before applying the variables achieved in the last step to the current one. We assume that the tensions applied to the cables passing through the base in counter-clockwise order in the WCS are ${\left\{T_{0,j}\right\}}_{j=1}^4$. Then if i is odd, we choose ${\alpha }_i=\alpha$, ${\left\{T_{i,j}\right\}}_{j=1}^4={\left\{T_{0,(j-1)}\right\}}_{j=1}^4$ (where $T_{0,0}=T_{0,4})$ and ${\left\{{\phi }_{i,j}\right\}}_{j=1}^4=\{0,-\alpha ,\pi ,\pi -\alpha \}$ in the LCS. Otherwise, ${\alpha }_i=-\alpha$, ${\left\{T_{i,j}\right\}}_{j=1}^4={\left\{T_{0,j}\right\}}_{j=1}^4$ and ${\left\{{\phi }_{i,j}\right\}}_{j=1}^4=\{0,\pi +\alpha ,\pi ,\alpha \}$. Moreover, we assume that the variables ${\theta }_{i-1}$, ${\mathbf{F}}_{ct}^i$ and $M_{ct}^i$ are achieved in the last static analysis on link-i, then in the current analysis, we have ${\theta }_{i-1}=-{\theta }_{i-1}$ and the bottom contact force and moment vectors are:

$$\left\{\begin{array}{c}{\mathbf{F}}_{cb}^{i-1}=-{\mathbf{R}}_z\left({\alpha }_i\right){\mathbf{R}}_y(-{\theta }_{i-1}){\mathbf{F}}_{ct}^i\hfill \\ {\mathbf{M}}_{cb}^{i-1}=-{\mathbf{R}}_z\left({\alpha }_i\right){\mathbf{R}}_y(-{\theta }_{i-1}){\mathbf{M}}_{ct}^i\hfill \end{array}\right..$$

(17)

3.3. Calculation of Tip Position

Since the shape of the robot has been achieved in the previous step, we can easily obtain the tip position, as illustrated in Algorithm 3. Let transformation matrices ${\mathbf{T}}_l\left(\mathbf{d}\right)={\mathbf{T}}_l\left(x,y,z\right)=\left[\begin{array}{cc}{\mathbf{I}}_{3\times 3}& \mathbf{d}\\ {\mathbf{0}}_{1\times 3}& 1\end{array}\right]$ be a pure translation of $\mathbf{d}$, and ${\mathbf{T}}_{ry}\left(\varphi \right)=\left[\begin{array}{cc}{\mathbf{R}}_y\left(\varphi \right)& {\mathbf{0}}_{3\times 1}\\ {\mathbf{0}}_{1\times 3}& 1\end{array}\right]$ & ${\mathbf{T}}_{rz}\left(\psi \right)=\left[\begin{array}{cc}{\mathbf{R}}_z\left(\psi \right)& {\mathbf{0}}_{3\times 1}\\ {\mathbf{0}}_{1\times 3}& 1\end{array}\right]$ be pure rotation matrices about the y and z-axes, respectively.

Algorithm 3: Calculation of Tip Position.

   For the base link, the transformation matrix between LCS $\left\{1\right\}$ and WCS $\left\{w\right\}$ is:

$${{}_1{}^w\mathbf{T}}_{}^{}={\mathbf{T}}_l({\mathbf{d}}_{\mathbf{1}})*{\mathbf{T}}_{rz}\left(-\pi +{\alpha }_1\right)*{\mathbf{T}}_{ry}\left(\pi \right),$$

(18)

where ${\mathbf{d}}_{\mathbf{1}}$ is the displacement between their origins. For the following links, the transformation matrix from LCS $\left\{i\right\}$ to LCS $\{i-1\}$$(i=2,3,\cdots ,n)$ is:

$$\begin{array}{c}\hfill {{}_i{}^{i-1}\mathbf{T}}_{}^{}={\mathbf{T}}_{rz}\left({\alpha }_i\right)*{\mathbf{T}}_{ry}\left(-{\theta }_{i-1}\right)*{\mathbf{T}}_l\left(x_0,0,z_0\right)\end{array},$$

(19)

where $x_0=-\frac{2ml}{m^2+1}$, $z_0=-\frac{2l}{m^2+1}$, $m=tan\frac{{\theta }_{i-1}}{2}$, $l=\frac{L}{2}-R\left(1-cos\frac{{\theta }_{i-1}}{2}\right)+mRsin\frac{{\theta }_{i-1}}{2}$.

Hence, the transformation matrix from LCS $\left\{i\right\}$ to WCS $\left\{w\right\}$ is:

$$\begin{array}{c}\hfill {{}_i{}^w\mathbf{T}}_{}^{}={{}_1{}^w\mathbf{T}}_{}^{}{{}_2{}^1\mathbf{T}}_{}^{}\cdots {{}_i{}^{i-1}\mathbf{T}}_{}^{}\end{array},$$

(20)

and the tip position in the WCS is: ${{}^w\mathbf{P}}_{tip}^{}={{}_n{}^w\mathbf{T}}_{}^{}{{}^n\mathbf{P}}_{tip}^{}$, where ${{}^n\mathbf{P}}_{tip}^{}$ is the tip of the distal link in the LCS $\left\{n\right\}$.

3.4. Complete Calculation Procedures

Equation (16), which is used to calculate bending angles ${\theta }_i$, can be regarded as a part of the system of nonlinear equations:

$$\begin{array}{c}\hfill \mathbf{F}=\left(f_1,f_2,\cdots ,f_{n-1}\right)=\mathbf{0}.\end{array}$$

(21)

To solve this nonlinear system, an iterative method is proposed in this paper. The complete calculation process of the method is presented in Algorithm 4, including the sub-processes described in Algorithms 1 and 2. It starts with an initial guess of the vector ${\mathbf{\theta }}^{\mathbf{0}}={\left[{\theta }_1^0,\cdots ,{\theta }_i^0,\cdots ,{\theta }_{n-1}^0\right]}^{\top }$ calculated in the case without gravity compensation. Then the sequence of bending angle vectors ${\left\{{\theta }_i^k\right\}}_{k=0}^{\infty }$ is generated, which will converge to the desired solution.

Algorithm 4: Complete process.

According to Equations (1)–(12) and (16), the function $f_i$ in the LCS on link-i is composed of the cable tensions, contact forces, gravity, and torques. Let k be the number of iterations for Equation (21) and ${{}^{*}\theta }_{i-1}^{k+1}$ be the solution of $f_i=0$ derived in the $(k+1)$th iteration. The parts of tension forces, contact forces and their torques are related to the angles $\{{\theta }_{n-1}^{k+1},{\theta }_{n-2}^{k+1},\cdots ,{\theta }_i^{k+1},{{}^{*}\theta }_{i-1}^{k+1}\}$, while those of gravity and its torque are related to the angles $\{{\theta }_1^k,{\theta }_2^k,\cdots ,{\theta }_{i-2}^k,{{}^{*}\theta }_{i-1}^{k+1}\}$. Thus, each nonlinear function can be expressed as:

$$\begin{array}{c}\hfill f_i\left({\theta }_1^k,{\theta }_2^k,\cdots ,{\theta }_{i-2}^k,{{}^{*}\theta }_{i-1}^{k+1},{\theta }_i^{k+1},\cdots ,{\theta }_{n-1}^{k+1}\right)=0\end{array},$$

(22)

which is the primary step of the nonlinear Gauss–Seidel iteration scheme [33]. To simplify the calculation, the parts of gravity and its torque can also be calculated by $\{{\theta }_1^k,{\theta }_2^k,\cdots ,{\theta }_{i-1}^k\}$. The relaxation parameter $\omega$ is also introduced to modify all the bending angles derived from the kth iteration before updating the gravity vectors:

$$\begin{array}{c}\hfill {\theta }_i^k={\theta }_i^{k-1}+\omega \left({{}^{*}\theta }_i^k-{\theta }_i^{k-1}\right)\end{array}.$$

(23)

Usually, the value of relaxation parameter $\omega$ is chosen within $\left(0,1\right]$ [34]. The iteration ends when the change in tip position is less than a predefined threshold $\epsilon$, i.e., when ${\parallel }^w{\mathbf{P}}_{tip}^{k+1}{-}^w{\mathbf{P}}_{tip}^k\parallel <\epsilon$. In all the simulations and experiments in this work, $\epsilon$ has been set to $1\times {10}^{-12}$.

During the calculation, the initial values of bending angles and the configuration of the value of relaxation parameter $\omega$ both affects the convergence and the computational time of the method. For example, the mean execution time for the ground-mounted steel-material spatial-orientation simulation case in Section 4 with $\epsilon =1\times {10}^{-12}$ was 0.1164 s for $\omega =0.1$ and 0.0085 s for $\omega =1$ when calculated a thousand times in MATLAB R2021b on a laptop with macOS 10.15.7, Intel Core i9 CPU (8-Core, 2.3 GHz), and 16 GB memory. To quickly achieve the specified accuracy [33] in the application, we can choose $\omega =1$ as the initial configuration for rapid convergence. Each time when the computation of the current step does not converge; the step will continue to iterate under the updated configuration with reduced relaxation parameter value (e.g., ${\omega }_{current}=\frac{{\omega }_{previous}}{2}$) using the angle values calculated in the last step.

4. Simulations and Experiments

Two sets of simulations and two sets of experiments were performed to validate the proposed estimation method. In the simulations, the effect of gravity on the snake-like robot’s shape with different material densities was analyzed for both planar- and spatial-orientation cases under ground- and ceiling-mounted setups. In the experiments, the accuracy of the proposed model was further validated using a real snake-like robot in planar and spatial motions with both mounting configurations.

4.1. Simulations

In the simulations, we used ADAMS to simulate the behaviors of the snake-like robots under different configurations and compared them with the calculated results in MATLAB using the proposed method. The simulations consisted of two groups: planar ($\alpha =0^{\circ }$ with 1 degree of freedom) and spatial ($\alpha ={90}^{\circ }$ with 2 degrees of freedom) cases, with one example for each group shown in Figure 3. In the literature, different materials have been used to fabricate the snake-like robot, such as steel [35], aluminum [36], and acrylonitrile butadiene styrene (ABS) [37]. To identify the effect of gravity on the robot with various materials, four popular materials for 3D printing have been chosen to parameterize the robot in simulation, and their densities were as follows: ABS (1.05 g/cm${}^3$), aluminum (2.68 g/cm${}^3$), titanium (4.41 g/cm${}^3$), and steel (7.86 g/cm${}^3$).

In all the simulations, each robot has six links with the following link parameters: Length $L=12$ mm, radii of contact surfaces $R=6$ mm, cable distance $r=3.5$ mm, and volume $V=0.851$ cm${}^3$. All the simulations started from the initial guess $\left\{{\theta }_i^0\right\}=\mathbf{0}$ with the gravitational acceleration $g=9.8$ m/s${}^2$.

4.1.1. Planar-Orientation Case

In this group of simulations, the forces applied to each cable were [0, 2.4, 0, 5.1] N in all cases. The simulation process of an example case (steel, ground-mounted) is illustrated in Figure 3a. The results are summarized in

Table 1. Estimation and simulation results of bending angles and tip positions for planar-orientation cases.

Platform	−	Ground-Mounted Case								Ceiling-Mounted Case
Material	−	ABS		Aluminum		Titanium		Steel		ABS		Aluminum		Titanium		Steel
Result	Est.${}^{*}$	Est.	Sim.	Est.	Sim.	Est.	Sim.	Est.	Sim.	Est.	Sim.	Est.	Sim.	Est.	Sim.	Est.	Sim.
${\theta }_1{(}^{\circ })$	28.99	31.91	31.06	36.57	37.29	41.46	46.01	50.44	51.86	26.22	27.36	22.31	24.02	18.79	21.26	13.56	13.38
${\theta }_2{(}^{\circ })$	28.99	31.22	30.65	34.61	33.63	37.93	39.80	43.26	46.61	26.80	28.12	23.62	24.70	20.65	23.32	16.04	16.93
${\theta }_3{(}^{\circ })$	28.99	30.28	30.13	32.08	31.20	33.59	32.24	35.35	34.10	27.65	28.73	25.58	26.58	23.52	24.58	20.10	23.07
${\theta }_4{(}^{\circ })$	28.99	29.51	29.74	30.14	30.07	30.54	30.13	30.62	30.19	28.41	29.18	27.43	28.64	26.39	27.66	24.50	25.36
${\theta }_5{(}^{\circ })$	28.99	29.10	29.53	29.21	28.20	29.24	29.50	29.11	29.51	28.86	29.41	28.62	29.28	28.34	29.17	27.80	28.80
x(mm)	47.04	46.23	46.12	44.16	44.78	41.26	39.78	34.98	33.23	47.39	46.78	47.05	46.92	45.78	46.51	41.94	42.32
y(mm)	0.00	0.00	−0.04	0.00	0.06	0.00	0.10	0.00	−0.02	0.00	−0.12	0.00	0.17	0.00	0.10	0.00	−0.01
z(mm)	14.85	10.19	11.16	3.45	4.02	−2.67	−6.31	−11.45	−13.34	19.55	16.78	26.54	23.25	33.12	27.94	43.11	40.43

Est.*: Estimation without gravity compensation [22]; Est.: Estimation with gravity compensation; Sim.: Simulation of ADAMS.

, including the bending angles of each joint and the displacement of the tip in the WCS.

In the ground-mounted cases, the z component of the tip position of simulation and estimation with gravity compensation both decrease as the density of the material increases. The mean position error between the estimation with gravity compensation and simulation $\parallel {\mathbf{P}}_{est}-{\mathbf{P}}_{sim}\parallel$ is 2.08 mm. The estimated positions without gravity compensation were fixed, i.e., $(x,y,z)=(47.04,0.00,14.85)$, as different material densities do not affect the model when gravity is not considered. The mean position error between the estimation without gravity compensation and the simulation is 17.16 mm, which is bigger than the compensated one.

In the ceiling-mounted cases, since gravity pulls the links away from the base, the z component of the tip position with gravity compensation enlarges while the density increases. The mean position errors between the estimation and simulation results with and without gravity compensation are 3.52 and 12.36 mm, respectively, showing the superior accuracy of the estimation with gravity compensation.

For both mounting configurations, the bending angles estimated without gravity compensation always kept the fixed value with the mean angle error $\parallel {\theta }_{i,est}-{\theta }_{i,sim}\parallel$ = 4.39${}^{\circ }$, while they are distinct from each other and change with different materials in the simulation. In comparison, the results with gravity compensation are more accurate, with a mean angle error of 0.48${}^{\circ }$ in the planar cases.

4.1.2. Spatial-Orientation Case

In this group of simulations, the tensions applied to each cable were [3.7, 2.4, 1.8, 5.1] N for all cases. The simulation process of an example case (steel, ground-mounted) is illustrated in Figure 3b. The results of the simulations are shown in

Table 2. Estimation and simulation results of bending angles and tip positions for spatial-orientation cases.

Platform	−	Ground-Mounted Case								Ceiling-Mounted Case
Material	−	ABS		Aluminum		Titanium		Steel		ABS		Aluminum		Titanium		Steel
Result	Est.${}^{*}$	Est.	Sim.	Est.	Sim.	Est.	Sim.	Est.	Sim.	Est.	Sim.	Est.	Sim.	Est.	Sim.	Est.	Sim.
${\theta }_1{(}^{\circ })$	10.58	11.08	11.32	11.92	12.63	12.94	13.65	15.40	17.17	10.12	10.06	9.47	9.28	8.84	8.61	7.77	7.68
${\theta }_2{(}^{\circ })$	15.48	15.88	17.34	16.54	18.39	17.28	19.49	18.89	21.26	15.09	16.21	14.51	15.49	13.94	14.71	12.90	13.48
${\theta }_3{(}^{\circ })$	10.58	10.85	11.26	11.29	11.87	11.82	12.52	13.08	13.70	10.33	10.66	9.98	10.28	9.63	9.91	9.03	9.32
${\theta }_4{(}^{\circ })$	15.48	15.63	16.97	15.87	17.35	16.14	17.75	16.71	18.65	15.33	16.55	15.11	16.27	14.88	15.97	14.47	15.43
${\theta }_5{(}^{\circ })$	10.58	10.62	10.99	10.68	11.05	10.75	11.15	10.91	11.34	10.55	10.90	10.50	10.86	10.45	10.78	10.36	10.68
x(mm)	18.56	19.13	19.60	20.09	21.04	21.23	22.14	23.88	25.55	18.02	18.23	17.24	17.28	16.48	16.54	15.17	15.36
y(mm)	−18.47	−18.82	−20.61	−19.37	−21.49	−19.99	−22.33	−21.30	−23.71	−18.14	−19.67	−17.64	−19.02	−17.13	−18.36	−16.20	−17.25
z(mm)	64.41	64.03	62.70	63.37	61.60	62.58	60.59	60.60	57.91	64.76	63.72	65.25	64.37	65.72	64.93	66.50	65.79

Est.*: Estimation without gravity compensation [22]; Est.: Estimation with gravity compensation; Sim.: Simulation of ADAMS.

.

The variation trends of angles and positions under various materials estimated with gravity compensation are consistent with those simulated in ADAMS. The mean position errors between the simulation and the estimation results with and without gravity compensation in ground-mounted cases are 3.10 and 6.28 mm, and those in ceiling-mounted cases are 1.57 and 2.15 mm. The mean angle errors between them in both ground-mounted and ceiling-mounted cases are 0.56${}^{\circ }$ and 1.52${}^{\circ }$. The influence of gravity is less vital when the density is relatively low in spatial orientation cases. However, the position errors of cases with and without gravity compensation under the highest density (steel) are 3.98 and 10.89 mm for the ground-mounted case and 1.28 and 3.69 mm for the ceiling-mounted case. Thus, when the density is relatively high, it is critical to implement gravity compensation.

4.2. Experiments

The proposed method was further validated with experiments on a real snake-like robot, which has 12 links with link length $L=12$ mm, radii of contact surfaces $R=20$ mm, cable distance $r=7.5$ mm, and link mass $m=3.8$ g, as shown in Figure 4 and Figure 5. The robot has two degrees of freedom with the orientation $\alpha ={90}^{\circ }$. Similarly to the simulations, both ground-mounted and ceiling-mounted setups were tested. In both configurations, a spirit level was used to make sure the robot base was horizontal. Different weights were added to the cables to adjust their tension.

All the data were collected at static equilibrium points along the paths. To reduce the impact of friction, the tensions started in larger values before it came to the predefined ones so that the robot could keep moving around before settling down. Tip positions were obtained by a real-time tracking system OptiTrack with 10 cameras, whose mean 3D error for overall re-projection was 0.307 mm. The bending angles of the robot were determined via images ($6016\times 4016pixels$) captured by a digital camera Nikon D750. Four optical markers were mounted to the frame of both setups to calibrate the $x,y$, and z-axes for the WCS. Another optical marker was attached to the tip of the robot to calibrate the origin of the WCS when the robot was held straight and to record its tip position during the experiment.

4.2.1. Planar-Motion Case

The experiments performed in planar motions and WCSs for ground- and ceiling-mounted platforms are illustrated in Figure 4a,b,f,g. As shown in Figure 4c–e,h–j, only the values of ${\theta }_i$$(i=2,4,\cdots ,10)$ have been recorded since ${\theta }_i=0$ for $i=1,3,\cdots ,11$. The payloads deployed in each experiment are shown in

Table 3. Estimated and measured results of bending angles for planar-motion cases.

Payloads(N)	Experiment 1: [0.98,0.98,0.98,1.96].					Experiment 2: [0.98,0.98,0.98,2.94].					Experiment 3: [0.98,0.98,0.98,3.92].
Results	Est*.1	G-M Est.1	G-M Exp.1	C-M Est.1	C-M Exp.1	Est*.2	G-M Est.2	G-M Exp.2	C-M Est.2	C-M Exp.2	Est*.3	G-M Est.3	G-M Exp.3	C-M Est.3	C-M Exp.3
${\theta }_2{(}^{\circ })$	8.97	27.17	26.49	4.16	4.10	14.97	31.35	30.35	7.87	6.64	19.25	33.53	32.50	11.16	11.23
${\theta }_4{(}^{\circ })$	8.97	23.42	22.93	4.85	4.83	14.97	27.82	27.12	8.94	8.50	19.25	30.33	29.34	12.44	11.79
${\theta }_6{(}^{\circ })$	8.97	18.07	18.49	6.02	6.34	14.97	22.85	23.81	10.72	10.82	19.25	25.90	25.85	14.53	13.67
${\theta }_8{(}^{\circ })$	8.97	13.23	13.78	7.38	7.74	14.97	18.54	19.24	12.72	13.70	19.25	22.16	22.13	16.80	16.31
${\theta }_{10}{(}^{\circ })$	8.97	10.06	10.19	8.53	8.80	14.97	15.86	15.46	14.35	15.58	19.25	19.96	20.39	18.58	18.18
x(mm)	0.00	0.00	0.00	0.00	0.05	0.00	0.00	−0.22	0.00	−2.15	0.00	0.00	−0.36	0.00	−2.32
y(mm)	−56.74	−106.23	−107.19	−35.87	−38.40	−84.84	−109.29	−110.68	−60.93	−62.41	−97.22	−106.43	−107.19	−77.57	−79.27
z(mm)	145.50	86.79	85.44	155.18	155.12	118.86	58.21	57.04	140.94	141.16	95.18	41.70	40.42	124.64	125.09

Est.*: Estimation without gravity compensation [22]; Est.: Estimation with gravity compensation; Exp.: Experiment; G-M: Ground-Mounted case; C-M: Ceiling-Mounted case.

. From Figure 4 and Table 3, the real shape (i.e., bending angles) of the robot in both ground-mounted and ceiling-mounted setups have a similar tendency to the estimated shape with gravity compensation. The result shows that the effect of gravity cannot be ignored here, and the shape varies with the direction of gravity.

As shown in Table 3, the mean errors of total bending angles of each case $\parallel {\sum }_{i=1}^{11}{\theta }_{i,est}-{\sum }_{i=1}^{11}{\theta }_{i,exp}\parallel$ for the estimation with gravity compensation are 0.72${}^{\circ }$ under ground-mounted and 1.28${}^{\circ }$ under ceiling-mounted configurations, and those for the cases without gravity compensation are 40.71${}^{\circ }$ and 19.23${}^{\circ }$. The mean tip position errors of estimation $\parallel {\mathbf{P}}_{est}-{\mathbf{P}}_{exp}\parallel$ with gravity compensation are 1.67 mm under ground-mounted and 2.69 mm under ceiling-mounted configurations, and those without gravity compensation are 67.04 mm and 29.12 mm.

4.2.2. Spatial-Motion Case

The experiments performed in spatial motions and WCSs for ground- and ceiling-mounted platforms are illustrated in Figure 5a–f. Nine tip positions $\{{\mathbf{p}}_1,{\mathbf{p}}_2,\cdots ,{\mathbf{p}}_9\}$ under different payloads have been recorded for each installation form. Under ground-mounted configurations, the tip of the robot tended to move outward, which is contrary to the ceiling-mounted configurations. The estimated tip positions are compared with the actual tracked tip position. As shown in

Table 4. Position errors (mm) between the estimated and measured tip positions for spatial-motion cases.

Tip No.	${\mathit{P}}_1$	${\mathit{P}}_2$	${\mathit{P}}_3$	${\mathit{P}}_4$	${\mathit{P}}_5$	${\mathit{P}}_6$	${\mathit{P}}_7$	${\mathit{P}}_8$	${\mathit{P}}_9$
Payload (N)	[1.96, 1.96, 1.96, 6.86]	[6.86, 1.96, 1.96, 8.82]	[8.82, 1.96, 1.96, 6.86]	[6.86, 1.96, 1.96, 3.92]	[6.86, 1.96, 1.96, 1.96]	[6.86, 3.92, 1.96, 1.96]	[8.82, 6.86, 1.96, 1.96]	[6.86, 8.82, 1.96, 1.96]	[1.96, 6.86, 1.96, 1.96]
G-M Est.${}^{*}$	28.39	21.87	23.42	32.74	40.86	32.67	25.03	21.74	28.43
G-M Est.	2.21	3.05	2.42	1.22	2.60	2.69	2.66	3.01	0.79
C-M Est.${}^{*}$	20.34	15.03	19.25	20.79	30.40	20.89	19.76	20.19	20.35
C-M Est.	2.88	3.63	3.25	3.26	2.21	3.87	2.55	3.82	2.81

Est.*: Estimation without gravity compensation [22]; Est.: Estimation with gravity compensation; G-M: Ground- Mounted; C-M: Ceiling-Mounted.

, the mean position errors of the estimation with gravity compensation are 2.29 mm under ground-mounted and 3.14 mm under ceiling-mounted configurations, and those without gravity compensation are 28.35 and 20.78 mm, respectively. From the results, it can be clearly seen that the introduction of gravity compensation has significantly improved the accuracy of the estimation.

5. Discussion and Conclusions

In this paper, we proposed a static model with gravity compensation to estimate the bending shape of the snake-like robot according to the tension of each driving cable and the mass of each link. The model employed an iterative algorithm with the effect of each link’s gravity and the bending angles constantly updated until convergence. The model works for a general installation configuration and has been verified by two special cases: ground-mounted and ceiling-mounted. Through simulations, it was found that the constant curvature hypothesis widely used in previous studies is violated when gravity is considered. The difference between a model with gravity compensation and one without is increasingly significant when the robot is made of denser materials. The superiority of the gravity compensation model was further verified by experiments on a real snake-like robot. The proposed model reduced the tip estimation error by 91.5% on average compared to a model without gravity compensation.

In the future, the proposed method will be extended to multi-segment snake-like robots with friction and clearance compensation, and the effect of other external forces will be studied as well.