Process of Learning from Demonstration with Paraconsistent Artificial Neural Cells for Application in Linear Cartesian Robots
Abstract
:1. Introduction
1.1. Related Works
1.2. Organization
2. Fundamentals of Learning from Demonstration (LfD)
2.1. Machine Learning
2.1.1. Supervised Learning
2.1.2. Demonstration Step Approaches
2.2. Data Modeling for Feature Extraction
2.3. Modeling
3. Paraconsistent Logic (PL)
y = λ → degree of unfavorable evidence, with 0 ≤ λ ≤ 1
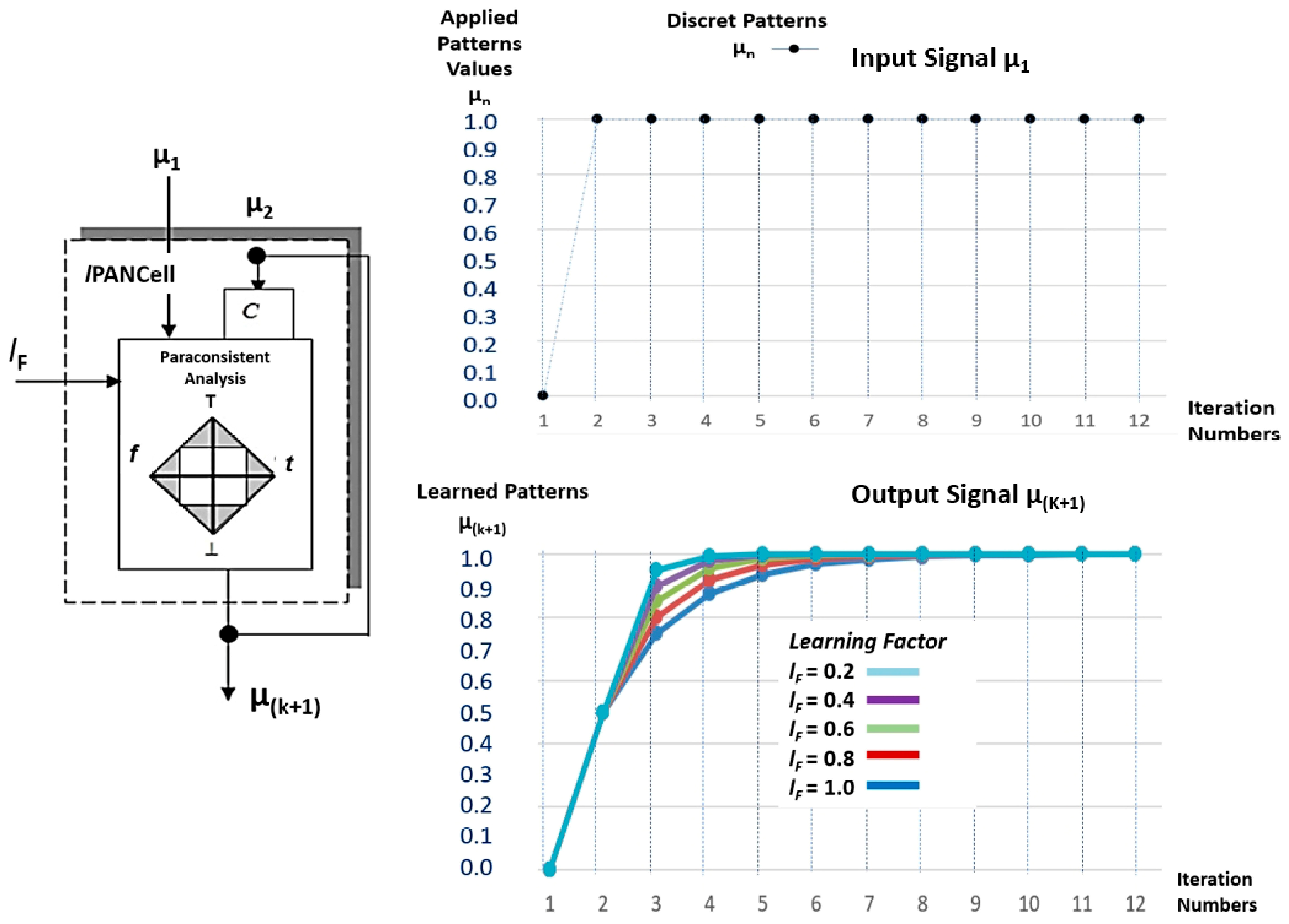
3.1. Paraconsistent Artificial Neural Cell of Learning (lPANCell)
| Algorithm 1: Paraconsistent Artificial Neural Cell of Learning—lPANCell |
| 1. Initial Condition and 2. Enter the value of the Learning Factor */Learning Factor */ 3. Transform the Degree of Evidence 2 into Unfavorable Degree of Evidence */Unfavorable Degree of Evidence */ 4. Enter the Pattern value (Degree of Evidence of input 1) */Degree of Evidence */ 5. Compute the Resultant Evidence Degree (Equation (6)). 6. Compute the Normalized Contradiction Degree (Equation (7)). 7. Present the current state of learning (Equation (10)). 8. Consider the condition If → Do and return to step 3 9. Stop |
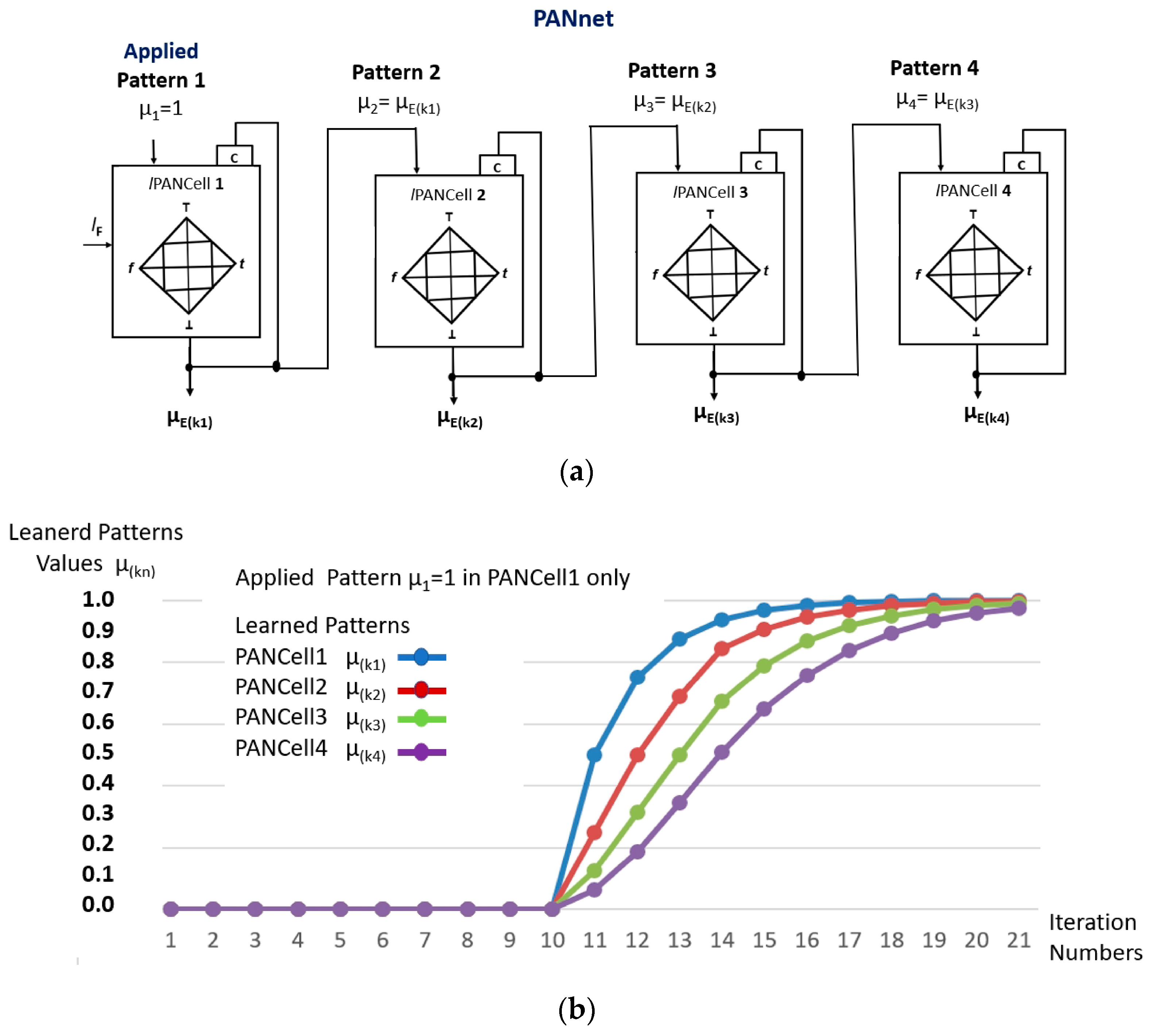
3.2. lPANnet—Paraconsistent Artificial Neural Network
4. Materials and Methods
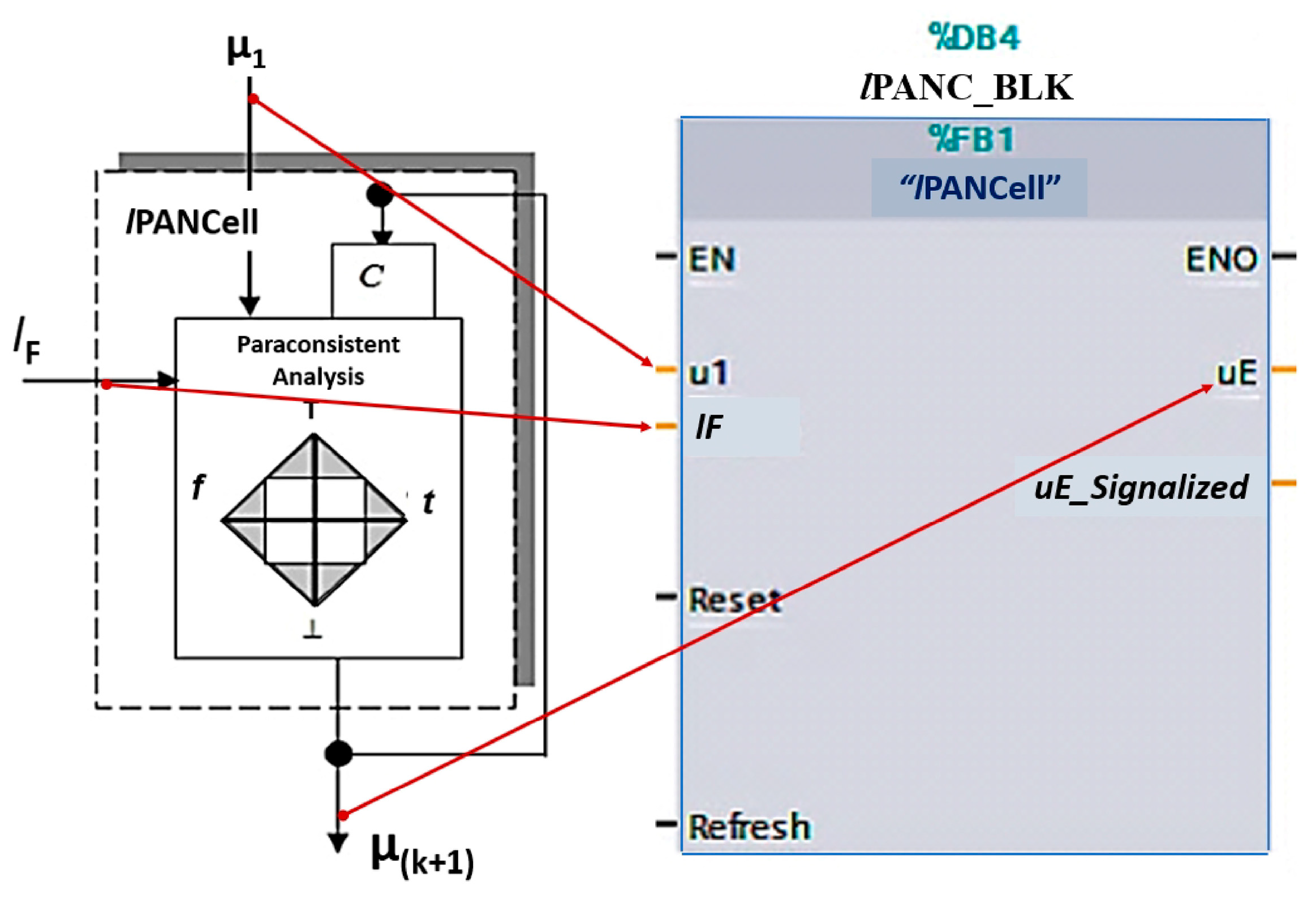
4.1. Functional Block (lPANC_BLK)
- (a)
- EN: Enable the block when its logic level is 1;
- (b)
- u1: Input pattern to be learned by lPANC_BLK in the range 0 to 100;
- (c)
- lF: Learning factor that corresponds to an adjustment of how quickly the cell will learn the input pattern—adjusted in the range of 0 to 100;
- (d)
- Reset: Restart the block, assigning the value 50 to the output μE.
- (e)
- Refresh: Updates the input pattern after receiving a pulse at logic level 1;
- (f)
- ENO: Provides logic level 1 when block is active;
- (g)
- uE: Evidence degree, which corresponds to the block output in the range of 0 to 100;
- (h)
- uE_Signaled: Signaling with a value of 100 when the block ends learning (or unlearning).
4.2. Linear Cartesian Robot and Pneumatic Machine Tool
4.3. Practical Application—Forms of Activation and Control
4.4. Paraconsistent Artificial Neural Network (lPANnet) Configured with lPANC_BLK Blocks
4.4.1. Planning
Y-axis trajectory: start Y0 = 0 mm finish Y(Target) = 500 mm
- Learning from demonstration on the x-axis determining the trajectory gx = X(Target) − X0;
- Learning from demonstration on the y-axis determining the trajectory gy = Y(Target) − Y0.
4.4.2. Learning Stage (Teleoperation)
- (a)
- First gx trajectory—Advance of the pneumatic cylinder on the x axis
- (b)
- Second gy trajectory—Advance of the pneumatic cylinder on the y axis
4.4.3. Imitation Step
5. Results and Discussion
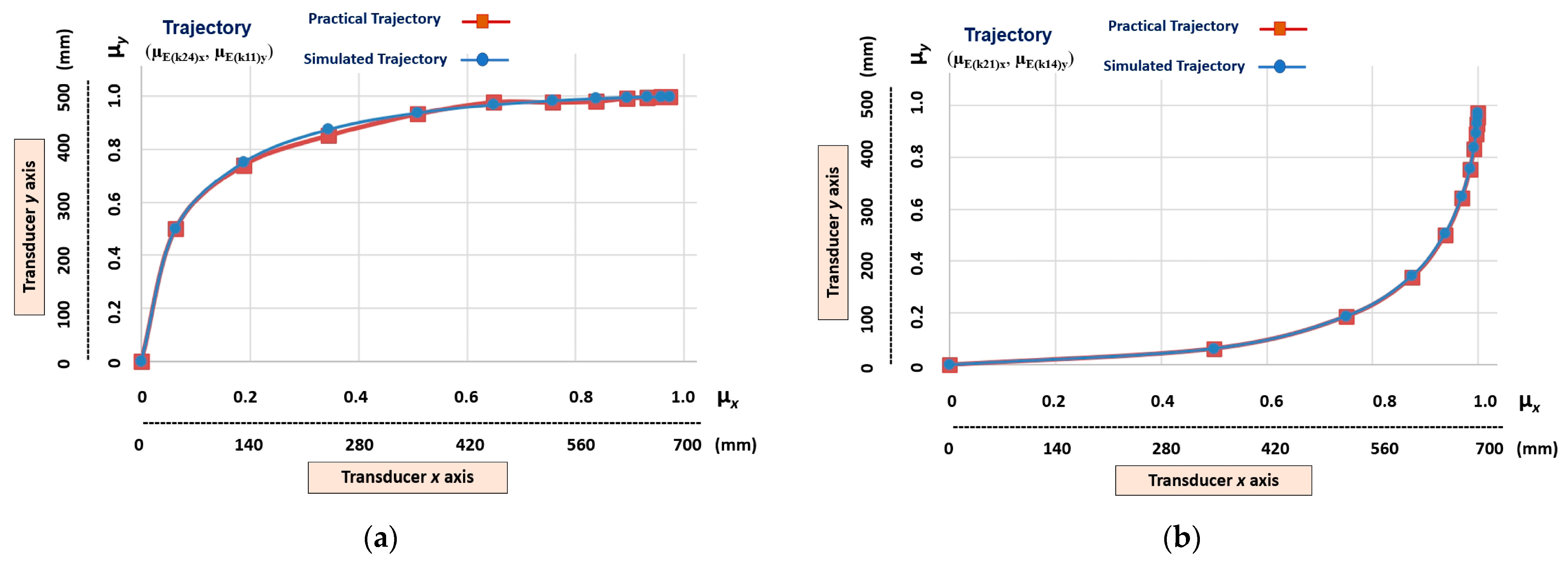
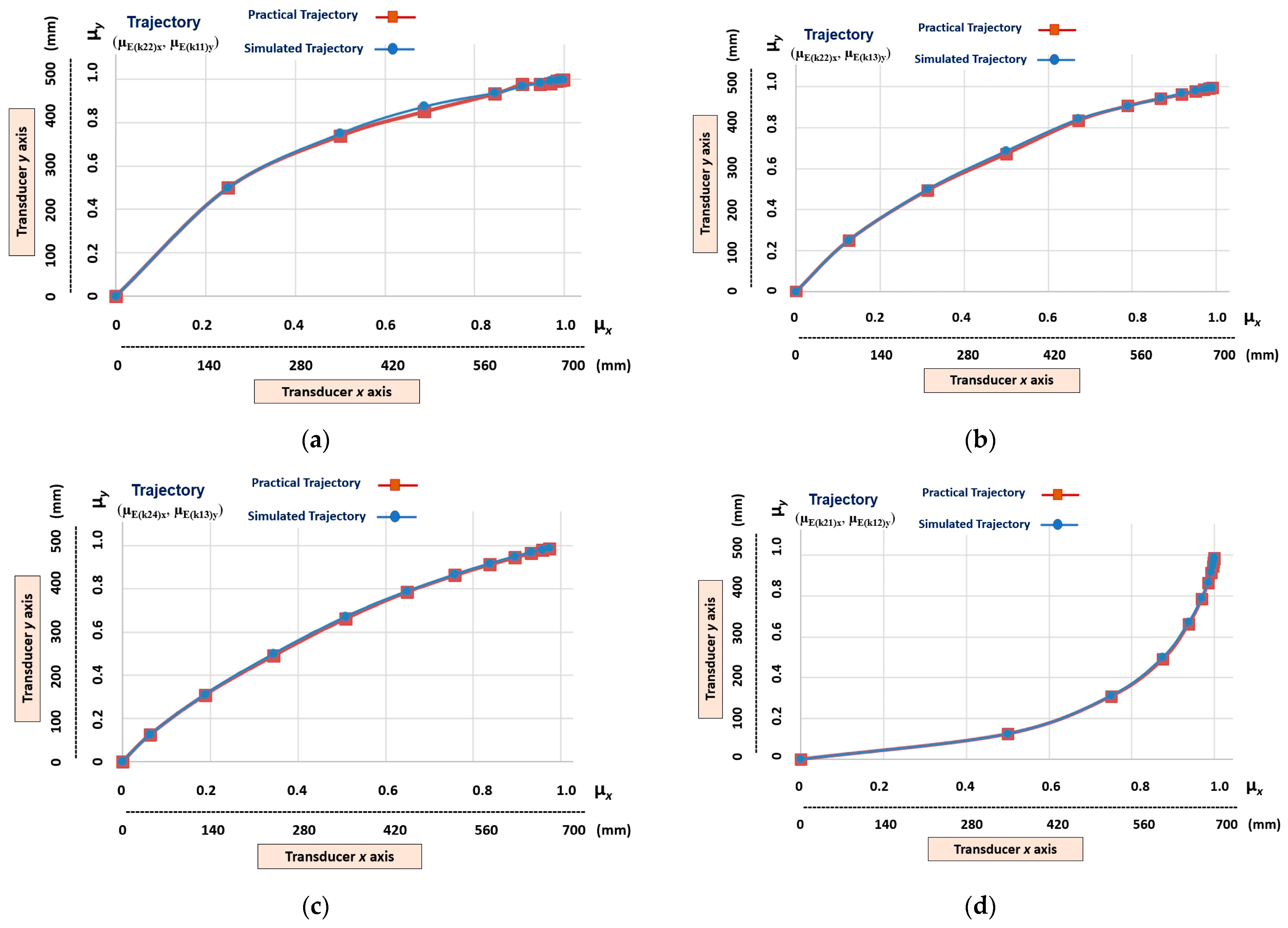
- Linear trajectories (g1n), which are obtained at the outputs (µE(k21)x, µE(k11)y), (µE(k22)x, µE(k12)y), (µE(k23)x, µE(k13)y), and (µE(k24)x, µE(k14)y);
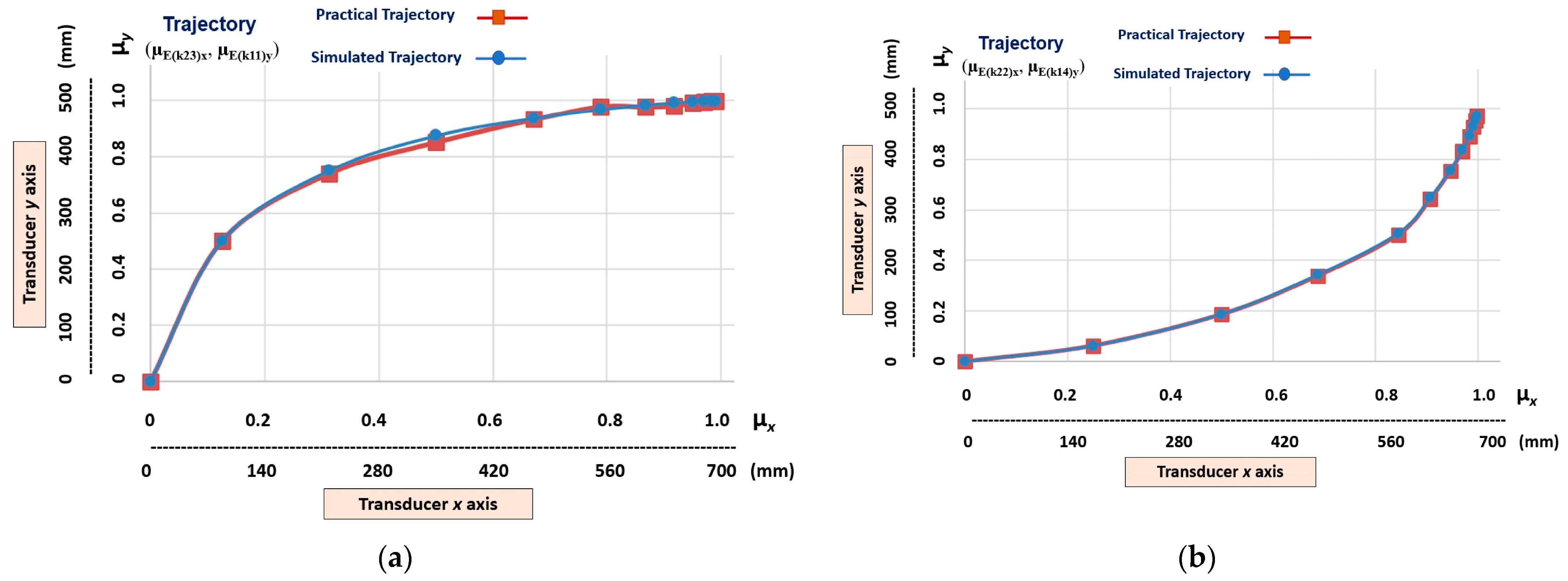
- Non-linear trajectories that have a higher level of slope (gnlh), which are those obtained at the outputs (µE(k24)x, µE(k11)y) and (µE(k21)x, µE(k14)y);
- Non-linear trajectories that present a medium level of non-linearity (gnlm), which are those obtained at the outputs (µE(k23)x, µE(k11)y), (µE(k24)x, µE(k12)y), (µE(k22)x, µE(k14)y) and (µE(k21)x, µE(k13)y);
- Non-linear trajectories that have a low level of non-linearity (gnll), which are those obtained at the outputs (µE(k22)x, µE(k11)y), (µE(k23)x, µE(k12)y), (µE(k24)x, µE(k13)y), (µE(k21)x, µE(k12)y), (µE(k22)x, µE(k13)y) and (µE(k23)x, µE(k14)y).
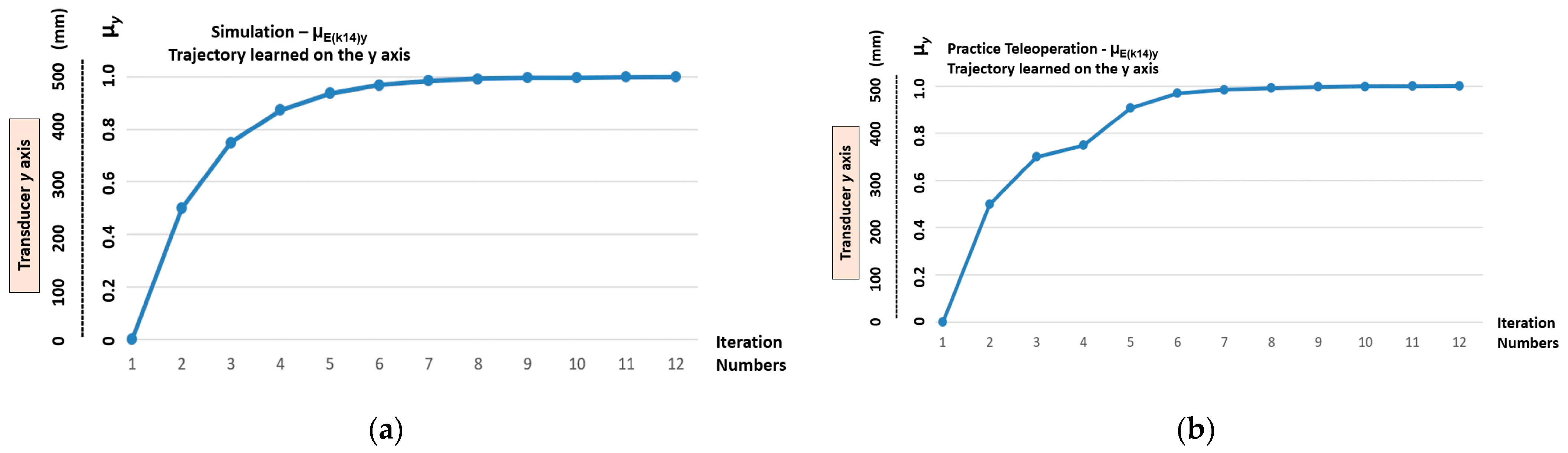
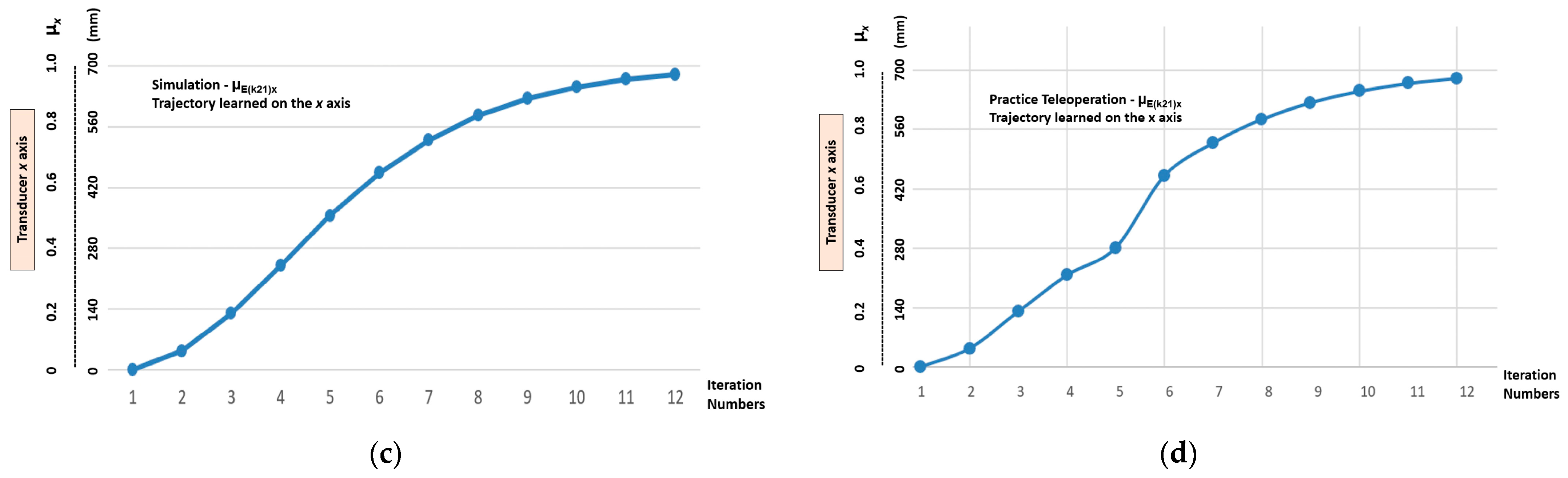
5.1. Learning Stage Results—Demonstration by Simulation
5.2. Learning Stage Results—Demonstration by Teleoperation
5.3. Imitation Step—Results
Practical Trajectory = (µE(k21)x, µE(k14)y) = (0.75, 0.3090).
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Haefner, N.; Wincent, J.; Parida, V.; Gassmann, O. Artificial intelligence and innovation management: A review, framework, and research agenda. Technol. Forecast. Soc. Chang. 2021, 162, 120392. [Google Scholar] [CrossRef]
- Angeles, J. Fundamentals of Robotic Mechanical Systems: Theory, Methods, and Algorithms, 3rd ed.; Springer: New York, NY, USA, 2007; ISBN 978-3-319-01850-8. [Google Scholar] [CrossRef]
- Craig, J.J. Introduction to Robotics: Mechanics and Control, 4th ed.; Pearson: Toronto, ON, Canada, 2022; ISBN 9780137848744. [Google Scholar]
- Torres, C.R.; Lambert-Torres, G.; Abe, J.M.; Da Silva Filho, J.I. The sensing system for the autonomous mobile robot Emmy III. In Proceedings of the 2011 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2011), Taipei, Taiwan, 27–30 June 2011; pp. 2928–2933. [Google Scholar] [CrossRef]
- Torres, C.R.; Abe, J.M.; Lambert-Torres, G.; Da Silva Filho, J.I.; Martins, H.G. A Sensing System for an Autonomous Mobile Robot Based on the Paraconsistent Artificial Neural Network. In Knowledge-Based and Intelligent Information and Engineering Systems; KES 2010; Lecture Notes in Computer Science; Setchi, R., Jordanov, I., Howlett, R.J., Jain, L.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6278. [Google Scholar] [CrossRef]
- Da Silva Filho, J.I.; Lambert-Torres, G.; Abe, J.M. Uncertainty Treatment Using Paraconsistent Logic—Introducing Paraconsistent Artificial Neural Networks; IOS Press: Amsterdam, The Netherlands, 2010; p. 320. ISBN 978-1-60750-557-0. [Google Scholar]
- Côrtes, H.M.; Santos, P.E.; Da Silva Filho, J.I. Monitoring electrical systems data-network equipment by means of Fuzzy and Paraconsistent Annotated Logic. Expert Syst. Appl. 2022, 187, 115865. [Google Scholar] [CrossRef]
- Ravichandar, H.; Polydoros, A.S.; Chernova, S.; Billard, A. Recent Advances in Robot Learning from Demonstration. Annu. Rev. Control Robot. Auton. Syst. 2020, 3, 297–330. [Google Scholar] [CrossRef]
- Argall, B.D.; Chernova, S.; Veloso, M.; Browning, B. A survey of robot learning from demonstration. Robot. Auton. Syst. 2009, 57, 469–483. [Google Scholar] [CrossRef]
- Verstaevel, N.; Régis, C.; Gleizes, M.P.; Robert, F. Principles and Experimentations of Self-Organizing Embedded Agents Allowing Learning From Demonstration in Ambient Robotics. Future Gener. Comput. Syst. 2016, 64, 78–87. [Google Scholar] [CrossRef]
- Ekvall, S.; Kragic, D. Robot learning from demonstration: A task-level planning approach. Int. J. Adv. Robot. Syst. 2008, 5, 223–234. [Google Scholar] [CrossRef]
- De Carvalho, A.; Da Silva Filho, J.I.; Mario, M.C.; Blos, M.F.; Da Cruz, C.M. A Study of Paraconsistent Artificial Neural Cell of Learning Applied as PAL2v Filter. IEEE Lat. Am. Trans. 2018, 16, 202–209. [Google Scholar] [CrossRef]
- Da Silva Filho, J.I.; da Cruz, C.M.; Rocco, A.; Garcia, D.V.; Ferrara, L.F.P.; Onuki, A.S.; Mario, M.C.; Abe, J.M. Paraconsistent Artificial Neural Network for Structuring Statistical Process Control in Electrical Engineering. In Towards Paraconsistent Engineering; Intelligent Systems Reference Library; Akama, S., Ed.; Springer: Cham, Stwitzerland, 2016; Volume 110. [Google Scholar] [CrossRef]
- Abe, J.M.; Torres, C.R.; Lambert-Torres, G.; Da Silva Filho, J.I.; Martins, H.G. Paraconsistent Autonomous Mobile Robot Emmy III. In Advances in Technological Applications of Logical and Intelligent Systems; Series Frontiers in Artificial Intelligence and Applications; IOS Press: Amsterdam, The Netherlands, 2009; Volume 186, pp. 236–258. [Google Scholar] [CrossRef]
- Nicolescu, M.N.; Mataric, M.J. Natural methods for robot task learning: Instructive demonstrations, generalization and practice. In Proceedings of the Second International Joint Conference on Autonomous Agents and Multiagent Systems, Melbourne, VIC, Australia, 14–18 July 2003; pp. 241–248. [Google Scholar]
- Billard, A.; Calinon, S.; Dillmann, R.; Schaal, S. Robot programming by demonstration. In Springer Handbook of Robotics; Siciliano, B., Khatib, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1371–1394. [Google Scholar]
- Mugan, J.; Kuipers, B. Autonomous learning of high-level states and actions in continuous environments. IEEE Trans. Auton. Ment. Dev. (TAMD) 2012, 4, 70–86. [Google Scholar] [CrossRef]
- Gienger, M.; Mühlig, M.; Steil, J.J. Imitating object movement skills with robots—A task-level approach exploiting generalization and invariance. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 1262–1269. [Google Scholar] [CrossRef]
- Mohseni-Kabir, A.; Rich, C.; Chernova, S.; Sidner, C.L.; Miller, D. Interactive hierarchical task learning from a single demonstration. In Proceedings of the Tenth Annual—ACM/IEEE International Conference on Human-Robot Interaction, HRI ’15, Portland, OR, USA, 2–5 March 2015; ACM: New York, NY, USA; pp. 205–212. [Google Scholar]
- Zimmerman, T.; Kambhampati, S. Learning-Assisted Automated Planning: Looking Back, Taking Stock, Going Forward. AI Mag. 2003, 24, 73. [Google Scholar] [CrossRef]
- Jiménez, S.; De La Rosa, T.; Fernández, S.; Fernández, F.; Borrajo, D. A review of machine learning for automated planning. Knowl. Eng. Rev. 2012, 27, 433–467. [Google Scholar] [CrossRef]
- Fikes, R.E.; Hart, P.E.; Nilsson, N.J. Learning and executing generalized robot plans. Artif. Intell. 1972, 3, 251–288. [Google Scholar] [CrossRef]
- Chrpa, L. Generation of macro-operators via investigation of action dependencies in plans. Knowl. Eng. Rev. 2010, 25, 281–297. [Google Scholar] [CrossRef]
- Hu, Y.; De Giacomo, G. Generalized planning: Synthesizing plans that work for multiple environments. In Proceedings of the IJCAI Proceedings-International Joint Conference on Artificial Intelligence, Catalonia, Spain, 16–22 July 2011; Volume 22, pp. 918–923. [Google Scholar]
- Zhuo, H.H.; Muñoz-Avila, H.; Yang, Q. Learning hierarchical task network domains from partially observed plan traces. Artif. Intell. 2014, 212, 134–157. [Google Scholar] [CrossRef]
- Ingrand, F.; Ghallab, M. Deliberation for autonomous robots: A survey. Artif. Intell. 2017, 247, 10–44. [Google Scholar] [CrossRef]
- Abe, J.M.; Da Silva Filho, J.I. Manipulating conflicts and uncertainties in robotics. J. Mult.-Valued Log. Soft Comput. 2003, 9, 147–169. [Google Scholar]
- De Carvalho, A.; Justo, J.F.; Angelico, B.A.; De Oliveira, A.M.; Da Silva Filho, J.I. Rotary Inverted Pendulum Identification for Control by Paraconsistent Neural Network. IEEE Access 2021, 9, 74155–74167. [Google Scholar] [CrossRef]
- Pastor, P.; Kalakrishnan, M.; Meier, F.; Stulp, F.; Buchli, J.; Theodorou, E.; Schaal, S. From dynamic movement primitives to associative skill memories. Robot. Auton. Syst. 2013, 61, 351–361. [Google Scholar] [CrossRef]
- Ijspeert, A.J.; Nakanishi, J.; Schaal, S. Movement imitation with nonlinear dynamical systems in humanoid robots. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA2002), Washington, DC, USA, 11–15 May 2002; pp. 1398–1403. [Google Scholar]
- Ijspeert, A.J.; Nakanishi, J.; Schaal, S. Learning rhythmic movements by demonstration using nonlinear oscillators. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS2002), EPFL, Lausanne, Switzerland, 30 September–4 October 2002; pp. 958–963. [Google Scholar]
- Zhu, Z.; Hu, H. Robot Learning from Demonstration in Robotic Assembly: A Survey. Robotics 2018, 7, 17. [Google Scholar] [CrossRef]
- Aleotti, J.; Caselli, S.; Reggiani, M. Leveraging on a virtual environment for robot programming by demonstration. Robot. Auton. Syst. 2004, 47, 153–161. [Google Scholar] [CrossRef]
- Schaal, S. Dynamic movement primitives—A framework for motor control in humans and humanoid robotics. In Adaptive Motion of Animals and Machines; Springer: Tokio, Japan, 2006; pp. 261–280. [Google Scholar]
- Niekum, S.; Osentoski, S.; Konidaris, G.; Chitta, S.; Marthi, B.; Barto, A.G. Learning grounded finite-state representations from unstructured demonstrations. Int. J. Robot. Res. 2015, 34, 131–157. [Google Scholar] [CrossRef]
- Sosa-Ceron, A.D.; Gonzalez-Hernandez, H.G.; Reyes-Avendaño, J.A. Learning from Demonstrations in Human–Robot Collaborative Scenarios: A Survey. Robotics 2022, 11, 126. [Google Scholar] [CrossRef]
- Sarker, I.H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar] [CrossRef]
- Akbari, E.; Mir, M.; Vasiljeva, M.V.; Alizadeh, A.; Nilashi, M. A Computational Model of Neural Learning to Predict Graphene Based ISFET. J. Electron. Mater. 2019, 48, 4647–4652. [Google Scholar] [CrossRef]
- Liu, T.; Lemeire, J. Efficient and Effective Learning of HMMs Based on Identification of Hidden States. Math. Probl. Eng. 2017, 2017, 7318940. [Google Scholar] [CrossRef]
- Kulić, D.; Ott, C.; Lee, D.; Ishikawa, J.; Nakamura, Y. Incremental learning of full body motion primitives and their sequencing through human motion observation. Int. J. Robot. Res. 2012, 31, 330–345. [Google Scholar] [CrossRef]
- Ijspeert, A.J.; Nakanishi, J.; Hoffmann, H.; Pastor, P.; Schaal, S. Dynamical Movement Primitives: Learning Attractor Models for Motor Behaviors. Neural Comput. 2013, 25, 328–373. [Google Scholar] [CrossRef]
- Guo, W.; Li, R.; Cao, C.; Gao, Y. Kinematics, dynamics, and control system of a new 5-degree-of-freedom hybrid robot manipulator. Adv. Mech. Eng. 2016, 8, 11. [Google Scholar] [CrossRef]
- Chi, M.; Yao, Y.; Liu, Y.; Zhong, M. Learning, Generalization, and Obstacle Avoidance with Dynamic Movement Primitives and Dynamic Potential Fields. Appl. Sci. 2019, 9, 1535. [Google Scholar] [CrossRef]
- Abe, J.M.; Lopes, H.F.D.S.; Anghinah, R. Paraconsistent artificial neural networks and Alzheimer disease: A preliminary study. Dement. Neuropsychol. 2007, 1, 241–247. [Google Scholar] [CrossRef]
- Kurfess, T.R. (Ed.) Robotics and Automation Handbook; CRC Press LLC.: Boca Raton, FL, USA, 2005. [Google Scholar]
- Sanchez-Sanchez, P.; Reyes-Cortes, F. Cartesian Control for Robot Manipulators. In Robot Manipulators Trends and Development; Jimenez, A., Al Hadithi, B.M., Eds.; IntechOpen: London, UK, 2010. [Google Scholar] [CrossRef]
- Cuesta, R.; Alvarez, J.; Miranda, M. Robust Tracking and Cruise Control of a Class of Robotic Systems. Math. Probl. Eng. 2015, 2015, 728412. [Google Scholar] [CrossRef]
- Da Costa, N.C.A.; Abe, J.M.; Subrahmanian, V.S. Remarks on annotated logic. Z. Math. Logik Grundl. Math. 1991, 37, 561–570. [Google Scholar]
- Garcia, D.V.; Da Silva Filho, J.I.; Silveira, L.; Pacheco, M.T.T.; Abe, J.M.; Carvalho, A.; Blos, M.F.; Pasqualucci, C.A.G.; Mario, M.C. Analysis of Raman spectroscopy data with algorithms based on paraconsistent logic for characterization of skin cancer lesions. Vib. Spectrosc. 2019, 103, 102929. [Google Scholar] [CrossRef]
- Da Silva Filho, J.I.; Abe, J.M.; Marreiro, A.D.L.; Martinez, A.A.G.; Torres, C.R.; Rocco, A.; Côrtes, H.M.; Mario, M.C.; Pacheco, M.T.T.; Garcia, D.V.; et al. Paraconsistent Annotated Logic Algorithms Applied in Management and Control of Communication Network Routes. Sensors 2021, 21, 4219. [Google Scholar] [CrossRef]
- Coelho, M.S.; Da Silva Filho, J.I.; Côrtes, H.M.; de Carvalho, A.; Blos, M.F.; Mario, M.C.; Rocco, A. Hybrid PI controller constructed with paraconsistent annotated logic. Control Eng. Pract. 2019, 84, 112–124. [Google Scholar] [CrossRef]
- Da Silva Filho, J.I.; de Oliveira, R.A.B.; Rodrigues, M.C.; Côrtes, H.M.; Rocco, A.; Mario, M.C.; Garcia, D.V.; Abe, J.M.; Torres, C.R.; Ricciotti, V.B.D.; et al. Predictive Controller Based on Paraconsistent Annotated Logic for Synchronous Generator Excitation Control. Energies 2023, 16, 1934. [Google Scholar] [CrossRef]
- Ferrara, L.F.P.; Yamanaka, K.; Da Silva Filho, J.I. A system of recognition of characters based on paraconsistent artificial neural networks. Front. Artif. Intell. Appl. 2005, 132, 127–134. [Google Scholar]
- John, K.H.; Tiegelkamp, M. IEC61131-3: Programing Industrial Automation Systems: Concepts and Programming Languages, Requirements for Programing Systems, Decision—Making Aids, 2nd ed.; Springer: New York, NY, USA, 2010; 390p. [Google Scholar]
- Salih, H.; Abdelwahab, H.; Abdallah, A. Automation design for a syrup production line using Siemens PLC S7-1200 and TIA Portal software. In Proceedings of the 2017 International Conference on Communication, Control, Computing and Electronics Engineering (ICCCCEE), Khartoum, Sudan, 16–18 January 2017; pp. 1–5. [Google Scholar] [CrossRef]










| Symbols/Abbreviations | Meaning |
|---|---|
| PL | Paraconsistent Logic |
| LfD | Learning from Demonstration process |
| PAL | Paraconsistent Annotated Logic |
| PAL2v | Paraconsistent Annotated Logic with Annotation of Two Values |
| PANCell | Paraconsistent Artificial Neural Cell |
| lPANCel | Learning Paraconsistent Artificial Neural Cell |
| lPANnet | Paraconsistent Artificial Neural Network |
| lPANC_BLK | Paraconsistent Artificial Neural Cell Programmed with IEC 61131-3 Rules as Functional Block |
| HMM | Hidden Markov Models |
| DMP | Dynamic Motion Primitives |
| μ | Favorable Evidence Degree |
| λ | Unfavorable Evidence Degree |
| (μ, λ) | Annotation of Two Values |
| USCP | Unit Square in the Cartesian Plane |
| P | Proposition |
| t | True Logical State |
| f | False Logical State |
| ⊥ | Paracomplete Logical State |
| T | Inconsistent Logical State |
| Dc | Certainty Degree |
| Dct | Contradiction Degree |
| DCR | Certainty Degree of Real Value |
| μER | Resulting Evidence Degree |
| Learning Factor |
| Pattern 1 | μ(k+1) | Pattern 2 | μ(k+1) | Pattern 3 | μ(k+1) | Pattern 4 | μ(k+1) | Pattern 5 | μ(k+1) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| μ1 | 0 | 0.5 | μ1 | 1 | 0.50048828 | μ1 | 0.4 | 0.6995122 | μ1 | 0.8 | 0.60029249 | μ1 | 1 | 0.89980497 |
| μ2 | 0 | 0.25 | μ2 | 1 | 0.75024414 | μ2 | 0.4 | 0.5497561 | μ2 | 0.8 | 0.70014625 | μ2 | 1 | 0.94990249 |
| μ3 | 0 | 0.125 | μ3 | 1 | 0.87512207 | μ3 | 0.4 | 0.47487805 | μ3 | 0.8 | 0.75007312 | μ3 | 1 | 0.97495124 |
| μ4 | 0 | 0.0625 | μ4 | 1 | 0.93756104 | μ4 | 0.4 | 0.43743902 | μ4 | 0.8 | 0.77503656 | μ4 | 1 | 0.98747562 |
| μ5 | 0 | 0.03125 | μ5 | 1 | 0.96878052 | μ5 | 0.4 | 0.41871951 | μ5 | 0.8 | 0.78751828 | μ5 | 1 | 0.99373781 |
| μ6 | 0 | 0.015625 | μ6 | 1 | 0.98439026 | μ6 | 0.4 | 0.40935976 | μ6 | 0.8 | 0.79375914 | μ6 | 1 | 0.99686891 |
| μ7 | 0 | 0.0078125 | μ7 | 1 | 0.99219513 | μ7 | 0.4 | 0.40467988 | μ7 | 0.8 | 0.79687957 | μ7 | 1 | 0.99843445 |
| μ8 | 0 | 0.0039062 | μ8 | 1 | 0.99609756 | μ8 | 0.4 | 0.40233994 | μ8 | 0.8 | 0.79843979 | μ8 | 1 | 0.99921723 |
| μ9 | 0 | 0.0019531 | μ9 | 1 | 0.99804878 | μ9 | 0.4 | 0.40116997 | μ9 | 0.8 | 0.79921989 | μ9 | 1 | 0.99960861 |
| μ10 | 0 | 0.0009765 | μ10 | 1 | 0.99902439 | μ10 | 0.4 | 0.40058498 | μ10 | 0.8 | 0.79960995 | μ10 | 1 | 0.99980431 |
| Pattern 1 μ(k+n) | μ(kn1) = Pattern 2 | μ(kn2) = Pattern 3 | μ(kn3) = Pattern 4 | μ(kn4) | |
|---|---|---|---|---|---|
| μ1 | 0 | 0 | 0 | 0 | 0 |
| μ2 | 1 | 0.5 | 0.25 | 0.125 | 0.0625 |
| μ3 | 1 | 0.75 | 0.5 | 0.3125 | 0.1875 |
| μ4 | 1 | 0.875 | 0.6875 | 0.5 | 0.34375 |
| μ5 | 1 | 0.9375 | 0.84375 | 0.671875 | 0.507813 |
| μ6 | 1 | 0.96875 | 0.90625 | 0.789063 | 0.648438 |
| μ7 | 1 | 0.984375 | 0.945313 | 0.867188 | 0.757813 |
| μ8 | 1 | 0.9921875 | 0.96875 | 0.917969 | 0.837891 |
| μ9 | 1 | 0.99609375 | 0.982422 | 0.950195 | 0.894043 |
| μ10 | 1 | 0.99804688 | 0.990234 | 0.970215 | 0.932129 |
| μ11 | 1 | 0.99902344 | 0.994629 | 0.982422 | 0.957275 |
| μ12 | 1 | 0.99951172 | 0.99707 | 0.989746 | 0.973511 |
| Simulation Results—x-Axis (X0)—lPANC_BLK x | Simulation Results—y-Axis (Y0)—lPANC_BLK y | |||||||
|---|---|---|---|---|---|---|---|---|
| μE(k21)x | μE(k22)x | μE(k23)x | μE(k24)x | μE(k11)y | μE(k12)y | μE(k13)y | μE(k14)y | |
| μ1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| μ2 | 0.5000000 | 0.250000 | 0.12500 | 0.062500 | 0.5000000 | 0.250000 | 0.125000 | 0.062500 |
| μ3 | 0.7500000 | 0.500000 | 0.31250 | 0.187500 | 0.7500000 | 0.500000 | 0.312500 | 0.187500 |
| μ4 | 0.8750000 | 0.687500 | 0.50000 | 0.343750 | 0.8750000 | 0.687500 | 0.500000 | 0.343750 |
| μ5 | 0.9375000 | 0.843750 | 0.671875 | 0.507813 | 0.9375000 | 0.843750 | 0.671875 | 0.507813 |
| μ6 | 0.9687500 | 0.906250 | 0.789063 | 0.648438 | 0.9687500 | 0.906250 | 0.789063 | 0.648438 |
| μ7 | 0.9843750 | 0.945313 | 0.867188 | 0.757813 | 0.9843750 | 0.945313 | 0.867188 | 0.757813 |
| μ8 | 0.9921875 | 0.968750 | 0.917969 | 0.837891 | 0.9921875 | 0.968750 | 0.917969 | 0.837891 |
| μ9 | 0.99609375 | 0.982422 | 0.950195 | 0.894043 | 0.99609375 | 0.982422 | 0.950195 | 0.894043 |
| μ10 | 0.99804688 | 0.990234 | 0.970215 | 0.932129 | 0.99804688 | 0.990234 | 0.970215 | 0.932129 |
| μ11 | 0.99902344 | 0.994629 | 0.982422 | 0.957275 | 0.99902344 | 0.994629 | 0.982422 | 0.957275 |
| μ12 | 0.99951172 | 0.997070 | 0.989746 | 0.973511 | 0.99951172 | 0.997070 | 0.989746 | 0.973511 |
| Teleoperation Results—x-Axis (X0)—lPANC_BLK x | Teleoperation Results—y-Axis (Y0)—lPANC_BLK y | |||||||
|---|---|---|---|---|---|---|---|---|
| μE(k21)x | μE(k22)x | μE(k23)x | μE(k24)x | μE(k11)y | μE(k12)y | μE(k13)y | μE(k14)y | |
| μ1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| μ2 | 0.500000 | 0.250000 | 0.125000 | 0.062500 | 0.500000 | 0.250000 | 0.125000 | 0.062500 |
| μ3 | 0.750000 | 0.500000 | 0.312500 | 0.187500 | 0.740000 | 0.495000 | 0.310000 | 0.186250 |
| μ4 | 0.875000 | 0.687500 | 0.500000 | 0.343750 | 0.852000 | 0.673500 | 0.491750 | 0.339000 |
| μ5 | 0.937500 | 0.843750 | 0.671875 | 0.507813 | 0.933500 | 0.836750 | 0.664250 | 0.501625 |
| μ6 | 0.968750 | 0.906250 | 0.789063 | 0.648438 | 0.978750 | 0.907750 | 0.786000 | 0.643813 |
| μ7 | 0.984375 | 0.945313 | 0.867188 | 0.757813 | 0.978375 | 0.943063 | 0.864531 | 0.754172 |
| μ8 | 0.9921875 | 0.968750 | 0.917969 | 0.837891 | 0.9821875 | 0.962625 | 0.913578 | 0.833875 |
| μ9 | 0.9960938 | 0.982422 | 0.950195 | 0.894043 | 0.9940938 | 0.978359 | 0.945969 | 0.889922 |
| μ10 | 0.9980469 | 0.990234 | 0.970215 | 0.932129 | 0.9970469 | 0.987703 | 0.966836 | 0.928379 |
| μ11 | 0.9990234 | 0.994629 | 0.982422 | 0.957275 | 0.9990234 | 0.993363 | 0.980100 | 0.954239 |
| μ12 | 0.99931172 | 0.996970 | 0.989696 | 0.973486 | 0.99981172 | 0.996587 | 0.988344 | 0.971291 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Da Silva Filho, J.I.; Fernandes, C.L.M.; Silveira, R.S.d.; Gomes, P.M.; Matos, S.L.d.C.; Santo, L.d.E.; Nunes, V.C.; Côrtes, H.M.; Lopes, W.A.C.; Mario, M.C.; et al. Process of Learning from Demonstration with Paraconsistent Artificial Neural Cells for Application in Linear Cartesian Robots. Robotics 2023, 12, 69. https://doi.org/10.3390/robotics12030069
Da Silva Filho JI, Fernandes CLM, Silveira RSd, Gomes PM, Matos SLdC, Santo LdE, Nunes VC, Côrtes HM, Lopes WAC, Mario MC, et al. Process of Learning from Demonstration with Paraconsistent Artificial Neural Cells for Application in Linear Cartesian Robots. Robotics. 2023; 12(3):69. https://doi.org/10.3390/robotics12030069
Chicago/Turabian StyleDa Silva Filho, João Inácio, Cláudio Luís Magalhães Fernandes, Rodrigo Silvério da Silveira, Paulino Machado Gomes, Sérgio Luiz da Conceição Matos, Leonardo do Espirito Santo, Vander Célio Nunes, Hyghor Miranda Côrtes, William Aparecido Celestino Lopes, Mauricio Conceição Mario, and et al. 2023. "Process of Learning from Demonstration with Paraconsistent Artificial Neural Cells for Application in Linear Cartesian Robots" Robotics 12, no. 3: 69. https://doi.org/10.3390/robotics12030069
APA StyleDa Silva Filho, J. I., Fernandes, C. L. M., Silveira, R. S. d., Gomes, P. M., Matos, S. L. d. C., Santo, L. d. E., Nunes, V. C., Côrtes, H. M., Lopes, W. A. C., Mario, M. C., Garcia, D. V., Torres, C. R., Abe, J. M., & Lambert-Torres, G. (2023). Process of Learning from Demonstration with Paraconsistent Artificial Neural Cells for Application in Linear Cartesian Robots. Robotics, 12(3), 69. https://doi.org/10.3390/robotics12030069








