Grasping Profile Control of a Soft Pneumatic Robotic Gripper for Delicate Gripping
Abstract
1. Introduction
- The design of an actuator set for controlling the SPG, comprising an air compressor pump with digital regulators and a pneumatic cylinder actuator along with its associated accessories.
- The development of a control technique that is capable of estimating unknown inputs of the system and effectively regulating the pressure and volume within the system.
2. Materials and Methods
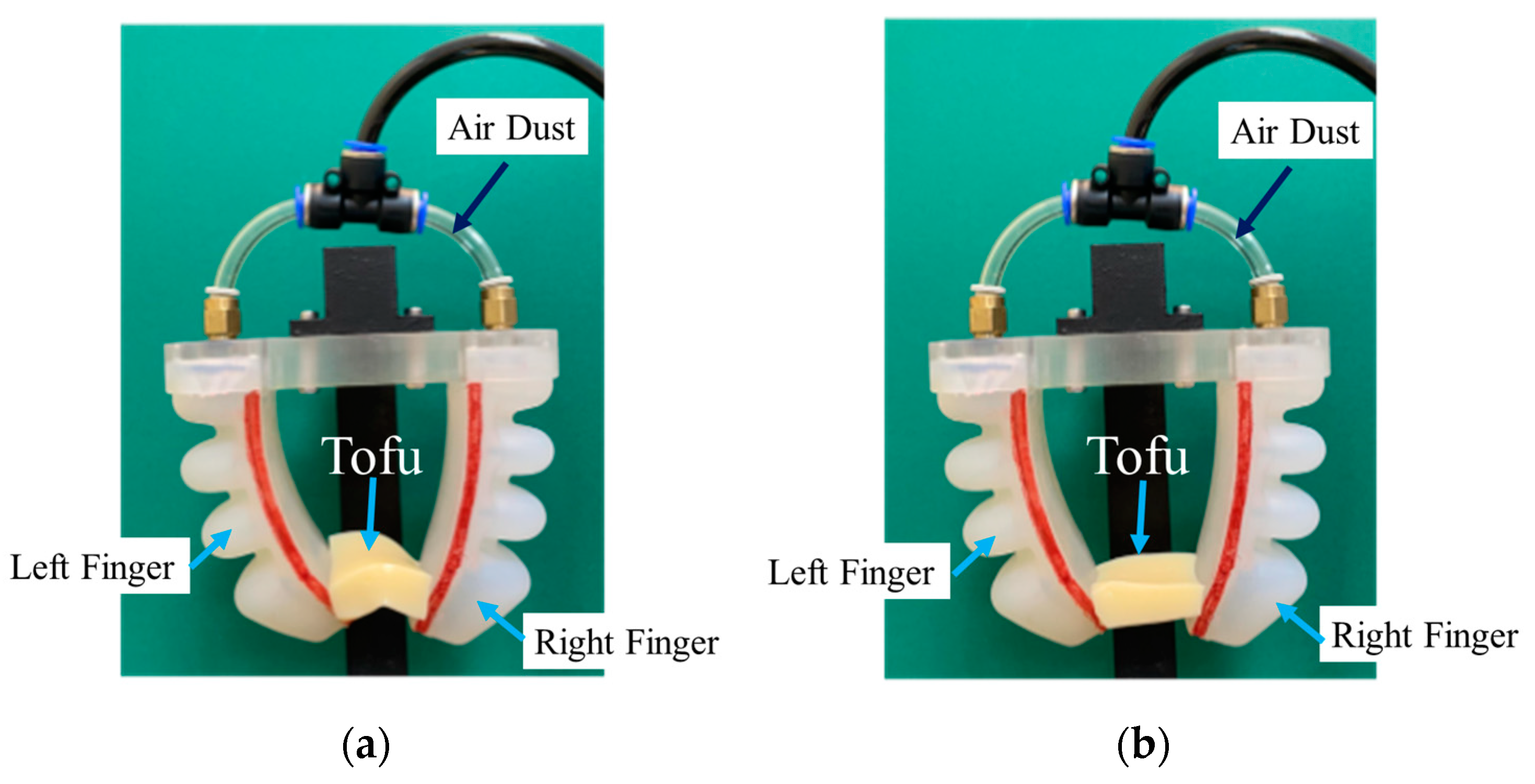
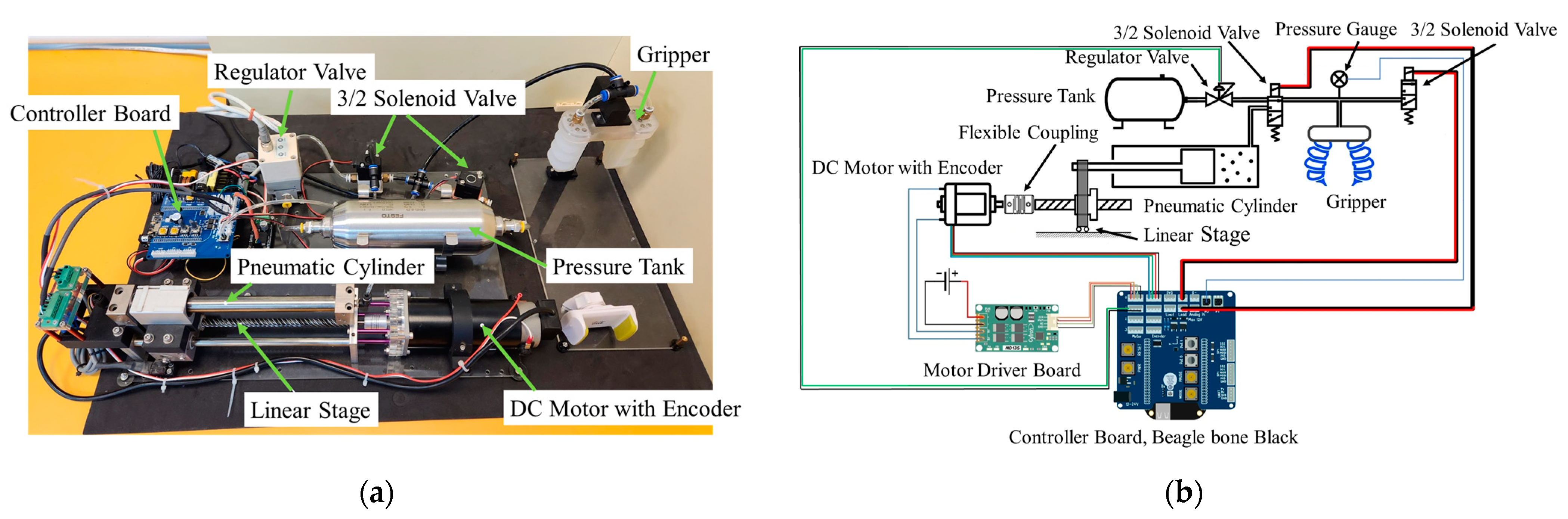
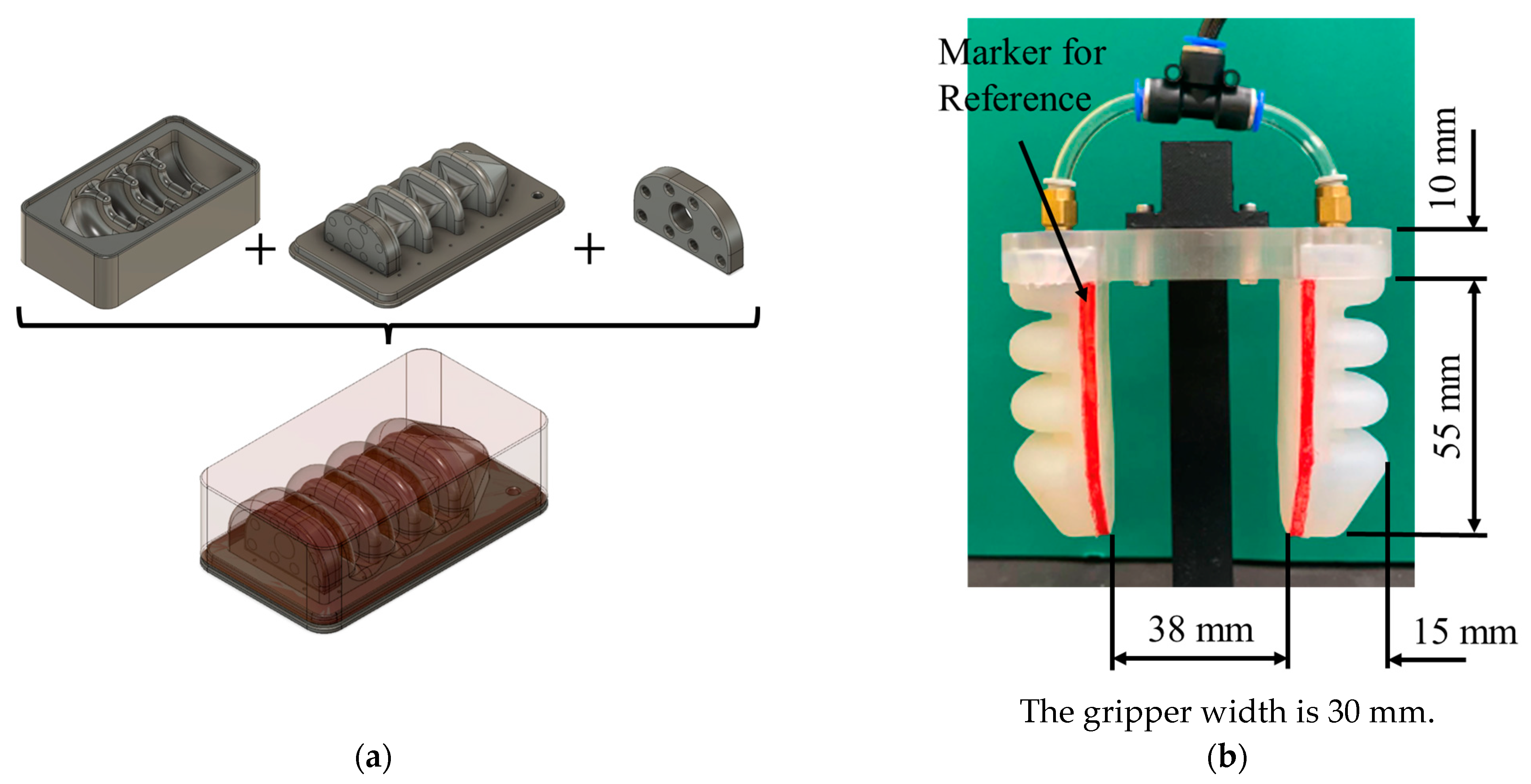
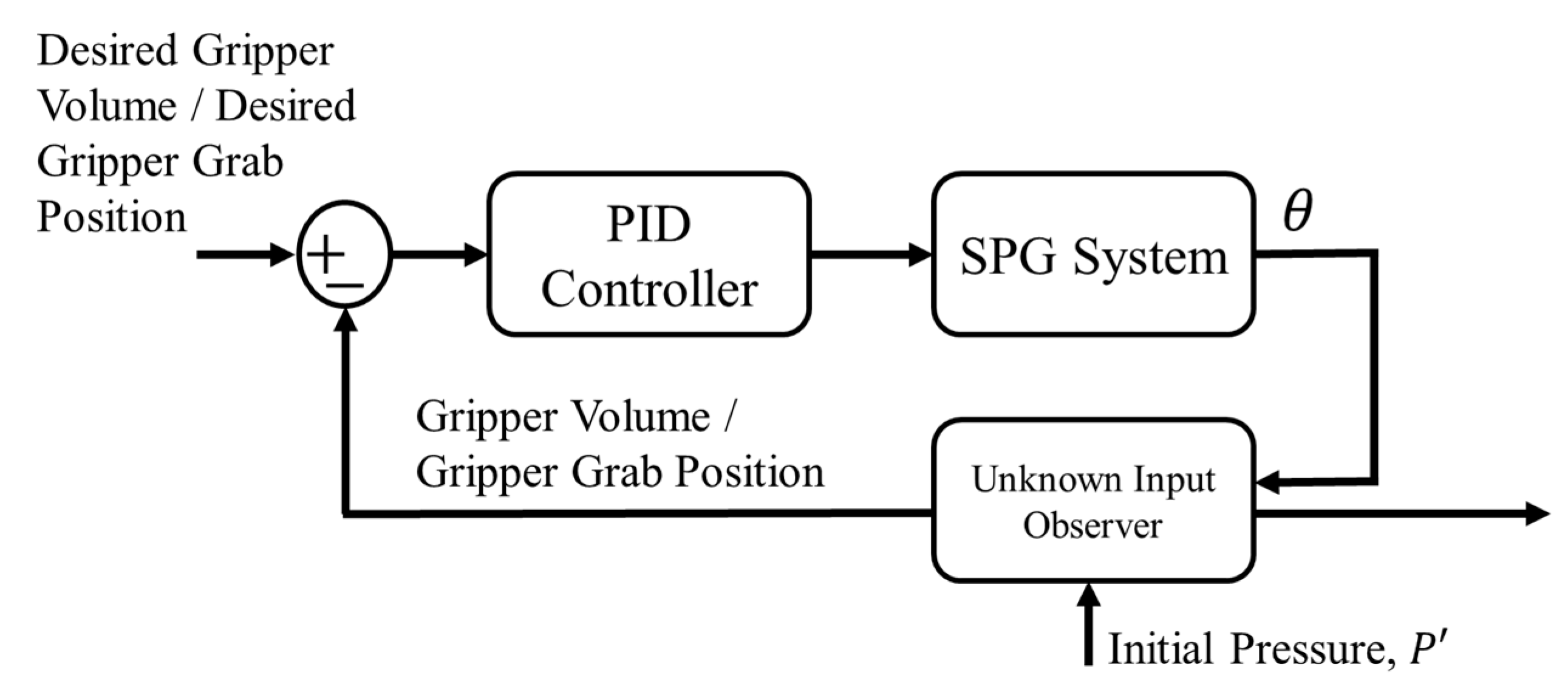
2.1. The System Architecture of Soft Pneumatic Gripper
2.2. Dynamic Model and Control Technique for the System
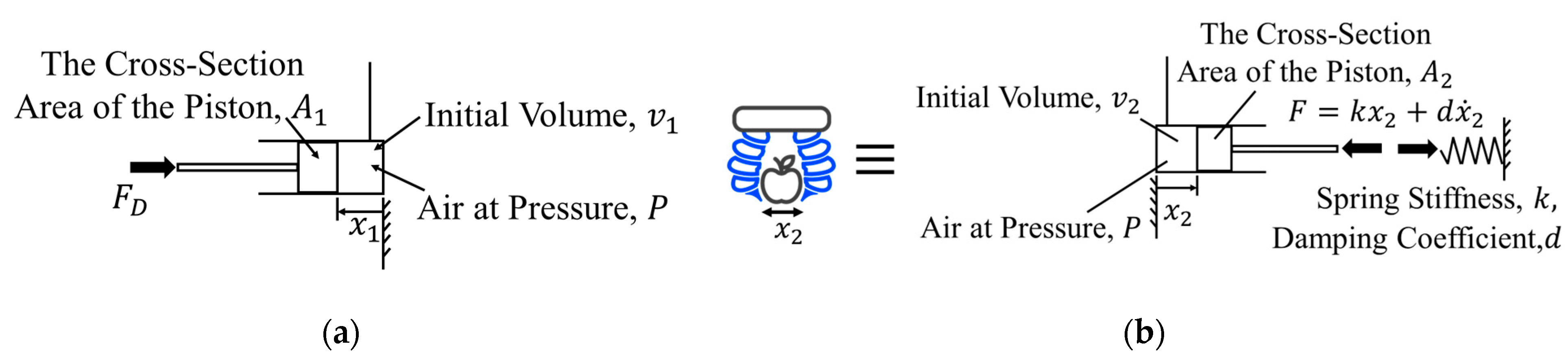
2.2.1. Dynamic Model of the System
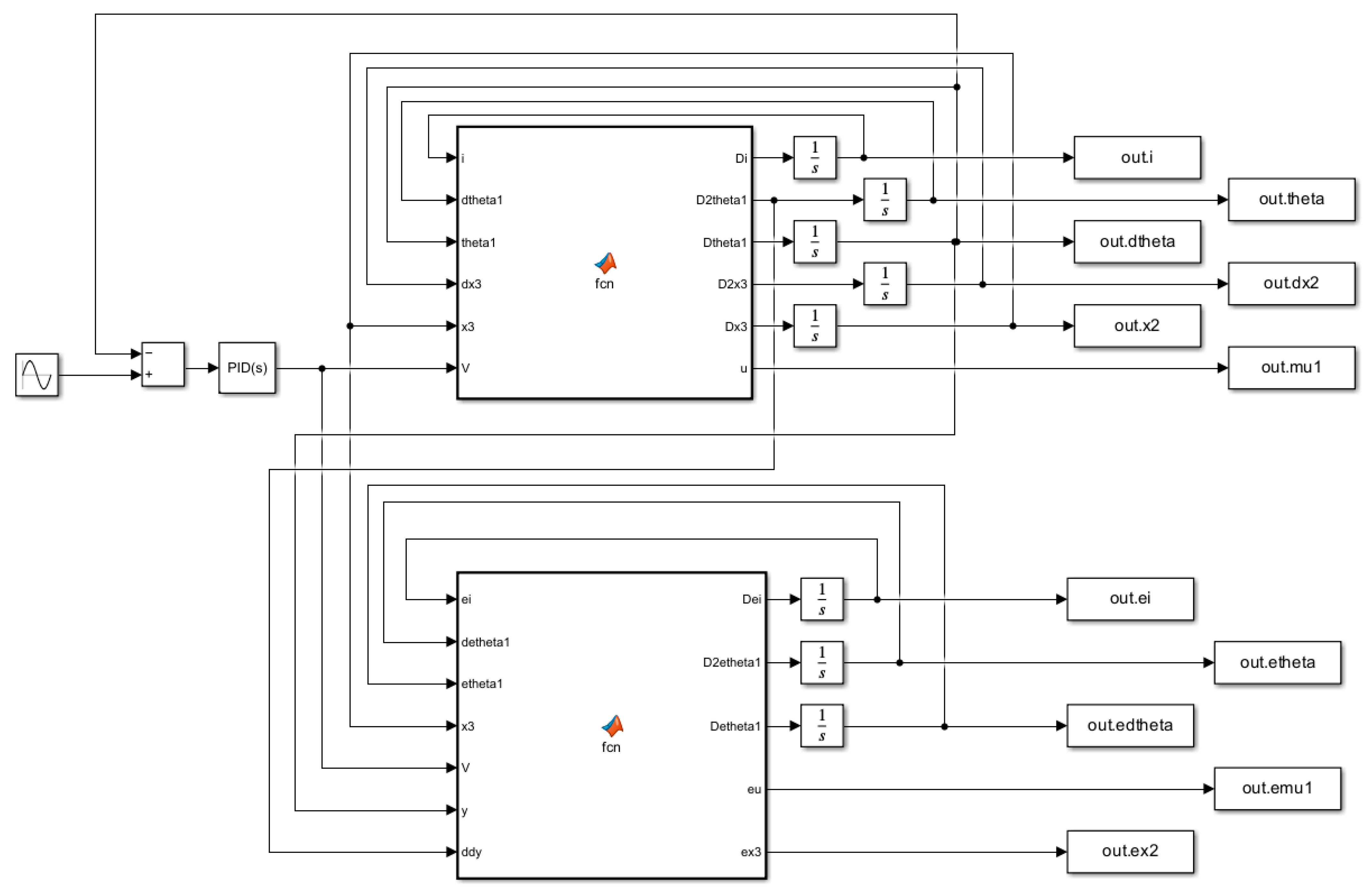
2.2.2. Unknown Input Observer
2.2.3. Control Technique
3. Experimental Results and Discussion
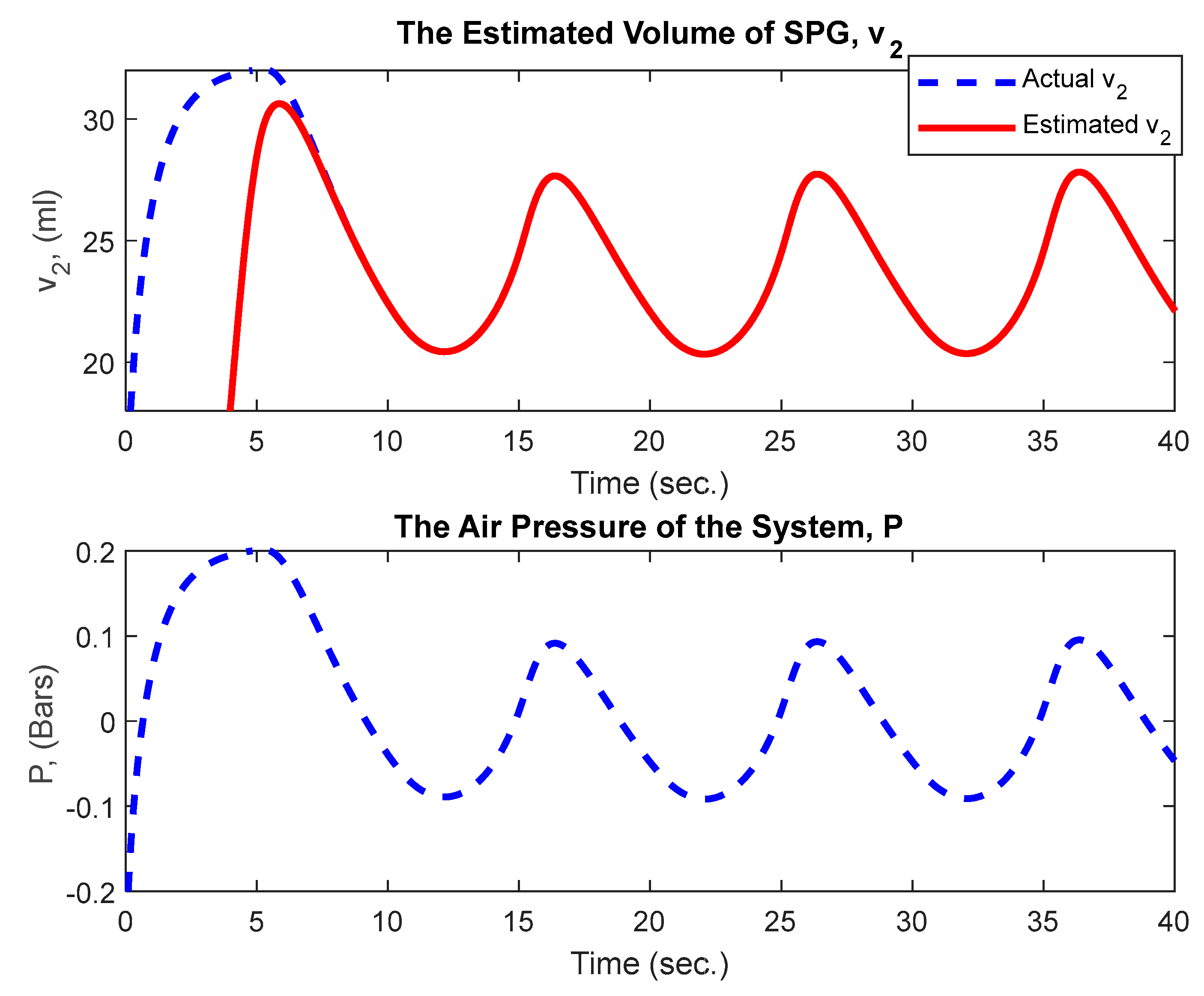
3.1. The Simulation Results of Unknown Input Observer
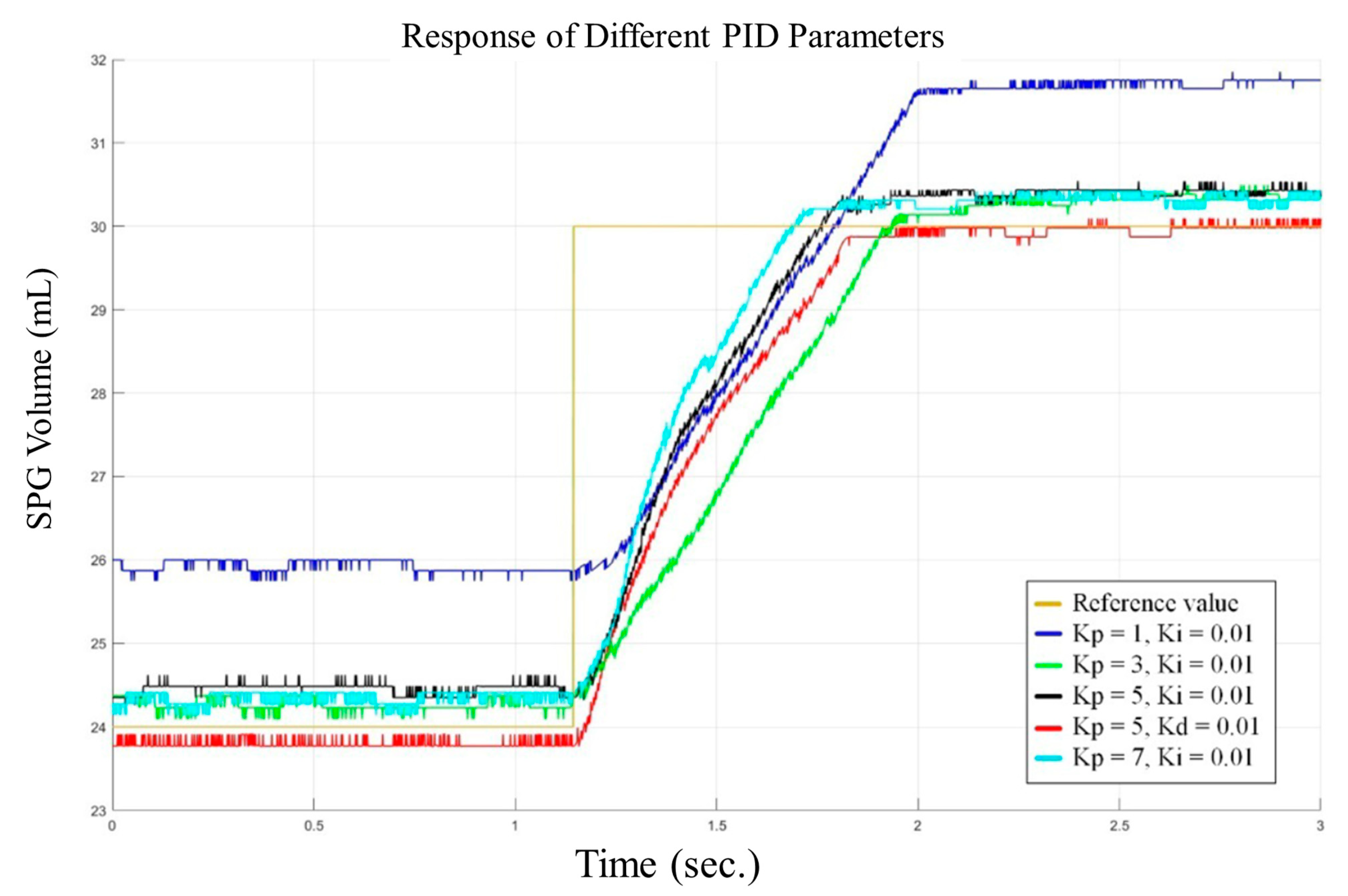
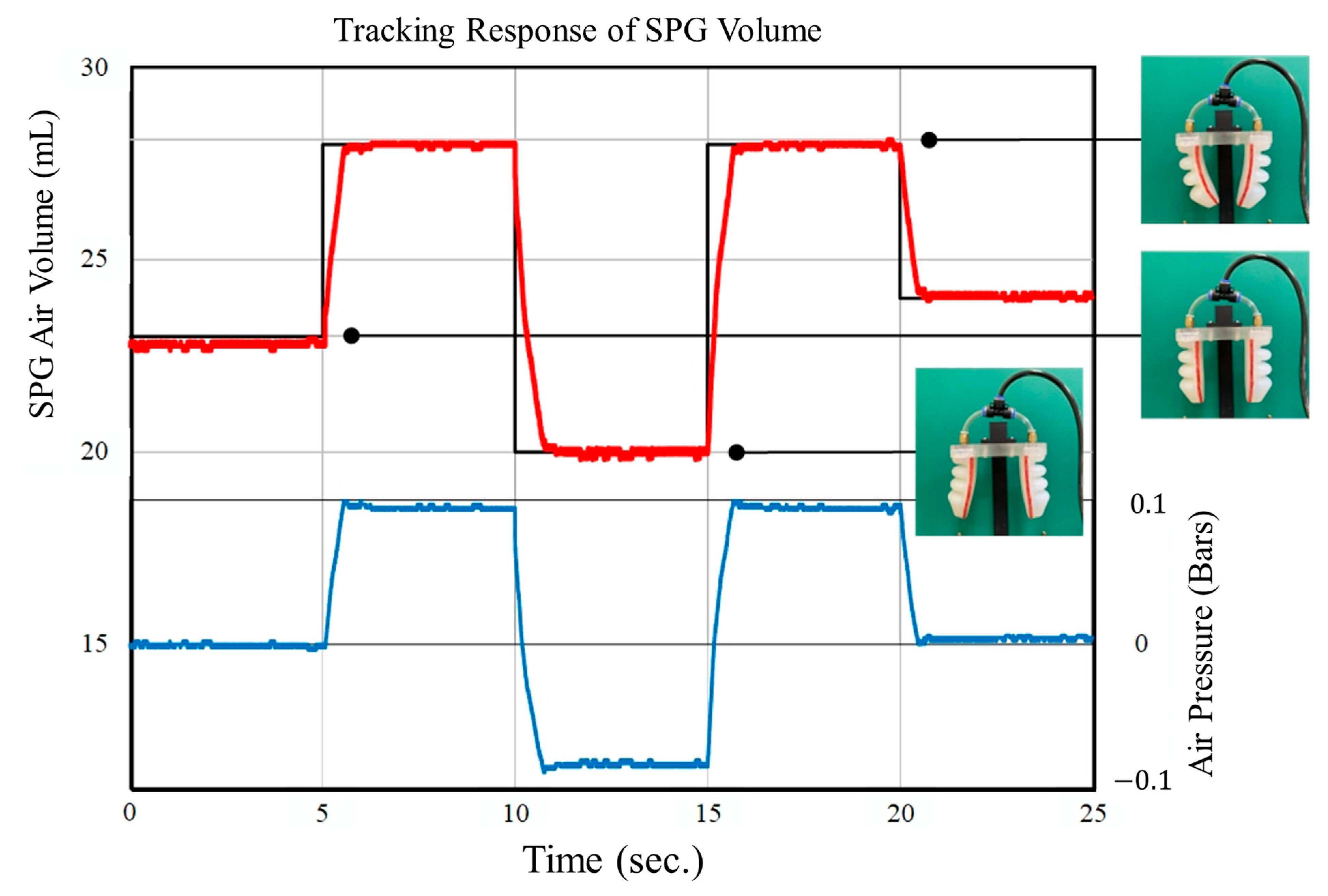
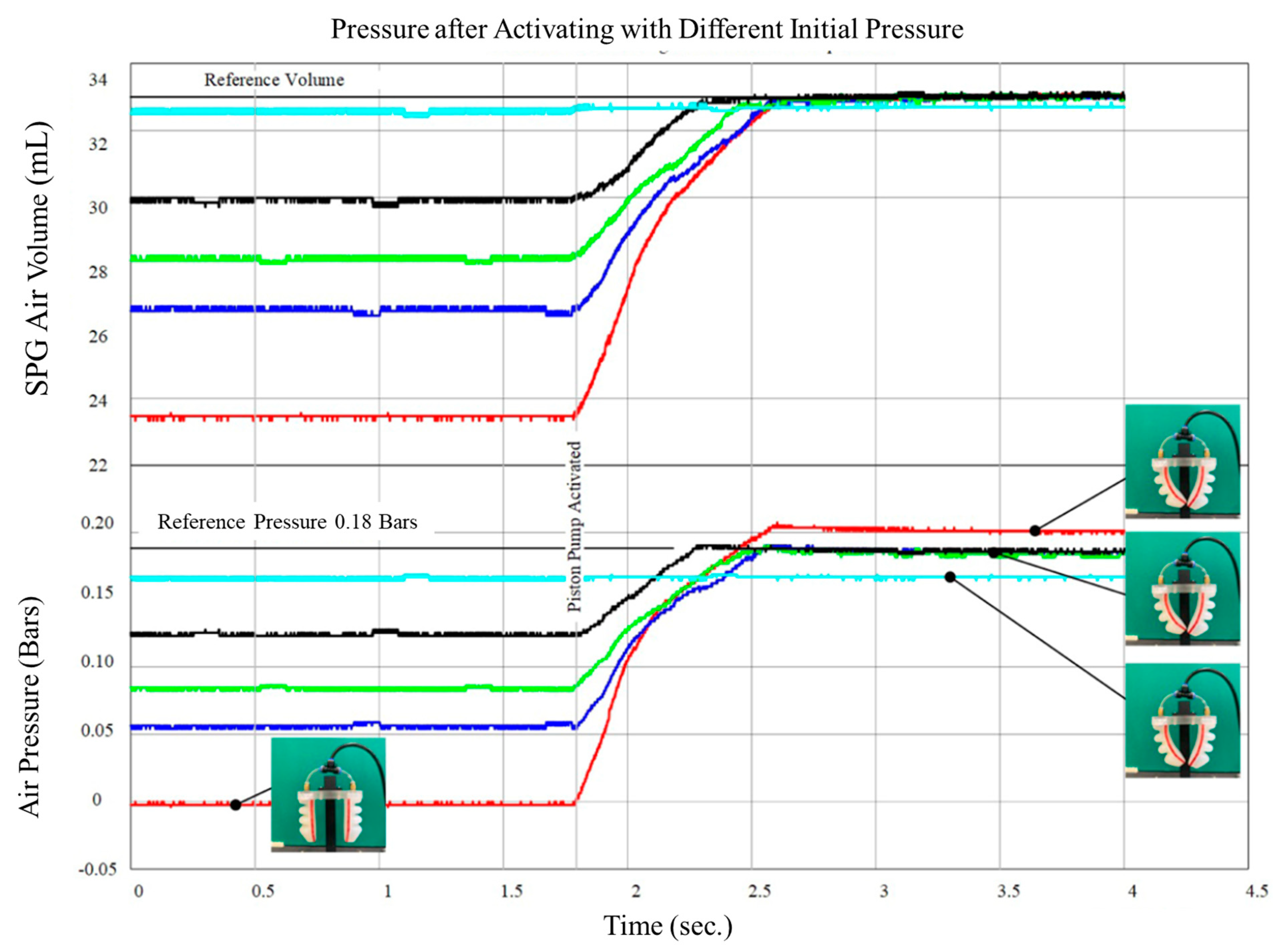
3.2. Experimental Results of the System
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, B.; Xie, Y.; Zhou, J.; Wang, K.; Zhang, Z. State-of-the-art robotic grippers, grasping and control strategies, as well as their applications in agricultural robots: A review. Comput. Electron. Agric. 2020, 177, 105694. [Google Scholar] [CrossRef]
- Samadikhoshkho, Z.; Zareinia, K.; Janabi-Sharifi, F. A brief review on robotic grippers classifications. In Proceedings of the 2019 IEEE Canadian Conference of Electrical and Computer Engineering (CCECE), Edmonton, AB, Canada, 5–8 May 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Birglen, L.; Schlicht, T. A statistical review of industrial robotic grippers. Robot. Comput.-Integr. Manuf. 2018, 49, 88–97. [Google Scholar] [CrossRef]
- Fujita, M.; Domae, Y.; Noda, A.; Garcia Ricardez, G.A.; Nagatani, T.; Zeng, A.; Song, S.; Rodriguez, A.; Causo, A.; Chen, I.M.; et al. What are the important technologies for bin picking? Technology analysis of robots in competitions based on a set of performance metrics. Adv. Robot. 2020, 34, 560–574. [Google Scholar] [CrossRef]
- Bader, F.; Rahimifard, S. A methodology for the selection of industrial robots in food handling. Innov. Food Sci. Emerg. Technol. 2020, 64, 102379. [Google Scholar] [CrossRef]
- Tai, K.; El-Sayed, A.-R.; Shahriari, M.; Biglarbegian, M.; Mahmud, S. State of the Art Robotic Grippers and Applications. Robotics 2016, 5, 11. [Google Scholar] [CrossRef]
- Hernandez, J.; Sunny, M.S.H.; Sanjuan, J.; Rulik, I.; Zarif, M.I.I.; Ahamed, S.I.; Ahmed, H.U.; Rahman, M.H. Current Designs of Robotic Arm Grippers: A Comprehensive Systematic Review. Robotics 2023, 12, 5. [Google Scholar] [CrossRef]
- Balaji, A.; Mithil, J.; Gousanal, J.J. Design and analysis of universal gripper for robotics applications. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1012, 012006. [Google Scholar] [CrossRef]
- Hu, Z.; Wan, W.; Koyama, K.; Harada, K. A mechanical screwing tool for parallel grippers—Design, optimization, and manipulation policies. IEEE Trans. Robot. 2021, 38, 1139–1159. [Google Scholar] [CrossRef]
- Zhang, H.; Peeters, J.; Demeester, E.; Kellens, K. Deep Learning Reactive Robotic Grasping With a Versatile Vacuum Gripper. IEEE Trans. Robot. 2022, 39, 1244–1259. [Google Scholar] [CrossRef]
- Tawk, C.; In Het Panhuis, M.; Spinks, G.M.; Alici, G. Bioinspired 3D printable soft vacuum actuators for locomotion robots, grippers and artificial muscles. Soft Robot. 2018, 5, 685–694. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; Yu, X.; Chai, H.; Li, Y.; Wu, H.; Jiang, S. Magnetic actuation bionic robotic gripper with bistable morphing structure. Compos. Struct. 2019, 229, 111422. [Google Scholar] [CrossRef]
- Dragusanu, M.; Marullo, S.; Malvezzi, M.; Achilli, G.M.; Valigi, M.C.; Prattichizzo, D.; Salvietti, G. The dressgripper: A collaborative gripper with electromagnetic fingertips for dressing assistance. IEEE Robot. Autom. Lett. 2022, 7, 7479–7486. [Google Scholar] [CrossRef]
- Gandarias, J.M.; Gómez-de-Gabriel, J.M.; García-Cerezo, A.J. Enhancing Perception with Tactile Object Recognition in Adaptive Grippers for Human–Robot Interaction. Sensors 2018, 18, 692. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.M.; Gerez, L.; Elangovan, N.; Zisimatos, A.; Liarokapis, M. On alternative uses of structural compliance for the development of adaptive robot grippers and hands. Front. Neurorobot. 2019, 13, 91. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, H.; Yuan, H.; Liang, B. A compliant adaptive gripper and its intrinsic force sensing method. IEEE Trans. Robot. 2021, 37, 1584–1603. [Google Scholar] [CrossRef]
- Glick, P.; Suresh, S.A.; Ruffatto, D.; Cutkosky, M.; Tolley, M.T.; Parness, A. A soft robotic gripper with gecko-inspired adhesive. IEEE Robot. Autom. Lett. 2018, 3, 903–910. [Google Scholar] [CrossRef]
- Reddy, P.V.P.; Suresh, V.V.N.S. A review on importance of universal gripper in industrial robot applications. Int. J. Mech. Eng. Robot. Res. 2013, 2, 255–264. [Google Scholar]
- Lundström, G. Industrial robot grippers. Ind. Robot: Int. J. 1974, 1, 72–82. [Google Scholar] [CrossRef]
- Giannaccini, M.E.; Georgilas, I.; Horsfield, I.; Peiris, B.H.P.M.; Lenz, A.; Pipe, A.G.; Dogramadzi, S. A variable compliance, soft gripper. Auton. Robot. 2014, 36, 93–107. [Google Scholar] [CrossRef]
- Sithiwichankit, C.; Chanchareon, R. Adaptive Pincer Grasping of Soft Pneumatic Grippers Based on Object Stiffness for Modellable and Controllable Grasping Quality. Robotics 2022, 11, 132. [Google Scholar] [CrossRef]
- Shintake, J.; Cacucciolo, V.; Floreano, D.; Shea, H. Soft robotic grippers. Adv. Mater. 2018, 30, 1707035. [Google Scholar] [CrossRef]
- Wang, Z.; Torigoe, Y.; Hirai, S. A prestressed soft gripper: Design, modeling, fabrication, and tests for food handling. IEEE Robot. Autom. Lett. 2017, 2, 1909–1916. [Google Scholar] [CrossRef]
- Wang, Z.; Or, K.; Hirai, S. A dual-mode soft gripper for food packaging. Robot. Auton. Syst. 2020, 125, 103427. [Google Scholar] [CrossRef]
- Hines, L.; Petersen, K.; Lum, G.Z.; Sitti, M. Soft Actuators for Small-Scale Robotics. Adv. Mater. 2017, 29, 1603483. [Google Scholar] [CrossRef]
- Polygerinos, P.; Correll, N.; Morin, S.A.; Mosadegh, B.; Onal, C.D.; Petersen, K.; Cianchetti, M.; Tolley, M.T.; Shepherd, R.F. Soft Robotics: Review of Fluid-Driven Intrinsically Soft Devices; Manufacturing, Sensing, Control, and Applications in Human-Robot Interaction. Adv. Eng. Mater. 2017, 19, 1700016. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, X.; Huang, Y.; Cao, L.; Liu, J. A Review of Soft Manipulator Research, Applications, and Opportunities. J. Field Robot. 2022, 39, 281–311. [Google Scholar] [CrossRef]
- Su, H.; Hou, X.; Zhang, X.; Qi, W.; Cai, S.; Xiong, X.; Guo, J. Pneumatic Soft Robots: Challenges and Benefits. Actuators 2022, 11, 92. [Google Scholar] [CrossRef]
- Suzumori, K.; Iikura, S.; Tanaka, H. Applying a Flexible Microactuator to Robotic Mechanisms. IEEE Control Syst. Mag. 1992, 12, 21–27. [Google Scholar] [CrossRef]
- Godage, I.S.; Wirz, R.; Walker, I.D.; Webster, R.J. Accurate and Efficient Dynamics for Variable-Length Continuum Arms: A Center of Gravity Approach. Soft Robot 2015, 2, 96–106. [Google Scholar] [CrossRef]
- Polygerinos, P.; Wang, Z.; Overvelde, J.T.B.; Galloway, K.C.; Wood, R.J.; Bertoldi, K.; Walsh, C.J. Modeling of Soft Fiber-Reinforced Bending Actuators. IEEE Trans. Robot. 2015, 31, 778–789. [Google Scholar] [CrossRef]
- Gerboni, G.; Diodato, A.; Ciuti, G.; Cianchetti, M.; Menciassi, A. Feedback Control of Soft Robot Actuators via Commercial Flex Bend Sensors. IEEE/ASME Trans. Mechatron. 2017, 22, 1881–1888. [Google Scholar] [CrossRef]
- Hao, Y.; Wang, T.; Ren, Z.; Gong, Z.; Wang, H.; Yang, X.; Guan, S.; Wen, L. Modeling and Experiments of a Soft Robotic Gripper in Amphibious Environments. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417707148. [Google Scholar] [CrossRef]
- Wang, Z.; Hirai, S. Soft Gripper Dynamics Using a Line-Segment Model with an Optimization-Based Parameter Identification Method. IEEE Robot. IEEE Robot. Autom. Lett. 2017, 2, 624–631. [Google Scholar] [CrossRef]
- Ibrahim, S.; Krause, J.C.; Olbrich, A.; Raatz, A. Modeling and Reconstruction of State Variables for Low-Level Control of Soft Pneumatic Actuators. Front. Robot. AI 2021, 8, 557830. [Google Scholar] [CrossRef]
- Xavier, M.S.; Fleming, A.J.; Yong, Y.K. Modelling and Simulation of Pneumatic Sources for Soft Robotic Applications. In Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 6–9 July 2020; pp. 916–921. [Google Scholar] [CrossRef]
- Terrile, S.; Argüelles, M.; Barrientos, A. Comparison of Different Technologies for Soft Robotics Grippers. Sensors 2021, 21, 3253. [Google Scholar] [CrossRef] [PubMed]
- Pandian, S.R.; Takemura, F.; Hayakawa, Y.; Kawamura, S. Pressure observer-controller design for pneumatic cylinder actuators. IEEE/ASME Trans. Mechatron. 2002, 7, 490–499. [Google Scholar] [CrossRef]
- Ohara, K.; Iwazawa, R.; Kaneko, M. Modeling and Analysis of a High-Speed Adjustable Grasping Robot Controlled by a Pneumatic Actuator. Robotics 2022, 11, 27. [Google Scholar] [CrossRef]
- The MathWorks Inc. Matlab. Available online: https://www.mathworks.com (accessed on 23 April 2023).
- Jintanawan, T.; Phanomchoeng, G.; Suwankawin, S.; Kreepoke, P.; Chetchatree, P.; U-viengchai, C. Design of Kinetic-Energy Harvesting Floors. Energies 2020, 13, 5419. [Google Scholar] [CrossRef]
- Phanomchoeng, G.; Chancharoen, R. Hybrid motor system for high precision position control of a heavy load plant. Eng. J. 2019, 23, 161–173. [Google Scholar] [CrossRef]
- Phanomchoeng, G.; Rajamani, R. Real-Time Estimation of Rollover Index for Tripped Rollovers with a Novel Unknown Input Nonlinear Observer. IEEE/ASME Trans. Mechatron. 2014, 19, 743–754. [Google Scholar] [CrossRef]
- Phanomchoeng, G.; Zemouche, A.; Jeon, W.; Rajamani, R.; Mazenc, F. H∞ Observer for Descriptor Nonlinear Systems with Nonlinear Output Equations. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 5952–5956. [Google Scholar] [CrossRef]


| Components | Parameters | Value | Unit |
|---|---|---|---|
| Pneumatic Cylinder | Volume, | 25.5 | |
| Cross-Section Area of the Piston, | 16.67 | ||
| Mass of the Piston, | 0.736 | ||
| Stroke Length | 153 | ||
| SPG | Volume, @1atm | 23.6 | |
| Mass of the Gripper | 0.1 | kg | |
| DC Motor | Moment of Inertia of the Rotor, | ||
| Electric Resistance, | 0.9 | ||
| Electric Inductance, | |||
| Electromotive Force Constant, | |||
| Motor Torque Constant, | |||
| Linear Stage | Pitch of the Ball Screw, | ||
| Efficiencies of the Thread of Ball Screw, | 0.9 | ||
| Efficiencies of the Thrust Bearing of Ball Screw, | 0.9 | ||
| Encoder | Pulse per Revolution | 4000 | |
| 1 Pulse of Encoder | 0.006375 | ||
| The System | Dead Volume | 17.15 | |
| Atmospheric Pressure | 1 |
| Gripper Volume Setting via a Syringe (mL) | Gripper Distance, D (mm)  | ||||
|---|---|---|---|---|---|
| Gripper Distance with Syringe Pressure Control | |||||
| 24 | 48.5 | 42.0 | - | - | - |
| 25 | 30.0 | 33.1 | - | - | - |
| 27 | 23.4 | 22.3 | 22.2 | - | - |
| 29 | 16.9 | 14.4 | 15.8 | 17.3 | - |
| 31 | 9.7 | 6.2 | 9.3 | 9.7 | 10.5 |
| 33 | 3.7 | 0 | 3.2 | 2.6 | 3.7 |
| 36 | 0 | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phanomchoeng, G.; Pitchayawetwongsa, P.; Boonchumanee, N.; Lin, S.; Chancharoen, R. Grasping Profile Control of a Soft Pneumatic Robotic Gripper for Delicate Gripping. Robotics 2023, 12, 107. https://doi.org/10.3390/robotics12040107
Phanomchoeng G, Pitchayawetwongsa P, Boonchumanee N, Lin S, Chancharoen R. Grasping Profile Control of a Soft Pneumatic Robotic Gripper for Delicate Gripping. Robotics. 2023; 12(4):107. https://doi.org/10.3390/robotics12040107
Chicago/Turabian StylePhanomchoeng, Gridsada, Patchara Pitchayawetwongsa, Nattaphat Boonchumanee, Saravut Lin, and Ratchatin Chancharoen. 2023. "Grasping Profile Control of a Soft Pneumatic Robotic Gripper for Delicate Gripping" Robotics 12, no. 4: 107. https://doi.org/10.3390/robotics12040107
APA StylePhanomchoeng, G., Pitchayawetwongsa, P., Boonchumanee, N., Lin, S., & Chancharoen, R. (2023). Grasping Profile Control of a Soft Pneumatic Robotic Gripper for Delicate Gripping. Robotics, 12(4), 107. https://doi.org/10.3390/robotics12040107








