Playing Checkers with an Intelligent and Collaborative Robotic System †
Abstract
1. Introduction
- the recognition of the board and positions of pieces with respect to the robot, piece color, and type, as well as the human player move;
- the decision of which is the optimal move to perform among all the possible ones according to a proper game strategy;
- the trajectory planning and control of the robot in order to physically execute the chosen move.
2. Related Works
3. Materials and Methods
3.1. Italian Checkers Rules
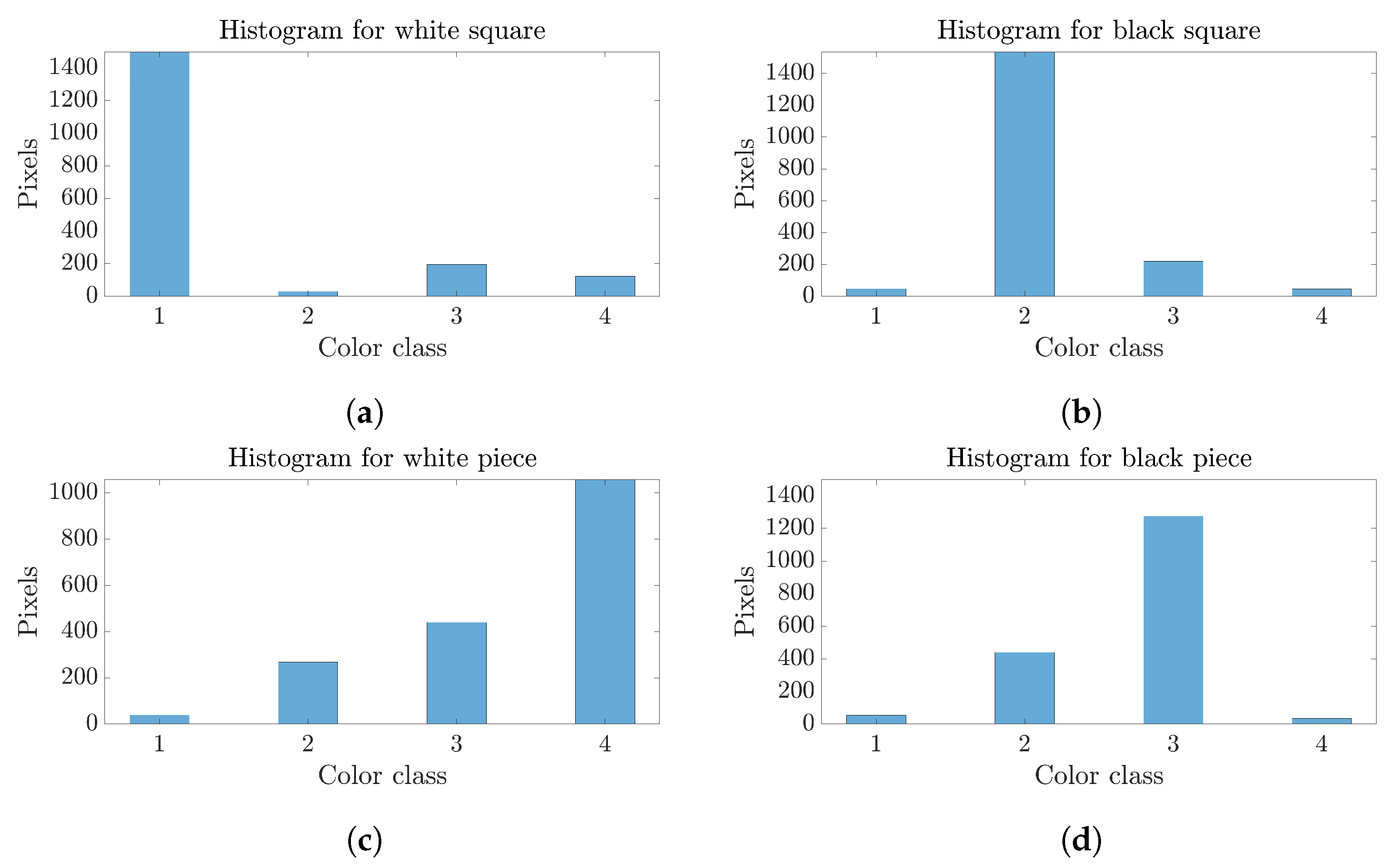
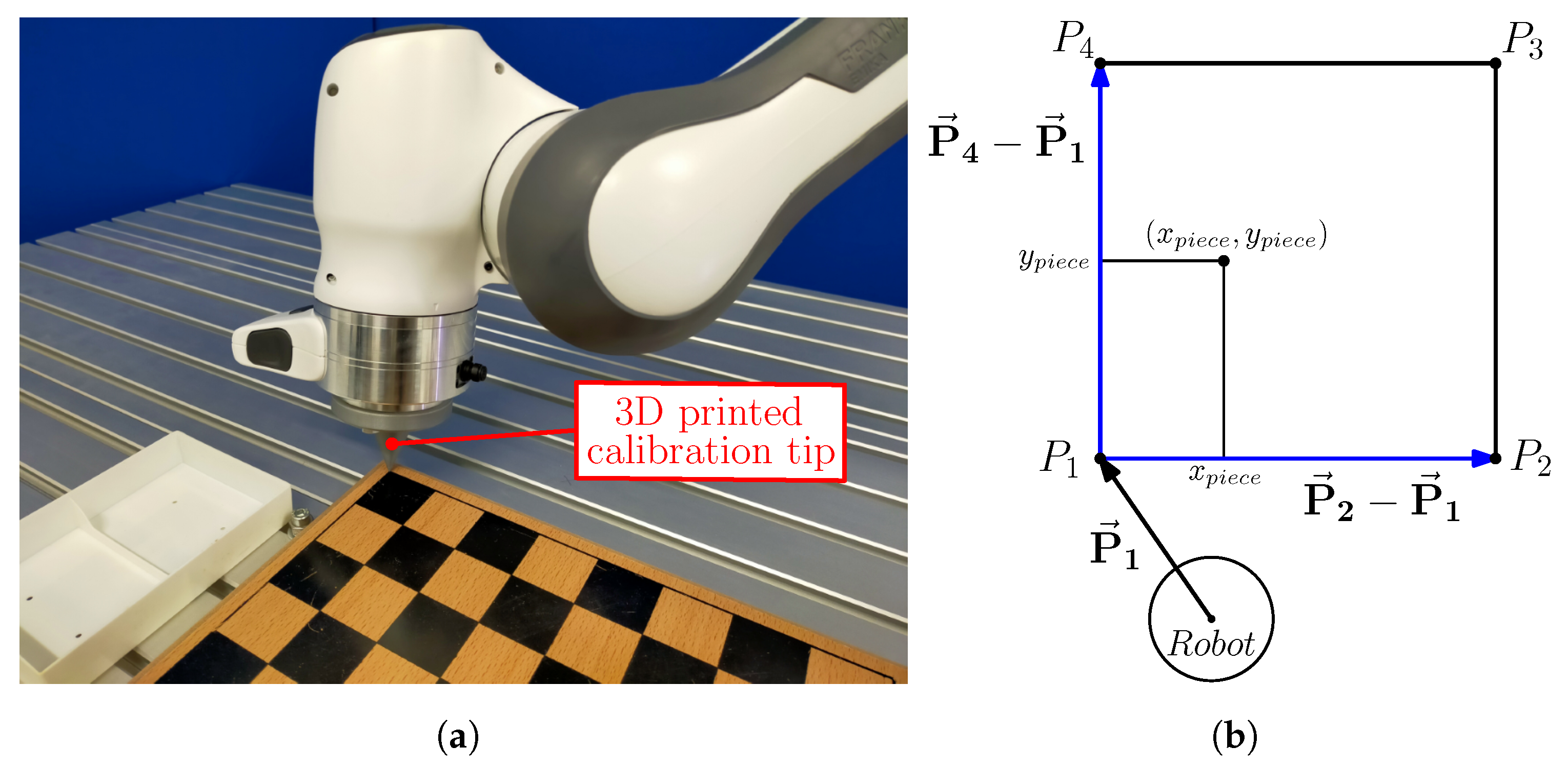
3.2. Game State Evaluation
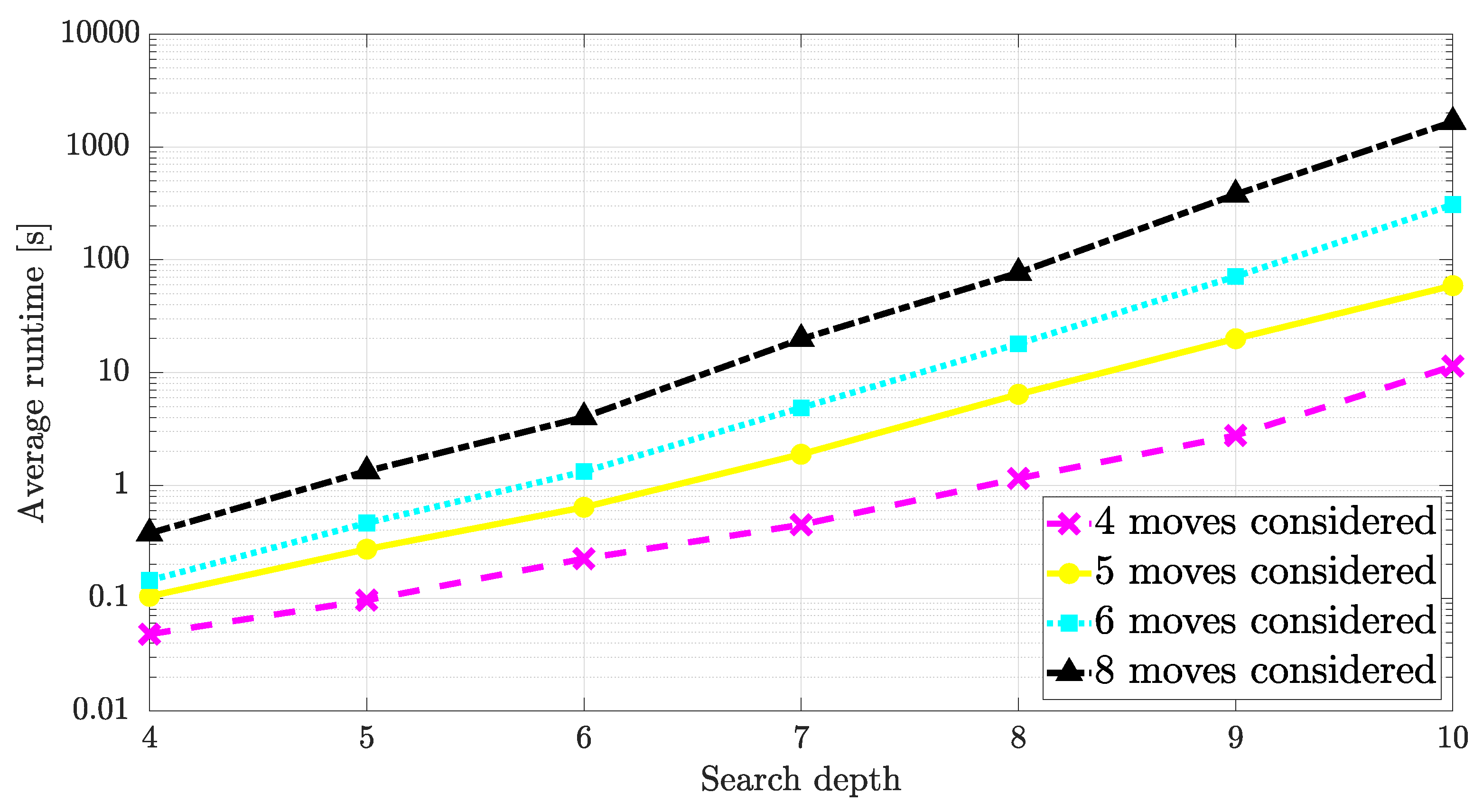
3.3. Game Engine
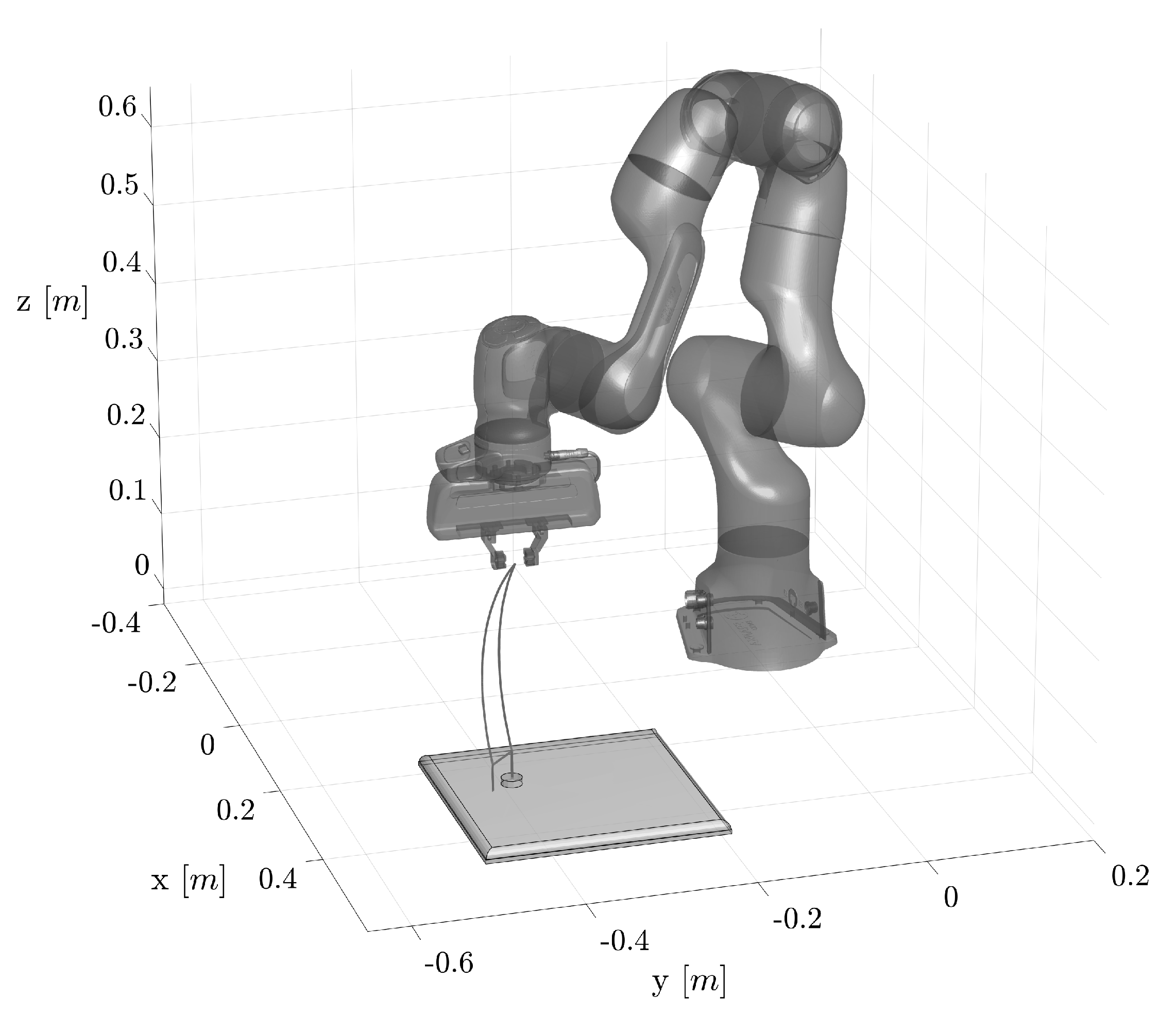
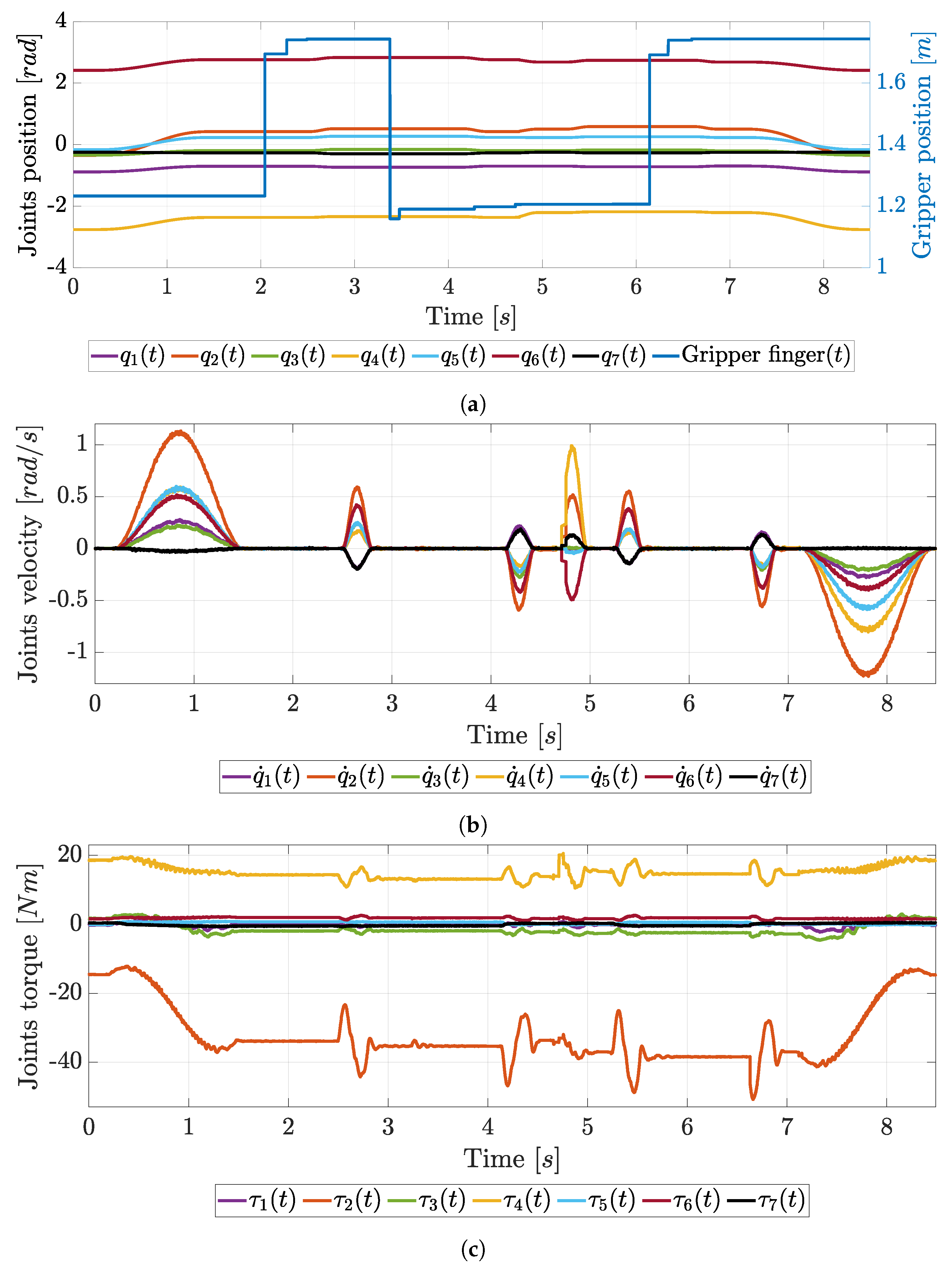
3.4. Trajectory Planning
- in the case of a simple movement, the robot positions the piece in the target square and then returns to the neutral pose;
- if a capture (including multiple ones) has to be made, the robot, after placing its piece in the target square, proceeds to eliminate from the board the opponent piece (or pieces) captured;
- when a move results in a man becoming a king, the robot avoids stacking pieces to make king by itself; instead, it removes the man from the board and takes the king, which is prepared in a reference position outside the board.
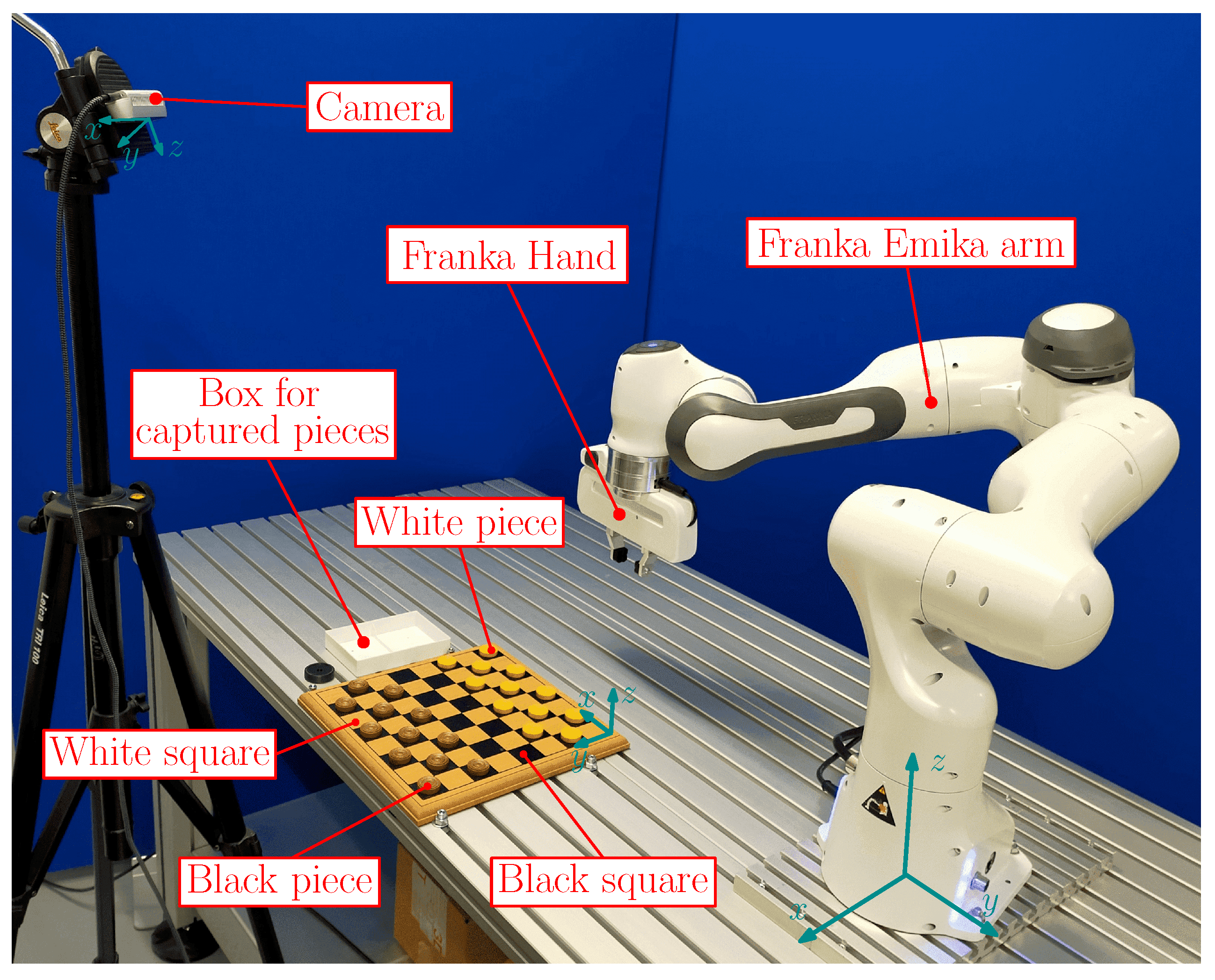
3.5. Experimental Setup
- robotic arm;
- computer and control system;
- camera;
- board and pieces.
4. Results
5. Conclusions
- •
- Vision system: the robustness and reliability of the computer vision algorithm will be improved through the implementation of an approach based on model recognition, which is more robust with respect to illumination, and an ad hoc illumination system;
- •
- Computational times: the alpha–beta pruning algorithm will be implemented to speed up the execution times of the gaming algorithm and enhance its overall performance;
- •
- Safety of the human player: safety strategies will be implemented to track the human position in real time and stop the robot in the case of a potential collision, as in [2]. Furthermore, the safety of the gripper will also be considered to avoid accidents, such as the one in 2022, when a chess robot broke a finger of 7-year-old boy during a tournament in Moscow [34].
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vicentini, F. Collaborative robotics: A survey. J. Mech. Des. 2021, 143, 040802. [Google Scholar] [CrossRef]
- Scalera, L.; Giusti, A.; Vidoni, R.; Gasparetto, A. Enhancing fluency and productivity in human-robot collaboration through online scaling of dynamic safety zones. Int. J. Adv. Manuf. Technol. 2022, 121, 6783–6798. [Google Scholar] [CrossRef]
- Dell’Ariccia, A.; Bremers, A.W.; Lee, W.-Y.; Ju, W. “Ah! he wants to win!”: Social responses to playing Tic-Tac-Toe against a physical drawing robot. In Proceedings of the 16th International Conference on Tangible, Embedded, and Embodied Interaction, Daejeon, Republic of Korea, 13–16 February 2022; pp. 1–6. [Google Scholar]
- Carbonari, L.; Forlini, M.; Scoccia, C.; Costa, D.; Palpacelli, M.-C. Disseminating Collaborative Robotics and Artificial Intelligence Through a Board Game Demo. In Proceedings of the 18th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Taipei, Taiwan, 28–30 November 2022; pp. 1–5. [Google Scholar]
- Karimov, A.; Kopets, E.; Leonov, S.; Scalera, L.; Butusov, D. A Robot for Artistic Painting in Authentic Colors. J. Intell. Robot. Syst. 2023, 107, 34. [Google Scholar] [CrossRef]
- Lin, J.-Y.; Kawai, M.; Nishio, Y.; Cosentino, S.; Takanishi, A. Development of performance system with musical dynamics expression on humanoid saxophonist robot. IEEE Robot. Autom. Lett. 2019, 4, 1684–1690. [Google Scholar] [CrossRef]
- Samuel, A.L. Some studies in machine learning using the game of checkers. IBM J. Res. Dev. 1959, 3, 210–229. [Google Scholar] [CrossRef]
- Schrittwieser, J.; Antonoglou, I.; Hubert, T.; Simonyan, K.; Sifre, L.; Schmitt, S.; Guez, A.; Lockhart, E.; Hassabis, D.; Graepel, T.; et al. Mastering atari, go, chess and shogi by planning with a learned model. Nature 2020, 588, 604–609. [Google Scholar] [CrossRef] [PubMed]
- Bernbaum, A.; Greenberg, B.; Latreille, J.; Mistry, S.; Pattison, L.; Ruegg, P.; Zhang, S. De3-rob1 Chess Group Documentation, Chess Project for the Robotics 1 Module in Design Engineering, Imperial College London. 2018. Available online: https://de3-rob1-chess.readthedocs.io/en/latest/ (accessed on 5 December 2023).
- Fabris, G.; Scalera, L.; Gasparetto, A. An interactive collaborative robotic system to play Italian checkers. In IFToMM World Congress on Mechanism and Machine Science; Springer: Berlin/Heidelberg, Germany, 2023; pp. 74–84. [Google Scholar]
- Juang, L.-H. Humanoid robots play chess using visual control. Multimed. Tools Appl. 2022, 81, 1545–1566. [Google Scholar] [CrossRef]
- Kołosowski, P.; Wolniakowski, A.; Miatliuk, K. Collaborative robot system for playing chess. In Proceedings of the International Conference Mechatronic Systems and Materials (MSM), Bialystok, Poland, 1–3 July 2020; pp. 1–6. [Google Scholar]
- Chen, A.T.-Y.; Wang, K.I.-K. Robust computer vision chess analysis and interaction with a humanoid robot. Computers 2019, 8, 14. [Google Scholar] [CrossRef]
- del Toro, C.; Robles-Algarín, C.; Rodríguez-Álvarez, O. Design and construction of a cost-effective didactic robotic arm for playing chess, using an artificial vision system. Electronics 2019, 8, 1154. [Google Scholar] [CrossRef]
- Barakova, E.I.; De Haas, M.; Kuijpers, W.; Irigoyen, N.; Betancourt, A. Socially grounded game strategy enhances bonding and perceived smartness of a humanoid robot. Connect. Sci. 2018, 30, 81–98. [Google Scholar] [CrossRef]
- Brooks, D.J.; McCann, E.; Allspaw, J.; Medvedev, M.; Yanco, H.A. Sense, plan, triple jump. In Proceedings of the IEEE International Conference on Technologies for Practical Robot Applications (TePRA), Woburn, MA, USA, 11–12 May 2015; pp. 1–6. [Google Scholar]
- Larregay, G.; Pinna, F.; Avila, L.; Morán, D. Design and Implementation of a Computer Vision System for an Autonomous Chess-Playing Robot. J. Comput. Sci. Technol. 2018, 18, 1–11. [Google Scholar] [CrossRef]
- Luqman, H.M.; Zaffar, M. Chess brain and autonomous chess playing robotic system. In Proceedings of the International Conference on Autonomous Robot Systems and Competitions (ICARSC), Bragança, Portugal, 4–6 May 2016; pp. 211–216. [Google Scholar]
- Gupta, V.; Kumar, A.; Agrawal, S.; Jaiswal, S. Autonomous Chess Playing Robot. Int. J. Eng. Res. Technol. 2015, 4. [Google Scholar]
- Kopets, E.E.; Karimov, A.I.; Kolev, G.Y.; Scalera, L.; Butusov, D.N. Interactive Robot for Playing Russian Checkers. Robotics 2020, 9, 107. [Google Scholar] [CrossRef]
- Rath, P.K.; Mahapatro, N.; Nath, P.; Dash, R. Autonomous Chess Playing Robot. In Proceedings of the 28th IEEE International Conference on Robot and Human Interactive Communication (RO-MAN), New Delhi, India, 14–18 October 2019; pp. 1–6. [Google Scholar]
- Escandon, E.R.; Campion, J. Minimax checkers playing GUI: A foundation for AI applications. In Proceedings of the XXV International Conference on Electronics, Electrical Engineering and Computing (INTERCON), Lima, Peru, 8–10 August 2018; pp. 1–4. [Google Scholar]
- Nasa, R.; Didwania, R.; Maji, S.; Kumar, V. Alpha-Beta Pruning in Mini-Max Algorithm–An Optimized Approach for a Connect-4 Game. Int. Res. J. Eng. Technol. 2018, 5, 1637–1641. [Google Scholar]
- Elnaggar, A.A.; Gadallah, M.; Aziem, M.A.; Aldeeb, H. Autonomous checkers robot using enhanced massive parallel game tree search. In Proceedings of the 2014 9th International Conference on Informatics and Systems, Cairo, Egypt, 15–17 December 2014; pp. 35–44. [Google Scholar]
- Rodrıguez-Sedano, F.J.; Esteban, G.; Inyesto, L.; Blanco, P.; Rodrıguez-Lera, F.J. Strategies for haptic-robotic teleoperation in board games: Playing checkers with Baxter. Strategies 2016, 31–37. [Google Scholar]
- Carrera, L.; Morales, F.; Tobar, J.; Loza, D. MARTI: A robotic chess module with interactive table, for learning purposes. In Proceedings of the World Congress on Engineering and Computer Science, San Francisco, CA, USA, 25–27 October 2017; pp. 25–27. [Google Scholar]
- Lukač, D. Playing chess with the assistance of an industrial robot. In Proceedings of the 3rd International Conference on Control and Robotics Engineering (ICCRE), Nagoya, Japan, 20–23 April 2018; pp. 1–5. [Google Scholar]
- Manurung, E.B. Gantry Robot System Checkers Player. ADI J. Recent Innov. 2023, 5, 9–19. [Google Scholar] [CrossRef]
- Matuszek, C.; Mayton, B.; Aimi, R.; Deisenroth, M.P.; Bo, L.; Chu, R.; Kung, M.; LeGrand, L.; Smith, J.R.; Fox, D. Gambit: An autonomous chess-playing robotic system. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 4291–4297. [Google Scholar]
- Italian Checkers Rules. Available online: https://www.boardgamecentral.com/rules/checkers-rules-italian.html (accessed on 2 October 2023).
- Diez, S.G.; Laforge, J.; Saerens, M. Rminimax: An optimally randomized MINIMAX algorithm. IEEE Trans. Cybern. 2012, 43, 385–393. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Andersson, J.A.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi: A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Gaz, C.; Cognetti, M.; Oliva, A.; Giordano, P.R.; De Luca, A. Dynamic identification of the franka emika panda robot with retrieval of feasible parameters using penalty-based optimization. IEEE Robot. Autom. Lett. 2019, 4, 4147–4154. [Google Scholar] [CrossRef]
- Chess Robot Grabs and Breaks Finger of Seven-Year-Old Opponent. Available online: https://www.theguardian.com/sport/2022/jul/24/chess-robot-grabs-and-breaks-finger-of-seven-year-old-opponent-moscow (accessed on 5 December 2023).




| First Author | Year | Ref. | Robot | Game | Game State Estimation | Game Engine |
|---|---|---|---|---|---|---|
| Barakova | 2018 | [15] | Humanoid (NAO) | Checkers | Camera, computer vision, based on relation between the coordinate systems of camera and board | Minimax + alpha–beta pruning |
| Bernbaum | 2018 | [9] | Franka Emika robot | Chess | Camera, computer vision, based on model recognition | Sunfish chess engine |
| Brooks | 2015 | [16] | Baxter robot | Checkers | Camera, computer vision, based on model recognition | Raven Checkers |
| Carrera | 2017 | [26] | Cartesian robot | Chess | Camera, computer vision, pieces recognition | Not specified |
| Chen | 2019 | [13] | Baxter robot | Chess | Camera, computer vision, based on model recognition | Stockfish |
| Del Toro | 2019 | [14] | Custom robot with four DOFs | Chess | Camera, computer vision, based on model recognition | Stockfish |
| Elnaggar | 2014 | [24] | Lynxmotion AL5D | Checkers | Camera, computer vision, based on color information | Negamax |
| Gupta | 2015 | [19] | Cartesian robot | Chess | LDR sensors under squares for pieces detection | Minimax + alpha–beta pruning |
| Juang | 2022 | [11] | Humanoid (NAO) | Chess | Camera, computer vision, based on model recognition | Not implemented |
| Kołosowski | 2020 | [12] | UR5 robot | Chess | Camera, computer vision, based on model recognition | Minimax + alpha–beta pruning |
| Kopets | 2020 | [20] | Custom robot with three DOFs | Russian checkers | Hall sensors under black squares detect magnetic pieces | Neural network based on AlphaZero |
| Larregay | 2018 | [17] | ABB model IRB120 | Chess | Camera, computer vision, dedicated lighting system | GNU Chess |
| Luqman | 2016 | [18] | Custom robot with four DOFs | Chess | Camera, computer vision, based on color information | Not specified |
| Manurung | 2023 | [28] | Gantry robot | Checkers | Camera, computer vision, based on color information | Minimax + alpha–beta pruning |
| Matuszek | 2011 | [29] | Gambit robot | Chess | Camera, computer vision, based on model recognition and point cloud information | Not specified |
| Rath | 2019 | [21] | Cartesian robot | Chess | Camera, computer vision, based on model recognition | Stockfish |
| Rodriguez-Sedano | 2016 | [25] | Baxter robot | Checkers | The operator sees the board configuration through a camera | Not implemented |
| Proposed approach | Franka Emika robot (minimum-time trajectories) | Italian checkers | Camera, computer vision based on color information | Minimax |
| Component | Main Features |
|---|---|
| Computer |
|
| Vision system |
|
| Game engine |
|
| Robotic player |
|
| Checkerboard |
|
| Pieces |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fabris, G.; Scalera, L.; Gasparetto, A. Playing Checkers with an Intelligent and Collaborative Robotic System. Robotics 2024, 13, 4. https://doi.org/10.3390/robotics13010004
Fabris G, Scalera L, Gasparetto A. Playing Checkers with an Intelligent and Collaborative Robotic System. Robotics. 2024; 13(1):4. https://doi.org/10.3390/robotics13010004
Chicago/Turabian StyleFabris, Giuliano, Lorenzo Scalera, and Alessandro Gasparetto. 2024. "Playing Checkers with an Intelligent and Collaborative Robotic System" Robotics 13, no. 1: 4. https://doi.org/10.3390/robotics13010004
APA StyleFabris, G., Scalera, L., & Gasparetto, A. (2024). Playing Checkers with an Intelligent and Collaborative Robotic System. Robotics, 13(1), 4. https://doi.org/10.3390/robotics13010004








