Structural–Parametric Synthesis of Path-Generating Mechanisms and Manipulators ^†

Abstract

This paper presents a structural–parametric synthesis of the four-link and Stephenson I, Stephenson II, and Stephenson III six-link path-generating mechanisms. The four-link path-generating mechanism is formed by connecting the output point and the base using an active closing kinematic chain (CKC) with two DOFs and a negative CKC of the type RR. The six-link path-generating mechanisms are formed by connecting the output point and the base by active, passive and negative CKCs. Active CKC has active kinematic pair, passive CKC has zero DOF, and negative CKC has a negative DOF. Active and negative CKCs impose geometrical constraints on the movement of the output point, and the geometric parameters of their links are determined by least-square approximation. Geometric parameters of the passive CKC are varied to satisfy the geometrical constraints of the active and negative CKCs. The CKCs of the active, passive and negative types, connecting the output point and the base, are the structural modules from which the different types of the path-generating mechanisms are synthesized. Numerical examples of the parametric synthesis of the four-link and six-link path-generating mechanisms are presented.

1. Introduction

Structural synthesis (type, number synthesis) and parametric synthesis (or dimensional, kinematic synthesis) are important in the design of mechanisms and robot manipulators. In structural synthesis, the structural schemes of mechanisms and manipulators with different numbers of links and types of kinematic pairs are defined by the given numbers of DOFs. In the parametric synthesis (kinematic, dimensional synthesis), according to the given laws of motions (or discrete positions) of the input and output links (output objects), the geometric parameters of links of mechanisms and manipulators are determined. The output object of the path-generating mechanisms is a point of a floating link moving according to the given laws of motion. Assur proposed a method for forming planar mechanisms from structural groups with zero DOF, which are called Assur groups [1]. There are various methods of the structural synthesis of mechanisms based on Assur groups, Baranov trusses, graph theory, screw theory, and the automatic method. For the structural synthesis of mechanisms based on Assur groups, Huang and Ding [2] and Chu and Cao [3] proposed a systematic method for synthesizing a complete set and corresponding databases of Assur groups with different links; Li, Wong, and Dai [4] and Morlin and Carboni [5] proposed an Assur-group inferred and matroid theory of planar mechanism structural synthesis. The structural synthesis of mechanisms using Baranov trusses [6] was carried out by Manolescu [7,8] based on the transforming Baranov trusses into planar kinematic chains using an idea called “graphization”. Rojas and Thomas [9] show how the characteristic polynomial of a Baranov truss determines the assembly modes of planar linkages. Huang and Ding [10] proposed the graph-from representation of Baranov trusses and its application for the structural synthesis of mechanisms. Graph theory in the structural synthesis of mechanisms has been applied by Crossley [11], Freudenstein, Dobrjanskyi [12], and Woo [13]. Schmidt, Shetty, and Chase [14] proposed a general graph grammar methodology for the structural synthesis of mechanisms. Sunkari and Schmidt [15] developed an algorithm belonging to one particular class called McKay-type for the structural synthesis of planar mechanisms. Ding, Huang, Zi, and Kecskemethy [16] developed an automatic synthesis of kinematic structures of complex mechanisms and robots. The fundamentals of the structural synthesis of parallel mechanisms using the screw theory are presented in the monographs by Kong and Gosselin [17] and Huang [18]. The synthesis approach in [17] is based on the concept of the virtual chain and the screw theory. Using the proposed approach, families of parallel mechanisms are constructed from a set of compositional units. In the monograph [18] based on the screw theory, a mobility analysis of parallel mechanisms was conducted and their special configurations were determined. The design of decoupled parallel manipulators by means of the screw theory is considered by Glazunov in [19]. In the automatic method of the structural synthesis of mechanisms and robots, Gogu [20] and Ding, Yang, and Kecskemethy [21] used the theory of linear transformations and evolutionary morphology, as well as isomorphism discrimination. Mruthyunjaya [22] and Tischler, Samuel, and Hunt [23,24] conducted a structural synthesis analysis by the transformation of binary chains and the new Melbourne method of enumeration of kinematic chains. A work [25] of Meng, Gao, Wu, and Ge is devoted to a framework and brief review of parallel-robot-mechanism-type synthesis.

The kinematic synthesis of mechanisms, including path-generating mechanisms, is carried out using exact and approximation methods. Exact (geometric) methods of kinematic synthesis are based on the Burmester theory [26]. The Burmester theory was developed in the works of Bottema and Roth [27], McCarthy [28], Hunt [29], and Luck and Modler [30]. In the works of Angeles and Bai [31,32] and Wu, Li, and Bai [33] a coupler curve synthesis of four-bar linkages is carried out via a novel formulation based on the Roberts–Chebyshev theorem and a fully analytical method. In the works of Xu, Myszka, and Murray [34], Sean, and Arthur [35], Yamine, Prini et al. [36], Sharma, Purwar, and Ge [37], and Brake, Hausenstein et al. [38], a kinematic synthesis of four-bar linkage, planar dyads and triads, and a parallel device for neurorehabilitation are carried out, respectively. An approximation (algebraic, optimization) synthesis of mechanisms was first formulated by Chebyshev [39]. In the works of Laribi, Mlika, Romdhane, and Seghloul [40], Larochelle [41], and Zhao, Ge X., Zi, and Ge Q. [42], the combined genetic algorithm–fuzzy logic method and the mixed exact and approximation motion method of kinematic synthesis are outlined. The approximation methods of the kinematic synthesis of planar dyads and tripods and four-link mechanisms have been developed in the works of Mather, and Erdman [43], Xuegang, Shimin, Qizheng, and Ying [44], and Dhingra, Cheng, and Kholi [45]. The works of Baskar and Plecnik [46], Plecnic and McCarthy [47], and Soh and McCarthy [48] are devoted to the kinematic synthesis of six-link path-generating mechanisms using random monodromy loops, polynomials, and constrained planar 3R chains. On the basis of geometric and approximation methods for the synthesis of mechanisms, an approximation kinematic geometry was formed. In the works of Sarkissyan, Gupta, and Roth [49,50], the kinematic geometry associated with the least-square and Chebyshev approximation with applications to planar kinematic synthesis is outlined. Based on approximation kinematic geometry, Baigunchekov, Laribi, Carbone et al. synthesized function generators with revolute joints [51], a RoboMech class parallel mechanism with two sliders [52], and a manipulator with two grippers [53], as well as path-generating mechanisms.

Existing methods of the structural synthesis of mechanisms do not take into account the functional purpose of the synthesized mechanisms, i.e., what type of mechanisms (function-generating, path-generating and motion-generating) they belong to. Existing methods of the kinematic (parametric) synthesis of mechanisms are devoted to determining the geometric parameters of links of mechanisms with given structural schemes. In this case, it is possible that a mechanism with a given structural scheme may not provide the required law of motion of the output link. It is known that it is quite difficult (practically impossible) to obtain analytical expressions associating the input and output parameters with the geometric parameters of links of six-link mechanisms. Therefore, in this paper, a structural–parametric synthesis of path-generating mechanisms is carried out; i.e., according to the given laws of motions (or discrete positions) of the output point and the input link, the structural schemes and geometric parameters of the links are simultaneously determined. In this case, the structural–parametric synthesis of the path-generating mechanisms is carried out starting with the smallest number of links of structural modules. The number of links of structural modules increases depending on the accuracy of the reproduction of the given laws of motion of the output point. Consequently, the optimal structural schemes and geometric parameters of the links of the synthesized mechanisms are determined.

In this paper, in Section 2, a structural synthesis of the planar four-link and six-link path-generating mechanisms is carried out; in Section 3 and Section 4, the methods of their parametric synthesis are presented [54]; and in Section 5, numerical examples of the parametric synthesis of the path-generating four-link mechanism, Stephenson I, Stephenson IIA, Stephenson IIB, and Stephenson III six-link mechanisms are presented.

2. Structural Synthesis of the Planar Four-Link and Six-Link Path-Generating Mechanisms

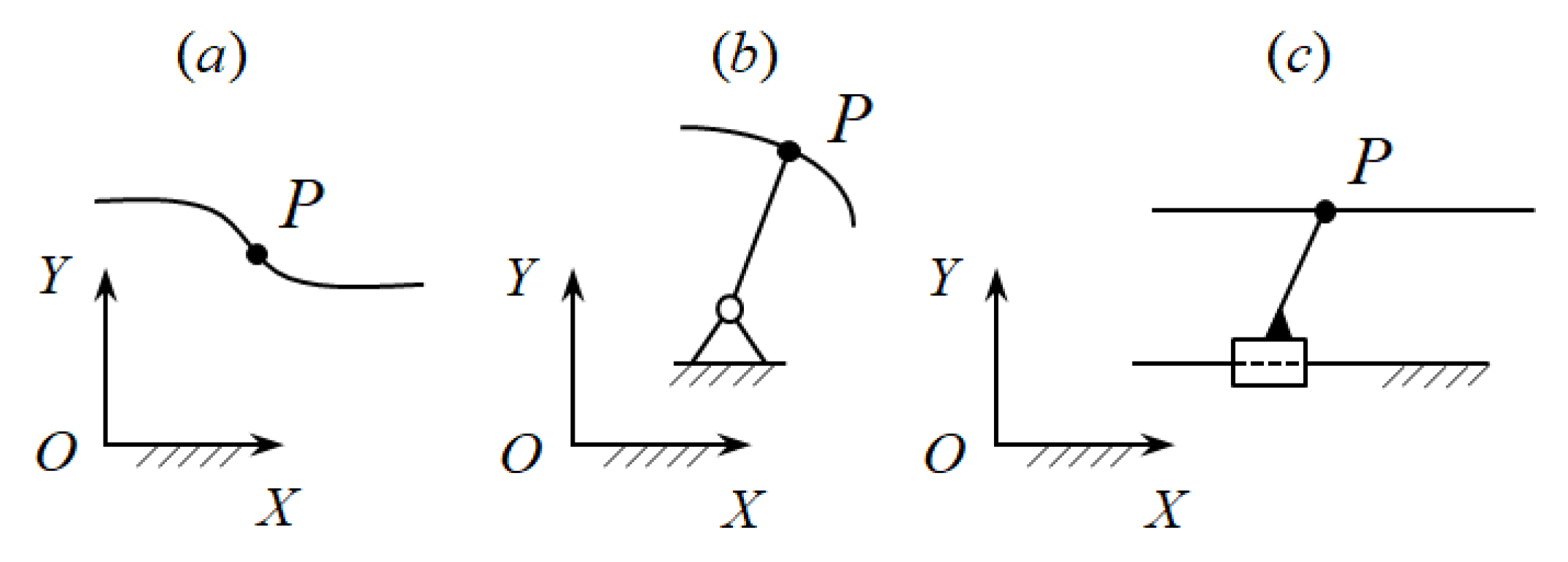
According to the developed principle [51], mechanisms and manipulators are formed by connecting the output objects (output links) with the base using active, passive, and negative CKCs. The output object of the function-generating mechanisms is a link with one DOF connected to a base, while of the path-generating mechanisms, it is a moving point with two DOFs, and of the motion-generating mechanisms, it is a moving body with three DOFs. Active and negative CKCs have positive and negative DOFs and they impose geometrical constraints on the motions of the output objects. Passive CKCs have zero DOF and they do not impose geometrical constraints on the motion of output objects. The connection of the output objects with the base begins with the simplest CKCs and with their subsequent complication, depending on the accuracy of reproducing the given laws of motions of the output objects. In the path-generating mechanisms, the simplest CKC connecting the output point P (Figure 1a) with the base is the link AP and the kinematic pair A, which can be revolute (Figure 1b) or prismatic (Figure 1c). In this case, the point P can only move in a circle or in a straight line. The link AP is a negative CKC having one negative DOF. This negative CKC imposes one geometrical constraint on the motion of the output point P.

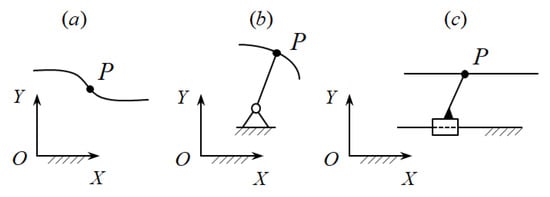
Figure 1. Output point P and the simplest form [54].

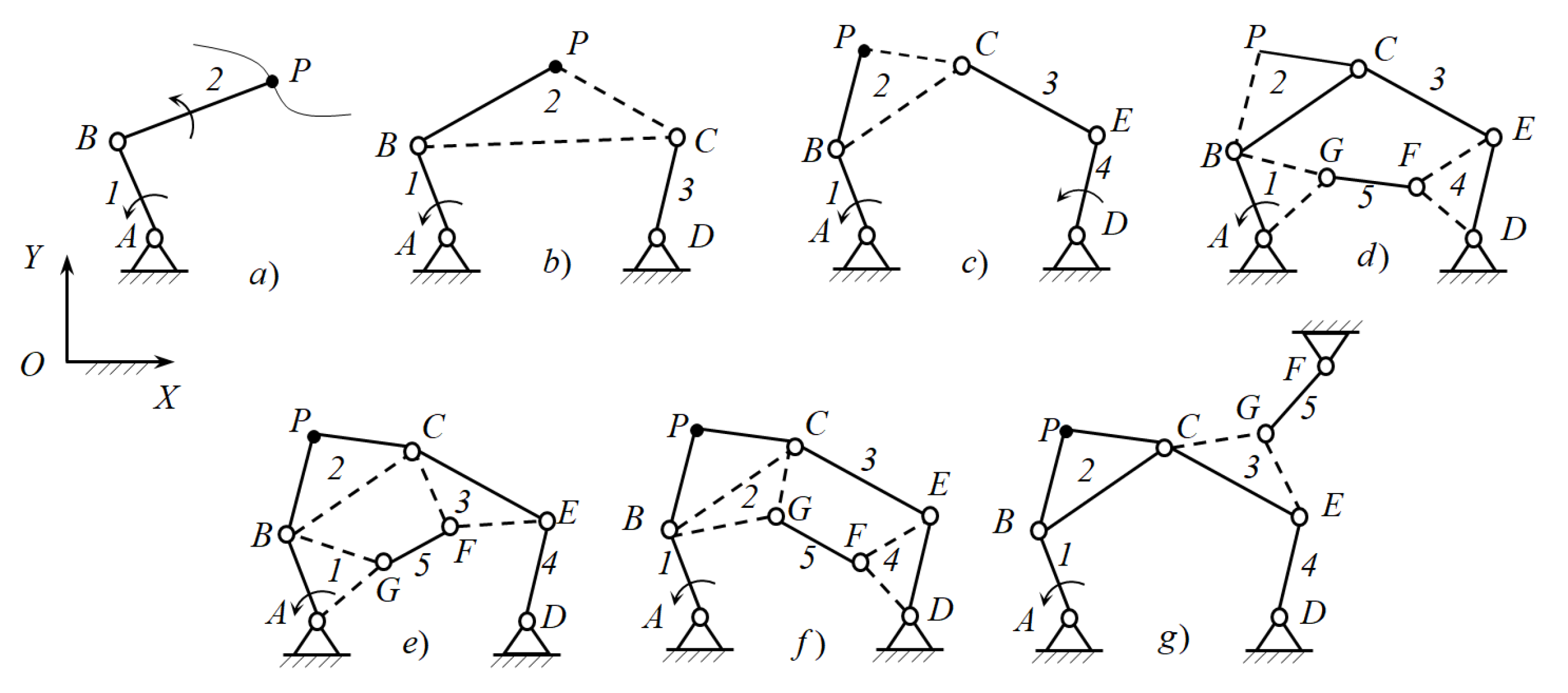
Since the point P on the plane has two generalized coordinates $X_P=X_P(t)$ and $Y_P=Y_P(t)$, i.e., two DOFs, then the CKC AP, imposing one geometrical constraint, limits its movement. Therefore, to ensure the arbitrary movement of the point P, it is necessary to connect it to the base using the CKC, which has two DOFs; it is the kinematic ABP (Figure 2a). As a result, we obtain a structural scheme of a planar serial manipulator with two DOFs. If we connect the link BP of this manipulator with the base using a negative CKC CD of the type RR, which has one negative DOF, we obtain a structural scheme of the four-link path-generating mechanism ABCD (Figure 2b).

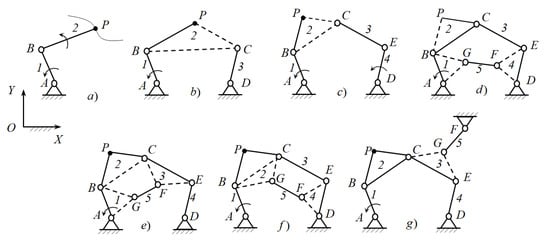
Figure 2. Structural synthesis of the path-generating mechanisms [54].

The link BP of the serial manipulator ABP is connected to the base using a binary link CD of the type RR in the case when the plane of the link BP has a point C that describes an arc of a circle in absolute motion. Such a point is called a circular point. The existence of a circular point in the planes of the moving links depends on the complexity of their movements, and the complexity of the movements of the planes of the moving links, in turn, depends on the complexity of the movements of the output objects.

If the plane of the link BP does not have a circular point, then this link is connected to the base using a passive CKC CED of the type RRR (a dyad), which has zero DOF. As a result, we obtain a planar five-link mechanism ABCED with two DOFs (Figure 2c).

To form single-moving six-link path-generating mechanisms from this five-link linkage ABCED, we connect its non-adjacent links using a negative CKC FG of the type RR. Figure 2d–g show structural schemes of the formed six-link path-generating mechanisms. If we connect links 1 and 4 of the five-link linkage ABCED by the binary link FG of the type RR, we obtain a Stephenson I path-generating mechanism (Figure 2d). If links 1 and 3 of the five-link linkage ABCED are connected by the binary link FG, we obtain a Stephenson IIA path-generating mechanism (Figure 2e). If links 2 and 4 of the five-bar linkage ABCED are connected by the binary link FG, we obtain a Stephenson IIB path-generating mechanism (Figure 2f). If link 3 of the five-link linkage ABCED is connected to the base by the binary link FG, we obtain a Stephenson III path-generating mechanism (Figure 2g). The types of Stephenson mechanisms can be found in ref. [51].

3. Parametric Synthesis of the Four-Link Path-Generating Mechanism

Let the N discrete positions of the output point P be

$$X_{Pi}=X_P(t_i), Y_{Pi}=Y_P(t_i), i=1,2,\dots N$$

(1)

and the angle of rotation of the input link 1 be

$${\phi }_{1i}={\phi }_1(t_i).$$

(2)

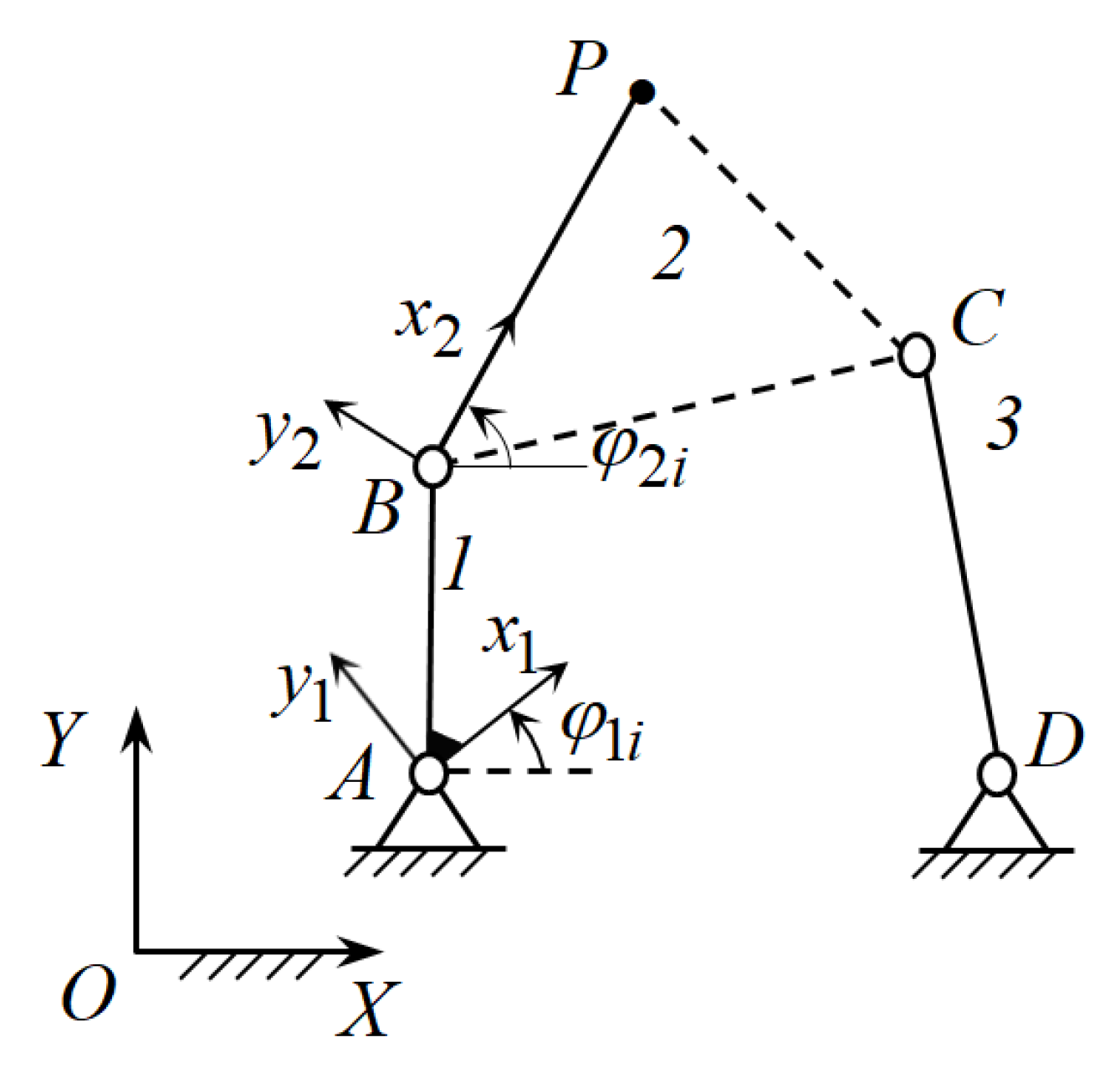
It is necessary to determine the geometric parameters of the links of the four-link path-generating mechanism (Figure 3) that implements Functions (1) and (2) within the required accuracy.

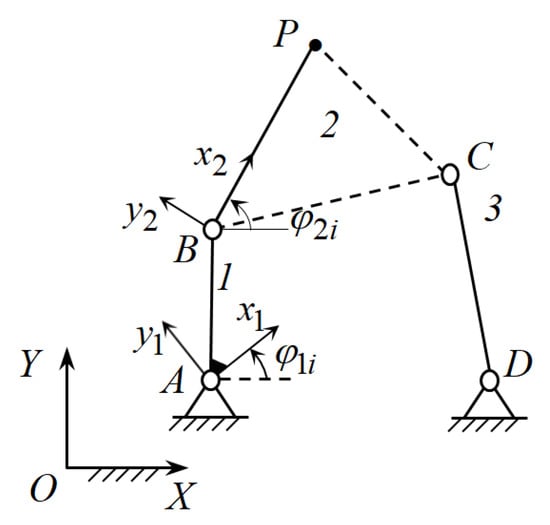
Figure 3. Four-link path-generating mechanism [54].

According to the structural synthesis of the four-link path-generating mechanism, its parametric synthesis consists of the parametric synthesis of the active CKC ABP and the negative CKC DC. Synthesis parameters of the active CKC ABP are $X_A,Y_A,x_B^{(1)},y_B^{(1)} ,l_{BP},$ and synthesis parameters of the negative CKC DC are $x_C^{(2)},y_C^{(2)},X_D,Y_D, l_{DC},$ where $X_A,Y_A$ and $X_D,Y_D$ are coordinates of the joints A and D in the absolute coordinate system OXY, respectively; $x_B^{(1)},y_B^{(1)}$ and $x_C^{(2)},y_C^{(2)}$ are coordinates of the joints B and C in moving coordinate systems $A{x}_1{y}_1$ and $B{x}_2{y}_2$ attached with the links AB and BP; and $l_{BP}$ and $l_{DC}$ are lengths of the links BP and DC.

For a parametric synthesis of the active CKC ABP, let us consider the movement of the point P relative to the coordinate system $A{x}_1{y}_1$. In this case, the point P moves along an arc of a circle with a center at point B and a radius l_BP. Let us derive the function weighted difference [51] as follows:

$$\Delta q_i={(x_{P_i}^{(1)}-x_B^{(1)})}^2+{(y_{P_i}^{(1)}-y_B^{(1)})}^2-l_{BP}^2,$$

(3)

where

$$\left[\begin{array}{c}{x}_{P_i}^{(1)}\\ y_{P_i}^{(1)}\end{array}\right]=\left[\begin{array}{cc}\cos {\phi }_{1i}& \sin {\phi }_{1i}\\ -\sin {\phi }_{1i}& \cos {\phi }_{1i}\end{array}\right]\cdot \left[\begin{array}{c}{X}_{P_i}-X_A\\ Y_{P_i}-Y_A\end{array}\right].$$

(4)

In Equations (3) and (4), $x_{P_i}^{(1)}$ and $y_{P_i}^{(1)}$ are the coordinates of the point P in the moving coordinate system Ax₁y₁.

Equation (3) is an equation of the geometrical constraint imposed by the active CKC ABP on the movement of the output point P. The parametric synthesis of the active CKC ABP consists of determining five geometric parameters $X_A,Y_A,x_B^{(1)},y_B^{(1)} ,l_{BP},$ from the minimum of Function (3).

Substituting the Expression (4) into Equation (3), and introducing the notations

$$\begin{array}{l}\left[\begin{array}{c}{p}_1\\ p_2\end{array}\right]=\left[\begin{array}{c}{x}_B^{(1)}\\ y_B^{(1)}\end{array}\right],\left[\begin{array}{c}{p}_4\\ p_5\end{array}\right]=\left[\begin{array}{c}{X}_A\\ Y_A\end{array}\right],p_3={\displaystyle \frac{1}{2}}(x_B^{{(1)}^2}+y_B^{{(1)}^2}+X_A^2+Y_A^2-l_{BP}^2),\\ f_{1i}=-X_{Pi}\cos {\phi }_{1i}-Y_{Pi}\sin {\phi }_{1i},f_{2i}=X_{Pi}\sin {\phi }_{1i}-Y_{Pi}\cos {\phi }_{1i},f_3=1, \\ f_{4i}=-X_{Pi}, f_{5i}=-Y_{Pi},f_{6i}=\cos {\phi }_{1i},f_{7i}=\sin {\phi }_{1i}, f_{0i}=-{\displaystyle \frac{1}{2}}(x_{Pi}^2+y_{Pi}^2),\end{array}$$

we obtain

$$\begin{array}{l}\Delta q_i=2[(p_1{f}_{1i}+p_2{f}_{2i}+p_3{f}_3+p_4{f}_{4i}+p_5{f}_{5i})+\\ +(p_1{p}_4+p_2{f}_5)f_{6i}+(p_1{p}_5-p_2{p}_4)f_{7i}-f_{0i}].\end{array}$$

(5)

Equation (5) is linear in the following two groups of synthesis parameters:

$$p^{(1)}={[p_1, p_2, p_3]}^T,p^{(2)}={[p_4, p_5, p_3]}^T$$

(6)

and is represented in two linear forms

$$\begin{array}{l}\Delta q_i^{(1)}=2[p_1(f_{1i}+p_4{f}_{4i}-p_2{f}_{7i})+p_2(f_{2i}+p_5{f}_{6i}-p_4{f}_{7i})+\\ +p_3{f}_3+(p_4{f}_{4i}+p_5{f}_{5i}-f_{0i})]\end{array}$$

(7)

and

$$\begin{array}{l}\Delta q_i^{(2)}=2[p_4(f_{4i}+p_1{f}_{6i}-p_2{f}_{7i})+p_5(f_{5i}+p_2{f}_{6i}+p_1{f}_{7i})+\\ +p_3{f}_3+(p_1{f}_{1i}+p_2{f}_{2i}-f_{0i})].\end{array}$$

(8)

Let us introduce the notations

$$\begin{array}{l}{g}_i^{(1)}={[g_{1i}^{(1)},g_{2i}^{(1)},g_{3i}^{(1)}]}^T, g_i^{(2)}={[g_{1i}^{(2)},g_{2i}^{(2)},g_{3i}^{(2)}]}^T, \\ g_{0i}^{(1)}=p_4{f}_{4i}+p_5{f}_{5i}-f_{0i}, g_{0i}^{(2)}=p_1{f}_{1i}+p_2{f}_{2i}-f_{0i},\end{array}$$

where

$$\begin{array}{l}{g}_{1i}^{(1)}=f_{1i}+p_4{f}_{6i}+p_5{f}_{7i}, g_{2i}^{(1)}=f_{2i}+p_5{f}_{6i}-p_4{f}_{7i}, g_{3i}^{(1)}=p_3{f}_3,\\ g_{1i}^{(2)}=f_{4i}+p_1{f}_{6i}-p_2{f}_{7i}, g_{2i}^{(2)}=f_{5i}+p_2{f}_{6i}+p_1{f}_{7i}, g_{3i}^{(2)}=p_3{f}_3.\end{array}$$

Then, Equations (7) and (8) take the form

$$\Delta q_i^{(k)}=2(g_i^{{(k)}^T}\cdot p^{(k)}-g_{0i}^{(k)}),k=1,2.$$

(9)

To determine the vectors $p^{(k)}$ of synthesis parameters, we minimize Function (9) by the least-square approximation, i.e., derive the following sums:

$$S^{(k)}={\displaystyle \sum _{i=1}^N{(\Delta q_i^{(k)})}^2},$$

(10)

for which, the necessary conditions for minimizing

$${\displaystyle \frac{\partial S^{(k)}}{\partial p^k}}=0$$

(11)

lead to two systems of linear equations with respect to two groups of synthesis parameters p^(k). This allows us to use a simple linear iteration method based on kinematic inversion [50]. Consequently, the minimization of nonlinear Function (10) is carried out on the basis of a linear iterative process. This article [51] also describes the parametric synthesis of the negative CKC CD connecting the plane of the link BP of the active CKC ABP with a base.

4. Parametric Synthesis of the Six-Link Path-Generating Mechanisms

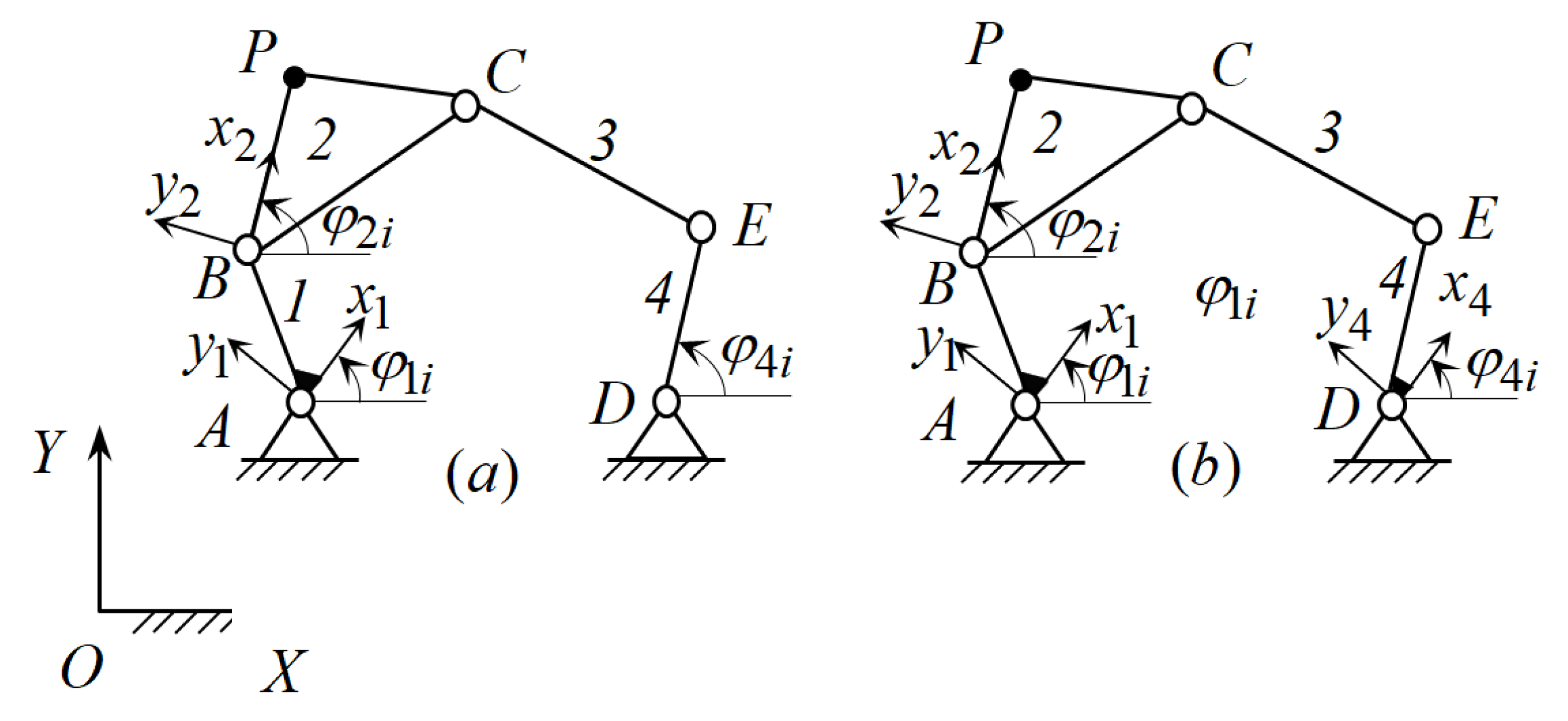
As previously noted, six-link path-generating mechanisms are formed by connecting non-adjacent links of the five-link path-generating mechanism by a negative CKC of the type RR. Therefore, the parametric synthesis of six-link path-generating mechanisms consists of the parametric synthesis of the five-bar path-generating mechanism and the negative CKC of the type RR. The five-link path-generating mechanism, in its turn, is formed by connecting the link BP of the active CKC ABP with the base by the CKC CED, when there is no circular point in the plane of the link BP in absolute motion. In this case, the CKC CED can be passive or active. If the CKC CED is passive (Figure 4a), then the angle ${\phi }_{4i}$ of link 4 is determined by solving the problem of positions of the dyad CED by the equation

$${\phi }_{4i}={\phi }_{D{C}_i}-{\cos }^{-1}{\displaystyle \frac{l_{DE}^2+l_{D{C}_i}^2-l_{CE}^2}{2l_{DE}\cdot l_{D{C}_i}}}.$$

(12)

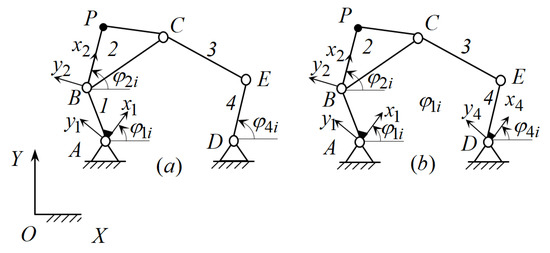
Figure 4. Five-link path-generating mechanisms with passive (a) and active (b) CKCs [54].

Passive CKC CED does not impose a geometrical constraint on the movement of the output point P, and its geometric parameters $x_C^{(2)},y_C^{(2)},X_D,Y_D,l_{CE},l_{DE}$ are varied to satisfy the geometrical constraint of the connecting negative CKC.

If the CKC CED is active (Figure 4b), then the values of the angle ${\phi }_{4i}$ of the moving coordinate system $D{x}_4{y}_4$ attached to link 4 are set. The active CKC CED imposes a geometrical constraint on the movement of the output point P and its geometric parameters $x_C^{(2)},y_C^{(2)},x_E^{(4)},y_E^{(4)},X_D,Y_D,l_{CE}$ are calculated.

For the parametric synthesis of the active CKC CED, let us consider the movement of the coordinate system $B{x}_2{y}_2$ relative to the coordinate system $D{x}_4{y}_4$ and derive the function of weighted difference

$$\Delta q_i={(x_{Ci}^{(4)}-x_E^{(4)})}^2+{(y_{Ci}^{(4)}-y_E^{(4)})}^2-l_{CE}^2,$$

(13)

where

$$\left[\begin{array}{c}{x}_{C_i}^{(4)}\\ y_{C_i}^{(4)}\end{array}\right]=\left[\begin{array}{cc}\cos {\phi }_{4i}& \sin {\phi }_{4i}\\ -\sin {\phi }_{4i}& \cos {\phi }_{4i}\end{array}\right]\cdot \left[\begin{array}{c}{X}_{C_i}-X_D\\ Y_{C_i}-Y_D\end{array}\right].$$

(14)

Substituting Expression (14) into Equation (13), and introducing the notations

$$\begin{array}{c}\left[\begin{array}{c}{p}_1\\ p_2\end{array}\right]=\left[\begin{array}{c}{x}_E^{(4)}\\ y_E^{(4)}\end{array}\right],\left[\begin{array}{c}{p}_4\\ p_5\end{array}\right]=\left[\begin{array}{c}{x}_C^{(2)}\\ y_C^{(2)}\end{array}\right],\left[\begin{array}{c}{p}_6\\ p_7\end{array}\right]=\left[\begin{array}{c}{X}_D\\ Y_D\end{array}\right],\\ p_3={\displaystyle \frac{1}{2}}(x_E^{{(4)}^2}+y_E^{{(4)}^2}+x_C^{{(2)}^2}+y_C^{{(2)}^2}+X_D^2+Y_D^2-l_{CE}^2),\\ f_{1i}=-(X_{Bi}\cos {\phi }_{4i}+Y_{Bi}\sin {\phi }_{4i}), f_{2i}=(X_{Bi}\sin {\phi }_{4i}-Y_{Bi}\cos {\phi }_{4i}),f_3=1, \\ f_{4i}=X_{Bi}\cos {\phi }_{2i}+Y_{Bi}\sin {\phi }_{2i},f_{5i}=-X_{Bi}\sin {\phi }_{2i}+Y_{Bi}\cos {\phi }_{2i}, f_{6i}=-X_{Bi},\\ f_{7i}=-Y_{Bi},f_{8i}=-\cos ({\phi }_{2i}-{\phi }_{4i}),f_{9i}=\sin ({\phi }_{2i}-{\phi }_{4i}),f_{10i}=\cos {\phi }_{4i},\\ f_{11i}=\sin {\phi }_{4i},f_{12i}=-\cos {\phi }_{2i},f_{13i}=\sin {\phi }_{2i}, f_{0i}=-{\displaystyle \frac{1}{2}}(X_{Bi}^2+Y_{Bi}^2),\end{array}$$

we obtain

$$\begin{array}{l}\Delta q_i=2[p_1{f}_{1i}+p_2{f}_{2i}+p_3{f}_3+p_4{f}_{4i}+p_5{f}_{5i}+p_6{f}_{6i}+p_7{f}_{7i}+\\ +(p_1{p}_4+p_2{p}_5)f_{8i}+(p_1{p}_5-p_2{p}_4)\cdot f_{9i}+(p_1{p}_6+p_2{p}_7)f_{10i}+\\ +(p_1{p}_7-p_2{p}_6)f_{11i}+(p_4{p}_6+p_5{p}_7)f_{12i}+(p_4{p}_7-p_5{p}_6)f_{13i}-f_{0i}].\end{array}$$

(15)

Equation (15) is linear in the following three groups of synthesis parameters:

$$p^{(1)}={[p_1, p_2, p_3]}^T,p^{(2)}={[p_4, p_5, p_3]}^T,p^{(3)}={[p_6, p_7, p_3]}^T$$

and is represented in three linear forms:

$$\begin{array}{l}\Delta q_i^{(1)}=2\{[p_1(f_{1i}+p_4{f}_{8i}+p_5{f}_{9i}+p_6{f}_{10i}+p_7{f}_{11i})+p_2(f_{2i}+\\ +p_5{f}_{8i}+p_4{f}_{9i}+p_7{f}_{10i}-p_6{f}_{11i})+p_3{f}_3]+[p_4{f}_{4i}+p_5{f}_{5i}+\\ +p_6{f}_{6i}+p_7{f}_{7i}+(p_4{p}_6+p_5{p}_7)f_{12i}+(p_4{p}_7-p_5{f}_6)f_{13i}-f_{0i}]\},\end{array}$$

(16)

$$\begin{array}{l}\Delta q_i^{(2)}=2\{[p_4(f_{4i}+p_1{f}_{8i}-p_2{f}_{9i}+p_6{f}_{12i}+p_7{f}_{13i})+p_5(f_{5i}+p_2{f}_{8i}+\\ +p_1{f}_{9i}+p_7{f}_{12i}-p_6{f}_{13i})+p_3{f}_3]+[p_1{f}_{1i}+p_2{f}_{2i}+p_6{f}_{6i}+p_7{f}_{7i}+\\ +(p_1{p}_6+p_2{p}_7)f_{10i}+(p_1{p}_7-p_2{f}_6)f_{11i}-f_{0i}]\},\end{array}$$

(17)

$$\begin{array}{l}\Delta q_i^{(3)}=2\{[p_6(f_{6i}+p_1{f}_{10i}-p_2{f}_{11i}+p_4{f}_{12i}-p_5{f}_{13i})+p_7(f_{7i}+p_2{f}_{10i}+\\ +p_1{f}_{11i}+p_5{f}_{12i}-p_4{f}_{13i})+p_3{f}_3]+[p_1{f}_{1i}+p_2{f}_{2i}+p_4{f}_{4i}+p_5{f}_{5i}+\\ +(p_1{p}_4+p_2{p}_5)f_{8i}+(p_1{p}_5-p_2{f}_4)f_{9i}-f_{0i}]\}.\end{array}$$

(18)

Then, Equations (16)–(18) take the form (9), where $k=1,2,3.$ To determine the synthesis parameter vectors $p^{(k)}$, we minimize the Function (9) by the least-square optimization method, i.e., derive the sums of the form (10), whose necessary minimum conditions (11) lead to three systems of linear equations relative to three groups of synthesis parameters $p^{(k)}$. This allows us to use a simple method of linear iterations based on kinematic inversion.

A parametric synthesis of a negative CKC of the type RR connecting non-adjacent links of the five-bar mechanism ABCED is considered in [51].

5. Numerical Examples

Let us consider the parametric synthesis of the four-link, Stephenson I, Stephenson IIA, Stephenson IIB, and Stephenson III path-generating mechanisms.

5.1. Four-Link Path-Generating Mechanism

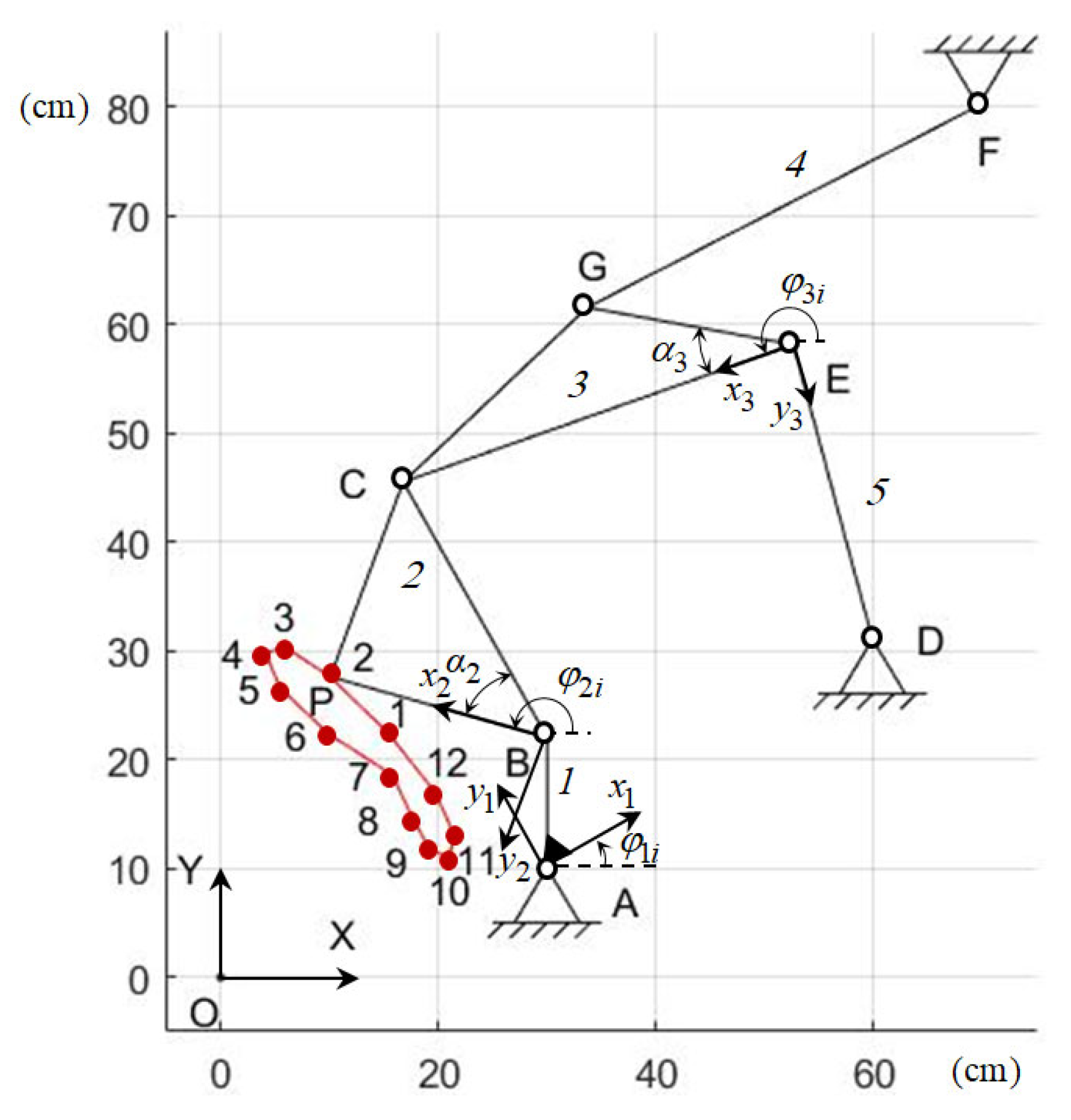
Table 1 gives the values of the point P coordinates $X_{Pi}$ and $Y_{Pi}$ in the absolute coordinate system OXY and input angle ${\phi }_{1i}$ for N = 12.

Table 1. Values of the point P coordinates and input angle ${\phi }_{1i}$.

i	1	2	3	4	5	6	7	8	9	10	11	12
$X_{Pi}, (\mathrm{cm})$	15.18	16.23	9.96	0.29	−7.90	−11.95	−11.41	−7.43	−1.39	5.26	10.72	13.43
$Y_{Pi}, (\mathrm{cm})$	51.46	65.35	69.27	65.91	57.00	45.03	33.07	23.67	18.20	17.52	22.29	33.52
${\phi }_{1i}$	0°	30°	60°	90°	120°	150°	180°	210°	240°	270°	300°	330°

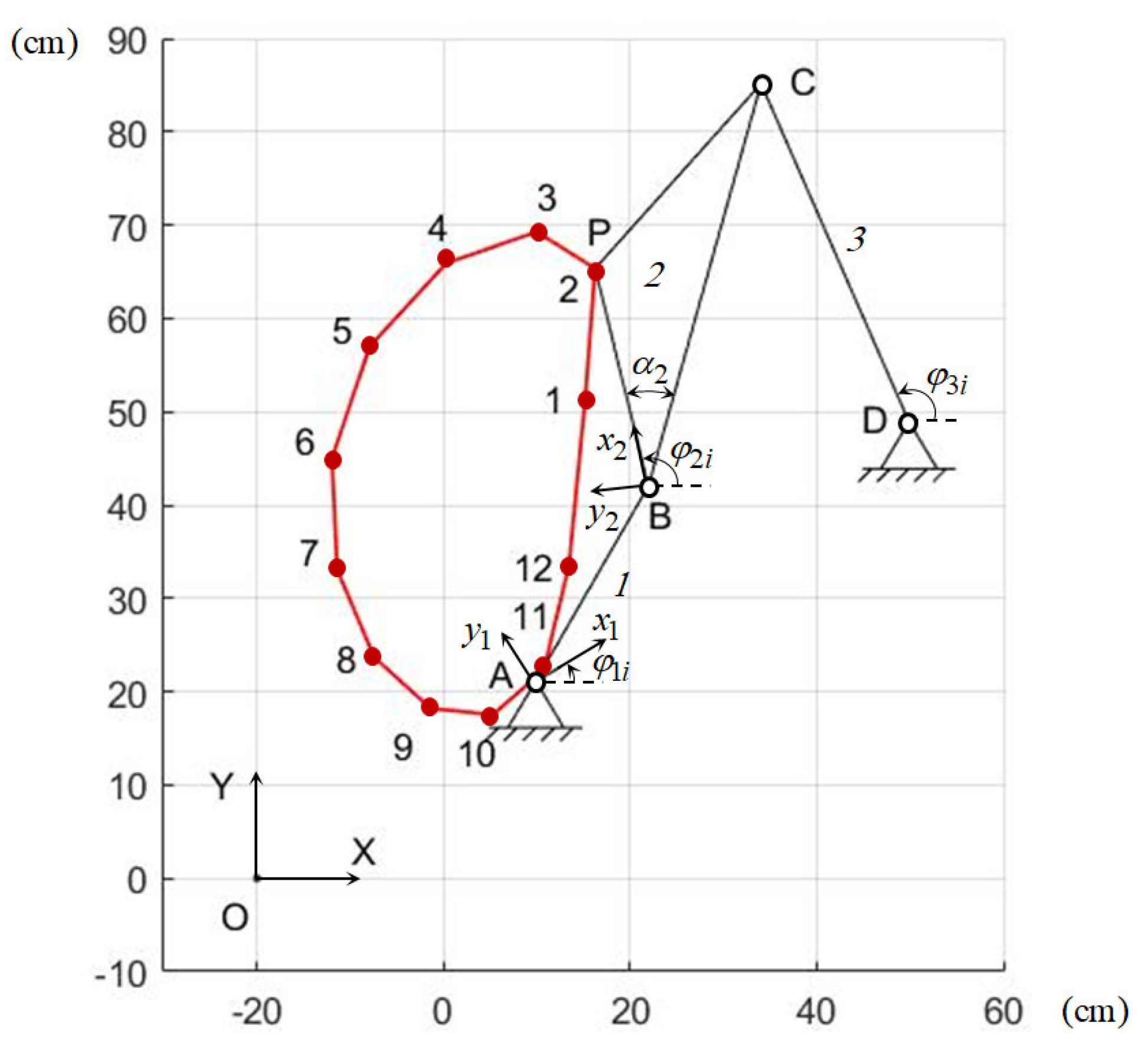
It is necessary to determine the synthesis parameters of the four-link path-generating mechanism (Figure 5), which reproduces the given values of the $X_{Pi}$ and $Y_{Pi}$ coordinates of the output point P for given values of the input angle ${\phi }_{1i}$. In Figure 8, the segment BC is not another separate segment.

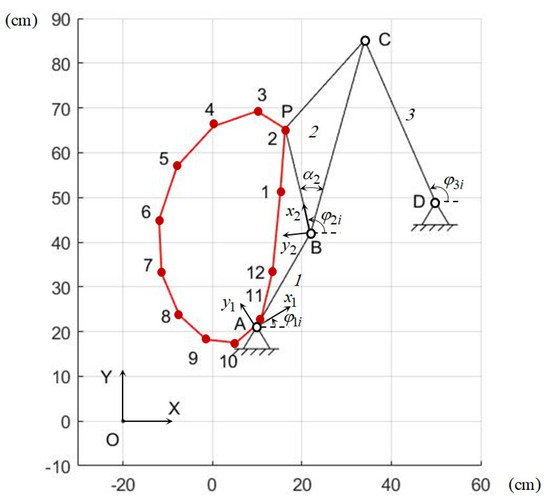
Figure 5. Four-link path-generating mechanism.

As noted above, the four-link path-generating mechanism is formed by connecting the active CKC ABP to the base using the negative CKC DC. Consequently, the synthesis parameters of the four-link path-generating mechanism are the synthesis parameters of the active CKC ABP: $X_A,Y_A,x_B^{(1)},y_B^{(1)},l_{BP}$ and the synthesis parameters of the negative CKC DC: $x_C^{(2)},y_C^{(2)},X_D,Y_D,l_{DC}$. The method for determining these synthesis parameters of the four-bar path-generating mechanism is described above.

Table 2 presents the obtained values of the synthesis parameters of the four-link path-generating mechanisms.

Table 2. Values of the synthesis parameters (cm).

$X_A$	$Y_A$	$x_B^{(1)}$	$y_B^{(1)}$	$l_{BP}$	$x_C^{(2)}$	$y_C^{(2)}$	$X_D$	$Y_D$	$l_{DC}$
9.87	21.12	20.89	12.06	24.01	39.02	−21.97	49.87	48.89	39.56

To check the parametric synthesis result of the four-link path-generating mechanism, determine the coordinates of the point P in the absolute coordinate system $OXY$. To perform this, it is necessary to solve the problem of the positions of the synthesized four-bar path-generating mechanism, which has the structural formula

$$\mathrm{I}(1)\to \mathrm{I}\mathrm{I}(2,3),$$

(19)

i.e., it belongs to the mechanism of the second class according to the Assur–Artobolevskiy classification [55].

The coordinates of the output point P relative to the absolute coordinate system $OXY$ are determined by the equation

$$\left[\begin{array}{c}{X}_{P_i}\\ Y_{P_i}\end{array}\right]=\left[\begin{array}{c}{X}_{B_i}\\ Y_{B_i}\end{array}\right]+l_{BP}\left[\begin{array}{c}\cos {\phi }_{2i}\\ \sin {\phi }_{2i}\end{array}\right],$$

(20)

where

$$\left[\begin{array}{c}{X}_{B_i}\\ Y_{B_i}\end{array}\right]=\left[\begin{array}{c}{X}_A\\ Y_A\end{array}\right]+\left[\begin{array}{cc}\cos {\phi }_{1i}& -\sin {\phi }_{1i}\\ \sin {\phi }_{1i}& \cos {\phi }_{1i}\end{array}\right]\cdot \left[\begin{array}{c}{x}_B^{(1)}\\ y_B^{(1)}\end{array}\right].$$

(21)

The values of the angle ${\phi }_{2i}$ in Equation (20) are determined by solving the problem of positions of the dyad BCD in the following sequence:

$${\phi }_{3i}={\phi }_{{(DB)}_i}-\cos {\displaystyle \frac{l_{DC}^2+l_{{(DB)}_i}^2-l_{BC}^2}{2l_{DC}{l}_{{(DB)}_i}}},$$

(22)

where

$$l_{{(DB)}_i}={\left[{(Y_{B_i}-Y_D)}^2+{(X_{B_i}-X_D)}^2\right]}^{{\displaystyle \frac{1}{2}}},$$

(23)

$${\phi }_{{(DB)}_i}={\mathrm{tg}}^{-1}{\displaystyle \frac{Y_{B_i}-Y_D}{X_{B_i}-X_D}},$$

(24)

$$l_{BC}^2=x_C^{{(2)}^2}+y_C^{{(2)}^2}.$$

(25)

Then, the coordinates of the joint C are determined in the absolute coordinate system $OXY$ by the equation

$$\left[\begin{array}{c}{X}_{C_i}\\ Y_{C_i}\end{array}\right]=\left[\begin{array}{c}{X}_D\\ Y_D\end{array}\right]+l_{DC}\left[\begin{array}{c}\cos {\phi }_{3i}\\ \sin {\phi }_{3i}\end{array}\right],$$

(26)

and the values of the angle ${\phi }_{2i}$ are determined by the equation

$${\phi }_{2i}=\mathrm{t}{\mathrm{g}}^{-1}{\displaystyle \frac{Y_{C_i}-Y_{B_i}}{X_{C_i}-X_{B_i}}}+{\alpha }_2,$$

(27)

where

$${\alpha }_2=\mathrm{t}{\mathrm{g}}^{-1}{\displaystyle \frac{y_C^{(2)}}{x_C^{(2)}}}.$$

(28)

Table 3 presents the obtained values of the coordinates of the point P, and Figure 5 shows a graph of its change.

Table 3. Values of the point P coordinates and input angle ${\phi }_{1i}$.

i	1	2	3	4	5	6	7	8	9	10	11	12
$X_{P_i}, (\mathrm{cm})$	15.17	16.24	9.96	0.30	−7.89	−11.94	−11.40	−7.42	−1.38	5.27	10.73	13.44
$Y_{P_i}, (\mathrm{cm})$	51.47	65.36	69.28	65.92	57.01	45.02	33.06	23.66	18.20	17.51	22.28	33.53
${\phi }_{1i}$	0°	30°	60°	90°	120°	150°	180°	210°	240°	270°	300°	330°

5.2. Stephenson I Path-Generating Mechanism

Table 4 gives the values of the point P coordinates $X_{P_i}$ and $Y_{P_i}$ in the absolute coordinates system $OXY$ and input angle ${\phi }_{1i}$ for N = 12.

Table 4. Values of the point P coordinates and input angle ${\phi }_{1i}$.

i	1	2	3	4	5	6	7	8	9	10	11	12
$X_{P_i}, (\mathrm{cm})$	25.44	37.44	40.24	29.08	13.51	−1.32	−11.55	−14.16	−8.95	1.33	12.64	20.98
$Y_{P_i}, (\mathrm{cm})$	44.07	73.88	84.30	85.26	79.74	68.40	52.55	35.21	20.67	12.38	12.01	20.96
${\phi }_{1i}$	0°	30°	60°	90°	120°	150°	180°	210°	240°	270°	300°	330°

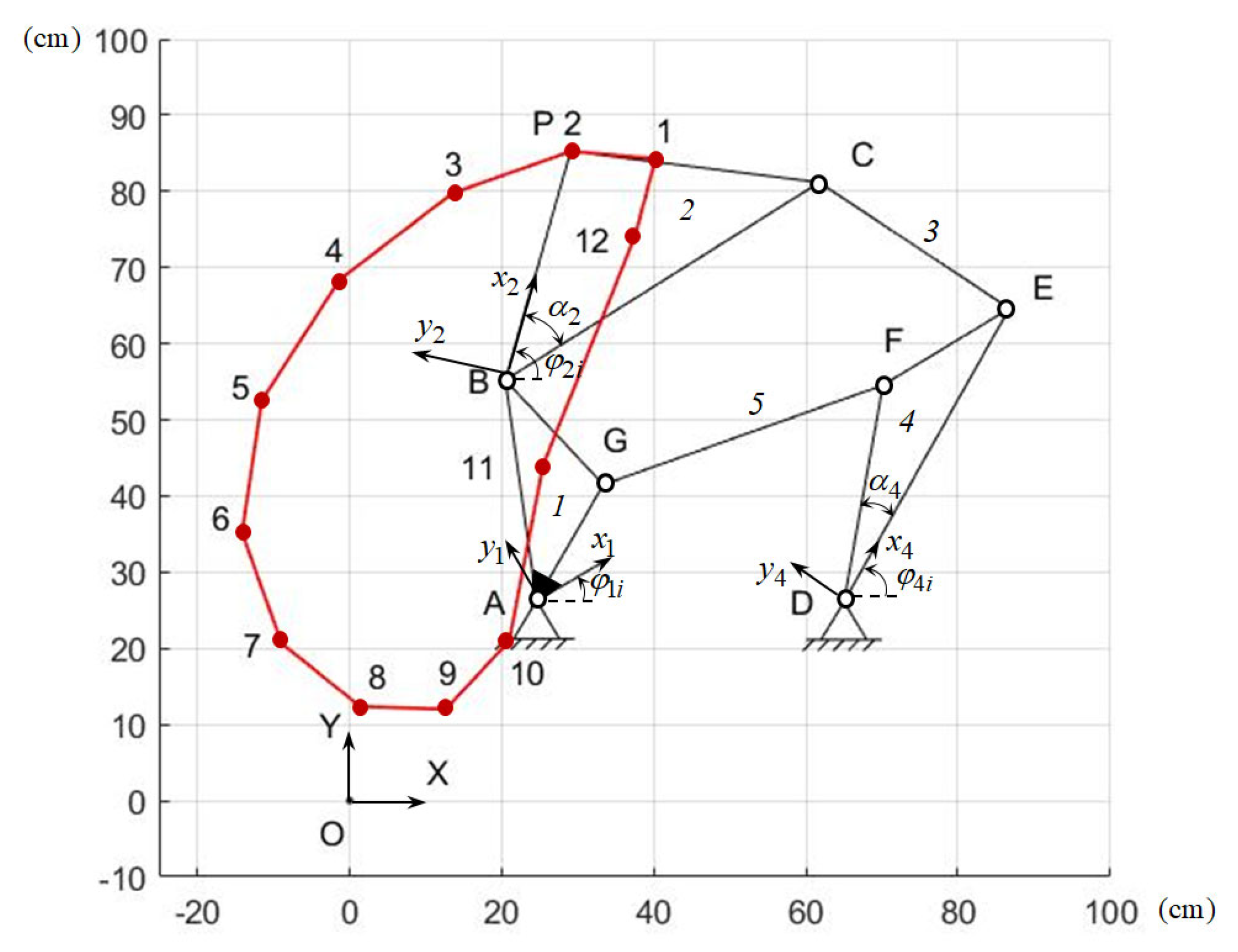
It is necessary to determine the synthesis parameters of the Stephenson I path-generating mechanism (Figure 6), which reproduces the given values of the $X_{P_i}$ and $Y_{P_i}$ coordinates of the output point P for given values of the input angle ${\phi }_{1i}$.

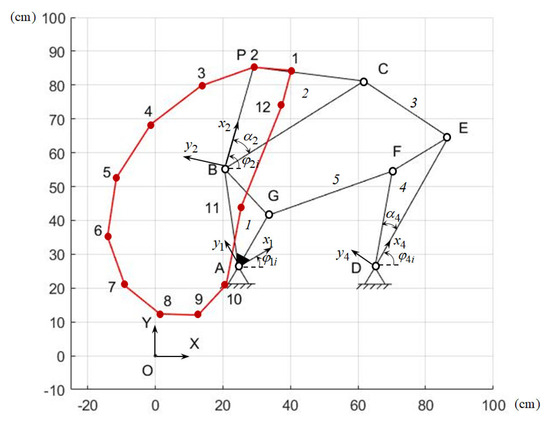
Figure 6. Stephenson I path-generating mechanism.

As noted above, the Stephenson I path-generating mechanism is formed by connecting links 1 and 4 of the five-link linkage ABCED by the binary link GF. Therefore, the parametric synthesis of the Stephenson I path-generating mechanism consists of the parametric synthesis of the five-link linkage ABCED and the binary link GF.

The five-link linkage ABCED in its turn is formed from the active CKC ABP and the passive CKC CED, so the synthesis parameters of the five-link linkage ABCED consist of the following synthesis parameters of the active CKC ABP: $X_A,Y_A,x_B^{(1)},y_B^{(1)},l_{BP}$, and the passive CKC CED: $x_C^{(2)},y_C^{(2)},X_D,Y_D,l_{CE},l_{ED}$.

The parametric synthesis of the active CKC ABP is considered above. Since the passive CKC CED does not impose a geometric constraint on the motion of the output object (output point P), its synthesis parameters are varied to satisfy the geometric constraint of the negative CKC GF.

To perform a parametric synthesis analysis of the binary link GF, it is necessary to determine the angle ${\phi }_{4i}$ by the equation

$${\phi }_{4i}={\phi }_{{(DC)}_i}-{\cos }^{-1}{\displaystyle \frac{l_{DE}^2+l_{{(DC)}_i}^2-l_{CE}^2}{2l_{DE}{l}_{{(DC)}_i}}},$$

(29)

where

$$l_{{(DC)}_i}={\left[{(X_{C_i}-X_D)}^2+{(Y_{C_i}-Y_D)}^2\right]}^{{\displaystyle \frac{1}{2}}},$$

(30)

$$\left[\begin{array}{c}{X}_{C_i}\\ Y_{C_i}\end{array}\right]=\left[\begin{array}{c}{X}_{B_i}\\ Y_{B_i}\end{array}\right]+\left[\begin{array}{cc}\cos {\phi }_{2i}& -\sin {\phi }_{2i}\\ \sin {\phi }_{2i}& \cos {\phi }_{2i}\end{array}\right]\cdot \left[\begin{array}{c}{x}_C^{(2)}\\ y_C^{(2)}\end{array}\right].$$

(31)

Then, the weighted difference function is derived:

$$\Delta q_i={\left(x_{F_i}^{(1)}-x_G^{(1)}\right)}^2+{\left(y_{F_i}^{(1)}-y_G^{(1)}\right)}^2-l_{GF}^2,$$

(32)

where

$$\left[\begin{array}{c}{x}_{F_i}^{(2)}\\ y_{F_i}^{(2)}\end{array}\right]=\left[\begin{array}{cc}\cos {\phi }_{1i}& \sin {\phi }_{1i}\\ -\sin {\phi }_{1i}& \cos {\phi }_{1i}\end{array}\right]\cdot \left[\begin{array}{c}{X}_{F_i}-X_A\\ Y_{F_i}-Y_A\end{array}\right],$$

(33)

$$\left[\begin{array}{c}{X}_{F_i}\\ Y_{F_i}\end{array}\right]=\left[\begin{array}{c}{X}_D\\ Y_D\end{array}\right]+\left[\begin{array}{cc}\cos {\phi }_{4i}& -\sin {\phi }_{4i}\\ \sin {\phi }_{4i}& \cos {\phi }_{4i}\end{array}\right]\cdot \left[\begin{array}{c}{x}_F^{(4)}\\ y_F^{(4)}\end{array}\right].$$

(34)

Based on the method described in [51], by minimizing the Function (32), the synthesis parameters of the binary link GF are determined.

Table 5 presents the obtained values of the synthesis parameters of the Stephenson I path-generating mechanism.

Table 5. Values of the synthesis parameters (cm).

$X_A$	$Y_A$	$x_B^{(1)}$	$y_B^{(1)}$	$l_{BP}$	$x_C^{(2)}$	$y_C^{(2)}$	$X_D$
24.58	26.26	10.90	27.14	31.25	38.38	−30.11	65.01
$Y_D$	$l_{CE}$	$l_{ED}$	$x_G^{(1)}$	$y_G^{(1)}$	$x_F^{(4)}$	$y_F^{(4)}$	$l_{GF}$
26.11	29.98	44.23	15.21	8.78	27.28	9.53	39.02

To check the parametric synthesis result of the Stephenson I path-generating mechanism, determine the coordinates of the point P in the absolute coordinate system $OXY$ using Equation (20).

To determine the angle ${\phi }_{2i}$, it is necessary to solve the problem of the positions of the synthesized Stephenson I path-generating mechanism, which has the structural formula

(35)

i.e., it belongs to the mechanism of the second class according to the Assur–Artobolevskiy classification, containing two dyads: $\mathrm{II}(5,4)$ and $\mathrm{II}(2,3)$.

The values of the angle ${\phi }_{2i}$ in Equation (20) are determined by sequentially solving problems of the positions of the dyads $\mathrm{II}(5,4)$ and $\mathrm{II}(2,3)$.

By solving the problem of the positions of dyad $\mathrm{II}(5,4)$, we determine the angle ${\phi }_{4i}$

$${\phi }_{4i}=\left({\phi }_{{(DG)}_i}-{\cos }^{-1}{\displaystyle \frac{l_{{(DG)}_i}^2+l_{DF}^2-l_{GF}^2}{2l_{{(DG)}_i}{l}_{DF}}}\right)-{\alpha }_4,$$

(36)

where

$$l_{{(DG)}_i}={\left[{(X_{G_i}-X_D)}^2+{(Y_{G_i}-Y_D)}^2\right]}^{{\displaystyle \frac{1}{2}}},$$

(37)

$${\phi }_{{(DG)}_i}=\mathrm{t}{\mathrm{g}}^{-1}{\displaystyle \frac{Y_{G_i}-Y_D}{X_{G_i}-X_D}},$$

(38)

$$\left[\begin{array}{c}{X}_{G_i}\\ Y_{G_i}\end{array}\right]=\left[\begin{array}{c}{X}_A\\ Y_A\end{array}\right]+\left[\begin{array}{cc}\cos {\phi }_{1i}& -\sin {\phi }_{1i}\\ \sin {\phi }_{1i}& \cos {\phi }_{1i}\end{array}\right]\cdot \left[\begin{array}{c}{x}_G^{(2)}\\ y_G^{(2)}\end{array}\right],$$

(39)

$${\alpha }_4=\mathrm{t}{\mathrm{g}}^{-1}{\displaystyle \frac{y_F^{(4)}}{x_F^{(4)}}}.$$

(40)

Then, knowing the value of the angle ${\phi }_{4i}$, we determine the values of the angle ${\phi }_{2i}$ by solving the problem of positions of the dyad $\mathrm{II}(2,3)$:

$${\phi }_{2i}=\left({\phi }_{{(BE)}_i}-{\cos }^{-1}{\displaystyle \frac{l_{{(BE)}_i}^2+l_{BC}^2-l_{CE}^2}{2l_{{(BE)}_i}{l}_{BC}}}\right)+{\alpha }_2,$$

(41)

where

$$l_{{(BE)}_i}={\left[{(X_{E_i}-X_{B_i})}^2+{(Y_{E_i}-Y_{B_i})}^2\right]}^{{\displaystyle \frac{1}{2}}},$$

(42)

$${\phi }_{{(BE)}_i}=\mathrm{t}{\mathrm{g}}^{-1}{\displaystyle \frac{Y_{E_i}-Y_{B_i}}{X_{E_i}-X_{B_i}}},$$

(43)

$$\left[\begin{array}{c}{X}_{E_i}\\ Y_{E_i}\end{array}\right]=\left[\begin{array}{c}{X}_D\\ Y_D\end{array}\right]+l_{DE}\left[\begin{array}{c}\cos {\phi }_{4i}\\ \sin {\phi }_{4i}\end{array}\right].$$

(44)

Table 6 presents the obtained values of the coordinates of the point P, and Figure 6 shows a graph of its change.

Table 6. Values of the point P coordinates and input angle ${\phi }_{1i}$.

i	1	2	3	4	5	6	7	8	9	10	11	12
$X_{P_i}, (\mathrm{cm})$	25.45	37.45	40.25	29.07	13.52	−1.33	−11.54	−14.16	−8.94	1.34	12.65	20.97
$Y_{P_i}, (\mathrm{cm})$	44.06	73.87	84.30	85.25	79.75	68.41	52.56	35.22	20.66	12.37	12.02	20.97
${\phi }_{1i}$	0°	30°	60°	90°	120°	150°	180°	210°	240°	270°	300°	330°

5.3. Stephenson IIA Path-Generating Mechanism

Table 7 gives the values of the point P coordinates $X_{P_i}$ and $Y_{P_i}$ in the absolute coordinate system $OXY$ and input angle ${\phi }_{1i}$ for N = 12.

Table 7. Values of the point P coordinates and input angle ${\phi }_{1i}$.

i	1	2	3	4	5	6	7	8	9	10	11	12
$X_{P_i}, (\mathrm{cm})$	45.65	41.00	33.24	25.16	18.89	15.88	16.97	22.18	29.68	47.37	52.83	49.69
$Y_{P_i}, (\mathrm{cm})$	72.45	70.65	70.22	69.80	66.80	62.08	57.44	54.79	16.96	29.67	54.16	66.72
${\phi }_{1i}$	0°	30°	60°	90°	120°	150°	180°	210°	240°	270°	300°	330°

It is necessary to determine the synthesis parameters of the Stephenson IIA path-generating mechanism (Figure 7), which reproduces the given values of the $X_{P_i}$ and $Y_{P_i}$ coordinates of the output point P for the given values of the input angle ${\phi }_{1i}$.

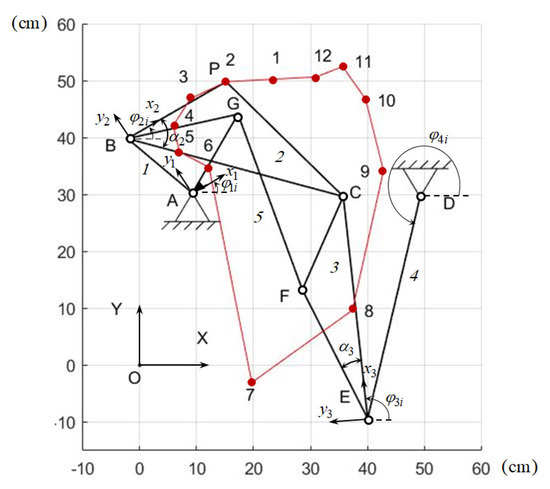
Figure 7. Stephenson IIA path-generating mechanism.

Stephenson IIA path-generating mechanism is formed by connecting the links 1 and 3 of the five-link linkage ABCED by the binary link GF. Therefore, the parametric syntesis of the Stephenson IIA path-generating mechanism consist of the parametric synthesis of the five-link linkage ABCED and the binary link GF. Parametric synthesis of the five-link linkage ABCED is considered above.

Synthesis parameters of the binary link GF are: $x_G^{(1)},y_G^{(1)},x_F^{(3)},y_F^{(3)},l_{GF}$. To parametric synthesis of the binary link GF, it is necessary to determine the angle ${\phi }_{3i}$ by the equation

$${\phi }_{3i}=\mathrm{t}{\mathrm{g}}^{-1}{\displaystyle \frac{Y_{C_i}-Y_{E_i}}{X_{C_i}-X_{E_i}}},$$

(45)

where

$$\left[\begin{array}{c}{X}_{E_i}\\ Y_{E_i}\end{array}\right]=\left[\begin{array}{c}{X}_D\\ Y_D\end{array}\right]+l_{DE}\left[\begin{array}{c}\cos {\phi }_{4i}\\ \sin {\phi }_{4i}\end{array}\right].$$

(46)

The angle ${\phi }_{4i}$ in Expression (46) is determined by Equation (29). Then, a weighted difference function of the form (32) is derived, where the coordinates $X_{F_i}$ and $Y_{F_i}$ of the joint F in the absolute coordinate system $OXY$ are determined by the equation

$$\left[\begin{array}{c}{X}_{F_i}\\ Y_{F_i}\end{array}\right]=\left[\begin{array}{c}{X}_{E_i}\\ Y_{E_i}\end{array}\right]+\left[\begin{array}{cc}\cos {\phi }_{3i}& -\sin {\phi }_{3i}\\ \sin {\phi }_{3i}& \cos {\phi }_{3i}\end{array}\right]\cdot \left[\begin{array}{c}{\mathrm{x}}_F^{(3)}\\ {\mathrm{y}}_F^{(3)}\end{array}\right].$$

(47)

The synthesis parameters of the GF binary link are determined by minimizing Function (32).

Table 8 presents the obtained values of the synthesis parameters of the Stephenson IIA path-generating mechanism.

Table 8. Values of the synthesis parameters (cm).

$X_A$	$Y_A$	$x_B^{(1)}$	$y_B^{(1)}$	$l_{BP}$	$x_C^{(2)}$	$y_C^{(2)}$	$X_D$
9.25	30.23	−5.09	13.99	19.99	11.96	−63.69	49.25
$Y_D$	$l_{CE}$	$l_{ED}$	$x_G^{(1)}$	$y_G^{(1)}$	$x_F^{(3)}$	$y_F^{(3)}$	$l_{GF}$
29.54	39.25	13.48	13.86	8.00	16.73	6.29	32.82

To check the parametric synthesis results of the Stephenson IIA path-generating mechanism, determine the coordinates of the point P in the absolute coordinate system $OXY$ using Equation (20). To determine the angle ${\phi }_{2i}$ in this equation, we solve the problem of the positions of the synthesized Stephenson IIA path-generating mechanism, which has the structural formula

$$\mathrm{I}(1)\to \mathrm{III}(2,3,4,5),$$

(48)

i.e., it belongs to the mechanism of the third class according to the Assur–Artobolevskiy classification.

To solve the problem of positions of this mechanism of the third class, we use the method of conditional generalized coordinates [51], according to which we remove the link GF by separating the elements of the joints G and F. Then, one additional DOF appears in the mechanism. If we choose the link 2 as a conditional input link and angle ${\phi }_{2i}$ as a conditional generalized coordinate, then the considered mechanism of the third class is transformed into a mechanism of the second class with the following structural formula:

$$\mathrm{I}(1)\to \mathrm{I}(2)\to \mathrm{II}(3,4).$$

(49)

Let us derive the residual function

$${\Delta }_i=l_{GF}-{\tilde{l}}_{{(GF)}_i},$$

(50)

where ${\tilde{l}}_{{(GF)}_i}$ is a variable distance between the centers of disconnected joints G and F, which is determined by the equation

$${\tilde{l}}_{{(GF)}_i}={\left[{\left(X_{F_i}-X_{G_i}\right)}^2+{\left(Y_{F_i}-Y_{G_i}\right)}^2\right]}^{{\displaystyle \frac{1}{2}}}.$$

(51)

Coordinates of the joints G and F in Expression (51) are determined by Equations (39) and (47), where the values of the angles ${\phi }_{3i}$ and ${\phi }_{4i}$ can be determined through the values of the angle ${\phi }_{2i}$, by solving the problem of positions of dyad CED

$${\phi }_{4i}={\phi }_{{(DC)}_i}-{\cos }^{-1}{\displaystyle \frac{l_{{(DC)}_i}^2+l_{DE}^2-l_{CE}^2}{2l_{{(DC)}_i}{l}_{DE}}},$$

(52)

$${\phi }_{3i}=\mathrm{t}{\mathrm{g}}^{-1}{\displaystyle \frac{Y_{C_i}-Y_{E_i}}{X_{C_i}-X_{E_i}}},$$

(53)

where

$$l_{{(DC)}_i}={\left[{(X_{C_i}-X_D)}^2+{(Y_{C_i}-Y_D)}^2\right]}^{{\displaystyle \frac{1}{2}}},$$

(54)

$${\phi }_{{(DC)}_i}=\mathrm{t}{\mathrm{g}}^{-1}{\displaystyle \frac{Y_{C_i}-Y_D}{X_{C_i}-X_D}}.$$

(55)

Consequently, the Residual (50) is a function of the conditional generalized coordinate ${\phi }_{2i}$. Minimizing Function (50) by the bisection method, we determine the value of the angle ${\phi }_{2i}$. In this case, the values of the angles ${\phi }_{3i}$ and ${\phi }_{4i}$ are simultaneously determined. By changing the values of the angle ${\phi }_{1i}$, the values of the angles ${\phi }_{2i},{\phi }_{3i},{\phi }_{4i}$ are similarly determined.

Table 9 presents the values of the coordinates $X_{P_i}$ and $Y_{P_i}$ of the point P, and Figure 7 shows a graph of its change.

Table 9. Values of the point P coordinates and input angle ${\phi }_{1i}$.

i	1	2	3	4	5	6	7	8	9	10	11	12
$X_{P_i}, (\mathrm{cm})$	45.66	41.01	33.23	25.17	18.88	15.87	16.96	22.19	29.67	47.36	52.84	49.69
$Y_{P_i}, (\mathrm{cm})$	72.44	70.64	70.21	69.81	66.81	62.09	57.45	54.80	16.95	29.66	54.17	66.71
${\phi }_{1i}$	0°	30°	60°	90°	120°	150°	180°	210°	240°	270°	300°	330°

5.4. Stephenson IIB Path-Generating Mechanism

Table 10 gives the values of the point P coordinates $X_{P_i}$ and $Y_{P_i}$ in the absolute coordinate system $OXY$ and input angle ${\phi }_{1i}$ for N = 12.

Table 10. Values of the point P coordinates and input angle ${\phi }_{1i}$.

i	1	2	3	4	5	6	7	8	9	10	11	12
$X_{P_i}, (\mathrm{cm})$	44.90	48.56	49.25	47.23	43.63	39.27	34.91	31.47	29.97	31.03	34.57	39.67
$Y_{P_i}, (\mathrm{cm})$	13.35	13.62	14.79	17.62	21.30	24.38	25.85	25.22	22.69	19.24	16.00	13.96
${\phi }_{1i}$	0°	30°	60°	90°	120°	150°	180°	210°	240°	270°	300°	330°

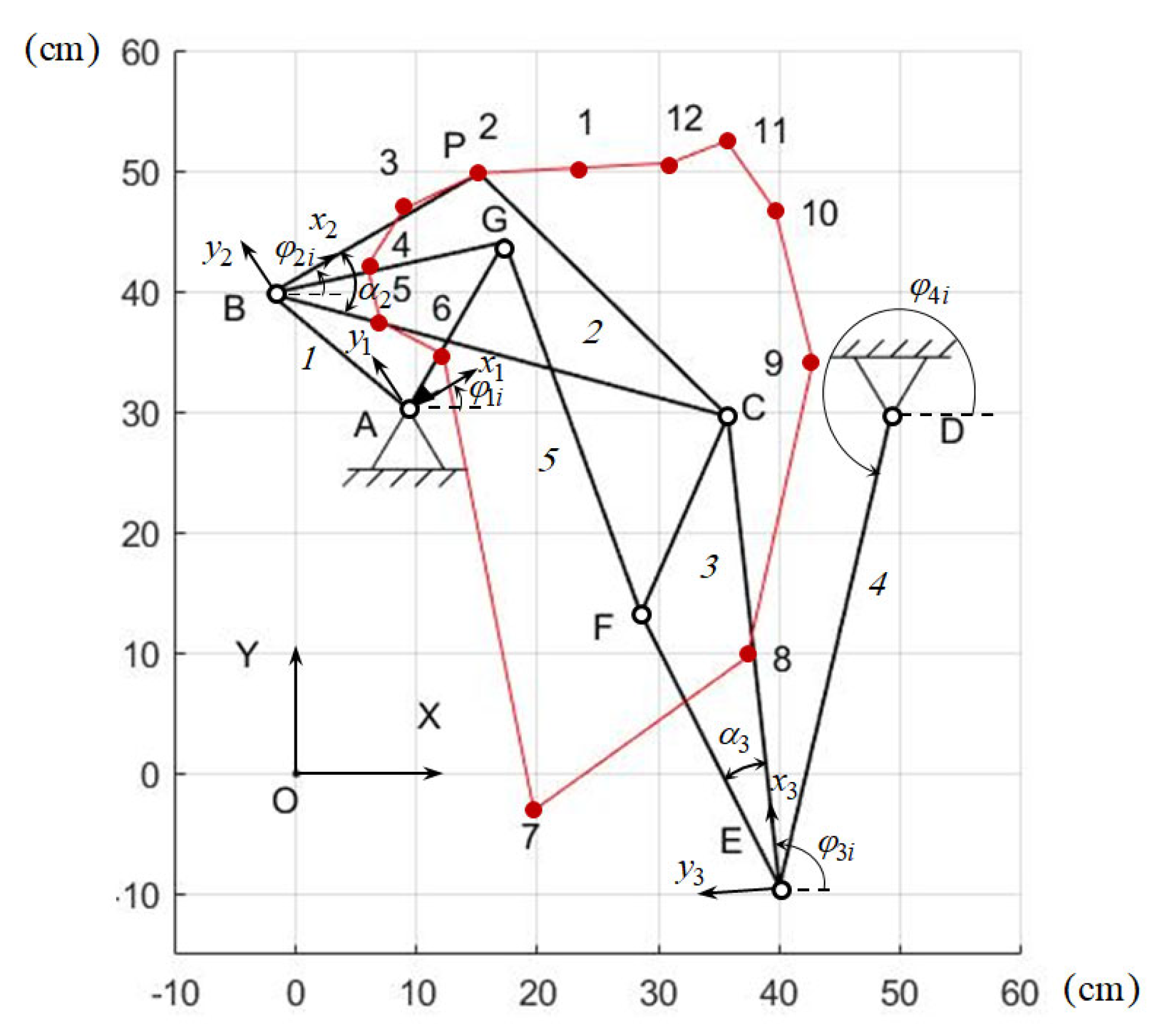
It is necessary to determine the synthesis parameters of the Stephenson IIB path-generating mechanism (Figure 8), which reproduces the given values of the $X_{P_i}$ and $Y_{P_i}$ coordinates of the output point P for given values of the input angle ${\phi }_{1i}$. In Figure 8, the segment BC is not another separate link.

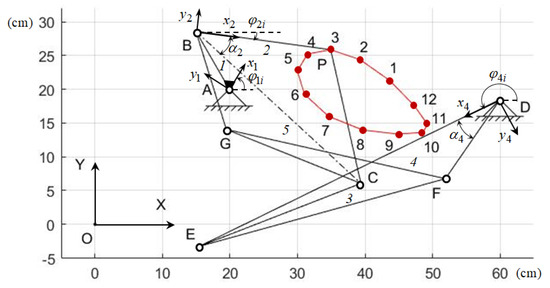
Figure 8. Stephenson IIB path-generating mechanism.

Stephenson IIB path-generating mechanism is formed by connecting links 2 and 4 of the five-link linkage ABCED by the binary link GF. Therefore, the parametric synthesis of the Stephenson IIB path generation mechanism consists of the parametric synthesis of the five-link linkage ABCED and the binary link GF. The synthesis parameters of the GF binary link are $x_G^{(2)},y_G^{(2)},x_F^{(4)},y_F^{(4)},l_{GF}$ to determine which weighted difference function is derived:

$$\Delta q_i={\left(x_{F_i}^{(2)}-x_G^{(2)}\right)}^2+{\left(x_{F_i}^{(2)}-x_G^{(2)}\right)}^2-l_{GF}^2,$$

(56)

where

$$\left[\begin{array}{c}{x}_{F_i}^{(2)}\\ y_{F_i}^{(2)}\end{array}\right]=\left[\begin{array}{cc}\cos {\phi }_{2i}& \sin {\phi }_{2i}\\ -\sin {\phi }_{2i}& \cos {\phi }_{2i}\end{array}\right]\cdot \left[\begin{array}{c}{X}_{F_i}-X_{B_i}\\ Y_{F_i}-Y_{B_i}\end{array}\right],$$

(57)

$${\phi }_{2i}=\mathrm{t}{\mathrm{g}}^{-1}{\displaystyle \frac{Y_{P_i}-Y_{B_i}}{X_{P_i}-X_{B_i}}}.$$

(58)

Synthesis parameters of the binary link GF are determined by minimizing Function (56). Table 11 presents the obtained values of the synthesis parameter of the Stephenson IIB path-generating mechanism.

Table 11. Values of the synthesis parameters (cm).

$X_A$	$Y_A$	$x_B^{(1)}$	$y_B^{(1)}$	$l_{BP}$	$x_C^{(2)}$	$y_C^{(2)}$	$X_D$
59.99	18.48	4.94	8.57	20.14	27.26	−19.01	59.99
$Y_D$	$l_{CE}$	$l_{ED}$	$x_G^{(2)}$	$y_G^{(2)}$	$x_F^{(4)}$	$y_F^{(4)}$	$l_{GF}$
18.48	25.69	49.58	6.42	−13.79	12.42	6.99	33.26

To check the parametric synthesis results of the Stephenson IIB path-generating mechanism, determine the coordinates of the point P in the absolute coordinate system $OXY$ using Equation (20). To determine the angle ${\phi }_{2i}$ in this equation, we solve the problem of positions of the synthesized Stephenson IIB path-generating mechanism, which has the structural formula

$$\mathrm{I}(1)\to \mathrm{I}\mathrm{V}(2,3,4,5),$$

(59)

i.e., it belongs to the mechanism of the fourth class according to the Assur–Artobolevskiy classification.

To solve the problem of the positions of the Stephenson IIB path-generating mechanism, as well as to analyze the position of the Stephenson IIA path-generating mechanism, we use the method of conditional generalized coordinates, i.e., we remove the link GF and transform this mechanism into a mechanism of the second class with the structural Formula (49). We derive the residual Function (50), where the coordinates of the joints G and F are determined by the equations

$$\left[\begin{array}{c}{X}_{G_i}\\ Y_{G_i}\end{array}\right]=\left[\begin{array}{c}{X}_{B_i}\\ Y_{B_i}\end{array}\right]+\left[\begin{array}{cc}\cos {\phi }_{2i}& -\sin {\phi }_{2i}\\ \sin {\phi }_{2i}& \cos {\phi }_{2i}\end{array}\right]\cdot \left[\begin{array}{c}{x}_G^{(2)}\\ y_G^{(2)}\end{array}\right],$$

(60)

$$\left[\begin{array}{c}{X}_{F_i}\\ Y_{F_i}\end{array}\right]=\left[\begin{array}{c}{X}_D\\ Y_D\end{array}\right]+\left[\begin{array}{cc}\cos {\phi }_{4i}& -\sin {\phi }_{4i}\\ \sin {\phi }_{4i}& \cos {\phi }_{4i}\end{array}\right]\cdot \left[\begin{array}{c}{x}_F^{(4)}\\ y_F^{(4)}\end{array}\right],$$

(61)

where the values of the angle ${\phi }_{4i}$ are determined by solving the problem of positions of the dyad CED using Equation (52).

Minimizing Function (50) via the bisection method, we determine the values of the angle ${\phi }_{4i}$. Table 12 presents the values of the coordinate $X_{P_i}$ and $Y_{P_i}$ of the point P, and Figure 8 shows a graph of its change.

Table 12. Values of the point P coordinates and input angle ${\phi }_{1i}$.

i	1	2	3	4	5	6	7	8	9	10	11	12
$X_{P_i}, (\mathrm{cm})$	44.91	48.57	49.24	47.22	43.64	39.26	34.92	31.46	29.98	31.04	34.56	39.67
$Y_{P_i}, (\mathrm{cm})$	13.36	13.61	14.80	17.63	21.31	24.39	25.84	25.21	22.70	19.25	16.01	13.97
${\phi }_{1i}$	0°	30°	60°	90°	120°	150°	180°	210°	240°	270°	300°	330°

5.5. Stephenson III Path-Generating Mechanism

Table 13 gives the values of the point P coordinates $X_{P_i}$ and $Y_{P_i}$ in the absolute coordinate system $OXY$ and input angle ${\phi }_{1i}$ for N = 12.

Table 13. Values of the point P coordinates and input angle ${\phi }_{1i}$.

i	1	2	3	4	5	6	7	8	9	10	11	12
$X_{P_i}, (\mathrm{cm})$	15.40	10.06	5.84	4.11	5.49	9.95	15.76	17.64	19.22	20.94	21.51	19.72
$Y_{P_i}, (\mathrm{cm})$	22.40	27.59	30.36	29.75	26.50	22.31	18.59	14.59	11.71	11.06	12.90	16.95
${\phi }_{1i}$	0°	30°	60°	90°	120°	150°	180°	210°	240°	270°	300°	330°

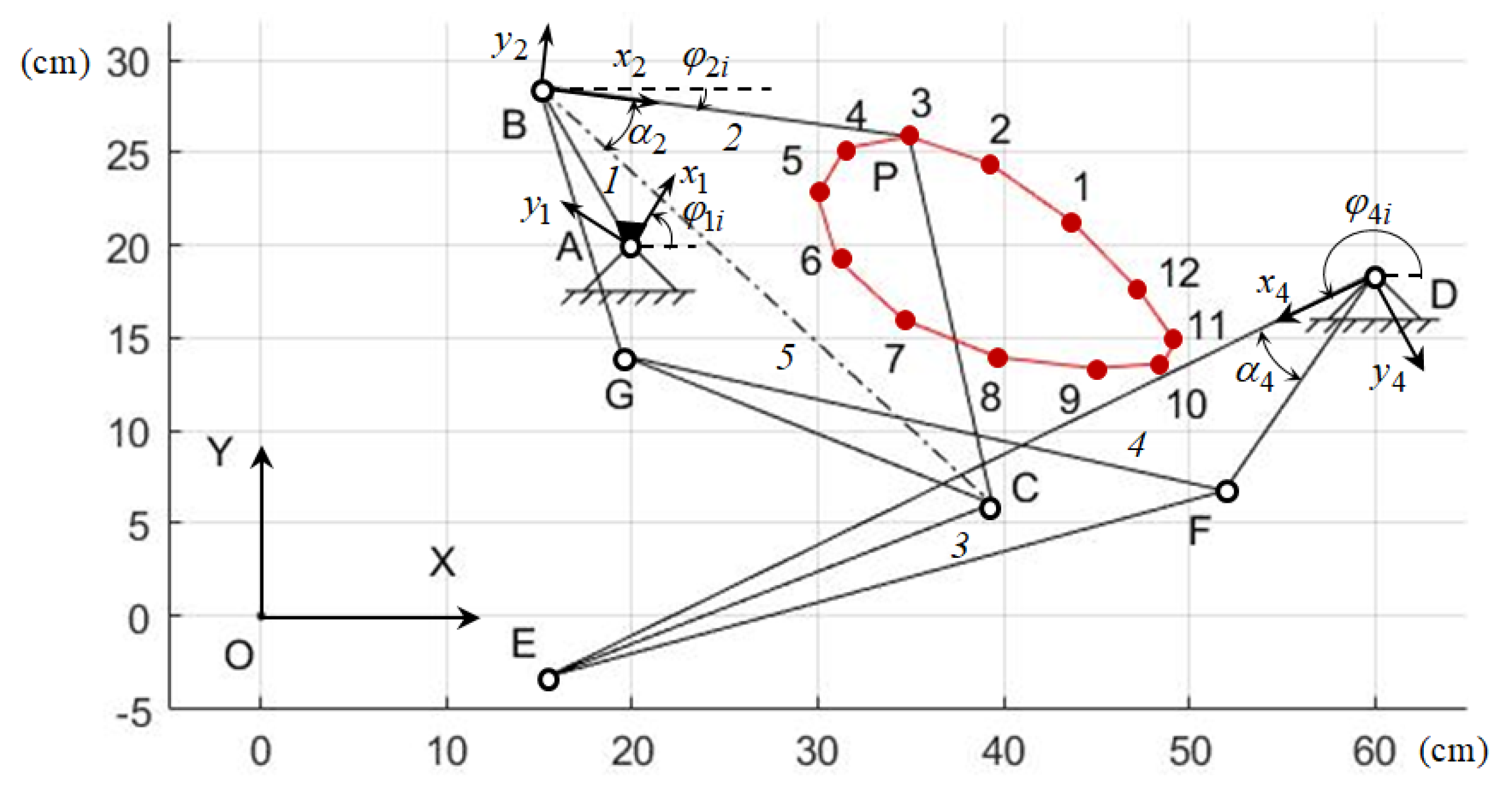
It is necessary to determine the synthesis parameters of the Stephenson III path generation mechanism (Figure 9), which reproduces the given values of the coordinates $X_{P_i}$ and $Y_{P_i}$ of the output point P at given values of the angle ${\phi }_{1i}$.

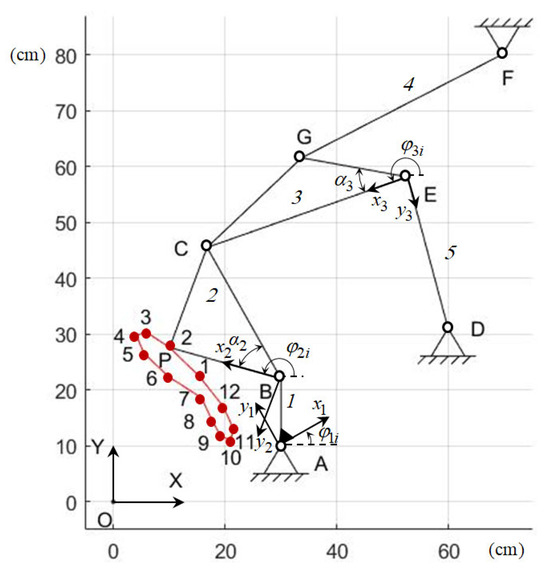
Figure 9. Stephenson III path-generating mechanism.

The Stephenson III path-generating mechanism is formed by connecting the link CE of the five-link linkage ABCED to the base by the binary link GF. Therefore, the parametric synthesis of the Stephenson III path-generating mechanism consists of the parametric synthesis of the five-link linkage ABCED and the binary link GF.

The synthesis parameters of the binary link GF are $x_G^{(3)},y_G^{(3)},X_F,Y_F,l_{GF}$ to determine which weighted difference function derives

$$\Delta q_i={\left(X_{G_i}-X_F\right)}^2+{\left(Y_{G_i}-Y_F\right)}^2-l_{GF}^2,$$

(62)

where

$$\left[\begin{array}{c}{X}_{G_i}\\ Y_{G_i}\end{array}\right]=\left[\begin{array}{c}{X}_{E_i}\\ Y_{E_i}\end{array}\right]+\left[\begin{array}{cc}\cos {\phi }_{3i}& -\sin {\phi }_{3i}\\ \sin {\phi }_{3i}& \cos {\phi }_{3i}\end{array}\right]\cdot \left[\begin{array}{c}{x}_G^{(3)}\\ y_G^{(3)}\end{array}\right].$$

(63)

The angle ${\phi }_{3i}$ in Equation (63) and the angle ${\phi }_{4i}$ for calculating the coordinates $X_{E_i}$ and $Y_{E_i}$ of the joint E are determined by Equations (52) and (53).

Table 14 presents the obtained values of the synthesis parameters of the Stephenson III path-generating mechanism.

Table 14. Values of the synthesis parameters (cm).

$X_A$	$Y_A$	$x_B^{(1)}$	$y_B^{(1)}$	$l_{BP}$	$x_C^{(2)}$	$y_C^{(2)}$	$X_D$
29.98	10.01	6.00	10.40	20.68	19.04	−19.03	59.89
$Y_D$	$l_{CE}$	$l_{ED}$	$x_G^{(3)}$	$y_G^{(3)}$	$X_F$	$Y_F$	$l_{GF}$
31.04	38.01	28.02	16.71	−9.51	69.59	80.03	40.38

To check the parametric synthesis results of the Stephenson III path-generating mechanism, determine the coordinates of the point P in the absolute coordinate system $OXY$ using Equation (20). To determine the angle ${\phi }_{2i}$ in this equation, we solve the problem of the positions of the synthesized Stephenson III path-generating mechanism, which has the structural Formula (48), i.e., it belongs to the mechanism of the third class according to the Assur–Artobolevskiy classification. The problem of the positions of the Stephenson III path-generating mechanism is solved similarly to the solution of the problem of the positions of the Stephenson IIA path-generating mechanism via the method of conditional generalized coordinates.

Table 15 presents the obtained values of the coordinates $X_{P_i}$ and $Y_{P_i}$ of the point P, and Figure 9 shows a graph of its change.

Table 15. Values of the point P coordinates and input angle ${\phi }_{1i}$.

i	1	2	3	4	5	6	7	8	9	10	11	12
$X_{P_i}, (\mathrm{cm})$	15.41	10.07	5.85	4.12	5.50	9.93	15.74	17.65	19.21	20.95	21.50	19.70
$Y_{P_i}, (\mathrm{cm})$	22.41	27.60	30.38	29.76	26.50	22.33	18.60	14.60	11.72	11.08	12.91	16.96
${\phi }_{1i}$	0°	30°	60°	90°	120°	150°	180°	210°	240°	270°	300°	330°

6. Conclusions

The structural synthesis of the four-link and six-link path-generating mechanisms with revolute joints has been carried out. A four-link path-generating mechanism is formed by connecting the output point and a base by the active and negative CKCs. Six-link path-generating Stephenson I, Stephenson IIA, Stephenson IIB, and Stephenson III mechanisms are formed by connecting the output point and base by active, passive, and negative CKCs. Active and negative CKCs impose the geometrical constraint on the movement of the output point and they work at certain values of the geometric parameters of their links, which are determined by least-square approximation. The geometric parameters of the links of the passive CKC vary to satisfy the constraints of the active and negative CKCs. Active, passive, and negative CKCs are structural modules. Structural and parametric syntheses of the path-generating mechanisms are carried out simultaneously, starting with the smallest number of links of structural modules. At the same time, the structural schemes and geometric parameters of the synthesized path-generating mechanisms are determined simultaneously. Numerical examples of the parametric synthesis of the four-link and six-link Stephenson I, Stephenson IIA, Stephenson IIB, and Stephenson III path-generating mechanisms are presented. The developed methods of the structural–parametric synthesis of path-generating mechanisms are the initial stage of their design. In future studies, their singular configurations and dynamics are planned.