Abstract
Simulation models are a valuable tool for exoskeleton development, especially for system optimization and evaluation. It allows an assessment of the performance and effectiveness of exoskeletons even at an early stage of their development without physical realization. Due to the closed physical interaction between the exoskeleton and the user, accurate modeling of the human–exoskeleton interaction in defined scenarios is essential for exoskeleton simulations. This paper presents a novel approach to simulate exoskeleton motion in response to human motion and the interaction forces at the physical interfaces between the human and the exoskeleton. Our approach uses a multibody model of a shoulder exoskeleton in MATLAB R2021b and imports human motion via virtual markers from a digital human model to simulate human–exoskeleton interaction. To validate the human-motion-based approach, simulated exoskeleton motion and interaction forces are compared with experimental data from a previous lab study. The results demonstrate the feasibility of our approach to simulate human–exoskeleton interaction based on human motion. In addition, the approach is used to optimize the support profile of an exoskeleton, indicating its potential to assist exoskeleton development prior to physical prototyping.
1. Introduction
Simulation models are useful tools for designing and optimizing exoskeletons by providing insight into their performance and effectiveness. Multibody and control system simulations are used primarily to evaluate the mechanical, actuator, and control behavior of the exoskeleton. Biomechanical simulation based on a human musculoskeletal model helps to understand the effect of the exoskeleton on the human body [1,2,3,4,5,6,7,8]. Due to the close interaction with the user, the user test is a conventional way to evaluate the performance of the exoskeleton. Compared to costly and time-consuming user testing, simulation models allow testing of extreme system configurations without compromising user health. This is especially important when developing rehabilitative exoskeletons for fragile patients. Moreover, simulation-based virtual prototyping reduces physical prototyping costs and iterations.
Exoskeletons interact closely with the human body and their movement is determined by human motion. Therefore, dynamic simulation of the human–exoskeleton interaction, especially the reaction of the exoskeleton to human motion, is crucial for mechanical and control design, as well as for optimization of the exoskeleton. Two groups of approaches can be identified in the literature to model the physical interaction between the human and the exoskeleton.
The first group models the physical human–exoskeleton interaction by importing the 3D model of the exoskeleton into a musculoskeletal human model. These approaches are often used in parametric studies to optimize exoskeleton hardware design [3,4,5,6,7,8] where the exoskeleton segments move with the coupled human model. The design parameters most commonly analyzed are spring stiffness [3,4,5], range of motion (ROM) [6], and material properties [8]. Additionally, the interaction between the exoskeleton and the musculoskeletal human model is also used for user-oriented control optimization [9,10,11]. Several studies model a rigid connection between the exoskeleton and the human model [6,8], where relative movement at the physical interface is not possible. These approaches assume that the human and exoskeleton joints are well aligned [6] or that there is some flexibility in the exoskeleton segments [8]. In other studies, the exoskeleton model is linked to the human model with additional degrees of freedom (DOF) [1,2,4,5,7]. This allows for relative motion between human and exoskeleton segments, thus approximating their connection at the physical interface in real operation. The interaction force at the physical interface is typically determined by contact models between two bodies, which is calculated by a spring-damper force [1,5]. The analysis of this group of approaches mostly focuses on the biomechanical impact of exoskeletons on the human body and helps improve the exoskeleton’s behavior concerning the user. However, using only musculoskeletal simulation has limitations in exploring the technical performance of exoskeletons, such as the robustness of the mechanical components and the computational efficiency of the controller.
The second group of approaches focuses on the technical behavior of the exoskeleton in interaction with humans. Mosconi et al. use human joint movements directly as the joint movements of the exoskeleton under the assumption of perfect joint alignment between humans and exoskeleton [12]. Chen et al. use a mathematical model to calculate the trajectory of the human foot for the dynamic simulation of a lower extremity exoskeleton [13]. Simplified 2D planar human models with rigid segments are often constructed for the dynamic simulation of the lower extremity [14,15]. Most approaches in this group build a 3D kinematic human model with rigid segments and couple it to the exoskeleton multibody model [16,17,18,19,20]. To reduce computational costs, these human models mostly use simplified kinematics and have a limited ability to mimic real human motions. The literature shows that it is important to simulate the behavior of the exoskeleton in response to human motion since the movement of the exoskeleton depends primarily on the motion of the user. However, building a human model within the exoskeleton simulation to mimic real human motion requires extensive effort.
The challenge of merging two models into a unified, monolithic simulation model without compromising their detailed representations is common for both groups of approaches discussed above. Therefore, there is a strong need for approaches that allow the simulation of exoskeleton behavior and human motion in a distributed but coordinated manner. In the domain of distributed simulation, the “gluing perspective” has demonstrated efficacy in establishing cohesive interactions between individual simulations of multibody systems [21,22,23]. To extend this to simulating exoskeleton behavior separate from the human model, an approach is needed that connects human motion to exoskeleton simulation and incorporates the physical interaction between the exoskeleton and the human body.
The present study addresses this need and introduces a novel approach to the dynamic simulation of exoskeleton behavior in response to realistic human motion. Our approach seamlessly integrates human motion into the exoskeleton simulation, avoiding the need to embed a human model. Furthermore, our approach allows us to simulate the realistic movements of the exoskeleton arms and interaction forces resulting from the relative motion between the user and the exoskeleton. A real shoulder exoskeleton is used as an example for the development and validation of this approach.
2. Human-Motion-Based Approach for Exoskeleton Simulation
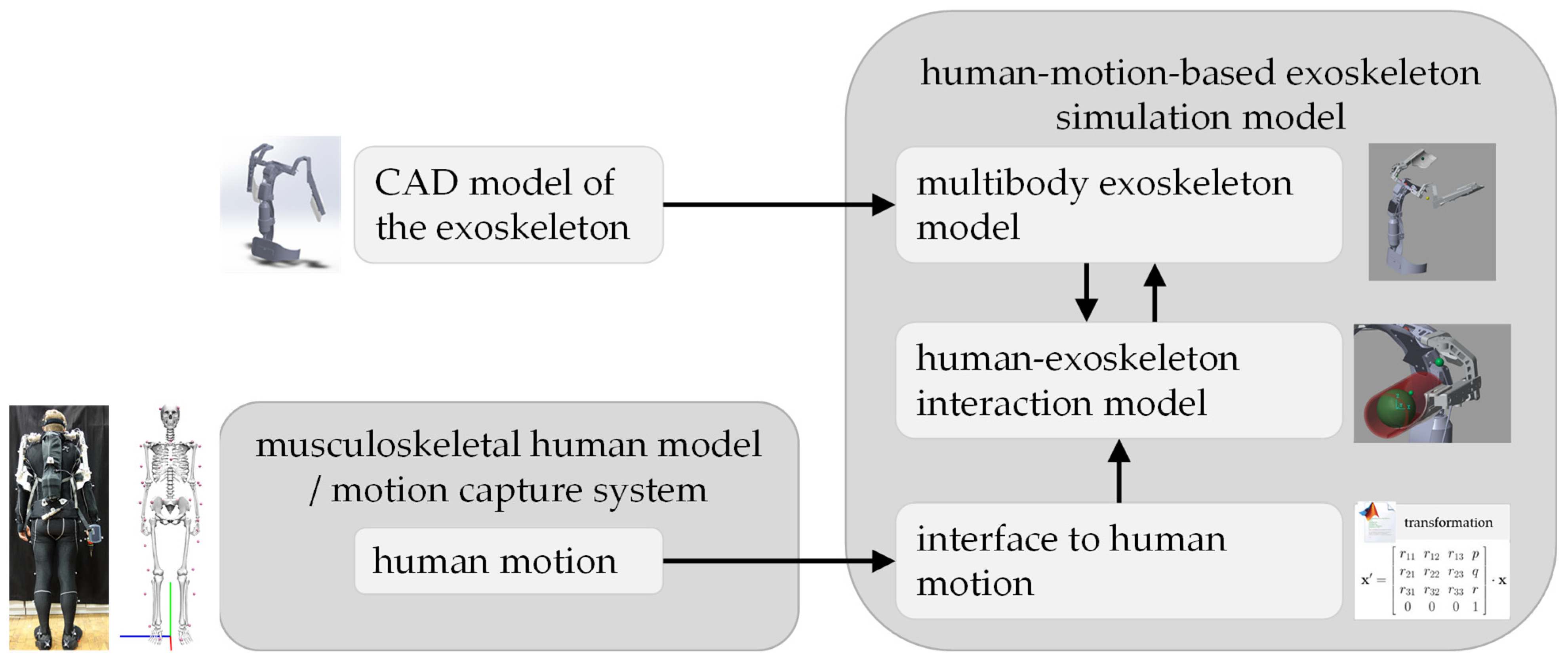
The presented approach is developed for simulative evaluation and optimization of exoskeleton behavior based on human motion, especially for the early stage of exoskeleton development, when a physical prototype is not available. As mentioned in the introduction, the motion of an exoskeleton is highly dependent on the motion of the user, and it is beneficial to simulate the behavior of the exoskeleton in response to human motion. Our approach constructs a human-motion-based exoskeleton simulation model that consists of three key elements (see Figure 1): a multibody model to describe the technical details of the exoskeleton, an interface to import human motion in the form of marker positions, and a human–exoskeleton interaction model to simulate the physical contact between the user and the exoskeleton as well as their interaction forces. In this way, no additional digital human model is required within the exoskeleton simulation model for human motion generation to realize human–exoskeleton interaction. The required human motion can be acquired by a motion capture system or simulated in a musculoskeletal human model. The multibody model is derived from the CAD design of the exoskeleton.
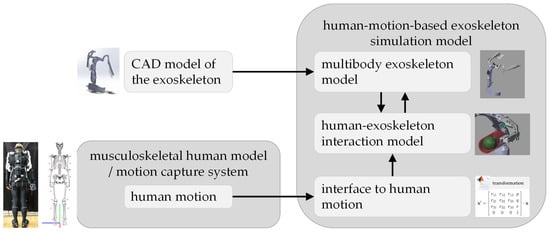
Figure 1.
Human-motion-based approach for exoskeleton simulation.
To validate the feasibility of this approach, this work uses a real shoulder exoskeleton Lucy [24] as an example to develop the human-motion-based simulation model, so that experimental data from user testing can be collected for comparison with the simulated data. The validation method is described in Section 3. The procedure for evaluating and optimizing the exoskeleton’s support profile for a specific task using this human-motion-based simulation approach is demonstrated as an example in Section 4. The results of the validation and the task-specific optimization are presented in Section 5.
2.1. Multibody Model of a Shoulder Exoskeleton
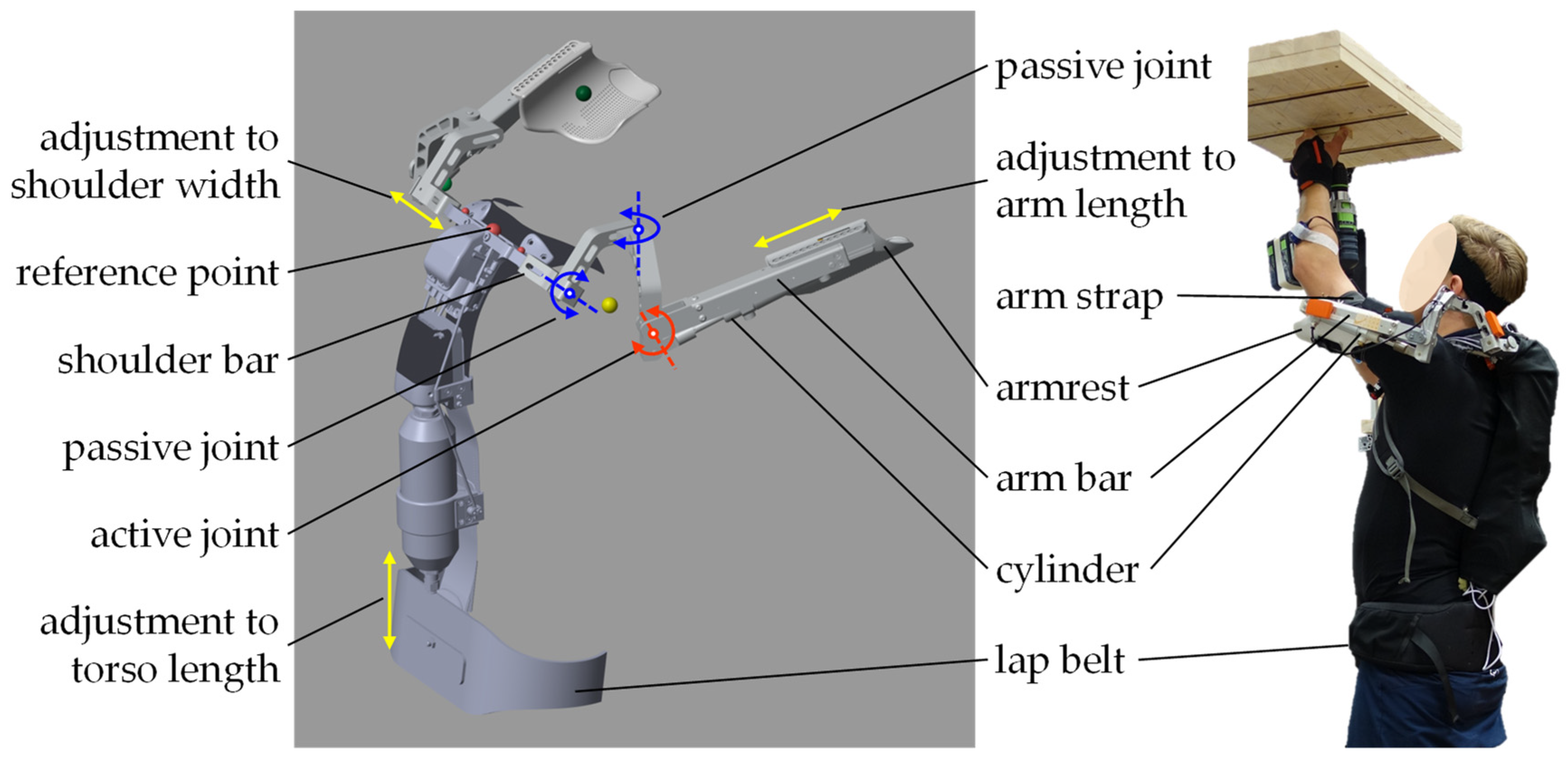
The shoulder exoskeleton Lucy is developed to assist users in raising and holding the arm for work at head level or above. The multibody exoskeleton model is built in MATLAB Simscape R2021b (MathWorks Inc., Natick, MA, USA), based on the CAD model of the exoskeleton Lucy built in SolidWorks 2022 SP 5.0 (SolidWorks Corporation, Concord, MA, USA). The key mechatronic features of Lucy are replicated in the multibody model, such as the joints’ range of motion (ROM), the possible mechanical adjustments, and control settings. The multibody model retains one active joint and two passive joints (red and blue curved arrows in Figure 2) in each exoskeleton arm, as well as three possibilities for individual adjustments in mechanical structure (yellow arrows in Figure 2). The model uses human anthropometric data such as upper arm length, shoulder width, and torso length to parameterize the position of the armrests, the shoulder bars, and the lap belt. Virtual sensors are added to the two active joints to measure the angular movements of the exoskeleton arms, which are used by the control model to determine the pressures for actuating the two pneumatic cylinders. A mathematical model derived from the technical characteristics of the cylinder is used to calculate the cylinder force. Cylinder forces create supporting moments at the active joints of each exoskeleton arm, helping to lift the human arm. Meanwhile, passive joints increase the degree of freedom of the shoulders. The control model contains the parameters for the support level and the support profile in relation to arm movement and the work task. The support level is the percentage of the maximum available cylinder force: 0% means that the exoskeleton is not providing any support, while 100% means that the exoskeleton is operating at full power of 7.8 N·m peak support torque with 6 bar supply pressure.
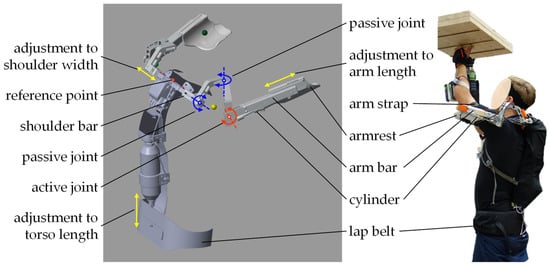
Figure 2.
The exoskeleton Lucy (right) and its multibody model in MATLAB Simscape R2021b (left).
2.2. Interface to Human Motion
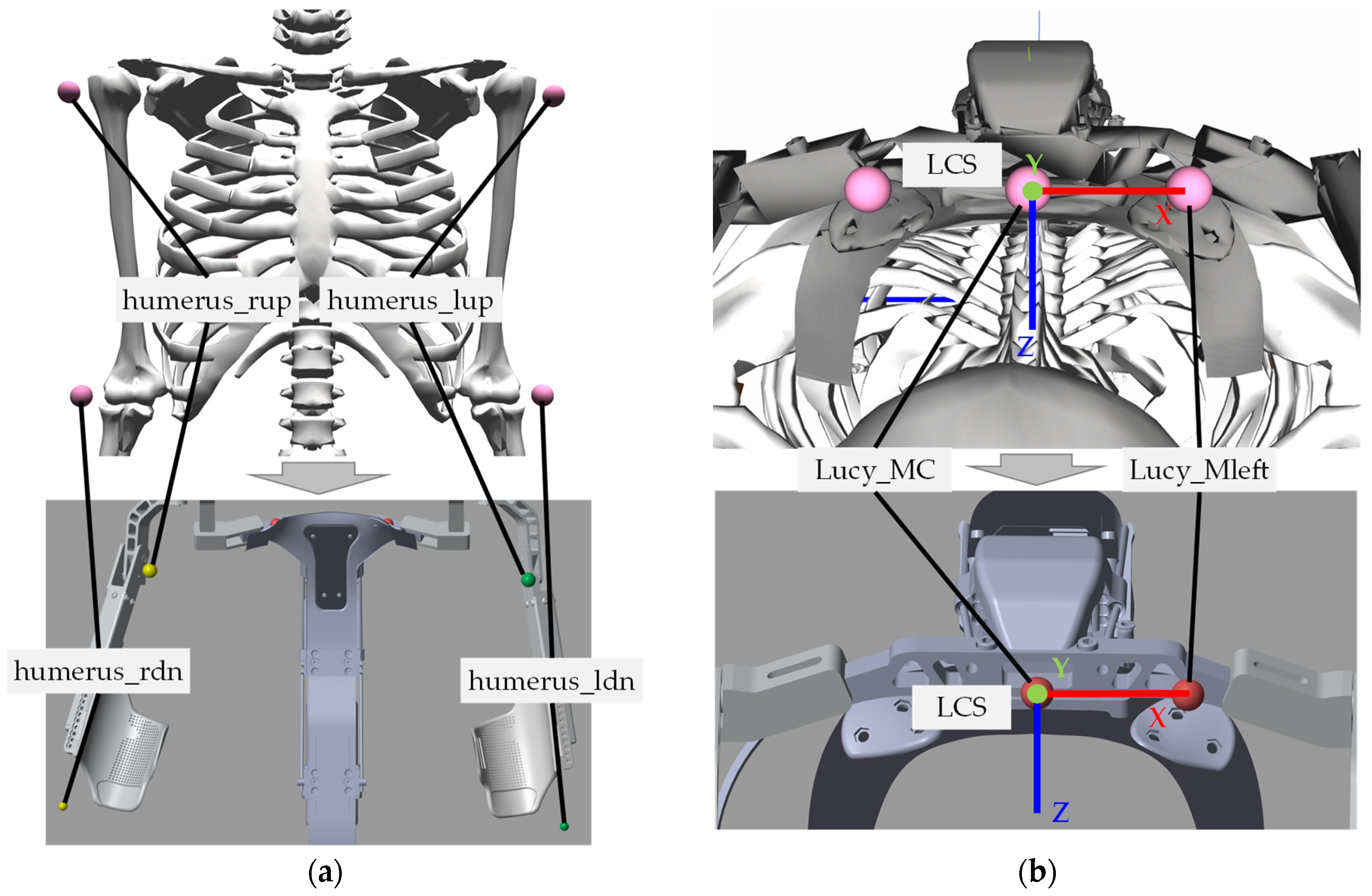
To simulate the movements of the exoskeleton arm, the upper arm movements of the user are required. The movements of the upper arm are imported into the exoskeleton multibody model through the positions of four virtual markers (humerus_rup, humerus_rdn, humerus_lup, humerus_ldn in Figure 3a) from a digital human model (DHM) [25] in OpenSim 4.3 (OpenSim, Stanford, US). It is a genetic full-body model built from partial models that specify the general musculoskeletal geometry of different parts of the human body. Its upper extremities are modeled by Holzbaur et al. [26] with 15 degrees of freedom for the shoulder, elbow, forearm, wrist, thumb, and index finger. The kinetic simulation of the DHM is based on the motions recorded by a motion capture system (Vicon Bonita, Oxford Metrics Ltd., Oxford, UK) during a previous lab study [27]. The marker placement follows the Vicon guide for the full-body model [28].
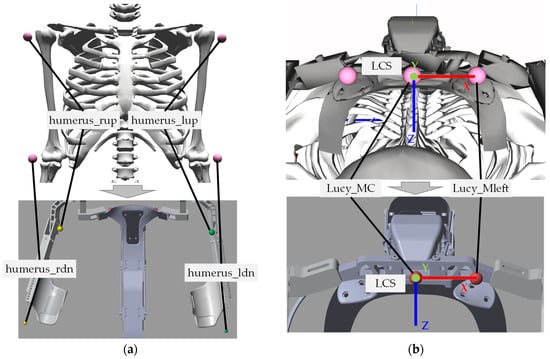
Figure 3.
Virtual markers for importing the upper arm movements from DHM into the exoskeleton model: (a) four markers on the humerus for motion input, the suffix “rup” stands for right-up, “ldn” for left-down, and so on; (b) two markers on the exoskeleton Lucy as reference points for the LCS.
The global coordinate systems (GCSs) of the human and exoskeleton models are different. In addition, the exoskeleton moves and rotates with the user, while the exoskeleton model is fixed to its GCS. Thus, the marker positions described in the GCS of the human model need to be transformed into a defined local coordinate system (LCS) for the exoskeleton model. Two reference points are defined on Lucy (see Figure 3b below) to define the LCS: Lucy_MC is the origin of the LCS, and Lucy_Mleft defines the direction of the x-axis of the LOS. Lucy_MC is on the middle line of Lucy, which should align with the spine of the user. Lucy_Mleft and Lucy_MC build a line along the shoulder bar, which is parallel to the user’s shoulder. In the previous study mentioned above, two markers are physically placed on the reference points on Lucy, and their positions are recorded by the motion capture system and then imported into the DHM. Alternatively, as shown in Figure 3b above, they can be virtually placed in the DHM by simply attaching the 3D model of the exoskeleton as a whole to the DHM without modeling each individual joint of the exoskeleton.
The marker positions from OpenSim are transformed from the GCS in the human model to the defined LCS in the exoskeleton model in three steps. First, the marker positions are translated from the origin of GCS to the origin of LCS through a translation matrix:
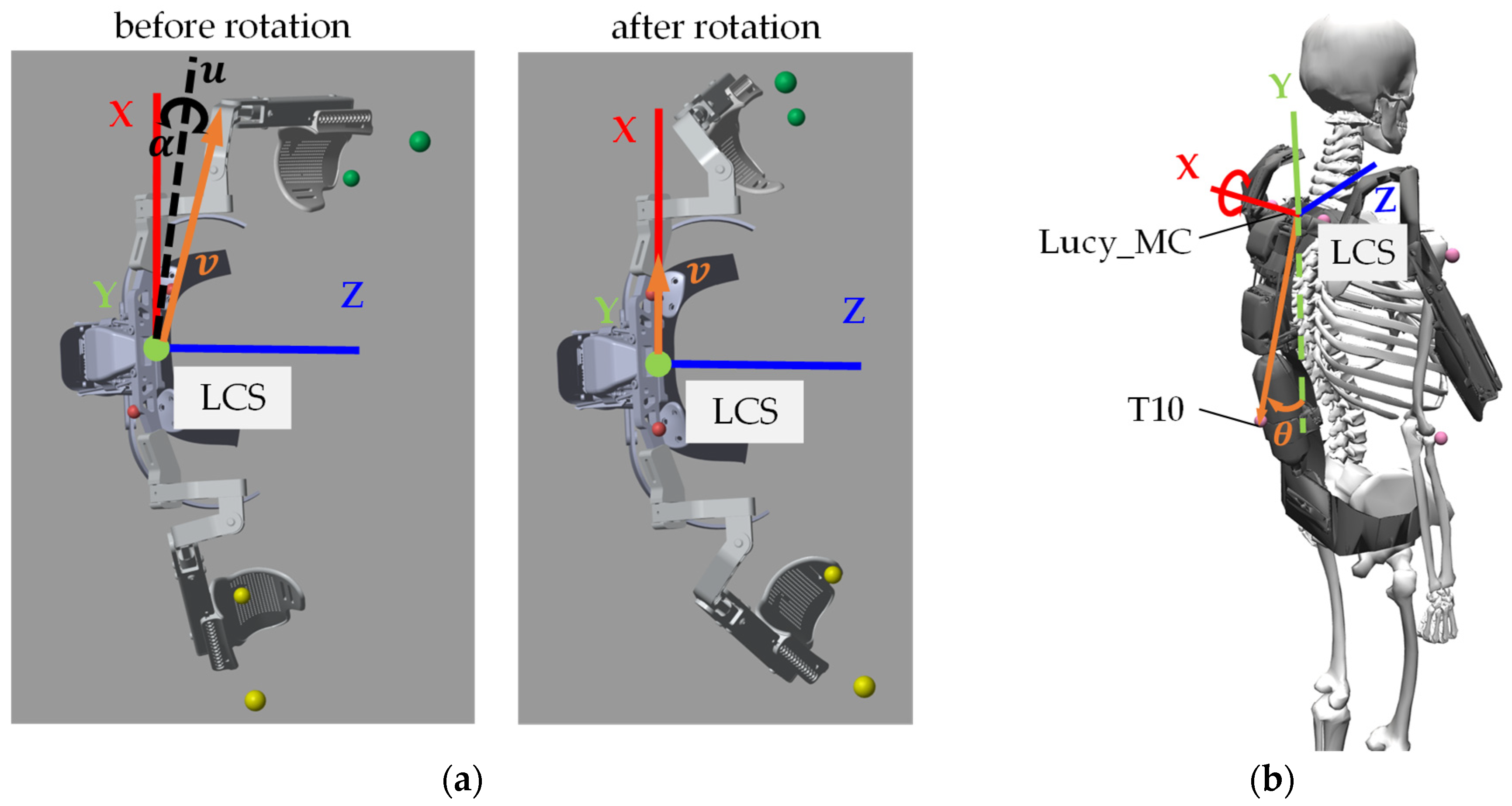
where is the position of Lucy_MC in GCS of DHM. Second, the rotation of the LCS following the upper body movements, e.g., rotation and lateral flexion, is determined by calculating the rotation matrix to align the vector (from Lucy_MC to Lucy_Mleft) (the orange vector in Figure 4a) to the x-axis of the LCS. is computed by two MATLAB functions: (1) the function vrrotvec determines the rotation axis and the angle that rotates around the axis (see Figure 4a left); (2) the function vrrotvec2mat converts the rotation axis and angle into rotation matrix :
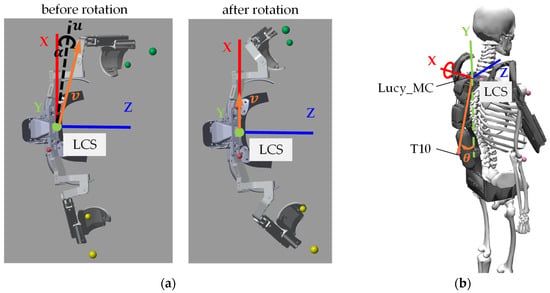
Figure 4.
(a) The first rotation () to align the vector to the x-axis of the LCS; (b) the second rotation () around the x-axis of the LCS.
Finally, to ensure that the y-axis of the LCS in the exoskeleton model is parallel to the y-axis of the GCS in the human model when the human is standing upright in the neutral position, a rotation on the x-axis of the LCS is required (see Figure 4b). To determine the rotation angle (see Figure 4b) around the x-axis, an additional marker T10 placed in the 10th thoracic vertebra is introduced. The second rotation matrix is given by:
The final transformation is summarized as follows:
where is the marker position in GCS of DHM, and is the transformed marker position in LCS of the exoskeleton model. The transformed positions of all the markers mentioned above are imported into the exoskeleton model in Simscape using bushing joints with the LCS at Lucy_MC as the base frame.
2.3. Human–Exoskeleton Interaction Model
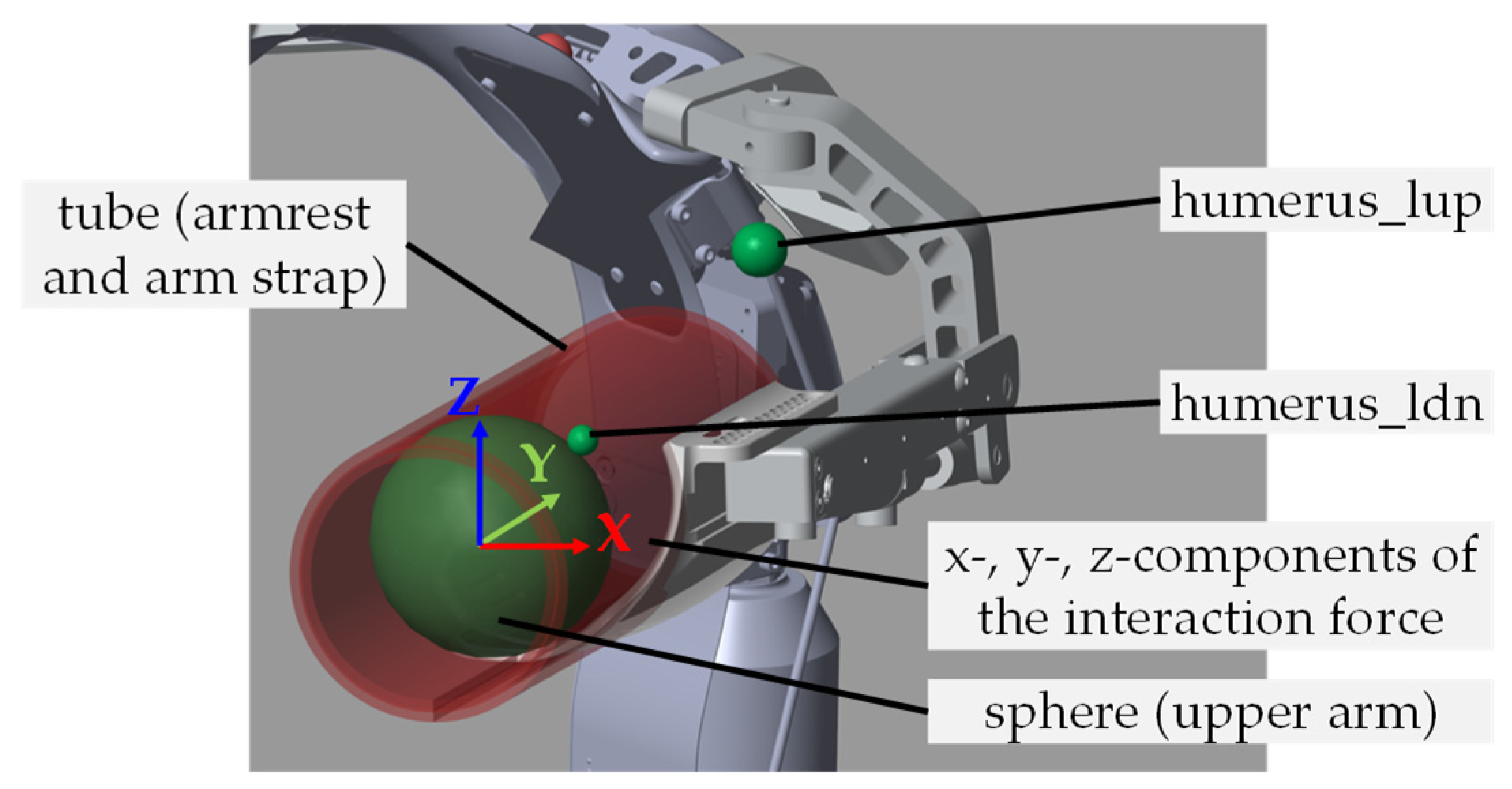
Because the human–exoskeleton interaction at the arm interfaces, including the armrest and arm strap (see Figure 2, at right, with label), is critical for the movements of the exoskeleton arm and the support torque, the interaction model focused on modeling the physical contact between the human upper arm and the exoskeleton arm interface, as well as the resulting interaction force. For this purpose, the entire arm interface is modeled as a tube, while the part of the human upper arm connected to the exoskeleton is modeled as a sphere inside the tube (see Figure 5). The contact force between the upper arm and the armrest is then implemented by the Sphere to Tube Contact Force model from the Simscape Multibody Contact Force Library [29]. The tubes are attached to the armrests by rigid transform blocks in Simscape. The motions of the spheres are driven by the transformed positions of markers humerus_rdn and humerus_ldn on the upper arms (see Figure 5). To mimic a proper connection between the upper arm and the exoskeleton without compressing the skin, the inner radius of the tube is set equal to the radius of the sphere. Due to the softness of the muscles and fabrics at the arm interface, small movements of the upper arm are still allowed inside the arm interface. Thus, a Cartesian joint with three linear degrees of freedom (DOFs) is connected between the sphere (human upper arm) and the tube (arm interface of the exoskeleton), with no specified limits in each DOF.
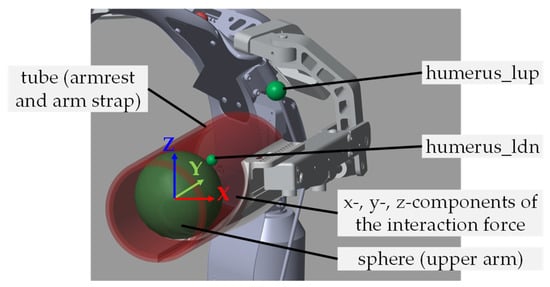
Figure 5.
Contact modeling between exoskeleton arm interface and human upper arm, left side as an example, with the coordinate system of the interaction force acting from the tube to the sphere.
The static and kinetic friction coefficients are set at 1 and 0.8, respectively, thus simulating fabric-to-fabric friction [30] between the cloth and the fabric surfaces of the arm interface. The contact force law of the model is set to linear with a stiffness of N/m and a damping of 10 N/(m/s) after tuning according to library recommendations [29]. The model calculates the contact force between the sphere and the tube caused by their relative motion and applies the force to both, resulting in changes in their motion. This allows the exoskeleton arm to follow the movement of the upper arm in the simulation, with or without the support of the cylinders, just as the system Lucy does in the real world. The coordinate system of the interaction force acting from the tube to the sphere is defined in Figure 5. The z-component of the force is regarded as the interaction force in this paper for the following validations and analysis. When the user raises the arms and the cylinders are off, i.e., no support, the simulated interaction force is negative because the user must work against the weight of the exoskeleton arm. When the arms are raised with support from the cylinder, a positive interaction force occurs in the simulation.
3. Validation of Human-Motion-Based Simulation Approach
Two groups of simulations are conducted, summarized in Table 1, for the validation of the human-motion-based simulation approach. Motion data of three participants (P1–P3) from the previous lab study of the exoskeleton Lucy [27] are used as input for the simulations. In the lab study, two overhead tasks (T1 and T2) with a screwdriver are defined. Task T2 is more demanding on the shoulder and wrist than task T1. Both tasks are carried out under three conditions: (S0) do not wear the exoskeleton Lucy, (S50) set Lucy at 50% of its maximum power, and (S100) set Lucy at 100% of its maximum power [27]. According to this setting, each group of exoskeleton simulation contains 12 simulation cases: 3 participants × 2 tasks × 2 supported conditions (S50, S100). The only difference between the two groups is the motion input of the simulation. Simulation group 1 uses the human motion from the same supported conditions (S50/S100), while simulation group 2 uses only the human motion from the unsupported condition (S0). For example, case P1T1S100 simulates the behavior of the exoskeleton in response to the motion of participant P1 while performing task T1. The support level of the exoskeleton model is set to Lucy’s full power. Simulation group 1 uses P1’s motion captured under condition S100 in the lab study, while simulation group 2 uses P1’s motion captured under condition S0.

Table 1.
An overview of the two simulation groups.
The validation of the human-motion-based simulation approach is conducted in two levels, summarized in Table 2. The first level aims to verify whether this approach can reproduce the exoskeleton behavior in response to the human motion recorded with the support of Lucy. At this level, simulated exoskeleton arm motions and the interaction forces from simulation group 1 are compared with the measured data from the same supported condition (S50 or S100) of the lab study. Besides the qualitative comparison of the curves, Mean Absolute Error (MAE) and Root Mean Square Deviation (RMSD) are calculated to quantitatively measure the deviation between the simulated and measured variables. To ensure comparability of the simulated and measured data, all simulations use the system setup documented in the lab study for the exoskeleton model, including the length of the shoulder bar, the position of the armrest, and the air pressure of the power supply. The elevation angle of the exoskeleton arm is recorded by the datalogger on Lucy during the lab study. The interaction force between the dominant upper arm and the arm interface is measured by a pressure sensing mat (X3 Pro System, LX205:50.100.10, Xsensor Technology Corporation, Calgary, AB, Canada). The screwdriver is held by the dominant hand, which is on the right for P1 and on the left for P2 and P3. Additionally, the plausibility of passive joint movements is also verified by comparing the simulation animation with the corresponding video recording from the lab study of the same motion cycle at the same time stamp.

Table 2.
The two validation levels.
The second validation level aims to evaluate the feasibility of the presented approach to simulate human–exoskeleton interaction based on human motion recorded without the use of the exoskeleton. This is important for simulative evaluation and optimization of exoskeletons in the absence of a physical prototype. For this purpose, the simulated variables from simulation group 1 are compared with those of the corresponding conditions from simulation group 2. The comparison is made qualitatively in terms of the shape and progression of the curve. For a quantitative comparison, the average differences between the results of simulation groups 1 and 2 are calculated. The key question for this level of validation is whether the simulation results are affected by the motion input from different conditions. If so, how critical is this to the simulative analysis of the exoskeleton’s behavior? To answer this question, the simulated shoulder elevation angles from the DHM are additionally considered in the comparison.
4. Simulative Optimization of the Support Profile
To demonstrate the application potential of the human-motion-based simulation approach, this section presents the methodological procedure for evaluating and optimizing the exoskeleton’s support profile for specific tasks using this approach, exemplified by the Lucy system and the two tasks described in the previous section. A solution for task-specific optimization is derived from the evaluation analysis and virtually implemented in the exoskeleton simulation model. The results of the optimization are presented in the next section.
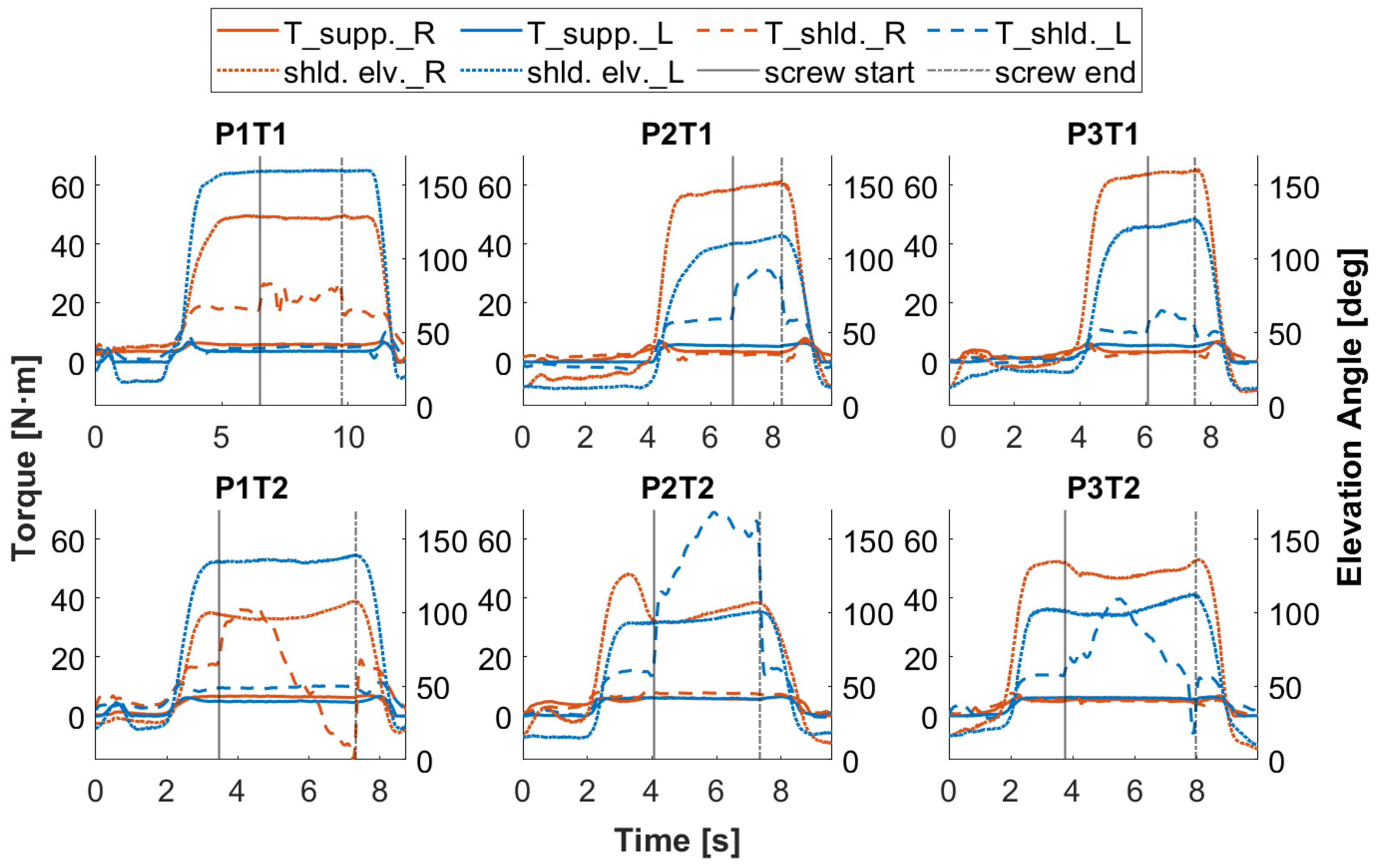
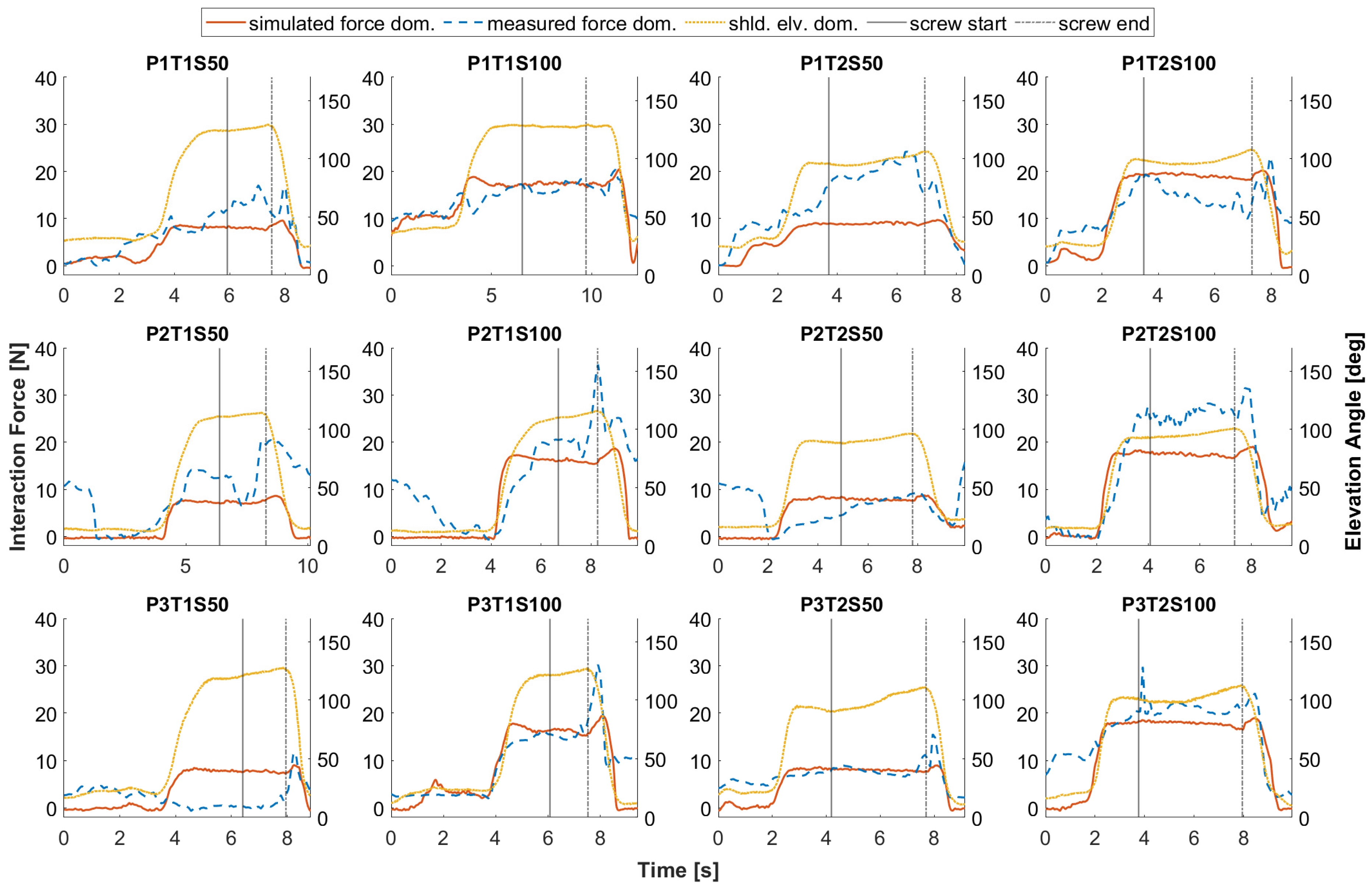
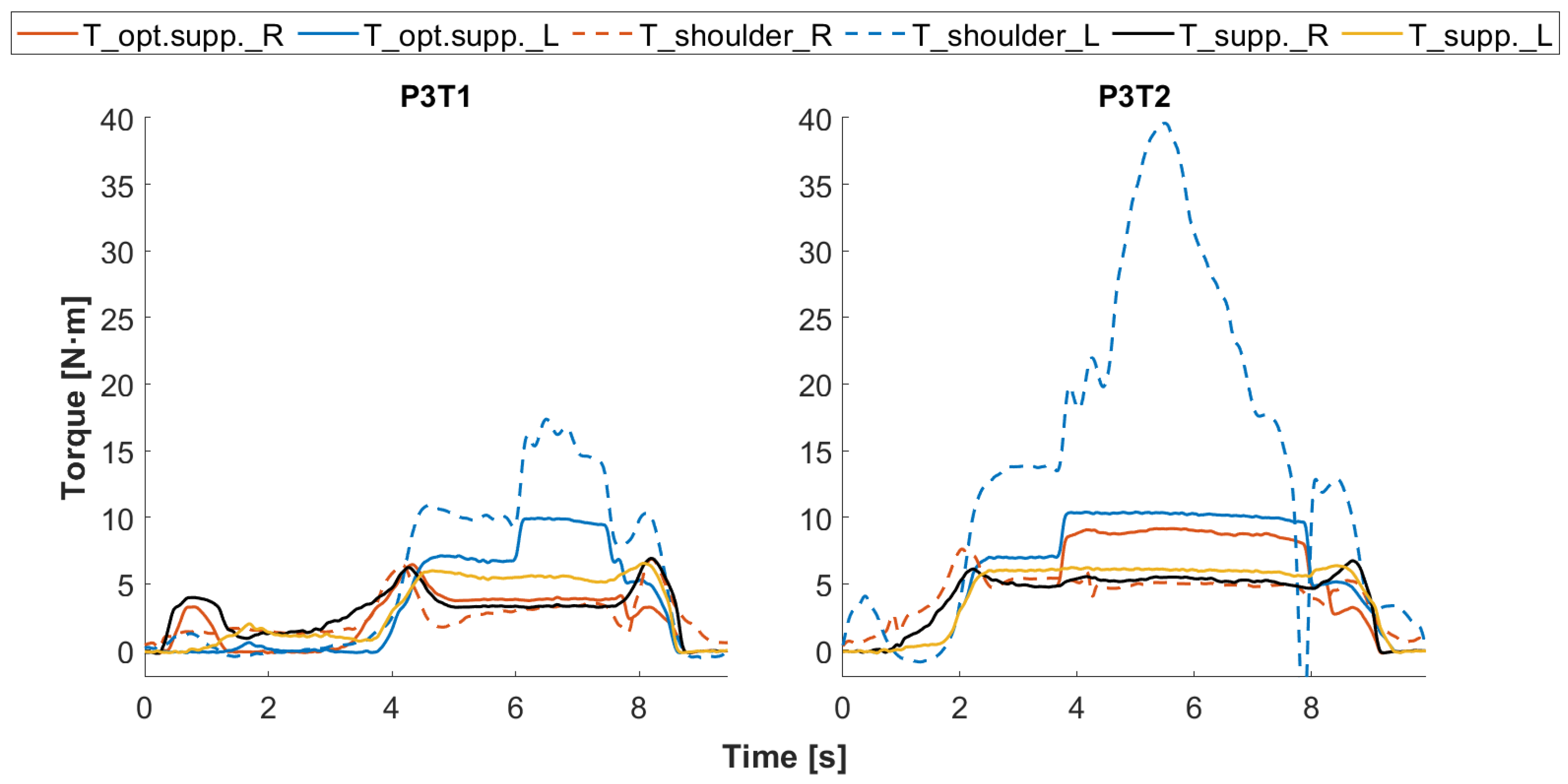
First, the simulated support torques (T_supp.) in both tasks (T1 and T2) under condition S100 are compared to the shoulder elevation torques (T_shld.) from the DHM (see Figure 6). The shoulder elevation torques are simulated in DHM based on the human motions captured in T1S100 and T2S100 with task-related loads but without the support of the exoskeleton. The task-related loads refer to the weight of the screwdriver and the force the user applies to the screwdriver while screwing [31]. The curves show that the shoulder elevation torques (T_shld.) increase in proportion to the shoulder elevation angles (shld.elv.) and jump to even higher values in the screw-in phase on the dominant side holding the screwdriver. Higher workloads in T2 than in T1 are confirmed by the shoulder elevation torques of the dominant side during phase screw-in. Compared to the simulated support torque, an increased support torque for the dominant side, especially during the screw-in phase, has a high potential to reduce further physical stress for the user, which is confirmed by the perceptions of the participants in the lab study [27]. This requires a more powerful cylinder, as the current one allows a peak support torque of 7.8 N·m at the active joint with 6 bar supply pressure. Considering force, weight, dimensions, and technical feasibility, a new cylinder providing a peak support torque of 12.8 N·m at 6 bar is selected and implemented in the exoskeleton model. Since the kinematic change caused by the new cylinder is small and this study focuses on the optimization potential of the support profile, the 3D models of the exoskeleton arm and the cylinder are not updated in the current multibody model of the exoskeleton.
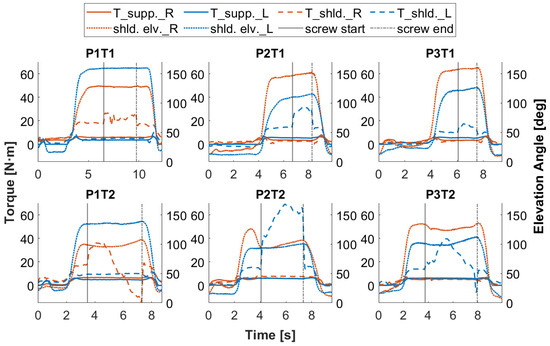
Figure 6.
Torques for shoulder elevation (dashed lines) without support of the exoskeleton and the supporting torques (solid lines) from the exoskeleton with 100% support level, red for the right and blue for the left side. Shoulder elevations in dotted lines as reference for the user’s arm movement, as well as solid and dash-dotted black lines for the start and end of the screw-in phase, respectively. For graphic titles, P: Participant; T: Task.
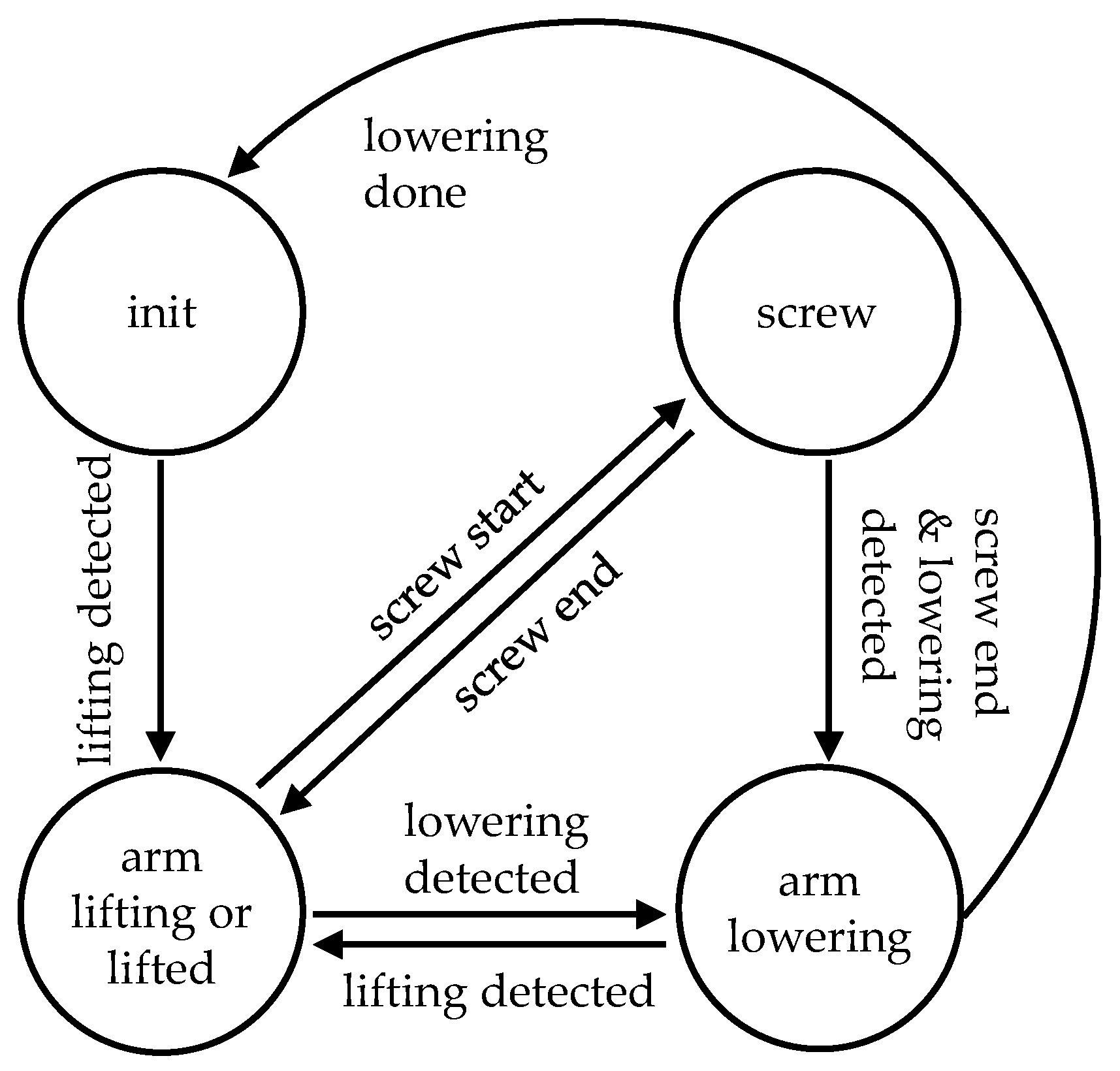
To detect the work phases and adjust the exoskeleton support according to the detected work phases, a state machine is integrated into the control model (see Figure 7). The arm lifting and lowering phases are detected by the elevation angle and angular velocity of the exoskeleton arm. The phase screw-in is detected by the current of the screwdriver [27] and imported as an external signal into the exoskeleton model. A Support Factor is used to adjust the exoskeleton support. It is a percentage of the maximum support level set via the user interface. The motion detection thresholds and Support Factor are determined based on simulation tuning. The results of the optimized simulation tuning and the support profiles for each task are presented in the next section.
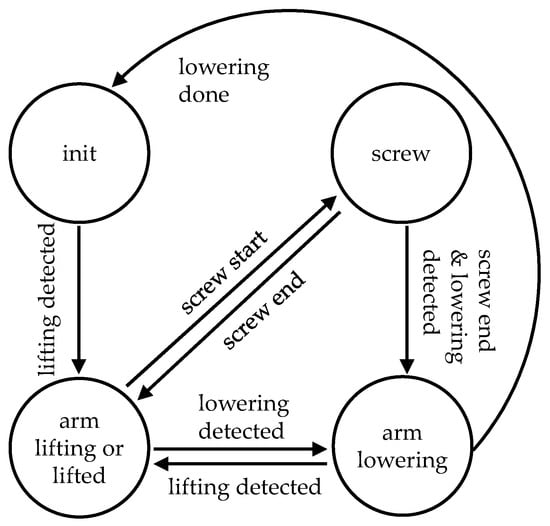
Figure 7.
State diagram for adjusting the exoskeleton support according to the work phases.
Besides the workload variation between the two tasks and between the working phases, the curves of shoulder elevation torque in Figure 6 also show a difference in amplitude between individuals, related to differences in arm weight and individual push force on the screwdriver. The optimization of the support profile for each individual is possible but not addressed in this work, as the optimization of this work focuses on the workload pattern of each task in terms of the human motion and effort required to tighten the screws. However, it is still possible to scale the overall amplitude of the support profile through the personal setting of the support level.
5. Results
The findings of the two validation studies as well as the optimization study are presented in three subsections. First, a comparative analysis of simulated and measured variables assesses the ability of our approach to represent exoskeleton behavior in response to realistic human motion. Subsequently, the feasibility of our approach for virtual prototyping of exoskeletons prior to physical realization is examined by comparing simulation outcomes based on human motion supported by the exoskeleton and without wearing the exoskeleton. Lastly, the results of the task-specific optimization of the support profile are presented, illustrating the practical use of our approach in the refinement of the exoskeleton control design.
5.1. Comparison of Simulated and Measured Variables
The feasibility of the present model as well as the human-motion-based simulation approach is first verified in two aspects: (1) the exoskeleton motion in response to human motion in respective supported conditions S50/100; (2) the interaction force between the dominant arm and the arm interface.
5.1.1. Exoskeleton Motion
The two passive joints on each exoskeleton arm are critical to the range of motion of the user’s shoulder and, therefore, affect the user’s comfort. Their movements also influence the elevation angle of the exoskeleton arm (active joint). Thus, the passive joint movements are examined first. In response to the human motions in both supported conditions (S50, S100), the simulated passive joint movements from the animation are very similar to the movements in the corresponding videos from the lab study. An example of comparing frames at the same moment of human motion in the animation and the corresponding video is shown in Figure 8. A video demonstration, including simulation animations and the video recording of the lab study, is available in the Supplementary Materials.

Figure 8.
Comparison between simulation animation and lab video recording of case P1T1S100, lateral views of the exoskeleton’s two passive joint movements at two different positions of the right upper arm: (a) shoulder elevation angel of 39° at 1 s of the motion cycle, (b) shoulder elevation angel of 129° at 6 s of the motion cycle.
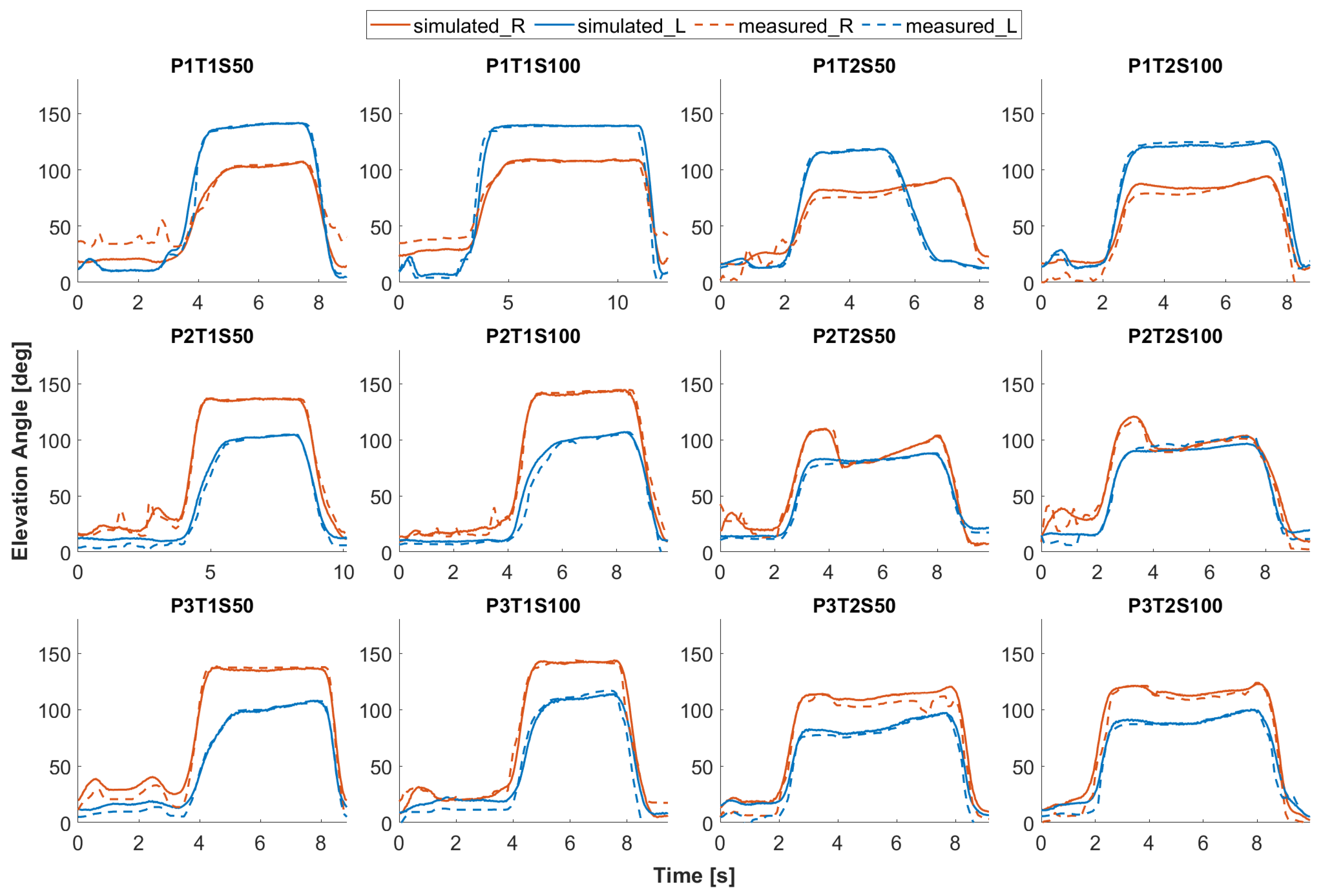
The curves of the simulated elevation angles of the exoskeleton arm match those measured during most of the motion (see Figure 9), especially during the work phases of arm lifting, screw-in, and lowering, where support is desired. In some cases, e.g., T1S50 and T1S100 of P1, there is a noticeable difference between the simulation and the measurement when the upper arm is near neutral and not elevated. The MAE and RMSD between the simulated and measured elevation angles of both exoskeleton arms are 4.8° and 7.1° for all simulation cases. Considering only the movements that require support in all cases, from the beginning of arm lifting to the end of arm lowering, the MAE and RMSD are 3.7° and 6.0°, respectively. These MAE and RMSD values are acceptable for the overhead position with shoulder elevation above 90°.
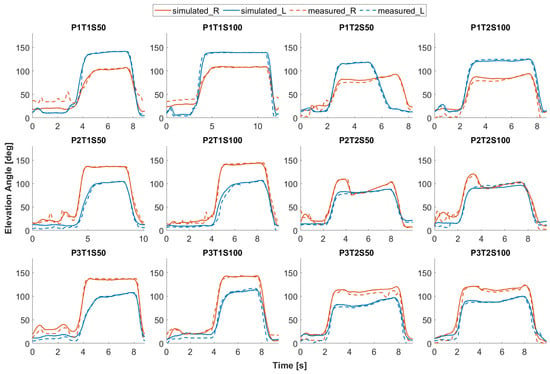
Figure 9.
Simulated elevation angles (solid lines) of the exoskeleton arms in comparison to the measured ones (dashed lines), red for the right and blue for the left side. For graphic titles, P: Participant; T: Task; S: Support Level.
5.1.2. Interaction Force at Arm Interface
The simulated and measured curves of the interaction forces are similar in shape, and both are proportional to the arm elevation angle during the work phases of arm lifting, screw-in, and arm lowering (see Figure 10). The MAE and RMSD are 4.3 N and 5.6 N, respectively, between the simulated and measured interaction force on the dominant side. An outlier is observed in the T1S50 measurement of P3, indicating poor contact between the upper arm and the armrest, which cannot be replicated by the simulation model. The presented simulation of human–exoskeleton interaction is performed under the assumption that the upper arms are in good contact with the arm interfaces. In certain cases, e.g., T1S50 and T2S50 of P1, the measured interaction force is clearly higher than the simulated one during the phase screw-in (between the two black lines in Figure 10). This may be relevant to the participant’s push force on the screwdriver to tighten the screw, which is not part of the simulation here. At the beginning of the arm lowering phase, when the user pushes down the exoskeleton arm, a jump in interaction force is observed in both simulated and measured values. However, the jump in the measured force is more significant than the jump in the simulated force, e.g., T1S100 and T2S50 of P3. A large difference between simulated and measured force is also observed in some cases, e.g., T1S50 and T2S50 of P2, when the upper arm is close to its neutral position and the cylinder is inactive. The interaction model assumes that the contact force between the upper arm and the arm interface is zero when the arm elevation is zero. However, this is not always the case in practice, as shown by the measurement data.
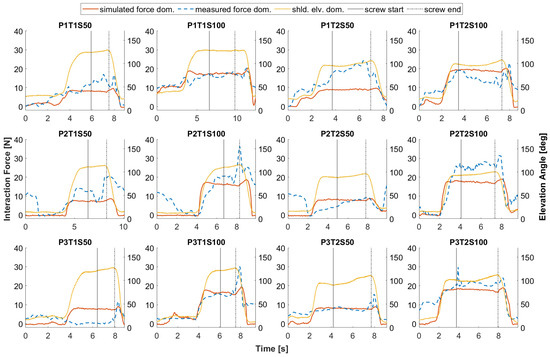
Figure 10.
Simulated interaction force (solid red lines) between the dominant arm and the arm interface compared to the measured force (dashed blue lines). Shoulder elevations in dotted yellow lines as reference for the user’s arm movement, as well as solid and dash-dotted black lines for the start and end of the screw-in phase respectively. For graphic titles, P: Participant; T: Task; S: Support Level.
5.2. Comparison of Unsupported and Supported Motion Simulation
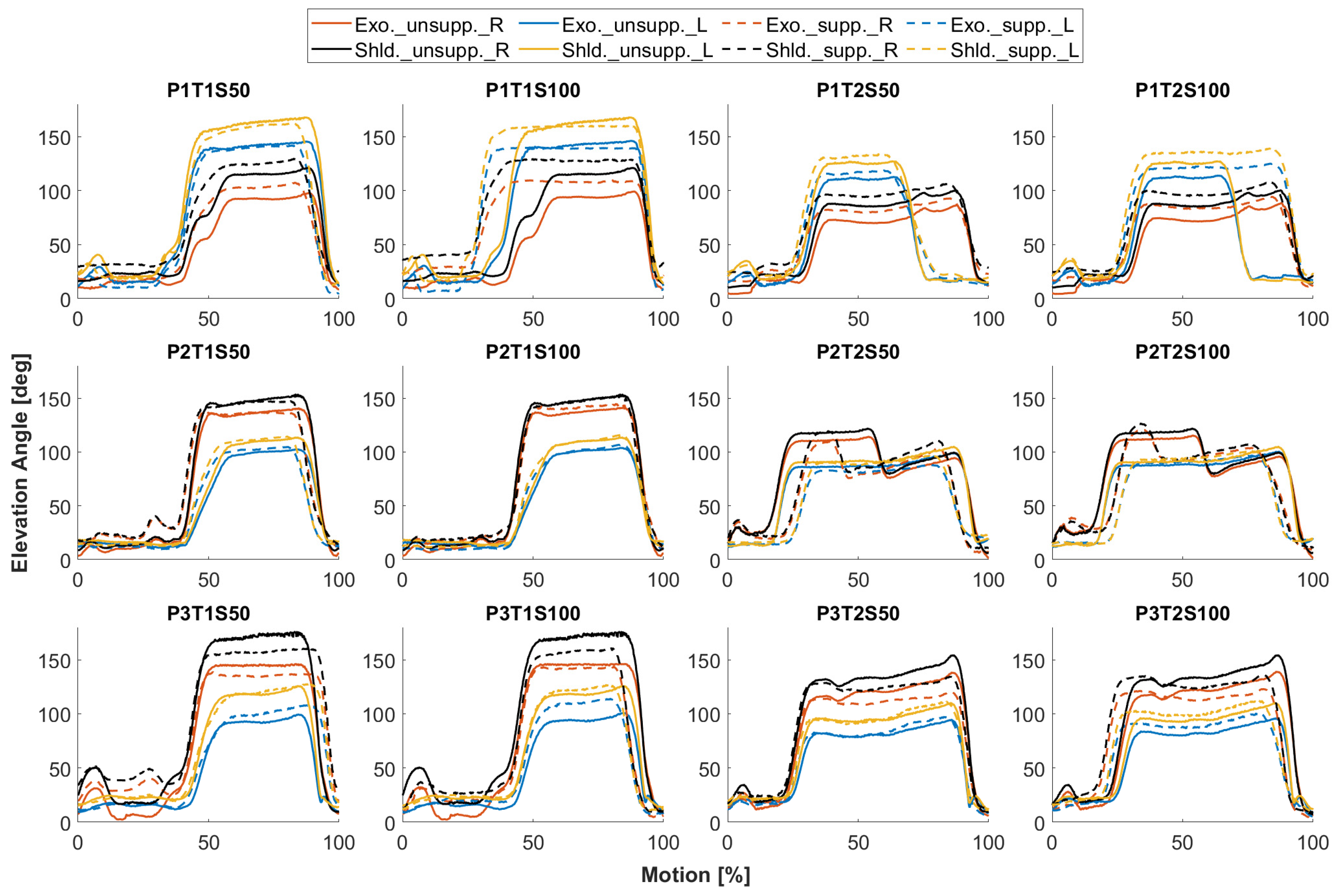
The core of the second validation study is to verify the feasibility of the present simulation approach for virtual prototyping of an exoskeleton with human motion without wearing the exoskeleton. In comparison to simulations using human motion from supported condition (S0), those based on human motions from unsupported conditions (S50/100) provide equivalent insights into the exoskeleton’s behavior. The same relationship with shoulder elevation is seen in the curves of the exoskeleton arm elevations and the interaction forces in Figure 11 and Figure 12. Since the duration of each recorded motion cycle is slightly different, the results are time-normalized for comparison. The variance in simulation outcomes between supported and unsupported human motions can be attributed to differences in shoulder elevations observed in these respective conditions. These differences are most apparent during the screw-in phase. Since the elevation angles and interaction forces are nearly constant during the screw-in phase, the average differences in their mean values are calculated. During the screw-in phase, the average difference in exoskeleton arm elevations simulated by supported and unsupported motion is 8.3°. This is almost equal to the variance in shoulder elevation in these respective conditions at 8.2°. What is striking in Figure 11 is that the user’s shoulder reaches a higher elevation angle than the exoskeleton arm under the same conditions, with an average difference of 13.8° during the screw phase. This highlights the importance of simulating the exoskeleton in response to human motion, rather than copying human joint motion directly to the exoskeleton joint.
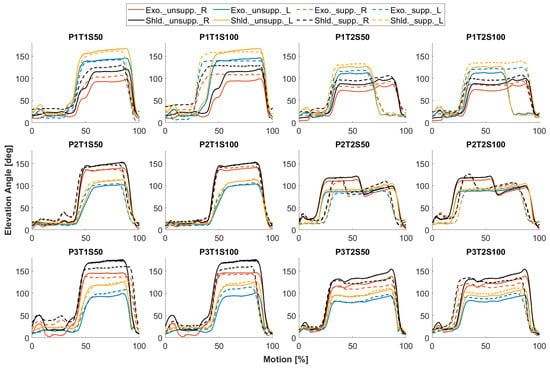
Figure 11.
Comparison of simulated elevation angle of exoskeleton (Exo.) based on unsupported (S0) and supported (S50/100) motion, paired with shoulder elevation angle (Shld.) from unsupported and supported motion. Solid lines represent angle curves for S0 condition and dashed lines for S50/100 condition. Red and blue indicate the right and left arm elevations of the exoskeleton, black and yellow indicate the right and left shoulder elevations of the user. For graphic titles, P: Participant; T: Task; S: Support Level.
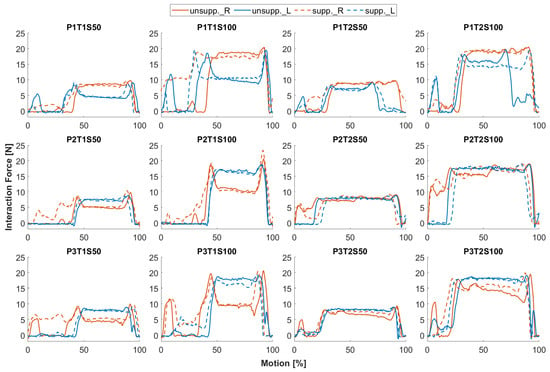
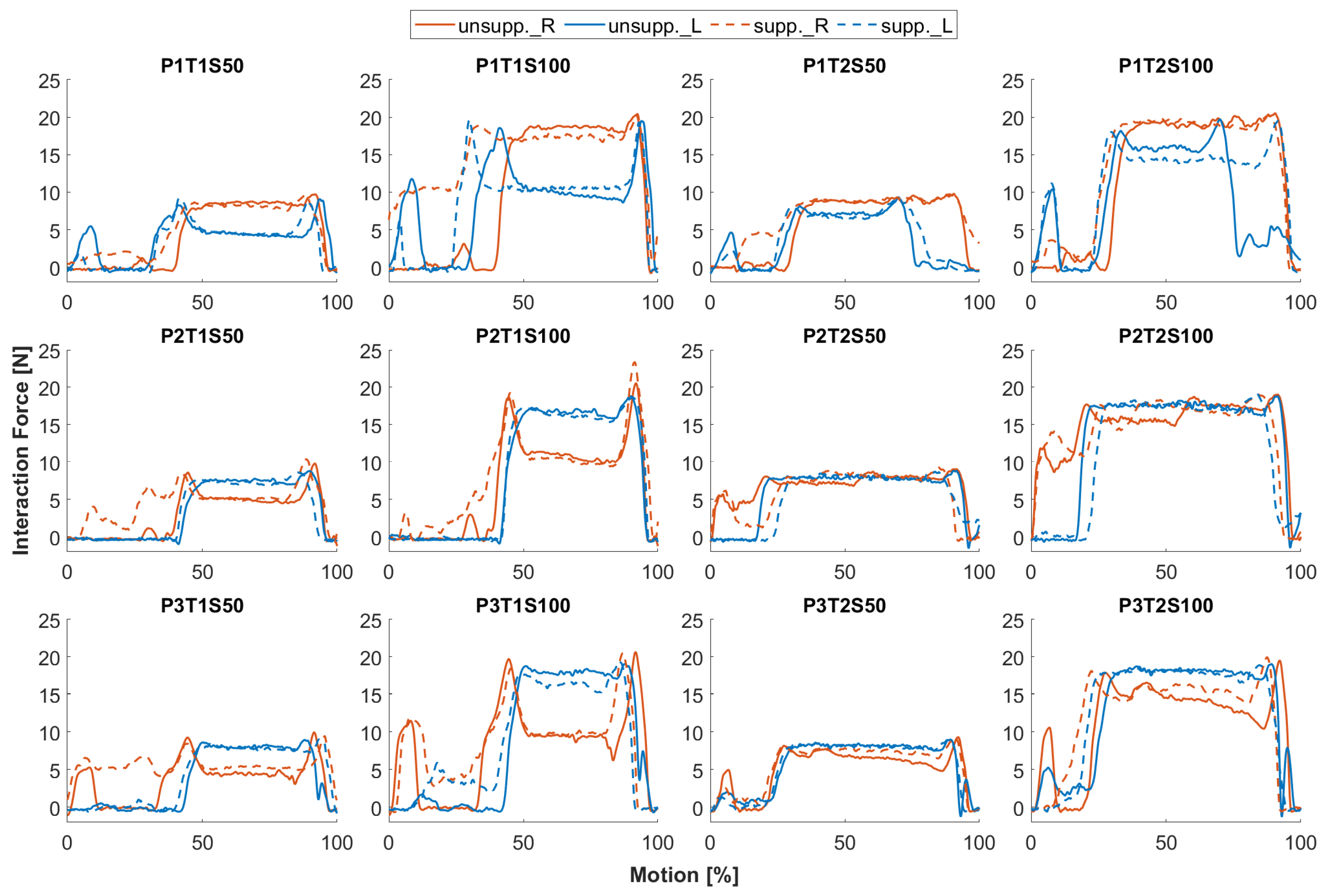
Figure 12.
Comparison of simulated interaction force at arm interface based on unsupported (S0) and supported (S50/100) motion. Solid lines represent angle curves for S0 condition and dashed lines for S50/100 condition. Red for the right arm, blue for the left. For graphic titles, P: Participant; T: Task; S: Support Level.
Interestingly, the interaction forces at the arm interfaces in response to human motion in the conditions S0 and S50/100 are not as obviously different as in the elevations of the exoskeleton arms (see Figure 12). The average difference in the mean interaction force on both sides during the screw phase is 0.66 N between the simulations with supported and unsupported human motion. The difference in interaction force is most noticeable in cases P1T1S100, P1T2S100, and P3T1S100, where the difference in exoskeleton arm elevation between conditions is visibly greater than the difference in shoulder elevation.
5.3. Task-Specific Support Profile
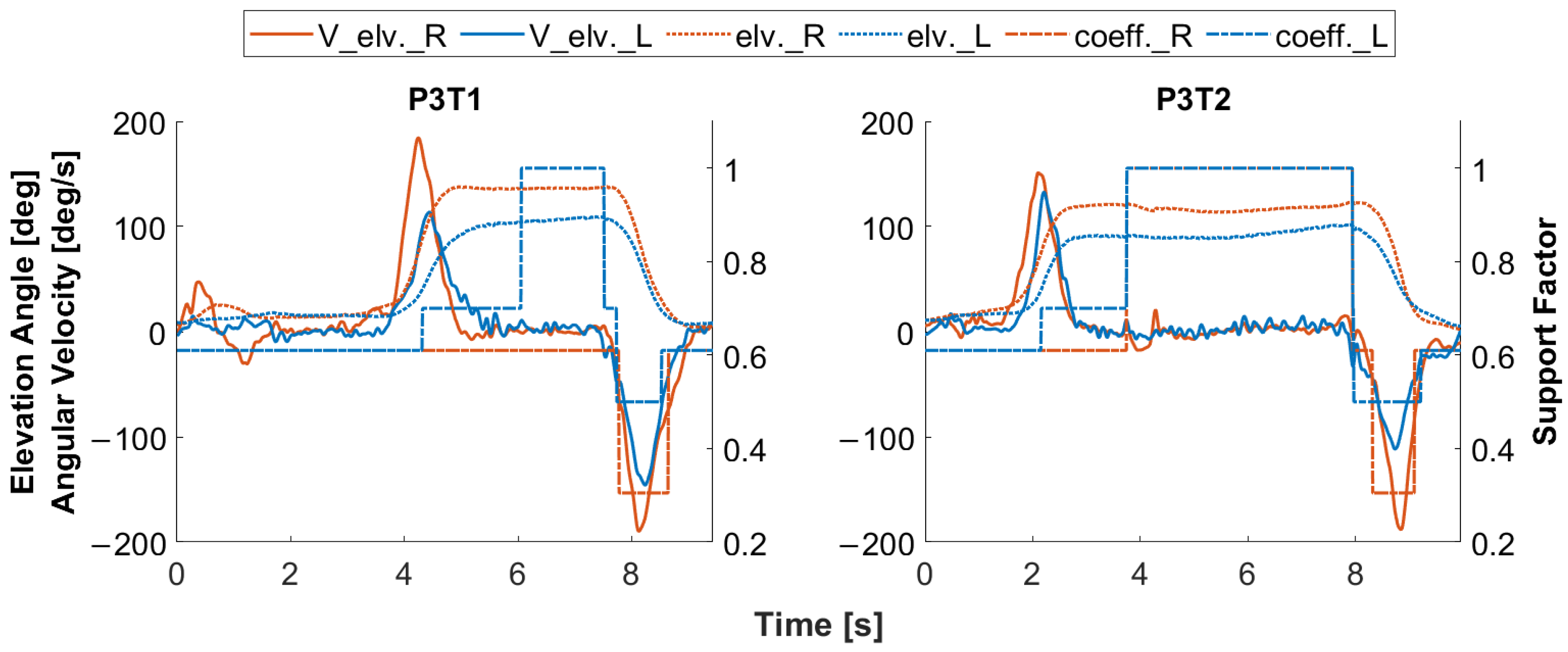
After validation, the current simulation model is used to optimize the support profile for two specified tasks to demonstrate its application potential in the exoskeleton development process. As a result of the simulation tuning, the Support Factor switching according to motion and screw detection is shown in Figure 13 using P3 as an example. The implemented state machine has the capability to recognize the beginning and end of the arm lifting and lowering phases according to the elevation angle and angular velocities of the Lucy arms. The task-specific Support Factors for the key work phases and both sides of the arm are summarized in Table 3. The Support Factors are percentages in decimal form. For example, a factor of one means 100% power of the current support level. The optimizations here are simulated at 6 bar supply pressure, providing a maximum force of 482 N for the new cylinder. At the same pressure, the current cylinder force is 60% of the new cylinder force. The Support Factor for lifting the dominant arm is set higher than for lifting the non-dominant arm due to the weight of the screwdriver. A higher Support Factor is established for the screw-in phase when an increase in shoulder elevation torque is observed. It should be noted that the pressure force in T2 to tighten the screw is applied by both hands, although an increase in the simulated shoulder elevation torque is only seen in the dominant arm. In the DHM simulation, the entire push force is applied to the dominant side because the distribution of the push force between the two hands could not be determined in the previous lab study due to the limitations of the measurement system. For the arm lowering phase, the factor is reduced following the evaluation results from the laboratory study, as explained in Section 4.
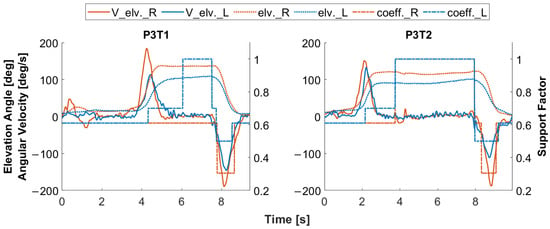
Figure 13.
Switching the Support Factor (dashed lines) according to the work phases in T1 and T2, in the example of P3, blue for the left and red for the right side. Elevation angle of the exoskeleton arm (elv.) in dashed line, angular velocity (V_elv.) in solid line. For graphic titles, P: Participant; T: Task.

Table 3.
Task-specific Support Factor (percentage in decimal form) for different work phases and arm sides.
As exemplary results of the task-specific optimization, the simulated supporting torques for both tasks based on the motion of P3 are shown in Figure 14. The optimized support torque curves (T_opt.supp.) show a closer match to the curves of shoulder elevation torque (T_shoulder) in terms of work phases when compared to the support torque before the optimization (T_supp.). This is consistent with the design expectations outlined in Section 4. The effect of the optimized support profile on the human body compared to the previous one needs to be investigated in future work in a DHM.
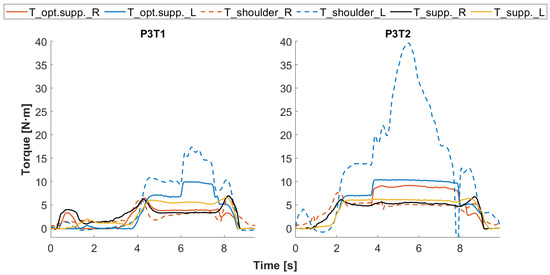
Figure 14.
Optimized support torques (T_opt.supp.) for both tasks compared to shoulder elevation torques (T_shoulder) and support torques before the optimization (T_supp.), in the example of P3. For graphic titles, P: Participant; T: Task.
6. Discussion
6.1. Comparison of Simulated and Measured Variables
The similarity between simulated and measured data confirms that the presented exoskeleton model and the simulation approach can reproduce plausible exoskeleton motion and the interaction forces at the arm interfaces, responding to human motions from the same supported condition. The MAE (4.8° for the full motion cycle and 3.7° only for work phases where support is desired) and RMSD (7.1° for the full motion cycle and 6.0° only for work phases where support is desired) between simulated and measured exoskeleton arm elevations are acceptable for the selected shoulder exoskeleton because its primary target support posture is with the shoulder elevated above 90°. This posture has been identified as a high potential risk for muscle fatigue [32,33,34]. Moreover, the resulting variation in support force caused by this deviation in exoskeleton arm elevation is barely perceived by the user. The deviation between the simulated and measured elevation angle of the exoskeleton arm when the upper arm is close to neutral is allowable for this work because the support profile and range of motion are not affected. If the movements of passive joints need to be validated, additional joint sensors can be added to the exoskeleton in the future.
Considering the theoretical support force, the amplitude of the simulated interaction force and its relationship to shoulder elevation are reasonable. The difference between the simulated and measured interaction forces is influenced by the limitations of both the measurement and the model. The measurement is sensitive to inadequate contact at the arm interface and external environmental forces, such as the participant’s push force on the screwdriver during the screw-in phase. The influence of the push force is not addressed here, as the primary focus of the current study is on the exoskeleton’s behavior in response to human motion. In this work, the interaction at the arm interface is modeled as a point contact between solid bodies. It does not accurately reproduce the deformation of the fabric padding at the arm interface and the soft tissues of the human arm, potentially influencing the interaction force. Furthermore, the point contact model assumes constant contact between the upper arm and the physical interface of the exoskeleton. In practice, however, the contact area varies, and the center of the contact area shifts as the user moves. To address these issues, the contact force model of soft bodies with the full contact force should be considered in future work. Moreover, appropriate measurement technology is expected in future work to validate friction and shear forces at the arm interface, which are crucial to user comfort.
6.2. Comparison of Unsupported and Supported Motion Simulation
The comparison of the simulation results with unsupported and supported human motion proves the feasibility of the human-motion-based simulation approach in replicating realistic exoskeleton behavior using human motion without wearing it. This allows not only the pre-development of a new exoskeleton concept prior to its physical implementation, but also the virtual evaluation of an exoskeleton’s application potential for new use cases. The differences between simulation outcomes using unsupported and supported human motion are highly dependent on the variances in the input human motions. It is important to note that the current model cannot simulate changes in human motion caused by exoskeleton support. This is not critical for the Lucy exoskeleton, as a previous study with a sample size of 30 showed that there were no significant changes in shoulder elevation with its support [35]. If the effect of the exoskeleton on human kinematics is unknown, it should be noted that a change in human motion may be observed during the physical implementation and testing of the exoskeleton. Predicting changes in human motion due to exoskeleton support is a potential challenge to be addressed in future work, especially if the changes are crucial to the control design. Dynamic reflex or response models that describe the human response to external forces while attempting to maintain stability could be explored as valuable candidates [10,36,37]. The results also reveal differences between shoulder elevation and the elevation of the exoskeleton arm, emphasizing the positive aspect of the proposed approach in achieving more realistic exoskeleton motion compared to directly applying human joint motion to the exoskeleton joint.
6.3. Task-Specific Support Profile
The simulative optimized support profiles demonstrate the potential of the current exoskeleton model and simulation approach to adapt the exoskeleton support profile for desired tasks using simulated user physical effort (e.g., shoulder elevation torque) and task process information (e.g., screw events). This allows for human-centered and task-specific optimization of the exoskeleton before its physical implementation, eliminating the risk and hassle of testing with human participants. The effect of the optimized support profile on the human body can first be investigated using a DHM. Nevertheless, achieving a smooth user experience requires individualized fine-tuning, a process that cannot be replicated through simulation alone. In addition, motion detection thresholds may need to be adjusted to account for the difference in noise between the simulation results and real sensor data.
Additionally, there are some other limitations of the current model, which can affect the results of the simulative optimization. Kinesthetic and cognitive user responses to the exoskeleton support are difficult to predict and cannot be addressed in the current simulation model. However, kinetic motion prediction can be considered as a compromise in future work. The current exoskeleton model does not simulate body sway, which could affect control decisions for tasks involving forward bending. An inverted pendulum model [38,39,40] could be considered to incorporate upper body motion into the exoskeleton model. In addition, there are typical deviations when translating real human motion to the model, whether it is the scaling of the model, the position of the markers on the model, or the relative motion caused by the influence of soft tissue. These deviations between the real human motion and the recorded or simulated human motion can affect the simulation results of the present model, since it is based on the recorded and simulated human motion.
7. Conclusions
This work has presented a novel approach to simulate exoskeleton behavior in response to human motion imported through marker positions. The main advantage of the presented approach is the ability to simulate the physical human–exoskeleton interaction without building a DHM in the exoskeleton model and the ability to simulate realistic exoskeleton movements based on human motion. In this paper, the simulations are performed using marker positions from a DHM. However, the presented approach also works with marker positions directly from a motion capture system if the markers are placed at the required positions. The results indicate that the presented modeling and simulation of the shoulder exoskeleton and its interaction with the human body are promising for the simulation analysis of exoskeleton behavior. This verified simulation approach is suitable not only for the task-specific evaluation and optimization of existing exoskeletons but also for the pre-development of new exoskeleton concepts in advance of physical realization.
To improve the capability of this approach for simulating human–exoskeleton interaction, further research should address the challenge of predicting changes in human motion caused by exoskeleton support and extending the current contact model to surface contact and soft bodies. The friction and shear forces should also be validated in the future to address user comfort in the simulation. The next step in the simulation-based optimization of the exoskeleton Lucy is to update the new cylinder in the multibody model to analyze the potential changes to the exoskeleton kinematics and its interaction with humans. In addition, the effect of the optimized support profile on the human body will be investigated in a co-simulation model combined with a DHM and compared with the current one.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/robotics13020027/s1, Video S1: A video demonstration of an exoskeleton simulation example, along with corresponding human motion simulations and recordings from the lab study.
Author Contributions
Conceptualization, Z.Y.; methodology, Z.Y.; software, Z.Y. and S.M.M.L.; validation, Z.Y.; formal analysis, Z.Y.; investigation, Z.Y.; resources, C.M., D.S., C.L. and J.S.; data curation, Z.Y. and S.M.M.L.; writing—original draft preparation, Z.Y.; writing—review and editing, S.M.M.L., C.M., D.S., J.S., J.M., S.W., A.L., S.M. and R.W.; visualization, Z.Y.; supervision, R.W.; funding acquisition, S.W., S.M. and R.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the German Research Foundation (DFG). The authors gratefully acknowledge the financial support of project 435242218 (WA 2913/41-1, MA 5940/11-1, and WE 6430/3-1).
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki and approved by the Institutional Ethics Committee of the Department of Psychology of Helmut-Schmidt University Hamburg (HSU).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Fournier, B.N.; Lemaire, E.D.; Smith, A.J.J.; Doumit, M. Modeling and Simulation of a Lower Extremity Powered Exoskeleton. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 1596–1603. [Google Scholar] [CrossRef] [PubMed]
- Fritzsche, L.; Gärtner, C.; Spitzhirn, M.; Galibarov, P.E.; Damsgaard, M.; Maurice, P.; Babič, J. Assessing the Efficiency of Industrial Exoskeletons with Biomechanical Modelling—Comparison of Experimental and Simulation Results. In Proceedings of the 21st Congress of the International Ergonomics Association (IEA 2021), Online, 13–18 June 2021; Black, N.L., Neumann, W.P., Noy, I., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 353–357. [Google Scholar]
- Agarwal, P.; Neptune, R.R.; Deshpande, A.D. A Simulation Framework for Virtual Prototyping of Robotic Exoskeletons. J. Biomech. Eng. 2016, 138, 061004. [Google Scholar] [CrossRef] [PubMed]
- Guan, X.; Ji, L.; Wang, R.; Huang, W. Optimization of an Unpowered Energy-Stored Exoskeleton for Patients with Spinal Cord Injury. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 5030–5033. [Google Scholar]
- Zhou, L.; Li, Y.; Bai, S. A Human-Centered Design Optimization Approach for Robotic Exoskeletons through Biomechanical Simulation. Robot. Auton. Syst. 2017, 91, 337–347. [Google Scholar] [CrossRef]
- Tröster, M.; Wagner, D.; Müller-Graf, F.; Maufroy, C.; Schneider, U.; Bauernhansl, T. Biomechanical Model-Based Development of an Active Occupational Upper-Limb Exoskeleton to Support Healthcare Workers in the Surgery Waiting Room. Int. J. Environ. Res. Public Health 2020, 17, 5140. [Google Scholar] [CrossRef]
- Ferrati, F.; Bortoletto, R.; Pagello, E. Virtual Modelling of a Real Exoskeleton Constrained to a Human Musculoskeletal Model. In Biomimetic and Biohybrid Systems; Lepora, N.F., Mura, A., Krapp, H.G., Verschure, P.F.M.J., Prescott, T.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 96–107. [Google Scholar]
- Imamura, Y.; Tanaka, T.; Suzuki, Y.; Takizawa, K.; Yamanaka, M. Motion-Based-Design of Elastic Material for Passive Assistive Device Using Musculoskeletal Model. J. Robot. Mechatron. 2011, 23, 978–990. [Google Scholar] [CrossRef]
- Kuhn, J.; Hu, T.; Schappler, M.; Haddadin, S. Dynamics Simulation for an Upper-Limb Human-Exoskeleton Assistance System in a Latent-Space Controlled Tool Manipulation Task. In Proceedings of the 2018 IEEE International Conference on Simulation, Modeling, and Programming for Autonomous Robots (SIMPAR), Brisbane, QLD, Australia, 16 May 2018; pp. 158–165. [Google Scholar]
- De Kruif, B.J.; Schmidhauser, E.; Stadler, K.S.; O’Sullivan, L.W. Simulation Architecture for Modelling Interaction Between User and Elbow-Articulated Exoskeleton. J. Bionic Eng. 2017, 14, 706–715. [Google Scholar] [CrossRef]
- Khamar, M.; Edrisi, M.; Zahiri, M. Human-Exoskeleton Control Simulation, Kinetic and Kinematic Modeling and Parameters Extraction. MethodsX 2019, 6, 1838–1846. [Google Scholar] [CrossRef]
- Mosconi, D.; Nunes, P.F.; Ostan, I.; Siqueira, A.A.G. Design and Validation of a Human-Exoskeleton Model for Evaluating Interaction Controls Applied to Rehabilitation Robotics. In Proceedings of the 2020 8th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob), New York, NY, USA, 29 November–1 December 2020; pp. 629–634. [Google Scholar]
- Chen, J.; Zhang, X.; Zhu, L. Kinematics Analysis and Three-Dimensional Simulation of the Rehabilitation Lower Extremity Exoskeleton Robot. arxiv 2014, arXiv:1401.6517. [Google Scholar] [CrossRef]
- Ostraich, B.; Riemer, R. Simulation of a Passive Knee Exoskeleton for Vertical Jump Using Optimal Control. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 2859–2868. [Google Scholar] [CrossRef]
- Inkol, K.A.; McPhee, J. Assessing Control of Fixed-Support Balance Recovery in Wearable Lower-Limb Exoskeletons Using Multibody Dynamic Modelling. In Proceedings of the 2020 8th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob), New York, NY, USA, 29 November–1 December 2020; pp. 54–60. [Google Scholar]
- Koch, H.; Mombaur, K. ExoOpt—A Framework for Patient Centered Design Optimization of Lower Limb Exoskeletons. In Proceedings of the 2015 IEEE International Conference on Rehabilitation Robotics (ICORR), Singapore, 11–14 August 2015; pp. 113–118. [Google Scholar]
- Low, K.H.; Liu, X.; Yu, H. Design and Implementation of NTU Wearable Exoskeleton as an Enhancement and Assistive Device. Appl. Bionics Biomech. 2006, 3, 209–225. [Google Scholar] [CrossRef]
- Derman, M.; Soliman, A.F.; Kuru, A.; Cevik, S.C.; Unal, R.; Bebek, O.; Ugurlu, B. Simulation-Based Design and Locomotion Control Implementation for a Lower Body Exoskeleton. In Proceedings of the 2022 IEEE 5th International Conference on Industrial Cyber-Physical Systems (ICPS), Coventry, UK, 24–26 May 2022; pp. 1–6. [Google Scholar]
- Pan, D.; Gao, F.; Miao, Y.; Cao, R. Co-Simulation Research of a Novel Exoskeleton-Human Robot System on Humanoid Gaits with Fuzzy-PID/PID Algorithms. Adv. Eng. Softw. 2015, 79, 36–46. [Google Scholar] [CrossRef]
- Panero, E.; Muscolo, G.G.; Gastaldi, L.; Pastorelli, S. Multibody Analysis of a 3D Human Model with Trunk Exoskeleton for Industrial Applications. In Multibody Dynamics 2019; Kecskeméthy, A., Geu Flores, F., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 43–51. [Google Scholar]
- Wang, J.; Ma, Z.-D.; Hulbert, G.M. A Gluing Algorithm for Distributed Simulation of Multibody Systems. Nonlinear Dyn. 2003, 34, 159–188. [Google Scholar] [CrossRef]
- Tseng, F.-C.; Hulbert, G.M. A Gluing Algorithm for Network-Distributed Multibody Dynamics Simulation. Multibody Syst. Dyn. 2001, 6, 377–396. [Google Scholar] [CrossRef]
- Rustin, C.; Verlinden, O.; Bombled, Q. A Cosimulation T-T Procedure Gluing Subsystems in Multibody Dynamics Simulations. In Proceedings of the ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference; American Society of Mechanical Engineers Digital Collection, San Diego, CA, USA, 30 August–2 September 2009; pp. 83–92. [Google Scholar]
- Otten, B.M.; Weidner, R.; Argubi-Wollesen, A. Evaluation of a Novel Active Exoskeleton for Tasks at or Above Head Level. IEEE Robot. Autom. Lett. 2018, 3, 2408–2415. [Google Scholar] [CrossRef]
- Miehling, J. Musculoskeletal Modeling of User Groups for Virtual Product and Process Development. Comput. Methods Biomech. Biomed. Eng. 2019, 22, 1209–1218. [Google Scholar] [CrossRef] [PubMed]
- Holzbaur, K.R.S.; Murray, W.M.; Delp, S.L. A Model of the Upper Extremity for Simulating Musculoskeletal Surgery and Analyzing Neuromuscular Control. Ann. Biomed. Eng. 2005, 33, 829–840. [Google Scholar] [CrossRef]
- Sänger, J.; Yao, Z.; Schubert, T.; Wolf, A.; Molz, C.; Miehling, J.; Wartzack, S.; Gwosch, T.; Matthiesen, S.; Weidner, R. Evaluation of Active Shoulder Exoskeleton Support to Deduce Application-Oriented Optimization Potentials for Overhead Work. Appl. Sci. 2022, 12, 10805. [Google Scholar] [CrossRef]
- Full Body Modeling with Plug-in Gait—Nexus 2.11 Documentation—Vicon Documentation. Available online: https://docs.vicon.com/display/Nexus211/Full+body+modeling+with+Plug-in+Gait#FullbodymodelingwithPluginGait-MarkerplacementforPlug-inGaitfullbodymodel (accessed on 13 October 2023).
- Miller, S. Simscape Multibody Contact Forces Library. Available online: https://github.com/mathworks/Simscape-Multibody-Contact-Forces-Library (accessed on 18 October 2023).
- Kothari, V.; Gangal, M. Assessment of Frictional Properties of Some Woven Fabrics. IJFTR 1994, 19, 151–155. [Google Scholar]
- Sänger, J.; Wirth, L.; Yao, Z.; Scherb, D.; Miehling, J.; Wartzack, S.; Weidner, R.; Lindenmann, A.; Matthiesen, S. ApOL-Application Oriented Workload Model for Digital Human Models for the Development of Human-Machine Systems. Machines 2023, 11, 869. [Google Scholar] [CrossRef]
- Alizadehkhaiyat, O.; Roebuck, M.M.; Makki, A.T.; Frostick, S.P. Subacromial Impingement Syndrome: An Electromyographic Study of Shoulder Girdle Muscle Fatigue. J. Electromyogr. Kinesiol. 2018, 38, 136–142. [Google Scholar] [CrossRef]
- Maenhout, A.; Dhooge, F.; Van Herzeele, M.; Palmans, T.; Cools, A. Acromiohumeral Distance and 3-Dimensional Scapular Position Change After Overhead Muscle Fatigue. J. Athl. Train. 2015, 50, 281–288. [Google Scholar] [CrossRef]
- Sommer, T.G.; Frost, P.; Svendsen, S.W. Combined Musculoskeletal Pain in the Upper and Lower Body: Associations with Occupational Mechanical and Psychosocial Exposures. Int. Arch. Occup. Environ. Health 2015, 88, 1099–1110. [Google Scholar] [CrossRef]
- Argubi-Wollesen, A. Entwicklung und Biomechanische Evaluation Eines Körpergetragenen Unterstützungssystems (Exoskelett) Für Arbeiten in und Über Kopfhöhe. Ph.D. Dissertation, University of Hamburg, Hamurg, Germany, 2021. [Google Scholar]
- Perreault, E.J.; Crago, P.E.; Kirsch, R.F. Estimation of Intrinsic and Reflex Contributions to Muscle Dynamics: A Modeling Study. IEEE Trans. Biomed. Eng. 2000, 47, 1413–1421. [Google Scholar] [CrossRef]
- Schouten, A.C.; Mugge, W.; van der Helm, F.C.T. NMClab, a Model to Assess the Contributions of Muscle Visco-Elasticity and Afferent Feedback to Joint Dynamics. J. Biomech. 2008, 41, 1659–1667. [Google Scholar] [CrossRef]
- Sakka, S.; Hayot, C.; Lacouture, P. A Generalized 3D Inverted Pendulum Model to Represent Human Normal Walking. In Proceedings of the 2010 10th IEEE-RAS International Conference on Humanoid Robots, Nashville, TN, USA, 6–8 December 2010; pp. 486–491. [Google Scholar]
- Loram, I.D.; Lakie, M. Human Balancing of an Inverted Pendulum: Position Control by Small, Ballistic-like, Throw and Catch Movements. J. Physiol. 2002, 540, 1111–1124. [Google Scholar] [CrossRef]
- Kwon, T.; Hodgins, J. Control Systems for Human Running Using an Inverted Pendulum Model and a Reference Motion Capture Sequence; The Eurographics Association: Eindhoven, The Netherlands, 2010; ISBN 978-3-905674-27-9. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).