A Review of Mechanical Design Approaches for Balanced Robotic Manipulation
Abstract
1. Introduction
2. Types of Balancing
2.1. Static and Gravity Balancing
2.2. Force Balancing
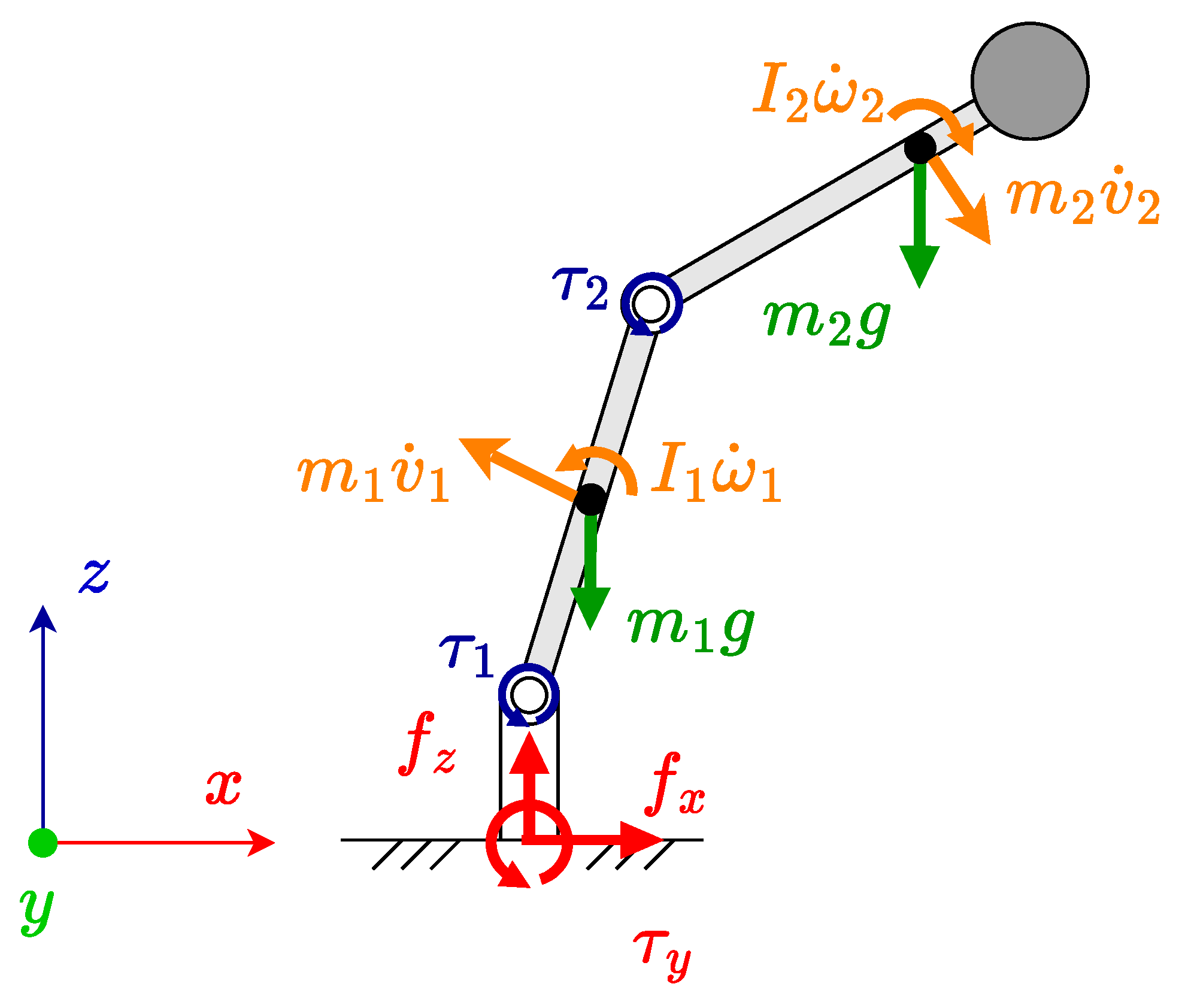
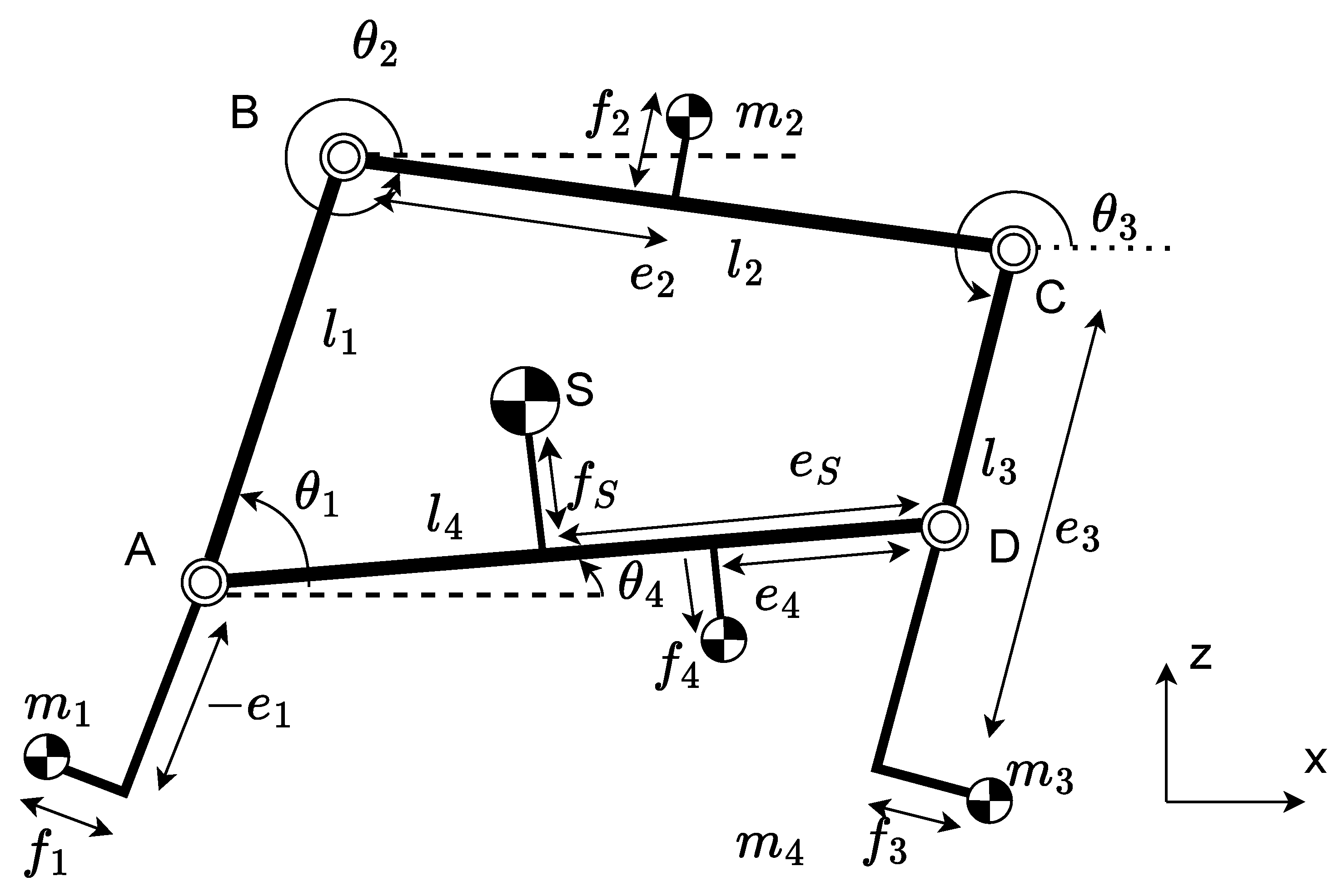
- As the change in linear momentum is caused by a net force on the manipulator , these are zero about the center of mass for any configuration:
- The linear momentum of the system can also be expressed in terms of the velocity of the manipulator center of mass, where is the total mass:As is constant, this means that in a force-balanced system , hence the center of mass remains static at fixed position :
2.3. Moment Balancing
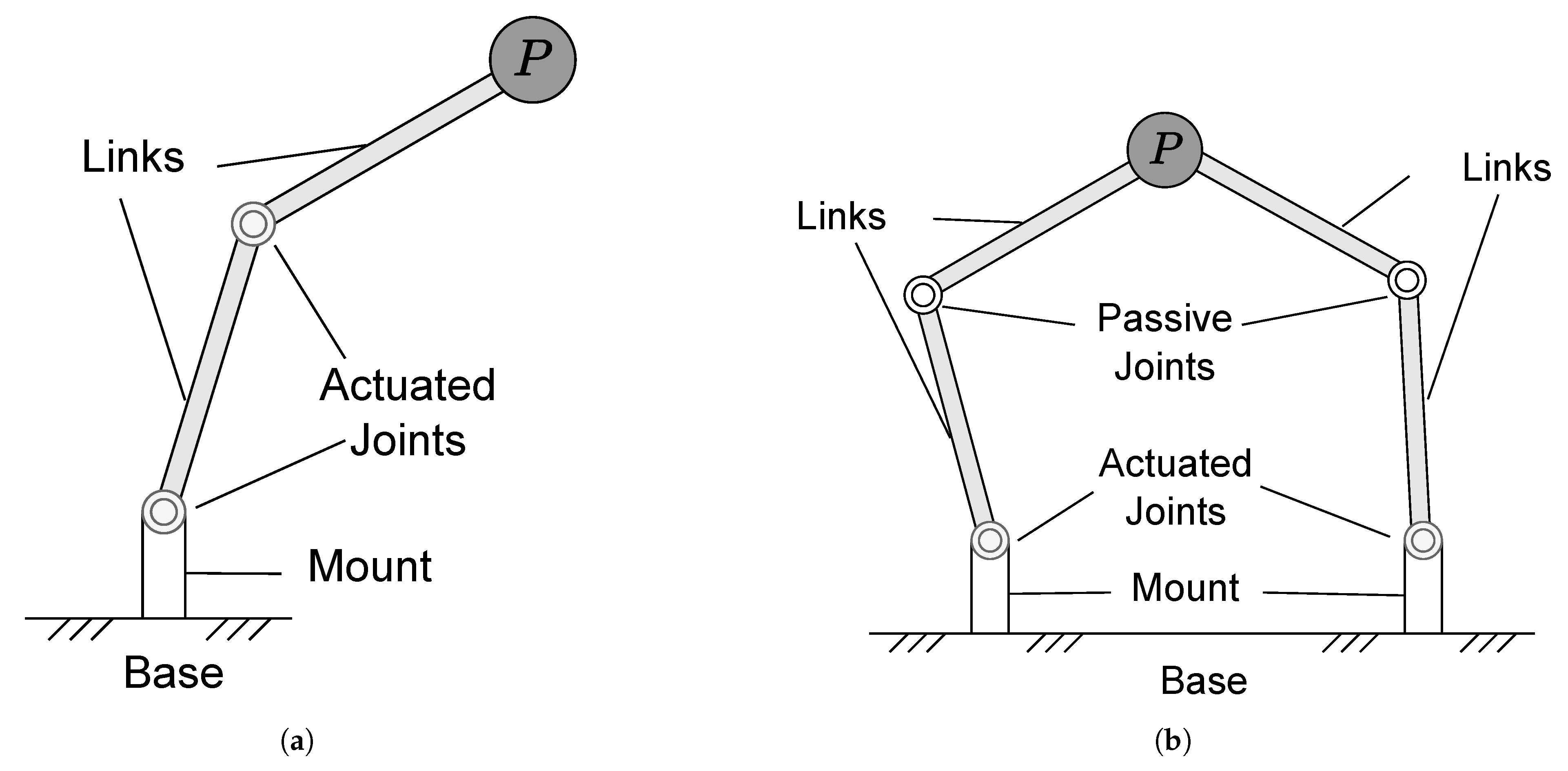
3. Approaches to Design Balanced Manipulators
3.1. Passive Component Addition
3.1.1. Springs
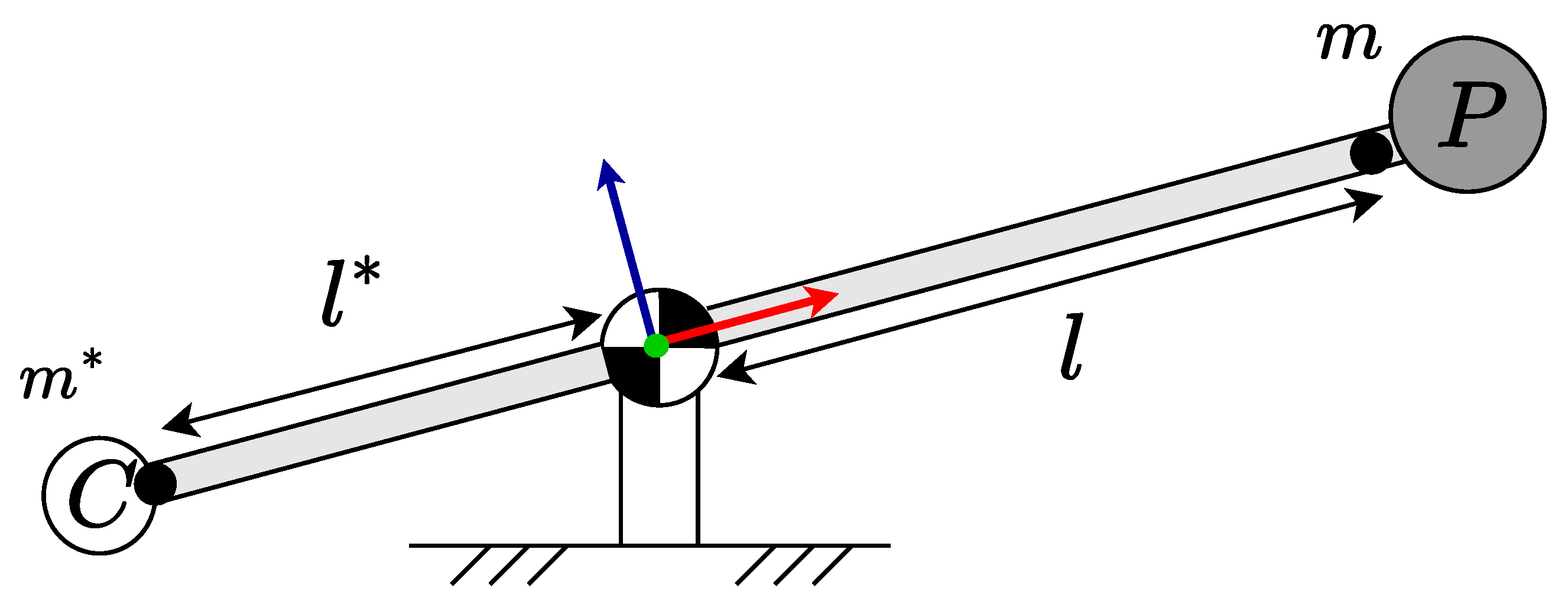
3.1.2. Counter Mass (CM)/Counter Inertia (CI)
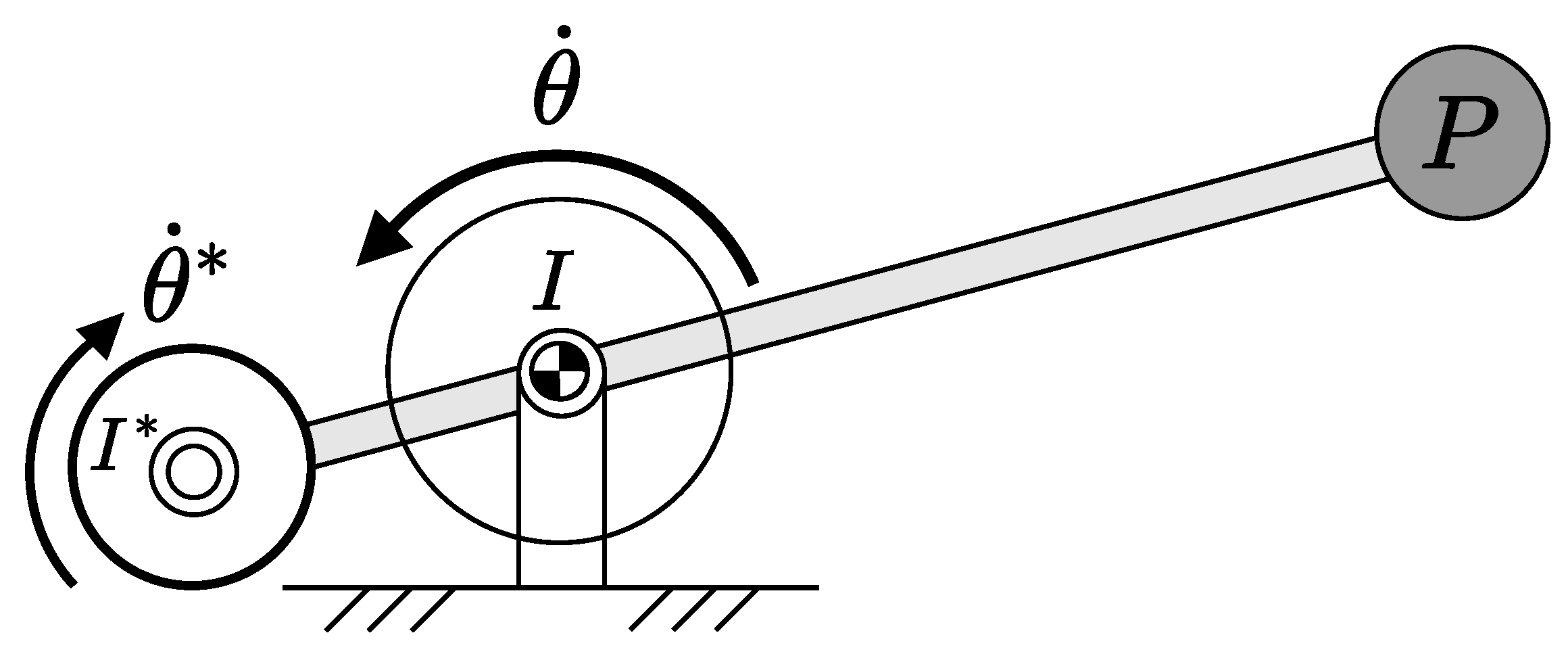
3.1.3. Counter Rotating Inertia (CR)/Counter Rotating Counter Mass (CRCM)
3.1.4. Additional Linkage Mechanism (ALM)
3.2. Active Component Addition
3.2.1. Active CM/CR/CRCM
3.2.2. Active Dynamic Balancing Unit (ADBU)
3.3. Inherent Balancing
3.3.1. Parallel Mechanisms
3.3.2. Principal Vector Method
3.4. Synthesis
3.5. Summary and Comparison of Approaches
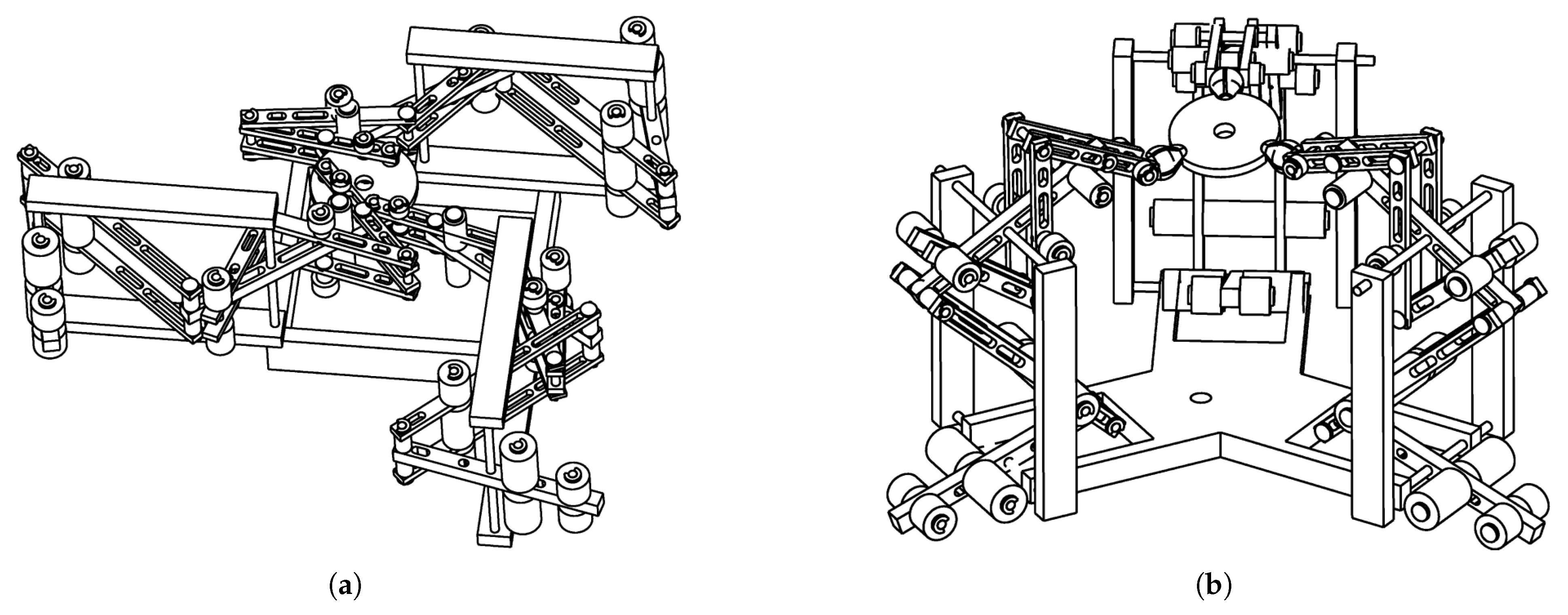
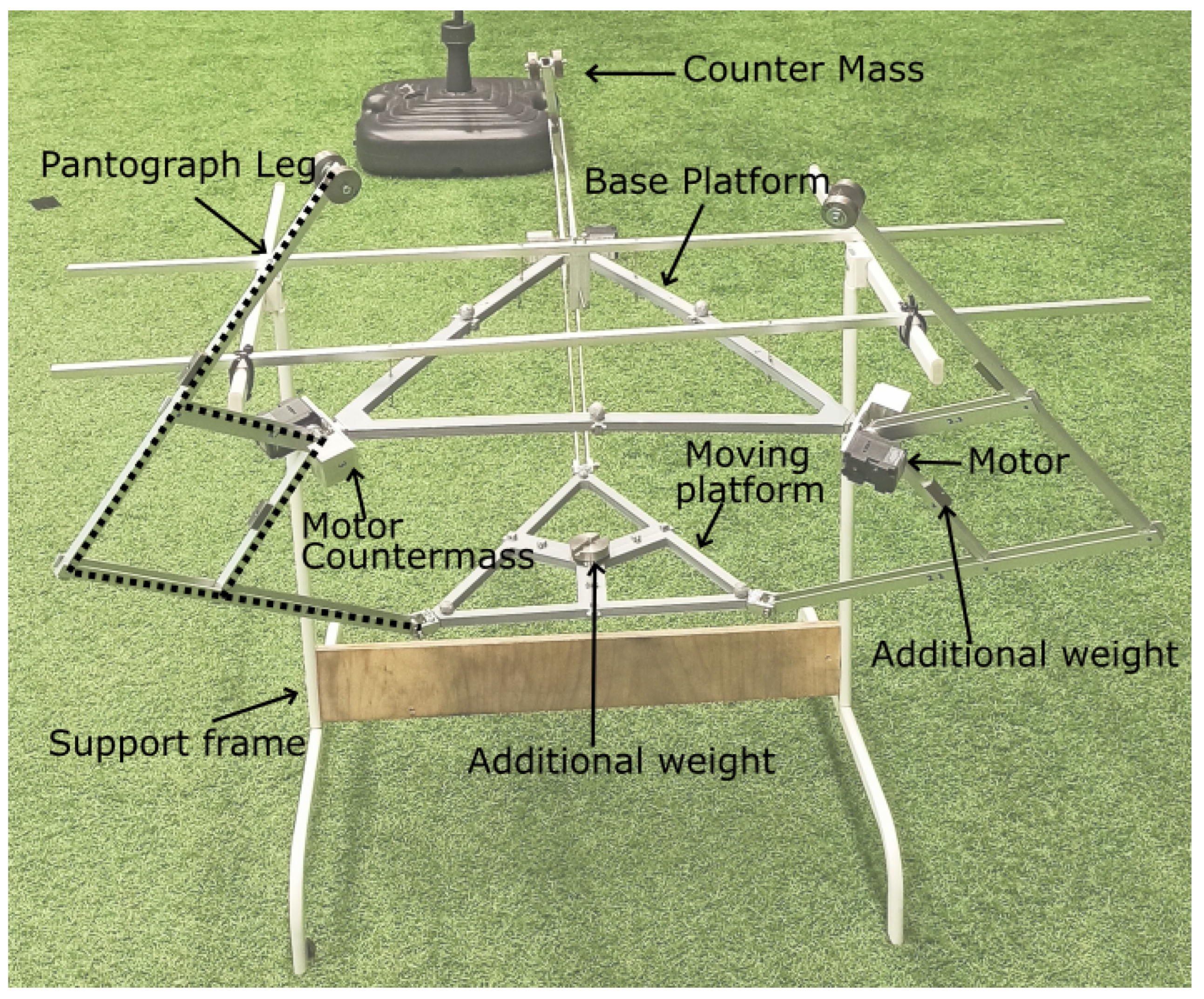
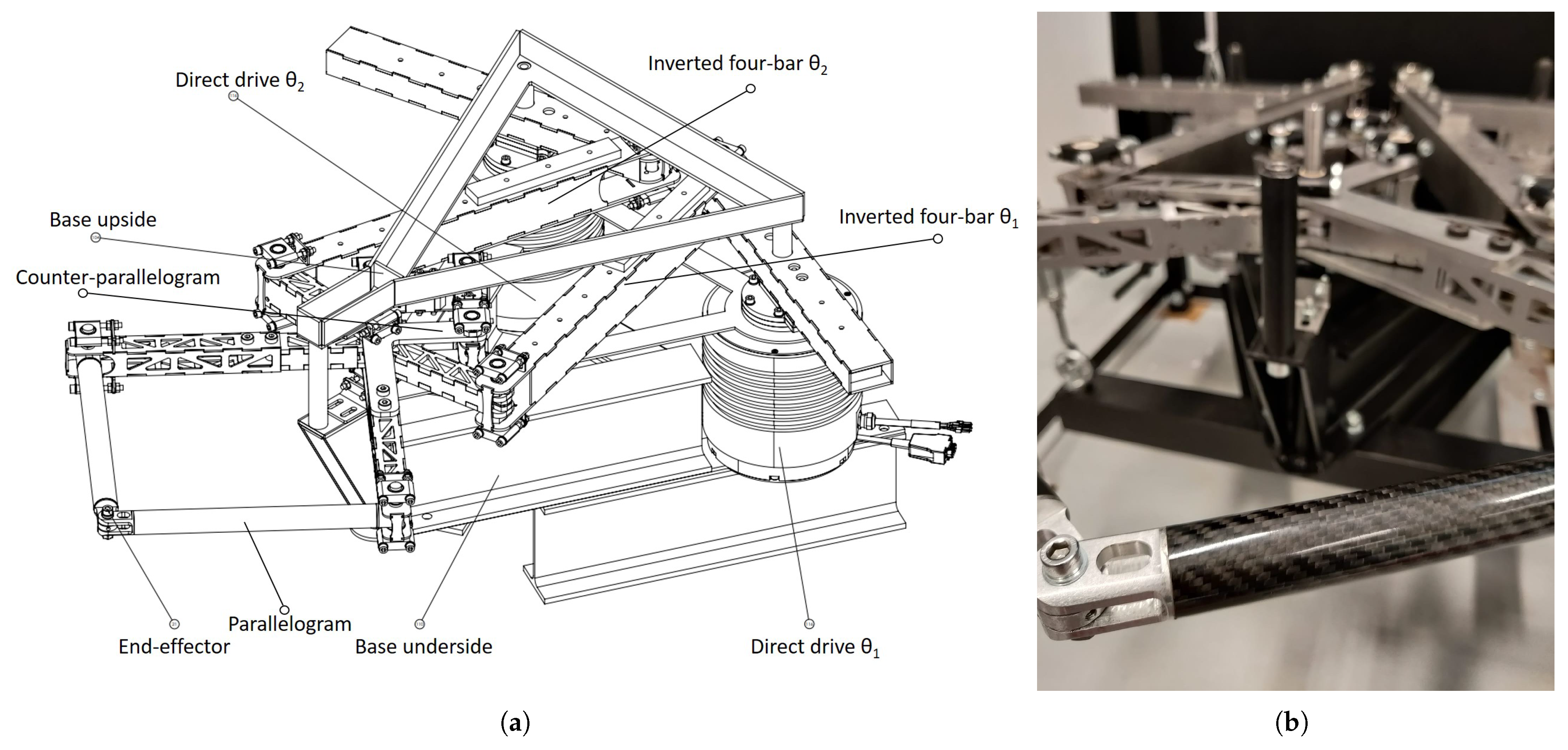
4. Experimental Prototypes
4.1. Gravity Balanced
4.2. Statically Balanced Manipulators
4.3. Force-Balanced Manipulators
4.4. Dynamically Balanced Manipulators
5. Conclusions
Challenges and Future Work
- Continued research in designing, building, and experimentally validating physical prototypes of abstract design concepts for real world applications. These will provide more examples for researchers on the practical issues involved in the design and manufacturing of balanced manipulators.
- Analysis and comparison of the practical mechanical implementation of abstract components (such as CRCM, ADBU, etc.) that comply with the design constraints inherent in real-world manipulator designs.
- More research into the design of low-mass and low-inertia components from a mechanical perspective, as mass and inertia increase poses a major challenge to the practical implementation of balanced manipulators in mobile platforms.
- Synthesis of mechanical design and control approaches for dynamic balancing. This idea was proposed in [28] and explored in some other studies. Control approaches have been extensively explored in the field of space manipulators [18]. However, real-world experimental results remain sparse in the literature. Designing dynamic balanced manipulators can be very difficult in practice; however, a synthesis of force balancing and control along reactionless trajectories can achieve this objective without requiring complex and precise designs.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADBU | Active Dynamic Balancing Unit |
| ALM | Additional Linkage Mechanism |
| DC | Direct Current |
| DOF | Degree of Freedom |
| CI | Counter Inertia |
| CM | Counter Mass |
| CR | Counter Rotation |
| CRCM | Counter Rotating Counter Mass |
| G | Gravitational-Force equivalent |
| PID | Proportional-Integral-Derivative (Control) |
| RRR | Revolute-Revolute-Revolute |
References
- Ghodsian, N.; Benfriha, K.; Olabi, A.; Gopinath, V.; Arnou, A. Mobile Manipulators in Industry 4.0: A Review of Developments for Industrial Applications. Sensors 2023, 23, 8026. [Google Scholar] [CrossRef]
- Billard, A.; Kragic, D. Trends and challenges in robot manipulation. Science 2019, 364, eaat8414. [Google Scholar] [CrossRef] [PubMed]
- Thakar, S.; Srinivasan, S.; Al-Hussaini, S.; Bhatt, P.M.; Rajendran, P.; Jung Yoon, Y.; Dhanaraj, N.; Malhan, R.K.; Schmid, M.; Krovi, V.N.; et al. A Survey of Wheeled Mobile Manipulation: A Decision-Making Perspective. J. Mech. Robot. 2022, 15, 020801. [Google Scholar] [CrossRef]
- Aldhaheri, S.; De Masi, G.; Pairet, E.; Ardón, P. Underwater Robot Manipulation: Advances, Challenges and Prospective Ventures. In Proceedings of the OCEANS 2022, Chennai, India, 21–24 February 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Ollero, A.; Tognon, M.; Suarez, A.; Lee, D.; Franchi, A. Past, Present, and Future of Aerial Robotic Manipulators. IEEE Trans. Robot. 2022, 38, 626–645. [Google Scholar] [CrossRef]
- Ruggiero, F.; Trujillo, M.; Cano, R.; Ascorbe, H.; Viguria, A.; Peréz, C.; Lippiello, V.; Ollero, A.; Siciliano, B. A multilayer control for multirotor UAVs equipped with a servo robot arm. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4014–4020, ISSN 1050-4729. [Google Scholar] [CrossRef]
- Khamseh, H.B.; Janabi-Sharifi, F.; Abdessameud, A. Aerial manipulation—A literature survey. Robot. Auton. Syst. 2018, 107, 221–235. [Google Scholar] [CrossRef]
- Papadopoulos, E.; Aghili, F.; Ma, O.; Lampariello, R. Robotic Manipulation and Capture in Space: A Survey. Front. Robot. AI 2021, 8, 686723. [Google Scholar] [CrossRef] [PubMed]
- Gosselin, C. Gravity Compensation, Static Balancing and Dynamic Balancing of Parallel Mechanisms. In Smart Devices and Machines for Advanced Manufacturing; Springer: London, UK, 2008; Chapter 2; pp. 27–48. [Google Scholar] [CrossRef]
- Arakelian, V. Inertia forces and moments balancing in robot manipulators: A review. Adv. Robot. 2017, 31, 717–726. [Google Scholar] [CrossRef]
- van der Wijk, V.; Krut, S.; Pierrot, F.; Herder, J. Generic Method for Deriving the General Shaking Force Balance Conditions of Parallel Manipulators with Application to a Redundant Planar 4-RRR Parallel Manipulator. In Proceedings of the IFToMM 2011 World Congress: The 13th World Congress in Mechanism and Machine Science, Guanajuato, Mexico, 19–25 June 2011; p. A12. [Google Scholar]
- Lim, T.G.; Cho, H.S.; Chung, W.K. Payload capacity of balanced robotic manipulators. Robotica 1990, 8, 117–123. [Google Scholar] [CrossRef]
- van der Wijk, V.; Herder, J.L. The Work of Otto Fischer and the Historical Development of His Method of Principal Vectors for Mechanism and Machine Science. In Explorations in the History of Machines and Mechanisms; History of Mechanism and Machine Science; Koetsier, T., Ceccarelli, M., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 521–534. [Google Scholar] [CrossRef]
- Lowen, G.G.; Berkof, R.S. Survey of investigations into the balancing of linkages. J. Mech. 1968, 3, 221–231. [Google Scholar] [CrossRef]
- Berkof, R.S.; Lowen, G.G. A New Method for Completely Force Balancing Simple Linkages. J. Eng. Ind. 1969, 91, 21–26. [Google Scholar] [CrossRef]
- Berkof, R.S. Complete force and moment balancing of inline four-bar linkages. Mech. Mach. Theory 1973, 8, 397–410. [Google Scholar] [CrossRef]
- Agrawal, S.K.; Fattah, A. Gravity-balancing of spatial robotic manipulators. Mech. Mach. Theory 2004, 39, 1331–1344. [Google Scholar] [CrossRef]
- Agrawal, S.K.; Fattah, A. Reactionless space and ground robots: Novel designs and concept studies. Mech. Mach. Theory 2004, 39, 25–40. [Google Scholar] [CrossRef]
- Arakelian, V.H.; Smith, M.R. Shaking Force and Shaking Moment Balancing of Mechanisms: A Historical Review with New Examples. J. Mech. Des. 2005, 127, 334–339. [Google Scholar] [CrossRef]
- Kochev, I.S. General theory of complete shaking moment balancing of planar linkages: A critical review. Mech. Mach. Theory 2000, 35, 1501–1514. [Google Scholar] [CrossRef]
- van der Wijk, V. Methodology for Analysis and Synthesis of Inherently Force and Moment-Balanced Mechanisms. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Wei, B.; Zhang, D. A Review of Dynamic Balancing for Robotic Mechanisms. Robotica 2020, 39, 55–71. [Google Scholar] [CrossRef]
- Arakelian, V.; Briot, S. Balancing of Linkages and Robot Manipulators; Number v.27 in Mechanisms and Machine Science Ser.; Springer International Publishing AG: Cham, Swizerland, 2015. [Google Scholar]
- Lee, S.; Cho, H.S. Dynamic characteristics of balanced robotic manipulators with joint flexibility. Robotica 1992, 10, 485–495. [Google Scholar] [CrossRef]
- Yu, Y.Q.; Lin, J. Active Balancing of a Flexible Linkage with Redundant Drives. J. Mech. Des. 2003, 125, 119–123. [Google Scholar] [CrossRef]
- Meijaard, J.P.; van der Wijk, V. Dynamic balancing of mechanisms with flexible links. Mech. Mach. Theory 2022, 172, 104784. [Google Scholar] [CrossRef]
- Yu, Y.Q.; Jiang, B. Analytical and experimental study on the dynamic balancing of flexible mechanisms. Mech. Mach. Theory 2007, 42, 626–635. [Google Scholar] [CrossRef]
- Papadopoulos, E.; Abu-Abed, A. On the Design of Zero Reaction Manipulators. J. Mech. Des. 1996, 118, 372–376. [Google Scholar] [CrossRef]
- Huang, P.; Xu, Y.; Liang, B. Dynamic Balance Control of Multi-Arm Free-Floating Space Robots. Int. J. Adv. Robot. Syst. 2005, 2, 13. [Google Scholar] [CrossRef]
- Vukobratovic, M.; Borovac, B. Dynamic balance concept and the maintenance of the dynamic balance in humanoid robotics. In Proceedings of the International Symposium on Intelligent Systems and Informatics (SISY), Subotica, Serbia, 26–27 September 2008; pp. 1–11, ISSN 1949-0488. [Google Scholar] [CrossRef]
- Huang, Y.; Bing, Z.; Zhang, Z.; Zhuang, G.; Huang, K.; Knoll, A. Optimizing Dynamic Balance in a Rat Robot via the Lateral Flexion of a Soft Actuated Spine. In Proceedings of the IEEE International Conference on Robotics and Automation, Yokohama, Japan, 13–17 May 2024; pp. 3442–3448. [Google Scholar] [CrossRef]
- Li, Z.; Ge, Q.; Ye, W.; Yuan, P. Dynamic Balance Optimization and Control of Quadruped Robot Systems with Flexible Joints. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 1338–1351. [Google Scholar] [CrossRef]
- Arakelian, V. Gravity compensation in robotics. Adv. Robot. 2016, 30, 79–96. [Google Scholar] [CrossRef]
- Saravanan, R.; Ramabalan, S.; Dinesh Babu, P. Optimum static balancing of an industrial robot mechanism. Eng. Appl. Artif. Intell. 2008, 21, 824–834. [Google Scholar] [CrossRef]
- Laliberte, T.; Gosselin, C.; Jean, M. Static balancing of 3-DOF planar parallel mechanisms. IEEE/ASME Trans. Mechatronics 1999, 4, 363–377. [Google Scholar] [CrossRef]
- Gosselin, C.M.; Wang, J. Static balancing of spatial six-degree-of-freedom parallel mechanisms with revolute actuators. J. Robot. Syst. 2000, 17, 159–170. [Google Scholar] [CrossRef]
- Wang, J.; Kong, X. A geometric approach to the static balancing of mechanisms constructed using spherical kinematic chain units. Mech. Mach. Theory 2019, 140, 305–320. [Google Scholar] [CrossRef]
- Baradat, C.; Arakelian, V.; Briot, S.; Guegan, S. Design and Prototyping of a New Balancing Mechanism for Spatial Parallel Manipulators. J. Mech. Des. 2008, 130, 072305. [Google Scholar] [CrossRef]
- Ebert-Uphoff, I.; Johnson, K. Practical considerations for the static balancing of mechanisms of parallel architecture. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2002, 216, 73–85. [Google Scholar] [CrossRef]
- Quaglia, G.; Yin, Z. Static balancing of planar articulated robots. Front. Mech. Eng. 2015, 10, 326–343. [Google Scholar] [CrossRef]
- Lessard, S.; Bigras, P.; Bonev, I.A. A New Medical Parallel Robot and Its Static Balancing Optimization. J. Med. Devices 2007, 1, 272–278. [Google Scholar] [CrossRef]
- Lee, W.B.; Kim, D.W.; Song, J.B. Novel 3-DOF counterbalance mechanism based on spring balancer for mobile robot arms. Mechatronics 2022, 82, 102734. [Google Scholar] [CrossRef]
- Nguyen, V.L.; Lin, C.Y.; Kuo, C.H. Gravity compensation design of Delta parallel robots using gear-spring modules. Mech. Mach. Theory 2020, 154, 104046. [Google Scholar] [CrossRef]
- Bayer, A.; Bohlken, W.; Berninger, A. Vorrichtung zum Gewichtsausgleich eines Roboterarms. EP Patent EP1125696B1, 15 March 2006. [Google Scholar]
- Lin, P.Y.; Shieh, W.B.; Chen, D.Z. Design of Statically Balanced Planar Articulated Manipulators with Spring Suspension. IEEE Trans. Robot. 2012, 28, 12–21. [Google Scholar] [CrossRef]
- Juang, C.W.; Chen, D.Z. Spring Configurations and Attachment Angles Determination for Statically Balanced Planar Articulated Manipulators. J. Mech. Robot. 2022, 14, 054502. [Google Scholar] [CrossRef]
- Cho, C.; Kang, S. Design of a Static Balancing Mechanism for a Serial Manipulator with an Unconstrained Joint Space Using One-DOF Gravity Compensators. IEEE Trans. Robot. 2014, 30, 421–431. [Google Scholar] [CrossRef]
- Briot, S.; Bonev, I.A.; Gosselin, C.M.; Arakelian, V. Complete shaking force and shaking moment balancing of planar parallel manipulators with prismatic pairs. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2009, 223, 43–52. [Google Scholar] [CrossRef]
- van der Wijk, V.; Herder, J.L. Guidelines for Low Mass and Low Inertia Dynamic Balancing of Mechanisms and Robotics. In Advances in Robotics Research; Springer: Berlin/Heidelberg, Germany, 2009; pp. 21–30. [Google Scholar] [CrossRef]
- Chung, W.K.; Cho, H.S. On the Dynamics and Control of Robotic Manipulators with an Automatic Balancing Mechanism. Proc. Inst. Mech. Eng. Part B Manag. Eng. Manuf. 1987, 201, 25–34. [Google Scholar] [CrossRef]
- Russo, A.; Sinatra, R.; Xi, F. Static balancing of parallel robots. Mech. Mach. Theory 2005, 40, 191–202. [Google Scholar] [CrossRef]
- Clark, A.B.; Baron, N.; Orr, L.; Kovac, M.; Rojas, N. On a Balanced Delta Robot for Precise Aerial Manipulation: Implementation, Testing, and Lessons for Future Designs. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 7359–7366. [Google Scholar] [CrossRef]
- Suryavanshi, K.; Hamaza, S.; van der Wijk, V.; Herder, J. ADAPT: A 3 Degrees of Freedom Reconfigurable Force Balanced Parallel Manipulator for Aerial Applications. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 11936–11942. [Google Scholar] [CrossRef]
- van der Wijk, V.; Herder, J.; Demeulenaere, B.; Gosselin, C. Comparative analysis and optimization for low-mass and low inertia dynamic balancing of a rotatable link balanced by a counter-mass. J. Mech. Robot. 2012, 4, 1–8. [Google Scholar] [CrossRef]
- van der Wijk, V.; Herder, J.L.; Demeulenaere, B. Comparison of Various Dynamic Balancing Principles Regarding Additional Mass and Additional Inertia. J. Mech. Robot. 2009, 1, 041006. [Google Scholar] [CrossRef]
- Feng, G. Complete shaking force and shaking moment balancing of 26 types of four-, five- and six-bar linkages with prismatic pairs. Mech. Mach. Theory 1990, 25, 183–192. [Google Scholar] [CrossRef]
- Baron, N.; Philippides, A.; Rojas, N. A Dynamically Balanced Kinematically Redundant Planar Parallel Robot. J. Mech. Des. 2021, 143, 083301. [Google Scholar] [CrossRef]
- van der Wijk, V.; Herder, J. Double Pendulum Balanced by Counter-Rotary Counter-Masses as Useful Element for Synthesis of Dynamically Balanced Mechanisms. In Proceedings of the IDETC/CIE 2008ASME 2008 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference, Brooklyn, NY, USA, 3–6 August 2008; Volume 2, pp. 1–11. [Google Scholar] [CrossRef]
- Laliberté, T.; Gosselin, C. Synthesis, optimization and experimental validation of reactionless two-DOF parallel mechanisms using counter-mechanisms. Meccanica 2016, 51, 3211–3225. [Google Scholar] [CrossRef]
- van der Wijk, V.; Herder, J.L. Force balancing of variable payload by active force-balanced reconfiguration of the mechanism. In Proceedings of the 2009 ASME/IFToMM International Conference on Reconfigurable Mechanisms and Robots, London, UK, 22–24 June 2009; pp. 323–330. [Google Scholar]
- van der Wijk, V.; Andreff, N.; Herder, J.; Gouttefarde, M.; Krut, S.; Pierrot, F. Dynamic balancing of mechanisms by using an actively driven couter-rotary counter-mass for low mass and low inertia. In Proceedings of the Second International Workshop on Fundamental Issues and Future Research Directions for Parallel Mechanisms and Manipulators, Montpellier, France, 21–22 September 2008; pp. 241–251. [Google Scholar]
- Otani, E.M.; Bartlett, D.S.; Akeel, H.A.; McGee, H.D.; Najdovski, L.; Hobson, J.C.; McClosky, S.H.; Bauer, R.V., Jr.; Frease, R. Intelligent Power Assisted Manual Manipulator. U.S. Patent US6612449B1, 2 September 2003. [Google Scholar]
- Hamaza, S.; Kovac, M. Omni-Drone: On the Design of a Novel Aerial Manipulator with Omni-directional Workspace. In Proceedings of the 2020 17th International Conference on Ubiquitous Robots (UR), Kyoto, Japan, 22–26 June 2020; pp. 153–158, ISSN 2325-033X. [Google Scholar] [CrossRef]
- AlAkhras, A.; Sattar, I.H.; Alvi, M.; Qanbar, M.W.; Jaradat, M.A.; Alkaddour, M. The Design of a Lightweight Cable Aerial Manipulator with a CoG Compensation Mechanism for Construction Inspection Purposes. Appl. Sci. 2022, 12, 1173. [Google Scholar] [CrossRef]
- Ohnishi, Y.; Takaki, T.; Aoyama, T.; Ishii, I. Development of a 4-joint 3-DOF robotic arm with anti-reaction force mechanism for a multicopter. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 985–991. [Google Scholar] [CrossRef]
- Luxton, C.; Sandino, J.; Vanegas, F.; Gonzalez, F. Design and Flight Testing of a Two DOF Decoupled Pantograph Aerial Manipulator for Commercial UAVs. In Proceedings of the 2022 International Conference on Unmanned Aircraft Systems (ICUAS), Dubrovnik, Croatia, 21–24 June 2022; pp. 1–10, ISSN 2575-7296. [Google Scholar] [CrossRef]
- Sun, J.; Zhou, C. AeroTail: A Bio-Inspired Aerodynamic Tail Mechanism for Robotic Balancing. In Proceedings of the IEEE International Conference on Automation and Computing (ICAC), Birmingham, UK, 30 August–1 September 2023; pp. 1–6. [Google Scholar] [CrossRef]
- van der Wijk, V.; Herder, J.L. Active Dynamic Balancing Unit for Controlled Shaking Force and Shaking Moment Balancing. In Proceedings of the ASME 2010 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference, American Society of Mechanical Engineers Digital Collection. Montreal, QC, Canada, 15–18 August 2011; pp. 1515–1522. [Google Scholar] [CrossRef]
- van der Wijk, V.; Herder, J.L. Dynamic Balancing of Clavel’s Delta Robot. In Proceedings of the Computational Kinematics; Kecskeméthy, A., Müller, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 315–322. [Google Scholar] [CrossRef]
- Chaudhary, K.; Chaudhary, H. Optimal dynamic balancing and shape synthesis of links in planar mechanisms. Mech. Mach. Theory 2015, 93, 127–146. [Google Scholar] [CrossRef]
- Chaudhary, K.; Chaudhary, H. Shape Optimization of Dynamically Balanced Planar Four-bar Mechanism. Procedia Comput. Sci. 2015, 57, 519–526. [Google Scholar] [CrossRef]
- Moore, B.; Schicho, J.; Gosselin, C.M. Determination of the complete set of shaking force and shaking moment balanced planar four-bar linkages. Mech. Mach. Theory 2009, 44, 1338–1347. [Google Scholar] [CrossRef]
- de Jong, J.J.; van Dijk, J.; Herder, J.L. A screw based methodology for instantaneous dynamic balance. Mech. Mach. Theory 2019, 141, 267–282. [Google Scholar] [CrossRef]
- Ricard, R.; Gosselin, C.M. On the Development of Reactionless Parallel Manipulators. In Proceedings of the Volume 7A: 26th Biennial Mechanisms and Robotics Conference, Baltimore, MD, USA, 10–13 September 2000; pp. 493–502. [Google Scholar] [CrossRef]
- Gosselin, C.; Vollmer, F.; Cote, G.; Wu, Y. Synthesis and design of reactionless three-degree-of-freedom parallel mechanisms. IEEE Trans. Robot. Autom. 2004, 20, 191–199. [Google Scholar] [CrossRef]
- Wu, Y.; Gosselin, C.M. On the Dynamic Balancing of Multi-DOF Parallel Mechanisms with Multiple Legs. J. Mech. Des. 2006, 129, 234–238. [Google Scholar] [CrossRef]
- Briot, S.; Goldsztejn, A. Topology Optimization of a Reactionless Four-Bar Linkage. In Proceedings of the Computational Kinematics; Zeghloul, S., Romdhane, L., Laribi, M.A., Eds.; Springer: Cham, Switzerland, 2018; pp. 413–421. [Google Scholar] [CrossRef]
- Emmanuel Ayala-Hernández, J.; Briot, S.; Jesús Cervantes-Sánchez, J. Structural Topology Optimization of Reactionless Four-Bar Linkages. J. Mech. Des. 2022, 144, 111701. [Google Scholar] [CrossRef]
- Alici, G.; Shirinzadeh, B. Optimum force balancing with mass distribution and a single elastic element for a five-bar parallel manipulator. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation (Cat. No.03CH37422), Taipei, Taiwan, 14–19 September 2003; Volume 3, pp. 3666–3671, ISSN 1050-4729. [Google Scholar] [CrossRef]
- Arakelian, V. Minimization of Shaking Moment in Fully Force Balanced Planar Four-Bar Linkages. In Proceedings of the Advances in Mechanism Design III; Beran, J., Bílek, M., Václavík, M., Žabka, P., Eds.; Springer: Cham, Switzerland, 2022; pp. 17–23. [Google Scholar] [CrossRef]
- Gosselin, C.M.; Wu, Y. On the Development of Reactionless Spatial 3-DOF Parallel-Piped Mechanisms. In Proceedings of the Volume 5: 27th Biennial Mechanisms and Robotics Conference, Montreal, QC, Canada, 29 September–2 October 2002. IDETC-CIE2002. [Google Scholar] [CrossRef]
- Wu, Y.; Gosselin, C. Design of reactionless 3-DOF and 6-DOF parallel manipulators using parallelepiped mechanisms. IEEE Trans. Robot. 2005, 21, 821–833. [Google Scholar] [CrossRef]
- Xi, F.; Sinatra, R. Effect of dynamic balancing on four-bar linkage vibrations. Mech. Mach. Theory 1997, 32, 715–728. [Google Scholar] [CrossRef]
- Kalas, V.J. Shaking Force Balance in Parallel Manipulators with Flexible Links. Ph.D. Thesis, Master Thesis, Laboratory of Mechanical Automation and Mechatronics, Faculty of Engineering Technology, University of Twente, Enschede, The Netherlands, 2016. Report WA-1588. [Google Scholar]
- Meijaard, J.P.; van der Wijk, V. Principal vectors and equivalent mass descriptions for the equations of motion of planar four-bar mechanisms. Multibody Syst. Dyn. 2020, 48, 259–282. [Google Scholar] [CrossRef]
- van der Wijk, V. Design and analysis of closed-chain principal vector linkages for dynamic balance with a new method for mass equivalent modeling. Mech. Mach. Theory 2017, 107, 283–304. [Google Scholar] [CrossRef]
- Agrawal, S.K.; Gardner, G.; Pledgie, S. Design and Fabrication of an Active Gravity Balanced Planar Mechanism Using Auxiliary Parallelograms. J. Mech. Des. 1999, 123, 525–528. [Google Scholar] [CrossRef]
- van der Wijk, V. The Spatial Pantograph and its Mass Balance. In Proceedings of the Advances in Robot Kinematics 2022; Springer Proceedings in Advanced Robotics; Altuzarra, O., Kecskeméthy, A., Eds.; Springer: Cham, Switzerland, 2022; pp. 426–433. [Google Scholar] [CrossRef]
- Girgenti, L.; van der Wijk, V. Techniques for Synthesis of Inherently Force Balanced Mechanisms. In Proceedings of the ROMANSY 24 - Robot Design, Dynamics and Control; CISM International Centre for Mechanical Sciences; Kecskeméthy, A., Parenti-Castelli, V., Eds.; Springer: Cham, Switzerland, 2022; pp. 263–271. [Google Scholar] [CrossRef]
- Collard, J.F.; Gosselin, C. Optimal Synthesis of a Planar Reactionless Three-Degree-of-Freedom Parallel Mechanism. J. Mech. Robot. 2011, 3, 041009. [Google Scholar] [CrossRef]
- van der Wijk, V.; Herder, J.L. Synthesis method for linkages with center of mass at invariant link point—Pantograph based mechanisms. Mech. Mach. Theory 2012, 48, 15–28. [Google Scholar] [CrossRef]
- Jean, M.; Gosselin, C. Static balancing of planar parallel manipulators. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; Volume 4, pp. 3732–3737, ISSN 1050-4729. [Google Scholar] [CrossRef]
- Wu, Y.; Gosselin, C.M. Synthesis of Reactionless Spatial 3-DoF and 6-DoF Mechanisms without Separate Counter-Rotations. Int. J. Robot. Res. 2004, 23, 625–642. [Google Scholar] [CrossRef]
- Fattah, A.; Agrawal, S. Gravity-balancing of classes of industrial robots. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, ICRA 2006, Orlando, FL, USA, 15–19 May 2006; pp. 2872–2877, ISSN 1050-4729. [Google Scholar] [CrossRef]
- Koser, K. A cam mechanism for gravity-balancing. Mech. Res. Commun. 2009, 36, 523–530. [Google Scholar] [CrossRef]
- Abdallah, M.; Wells, J.; Cresmeri, P. Balance Mechanism for Robot Auxiliary Equipment. CN Patent CN114905543B, 12 March 2024. [Google Scholar]
- van der Wijk, V.; Krut, S.; Pierrot, F.; Herder, J.L. Design and experimental evaluation of a dynamically balanced redundant planar 4-RRR parallel manipulator. Int. J. Robot. Res. 2013, 32, 744–759. [Google Scholar] [CrossRef]
- Papadopoulos, E.; Abu-Abed, A. Design and motion planning for a zero-reaction manipulator. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; Volume 2, pp. 1554–1559. [Google Scholar] [CrossRef]
- Ouyang, P.R.; Li, Q.; Zhang, W.J. Integrated design of robotic mechanisms for force balancing and trajectory tracking. Mechatronics 2003, 13, 887–905. [Google Scholar] [CrossRef]
- Geng, J.; Arakelian, V. Partial Shaking Force Balancing of 3-RRR Parallel Manipulators by Optimal Acceleration Control of the Total Center of Mass. In Multibody Dynamics 2019; Kecskeméthy, A., Geu Flores, F., Eds.; Springer: Cham, Switzerland, 2020; pp. 375–382. [Google Scholar] [CrossRef]
- Briot, S.; Arakelian, V.; Guégan, S. PAMINSA: A new family of partially decoupled parallel manipulators. Mech. Mach. Theory 2009, 44, 425–444. [Google Scholar] [CrossRef]
- Gosselin, C.M. Static Balancing of Spherical 3-DOF Parallel Mechanisms and Manipulators. Int. J. Robot. Res. 1999, 18, 819–829. [Google Scholar] [CrossRef]
- Chung, W.K.; Cho, H. On the dynamic characteristics of a balance PUMA-760 robot. IEEE Trans. Ind. Electron. 1988, 35, 222–230. [Google Scholar] [CrossRef]
- Arakelian, V.; Briot, S. Dynamic Balancing of the SCARA robot. In Proceedings of the 17th CISM-IFToMM Symposium on Robot Design, Dynamics, and Control (RoManSy 2008), Tokyo, Japan, 5–9 July 2008. [Google Scholar]
- van der Wijk, V.; Demeulenaere, B.; Gosselin, C.; Herder, J.L. Comparative Analysis for Low-Mass and Low-Inertia Dynamic Balancing of Mechanisms. J. Mech. Robot. 2012, 4, 031008. [Google Scholar] [CrossRef]
- Arakelian, V. Optimum Shaking Force Balancing of Planar 3-RRR Parallel Manipulators by means of an Adaptive Counterweight System. J. Robot. Mech. Eng. Res. 2015, 1, 36–41. [Google Scholar] [CrossRef]
- Acevedo, M.; Ceccarelli, M.; Carbone, G. Application of Counter-Rotary Counterweights to the Dynamic Balancing of a Spatial Parallel Manipulator. Appl. Mech. Mater. 2012, 162, 224–233. [Google Scholar] [CrossRef]
- Imanberdiyev, N.; Sood, S.; Kircali, D.; Kayacan, E. Design, development and experimental validation of a lightweight dual-arm aerial manipulator with a COG balancing mechanism. Mechatronics 2022, 82, 102719. [Google Scholar] [CrossRef]
- Mirz, C.; Hüsing, M.; Takeda, Y.; Corves, B. Active Dynamic Balancing of Delta Robots in Pick and Place Tasks. In Advances in Mechanism and Machine Science; Okada, M., Ed.; Springer: Cham, Switzerland, 2023; pp. 255–265. [Google Scholar] [CrossRef]
- Fattah, A.; Agrawal, S.K. Design and simulation of a class of spatial reactionless manipulators. Robotica 2005, 23, 75–81. [Google Scholar] [CrossRef]
- Alici, G.; Shirinzadeh, B. Optimum dynamic balancing of planar parallel manipulators. In Proceedings of the IEEE International Conference on Robotics and Automation, Proceedings, ICRA ’04, New Orleans, LA, USA, 26 April–1 May 2004; pp. 4527–4532. [Google Scholar] [CrossRef]
- Ouyang, P.R.; Zhang, W.J. Force Balancing of Robotic Mechanisms Based on Adjustment of Kinematic Parameters. J. Mech. Des. 2004, 127, 433–440. [Google Scholar] [CrossRef]
- Campeau-Lecours, A.; Gosselin, C. Reactionless Two-Degree-of-Freedom Planar Parallel Mechanism with Variable Payload. ASME J. Mech. Robot. 2010, 2, 887–896. [Google Scholar] [CrossRef]
- Ilia, D.; Sinatra, R. A novel formulation of the dynamic balancing of five-bar linkages with applications to link optimization. Multibody Syst. Dyn. 2009, 21, 193–211. [Google Scholar] [CrossRef]
- Arakelian, V.H.; Smith, M.R. Design of planar 3-DOF 3-RRR reactionless parallel manipulators. Mechatronics 2008, 18, 601–606. [Google Scholar] [CrossRef]
- Fattah, A.; Agrawal, S.K. On the design of reactionless 3-DOF planar parallel mechanisms. Mech. Mach. Theory 2006, 41, 70–82. [Google Scholar] [CrossRef]
- Chaudhary, H.; Saha, S.K. An optimization technique for the balancing of spatial mechanisms. Mech. Mach. Theory 2008, 43, 506–522. [Google Scholar] [CrossRef]
- Zomerdijk, M.J.J.; van der Wijk, V. Structural Design and Experiments of a Dynamically Balanced Inverted Four-Bar Linkage as Manipulator Arm for High Acceleration Applications. Actuators 2022, 11, 131. [Google Scholar] [CrossRef]
- Ulrich, N.; Kumar, V. Passive mechanical gravity compensation for robot manipulators. In Proceedings of the 1991 IEEE International Conference on Robotics and Automation Proceedings, Sacramento, CA, USA, 9–11 April 1991; Volume 2, pp. 1536–1541. [Google Scholar] [CrossRef]
- Cho, C.; Lee, W.; Kang, S. Static balancing of a manipulator with hemispherical work space. In Proceedings of the 2010 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Montreal, QC, Canada, 6–9 July 2010; pp. 1269–1274, ISSN 2159-6255. [Google Scholar] [CrossRef]
- Sajjapongse, K.; Wannasuphoprasit, W. Single Spring Gravity Compensator for a Multi-DOF Manipulator. IEEE Access 2024, 12, 64416–64426. [Google Scholar] [CrossRef]
- Vermeulen, M.; Wisse, M. Intrinsically Safe Robot Arm: Adjustable Static Balancing and Low Power Actuation. Int. J. Soc. Robot. 2010, 2, 275–288. [Google Scholar] [CrossRef]
- Boere, D.; van der Wijk, V.; Herder, J.; Meijaard, J. The Constant Inertia Mechanism and Its Use in a High-Speed 2-DoF Inherently Dynamically Balanced Parallel Manipulator. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2022. [Google Scholar]
- Foucault, S.; Gosselin, C.M. Synthesis, Design, and Prototyping of a Planar Three Degree-of-Freedom Reactionless Parallel Mechanism. J. Mech. Des. 2005, 126, 992–999. [Google Scholar] [CrossRef]
- Suryavanshi, K. ADAPT: A 3 Degrees of Freedom Reconfigurable Force Balanced Parallel Manipulator for Aerial Applications. Master’s Thesis, TU Delft, Delft, The Netherlands, 2022. [Google Scholar]
- Zlatanov, D.; Bonev, I.A.; Gosselin, C.M. Constraint Singularities as C-Space Singularities. In Advances in Robot Kinematics; Lenarčič, J., Thomas, F., Eds.; Springer: Dordrecht, The Netherlands, 2002; pp. 183–192. [Google Scholar] [CrossRef]
- van der Wijk, V.D. Robot Manipulator. WO Patent WO2024063645A1, 28 March 2024. [Google Scholar]
- Bom, A. Design of an Inherently Fully Dynamically Balanced Aerial Manipulator with Omnidirectional Workspace. Master’s Thesis, TU Delft, Delft, The Netherlands, 2024. [Google Scholar]
- Foucault, S.; Gosselin, C.M. On the Development of a Planar 3-DOF Reactionless Parallel Mechanism. In Proceedings of the ASME 2002 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Montreal, QC, Canada, 29 September–2 October 2002; pp. 985–993. [Google Scholar] [CrossRef]
- van der Wijk, V.; Krut, S.C.; Pierrot, F.; Herder, J.L. Manipulator Comprising a Fixed Base and a Movable Platform, with Four Motor-Driven Chains of Articulated Links. EP Patent EP2720835B1, 12 August 2015. [Google Scholar]









| Category | Approach | Advantages | Disadvantages | Relevant Papers |
|---|---|---|---|---|
| Passive Component Addition | Springs | - Lightweight - Compact - Low Mass Addition | - Only achieves static balance - Expends energy during motion from equilibrium - Constrains the motion to be within the linear elastic region of deflection | [17,35,36,37,40,41,43,51,79,89,102] |
| Counter Mass (CM) Counter Inertia (CI) | - Simple modifications to an existing mechanism - Kinematic equations do not increase in complexity - Can be implemented compactly | - CM Only achieves force balance - Increases overall mass and inertia - Tradeoff between mass/inertia and space increase - Can increase moments/joint torques at high accelerations - CI requires precise modifications of link inertia | [12,49,52,54,56,59,60,63,64,69,103,104,105,106] | |
| Counter Rotating Counter Mass (CRCM) | - Simultaneously low mass and low space addition | - Complex kinematic design - Mechanically complex to implement in practice | [49,55,56,58,105,107] | |
| Additional Linkage mechanism (ALM) | - Low mass addition - Increases stiffness and rigidity | - Significant increase in space - Can restrict workspace due to additional complexity in kinematics | [17,48,51,55,59,87,105,108] | |
| Active Component Addition | Active CRCM/ADBU | - Highly Compact - Low Mass/Inertia addition - Can be placed in a variety of locations - Can balance all forces and torques simultaneously | - Requires actuation - Mechanical limits to forces and torques that can be balanced - Complex to design and implement | [61,67,68,69,109] |
| Inherent Dynamic Balancing | Parallel Mechanisms | - Can synthesize to form higher DOF planar or spatial mechanisms. - Lower mass increase than CM/CI applied to serial mechanisms - Multiple kinematic designs for any set of balancing conditions | - Designs can restrict workspace due to interference or singularities - Complex kinematics and mechanical design | [11,16,57,71,74,75,77,78,93,98,101,110,111,112,113,114,115,116,117,118] |
| Principal Vector Designs | - Low mass increase - Well-established mathematical methods of solving for balance | - Very large mass and inertia - Complex mechanical design (particularly joint design) | [85,88,91] | |
| Parallel-Piped | - Design optimizes in 3D for balance conditions | - Large mass increase - Complex mechanical design (particularly joint design) | [81,82] | |
| Synthesized mechanisms | - Can combine the advantages of different methods (from the above) - Build complex mechanisms from simpler balanced components which are easier to solve for balance | - Complex combinations of designs which can be difficult to implement practically - Redundant components (masses, inertias) are added which could be reduced if the entire mechanism is optimized | [35,53,76,82,90,91,92,93,94,97,98,99,116] |
| Type of Balance | Dimension | Balanced DOF | Motion DOF | Paper | Method | Experimental metrics |
|---|---|---|---|---|---|---|
| Gravity | Planar | 1 | 2 | [119] | Spring | Joint torques |
| 1 | 2 | [120] | Spring | Joint angles | ||
| 1 | 3 | [87] | ALM, Active CM | Joint angles | ||
| 1 | 3 | [42] | Spring | Joint torques | ||
| 1 | 3 | [121] | Spring | Joint torques | ||
| Spatial | 1 | 3 | [38] | Active ALM | Joint torques, end-effector position | |
| Static | Planar | 1 | 2 | [66] | Active CM | Reaction moments, base position |
| 1 | 3 | [64] | Active CM | Base rotation | ||
| 1 | 5 | [6] | Active CM | Joint torques, base orientation | ||
| 3 | 3 | [35] | CM/CR, CRCM, ALM | Joint torques (simulation) | ||
| Spatial | 3 | 4 | [122] | Spring, ALM | Joint torques | |
| 3 | 6 | [108] | Active ALM | Base displacement | ||
| Static and Moment | Planar | 2 | 3 | [65] | Active CM, Inherent Balancing | Base orientation |
| Force | Planar | 2 | 2 | [103] | CM | Joint Torques |
| Spatial | 3 | 3 | [53] | Synthesized Mechanism | Reaction forces | |
| 3 | 4 | [101] | Synthesized Mechanism | Actuator torques | ||
| 3 | 6 | [52] | CM | Reaction forces and moments | ||
| Dynamic | Planar | 3 | 1 | [118] | Inherent Balancing | Angular acceleration, joint torque |
| 3 | 2 | [123] | Inherent Balancing | Reaction forces and moment | ||
| 3 | 2 | [59] | ALM, CM/CR, CRCM | Joint torques | ||
| 3 | 3 | [124] | Synthesized Mechanism | End-effector position | ||
| 3 | 4 | [97] | Synthesized Mechanism | End-effector position, reaction forces/moments | ||
| Spatial | 3 | 4 | [109] | ADBU | End-effector position |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vyas, Y.J.; van der Wijk, V.; Cocuzza, S. A Review of Mechanical Design Approaches for Balanced Robotic Manipulation. Robotics 2025, 14, 151. https://doi.org/10.3390/robotics14110151
Vyas YJ, van der Wijk V, Cocuzza S. A Review of Mechanical Design Approaches for Balanced Robotic Manipulation. Robotics. 2025; 14(11):151. https://doi.org/10.3390/robotics14110151
Chicago/Turabian StyleVyas, Yash J., Volkert van der Wijk, and Silvio Cocuzza. 2025. "A Review of Mechanical Design Approaches for Balanced Robotic Manipulation" Robotics 14, no. 11: 151. https://doi.org/10.3390/robotics14110151
APA StyleVyas, Y. J., van der Wijk, V., & Cocuzza, S. (2025). A Review of Mechanical Design Approaches for Balanced Robotic Manipulation. Robotics, 14(11), 151. https://doi.org/10.3390/robotics14110151







