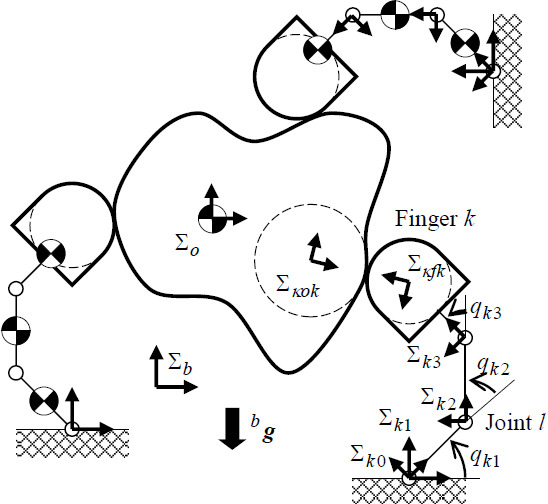
Static Stability Analysis of a Planar Object Grasped by Multifingers with Three Joints
Abstract
:1. Introduction
| Dimensions | Local Curvature of the Finger Surface | Curvature Deviation (Positive Definiteness) | Contact Condition | Contact Condition Diff. (Positive Definiteness) | Joint Stiffness | Nr. of Links | Link Mass | Mass Deviation | |
|---|---|---|---|---|---|---|---|---|---|
| Hanafusa [1] | 2D | - | - | PC | - | - | - | - | - |
| Nguyen [2] | 3D | - | - | PC, PCWF, | - | - | - | - | - |
| Li [3] | 3D | - | - | PCWF | - | - | - | - | - |
| Cutkosky [4] | 3D | - | - | PCWF | - | O | O | - | - |
| Carbone [5] | 3D | - | - | PCWF | - | O | O | - | - |
| Kim [6] | 3D | - | - | PCWF | - | - | O | - | - |
| Babiccini [7] | 3D | - | - | PCWF | - | - | - | - | - |
| Malvezzi [8] | 2D | - | - | PCWF | - | - | - | - | - |
| Shapiro [9] | 3D | - | - | PC | - | - | - | - | - |
| Montana [10] | 3D | included | - | RC | - | - | - | - | - |
| Xiong [11] | 3D | included | - | RC | - | - | - | - | - |
| Choi [12] | 3D | included | - | RC | - | - | - | - | - |
| Michalec [13] | 3D | included | - | RC | - | - | O | O | - |
| Funahashi [14] | 2D | included | - | RC, SC(1D) | - | - | - | - | - |
| Howard [15] | 3D | included | - | RC, SC(1D) | - | O | O | - | - |
| Howard [16] | 3D | included | - | RC, SC(1D) | - | - | - | - | - |
| Lin [17] | 2D | included | - | SC(1D) | - | - | - | - | - |
| Yamada [18] | 2D | included | - | RC, SC | - | - | - | - | - |
| Yamada [19,20,21] | 3D | included | - | RC, SC | - | - | - | - | - |
| Yamada [22] | 2D | included | treated | RC, SC | treated | O | 2 | - | - |
| This paper | 2D | included | treated | RC, SC | treated | O | 3 | O | O |
2. Problem Definitions

2.1. Assumptions
2.2. Nomenclature

3. Formulation
3.1. Joint Position and Local Coordinate Frame
3.2. Potential Energy of the Finger
3.3. Contact Constraint and Its Partial Derivative
3.4. Partial Derivatives of the Energy
3.5. Frictionless Sliding Contact Case
3.5.1. Wrench Vector and Stiffness Matrix
3.5.2. Local Curvature Effect
3.6. Pure Rolling Contact Case
3.6.1. Wrench Vector and Stiffness Matrix
3.6.2. Local Curvature Effect
3.7. Contact Condition Effect
3.8. Grasp Wrench and Stiffness Matrix
4. Numerical Examples
4.1. Example 1


| Gravity acceleration | g = 9.8 (m/s2) |
| Gravity acceleration vector | bg = |
| Mass of the object | mo |
| Mass of the link | mkl = 0.04 (kg) |
| Object half length | lo = 0.02 (m) |
| Finger link length | lkl = 0.03 (m) |
| Local curvature of the object | κok = 100 (1/m) |
| Local curvature of the finger | κfk = 200 (1/m) |
| Joint stiffness matrix | Sk = diag[1,1,1] (N∙m/rad) |
| Joint angles of the finger 1 | (q11, q12, q13) = (, , ) (rad) |
| Joint angles of the finger 2 | (q21, q22, q23) = (, , ) (rad) |
| Directions of the contact points | (θ1, θ2) = (, ) (rad) |
| Center of the object mass | |
| Local contact frames on the object | , |
| Frames of the finger | , , , |
| Finger base frames | , |
| Center of the link mass | |
| Contact force | f := = 10 (N) |
4.2. Example 2


4.3. Example 3


4.4. Example 4

4.5. Example 5

4.6. Example 6


5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Partial Derivatives of the Potential Energy of the Finger Link Mass
Appendix B. Partial Derivatives of the Contact Constraint
Appendix C. Wrench Vector and Stiffness Matrix of the Sliding Contact Case
Appendix D. Wrench Vector and Stiffness Matrix of the Rolling Contact Case
Appendix E. Partial Derivatives with Respect to the Object Mass in Example 1
Appendix F. Partial Derivatives with Respect to the Link Mass in Example 1
References
- Hanafusa, H.; Asada, H. Stable prehension by a robot hand with elastic fingers. In Robot Motion; MIT Press: Cambridge, MA, USA, 1982; pp. 323–335. [Google Scholar]
- Nguyen, V.D. Constructing stable grasps. Int. J. Robot. Res. 1988, 7, 3–16. [Google Scholar] [CrossRef]
- Li, J.; Kao, I. Grasp Stiffness Matrix-Fundamental Properties in Analysis of Grasping and Manipulation. In Proceedings of the IEEE/RSJ International Conference Intelligent Robots and Systems (IROS1995), Pittsburgh, PA, USA, 5–9 August 1995; Volume 2, pp. 381–386.
- Cutkosky, M.R.; Kao, I. Computing and Controlling the Compliance of a Robotic Hand. IEEE Trans. Robot. Autom. 1989, 5, 151–165. [Google Scholar] [CrossRef]
- Carbone, G. Stiffness Analysis for Grasping Tasks. Grasping Robot. Mech. Mach. Sci. 2013, 10, 17–55. [Google Scholar]
- Kim, B.; Yi, B.; Oh, S.; Suh, I.H. Task-based compliance planning for multi-fingered robotic manipulations. Adv. Robot. 2004, 18, 23–44. [Google Scholar] [CrossRef]
- Gabiccini, M.; Farnioli, E.; Bicchi, A. Grasp analysis tools for synergistic underactuated robotic hands. Int. J. Robot. Res. 2013, 32, 1553–1576. [Google Scholar] [CrossRef]
- Malvezzi, M.; Prattichizzo, D. Evaluation of Grasp Stiffness in Underactuated Compliant Hands. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA 2013), Karlsruhe, Germany, 6–10 May 2013; pp. 2074–2079.
- Shapiro, A.; Rimon, E.; Shoval, S. On the Passive Force Closure Set of Planar Grasps and Fixtures. Int. J. Robot. Res. 2010, 29, 1435–1454. [Google Scholar] [CrossRef]
- Montana, D.J. Contact Stability for Two-Fingered Grasps. IEEE Trans. Robot. Autom. 1992, 8, 421–430. [Google Scholar] [CrossRef]
- Xiong, C.; Li, Y.; Ding, H.; Xiong, Y. On the Dynamic Stability of Grasping. Int. J. Rob. Res. 1999, 18, 951–958. [Google Scholar] [CrossRef]
- Choi, K.K.; Jing, S.L.; Li, Z. Grasping with Elastic Finger Tips. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA1999), Detroit, MI, USA, 10–15 May 1999; pp. 920–925.
- Michalec, R.; Micaelli, A. Stiffness Modeling for Multi-Fingered Grasping with Rolling Contacts. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Nashville, TN, USA, 6–8 December 2010; pp. 601–608.
- Funahashi, Y.; Yamada, T.; Tate, M.; Suzuki, Y. Grasp Stability Analysis Considering the Curvatures at Contact Points. In Proceedings of the IEEE International Conference Robotics and Automation (ICRA1996), Minneapolis, MN, USA, 22–28 April 1996; pp. 3040–3046.
- Howard, W.S.; Kumar, V. Modeling and Analysis of the Compliance and Stability of Enveloping Grasps. In Proceedings of the IEEE International Conference Robotics and Automation (ICRA1995), Nagoya, Aichi, Japan, 21–27 May 1995; pp. 1367–1372.
- Howard, W.S.; Kumar, V. On the stability of Grasped Objects. IEEE Trans. Robot. Autom. 1996, 12, 904–917. [Google Scholar] [CrossRef]
- Lin, Q.; Burdick, J.; Rimon, E. Computation and Analysis of Natural Compliance in Fixturing and Grasping Arrangements. IEEE Trans. Robot. 2004, 20, 651–667. [Google Scholar] [CrossRef]
- Yamada, T.; Saha, S.K.; Mimura, N.; Funahashi, Y. Stability Analysis of Planar Grasp with 2D-Virtual Spring Model. J. Robot. Mech. 1999, 11, 274–281. [Google Scholar]
- Yamada, T.; Taki, T.; Yamada, M.; Funahashi, Y.; Yamamoto, H. Static Stability Analysis of Spatial Grasps Including Contact Surface Geometry. Adv. Robot. 2011, 25, 447–472. [Google Scholar] [CrossRef]
- Yamada, T.; Taki, T.; Yamada, M.; Yamamoto, H. Static Grasp Stability Analysis of Two Spatial Objects Including Contact Surface Geometry. Trans. Control Mech. Syst. 2012, 1, 218–228. [Google Scholar]
- Yamada, T.; Yamamoto, H. Grasp stability analysis of multiple objects including contact surface geometry in 3D. In Proceedings of the IEEE International Conference Mechatronics and Automation (ICMA2013), Takamatsu, Kagawa, Japan, 4–7 August 2013; pp. 36–43.
- Yamada, T.; Yamada, M.; Yamamoto, H. Static Stability Analysis of a Single Planar Object Grasped by a Multifingered Hand. J. Mech. Eng. Autom. 2012, 2, 606–627. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamada, T.; Johansson, R.; Robertsson, A.; Yamamoto, H. Static Stability Analysis of a Planar Object Grasped by Multifingers with Three Joints. Robotics 2015, 4, 464-491. https://doi.org/10.3390/robotics4040464
Yamada T, Johansson R, Robertsson A, Yamamoto H. Static Stability Analysis of a Planar Object Grasped by Multifingers with Three Joints. Robotics. 2015; 4(4):464-491. https://doi.org/10.3390/robotics4040464
Chicago/Turabian StyleYamada, Takayoshi, Rolf Johansson, Anders Robertsson, and Hidehiko Yamamoto. 2015. "Static Stability Analysis of a Planar Object Grasped by Multifingers with Three Joints" Robotics 4, no. 4: 464-491. https://doi.org/10.3390/robotics4040464