Vine-Inspired Continuum Tendril Robots and Circumnutations
Abstract
1. Introduction
2. Materials and Methods
2.1. Plant-Inspired Innovations
2.1.1. Plant-Inspired Environmental Contact Hardware
2.1.2. Plant-Inspired Motion Planning: Circumnutation
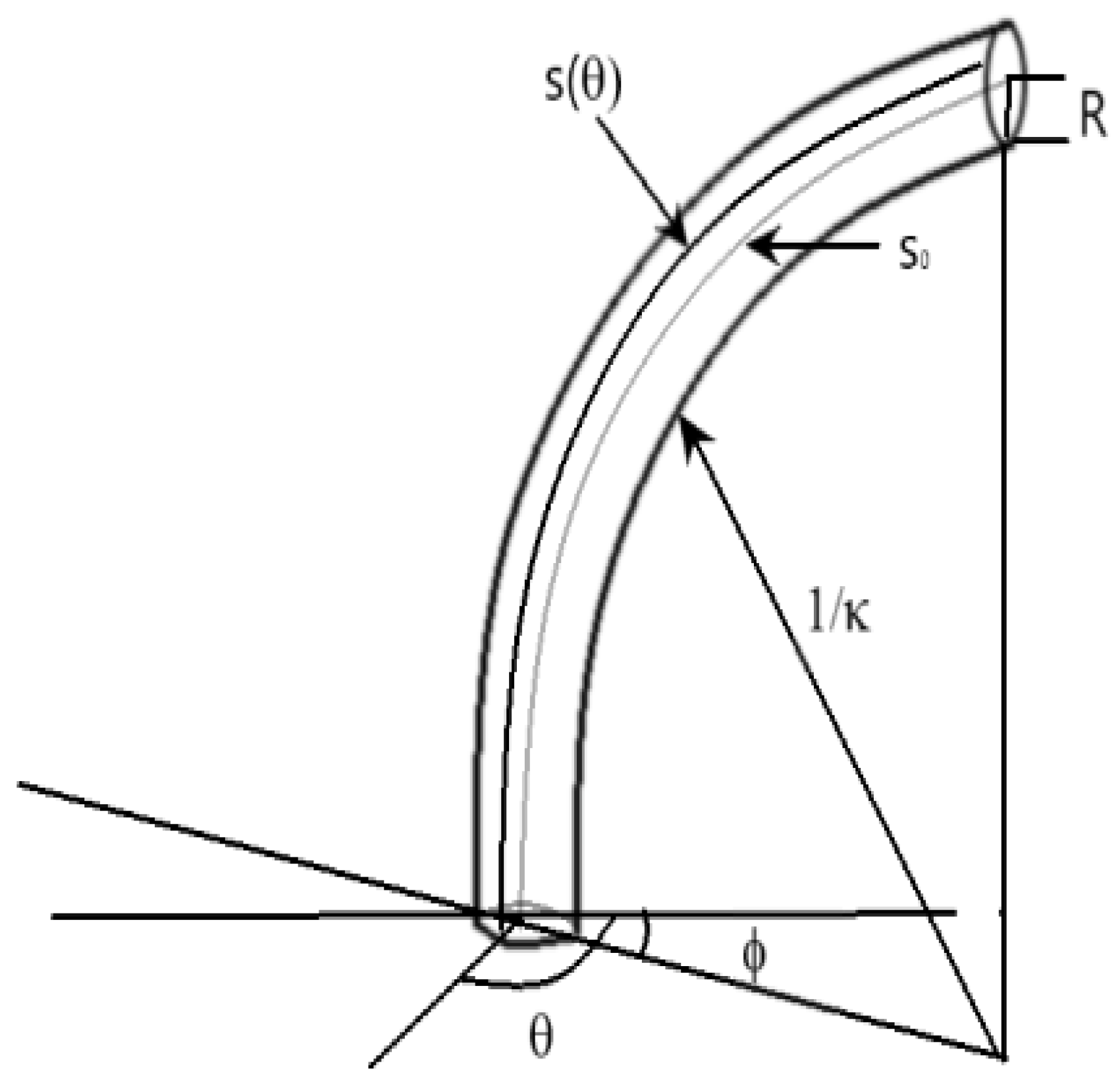
- the radius of the section is R, a constant value
- the backbone section considered has constant curvature with respect to s at any given time t
- the initial curvature of the section is
- the initial length along center line of the section is
- the initial orientation of maximum curvature is , with respect to a fixed coordinate frame fixed at the section base with the z-axis aligned with the section tangent at that point
3. Results
- The user chooses the motors and therefore sections to circumnutate, along with the number of motors included in the movement
- These values are then stored into an array
- (a)
- i.e., the distal section is controlled by Motors 6, 7, and 8, 3, and so on
- Wind the motors to maximum compression
- Unwind the first motor in each set by a predetermined length
- Enter a loop structure that is set to execute a predetermined number of times
- (a)
- Loop until all motors have unwound by a small amount (usually three)
- i
- Unwind the next motor in the sequence to a length greater than the previous one
- ii
- Go to 5-a until the condition is met
- (b)
- Increment the counter
- (c)
- Go to 4 unless the increment of the counter equals the max iterations
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| OD | outer diameter |
| ID | inner diameter |
| DC | direct current |
| PWM | pulse width modulated |
| RMS | root mean square |
References
- Trivedi, D.; Rahn, C.D.; Kier, W.M.; Walker, I.D. Soft Robotics: Biological Inspiration, State of the Art, and Future Research. Appl. Bionics Biomech. 2008, 5, 99–117. [Google Scholar] [CrossRef]
- Meyer, J.A.; Guillot, A. Biologically Inspired Robots. In Springer Handbook of Robotics; Springer-Verlag Berlin Heidelberg: Berlin, Germany, 2008; pp. 1395–1418. [Google Scholar]
- Walker, I.D. Continuous Backbone “Continuum” Robot Manipulators: A Review. ISRN Robot. 2013, 2013. [Google Scholar] [CrossRef]
- Robinson, G.; Davies, J. Continuum Robots—A State of the Art. In Proceedings of the IEEE International Conference on Robotics and Automation, Detroit, MI, USA, 10–15 May 1999; pp. 2849–2854. [Google Scholar]
- Burgner-Kars, J.; Rucker, D.; Choset, H. Continuum Robots for Medical Applications: A Survey. IEEE Trans. Robot. 2015, 31, 1261–1280. [Google Scholar] [CrossRef]
- Chitalia, Y.; Wang, X.; Desai, J.P. Design, Modeling and Control of a 2-DoF Robotic Guidewire. In Proceedings of the IEEE International Conference on Robotics and Automation, Brisbane, Australia, 21–25 May 2018; pp. 32–37. [Google Scholar]
- Liu, N.; Abdelaziz, M.E.M.K.; Shen, M.; Yang, G.Z. Design and Kinematics Characterization of a Laser-Profiled Continuum Manipulator for the Guidance of Bronchoscopic Instruments. In Proceedings of the IEEE International Conference on Robotics and Automation, Brisbane, Australia, 21–25 May 2018; pp. 25–31. [Google Scholar]
- Webster III, R.J.; Jones, B.A. Design and Kinematic Modeling of Constant Curvature Continuum Robots: A Review. Int. J. Robot. Res. 2010, 29, 1661–1683. [Google Scholar] [CrossRef]
- Walker, I.D. Robot Strings: Long, Thin Continuum Robots. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013; pp. 1–12. [Google Scholar]
- Mehling, J.; Diftler, M.; Chu, M.; Valvo, M. A Minimally Invasive Tendril Robot for In-Space Inspection. In Proceedings of the International Conference on BioRobotics, Pisa, Italy, 20–22 February 2006; pp. 690–695. [Google Scholar]
- Moravec, H. Mind Children: The Future of Robot and Human Intelligence; Harvard University Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Martone, P.; Boller, M.; Burgert, I.; Dumais, J.; Edwards, J.; Mach, K.; Rowe, N.; Rueggeberg, M.; Seidel, R.; Speck, T. Mechanics Without Muscle: Biomechanical Inspiration from the Plant World. Integr. Comp. Biol. 2010, 50, 888–907. [Google Scholar] [CrossRef] [PubMed]
- Wooten, M.; Walker, I. A Novel Vine-Like Robot for In-Orbit Inspection. In Proceedings of the 45th International Conference on Environmental Systems, Bellevue, WA, USA, 12–16 July 2015; pp. 1–11. [Google Scholar]
- Hawkes, E.W.; Blumenschein, L.H.; Greer, J.D.; Okamura, A.M. A soft robot that navigates its environment through growth. Sci. Robot. 2017. [Google Scholar] [CrossRef]
- Blumenschein, L.H.; Okamura, A.M.; Hawkes, E.W. Modeling of Bioinspired Apical Extension in a Soft Robot. In Conference on Biomimetic and Biohybrid Systems; Living Machines: Stanford, CA, USA, 2017; pp. 522–531. [Google Scholar]
- Mazzolai, B.; Beccai, L.; Mattoli, V. Plants as Model in Biomimetics and Biorobotics: New Perspectives. Front. Bioeng. Biotechnol. 2014, 2, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Sadeghi, A.; Tonazzini, A.; Popova, I.; Mazzolai, B. Robotic Mechanism for Soil Penetration Inspired by Plant Root. In Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3457–3462. [Google Scholar]
- Del Dottore, E.; Mondini, A.; Sadeghi, A.; Mattoli, V.; Mazzolai, B. Circumnutations as a penetration strategy in a plant-root-inspired robot. In Proceedings of the IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 16–21 May 2016; pp. 4722–4728. [Google Scholar]
- Del Dottore, E.; Sadeghi, A.; Mondini, A.; Mazzolai, B. Continuous growth in plant-inspired robots through 3D additive manufacturing. In Proceedings of the IEEE International Conference on Robotics and Automation, Brisbane, Australia, 21–25 May 2018; pp. 3454–3460. [Google Scholar]
- Greer, J.D.; Blumenschein, L.H.; Okamura, A.M.; Hawkes, E.W. Obstacle-Aided Navigation of a Soft Growing Robot. In Proceedings of the IEEE International Conference on Robotics and Automation, Brisbane, Australia, 21–25 May 2018; pp. 4165–4172. [Google Scholar]
- Goriely, A.; Neukirch, S. Mechanics of Climbing and Attachment in Twining Plants. Phys. Rev. Lett. 2006, 97, 184302. [Google Scholar] [CrossRef] [PubMed]
- Putz, F.; Mooney, H. The Biology of Vines; Cambridge University Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Darwin, C. The Movements and Habits of Climbing Plants; John Murray: London, UK, 1875. [Google Scholar]
- Isnard, S.; Silk, W. Moving with Climbing Plants from Charles Darwin’s Time into the 21st Century. Am. J. Bot. 2009, 96, 1205–1221. [Google Scholar] [CrossRef] [PubMed]
- Bastien, R.; Meroz, Y. The Kinematics of Plant Nutation Reveals a Simple Relation Between Curvature and the Orientation of Differential Growth. PLOS Comput. Biol. 2016, 12, e1005238. [Google Scholar] [CrossRef] [PubMed]
- Neumann, M.; Burgner-Kahrs, J. Considerations for Follow-The-Leader Motion of Extensible Tendon-driven Continuum Robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 16–21 May 2016; pp. 917–923. [Google Scholar]
- Wooten, M.B.; Walker, I.D. Circumnutation: From Plants to Robots. In From Animals to Animats 14, Proceedings of the 14th International Conference on Simulation of Adaptive Behavior, SAB 2016, Aberystwyth, UK, 23–26 August 2016; Tuci, E., Giagkos, A., Wilson, M., Hallam, J., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 1–11. [Google Scholar]
- Wooten, M.; Frazelle, C.; Walker, I.; Kapadia, A.; Lee, J. Exploration and Inspection with Vine-Inspired Continuum Robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Brisbane, Australia, 21–25 May 2018; pp. 5526–5533. [Google Scholar]
- Tonapi, M.; Godage, I.; Vijaykumar, A.; Walker, I. Spatial Kinematic Modeling of a Long and Thin Continuum Robotic Cable. In Proceedings of the IEEE International Conference on Robotics and Automation, Seattle, WA, USA, 26–30 May 2015; pp. 3755–3761. [Google Scholar]
- Jones, B.; Walker, I. Kinematics for Multisection Continuum Robots. IEEE Trans. Robot. 2006, 22, 43–57. [Google Scholar] [CrossRef]
- Li, J.; Teng, Z.; Xiao, J.; Kapadia, A.; Bartow, A.; Walker, I. Autonomous Continuum Grasping. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 4569–4576. [Google Scholar]
- Buckingham, R. Snake Arm Robots. Ind. Robot Int. J. 2002, 29, 242–245. [Google Scholar] [CrossRef]
- Truong-Thinh, N.; Ngoc-Phuong, N. Design and Development of a Continuum Structure for Robotic Flower. In Proceedings of the IEEE Conference on Robotics and Biomimetics, Phuket, Thailand, 7–11 December 2011; pp. 118–123. [Google Scholar]
- Book, W.; Le, S.; Sangveraphunsiri, V. The bracing strategy for robot operation. In Proceedings of the 5th Symposium on Theory and Practise of Robots and Manipulators, Udine, Italy, 26–29 June 1984; pp. 179–186. [Google Scholar]
- Bullock, I.; Ma, R.; Dollar, A. A hand-centric classification of human and robot dexterous manipulation. IEEE Trans. Haptics 2013, 6, 129–144. [Google Scholar] [CrossRef] [PubMed]
- Hollis, R.; Hammer, R. Real and virtual coarse-fine robot bracing strategies for precision assembly. In Proceedings of the IEEE International Conference on Robotics and Automation, Nice, France, 12–14 May 1992; pp. 767–774. [Google Scholar]
- Brown, A. Circumnutations: From Darwin to Space Flights. Plant Physiol. 1993, 101, 345–348. [Google Scholar] [CrossRef] [PubMed]
- Niklas, K.J.; Spatz, H.C. Plant Physics; University of Chicago Press: Chicago, IL, USA, 2012. [Google Scholar]
- MathWorks. MATLAB, 2017. Available online: www.mathworks.com (accessed on 18 September 2018).
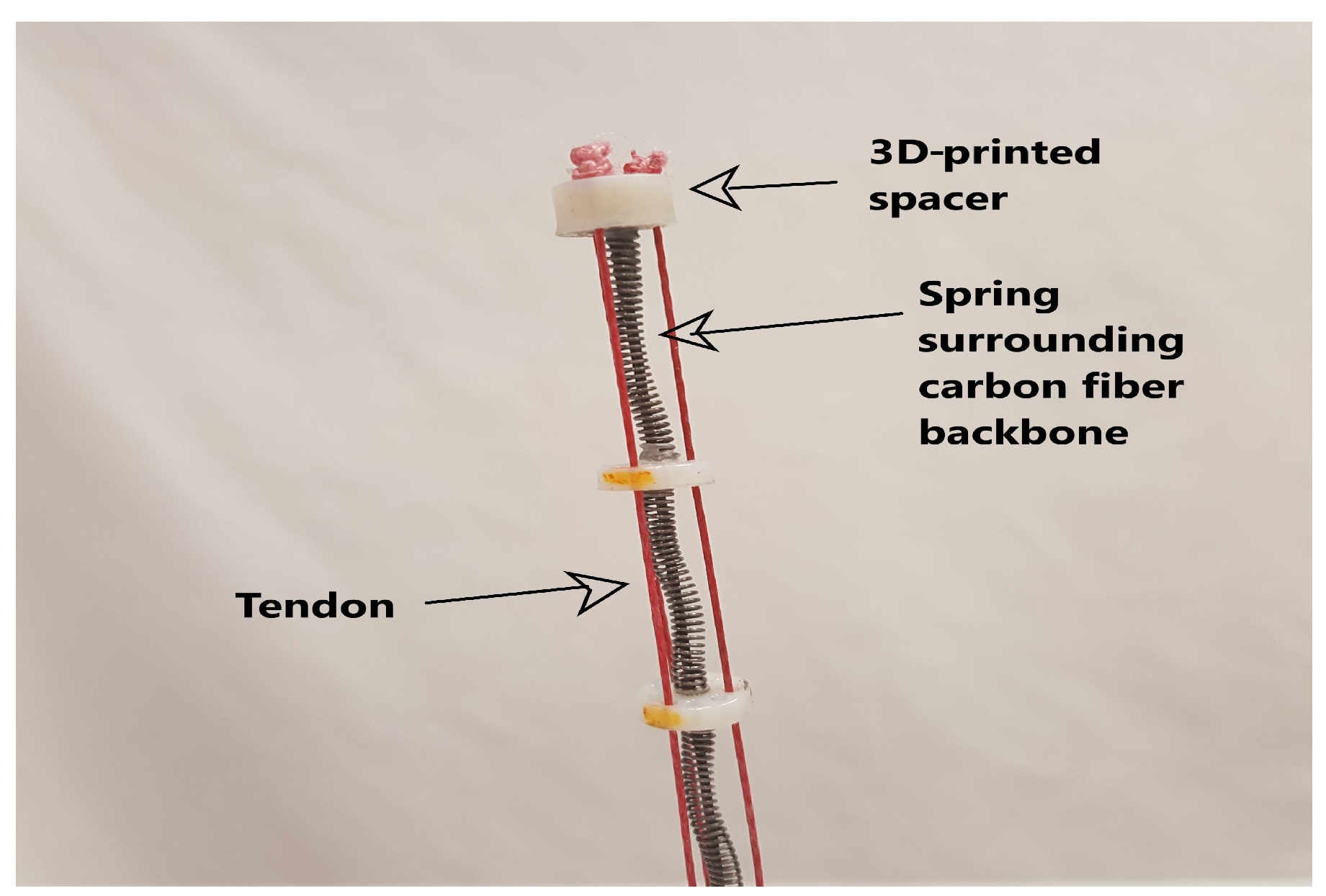






| Section | Maximal Length (mm) | Minimal. Length (mm) | Tube OD (mm) | Tube ID (mm) |
|---|---|---|---|---|
| Base | 616 | N/A | 2.5 | 1.5 |
| Middle | 502 | 290 | 1.5 | 0.7 |
| Tip | 208 | 98 | 0.7 | 0.3 |
| Section | Spring Length (mm) | Spring Rate (N/mm) | Spacer Diameter (mm) | Spacer Count |
|---|---|---|---|---|
| Base | N/A | N/A | 14.0 | 13 |
| Middle | 38.1 | 0.175 | 8.0 | 13 |
| Tip | 25.2 | 0.403 | 7.5 | 8 |
| Motor 6 Tendon (mm) | Motor 7 Tendon (mm) | Motor 8 Tendon (mm) |
|---|---|---|
| 0 | 0 | 0 |
| 5.1 | 0 | 0 |
| 0 | 10.2 | 0 |
| 0 | 0 | 15.3 |
| 15.3 | 0 | 0 |
| 0 | 15.3 | 0 |
| 0 | 0 | 15.3 |
| 15.3 | 0 | 0 |
| Sample Number | X Value (mm) | Y Value (mm) | Z Value (mm) |
|---|---|---|---|
| 1 | −4 | 18 | 92 |
| 2 | −8 | 15 | 91 |
| 3 | −12 | 10 | 92 |
| 4 | −19 | 6 | 93 |
| 5 | −22 | 2 | 89 |
| 6 | −23 | 0 | 89 |
| 7 | −18 | −7 | 90 |
| 8 | −10 | −12 | 94 |
| 9 | −5 | −14 | 97 |
| 10 | 2 | −15 | 98 |
| 11 | 8 | −15 | 95 |
| 12 | 12 | −15 | 98 |
| 13 | 12 | −15 | 96 |
| 14 | 12 | −15 | 96 |
| 15 | 12 | −15 | 96 |
| 16 | 12 | −15 | 96 |
| 17 | 13 | −8 | 98 |
| 18 | 12 | 0 | 100 |
| 19 | 12 | 8 | 100 |
| 20 | 12 | 12 | 100 |
| 21 | 12 | 15 | 99 |
| 22 | 12 | 19 | 99 |
| 23 | 12 | 19 | 99 |
| 24 | 12 | 19 | 99 |
| 25 | 12 | 19 | 99 |
| 26 | 8 | 15 | 104 |
| 27 | 3 | 13 | 106 |
| 28 | −3 | 12 | 108 |
| 29 | −8 | 10 | 110 |
| 30 | −13 | 9 | 110 |
| 31 | −19 | 6 | 109 |
| 32 | −20 | 6 | 108 |
| 33 | −20 | 6 | 108 |
| 34 | −20 | 6 | 108 |
| 35 | −19 | 2 | 110 |
| 36 | −16 | −3 | 111 |
| 37 | −11 | −8 | 112 |
| 38 | −8 | −12 | 113 |
| 39 | −1 | −14 | 113 |
| 40 | 3 | −17 | 113 |
| 41 | 9 | −18 | 112 |
| 42 | 9 | −18 | 111 |
| 43 | 9 | −18 | 111 |
| 44 | 9 | −10 | 116 |
| 45 | 9 | 0 | 118 |
| 46 | 11 | 6 | 119 |
| 47 | 12 | 11 | 118 |
| 48 | 12 | 14 | 118 |
| 49 | 12 | 14 | 118 |
| 50 | 12 | 14 | 118 |
| 51 | 12 | 14 | 118 |
| 52 | 12 | 14 | 118 |
| 53 | 9 | 12 | 120 |
| 54 | 1 | 10 | 122 |
| 55 | −5 | 9 | 124 |
| RMS of X (mm) | RMS of Y (mm) | RMS of Z (mm) |
|---|---|---|
| 23 | 8 | 92 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wooten, M.B.; Walker, I.D. Vine-Inspired Continuum Tendril Robots and Circumnutations. Robotics 2018, 7, 58. https://doi.org/10.3390/robotics7030058
Wooten MB, Walker ID. Vine-Inspired Continuum Tendril Robots and Circumnutations. Robotics. 2018; 7(3):58. https://doi.org/10.3390/robotics7030058
Chicago/Turabian StyleWooten, Michael B., and Ian D. Walker. 2018. "Vine-Inspired Continuum Tendril Robots and Circumnutations" Robotics 7, no. 3: 58. https://doi.org/10.3390/robotics7030058
APA StyleWooten, M. B., & Walker, I. D. (2018). Vine-Inspired Continuum Tendril Robots and Circumnutations. Robotics, 7(3), 58. https://doi.org/10.3390/robotics7030058





