Sparse in the Time Stabilization of a Bicycle Robot Model: Strategies for Event- and Self-Triggered Control Approaches
Abstract
:1. Introduction
2. Mathematical Model of the Considered 2DoF Bicycle Robot Model
3. Considered Control Strategies
3.1. Introduction
3.2. Preliminaries—Standard LQR Control
3.3. The Event-Triggered Control Approach
3.4. The Self-Triggered Control Approach
3.5. The Improved Self-Triggered Control Approach
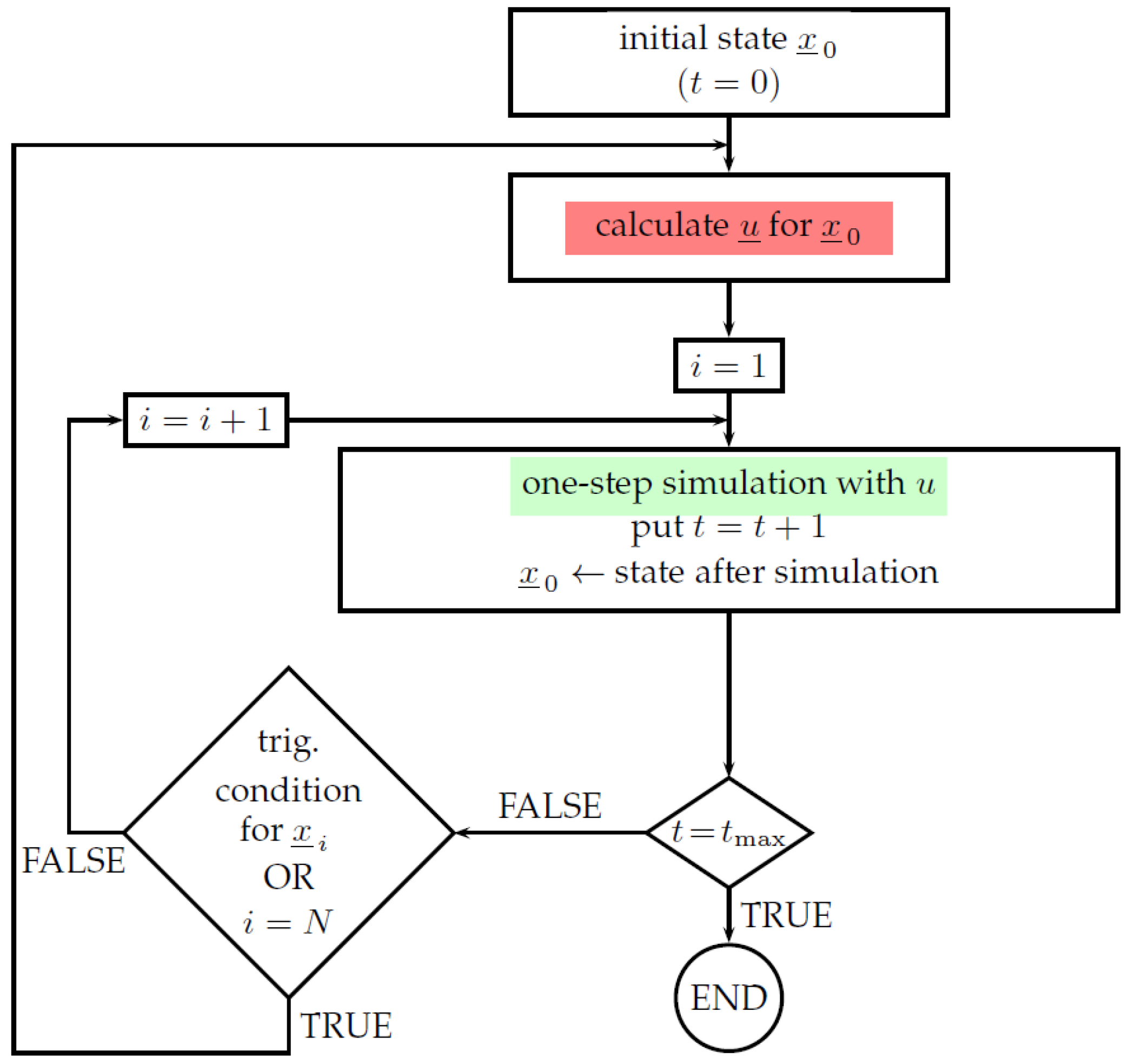
4. Simulation Study
- standard LQR control, where the following weighting matrices have been taken: , , and the control signal is updated at every step with sampling period ,
- event-triggered control, where it is assumed that the control update should be made no less than every 10 sampling periods, which forms an additional triggering condition, , and
- self-triggered control/improved-self triggered control based on prediction from the linearized model, where it is also assumed that control update should be made no less than every 10 sampling periods, .
5. Summary and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Clayton, N. A Short History of the Bicycle; Amberley: Gloucestershire, UK, 2016. [Google Scholar]
- Hadland, T.; Lessing, H.E.; Clayton, N.; Sanderson, G.W. Bicycle Design: An Illustrated History; The MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Herlihy, D.V. Bicycle: The History; Yale University Press: New Haven, CT, USA, 2004. [Google Scholar]
- Tehrani, E.S.; Khorasani, K.; Tafazoli, S. Dynamic neural network-based estimator for fault diagnosis in reaction wheel actuator of satellite attitude control system. In Proceedings of the International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005; pp. 2347–2352. [Google Scholar]
- Halliday, D.; Recnick, R.; Walker, J. Fundamentals of Physics Extended, 10th ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Acosta, V.; Cowan, C.L.; Graham, B.J. Essentials of Modern Physics; Harper & Row: New York, NY, USA, 1973. [Google Scholar]
- Norwood, J. Twentieth Century Physics; Prentice-Hall: Upper Saddle River, NJ, USA, 1976. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Bapiraju, B.; Srinivas, K.N.; Prem, P.; Behera, L. On balancing control strategies for a reaction wheel pendulum. In Proceedings of the IEEE INDICON, Khangapur, India, 20–24 December 2004; pp. 199–204. [Google Scholar]
- Gao, Q. Universal Fuzzy Controllers for Non-Affine Nonlinear Systems; Springer: Singapore, 2017. [Google Scholar]
- Fahimi, F. Autonomous Robots: Modeling, Path Planning, and Control; Springer: Berlin, Germany, 2008. [Google Scholar]
- Maciejowski, J.M. Predictive Control with Constraints; Prentice Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Miller, W.T., III; Sutton, R.S.; Werbos, P.J. Neural Networks for Control; MIT Press: Cambridge, UK, 1995. [Google Scholar]
- Carpenter, S. Lit Motors Hopes Its C-1 Becomes New Personal Transportation Option. Available online: http://www.latimes.com/business/autos/la-fi-motorcycle-car-20120526,0,4147294.story (accessed on 16 June 2012).
- Cameron, K. Honda Shows Self-Balancing but Non-Gyro Bike. Available online: https://www.cycleworld.com/honda-self-balancing-motorcycle-rider-assist-technology (accessed on 6 January 2017).
- Horla, D.; Owczarkowski, A. Robust LQR with actuator failure control strategies for 4DOF model of unmanned bicycle robot stabilised by inertial wheel. In Proceedings of the 15th International Conference IESM, Seville, Spain, 21–23 October 2015; pp. 998–1003. [Google Scholar]
- Owczarkowski, A.; Horla, D. A Comparison of Control Strategies for 4DoF Model of Unmanned Bicycle Robot Stabilised by Inertial Wheel. In Progress in Automation, Robotics and Measuring Techniques, Advances in Intelligent Systems and Computing; Roman, S., Ed.; Springer: Basel, Switzerland, 2015; pp. 211–221. [Google Scholar]
- Owczarkowski, A.; Horla, D. Robust LQR and LQI control with actuator failure of 2DoF unmanned bicycle robot stabilized by inertial wheel. Int. J. Appl. Math. Comput.Sci. 2016, 26, 325–334. [Google Scholar] [CrossRef]
- Zietkiewicz, J.; Horla, D.; Owczarkowski, A. Robust Actuator Fault-Tollerant LQR Control of Unmanned Bicycle Robot. A Feedback Linearization Approach; Challenges in Automation, Robotics and Measurement Techniqies; Szewczyk, R., Zieliński, C., Kaliczynska, M., Eds.; Springer: Berlin, Germany, 2016; pp. 411–421. [Google Scholar]
- Zietkiewicz, J.; Owczarkowski, A.; Horla, D. Performance of Feedback Linearization Based Control of Bicycle Robot in Consideration of Model Inaccuracy; Challenges in Automation, Robotics and Measurement Techniqies; Szewczyk, R., Zieliński, C., Kaliczynska, M., Eds.; Springer: Berlin, Germany, 2016; pp. 399–410. [Google Scholar]
- Horla, D.; Zietkiewicz, J.; Owczarkowski, A. Analysis of Feedback vs. Jacobian Linearization Approaches Applied to Robust LQR Control of 2DoF Bicycle Robot Model. In Proceedings of the 17th International Conference on Mechatronics, Prague, Czech Republic, 7–9 December 2016; pp. 285–290. [Google Scholar]
- Owczarkowski, A.; Horla, D.; Zietkiewicz, J. Introduction of feedback linearization to robust LQR and LQI control—Analysis of results from an unmanned bicycle robot with reaction wheel. Asian J. Control 2019, 21, 1–13. [Google Scholar] [CrossRef]
- Muehlebach, M.; D’Andrea, R. Nonlinear analysis and control of a reaction-wheel-based 3-D inverted pendulum. IEEE Trans. Control Syst. Technol. 2016, 25, 235–246. [Google Scholar] [CrossRef]
- Åström, K.J.; Klein, R.E.; Lennartsson, A. Bicycle dynamics and control: Adapted bicycles for education and research. IEEE Control Syst. 2005, 25, 26–47. [Google Scholar]
- Åström, K.J.; Block, D.J.; Spong, M.W. The Reaction Wheel Pendulum; Morgan & Claypool: San Rafael, CA, USA, 2007. [Google Scholar]
- Kwakernaak, H.; Sivan, R. Linear Optimal Control Systems; Wiley-Interscience: Hoboken, NJ, USA, 1972. [Google Scholar]
- Heemels, W.P.M.H.; Donkers, M.C.F.; Teel, A.R. Periodic Event-Triggered Control for Linear Systems. IEEE Trans. Autom. Control 2013, 58, 847–861. [Google Scholar] [CrossRef]
- Liu, T.; Jiang, Z.-P. Event-based control of nonlinear systems with partial state and output feedback. Automatica 2015, 53, 10–22. [Google Scholar] [CrossRef]
- Heemels, W.P.M.H.; Johansson, K.H.; Tabuda, P. An Introduction to Event-triggered and Self-triggered Control. In Proceedings of the 51st IEEE Conference on Decision and Control, Maui, HI, USA, 10–13 December 2012. [Google Scholar]
- Barradas Berglind, J.D.J.; Gommans, T.M.P.; Heemels, W.P.M.H. Self-triggered MPC for constrained linear systems and quadratic costs. In Proceedings of the 4th IFAC Nonlinear Model Predictive Control Conference, Noordwijkerhout, The Netherlands, 23–27 August 2012. [Google Scholar]
- Gommans, T.; Antunes, D.; Donkers, T.; Tabuda, P.; Heemels, M. Self-triggered linear quadratic control. Automatica 2014, 50, 1279–1287. [Google Scholar] [CrossRef]
- Wang, W.; Li, H.; Yan, W.; Shi, Y. Self-Triggered Distributed Model Predictive Control of Nonholonomic Systems. In Proceedings of the 11th Asian Control Conference, Gold Coast, Australia, 17–20 December 2017. [Google Scholar]
- Heshmati-Alamdari, S.; Eqtami, A.; Karras, G.C.; Dimarogonas, D.V.; Kyriakopoulos, K.J. A self-triggered visual servoing model predictive control scheme for under-actuated underwater robotic vehicles. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation ICRA, Hong Kong, China, 31 May–5 June 2014; pp. 3826–3831. [Google Scholar]
- Durand, D.; Castellanos, F.G.; Marchand, N.; Sánchez, W.F.G. Event-Based Control of the Inverted Pendulum: Swing up and Stabilization. J. Control Eng. Appl. Inform. SRAIT 2013, 15, 96–104. [Google Scholar]
- Hashimoto, K.; Adachi, A.; Dimarogonas, D.V. Self-Triggered Model Predictive Control for Nonlinear Input-Affine Dynamical Systems via Adaptive Control Samples Selection. IEEE Trans. Autom. Control 2017, 62, 177–189. [Google Scholar] [CrossRef] [Green Version]
- Brunner, F.D.; Heemels, W.P.M.H. Robust Self-Triggered MPC for Constrained Linear Systems. In Proceedings of the European Control Conference, Strasbourg, France, 24–26 June 2014. [Google Scholar]







| Symbol | Meaning |
|---|---|
| state vector | |
| vertical deflection angle of the robot | |
| angular velocity of the robot | |
| angle of rotation of the reaction wheel | |
| angular velocity of the reaction wheel | |
| control signal (current of the motor) | |
| weight of the robot | |
| moment of inertia of the reaction wheel | |
| moment of inertia of the rotor of the motor | |
| moment of inertia of the robot (rel. to the ground) | |
| distance between the ground and the center of mass of the robot | |
| gravity force | |
| constant of the motor | |
| friction coefficient in rotational movement | |
| friction coefficient in the rotation of the reaction wheel | |
| , | contact points of the wheels with the ground |
| center of the rear wheel | |
| center of the front wheel | |
| LQR | linear-quadratic regulator |
| ETC | event-triggered control |
| STC | self-triggered control |
| ISTC | improved self-triggered control |
| Parameter | Value | Description |
|---|---|---|
| weight of the robot | ||
| moment of inertia (MOI) of the reaction wheel | ||
| MOI of the rotor | ||
| MOI of the robot related to the ground | ||
| distance from the ground to the center of mass | ||
| g | gravity constant | |
| motor constant | ||
| friction coefficient in the robot rotation | ||
| friction coefficient of the reaction wheel |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zietkiewicz, J.; Horla, D.; Owczarkowski, A. Sparse in the Time Stabilization of a Bicycle Robot Model: Strategies for Event- and Self-Triggered Control Approaches. Robotics 2018, 7, 77. https://doi.org/10.3390/robotics7040077
Zietkiewicz J, Horla D, Owczarkowski A. Sparse in the Time Stabilization of a Bicycle Robot Model: Strategies for Event- and Self-Triggered Control Approaches. Robotics. 2018; 7(4):77. https://doi.org/10.3390/robotics7040077
Chicago/Turabian StyleZietkiewicz, Joanna, Dariusz Horla, and Adam Owczarkowski. 2018. "Sparse in the Time Stabilization of a Bicycle Robot Model: Strategies for Event- and Self-Triggered Control Approaches" Robotics 7, no. 4: 77. https://doi.org/10.3390/robotics7040077
APA StyleZietkiewicz, J., Horla, D., & Owczarkowski, A. (2018). Sparse in the Time Stabilization of a Bicycle Robot Model: Strategies for Event- and Self-Triggered Control Approaches. Robotics, 7(4), 77. https://doi.org/10.3390/robotics7040077







