Simulation Assessment of the Performance of a Redundant SCARA
Abstract
:1. Introduction
2. Robot Design and Basic Characteristics
3. Kinematic and Dynamic Characterisation of Robot Performance
3.1. Kinematic and Dynamic Characterisation of Robot Performance
3.2. Dynamic Performance for a Specific Task
- (a)
- quick motion from a given position A and a given joint configuration to a new position B to be reached with the most convenient joint configuration ;
- (b)
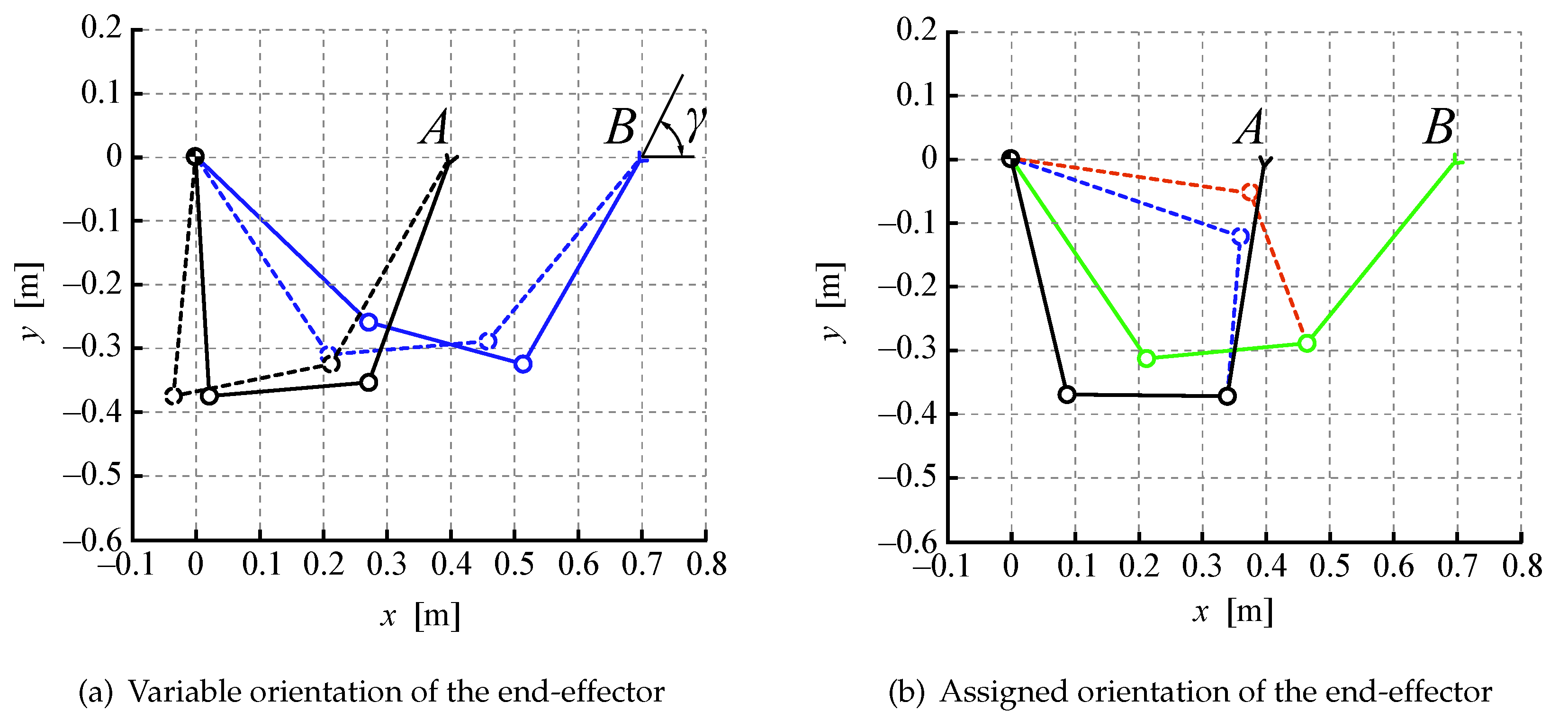
- repeated motion cycles between two fixed positions A and B to be performed with optimal joint configurations and (Figure 9);
- (c)
- repeated motion cycles between two positions to be performed with optimal joint configurations, where the initial (and/or final) position could be given by different locations on a moving conveyor, and the final (and/or initial) position could be a random location in a pallet.
- the robot is initially at the home position , with a corresponding joint configuration and assigned joint velocity ;
- a point appears in area A with assigned position and assigned velocity (position and velocity may change at each cycle);
- the robot starts moving to reach the moving set points;
- when the set point is reached (point ), it is tracked while performing the requested task (grasping, releasing or other) until point is reached;
- a point appears in area B with assigned position and assigned velocity;
- the robot starts moving to reach the moving set points;
- when the set point is reached (point ), it is tracked while performing the requested task (grasping, releasing, or other), which ends in ;
- the cycle is repeated from step 2.
- at the time , the robot is in point A and a set point appears in coordinate , so the algorithm discussed in the previous section is executed to find the best configuration to reach assuming null velocity at the end and the corresponding value of the joint coordinates and this value is assumed as reference position for the joint motion.
- while the robot is moving toward , its coordinates change at each instant of time. Data are updated at regular time interval of duration . Consequently, at each time t, the reference value for the joint coordinates is updated as to assure smooth motion during the tracking of the object. is the Moore–Penrose pseudoinverse of the Jacobian matrix [20], which, in the case of the traditional SCARA, coincides with the inverse of , whereas it is a matrix for the redundant manipulator.
- the value for the joint coordinates, velocity and acceleration are evaluated by processing with the mentioned nonlinear filter.
- at the time the moving point is reached with a sufficient precision and the next activity is started (moving z axis, object manipulation, ...) while the position is continuously tracked.
- at the time the activity is terminated and the robot starts moving to the new moving points appeared in area A using the same procedure used to reach point B (initial evaluation of and its iterative updating)
- the moving point A is reached at time and the manipulating tasks are performed until the time while continuing to track the moving point
- operations are cyclically repeated as above.
4. Main Simulation Results
- (a)
- The comparison between velocity ellipses of SCARA-Trad and SCARA-Red has shown better kinematic behaviour of the redundant SCARA with respect to the conventional one in terms of higher gripper velocity and with the possibility to use the redundancy to improve its performance.
- (b)
- The redundant robot has shown a better behaviour even for Cartesian accelerations, but the difference decreases when the end-effector moves towards the border of the workspace. Some tests have also shown that Coriolis and Centrifugal terms have a heavier weight for the redundant robot than for the conventional SCARA
- (c)
- Robots’ motion is characterized by high speed cycles which do not allow for obtain high velocities; in fact, they are significantly lower than the maximum velocities that the robots can reach. Trapezoidal velocity profiles degenerate in triangular profiles, showing the importance of acceleration abilities with respect to velocity performance. Joint accelerations of the redundant robot, obtained at nominal torque of the motors, has proved to be quite small if compared with joint accelerations of the conventional SCARA, not allowing a full exploitation of the redundant SCARA performances. A better dimensioning of the speed reducers and of the motors can be dealt with in order to improve the redundant robot performance.
- (d)
- Research about the vertical motion and the rotation of the end-effector has shown some limitations given by motors and speed reducers responsible of such motion. In fact, rated torques associated with such motors are small and they do not allow joint axes to reach high velocities.
- (e)
- The load at the end-effector has a significant influence on robots’ dynamics. The acceleration used in the planning algorithms could be increased according to the load applied at the end-effector.
- (f)
- Five layouts have been considered as actual work-cells for the definition of tasks. Referring to rated torque values, robots have shown a comparable behaviour in terms of cycle times for different tasks. Therefore, the optimization of the planning algorithm is vital in order to improve the performance of the redundant SCARA. In any case, the redundant robot is better than the conventional robot for specific movements.
- (g)
- Simulation results are highly dependent on construction parameters, e.g., mass distribution, speed ratios and performance of motors. Therefore, a different mechanical design could lead to different conclusions. Moreover, it is possible that one of the two architectures performs better in a task, whereas the other performs better in another.
- (h)
- Velocity capabilities of the manipulators deeply depend on the position within the working space.
- (i)
- Accelerations depend on dynamic parameters of the manipulator and are limited by the available motor torques. It results that, if a single threshold value for the acceleration is selected for each motor, it is necessary to choose a “limited” value that could be “guaranteed” in any situation. Both the limit of the maximum instantaneous torque (intermittent field) and the root mean square (RMS) rate torque (continuous field) have been considered.
- (j)
- In standard cycles between fixed points, the redundant SCARA manipulator performs much better than the classical one reducing the time in a range between and ( in average). These results are obtained with the “guaranteed” accelerations.
- (k)
- In standard cycles with moving points (the five layouts considered), the superiority of the redundant manipulator is less evident and in one case the traditional SCARA performs better. On average, the redundant manipulator performances are better by about .
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Makino, H. Assembly Robot. U.S. Patent 434,150,207, 27 July 1982. [Google Scholar]
- Clavel, R. Conception d’un robot parallèle rapide à 4 degrés de liberté. Ph.D Thesis, EPFL (Ecole Polytechnique Fédérale de Lausanne), Lausanne, Switzerland, 1991. [Google Scholar]
- Tosi, D.; Legnani, G.; Pedrocchi, N.; Righettini, P.; Giberti, H. Cheope: A new reconfigurable redundant manipulator. Mech. Mach. Theory 2010, 45, 611–626. [Google Scholar] [CrossRef]
- Carricato, M. Fully Isotropic Four-Degrees-of-Freedom Parallel Mechanisms for Schoenflies Motion. Int. J. Robot. Res. 2005, 24, 397–414. [Google Scholar] [CrossRef]
- Altuzarra, O.; Şandru, B.; Pinto, C.; Petuya, V. A symmetric parallel Schönflies-motion manipulator for pick-and-place operations. Robotica 2011, 29, 853–862. [Google Scholar] [CrossRef]
- Xie, F.; Liu, X. Design and Development of a High-Speed and High-Rotation Robot With Four Identical Arms and a Single Platform. ASME J. Mech. Robot. 2015, 7, 041015. [Google Scholar] [CrossRef]
- Reiter, A.; Müller, A.; Gattringer, H. Inverse kinematics in minimum-time trajectory planning for kinematically redundant manipulators. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 6873–6878. [Google Scholar]
- Urrea, C.; Mun˜oz, R. Joints Position Estimation of a Redundant Scara Robot by Means of the Unscented Kalman Filter and Inertial Sensors. Asian J. Control 2016, 18, 481–493. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, V.; Gaidhane, P.J. Optimal Design of Fuzzy Fractional Order PIλDμ Controller for Redundant Robot. Procedia Comput. Sci. 2018, 125, 442–448. [Google Scholar] [CrossRef]
- Risse, W.; Hiller, M. Dextrous motion control of a redundant SCARA robot. In Proceedings of the 24th Annual Conference of the IEEE Industrial Electronics Society (IECON ’98), Aachen, Germany, 31 August–4 September 1998; Cat. No. 98CH36200. Volume 4, pp. 2446–2451. [Google Scholar]
- Boscariol, P.; Richiedei, D. Trajectory Design for Energy Savings in Redundant Robotic Cells. Robotics 2019, 8, 15. [Google Scholar] [CrossRef]
- Bowling, A.; Khatib, O. Modular Decomposition for Optimal Dynamic Design of Redundant Macro/Mini Manipulators; Springer: Dordrecht, Netherlands, 1996; pp. 29–38. [Google Scholar]
- Callegari, M.; Palmieri, G.; Palpacelli, M.C.; Bussola, R.; Legnani, G. Performance Analysis of a High-Speed Redundant Robot. In Proceedings of the MESA 2018—14th ASME/IEEE International Conference on Mechatronic & Embedded Systems & Applications, Oulu, Finland, 2–4 July 2018; pp. 6873–6878. [Google Scholar]
- Yoshikawa, T. Manipulability of Robotic Mechanisms. Int. J. Robot. Res. 1985, 4, 3–9. [Google Scholar] [CrossRef]
- Yoshikawa, T. Dynamic manipulability of robot manipulators. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; Volume 2, pp. 1033–1038. [Google Scholar]
- Kim, J.-O.; Khosla, K. Dexterity measures for design and control of manipulators. In Proceedings of the IROS ’91:IEEE/RSJ International Workshop on Intelligent Robots and Systems ’91, Osaka, Japan, 3–5 November 1991; Volume 2, pp. 758–763. [Google Scholar]
- Patel, S.; Sobh, T. Manipulator Performance Measures—A Comprehensive Literature Survey. J. Intell. Robot. Syst. 2015, 77, 547–570. [Google Scholar] [CrossRef]
- Zanasi, R.; Bianco, C.L.; Tonielli, A. Nonlinear filters for the generation of smooth trajectories. Automatica 2000, 36, 439–448. [Google Scholar] [CrossRef]
- Gerelli, O.; Bianco, C.G.L. A discrete-time filter for the online generation of trajectories with bounded velocity, acceleration, and jerk. In Proceedings of the ICRA 2010—IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 3989–3994. [Google Scholar]
- Ben-Israel, A.; Greville, T. Generalized Inverses: Theory and Applications; Springer: New York, NY, USA, 2003. [Google Scholar]














| Axis Motor | Gear Ratios | Mass (kg) | Inertia (kgm) | |||||
|---|---|---|---|---|---|---|---|---|
| SCARA-Trad | joint 1 | 9.5 | 19 | 5000 | 30 | 12 | 0.58 | |
| joint 2 | (at 2000 rpm) | (at 2000 rpm) | 20 | 4.8 | 0.21 | |||
| SCARA-Red | joint 1 | 9.5 (at 2000 rpm) | 19 (at 2000 rpm) | 5000 | 30 | 11 | 0.34 | |
| joint 2 | 15 | 6.8 | 0.15 | |||||
| joint 3 | 15 | 4.4 | 0.15 | |||||
| end effector | spin | 1.59 | 3.18 | 6000 | 15 | – | – | – |
| z-axis | (at 3000 rpm) | (at 3000 rpm) | 40 mm/turn | – | – | – | ||
| Cycle # | Length [m] | ||||
|---|---|---|---|---|---|
| 1 T | A1 | B1 | 1.400 | 0.899 | 10% |
| 2 T | A2 | B2 | 1.200 | 0.741 | 26% |
| 3 T | A3 | B3 | 0.800 | 0.848 | 15% |
| 4 R | A4 | B4 | 0.300 | 0.809 | 19% |
| 5 D | A5 | B5 | 0.721 | 0.719 | 28% |
| 6 T | A6 | B6 | 0.600 | 0.639 | 36% |
| 7 R | A7 | B7 | 0.600 | 0.973 | 3% |
| 8 R | A8 | B8 | 0.300 | 0.948 | 5% |
| 9 D | A9 | B9 | 0.361 | 0.858 | 14% |
| 10 D | A10 | B10 | 0.361 | 0.723 | 28% |
| 11 T | A11 | B11 | 0.300 | 0.631 | 37% |
| R = radial direction | maximum | 0.973 | 3% | ||
| D = diagonal direction | minimum | 0.631 | 37% | ||
| T = tangential direction | average | 0.799 | 20% | ||
| Layout | Optimized Acceleration | Guaranteed Acceleration | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 | ||||||||
| 5 | ||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bussola, R.; Legnani, G.; Callegari, M.; Palmieri, G.; Palpacelli, M.-C. Simulation Assessment of the Performance of a Redundant SCARA. Robotics 2019, 8, 45. https://doi.org/10.3390/robotics8020045
Bussola R, Legnani G, Callegari M, Palmieri G, Palpacelli M-C. Simulation Assessment of the Performance of a Redundant SCARA. Robotics. 2019; 8(2):45. https://doi.org/10.3390/robotics8020045
Chicago/Turabian StyleBussola, Roberto, Giovanni Legnani, Massimo Callegari, Giacomo Palmieri, and Matteo-Claudio Palpacelli. 2019. "Simulation Assessment of the Performance of a Redundant SCARA" Robotics 8, no. 2: 45. https://doi.org/10.3390/robotics8020045
APA StyleBussola, R., Legnani, G., Callegari, M., Palmieri, G., & Palpacelli, M.-C. (2019). Simulation Assessment of the Performance of a Redundant SCARA. Robotics, 8(2), 45. https://doi.org/10.3390/robotics8020045








