The omnidirectional movement based on wheels can be achieved with conventional wheels with a rotational mechanism to change the wheels’ orientation, or with omnidirectional wheels [
18]. The working principle of an omnidirectional wheel is based on providing traction in the direction normal to the motor axis and using inner passive wheels or rollers that are free to rotate and slide in the direction of the motor axis. The inner passive wheels or rollers are placed along the periphery of the main wheel, allowing the spin of the main wheel and allowing perpendicular wheel displacements and direct displacement in any direction [
19,
20]. Indiveri et al. [
21] classified the omnidirectional wheels as Swedish or Mecanum according to the orientation of the passive rollers, which is defined by the angle (γ) between the rolling direction of the passive wheels and the main wheel hub axis direction (typical values are γ = 45° for Mecanum and γ = 0° for Swedish wheels). Moreno et al. [
22] classified them according to their implementation: free-rotation inner passive wheels, overlapping passive rollers (also called Mecanum), alternated passive rollers, or double parallel passive rollers. Moreno et al. [
22] also summarized the motion system of an omnidirectional mobile robot depending on the element in contact with the ground: wheels, tracks, ball-shaped wheels or legs.
The main advantage of an omnidirectional motion system applied in a mobile robot is the high-mobility capabilities obtained to navigate in tight indoor spaces [
23], being able to move in any direction without performing intermediate rotation maneuvers. The main disadvantages are the complexity of its kinematics [
22] and control in order to follow a target trajectory.
3.1. Omnidirectional Wheel Design Used as a Reference
The design presented in this paper has been inspired by the work of Clotet et al. [
24] that describes the design and implementation of a versatile human-sized assistant personal robot (APR), which includes a holonomic motion system with three omnidirectional wheels shifted 120° (
Figure 1). The APR prototypes have been used as a tele-operated assisted living robot [
24], as a tool for automatic supervision of environmental parameters [
25], as a walk-helper application [
26], as a support tool for gas leakage localization [
27], and as an experimentation tool [
28]. However, the weight (38.5 kg) and size (Ø55 mm × 1680 mm) of this mobile robot has limited its application as a tool to learn or teach robotics. The design and FDM/FFF implementation of a compact omnidirectional wheel for a mobile robot is a first step to overcome this limitation.
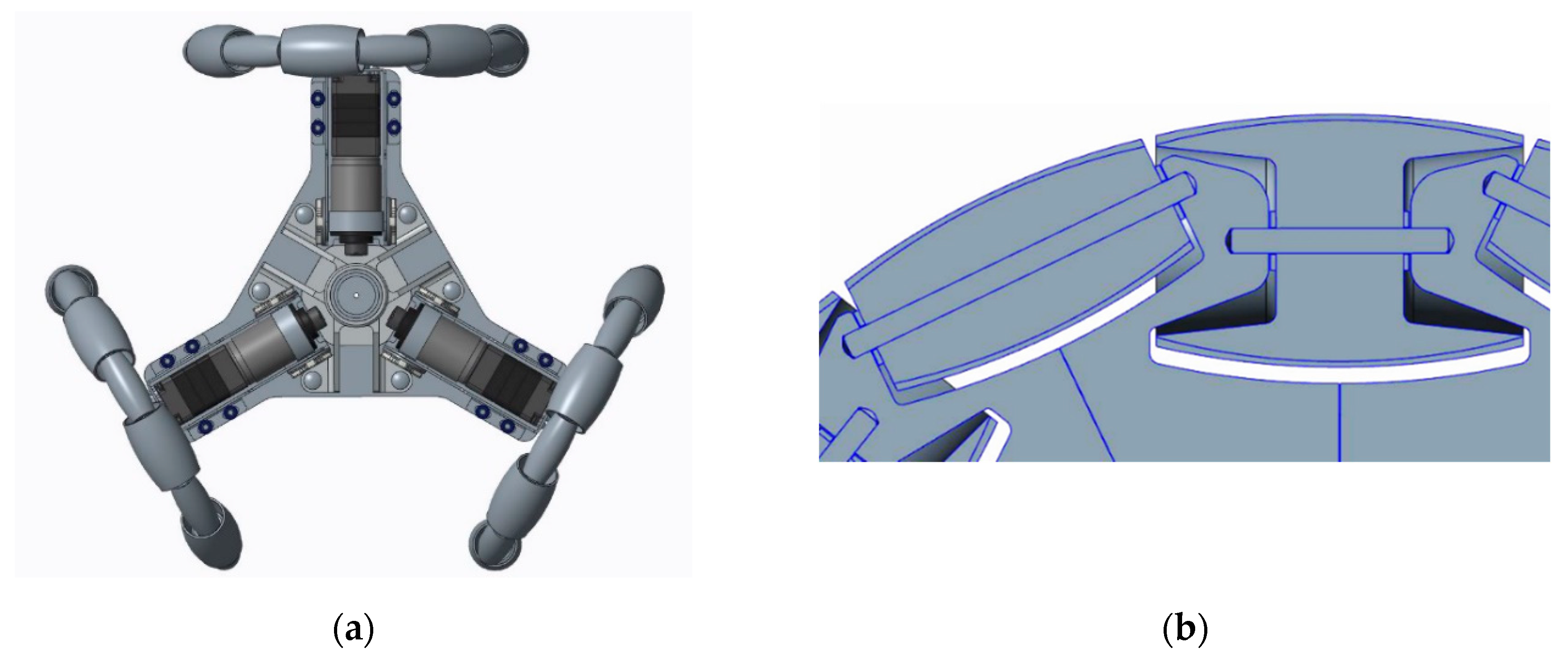
Figure 1a shows the top view of the APR motion system which is based on three omnidirectional wheels attached to three DC (direct current) geared motors shifted 120°. These omnidirectional wheels are based on the use of alternated passive rollers with two different sizes and shapes [
22]. This optimal design reduces the gap between passive rollers and minimizes the generation of vibrations, which have been further reduced with the development of a suspension system [
29].
Figure 1b shows a Computer-Aided Design (CAD) detail of the roller brackets, passive rollers and their links. This implementation is optimal for a big wheel (300 mm diameter) but the application of this original design in a compact mobile robot is limited by the size of the rollers and its ball bearings. This paper proposes the development of thin inner passive wheels to overcome this scale down limitation.
3.2. Omnidirectional Wheel Design
Figure 2a shows the basic design of an omnidirectional wheel based on free-rotating inner passive wheels.
Figure 2b shows the exploded view of its characteristic T-shaped piece (or T-structure) that holds two passive wheels (instead of complex passive rollers). The main structure of the omnidirectional wheel is its central circular part, which is attached to the motor shaft and holds the T-structure assemblies. The T-structure is a rectangular stick which includes two axes at the end. The axes are tilted in order to fit and properly orientate the passive wheels to the center of the omnidirectional wheel. Each passive wheel also includes a toric joint as a soft cover to increase grip and contribute to the absorption of impacts with the ground.
The diameter of this omnidirectional wheel is correlated with the number of T-shaped pieces.
Figure 3 shows the main parameters that define the wheel structure: Rout is the total outer wheel radius; Rcenter is the wheel radius measured until the center of the axes that support the passive wheels; Rsupport is the radius of the central part of the wheel; Øin is the inner diameter of the passive wheel; Øext is the outer diameter of the passive wheel; Øtot is the total diameter of the passive wheel including the cover; Ww is the passive wheel width; Ω is the angle between two passive wheels; Ws is the width of the T-structure; d is the distance between the stick of the T-structure and the passive wheel; Øt is the toric joint width; Gd is the U-groove depth required to fix the cover (toric joint) to the passive wheel; and finally, gap is the characteristic distance between wheels.
The gap is the linear distance between two inner passive wheels in contact with the floor. This gap generates impact vibrations but the passive wheels includes soft plastic torics to reduce the amplitude of these vibrations as well as to increase the grip.
Figure 4 shows a representation of the gap between two inner wheels in contact with the ground. This gap is always the same in order to generate vibration impulses with only one main oscillation frequency.
The constructive features of the wheel depend on the number (N) of passive rollers, the width of the T-shaped structure (Ws), the width of the inner wheel (Ww), the width of the toric joint (Øt), the depth of the groove in the wheel (Gd), the diameter of the passive wheel (Øext) and the distance (d) between the stick of the T-shaped structure and the passive wheel that is holding. The distance (d) and the number of passive rollers (N) are restrictive factors that have a great impact in the wheel radius and in the gap. However, the inner distance (d) must have a reasonable value in order to avoid wheel blockage by dirt particles. Mølhave et al. [
30] concluded that the dirt particles in a normal office are usually in a size range from 1 µm to 1 mm so this inner distance (d) has been fixed to 1 mm.
The external radius of the wheel that guarantees the maximum number of passive rollers is calculated with Equation (1):
and the gap is obtained with Equation (2):
The design of the passive wheel and the T-shaped structure determines the operational parameters of the omnidirectional wheel. Examples of feasible parameter values are: passive wheel diameter (Øext) from 10 to 14 mm, passive wheel width (Ww) from 3 to 4 mm, T-shaped structure width (Ws) of 2 mm, toric joint width (Øt) of 2.62 mm, U-groove depth (Gd) of 0.4 mm and distance (d) of 1 mm.
Figure 5 shows that the total external radius (Rout) of the complete omnidirectional wheel increases linearly as the number of passive wheels (N) also increases. The radius of the omnidirectional wheel (Rout) decreases approximately 2 mm when decreasing the diameter of the inner passive wheels (Øext) 2 mm (from 14 to 12 mm) while maintaining its width to 4 mm. The reduction of the total radius of the wheel (Rout) is more significant as the number of passive rollers increases and when reducing the diameter of the inner passive wheels (Øext) from 14 to 12 mm as well as the wheel width (Ww) from 4 to 3 mm.
Figure 6 shows that the gap (gap) of the omnidirectional wheel decreases almost exponentially in relation to the number of inner passive wheels (N). In this case, increasing the total external radius of the omnidirectional wheel (Rout) has the effect of reducing the angle between inner passive wheels (Ω) and then reducing the gap (gap). However, the value of the gap is almost constant for a number of passive wheels higher than 20. Similar to
Figure 5, the different feasible cases plotted in
Figure 6 show that the effect of reducing the wheel width (Ww) as well as its diameter (Øext) has more impact on the gap reduction than just reducing the inner passive wheel diameter (Øext). Therefore, the general recommendation for an optimized omnidirectional wheel design is the selection of inner passive wheels with the minimum diameter (Øext) and the minimum width (Ww).
3.3. T-Shaped Structure and Inner Passive Wheel Design and Implementation
Table 1 presents three practical alternative implementations of the T-assembly and a detail of the omnidirectional wheel obtained with each proposal. These proposals are based on different combinations of commercial mass-produced parts and 3D printed parts in order to create a compact omnidirectional wheel implementation. The pieces shown on
Table 1 are made with transparent PLA 3D850 although these designs have been also implemented with ABS.
The first alternative (
Table 1, Design 1) consists of a 3D printed T-shaped structure with two axes for passive wheel attachment. In this case, the inner passive wheel is a fixed assembly of a ball bearing with an additional U-grooved (3D printed) cover that holds a toric joint. As an example,
Table 2, Design 1 shows some feasible constructive parameters of the passive wheel when using a commonly available ball bearing with an external diameter of 10 mm, inner diameter of 3 mm and width of 4 mm. This design is assembled under pressure and the passive wheels rotate with almost no friction.
The second alternative (
Table 1, Design 2) consists of a basic plastic T-shaped structure with two axes. In this case, the passive roller is a commercial ball bearing with a V-groove on its outer perimeter that directly holds the outer toric joint. V-grooved ball bearings seem to be more convenient for the implementation presented but, unfortunately, they are less common and can be up to 6 times more expensive than U-grooved ball bearings. As an example,
Table 2, Design 2 shows some feasible constructive parameters of the passive wheel when using a commercially available V-grooved ball bearing with and external diameter of 12 mm, inner diameter of 3 mm and width of 4 mm. This design is assembled under pressure and the passive wheels rotate with almost no friction.
The third alternative (
Table 1, Design 3) only consists of one toric joint and 3D printed elements: the T-shaped structure is made of a central stick structure with a tilted hole to fit two small axes, and passive wheels are solid 3D printed cylinders with a U-groove shape in their outer perimeter to fit the soft toric joint. This design does not include bearings, so the passive wheel cannot be fixed to the axes as it must rotate freely. Therefore, the axes are built as separated pieces in order to provide a mechanical lock for the wheels and allow their spin. This design has the advantage that the dimensions of the passive wheel do not depend on standardized ball bearing elements, increasing the possibilities of creating smaller omnidirectional wheels. However, this design also has several disadvantages. It is not as rigid as the previous alternatives because of the amount of clearance required for rotation between the hole of the inner passive wheel and the axis, so inner passive wheels tend to swivel. The rotation of the inner passive wheels has more friction than the previous alternatives due to the inexistence of a ball bearing. As an example,
Table 2, Design 3 shows some feasible constructive parameters of a passive wheel. Assembling this design requires the adhesion of the axes to the central stick with strong glue in a delicate time-consuming manual operation.
The experience of assembling and testing these designs can be summarized as follows: Design 1 is easy to assemble and the metallic ball bearing has practically no friction during the rotation; Design 2 is similar to Design 1 but based on a special V-grooved metallic ball bearing which has the disadvantages of limited availability, extra weight and extra cost (1.5 times the weight and 3 times the cost of a standard ball bearing); Design 3 has de disadvantages of poor axis alignment (due to the manual gluing of the axes) and the existence of friction between the axes and the passive wheels. Consequently, Design 1, based on a 3D printed U-grooved ring, a standard metallic ball bearing and a 3D printed T-shaped structure, has been selected as the optimal implementation.
3.4. T-Shaped Structure Deformation Test
This section presents an empirical assessment of the deformation of the most critical part of the omnidirectional wheel which is located in the T-shaped structure, in the union between the central rectangular stick and the axes that hold the inner passive wheels. This union is especially susceptible to deformation, tensions and rupture due to its reduced dimensions and the fatigue caused by the repeated forces generated when inner passive wheels contact with the floor. This union will be empirically evaluated by performing repetitive deformation tests with sets of 10 T-shaped structures 3D printed using ABS (
Figure 7) and PLA 3D850 (
Figure 8). These test T-structures only have one axis in order to simplify the 3D printing process of large sets of pieces.
The a priori comparison of the flexural strength of the selected printing filaments shows that PLA 3D850 should break with higher values of forces applied. The comparison of the flexural modulus also shows that PLA 3D850 is stiffer than ABS, so ABS is expected to deform more than PLA 3D850 with the same load applied. Finally, the Izod impact strength shows that ABS absorbs more energy per unit of thickness than PLA 3D850 and then, ABS must be tougher than PLA 3D850. All these expected properties can be affected by the design of the piece and the parameters of the 3D printing process [
14,
15] and will be empirically verified. The deformation tests will compare the mechanical properties [
7,
14] of T-structures 3D printed in ABS and PLA 3D805 depending on the printing orientation, the infill density (30% and 100% or solid) and the width of the T-structure (2 and 4 mm). In this paper the term vertical printing orientation means that the T-structure has been printed with the axes perpendicular to the build surface (see
Figure 7 and
Figure 8a) and the term horizontal printing orientation means that the T-structure has the axes parallel to the build surface (see
Figure 7 and
Figure 8b). The images of
Figure 7 and
Figure 8 show a detail of the layered structure originated by AM using FDM/FFF.
Figure 9a shows an illustrative image of the development of a deformation experiment. In this case a passive wheel (composed by a U-grooved ring inserted over a metallic ball bearing) has been inserted in the axis of a half T-structure. Then, the passive wheel has been fixed horizontally in order to apply a deformation force at the end of the stick of the T-structure (see
Figure 9). On the one hand, the deformation force has been increased in discrete steps during the experiments and, on the other hand, the reduced size of the pieces has limited the effective resolution of the angular measurements to approximately 1.3°. The combination of both effects has generated a digitalization step effect in the results shown in
Figure 10,
Figure 11 and
Figure 12. The point clouds of the different groups have been slightly shifted in the deformation axis in order to improve the visualization and interpretation of the results. Finally,
Figure 9b shows a sample piece that has exceeded its elastic deformation limit, a case that is not included in the results shown in this section because then the omnidirectional wheel will not rotate properly.
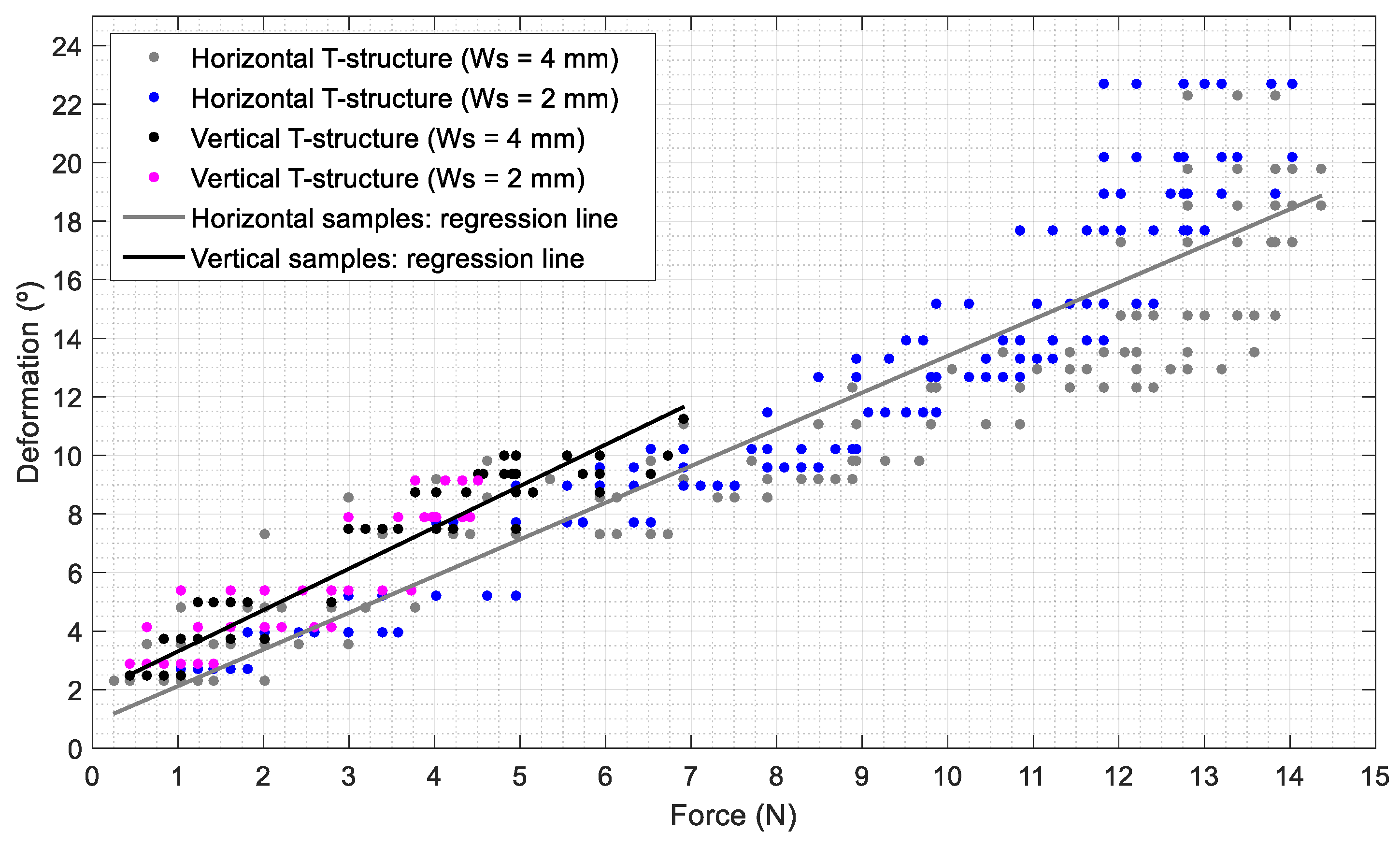
Figure 10 shows the relationship between the force applied and the angular deformation measured in four different groups of T-structures 3D printed using ABS with a 100% infill (solid piece), with different orientations and different holding structure widths (see
Figure 7). The groups compared are: (1) T-structures printed horizontally with a wide 4 mm central holding structure (Ws = 4 mm,
Figure 10 gray dots); (2) T-structures printed horizontally with a thin 2 mm central holding structure (Ws = 2 mm,
Figure 10 blue dots); (3) T-structures printed vertically with a wide 4 mm central holding structure (Ws = 4 mm,
Figure 10 black dots); (4) T-structures printed vertically with a thin 2 mm central holding structure (Ws = 2 mm,
Figure 10 magenta dots).
Figure 10 shows that the pieces printed vertically can be deformed up to 10° before breaking (or reaching its maximum deformation limit) and support up to 6.5 N, whereas the pieces printed horizontally can be deformed up to 22.5° (125% more) and support up to 13 N (100% more). In general,
Figure 10 shows a similar deformation tendency in all groups of pieces printed vertically and horizontally regardless of the width of the T-structure. The linear regressions of both cases show similar rates (horizontally: 1.25 °/N, vertically: 1.41 °/N) with an offset that depends on the printing direction. Therefore, the conclusion of this experiment is that ABS T-structures printed horizontally are less deformed and support more force. A similar conclusion has been obtained when repeating this experiment with PLA 3D850 (
Figure 8a,b). Consequently, the implementation of the omnidirectional wheels and the next experiments will be performed with horizontally printed pieces.
Figure 11 shows the relationship between the angular deformation of the axis and the force applied to two different groups of T-structures 3D printed horizontally using PLA 3D850 with two infill densities: 100% and 30%, and the same width (Ws = 4 mm).
Figure 11 shows that samples with 30% infill density (magenta dots) have an elastic deformation response with forces up to 9 N, while the samples with a 100% infill density (black dots) have an elastic deformation response with 19 N (are more deformable). The linear regressions of both cases show average sensitivities of 1.52 °/N (100% infill) and 0.64 °/N (30% infill). Therefore, the conclusion of this experiment is that the T-structures of PLA 3D850 printed horizontally with a 100% infill (solid piece) have higher resistance to deformation (are less deformed and support more force). Consequently, the implementation of the omnidirectional wheels and the next experiments will be performed with horizontally printed pieces with a 100% infill density.
Figure 12 shows the relationship between the angular deformation of the axis and the force applied to two different groups of T-structures printed horizontally using ABS and PLA 3D 850 with a thin central part (Ws = 2 mm).
Figure 12 shows that ABS pieces (magenta dots) are more deformable than the PLA 3D850 ones (black dots). In this piece, ABS offers an elastic deformation response with forces up to 11 N, whereas PLA 3D850 offers an elastic deformation response with forces up to 19 N (72% more). These results agree with the claimed mechanical properties of both materials. The linear regression of both cases show average sensitivities of 1.34 °/N for the ABS (magenta line) and 0.96° /N for the PLA 3D850 (black line).
Therefore, the final conclusion of this experimental section is that PLA 3D850 T-structures printed in horizontal orientation, with a 100% infill density (solid piece), and a width of 2 mm have higher resistance to deformation (are less deformed and support more force). This conclusion agrees with Rodríguez et al. [
14] that concluded that the PLA was stiffer and had greater flexural strength than ABS when analyzing the influence of printing parameters in the mechanical behavior of PLA and ABS samples. Consequently, PLA 3D850 is the most adequate printing material to implement the compact omnidirectional wheel proposed in this paper. Another interesting experimental conclusion is that the width of the T-structure has no influence on the deformation of the axis that supports the passive wheels. The use of a small width in the T-structures has the advantages of reducing the gap between the inner passive wheels, reducing the time between impacts, and the amplitude of the vibrations generated by these impacts [
29].
3.5. Complete Omnidirectional Wheel Implementation
Figure 13a shows an application example of the final design of the complete omnidirectional wheel proposed in this paper. The central structure also includes a connection for the shaft of a small motor. After some practical usage tests, the attachment between the T-structures and the central structure (
Figure 13b) has been modified to include a cylindrical feature in order to block the radial displacement and to improve the mechanical fixation between the T-structures and the central structure.
A feasible value of the diameter of a compact omnidirectional wheel can be around 120 mm so, according to this limitation, the number of passive rollers must be 30 (N = 30) and then the resulting gap between passive wheels is 11.3609 mm (gap = 11.3609 mm) and the final wheel radius is 54.38 mm (Rout = 54.38 mm). The total weight of a complete omnidirectional wheel using PLA 3D850, mechanical ball bearings and toric joints is 86.78 g, see
Table 2, Design 1 to obtain other implementation details. The assembling of a complete omnidirectional wheel involves attachment under pressure between the U-grooved rings and the metallic ball bearings and between the T-structures and the central part of the wheel (
Figure 13b). This screw-less design allows fast part replacement in the case of failure or rupture, but requires an accurate definition of the 3D printing tolerances, which may require fine adjustment depending on the 3D printer used. For example, in this application example the diameter of the insertion holes in the central wheel was 5.4 mm, the diameter of the equivalent blocking cylinder in the T-Structures was 5.0 mm; the width of the stick of the T-structures was 2.0 mm and the width of the equivalent insertion in the central wheel was 2.2 mm.
Figure 14 shows a first demonstrative mobile robot implementation. The mobile robot consists of a support structure with a radius of 115 mm and a width of 4 mm, printed with standard red PLA with a honeycomb infill density of 10% and a total weight of 82.29 g. This support structure holds a Discovery 3TM32F7 control board (130 mm high and 80 mm wide), two 5 V, 1500 mAh power banks, three low-cost geared DC motors (also known as Arduino motor: voltage range 3–6 VDC, gear 1:48, 100 rpm at 6 VDC and 22.3 mm wide, 65 mm high and 19 mm depth) and three omnidirectional wheels. This mobile robot prototype has a diameter of 330 mm and a total weight of 422 g, defining a compact, portable and low-cost omnidirectional mobile robot suitable for its application as an engaging material in the teaching of robotics and 3D printing to students. The results of the first qualitative usage tests have confirmed the expected omnidirectional trajectory capabilities of the omnidirectional wheels.