Abstract
One of the top concerns for travelers when choosing public transportation is whether they can reach their destination in limited time and monetary cost on the basis of ensured reliability. However, the existing literature shows no studies on how to evaluate bi-objective multimodal accessibility under travel time uncertainty. In order to fill this research gap, this paper creates a multimodal super network based on smart card data in which the transfers among taxi, bus, and subway modes are developed and applied. Next, we propose a two-stage opportunity accessibility model to calculate bi-objective multimodal accessibility under travel time uncertainty. Then we propose a multimodal reliability path finding model and a reliability boundary convergence algorithm to solve this problem. Finally, we conduct a large-scale real-world case study. It is found that the impedance heterogeneity between different modes is significant, and multimodal travel has better accessibility than a unimodal one. Although multimodal accessibility decreases as the reliability increases, the advantage of multimodal over unimodal accessibility increases with reliability, and it can be improved up to 14.61% by multimodal transfers. This model can effectively guide traffic management departments to improve traffic accessibility in terms of time and cost and advise commuters to choose living places.
1. Introduction
Accessibility is an effective indicator for evaluating the ease of transportation, which can guide traffic departments to optimize transportation systems and assist urban residents to choose living and working places to access more opportunities for medical care, education and other activities. Public transportation consumes less energy and is conducive to sustainable development [1]. Unscientific accessibility assessment may lead to unreasonable public transportation planning, resulting in a great waste of resources.
Due to the effect of various factors, such as holidays, weather and peak hours, travel time is highly uncertain, which may result in late arrivals and cause penalties [2]. Thus, when travelers choose public transportation modes, including bus, subway, taxi, etc., they are eager to find the most reliable mode and path in multimodal networks to reduce the penalty caused by late arrival. However, due to the limitation of cost budget, people may not choose the most reliable mode and path. Since the multimodal combined mode can integrate the advantages of various modes, it provides a new approach for traffic departments to improve regional accessibility. Therefore, how to evaluate multimodal accessibility in limited time and monetary cost on the basis of ensured reliability has become a major challenge in the field of accessibility research.
In the existing research studies, the typical accessibility search models include potential models [3], cumulative opportunity models [4], utility models [5], and space–time prism models [6]. Although the potential model considers impedance attenuation, its friction coefficient is difficult to be determined. The cumulative opportunity model uses the impedance threshold, though it does not consider the impedance attenuation characteristics, making it easy to understand. The utility model is mainly used to study travelers’ behavior. The space–time prism model is used to analyze the accessibility of individual travel but has high requirements for data, especially personal trajectory data.
Transportation accessibility is generally measured based on deterministic travel time. In practical cases, due to different travel conditions, such as weather, traffic control, morning and evening peak hours, travel time is uncertain. People cannot be sure of the exact punctual arrival time of a path. Thus, transport modelers typically define reliability indicators to quantitatively measure the uncertainty of travel time using statistical range methods, such as the buffer time method, tardy-trip method, or probabilistic method. The probability method [2] is currently widely used in accessibility research, which uses on-time arrival probability to represent travel time reliability, with different distribution assumptions of travel time, e.g., normal distribution [7], lognormal distribution [8], and extended shifted lognormal distribution [2].
In addition, studies on traditional accessibility mainly focus on unimodal points of view [9]. Initially, Hansen [3] evaluated regional accessibility under travel time certainty using the shortest highway route. However, the environment is often uncertain in real life [10]. Meanwhile, the research object has shifted from a virtual network to an actual large-scale network [11]. To address this issue, the multi-criteria shortest path algorithm [12], reliability convergence boundary algorithm [2], etc., have been proposed, according to different travel time distributions.
Scholars have gradually realized that travel time is no longer the only concern, considering the impact of monetary costs, traffic congestion, energy consumption and other factors. Matisziw et al. [13] analyzed accessibility under travel time certainty, using generalized travel costs. Jiang [14] developed a two-stage single-objective accessibility model to improve the computational efficiency of accessibility. Shen et al. [7] established a bi-objective reliable path planning model to calculate a non-dominant solution. In the study of unimodal accessibility, considering time as a single factor is not problematic because costs increase over time. However, the cost difference between modes is far larger. Therefore, most of the existing studies on multimodal accessibility focus on time while ignoring the impact of cost, leading to incorrect accessibility results.
Similar to unimodal research, scholars have gradually shifted their focus to the assessment of multimodal accessibility under travel time uncertainty. Mavoa et al. [15] created a multimodal network by ArcGIS 9.2 with deterministic travel time as the network impedance. Salonen et al. [16] proposed a door-to-door method to evaluate multimodal accessibility. Based on the methods of Mavoa et al. [15] and Salonen et al. [16], Liu et al. [9] considered the impact of multimodal combined travel on the deterministic shortest time in accessibility assessment. Chen et al. [17] evaluated the accessibility of multimodal combined travel of bus and subway with online software. Xia et al. [18] used the weighted average travel time to represent the overall accessibility for each populated area in multimodal networks. Zhang et al. [19] used time as a single impedance to evaluate the accessibility of urban buses and subways under travel time uncertainty.
In the assessment of multimodal transportation accessibility, multimodal network construction is one of the core tasks. Initially proposed by Sheffi [20], super network refers to the network for different modes or activities. We adopt this concept to build the multimodal transport network, which is one type of super network with more than one transport mode. Arentze et al. [21] considered the impact of activities to develop a super network by using generalized costs. Liao et al. [22] further studied the factors of the personalization and travel time uncertainty to carry out activity planning research. Later, Li et al. [23] conducted an in-depth study on the shared bicycles based on this network. Among them, the construction of public transportation networks is much more complicated than that of private car networks. Two of the most well-known network construction methods in the literature are the time-dependent method and network expansion method, of which the former takes schedule events as attributes of the link, while the latter takes schedule events as nodes [24]. Zhang [25] proposed a multimodal network construction method integrating the time-dependent method for private vehicles and the time-expanded method for public transportation into one network.
In this paper, we mainly distinguish between unimode and multimode in terms of networks and paths. In the case of networks, the unimodal network refers to a network made with only one transport mode, while the multimodal network refers to a network made with more than one transport mode [17,19,20,21,25]. In the case of paths, the unimodal path refers to a path made with only one transport mode, while the combined mode path refers to a path made with more than one transport mode. The accessibility approach based on multi-modal networks is to find the optimal solution to evaluate accessibility. Since the optimal solution may be a unimodal path or a combined mode path, for simplicity, we refer to both as multimodal paths in this paper, i.e., multimodal path refers to a path made in multimodal networks.
For the multimodal network construction under travel time uncertainty, the road network sets the link time as being uncertain. Station-type networks usually have two processing methods, one of which is to process the network into a deterministic network according to the timetable, while the other is the same as the deterministic network structure, except that the travel time between the two stations is set to be uncertain according to the transit lines instead of the timetable [19]. At present, smart cards are widely adopted in public transportation. However, there is still no research considering transfers between the taxi mode and the bus and subway modes and building a super network based on smart card data. A novel idea is to build a super network based on smart card data while ignoring the lines, in which links exist when traffic flow meets the constraints between two stations its attributes include all time and monetary cost, such as waiting time and in-vehicle time. The different mode networks are connected by a foot network. Thus, the number of paths that people would not choose in reality is reduced, while the problems of route collinear and fare calculation are easier to be solved.
Moreover, when evaluating multimodal accessibility, time is not the only factor that needs to be considered; travel time reliability, monetary cost and multimodal transfers are also important factors. The single-objective method (the travel time method) or the generalized cost method can result in some gaps with real situations. Travelers care more about money and time when choosing travel modes and paths, and prefer higher arrival reliability to reduce penalties caused by late arrival. However, most of the existing studies on multimodal accessibility and popular route planners, such as Google map and Baidu map, focus on time while ignoring the impact of cost, travel time uncertainty, and especially transfers between the taxi mode and the bus and subway modes, leading to incorrect accessibility results, as summarized in Table 1. Thus, there is still no research on the problem of how to evaluate bi-objective multimodal accessibility under travel time uncertainty and analyze the impacts of bi-objective multimodal travel on public transportation accessibility.

Table 1.
Categories of existing studies.
To fill these above-mentioned gaps, this paper proposes a novel data-based bi-objective approach to explore multimodal accessibility under travel time uncertainty and attempts to make three main contributions beyond those of previous studies.
(1) We first use smart card data to extend the traditional multimodal network to incorporate the transfer between the taxi mode and the bus and subway mode under travel time uncertainty. This network makes it easy to solve the problems of route collinear and the fare calculation of the multimodal combined trip.
(2) We develop a two-stage bi-objective opportunity model and a multimodal reliability path finding model, and propose the reliability boundary convergence algorithm to solve this accessibility problem. In particular, the proposed algorithm is applicable to the studies of multimodal bi-objective accessibility under various risk-preference conditions, including risk-averse, risk-neutral, and risk-seeking.
(3) We use a large-scale real-world case study to verify the effectiveness and efficiency of the proposed models and algorithm. It is found that although multimodal accessibility decreases as the reliability increases, the advantage of multimodal over unimodal accessibility increases with reliability, and it can be improved up to 14.61% by multimodal transfers.
The rest of this paper is organized as follows. In Section 2, a multimodal super network based on smart card data is developed. In Section 3, a two-stage bi-objective opportunity model is established. In Section 4, data collection and processing are presented. In Section 5, multimodal accessibility is analyzed, using Beijing as an example. In Section 6, this paper is discussed and summarized.
2. A Data-Based Multimodal Network Model
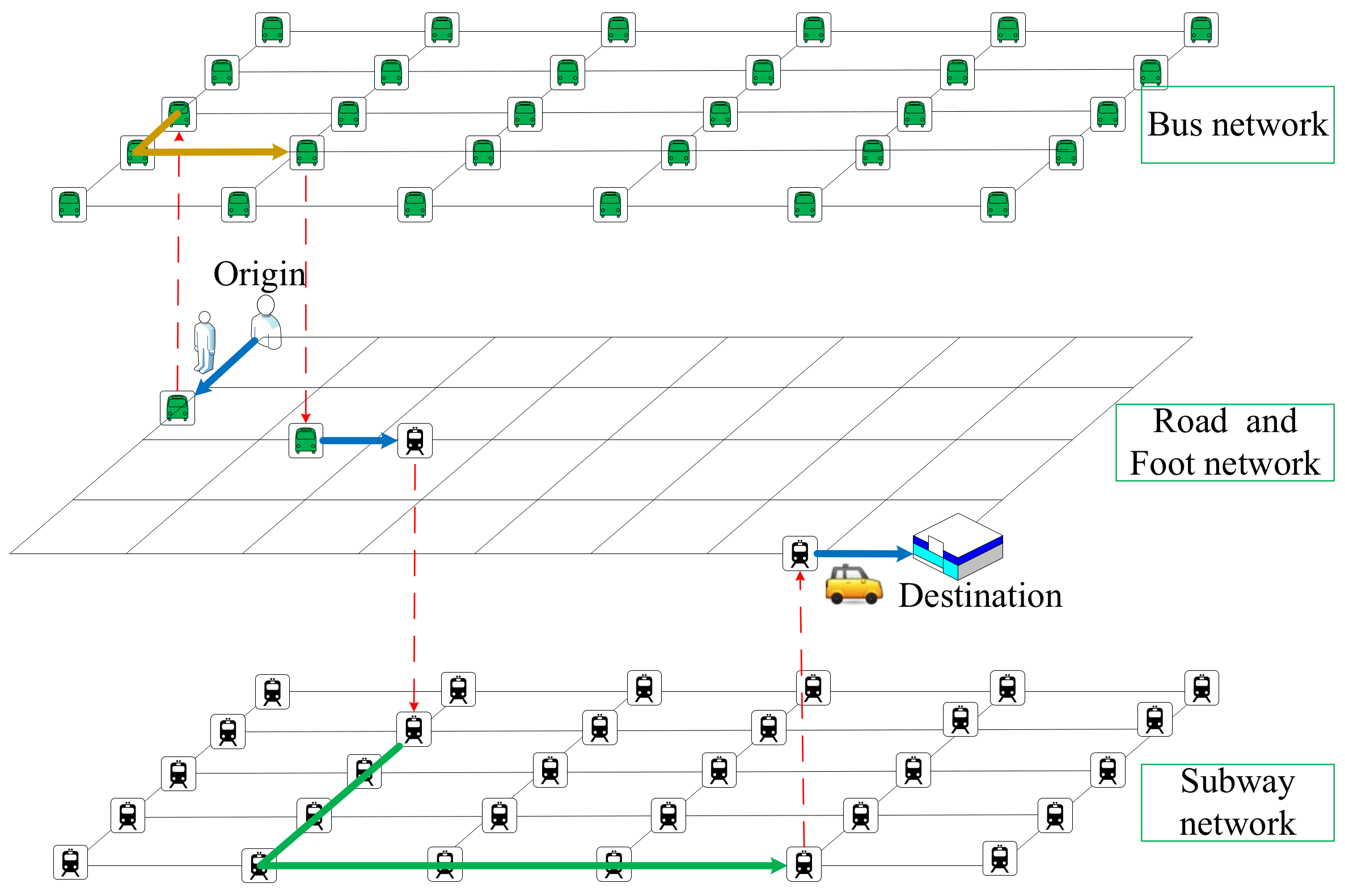
A multimodal path is shown in Figure 1 in the form of a hierarchical network.
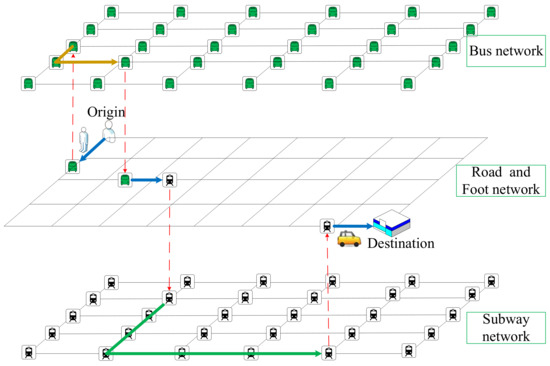
Figure 1.
A hierarchical multimodal network diagram.
A traveler starts from the origin, walks to a bus station, transfers to a subway, and then takes a taxi to the destination. This trip involves three transportation facilities, namely, bus, subway, and taxi. It is a combined multimodal trip, including bus to subway and subway to taxi. Big data provide multi-source information for studying multimodal accessibility. However, due to the diversity of transportation data, it is difficult to extract individual multimodal combined travel chains from multi-source data. Therefore, it is necessary to establish a multimodal super network so as to study combined multimodal accessibility.
2.1. Basic Assumption
Since the path travel time can be well approximated by a normal distribution [31], the following assumptions are made to simplify the problem and to present the core idea.
A1. It is assumed that link travel times are mutually independent and follow normal distributions [30,31,32].
A2. Taxi has a flag-down fare for an initial certain mileage, and thereafter, the price increases monotonically with distance.
2.2. Multimodal Network Model
To effectively study the bi-objective multimodal accessibility under travel time uncertainty, we develop a multimodal super network model based on smart card data to realize the transfers between the multimodal transportation modes, making it easier to calculate the time and monetary cost of the path, especially of that with transfers between taxi and subway modes.
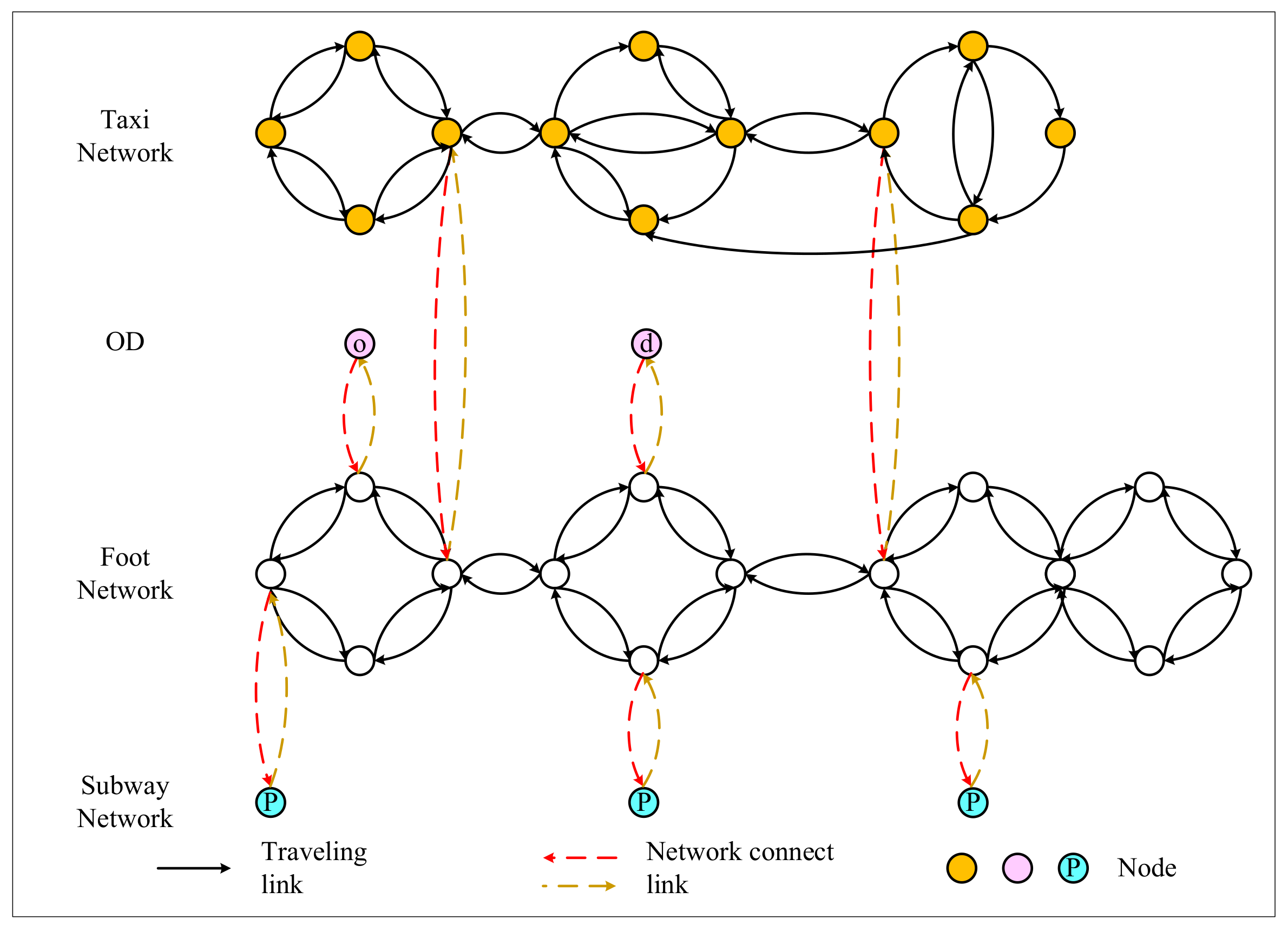
We take five steps to build a multimodal network: mode selection, node selection, node connection inside mode, node connection between modes, and OD (origin–destination) nodes connection.
Mode selection: Foot networks are the fundamental of a multimodal network. Generally, public transportation networks include buses, subways, taxis, shared bicycles, etc., while private ones include private cars, private bicycles, etc. Almost all trips start and end on foot. In the process of one’s journey, only the process between the stations is performed by vehicle, while the rest is completed on foot. Therefore, the foot network is an essential basic one for public and private transportation. When constructing a multimodal network, we build a network for each mode and a walking network at the same time.
Node selection: For road networks, such as the foot network and taxi network, the connecting points between roads are selected as nodes. For station networks, such as bus networks and subway networks, stations are selected as nodes. Points and stations are collectively referred to as nodes for ease of presentation.
Node connection inside mode: Considering the bi-objective of uncertain travel time and monetary cost, we provide a novel idea to connect nodes inside mode by using bus and subway smart card data. Firstly, we set links between two stations where travel data exist to reduce the number of links that people would not choose on their actual trips. Then, we adopt travel time in the form of a distribution function based on smart card data as the time of the link to reflect the uncertainty of travel time, where travel time includes waiting time and in-vehicle time. Next, we calculate the fares between stations based on smart card data and take it as the link cost. As this multimodal network is based on smart card data, it does not need to consider collinear issues and is capable of providing all accessible paths between stations at one time. Meanwhile, the travel time distribution and monetary cost between stations can be extracted directly from smart card data. The impedance heterogeneity within modes is far smaller than that between the modes, so it can be ignored, and the average monetary cost is adaptable. The difference between bus and subway lies in the fact that the subway data include the internal transfer time. In contrast, bus data do not include this time, so subway data can better reflect people’s actual travel behavior. This method differs from the existing networks in terms of reliability and the data-based construction method.
Nodes connection between modes: Based on the foot network, each modal node is connected to the nodes of the foot network. There are two most commonly used methods: one is to attach the points to the nearest foot network nodes, and the other is to insert vertical nodes, which is more accurate than the former one, as it increases the number of nodes and links and thus, will consume more time. Meanwhile, when a transfer is required between modes, the corresponding waiting time and walking time should be set in links.
OD nodes connection: Like other network nodes, OD nodes are connected to the foot network in the same way to achieve an OD pair connection.
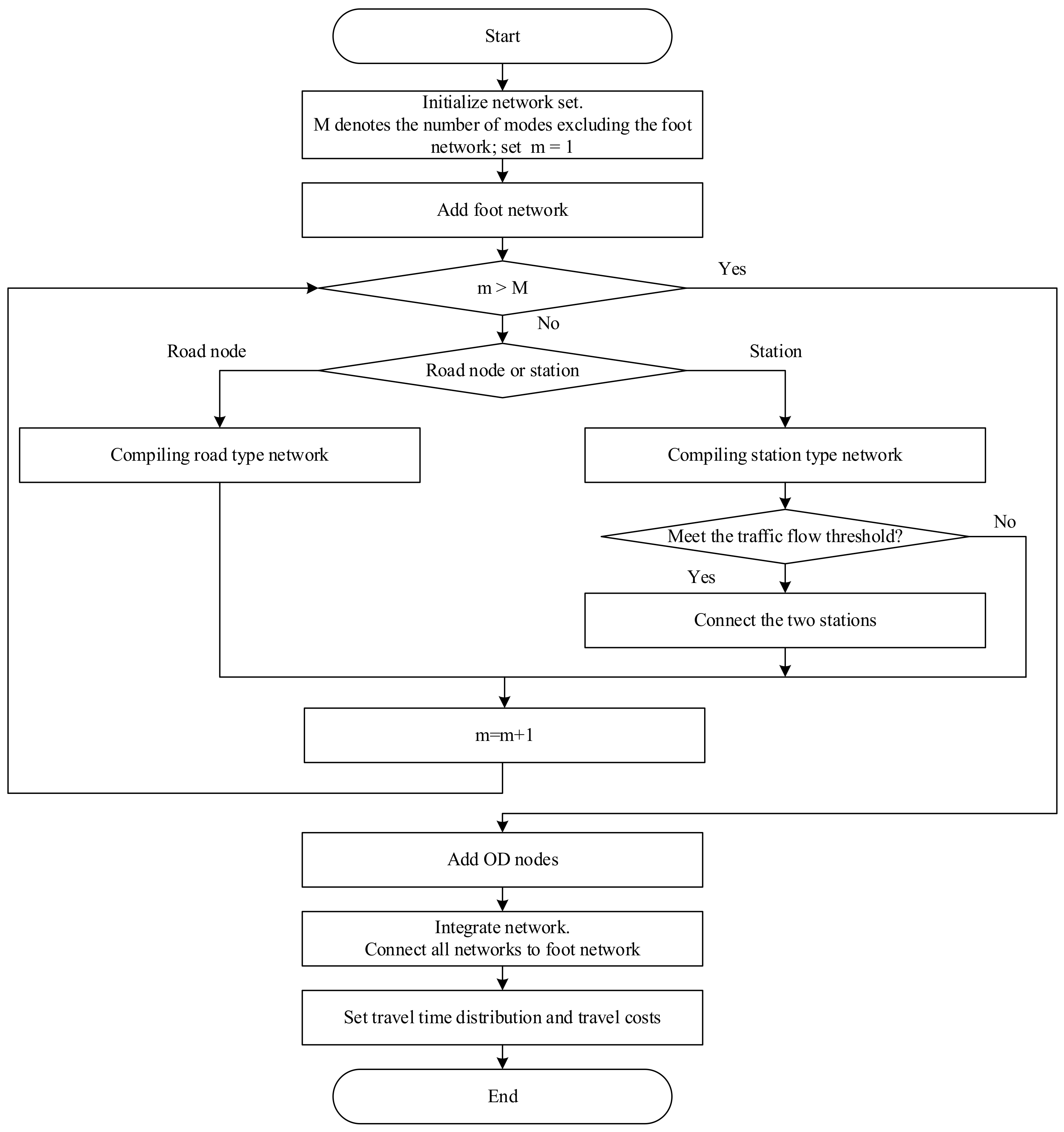
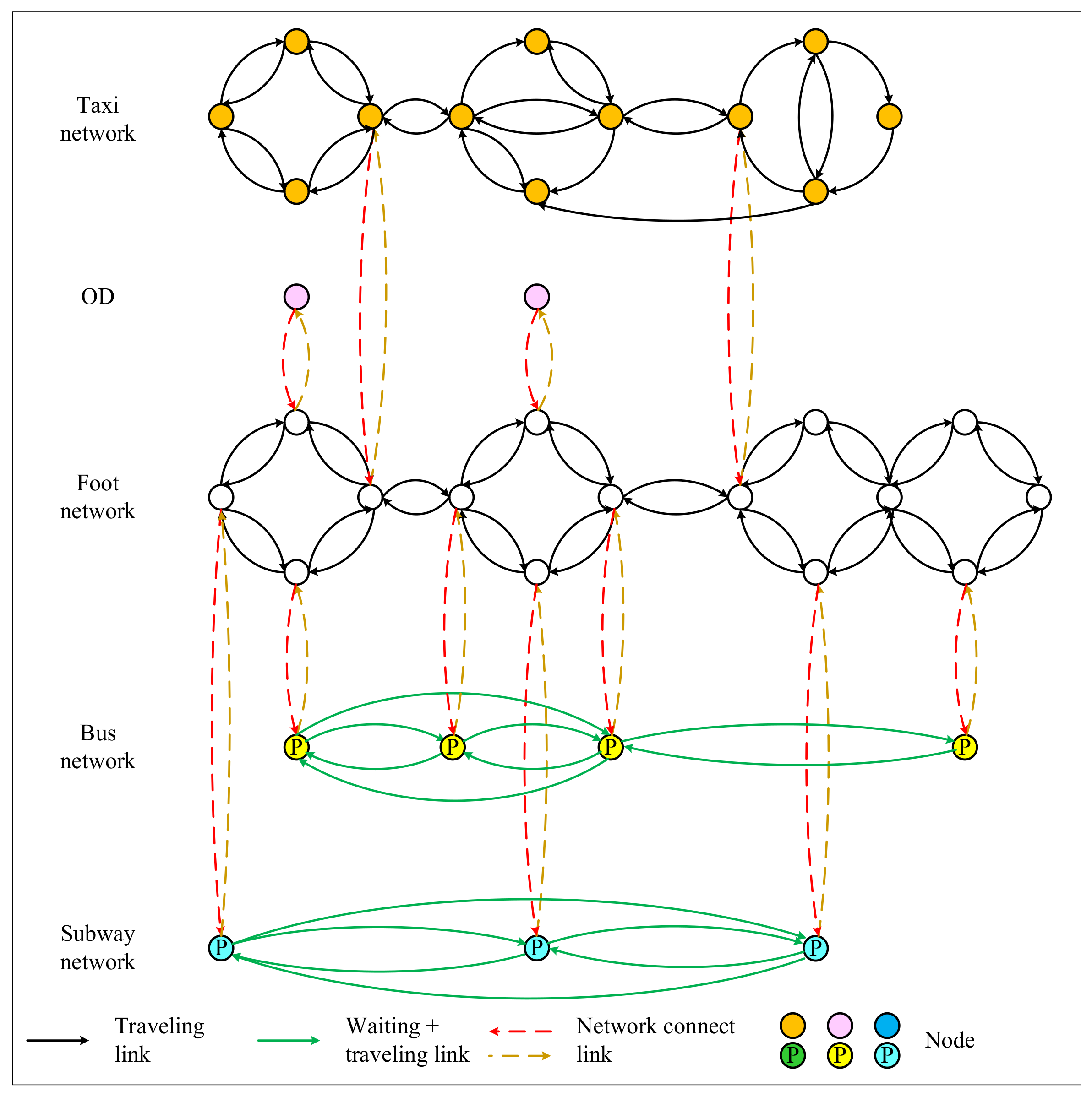
Based on the above description, we have drawn a flow chart of data-based multimodal super network construction under travel time uncertainty, as shown in Figure 2. Figure 3 shows a directed graph of a multimodal network, including taxi, subway, and bus. This method is not limited to the above modes but can be extended to any multimodal network. In this paper, the multimodal network is expressed as , including a set of nodes () and links (). By considering the uncertainty of travel time, each link has randomly distributed travel time . The uncertainty in this paper is represented by the on-time arrival probability () in the normal distribution. Under the basic assumption that link travel times are mutually independent and follow normal distributions, the travel time of paths can be obtained by adding link travel time. Then, effective travel time can be expressed as the sum of average time and safety margin time [26,33], as shown in Equations (A1)–(A8) in Appendix A.
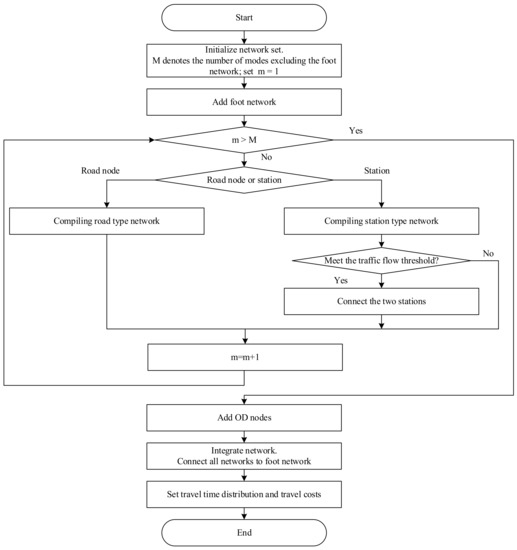
Figure 2.
A flow chart of data-based multimodal network construction.
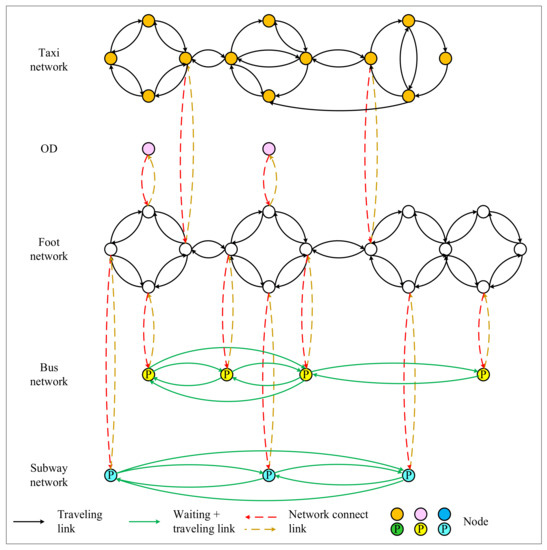
Figure 3.
A data-based multimodal super network.
3. Analysis Methods
3.1. A Two-Stage Bi-Objective Opportunity Model
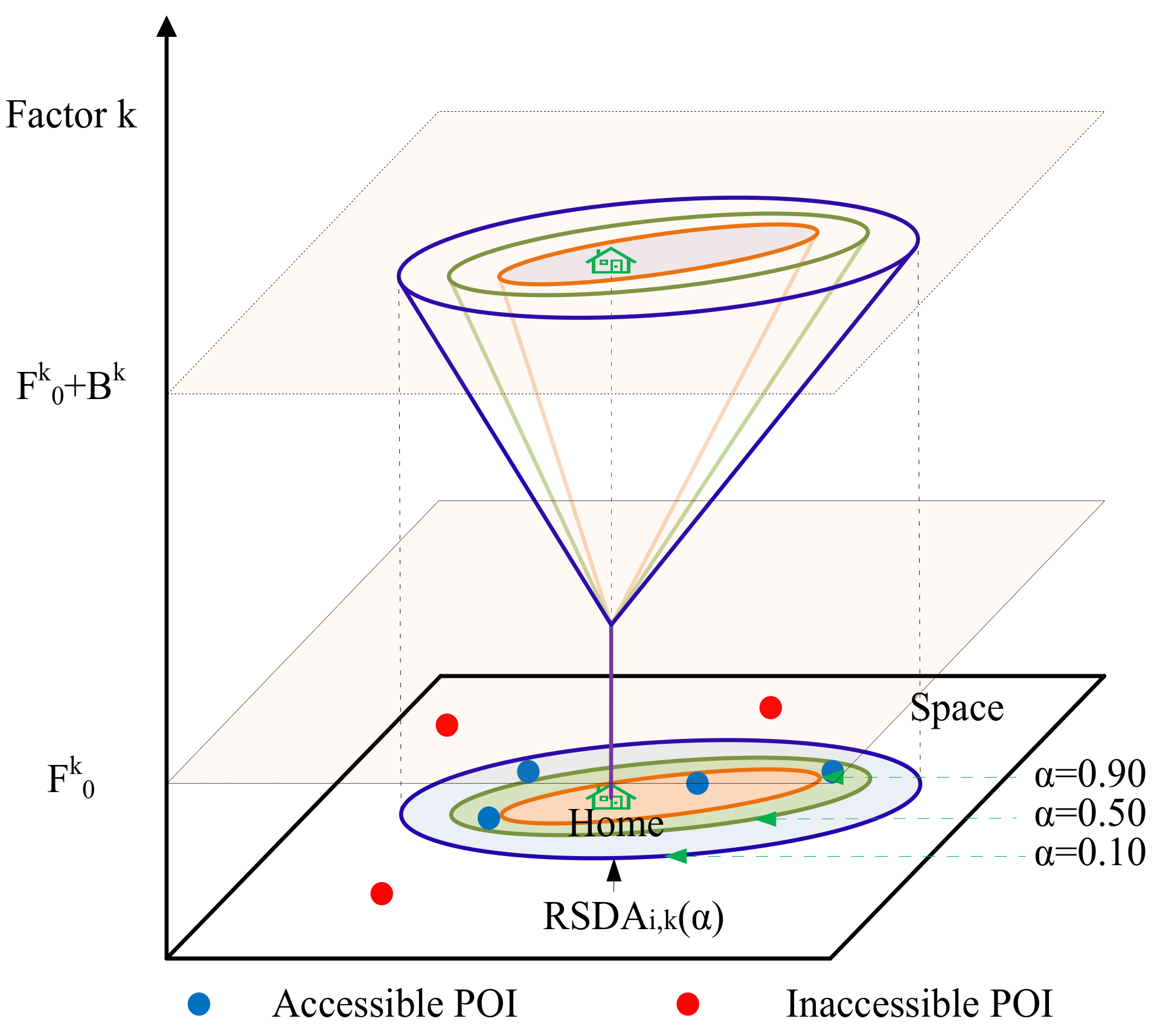
After establishing the multimodal network, we start to develop a bi-objective opportunity model in order to evaluate accessibility with budgets of time and monetary cost under travel time uncertainty. Since accessibility increases with budgets, from the perspective of the single impedance constraint, we use the reliable single dimension area () to represent the accessibility of the node in the dimension, as shown in Figure 4.
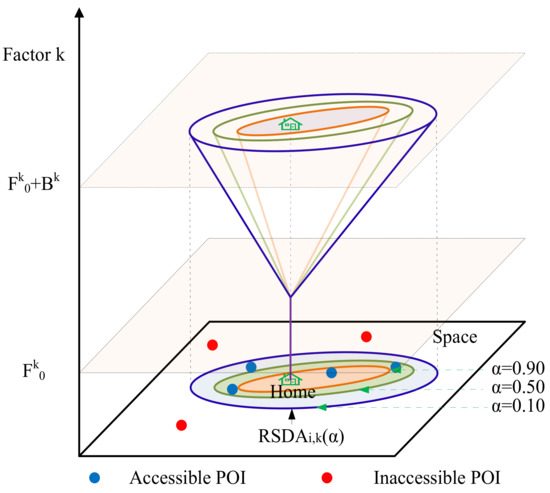
Figure 4.
The bi-objective opportunity model: is the initial value and is the budget.
By calculating the intersection of the areas of various dimensions, we can obtain the reliable multi-dimension area (). Then, we use POI (point of interest) to represent opportunities and take the number of opportunities in to represent the position accessibility. The formula of the bi-objective opportunity model is shown in Equations (1)–(3).
where is the cumulative opportunity accessibility of the location under reliability ; is a binary variable, indicates p is in , and otherwise. and respectively represent effective travel time and monetary cost for the location to obtain the opportunity . and represent budgets of travel time and monetary cost, respectively.
Since each POI needs to be determined separately, a two-stage bi-objective opportunity model is proposed to improve the computational efficiency of accessibility. At the first stage, the grid is divided, whose opportunities are represented by POI in the grid, as shown in Equations (4) and (5). At the second stage, the accessibility of the grid area is calculated using the grid centroid, as shown in Equations (6)–(8).
The first stage is as follows:
The second stage is as follows:
where is the grid . is the number of opportunities within . is a binary variable, indicates p is within , and otherwise. is a binary variable, indicates is within , and otherwise.
3.2. A Multimodal Reliability Path Finding Model
The most critical content in the accessibility evaluation is whether the two points are accessible under the constraints of monetary cost and time under uncertainty. Here, we establish a bi-objective multimodal reliability path model to find a feasible solution, as shown in Equations (9)–(12). Since a multimodal path includes more than one transportation mode, which is charged in different ways, its costs should be calculated in segments.
Subject to
where is the monetary cost of the trip in the path k; is the total monetary cost. Objective functions (9) and (10) represent the minimum effective travel time and minimum monetary cost, respectively. Constraint (11) represents the flow balance constraint. Constraint (12) represents the binary variable for link-path incidence.
The common method is to solve the Pareto solution set and then determine the accessibility based on the set and the impedance threshold. By evaluating the travel time and monetary cost of the path, it can be determined whether the OD points are accessible under certain constraints, as shown in Equations (13) and (14).
where indicates whether the path in the Pareto set is accessible.
In a large-scale multimodal network, the scale of the Pareto set is large, making it difficult to compute. In order to improve the computation efficiency, we reconstruct the network by dividing the network to eliminate the constraint of monetary cost. Taxis, buses, and subways are the main modes of urban public transportation. Their monetary cost calculation method is quite different. The monetary cost of taxis is relatively high. In actual public transportation, people usually use the time-effective shortest path to travel. Considering the difference in monetary cost among modes, we divide the multimodal network into seven networks, according to monetary cost. Then, the bi-objective problem is transformed into a single-objective problem by calculating the shortest path of each network separately. According to the transport modes that people use in daily life, we divide the network into unimodal networks and combined modal networks, as is shown in Table 2.

Table 2.
Network segmentation.
The unimodal network set includes the following: foot network + taxi network, foot network + bus network, foot network + subway network, namely [G1, G2, G3]. It is more common to take a taxi to a subway station, but less common to take a taxi to a bus station. Therefore, we build the combined networks by linking taxi nodes to subway stations in order to realize the transfers between the taxi network and the bus and subway networks. In the combined modal networks, buses and subways are low-monetary cost modes, while taxi is a high-monetary cost mode. It is especially worth noting that a trip may include two taxi rides: one from the origin to a station and one from a station to the destination. Therefore, further considering the difference in taxi costs, the combined modal networks are further divided into four scenarios: foot network + bus network + subway network, foot network + bus network + subway network + taxi transfer to subway from the origin, foot network + bus network + subway network + subway transfer to taxi to the destination, foot network + bus network + subway network+ taxi transfer to subway from the origin + subway transfer to taxi to the destination, namely [G4, G5, G6, G7].
By calculating the time and monetary cost of the shortest path of effective travel time for seven networks, respectively, as shown in Equations (15)–(17), multimodal accessibility can be evaluated based on Equations (18)–(20).
Subject to
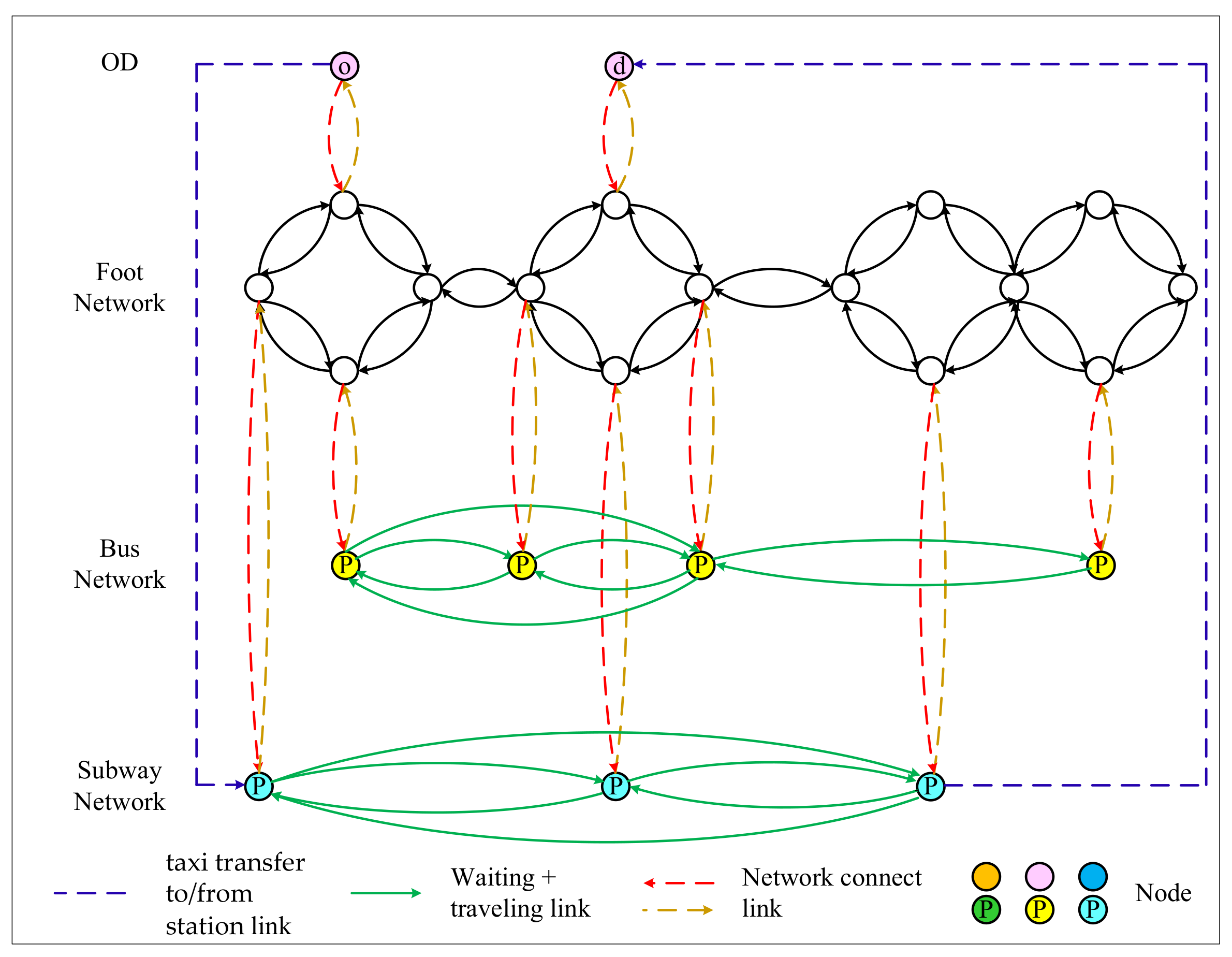
Taking the network, foot network + bus network + subway network+ taxi transfer to subway from the origin + subway transfer to taxi to the destination, as an example, we present the steps of network division as follows.
Step 1: Calculate the closest subway stations to the OD points. In this paper, is taken as four, indicating that travelers can take a taxi to four subway stations, or reach their destination from the nearest four stations.
Step 2: Use the network in Figure 5 to calculate the travel time distribution and monetary cost of the most reliable path from OD to each subway station.
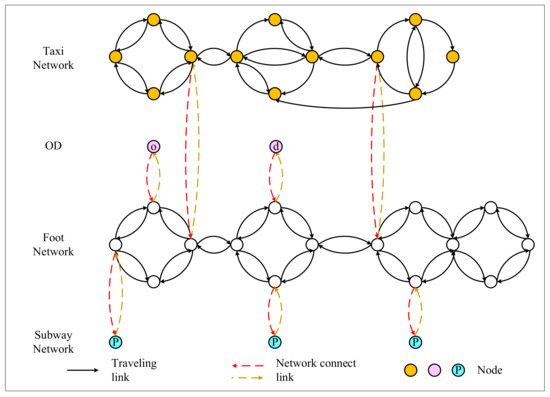
Figure 5.
Transactions between subway and taxi.
Step 3: Add the link between the OD and the closest station in the multimodal network, as shown in Figure 6, and then the combined modal network, foot network + bus network + subway network+ taxi transfer to subway from the origin + subway transfer to taxi to the destination, is completed.
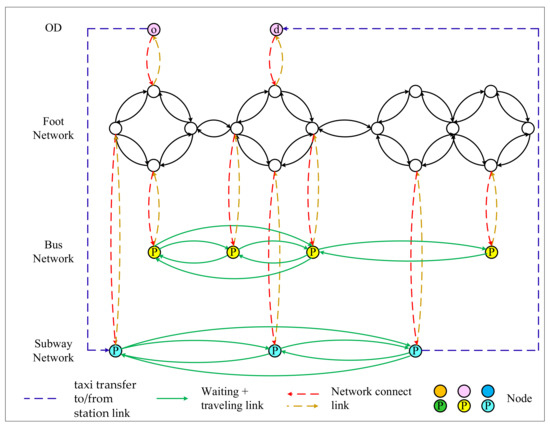
Figure 6.
A combined multimodal network.
3.3. Reliability Boundary Convergence Algorithm
The reliability boundary convergence algorithm for the normal distribution is proposed to solve the problem of the shortest path of effective travel time with the bi-objective of energy consumption and travel time [7]. However, their method works for finding the shortest paths but not for evaluating accessibility; the algorithm for risk-seeking travelers is not given. Hence, we adjust the algorithm process and termination conditions to meet the requirements of accessibility assessment, making it applicable to the studies of multimodal bi-objective accessibility under various risk-preference conditions, including risk-averse, risk-neutral, and risk-seeking.
According to the characteristics of the normal distribution, the following inequalities can be obtained.
(1) When and , travelers are risk-averse:
Set upper boundary and lower boundary :
(2) When and , travelers are risk-neutral:
Set upper boundary and lower boundary :
(3) When and , travelers are risk-seeking:
Set upper boundary and lower boundary :
Based on the above inequality, the upper and lower boundaries of the effective travel time of path can be determined so that the lower boundary can be monotonically increased by using the method of the K-shortest algorithm [34] to reduce the difference between the upper and lower boundaries. When the relative difference between the upper and lower boundaries of the reliability, , meets the requirements of the error threshold or reaches the maximum number of path searches, the algorithm will stop.
The bi-objective multimodal accessibility evaluation algorithm (Algorithm 1) based on the reliability boundary convergence is described as follows.
| Algorithm 1 The reliability boundary convergence algorithm |
| 1: Input: |
| 2: Output: . |
| 3: Other Notations: Construct a multimodal network based on the foot network, and divide the networks into seven parts . |
| 4: Step 1: Initialization |
| 5: Set: |
| 6: Step 2: Calculate the travel time and monetary cost of each transfer link in the multimodal network. |
| 7: Step 3: Evaluate accessibility. |
| 8: If : |
| 9: |
| 10: Elseif: |
| 11: |
| 12: Else: |
| 13: |
| 14: Step 4: Evaluate the cumulative opportunity accessibility of location by adding up POIs of all accessible grids. |
| 15: Def acc_probabilityless50( ): |
| 16: For G in [ G1, G2, G3, G4, G5, G6, G7 ]: |
| 17: Set i = 1 |
| 18: Do while: |
| 19: If : |
| 20: Find the i-shortest path with the link-time by using the K-shortest algorithm, then calculate its lower boundary travel time , effective travel time , effective path monetary cost , and upper boundary travel time . |
| 21: Set |
| 22: If: |
| 23: |
| 24: |
| 25: Else if: |
| 26: |
| 27: |
| 28: |
| 29: Else: |
| 30: Find the i-shortest path with the link-time by using the K-shortest algorithm, then calculate its lower boundary travel time , effective travel time , effective path monetary cost , and upper boundary travel time . |
| 31: Set |
| 32: If: |
| 33: |
| 34: |
| 35: Else if: |
| 36: |
| 37: |
| 38: |
| 39: Return |
| 40: Def acc_probabilityequal50( ): |
| 41: For G in [ G1, G2, G3, G4, G5, G6, G7 ]: |
| 42: Find the shortest path with the link time of the classic Dijkstra algorithm, and then calculate its effective travel time and effective path monetary cost . |
| 43: If: |
| 44: |
| 45: |
| 46: Return |
| 47: Def acc_probabilitymore50( ): |
| 48: For G in [ G1, G2, G3, G4, G5, G6, G7 ]: |
| 49: Set i = 1 |
| 50: Do while: |
| 51: If : |
| 52: Find the i-shortest path with the link-time by using the K-shortest algorithm, and then calculate its lower boundary travel time , effective travel time , effective path monetary cost , and upper boundary travel time . |
| 53: Set |
| 54: If: |
| 55: |
| 56: |
| 57: Else if: |
| 58: |
| 59: |
| 60: |
| 61: Else: |
| 62: Find the i-shortest path with the link-time by using the K-shortest algorithm, and then calculate its lower boundary travel time , effective travel time , effective path monetary cost , and upper boundary travel time . |
| 63: Set |
| 64: If: |
| 65: |
| 66: |
| 67: Else if: |
| 68: |
| 69: |
| 70: |
| 71: Return |
3.4. Evaluation Indicators
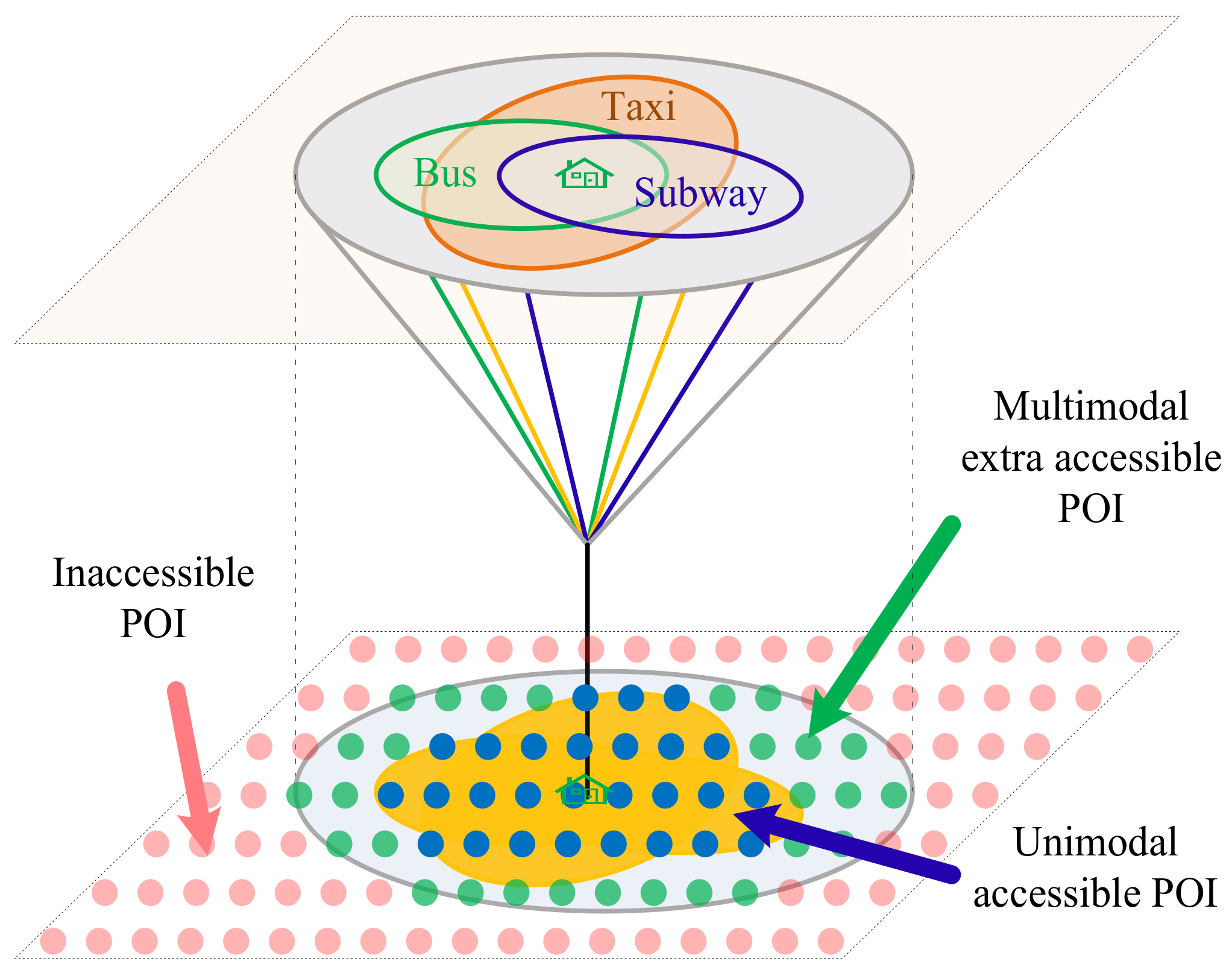
By using multimodal instead of unimodal transportation modes, travelers can access more opportunities, as shown in Figure 7. In order to effectively evaluate the impact of multimodal transportation, the difference value and ratio are used as the evaluation indicator to demonstrate the advantages of multimodal accessibility over unimodal accessibility (1 + 1 ≥ 2), as shown in Equations (29) and (30).
where is the cumulative opportunity accessibility of all unimodal accessibility opportunities, i.e., the union of all unimodal accessibility opportunities. is the cumulative opportunity accessibility of the multimodal network.
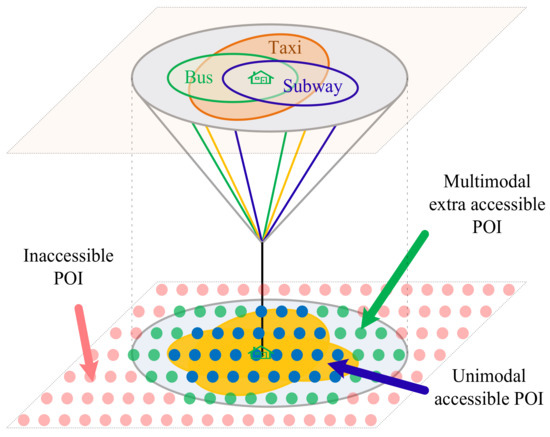
Figure 7.
Advantages of multimodal accessibility.
4. Study Area and Data Collection
Taking Beijing Fifth Ring Road as the research area, this paper constructs three transportation modes, including bus, subway, and taxi. There are 203 subway stations and 2698 bus stations. The area is divided into 482 grids by hexagonal grids with a length of 0.76 km. The following data are used: (1) bus and subway smart card data from 3 August to 9 August 2015, and its schedule data obtained through the mapbar website and Gaode map application; (2) openstreet map road network data; (3) actual detected data of road conditions; (4) Beijing POI data; and (5) population data in Beijing.
Monetary cost calculation: Considering the impact of distance on cost, we can use the monetary cost equation from the official website of Beijing. The monetary cost for taxi can be calculated by Equation (31) (http://fgw.beijing.gov.cn/bmcx/djcx/cxldj/202003/t20200331_1752789.htm, accessed on 1 August 2021). The monetary cost for bus and subway can be calculated by Equations (32) and (33) (http://fgw.beijing.gov.cn/bmcx/djcx/cxldj/202003/t20200331_1752788.htm, accessed on 1 August 2021). In this paper, we set the waiting time for taxi mode to 5 min and assume that taxis are available at the station.
where , and are the one-time ride distance by taxi, bus, and subway, km, respectively. , and are the one-time ride monetary cost by taxi, bus, and subway, RMB, respectively.
5. Results
5.1. The Impedance Heterogeneity
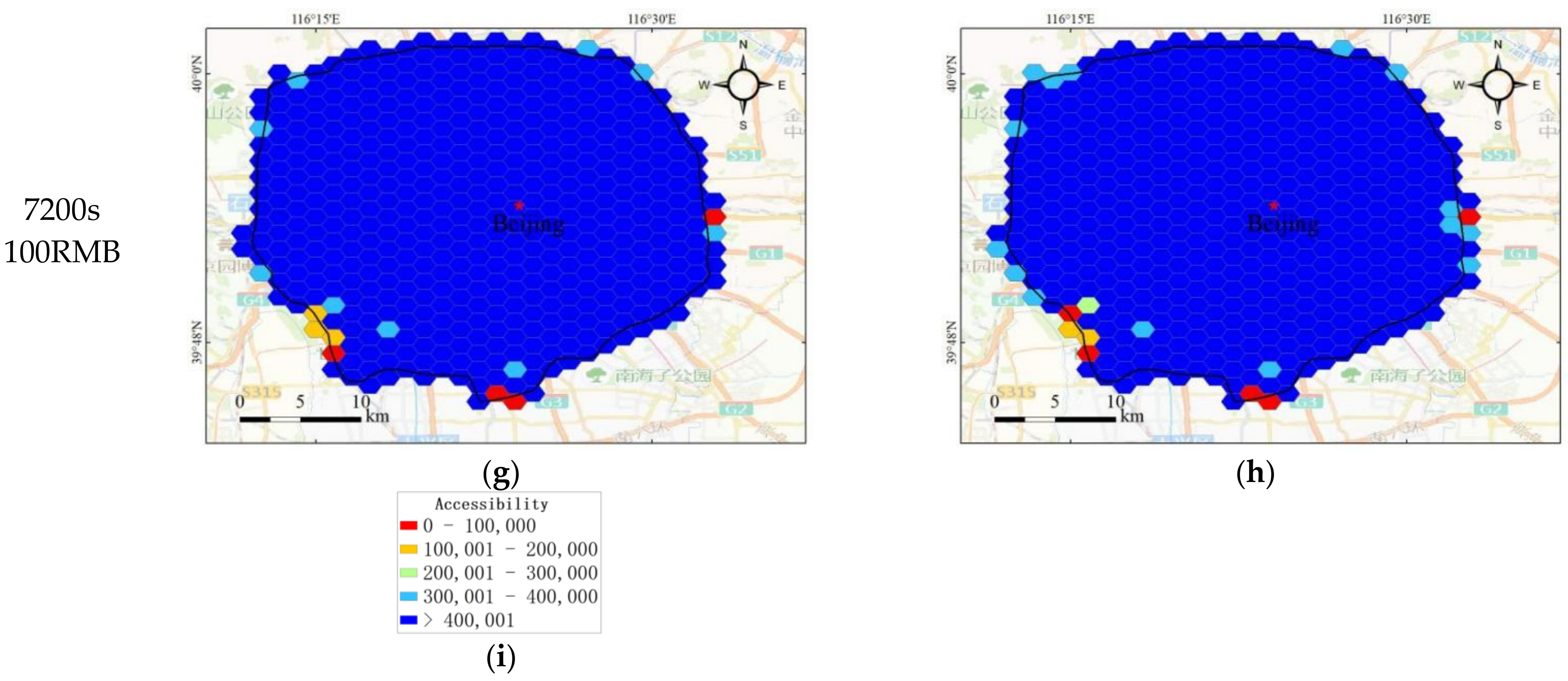
We use the proposed method to evaluate under travel time uncertainty; we set to 50% and 90%, the time to 3600 s and 7200 s, and the monetary cost to RMB 20 and RMB 100. The results are shown in Figure 8, in which Figure 8a–h show the accessibility results of Beijing Fifth Ring Road, and Figure 8i shows the chroma bar. By comparing the accessibility results of different reliability levels under the conditions of the same time and monetary cost, it can be seen that a higher reliability level leads to worse accessibility. By comparing the accessibility results of the same reliability with different levels of time and monetary cost conditions, higher monetary cost constraint leads to better accessibility, as shown in Figure 8a vs. Figure 8c, Figure 8b vs. Figure 8d, Figure 8e vs. Figure 8g, and Figure 8f vs. Figure 8h. Higher time constraint leads to better accessibility, as shown in Figure 8a vs. Figure 8e, Figure 8c vs. Figure 8f, Figure 8b vs. Figure 8f, and Figure 8d vs. Figure 8h. As can be seen, it is necessary to take into account the impact of multiple constraints, such as time and monetary costs, when assessing accessibility under travel time uncertainty. The impedance heterogeneity between different modes is significant, so it is biased to take time as the only impedance. In addition, regional accessibility is high in the central area, gradually decreasing toward the suburbs.
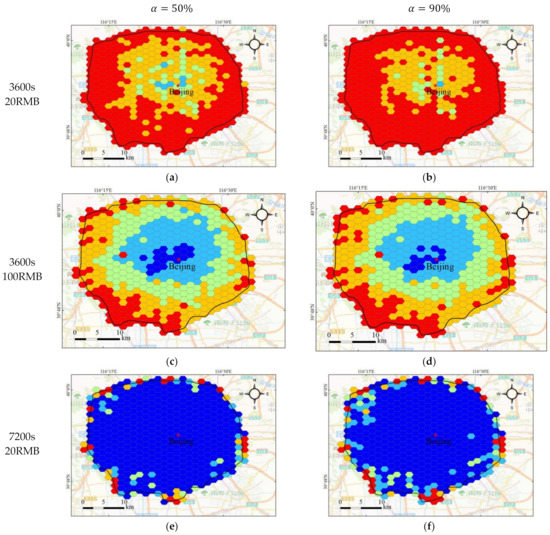
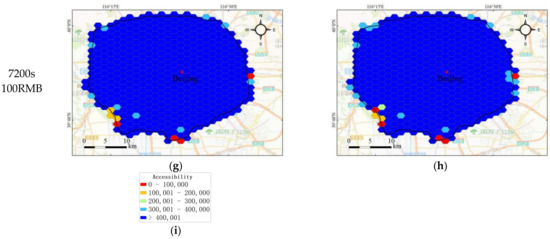
Figure 8.
Accessibility of Beijing Fifth Ring Road: (a–h) the accessibility under different conditions, and (i) the colorimetric bar of accessibility. (Note: there are 502,180 POIs within Beijing’s 5th Ring Road, and the equalization method is used to classify the accessibility level, which is divided into five levels after rounding).
5.2. Advantages of Multimodal Compared with Unimodal
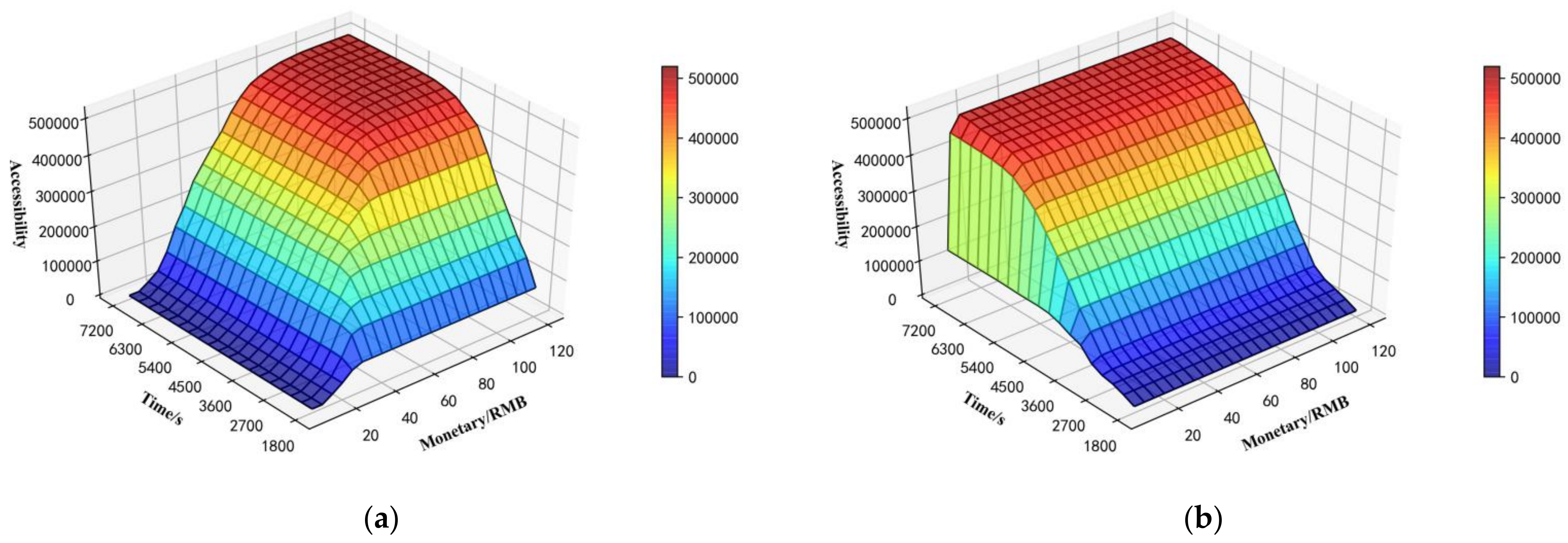
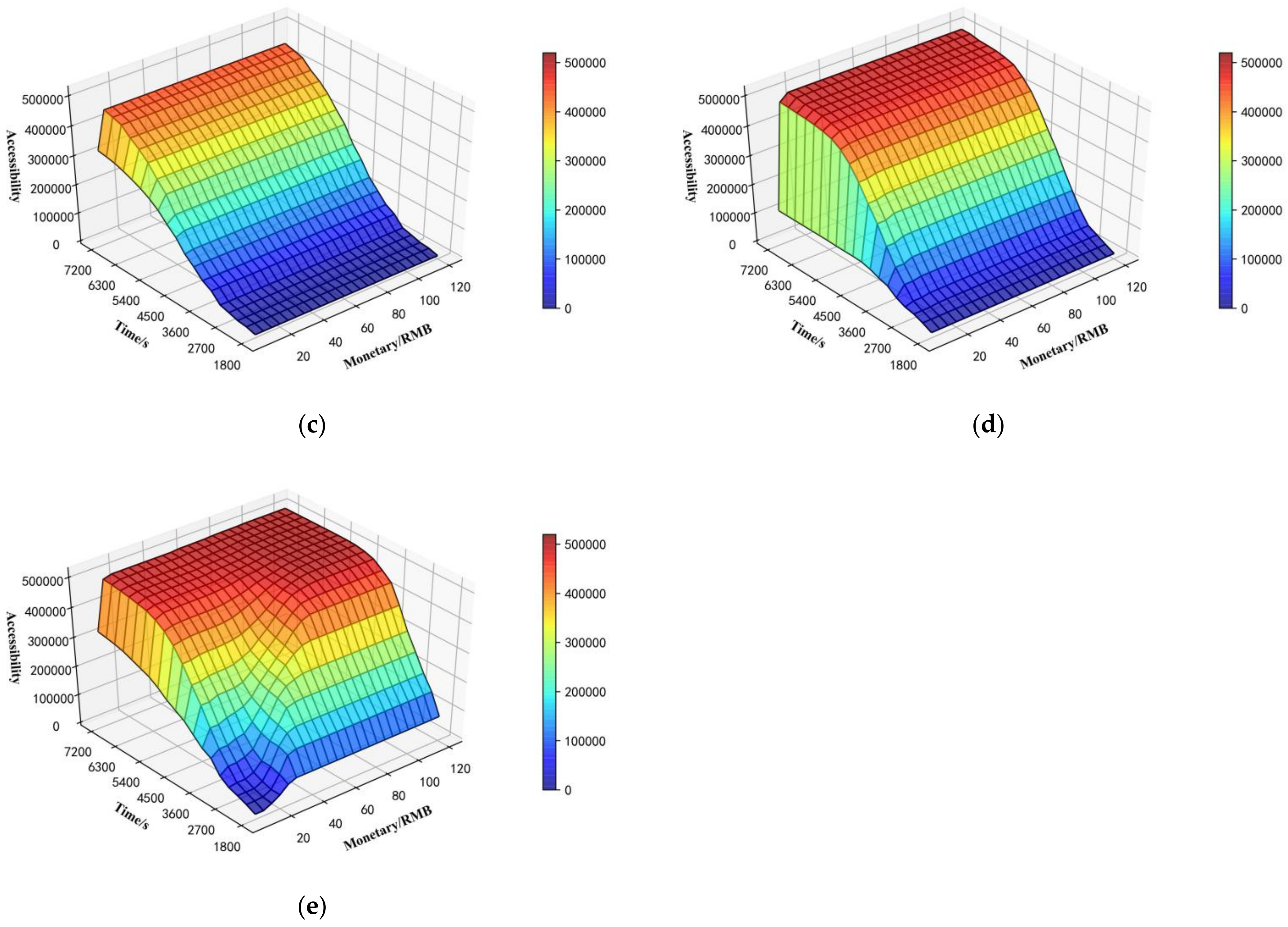
We take the central grid as an example to analyze the advantages of multimodal networks over the unimodal network, where Tiananmen Square is located. We plot the accessibility of each mode under the condition of different times and monetary costs, as shown in Figure 9. According to Figure 9a, the accessibility of the taxi mode is mainly limited by travel monetary cost constraints. For the mode of bus or subway, however, according to Figure 9b,c, the accessibility of the bus or subway mode is mainly limited by travel time constraints. Figure 9d shows that the accessibility trend of combined transportation is the same as that of the public transportation subway, which is mainly restricted by travel time constraints. This is because the network division method proposed in this paper was used to obtain the combined transportation networks, with bus or subway as the main transportation mode. Comparing Figure 9d,e, the accessibility of the combined mode is worse than that of the unimode under certain budgets. Compared with Figure 9a–d, Figure 9e indicates that multimodal can effectively improve the accessibility of the area. Due to the limitation of the research area, when accessibility grows to a certain level, it no longer grows.
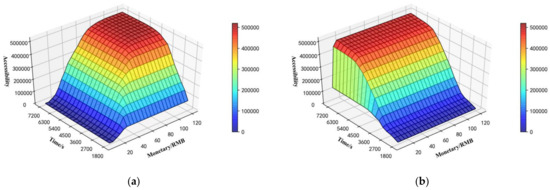
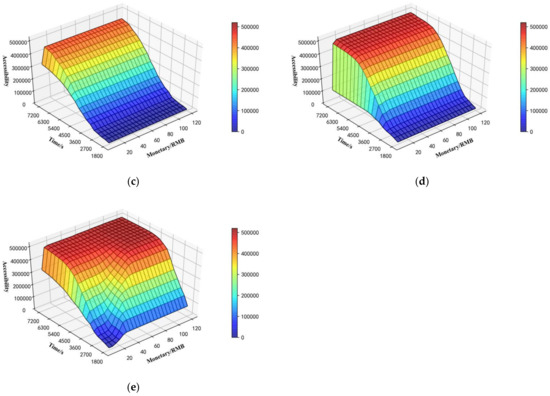
Figure 9.
Accessibility of various modes in the central area: (a) taxi accessibility, (b) bus accessibility, (c) subway accessibility, (d) combined-mode accessibility, and (e) multimodal accessibility.
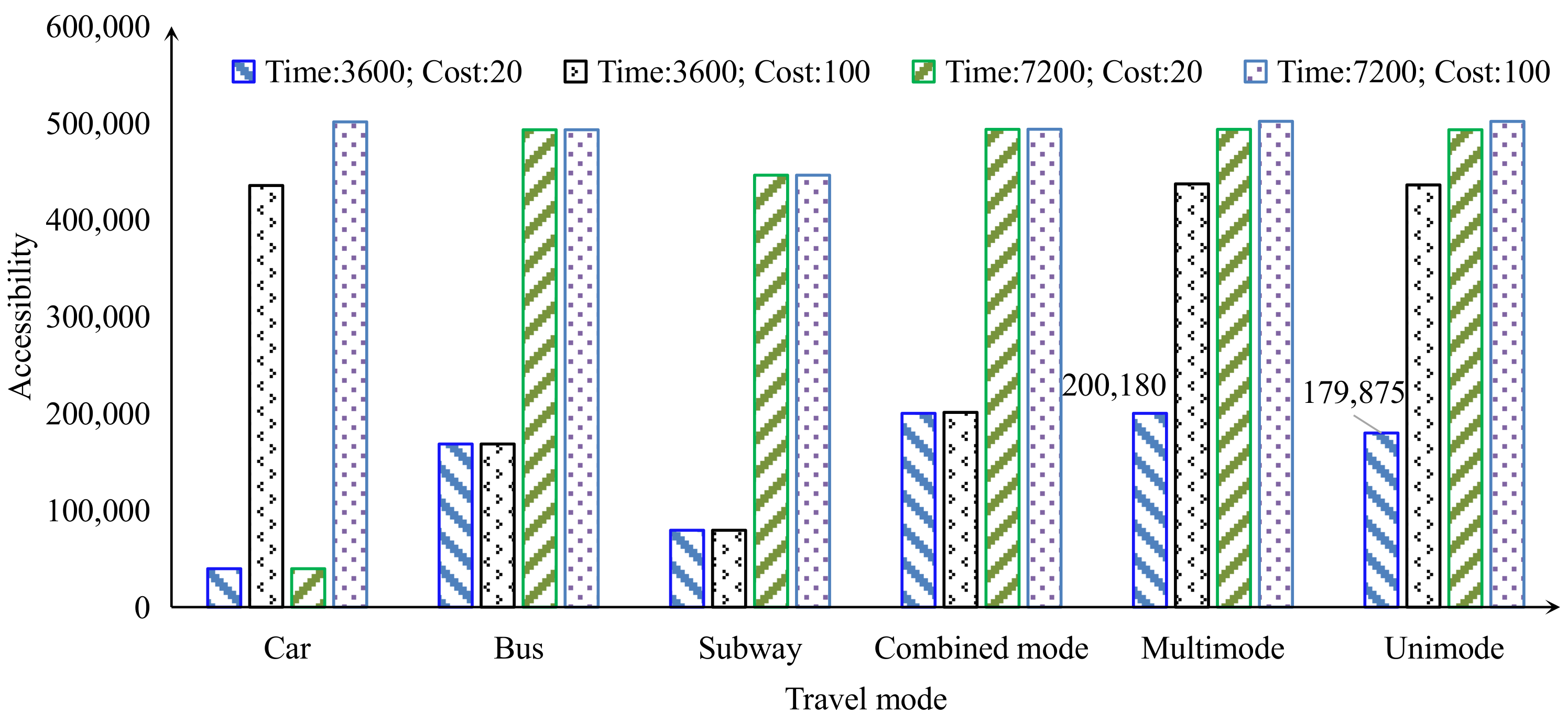
We use three points from Figure 9 to illustrate the impact of time and monetary cost on accessibility, as shown in Figure 10. It shows that monetary cost and time heterogeneity between modes varies greatly. Therefore, it can be verified that multimodal transportation cannot use travel time as the unique impedance for accessibility evaluation. Multi-impedance constraint is a typical feature of distinguishing multimodal from unimodal when studying accessibility. In addition, any mode can be the most effective under specific time and cost conditions, so no fixed mode is optimal.
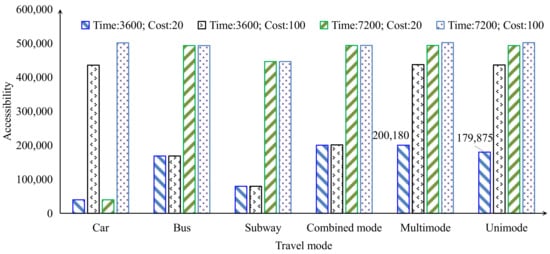
Figure 10.
Accessibility at different times and costs.
5.3. Advantages of Multi-Modal Transfers under Different Risk-Preference Conditions
We plot the difference and ratio between unimodal accessibility and multimodal accessibility, as shown in Figure 11. In [2700 s, 5400 s] and [RMB 10, RMB 40], the advantage of multimodal accessibility is more obvious. The advantage reaches the maximum value around 3600 s and RMB 20, showing a central symmetry. As the impedance threshold increases, all POIs in the research area can be reached, so that the level of advantage tends to become zero. In terms of the central research grid, with the increase in , the accessibility of multimode is better than that of unimode. The reason is that a higher allows travelers to reach a smaller travel range. The number of POIs in Beijing decreases from the center to the suburbs. Therefore, the multimode can obtain a relatively larger number of POIs than the unimode, resulting in obvious advantages, i.e., . The advantage of multimodal over unimodal accessibility increases with reliability, and it can be improved up to 14.61% by multimodal transfers (see Figure 11f).
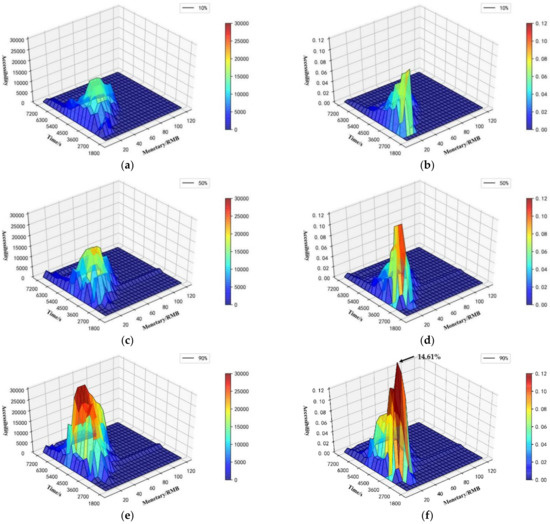
Figure 11.
The difference and ratio between unimodal accessibility and multimodal accessibility: (a,b) the difference and ratio at 10% reliability, (c,d) the difference and ratio at 50% reliability, and (e,f) the difference and ratio at 90% reliability.
5.4. Impacts of Reliability
The probability of on-time arrival is set to 10%, 50%, and 90% to analyze the impact of reliability on accessibility with different multimodal transport modes. From Figure 12a–c, it can be seen that travel time reliability can affect regional accessibility, i.e., the higher the reliability, the lower the accessibility. In particular, reliability has the smallest impact on subways and the greatest impact on buses. Since the subway runs on a separate track, it is less affected by travel time uncertainty, while the bus needs to run on the road, which is severely affected by road congestion and is more affected by travel time uncertainty. Furthermore, in all models, the impact of reliability increases first and decreases finally as travel time, because reliability affects the effective travel time. The greater the reliability level, the longer the effective travel time.
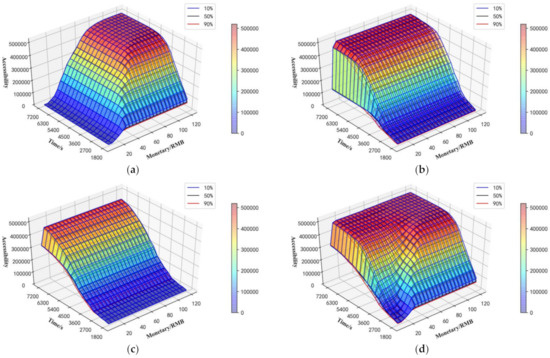
Figure 12.
The impact of reliability on accessibility: (a) taxi, (b) bus, (c) subway, and (d) multimode.
Therefore, as the threshold of travel time increases, the difference in accessibility increases. After that, due to the limitation of the research area, all areas can be reached by travelers, so the impact of reliability on accessibility is ultimately reduced. Comparing the blue, black, and red surfaces of each subgraph in Figure 12, we can see that risk-seeking travelers have the greatest accessibility, indicating that no matter what value takes, the multimodal accessibility will always decrease with the increase in reliability.
5.5. Comparison of Different Methods
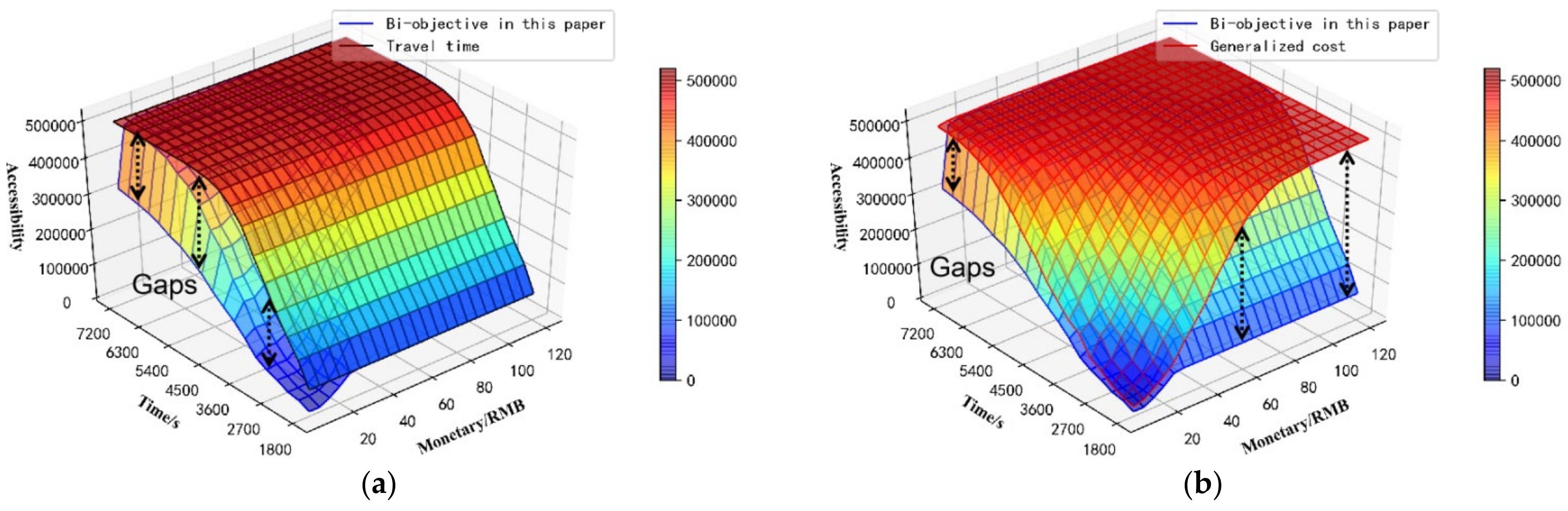
In order to verify the superiority of the accessibility model and algorithm, we set to 90% and VOT (value of time) to RMB 52.7, according to the average salary in Beijing, and use three different types of methods to calculate accessibility, as shown in Figure 13. Compared with the travel time method [19], our bi-objective accessibility method can effectively reflect accessibility with low-cost budgets and eliminate the gaps caused by ignoring cost budgets (see Figure 13a). Compared with the generalized cost method [23,25], our proposed method can effectively reflect accessibility with low-cost and high-time budgets or low-time and high-cost budgets, and eliminate the gaps caused by converting time to generalized cost budgets (see Figure 13b). Thus, the superiority of the two-stage bi-objective opportunity model is validated.
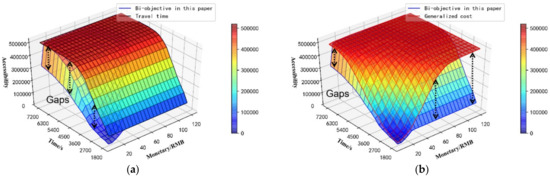
Figure 13.
Comparison of different methods: (a) the travel time method, and (b) the generalized cost method.
5.6. Applications in Transportation Planning
To verify the effectiveness of the proposed method, we classify the grids by analyzing the relationship between multimodal accessibility and population, and thus propose corresponding planning suggestions for each grid type.
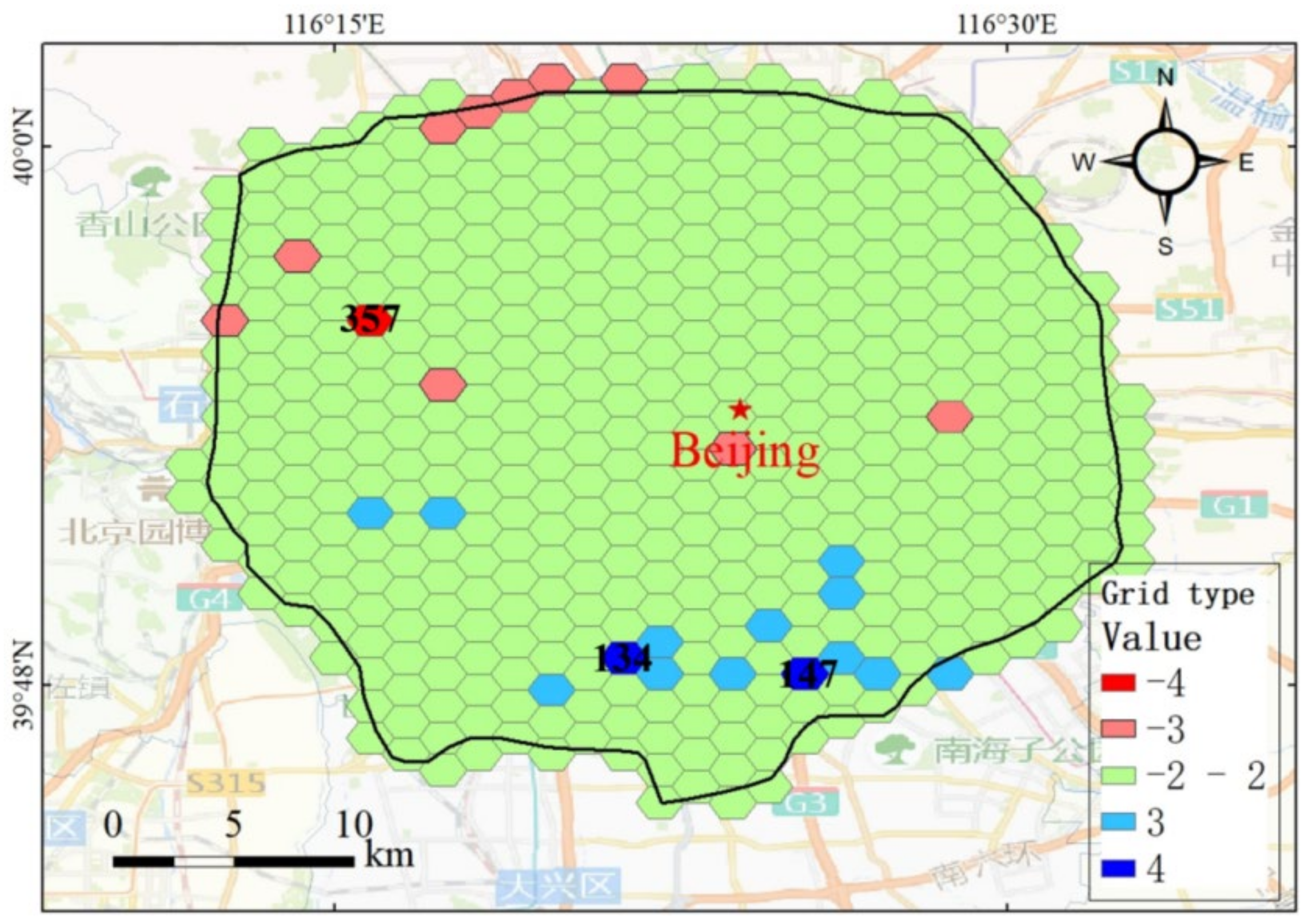
We set the time threshold to 3600 s, the reliability to 90%, and the cost threshold to RMB 10, RMB 20, and RMB 100 in order to respectively calculate bus and subway accessibility, one taxi transaction accessibility, and combined accessibility, including all modes. We rank the population in each grid from small to large and equally divide it into five levels (i.e., low, lower, medium, higher, and high) marked with 1, 2, 3, 4, and 5, respectively. Similarly, accessibility is also divided into five levels from low to high. When the cost threshold is set to RMB 10, by subtracting the population level value from the accessibility level value, we can identify grids with high accessibility and small population according to result ≥ 3, as shown in blue grids in Figure 14, in which Grid 134 and Grid 147 are the most prominent. Due to greater accessibility of these grids, including low-cost public transportation, such as buses and subways, as well as smaller populations, we recommend that commuters in Beijing choose to live in these places, as they can get to work more reliably to reduce penalties for late arrival.
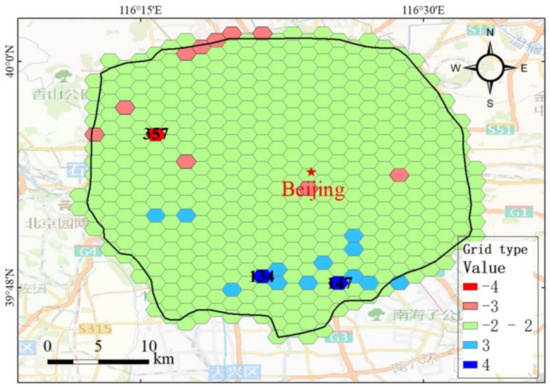
Figure 14.
Grid type.
Similarly, grids with low accessibility and large population can be identified according to result ≤−3, as shown in the red grid in Figure 14, in which Grid 357 is the most prominent. Due to the lower accessibility and the larger population of these grids, it is suggested that the government should take some traffic demand management measures, such as increasing bus stations and optimizing subway network to improve the low-cost accessibility of the grid to meet the commuting demand.
In order to elaborate more on the characteristics of grids 357, 134, 147, we analyze POI types. We find that the main POI types of Grids 134 and 147 are business facilities, in which their shopping and restaurant POIs account for 55.27% and 47.09% respectively, and only 28.75% of grid 357. So, Grids 134 and 147 are mainly business areas. For grid 357, its housing and education POI types account for 18.47%, and only 10.92% and 8.02% of Grids 134 and 147. So, Grid 357 is mainly a residential area.
Moreover, Table 3 shows that transactions between taxis and subways can improve accessibility, especially for girds with low accessibility and large population. When only considering the objective of travel time, the accessibility of Grid 357 (185,823) is even better than that of Grid 134 (177,144) and Grid 147 (176,865). However, its low-cost accessibility is poorer if the bi-objectives of time and cost are considered. Thus, the proposed method can effectively guide traffic management departments to improve traffic accessibility from the perspective of cost and time under travel time uncertainty and advise commuters to choose living places.

Table 3.
Grid classification.
6. Conclusions
In this paper, we proposed a multimodal super network based on smart card data, which can reduce the total set of paths that people would not choose in reality and solved the problems of route collinearity and fare calculation. Then, we established a two-stage opportunity accessibility model to evaluate accessibility with budgets of time and monetary cost under travel time uncertainty. Next, we divided this network into seven parts covering the common modes to make it possible to evaluate bi-objective accessibility under travel time uncertainty in large-scale multimodal networks. Moreover, we created a multimodal reliability path finding model for each section and improved the reliability boundary convergence algorithm to calculate bi-objective accessibility under travel time uncertainty. Finally, we demonstrated that the impedance heterogeneity among different modes is obvious, and there is a bias in taking time as the only factor for accessibility assessment. Multimodal travel has better accessibility than the unimodal one, which verifies the problem of “1 + 1 ≥ 2”, i.e., the multimode can obtain a relatively larger number of POIs than the unimode, resulting in obvious advantages.
Although multimodal accessibility decreases as the reliability increases, the advantage of multimodal over unimodal accessibility increases with reliability, and it can be improved up to 14.61% by multimodal transfers. Furthermore, we identified grids with high accessibility and small population under the condition of 90% reliability, and recommended commuters to choose these places to reduce the penalty caused by late arrival. Similarly, we identified grids with low accessibility and a large population, and recommended the government to focus on improving low-cost accessibility of these grids to meet the commuting demand, which verified the effectiveness of the proposed method.
The limitation of this paper is that the scope of the study is within a city, i.e., Beijing. It requires further in-depth research and extensive data to assess inter-city accessibility and to provide policy recommendations for national urban planning. In future studies, we will further evaluate inter-city accessibility to improve regional equity. Furthermore, it can be extended to the reliability of facilities, such as the reliability of available parking space when arriving at a parking lot. Moreover, it can be further extended to the multi-objective study, including environmental and service-quality factors.
Author Contributions
Conceptualization, Huijun Sun; methodology, Wentao Yu and Tao Feng; software, Wentao Yu; validation, Guangyu Xin; formal analysis, Ying Lv; investigation, Guangyu Xin; resources, Huijun Sun; data curation, Jianjun Wu; writing—original draft preparation, Wentao Yu; writing—review and editing, Huijun Sun and Tao Feng; visualization, Ying Lv; supervision, Huijun Sun; project administration, Wentao Yu; funding acquisition, Huijun Sun. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China (71890972/71890970; 91846202; 72171020), the 111 Project (No. B20071), and the Fundamental Research Funds for the Central Universities (No. 2021RC237).
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the anonymous reviewers and the editors for their constructive comments that helped to improve the paper significantly.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The equations to calculate the effective travel time on a path are shown as follows.
where and are the mean and the standard deviation of travel time, respectively. and are the mean and standard deviation of the travel time of the path between , respectively. and are the travel time distribution of link and path , respectively. is the path-link incidence, i.e., means that the link is on the path , and otherwise. , is the effective travel time of link and path . is the on-time arrival probability. is an inverse function of the standard normal cumulative distribution function. is the upper of the standard normal cumulative distribution. and are the safety margin of link and path, respectively.
References
- Jia, S.; Yuan, Q.; Cai, W.; Lv, J.; Hu, L. Establishing prediction models for feeding power and material drilling power to support sustainable machining. Int. J. Adv. Manuf. Technol. 2019, 100, 2243–2253. [Google Scholar] [CrossRef]
- Yang, Z.; Gao, Z.; Sun, H.; Liu, F.; Zhao, J. Finding most reliable path with extended shifted lognormal distribution. IEEE Access 2018, 6, 72494–72505. [Google Scholar] [CrossRef]
- Hansen, W.G. How Accessibility Shapes Land Use. J. Am. Plan. Assoc. 1959, 25, 73–76. [Google Scholar] [CrossRef]
- Wachs, M.; Kumagai, T.G. Physical accessibility as a social indicator. Socio-Econ. Plan. Sci. 1973, 7, 437–456. [Google Scholar] [CrossRef]
- Uncles, M.D. Discrete Choice Analysis: Theory and Application to Travel Demand. J. Oper. Res. Soc. 1987, 38, 370–371. [Google Scholar] [CrossRef]
- Miller, H.J. Modelling accessibility using space-time prism concepts within geographical information systems. Int. J. Geogr. Inf. Syst. 1991, 5, 287–301. [Google Scholar] [CrossRef]
- Shen, L.; Shao, H.; Wu, T.; Lam, W.H.K.; Zhu, E.C. An energy-efficient reliable path finding algorithm for stochastic road networks with electric vehicles. Transp. Res. Part C Emerg. Technol. 2019, 102, 450–473. [Google Scholar] [CrossRef]
- Kaparias, I.; Bell, M.G.H.; Belzner, H. A new measure of travel time reliability for in-vehicle navigation systems. J. Intell. Transp. Syst. Technol. Plan. Oper. 2008, 12, 202–211. [Google Scholar] [CrossRef]
- Liu, R.; Chen, Y.; Wu, J.; Xu, T.; Gao, L.; Zhao, X. Mapping spatial accessibility of public transportation network in an urban area—A case study of Shanghai Hongqiao Transportation Hub. Transp. Res. Part D Transp. Environ. 2018, 59, 478–495. [Google Scholar] [CrossRef]
- Chen, A.; Ji, Z. Path finding under uncertainty. J. Adv. Transp. 2005, 39, 19–37. [Google Scholar] [CrossRef]
- Nie, Y.; Wu, X. Shortest path problem considering on-time arrival probability. Transp. Res. Part B Methodol. 2009, 43, 597–613. [Google Scholar] [CrossRef]
- Chen, B.Y.; Li, Q.; Wang, D.; Shaw, S.L.; Lam, W.H.K.; Yuan, H.; Fang, Z. Reliable Space-Time Prisms Under Travel Time Uncertainty. Ann. Assoc. Am. Geogr. 2013, 103, 1502–1521. [Google Scholar] [CrossRef]
- Matisziw, T.C.; Grubesic, T.H. Evaluating locational accessibility to the US air transportation system. Transp. Res. Part A Policy Pract. 2010, 44, 710–722. [Google Scholar] [CrossRef]
- Jiang, S. Urban Public Transit System Accessibility Evaluation and Optimization Method. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2019. [Google Scholar]
- Mavoa, S.; Witten, K.; McCreanor, T.; O’Sullivan, D. GIS based destination accessibility via public transit and walking in Auckland, New Zealand. J. Transp. Geogr. 2012, 20, 15–22. [Google Scholar] [CrossRef]
- Salonen, M.; Toivonen, T. Modelling travel time in urban networks: Comparable measures for private car and public transport. J. Transp. Geogr. 2013, 31, 143–153. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Ni, J.; Xi, C.; Li, S.; Wang, J. Determining intra-urban spatial accessibility disparities in multimodal public transport networks. J. Transp. Geogr. 2017, 65, 123–133. [Google Scholar] [CrossRef]
- Xia, N.; Cheng, L.; Li, M. Transnational Accessibility between Residential Areas Based on Multimodal Transport System. ISPRS Int. J. Geo-Inform. 2021, 10, 136. [Google Scholar] [CrossRef]
- Zhang, T.; Dong, S.; Zeng, Z.; Li, J. Quantifying multi-modal public transit accessibility for large metropolitan areas: A time-dependent reliability modeling approach. Int. J. Geogr. Inf. Sci. 2018, 32, 1649–1676. [Google Scholar] [CrossRef]
- Sheffi, Y. Urban Transportation Networks: Equilibrium Analysis with Mathematical Programming Methods; Prentice-Hall: Englewood Cliff, NJ, USA, 1985. [Google Scholar]
- Arentze, T.; Timmermans, H. Multistate supernetwork approach to modelling multi-activity, multimodal trip chains. Int. J. Geogr. Inf. Sci. 2004, 18, 631–651. [Google Scholar] [CrossRef]
- Liao, F.; Arentze, T.A.; Timmermans, H.J.P. Constructing personalized transportation networks in multi-state supernetworks: A heuristic approach. Int. J. Geogr. Inf. Sci. 2011, 25, 1885–1903. [Google Scholar] [CrossRef]
- Li, Q.; Liao, F.; Timmermans, H.J.P.; Huang, H.; Zhou, J. Incorporating free-floating car-sharing into an activity-based dynamic user equilibrium model: A demand-side model. Transp. Res. Part B Methodol. 2018, 107, 102–123. [Google Scholar] [CrossRef]
- Pajor, T. Multi-Modal Route Planning Supervisors. Master’s Thesis, University of Karlsruhe (TH), Karlsruhe, Germany, 2009. [Google Scholar]
- Zhang, J. Personalized Route Finding in Multimodal Transportation Networks. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 2016. [Google Scholar]
- Shao, H.; Lam, W.H.K.; Tam, M.L. A Reliability-Based Stochastic Traffic Assignment Model for Network with Multiple User Classes under Uncertainty in Demand. Netw. Spat. Econ. 2006, 6, 173–204. [Google Scholar] [CrossRef]
- Tang, J.; Liang, J.; Zhang, S.; Huang, H.; Liu, F. Inferring driving trajectories based on probabilistic model from large scale taxi GPS data. Phys. A Stat. Mech. Appl. 2018, 506, 566–577. [Google Scholar] [CrossRef]
- Zhang, J.; Liao, F.; Arentze, T.; Timmermans, H. A multimodal transport network model for advanced traveler information systems. Proc.-Soc. Behav. Sci. 2011, 20, 313–322. [Google Scholar] [CrossRef] [Green Version]
- Tomasiello, D.B.; Giannotti, M.; Arbex, R.; Davis, C. Multi-temporal transport network models for accessibility studies. Trans. GIS 2019, 23, 203–223. [Google Scholar] [CrossRef]
- Liao, F.; Rasouli, S.; Timmermans, H. Incorporating activity-travel time uncertainty and stochastic space-time prisms in multistate supernetworks for activity-travel scheduling. Int. J. Geogr. Inf. Sci. 2014, 28, 928–945. [Google Scholar] [CrossRef]
- Chen, B.Y.; Shi, C.; Zhang, J.; Lam, W.H.K.; Li, Q.; Xiang, S. Most reliable path-finding algorithm for maximizing on-time arrival probability. Transp. B 2017, 5, 253–269. [Google Scholar] [CrossRef]
- Chen, B.Y.; Li, Q.; Lam, W.H.K. Finding the k reliable shortest paths under travel time uncertainty. Transp. Res. Part B Methodol. 2016, 94, 189–203. [Google Scholar] [CrossRef]
- Lo, H.K.; Luo, X.W.; Siu, B.W.Y. Degradable transport network: Travel time budget of travelers with heterogeneous risk aversion. Transp. Res. Part B Methodol. 2006, 40, 792–806. [Google Scholar] [CrossRef]
- Yen, J.Y. Finding the K Shortest Loopless Paths in a Network. Manag. Sci. 1971, 17, 712–716. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).