Dynamic Intervisibility Analysis of 3D Point Clouds
Abstract
:1. Introduction
- (1)
- On the one hand, such as unsupervised methods: point cloud-constructed Delaunay triangle meshes can derive inactive triangulation [24], features extraction of point cloud information from point cloud Voronoi diagrams with different geometrical shapes of plates, spheres, and rods [25]; these similar pathway-based approaches [26,27] are time-consuming, susceptible to noise, and do not conform to the true surface topology of the point cloud.
- (2)
- On the other hand, such as supervised methods based on deep learning [28,29]: convolutional neural network-based feature map calculation by the maximum, minimum, and average value of the points in grids generates with the neighborhoods of points [30], features extraction and optimization of point cloud information from the probability distribution and decision tree are obtained by multi-scale convolutional neural network-based points cloud learning [31]; these similar pathway-based approaches [32] only extract the characteristics of independent points, lose part of the spatial information of the point cloud, and affect the generalization ability of the network [33,34,35].
- (1)
- Multi-dimensional points coordinates of camera-based images and LiDAR-based point clouds are aligned to estimate the spatial parameters and point clouds within the FOV of the traffic environment for autonomous driving, including the viewpoint location and FOV range. This contribution determines the effective FOV, reduces the impact of redundant noise, reduces the computational complexity of visual analysis, and is suitable for the dynamic needs of autonomous driving.
- (2)
- Point clouds computation is transferred from Euclidean space to Riemannian space for manifold learning to construct Manifold Auxiliary Surfaces (MAS) for through-view analysis. This contribution makes fast multi-dimensional data processing possible, effectively controls the problems of large amounts, spatial discreteness, and uneven distribution of original point clouds, and makes the calculation of the distance relationship between points more accurate for the real application scenarios of autonomous driving.
- (3)
- The spectral graph analysis for the finite element-composed topological structure of the manifold auxiliary surface is constructed to innovatively realize the intervisibility analysis of points and point clouds in the Mix-Planes Calculation Structure (MPCS). This contribution has resulted in fast, efficient, robust, and accurate results, which can dynamically handle every motion movement in autonomous driving.
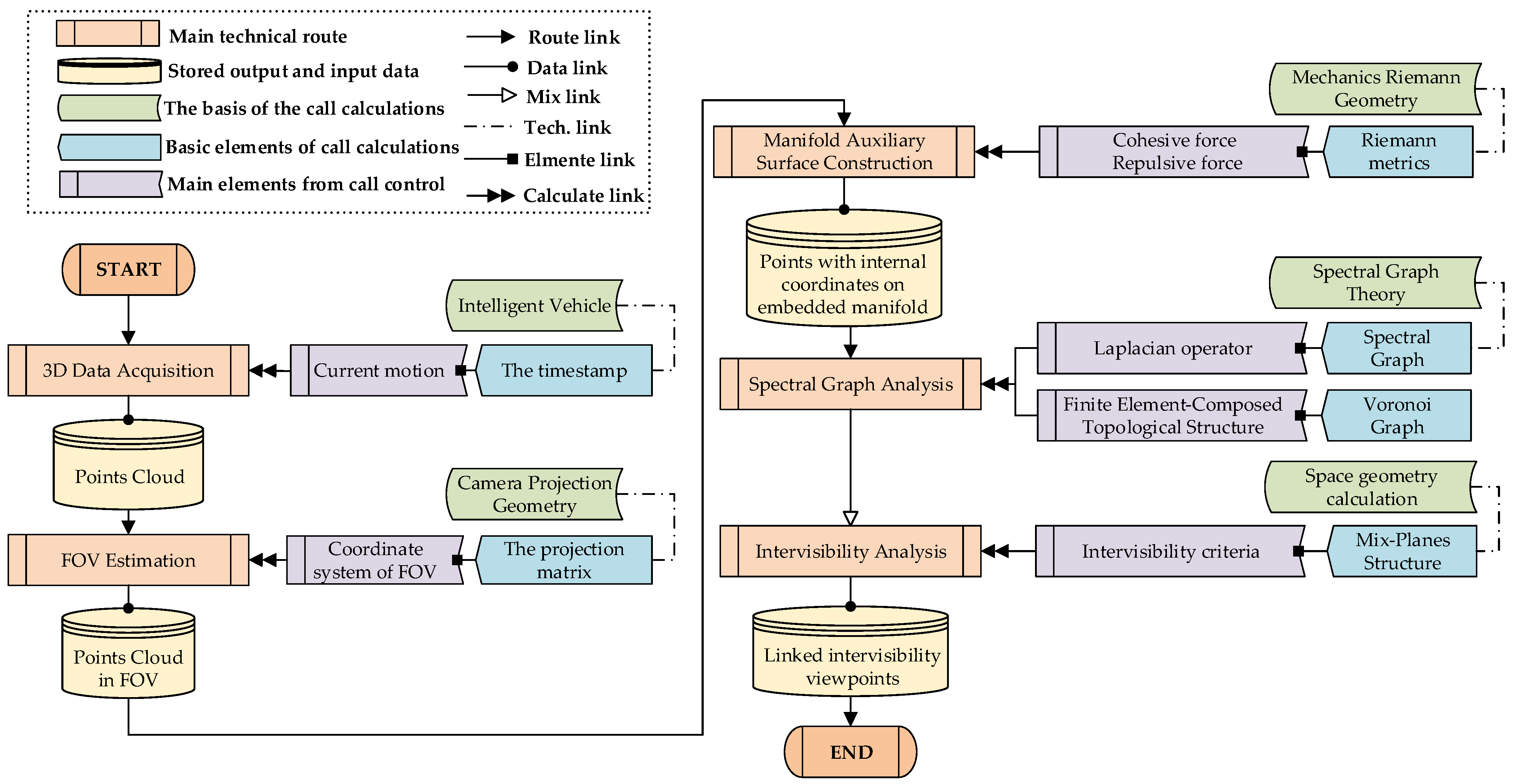
2. Method
- (1)
- FOV estimation and point cloud generation at the current motion time of the intelligent vehicle;
- (2)
- Metrics construction of point cloud’s manifold auxiliary surface;
- (3)
- Spectral graph analysis of the finite element-composed topological structure on the manifold auxiliary surface, and the intervisibility analysis under the criterion based on the geometric calculation conditions of the mix-planes structure.
2.1. Estimation of Motion Field-of-View
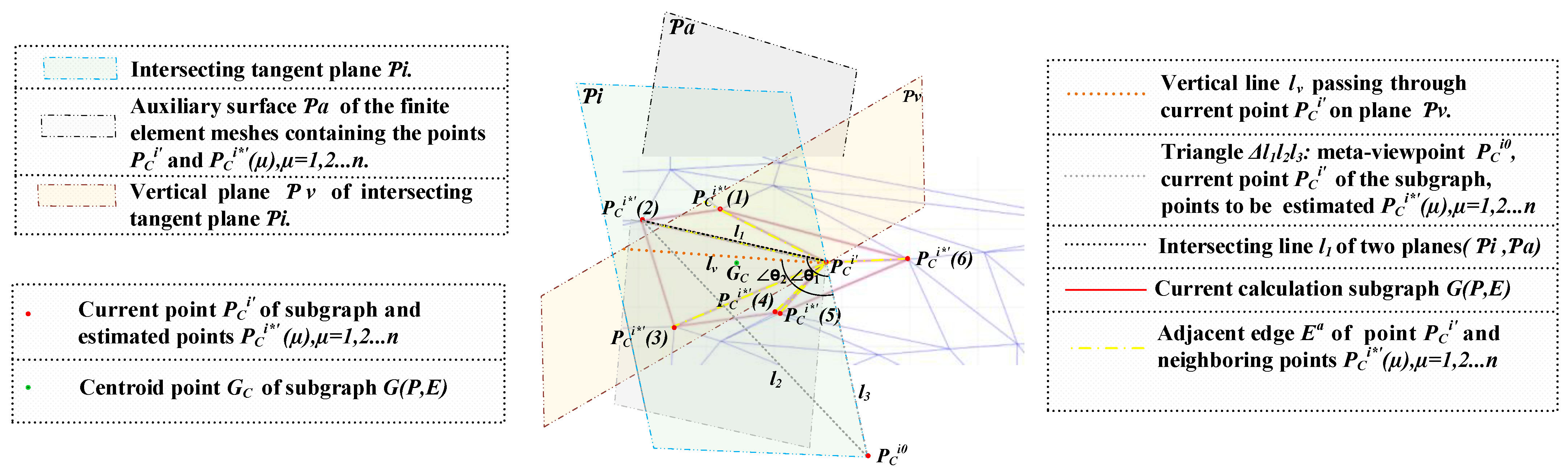
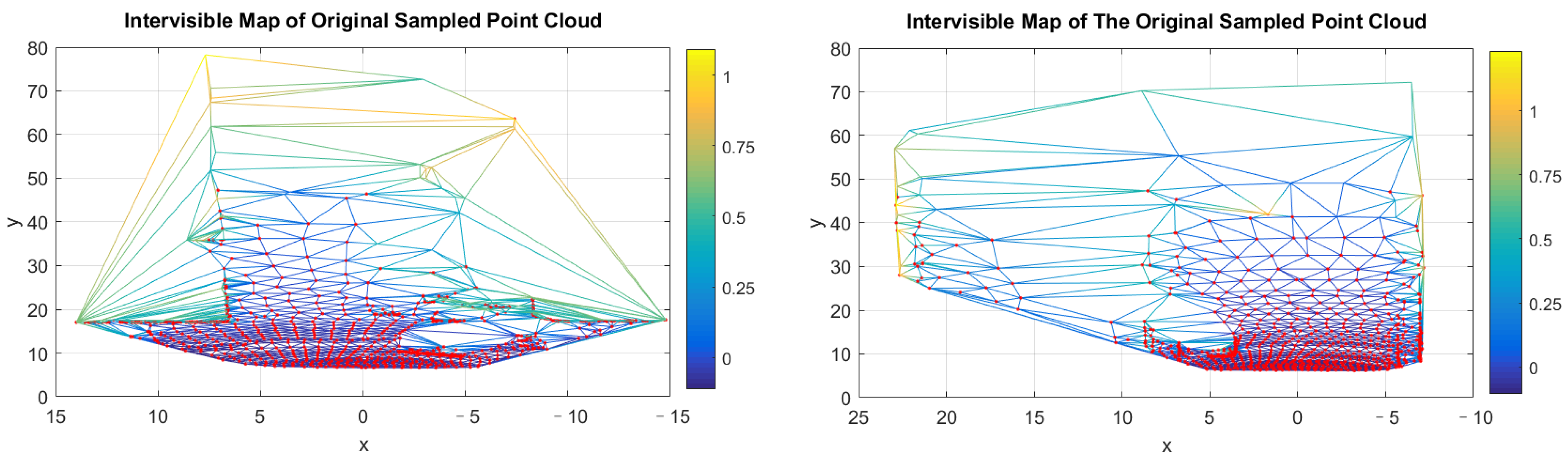
2.2. Manifold Auxiliary Surface for Intervisibility Computing
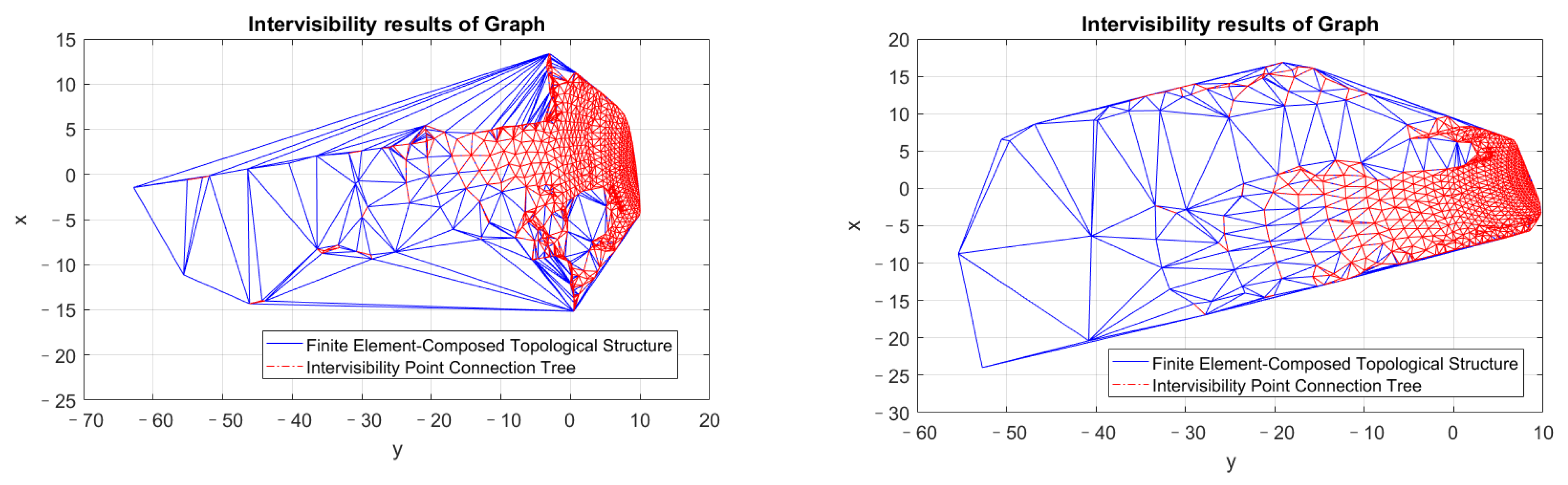
2.3. Spectral Graph Analysis of Finite Element-Composed Topological Structure
| Algorithm 1 The criteria determination process of reachable intervisibility points | |
| 1: | for of and do |
| 2: | if for then |
| 3: | update for ; |
| 4: | end if |
| 5: | else if then |
| 6: | find for ; |
| 7: | update of and ; |
| 8: | find for ; |
| 9: | update of and ; |
| 10: | end if |
| 11: | end for |
| 12: | return |
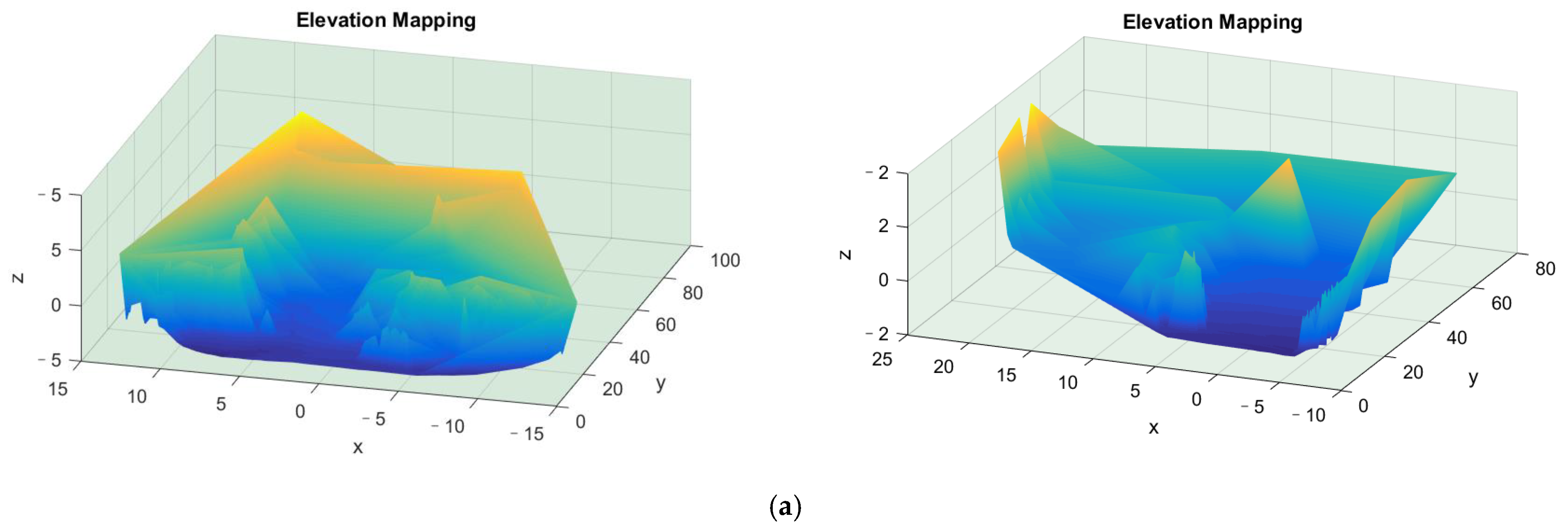
3. Results
4. Results Analysis and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Claussmann, L.; Revilloud, M.; Gruyer, D.; Glaser, S. A review of motion planning for highway autonomous driving. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1826–1848. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Jian, Z.; Huang, Y.; Chen, Y.; Zhou, Z.; Zheng, N. Autonomous driving: Cognitive construction and situation understanding. Sci. China Inf. Sci. 2019, 62, 81101. [Google Scholar] [CrossRef] [Green Version]
- Fisher, P.F. First experiments in viewshed uncertainty: The accuracy of the viewshed area. Photogramm. Eng. Remote Sens. 1991, 57, 1321–1327. [Google Scholar]
- Murgoitio, J.J.; Shrestha, R.; Glenn, N.F.; Spaete, L.P. Improved visibility calculations with tree trunk obstruction modeling from aerial LiDAR. Int. J. Geogr. Inf. Sci. 2013, 27, 1865–1883. [Google Scholar] [CrossRef]
- Popelka, S.; Vozenilek, V. Landscape visibility analysis and their visualisation. ISPRS Arch. 2010, 38, 1–6. [Google Scholar]
- Guth, P.L. Incorporating vegetation in viewshed and line-of-sight algorithms. In Proceedings of the ASPRS/MAPPS 2009 Conference, San Antonio, TX, USA, 16–19 November 2009; pp. 1–7. [Google Scholar]
- Zhang, G.; Van Oosterom, P.; Verbree, E. Point Cloud Based Visibility Analysis: First experimental results. In Proceedings of the Societal Geo-Innovation: Short Papers, Posters and Poster Abstracts of the 20th AGILE Conference on Geographic Information Science, Wageningen, The Netherlands, 9–12 May 2017; pp. 9–12. [Google Scholar]
- Zhu, J.; Sui, L.; Zang, Y.; Zheng, H.; Jiang, W.; Zhong, M.; Ma, F. Classification of airborne laser scanning point cloud using point-based convolutional neural network. ISPRS Int. J. Geo-Inf. 2021, 10, 444. [Google Scholar] [CrossRef]
- Qu, Y.; Huang, J.; Zhang, X. Rapid 3D Reconstruction for Image Sequence Acquired from UAV Camera. Sensors 2018, 18, 225. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Liu, X.J.; Wu, Y.G. Depth Reconstruction from Single Images Using a Convolutional Neural Network and a Condition Random Field Model. Sensors 2018, 18, 1318. [Google Scholar] [CrossRef] [Green Version]
- Gerdes, K.; Pedro, M.Z.; Schwarz-Schampera, U.; Schwentner, M.; Kihara, T.C. Detailed Mapping of Hydrothermal Vent Fauna: A 3D Reconstruction Approach Based on Video Imagery. Front. Mar. Sci. 2019, 6, 96. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Li, D.; Wang, M.; Wang, Z. 3D Change Detection Using Adaptive Thresholds Based on Local Point Cloud Density. ISPRS Int. J. Geo-Inf. 2021, 10, 127. [Google Scholar] [CrossRef]
- Ponciano, J.J.; Roetner, M.; Reiterer, A.; Boochs, F. Object Semantic Segmentation in Point Clouds—Comparison of a Deep Learning and a Knowledge-Based Method. ISPRS Int. J. Geo-Inf. 2021, 10, 256. [Google Scholar] [CrossRef]
- Pan, H.; Guan, T.; Luo, K.; Luo, Y.; Yu, J. A visibility-based surface reconstruction method on the GPU. Comput. Aided Geom. Des. 2021, 84, 101956. [Google Scholar] [CrossRef]
- Loarie, S.R.; Tambling, C.J.; Asner, G.P. Lion hunting behaviour and vegetation structure in an African savanna. Anim. Behav. 2013, 85, 899–906. [Google Scholar] [CrossRef] [Green Version]
- Vukomanovic, J.; Singh, K.K.; Petrasova, A.; Vogler, J.B. Not seeing the forest for the trees: Modeling exurban viewscapes with LiDAR. Landsc. Urban Plan. 2018, 170, 169–176. [Google Scholar] [CrossRef]
- Zong, X.; Wang, T.; Skidmore, A.K.; Heurich, M. The impact of voxel size, forest type, and understory cover on visibility estimation in forests using terrestrial laser scanning. GISci. Remote Sens. 2021, 58, 323–339. [Google Scholar] [CrossRef]
- Fisher, G.D.; Shashkov, A.; Doytsher, Y. Voxel based volumetric visibility analysis of urban environments. Surv. Rev. 2013, 45, 451–461. [Google Scholar] [CrossRef]
- Choi, B.; Chang, B.; Ihm, I. Construction of efficient kd-trees for static scenes using voxel-visibility heuristic. Comput. Graph. 2012, 36, 38–48. [Google Scholar] [CrossRef]
- Krishnan, S.; Manocha, D. Partitioning trimmed spline surfaces into nonself-occluding regions for visibility computation. Graph. Models 2000, 62, 283–307. [Google Scholar] [CrossRef] [Green Version]
- Katz, S.; Tal, A.; Basri, R. Direct visibility of point sets. In ACM SIGGRAPH 2007 Papers; ACM: San Diego, CA, USA, 2007; p. 24-es. [Google Scholar]
- Katz, S.; Tal, A. On the visibility of point clouds. In Proceedings of the IEEE International Conference on Computer Vision International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1350–1358. [Google Scholar]
- Silva, R.; Esperanca, C.; Marroquim, R.; Oliveira, A.A.F. Image space rendering of point clouds using the HPR operator. Comput. Graph. Forum 2014, 33, 178–189. [Google Scholar] [CrossRef]
- Liu, N.; Lin, B.; Lv, G.; Zhu, A.; Zhou, L. A Delaunay triangulation algorithm based on dual-spatial data organization. PFG–J. Photogramm. Remote Sens. Geoinf. Sci. 2019, 87, 19–31. [Google Scholar] [CrossRef]
- Dey, T.; Wang, L. Voronoi-based feature curves extraction for sampled singular surfaces. Comput. Graph. 2013, 37, 659–668. [Google Scholar] [CrossRef] [Green Version]
- Tong, G.; Li, Y.; Zhang, W.; Chen, D.; Zhang, Z.; Yang, J.; Zhang, J. Point Set Multi-Level Aggregation Feature Extraction Based on Multi-Scale Max Pooling and LDA for Point Cloud Classification. Remote Sens. 2019, 11, 2846. [Google Scholar] [CrossRef] [Green Version]
- Shi, P.; Ye, Q.; Zeng, L. A Novel Indoor Structure Extraction Based on Dense Point Cloud. ISPRS Int. J. Geo-Inf. 2020, 9, 660. [Google Scholar] [CrossRef]
- Pastucha, E.; Puniach, E.; Ścisłowicz, A.; Ćwiąkała, P.; Niewiem, W.; Wiącek, P. 3D Reconstruction of Power Lines Using UAV Images to Monitor Corridor Clearance. Remote Sens. 2020, 12, 3698. [Google Scholar] [CrossRef]
- Bello, S.A.; Yu, S.; Wang, C.; Adam, J.M.; Li, J. Review: Deep Learning on three-dimensional Point Clouds. Remote Sens. 2020, 12, 1729. [Google Scholar] [CrossRef]
- Hu, X.; Yuan, Y. Deep-Learning-Based Classification for DTM Extraction from ALS Point Cloud. Remote Sens. 2016, 8, 730. [Google Scholar] [CrossRef] [Green Version]
- Zhao, R.; Pang, M.; Wang, J. Classifying airborne LiDAR point clouds via deep features learned by a multi-scale convolutional neural network. Int. J. Geogr. Inf. Sci. 2018, 32, 960–979. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for three-dimensional Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar]
- Mirsu, R.; Simion, G.; Caleanu, C.D.; Pop-Calimanu, I.M. A PointNet-Based Solution for three-dimensional Hand Gesture Recognition. Sensors 2020, 20, 3226. [Google Scholar] [CrossRef]
- Xing, Z.; Zhao, S.; Guo, W.; Guo, X.; Wang, Y. Processing Laser Point Cloud in Fully Mechanized Mining Face Based on DGCNN. ISPRS Int. J. Geo-Inf. 2021, 10, 482. [Google Scholar] [CrossRef]
- Young, M.; Pretty, C.; Agostinho, S.; Green, R.; Chen, X. Loss of Significance and Its Effect on Point Normal Orientation and Cloud Registration. Remote Sens. 2019, 11, 1329. [Google Scholar] [CrossRef] [Green Version]
- Sharma, R.; Badarla, V.; Sharma, V. PCOC: A Fast Sensor-Device Line of Sight Detection Algorithm for Point Cloud Representations of Indoor Environments. IEEE Commun. Lett. 2020, 24, 1258–1261. [Google Scholar] [CrossRef]
- Zhang, X.; Bar-Shalom, Y.; Willett, P.; Segall, I.; Israel, E. Applications of level crossing theory to target intervisibility: To be seen or not to be seen? IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 840–852. [Google Scholar] [CrossRef]
- Zhi, J.; Hao, Y.; Vo, C.; Morales, M.; Lien, J.M. Computing 3-D From-Region Visibility Using Visibility Integrity. IEEE Robot. Autom. Lett. 2019, 4, 4286–4291. [Google Scholar] [CrossRef]
- Gracchi, T.; Gigli, G.; Noël, F.; Jaboyedoff, M.; Madiai, C.; Casagli, N. Optimizing Wireless Sensor Network Installations by Visibility Analysis on 3D Point Clouds. ISPRS Int. J. Geo-Inf. 2019, 8, 460. [Google Scholar] [CrossRef] [Green Version]

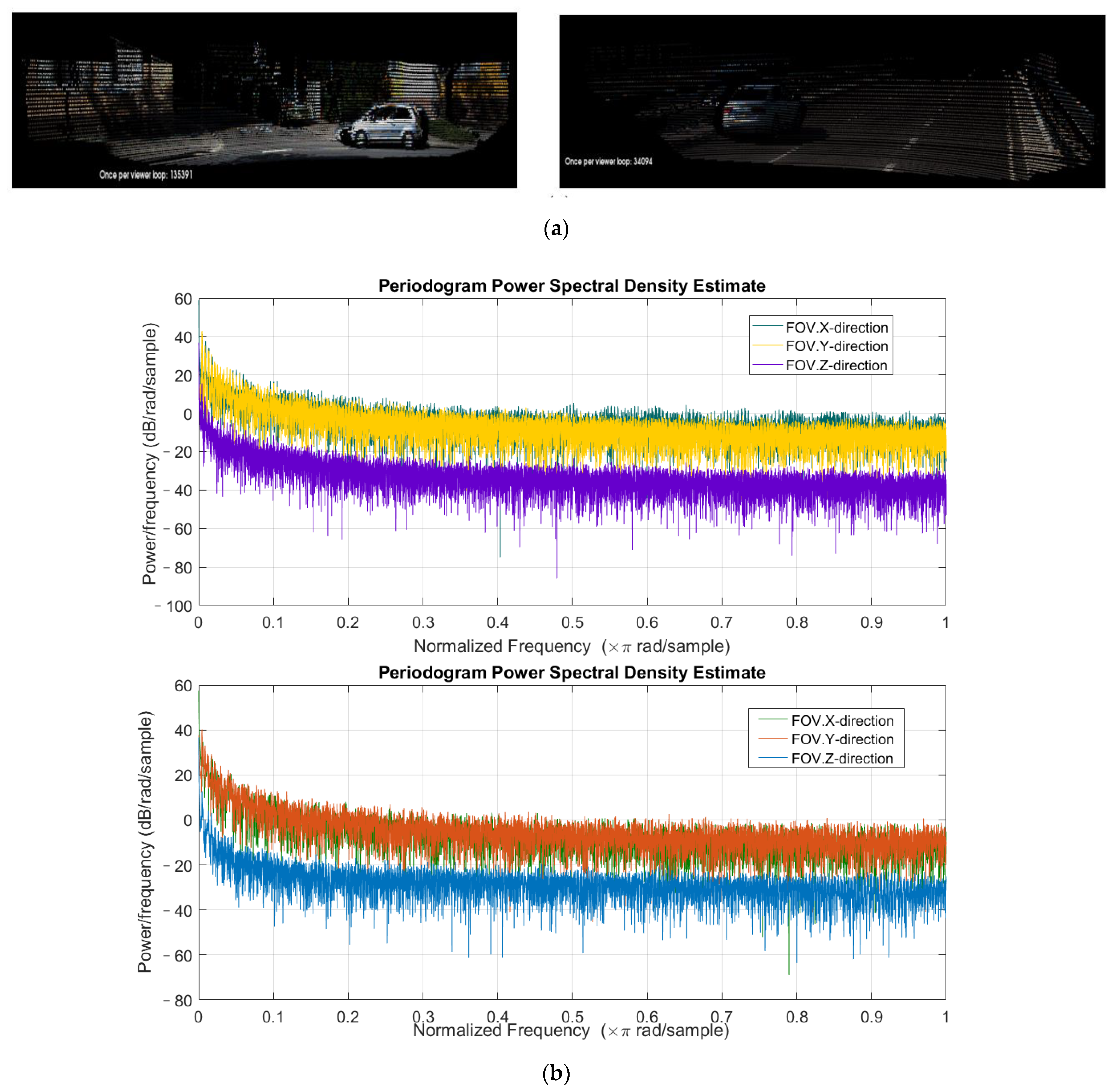
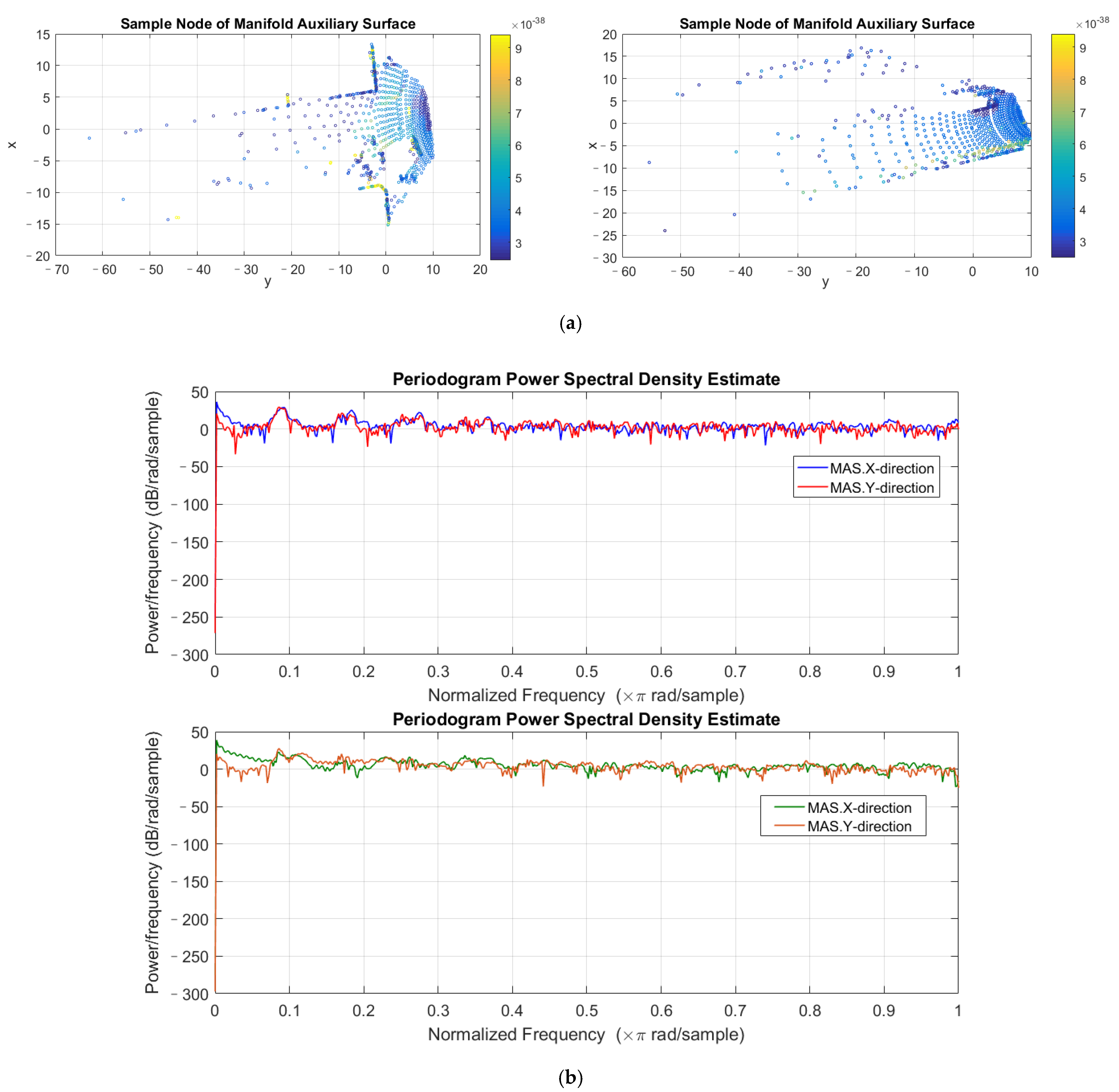



| Experimental Environments | |
|---|---|
| Equipment | Camera: 1.4 Megapixels: Point Grey Flea 2 (FL2-14S3C-C) LiDAR: Velodyne HDL-64E rotating 3D laser scanner, 10 Hz, 64 beams, 0.09-degree angular resolution, 2 cm distance accuracy |
| Platform | Visual studio 2016, Matlab 2016a, OpenCV 3.0, PCL1.8.0 |
| Environment | Ubuntu 16.04/Windows 10, Intel(R) Core(TM) i7-8750H CPU @ 2.20GHz, NVIDIA GeForce GTX 1060/Intel(R) UHD Graphics 630 |
| Samplings | N | SP | ARR (%) | TPI (%) | DCP (%) |
|---|---|---|---|---|---|
| 10 | 3982 | 5982 | 98.40 | 47.61 | 95.46 |
| 20 | 1984 | 2984 | 99.20 | 44.17 | 97.90 |
| 30 | 1320 | 1986 | 99.47 | 41.04 | 98.70 |
| 40 | 987 | 1487 | 99.60 | 38.57 | 99.09 |
| 50 | 786 | 1186 | 99.68 | 35.79 | 99.33 |
| 60 | 653 | 986 | 99.73 | 35.78 | 99.44 |
| 70 | 557 | 842 | 99.77 | 33.87 | 99.55 |
| 80 | 488 | 738 | 99.80 | 30.94 | 99.64 |
| 90 | 432 | 654 | 99.82 | 31.33 | 99.68 |
| 100 | 388 | 588 | 99.84 | 30.50 | 99.72 |
| Samplings | S1 (s) | S2 (s) | S3 (s) | TIME (s) | AS1 (s) | AS2 (s) | AS3 (s) | ATIME (s) | VAR (%) | STD (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 0.0010 | 0.0053 | 0.3854 | 0.3917 | 0.00083 | 0.00515 | 0.36934 | 0.37532 | 0.9197 | 0.9695 |
| 20 | 0.0008 | 0.0026 | 0.1696 | 0.1730 | 0.00080 | 0.00281 | 0.16817 | 0.17178 | 0.5848 | 0.6165 |
| 30 | 0.0008 | 0.0018 | 0.1105 | 0.1131 | 0.00076 | 0.00183 | 0.11383 | 0.11642 | 0.2544 | 0.2682 |
| 40 | 0.0008 | 0.0015 | 0.0858 | 0.0881 | 0.00075 | 0.00150 | 0.08842 | 0.09067 | 0.1532 | 0.1615 |
| 50 | 0.0008 | 0.0013 | 0.0808 | 0.0829 | 0.00074 | 0.00157 | 0.08625 | 0.08856 | 0.2615 | 0.2757 |
| 60 | 0.0009 | 0.0011 | 0.0619 | 0.0639 | 0.00078 | 0.00116 | 0.06341 | 0.06535 | 0.1819 | 0.1918 |
| 70 | 0.0007 | 0.0011 | 0.0651 | 0.0669 | 0.00079 | 0.00107 | 0.06327 | 0.06513 | 0.4069 | 0.4289 |
| 80 | 0.0009 | 0.0010 | 0.0592 | 0.0611 | 0.00075 | 0.00091 | 0.05188 | 0.05354 | 0.1563 | 0.1648 |
| 90 | 0.0009 | 0.0009 | 0.0521 | 0.0539 | 0.00072 | 0.00093 | 0.05130 | 0.05295 | 0.1732 | 0.1825 |
| 100 | 0.0008 | 0.0008 | 0.0459 | 0.0475 | 0.00073 | 0.00088 | 0.04672 | 0.04833 | 0.2473 | 0.2607 |
| Methods | Nodes | ARR (%) | TPI (%) | DCP (%) | TIME (s) |
|---|---|---|---|---|---|
| Global Points | 12,5148 | - | 50.72 | - | 1163.876 |
| Interpolation Points | 20,008 | 84.01 | 50.01 | 52.08 | 17.537 |
| OURS | 572 | 99.54 | 50.25 | 98.65 | 0.1044 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, L.; Li, Y.; Cen, M. Dynamic Intervisibility Analysis of 3D Point Clouds. ISPRS Int. J. Geo-Inf. 2021, 10, 782. https://doi.org/10.3390/ijgi10110782
Bai L, Li Y, Cen M. Dynamic Intervisibility Analysis of 3D Point Clouds. ISPRS International Journal of Geo-Information. 2021; 10(11):782. https://doi.org/10.3390/ijgi10110782
Chicago/Turabian StyleBai, Ling, Yinguo Li, and Ming Cen. 2021. "Dynamic Intervisibility Analysis of 3D Point Clouds" ISPRS International Journal of Geo-Information 10, no. 11: 782. https://doi.org/10.3390/ijgi10110782
APA StyleBai, L., Li, Y., & Cen, M. (2021). Dynamic Intervisibility Analysis of 3D Point Clouds. ISPRS International Journal of Geo-Information, 10(11), 782. https://doi.org/10.3390/ijgi10110782





