An Automatic Extraction Method for Hatched Residential Areas in Raster Maps Based on Multi-Scale Feature Fusion
Abstract
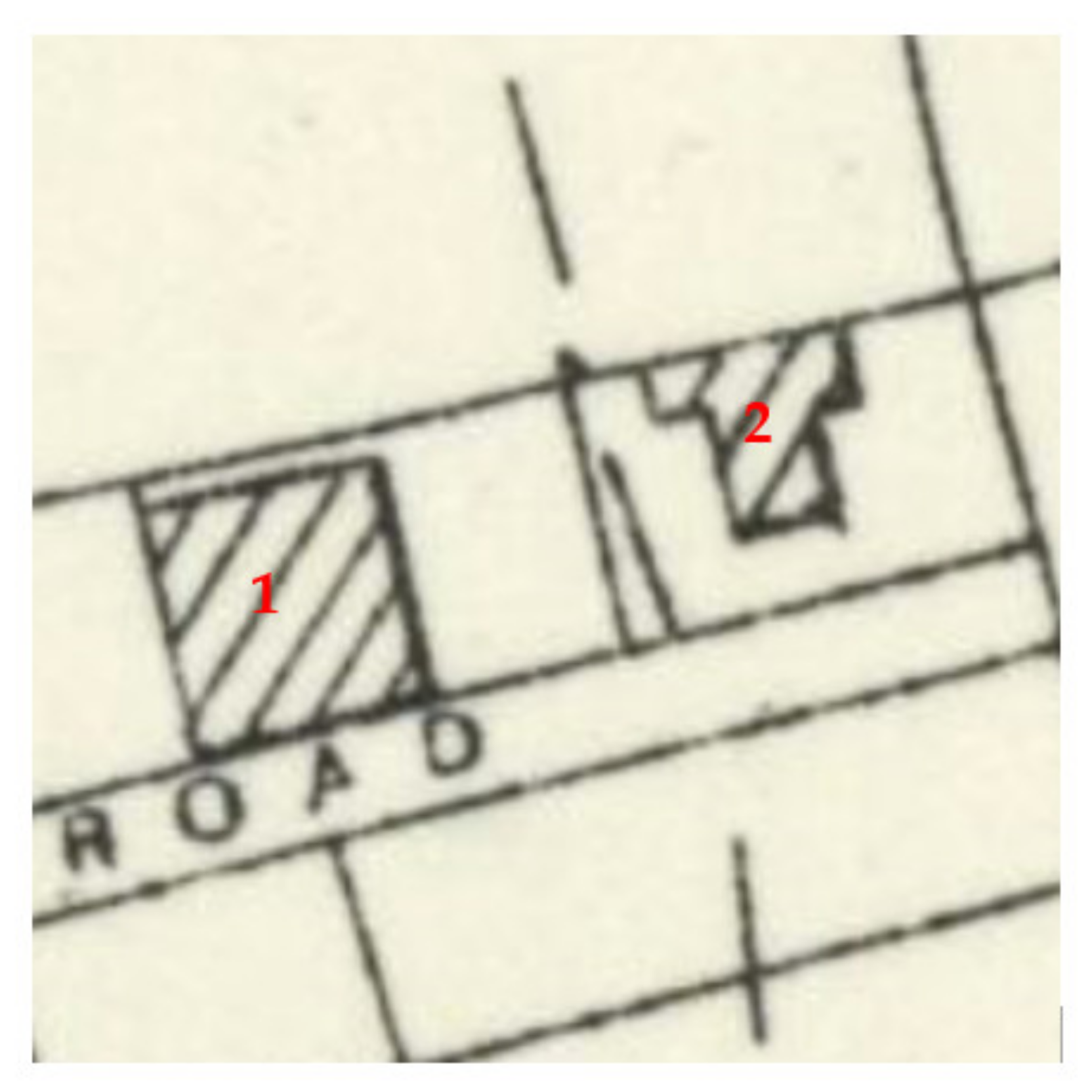
:1. Introduction
- Lack of adaptability: It is difficult to apply the identification method to cases with low image resolution, blurred hatched lines after magnification or irregular structure of the hatched lines in residential areas (e.g., unequal spacing of the hatched lines or broken hatched lines);
- Poor identification ability: The shapes of the identified residential areas are not ideal, the accuracy of the location of the residential areas contour is not high and it is easy to incorrectly identify map elements that are similar in structure to polygons with hatched lines;
- Impracticality: It is difficult for the parameter-dependent method to perfectly grasp the threshold value and it is also difficult to obtain good results in the segmentation task of complex and large images. Moreover, because most of the literature has involved carrying out experiments on partial regions of the entire map image, it was difficult to process map sheet-level raster images and the performance of the algorithms was also less than ideal, which led to the reduced applicability of the algorithms.
2. Methods
2.1. The AEHRA Approach
2.2. Sample Data Set Production Method
2.3. Architecture of the MSU-Net
2.4. Fully Connected CRFs Post-Processing
2.5. Evaluation Metrics
3. Experiments, Result Analysis and Applications
3.1. Experimental Data Description
3.2. Model Training and Parameter Setting
3.3. Experimental Results and Comparative Analysis
3.4. Identifying Residential Areas from a Sheet of Raster Maps
3.5. Land Change Monitoring Application
4. Conclusions
- We developed a novel deep learning model, called MSU-Net, which combines multi-scale features, outputs a feature image at each scale and fuses the feature images. This solved the problem that the up-sampling of a single chain of classical U-Net network cannot fully transfer the scale information;
- We combined the post-processing method of fully connected CRFs, used the probability distribution map output by the MSU-Net model as a unary potential and used the original map as a binary potential. The prediction results can be optimized by a calculation of the similarity of two pixels nodes in color and position, which can eliminate the isolated island and cavity phenomena;
- The research results of this paper can help historians to understand the relationship between human activities and the physical geographical environment, support land change monitoring and benefit the vectorization of raster maps. In short, it has significant application value.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhigang, S. Automatic Recognition of Hatched Residential Areas in Topographic Maps; Jiangxi Normal University: Nanchang, China, 2017. [Google Scholar]
- Shi-Ying, H.; Yuan-Hua, Z. Kohonen Clustering Networks with Fuzzy Selective Multiresolution for Intensity Image Segmentation. Acta Electron. Sin. 1999, 27, 34–37. [Google Scholar]
- Xue, L.; Jiana, H. Algorithems for Recognition of Urban Roads in Large scaled Topographical Maps Based on Integration of Segmentation and Recognition. Signal. Process. 1998, 14, 80–83. [Google Scholar]
- Zhongliang, F. Ditu Saomiao Yingxiang Zidong Shibie Jishu; The Mapping Publishing Group: Beijing, China, 2003. [Google Scholar]
- Huali, Z.; Xianzhong, Z.; Jianyu, W. Research and Implementation of Automatic Color Segmentation Algorithm for Scanned Color Maps. J. Comput. Aided Des. Comput. Graph. 2003, 15, 29–33. [Google Scholar]
- Yun, Y.; Changqing, Z.; Qun, S. Extraction and vectorization of street blocks on scanned topographic maps. Sci. Surv. Mapp. 2007, 32, 88–90. [Google Scholar]
- Wu, J.; Wei, P.; Yuan, X.; Shu, Z.; Chiang, Y.; Fu, Z.; Deng, M. A New Gabor Filter-Based Method for Automatic Recognition of Hatched Residential Areas. IEEE Access 2019, 7, 40649–40662. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet Classification with Deep Convolutional Neural Networks; ACM: New York, NY, USA, 2017; Volume 60, pp. 84–90. [Google Scholar]
- Kim, Y. Convolutional Neural Networks for Sentence Classification. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2015. [Google Scholar]
- Zhang, W.; Tang, P.; Zhao, L. Fast and accurate land-cover classification on medium-resolution remote-sensing images using segmentation models. Int. J. Remote Sens. 2021, 42, 3277–3301. [Google Scholar] [CrossRef]
- He, T.; Zhang, Z.; Zhang, H.; Zhang, Z.; Xie, J.; Li, M. Bag of tricks for image classification with convolutional neural networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), IEEE, Manhattan, NY, USA, 16–20 June 2019; pp. 558–567. [Google Scholar]
- Sermanet, P.; Eigen, D.; Zhang, X.; Mathieu, M.; Fergus, R.; Lecun, Y. OverFeat: Integrated Recognition, Localization and Detection using Convolutional Networks. arxiv 2013, arXiv:1312.6229. [Google Scholar]
- Xi, W.; Ming, Y.; Hong, E.R. Remote sensing image semantic segmentation combining UNET and FPN. Chin. J. Liq. Cryst. Disp. 2021, 36, 475–483. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manzo, M.; Pellino, S. Fighting together against the pandemic: Learning multiple models on tomography images for COVID-19 diagnosis. AI 2021, 2, 16. [Google Scholar] [CrossRef]
- Luo, H.; He, B.; Guo, R.; Wang, W.; Kuai, X.; Xia, B.; Wan, Y.; Ma, D.; Xie, L. Urban Building Extraction and Modeling Using GF-7 DLC and MUX Images. Remote Sens. 2021, 13, 3414. [Google Scholar] [CrossRef]
- Jiao, C.; Heitzler, M.; Hurni, L. A survey of road feature extraction methods from raster maps. Trans. GIS 2021, 1–30. [Google Scholar] [CrossRef]
- Shunping, J.; Shiqing, W. Buidling extraction via convolutional neural networks from an open remote sensing building dataset. Acta Geod. Cartogr. Sin. 2019, 48, 448–459. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 39, 640–651. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Proceedings of the 18th International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep Sparse Rectifier Neural Networks. J. Mach. Learn. Res. 2011, 15, 315–323. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef]
- Zhang, C.S.; Jia, X.; Wu, R.R.; Cui, W.H.; Shi, S.; Guo, B.X. Object oriented semi-automatic extraction of typical natural areas from high-resolution remote sensing image. J. Geo-Inf. Sci. 2021, 23, 1050–1062. [Google Scholar]
- Wang, Z.H.; Zhong, Y.F.; He, W.W.; Qu, N.Y.; Xu, L.Z.; Zhang, W.Z.; Liu, Z.X. Island shoreline segmentation in remote sensing image based on improved Deeplab network. J. Image Graph. 2020, 25, 768–778. [Google Scholar]
- Huang, X.X.; Li, H.G. Water body extraction of high resolution remote sensing image based on improved U-Net network. Int. J. Geo-Inf. Sci. 2020, 22, 2010–2022. [Google Scholar]












| Parameter | Value |
|---|---|
| Training samples | 2800 |
| Validation samples | 800 |
| Batch size | 8 |
| Weight decay | 5 × 10−4 |
| Learning rate | 1 × 10−4 |
| Optimizer | Adam |
| Epoch | 20 |
| Indicator | Fold 1 | Fold 2 | Fold 3 | Fold 4 | Fold 5 |
|---|---|---|---|---|---|
| Dice% | 97.47 | 94.46 | 96.09 | 94.72 | 96.92 |
| IoU% | 95.07 | 89.51 | 92.48 | 89.97 | 94.03 |
| Recall% | 95.08 | 84.06 | 89.99 | 88.70 | 93.97 |
| Precision% | 95.33 | 94.50 | 94.85 | 89.66 | 94.03 |
| Accuracy% | 99.34 | 98.93 | 99.19 | 99.49 | 99.41 |
| Indicator | FCN-8s | U-Net | MSU-Net | AEHRA |
|---|---|---|---|---|
| Dice % | 95.58 | 96.21 | 97.02 | 97.05 |
| IoU % | 91.54 | 92.70 | 94.23 | 94.26 |
| Recall % | 93.85 | 91.92 | 94.90 | 94.92 |
| Precision % | 88.96 | 92.87 | 93.45 | 93.52 |
| Accuracy % | 99.26 | 99.39 | 99.50 | 99.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Xiong, J.; Zhao, Y.; Hu, X. An Automatic Extraction Method for Hatched Residential Areas in Raster Maps Based on Multi-Scale Feature Fusion. ISPRS Int. J. Geo-Inf. 2021, 10, 831. https://doi.org/10.3390/ijgi10120831
Wu J, Xiong J, Zhao Y, Hu X. An Automatic Extraction Method for Hatched Residential Areas in Raster Maps Based on Multi-Scale Feature Fusion. ISPRS International Journal of Geo-Information. 2021; 10(12):831. https://doi.org/10.3390/ijgi10120831
Chicago/Turabian StyleWu, Jianhua, Jiaqi Xiong, Yu Zhao, and Xiang Hu. 2021. "An Automatic Extraction Method for Hatched Residential Areas in Raster Maps Based on Multi-Scale Feature Fusion" ISPRS International Journal of Geo-Information 10, no. 12: 831. https://doi.org/10.3390/ijgi10120831
APA StyleWu, J., Xiong, J., Zhao, Y., & Hu, X. (2021). An Automatic Extraction Method for Hatched Residential Areas in Raster Maps Based on Multi-Scale Feature Fusion. ISPRS International Journal of Geo-Information, 10(12), 831. https://doi.org/10.3390/ijgi10120831





