Micro-Fabric Analyzer (MFA): A New Semiautomated ArcGIS-Based Edge Detector for Quantitative Microstructural Analysis of Rock Thin-Sections
Abstract
:1. Introduction
2. Materials and Methods
2.1. Input Images
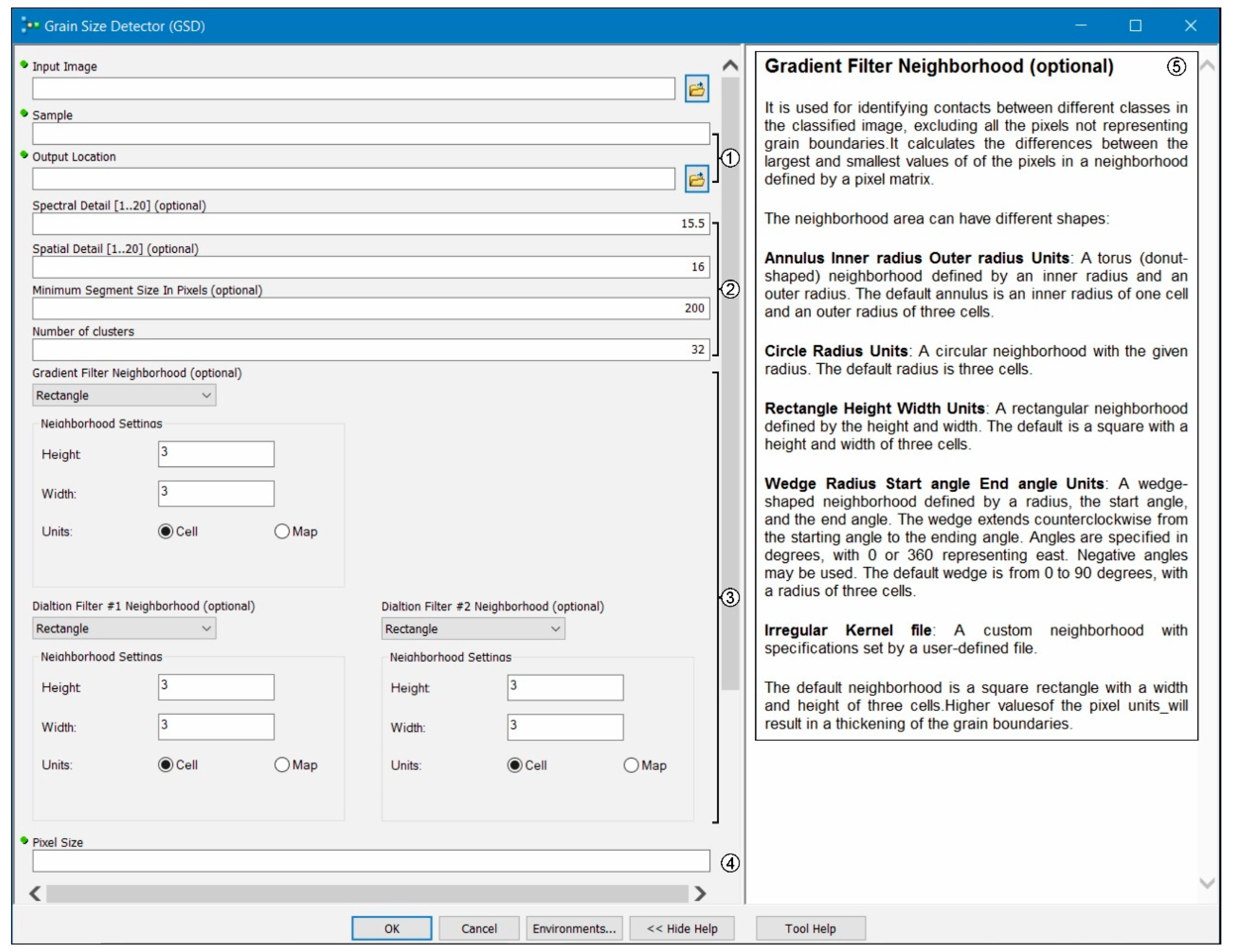
2.2. The Micro-Fabric Analyzer Toolbox: Grain Size Detector (GSD) Tool
- (i)
- The data storage management through the creation of directories where the outputs will be stored. In this case, the tool prompts the user to specify both the name of the analyzed sample and the path where the output folder will be created (Figure 2);
- (ii)
- The image segmentation performed by the application of the SMS followed by Iterative self-organization (Iso) cluster classification.
- (i)
- (i)
- The vectorization step to convert, in vector format (i.e., polylines), the rasterized skeleton of the boundaries. Where the intersections between these polylines form a closed area, polygons (containing attributes regarding their area and perimeter in pixels), representative of rock-forming grains, are automatically digitized. This operation is performed throughout the whole image, obtaining the thin section grains (Figure 4f);
- (ii)
- The collection of measurements, by adopting the Minimum Bounding Geometry (MBG) algorithm e.g., [5]. Such a tool creates boxes having the smallest width enclosing each polygon (Figure 4g), in order to collect data about elongation (i.e., length and width axes) and orientation of the grains (Figure 4h). Furthermore, by combining data of the area, perimeter, length, and width of the grains, the tool calculates five fabric parameters more (i.e., aspect ratio, equivalent diameter, roundness, shape factor 1, shape factor 2; Table 2) as defined in the Appendix A. In this case, the tool prompts the user to specify the pixel size of the input image.
2.3. Classification of Rock-Forming Minerals via the Q-XRMA Tool
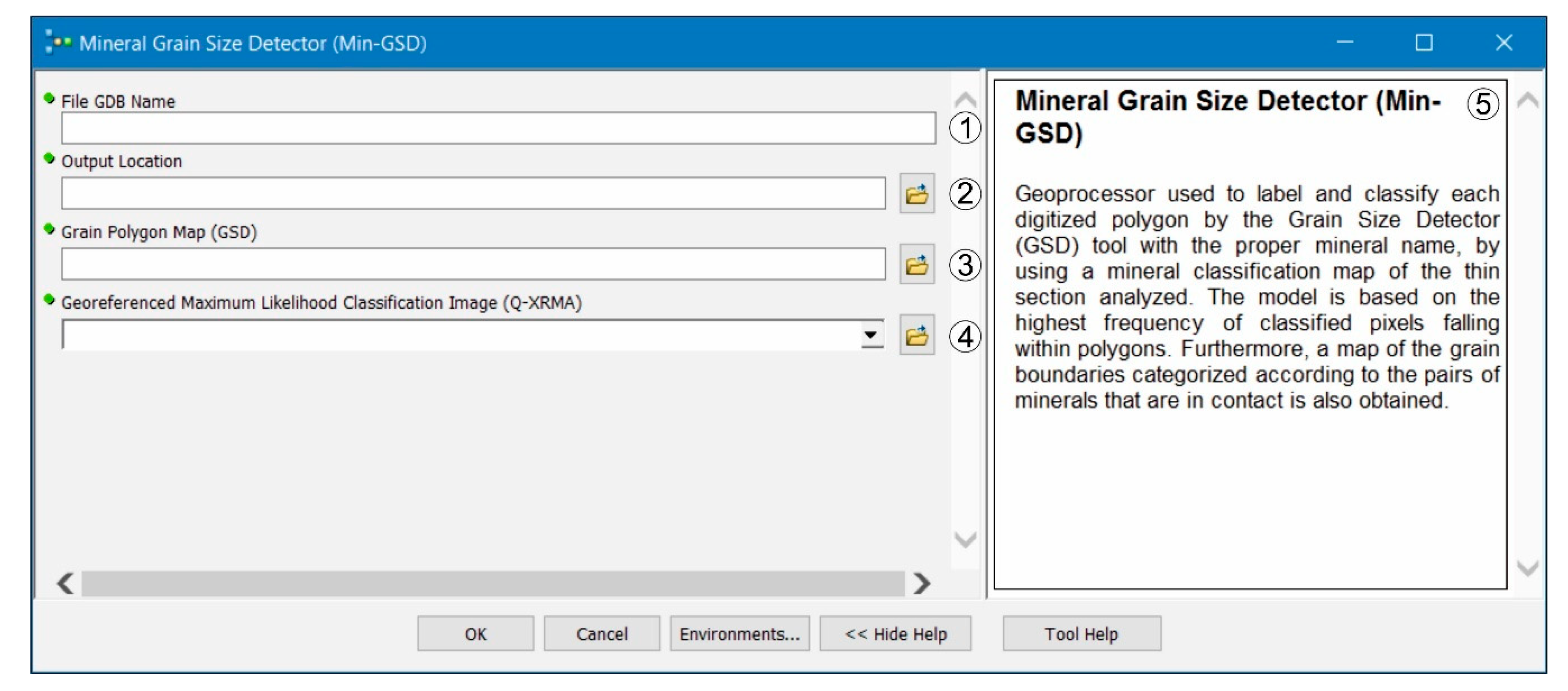
2.4. The Micro-Fabric Analyzer Toolbox: Mineral Grain Size Detector (Min-GSD) Tool
- (i)
- The data storage management. Analogous to the GSD, the tool asks the user to specify both the name of the analyzed sample and the path where the output folder will be created;
- (ii)
- A raster to vector conversion applied to the map of classified minerals, in which a point feature is created at the center of each pixel (Figure 6b). Each point preserves (as an attribute) the mineral phase of the parent pixel in the classified map;
- (iii)
- The join, based on the spatial relationships, between the attributes of the map of polygons obtained through the GSD tool and the points storing the mineral phase attribute. With this operation, the tool appends, through the “Contains Clementini” function [57], the mineral phase attribute to the attributes of the map of polygons, with the exception that if the join feature (i.e., the points) is entirely on the boundary (no part is properly inside or outside) of the target feature (i.e., the polygons), the feature will not be matched. The “Contain Clementini” function defines the boundary of the polygon as the line separating inside and outside, the boundary of a line is defined as its endpoints, and the boundary of a point is always empty. To ensure a reliable assignment of the mineral attribute to the polygon, the tool calculates the most frequent mineral phase attribute among the points enclosed within each polygon. When it is impossible to determine the most frequent mineral phase attribute among the points enclosed within a given polygon, this will not be assigned to any mineral phase, and it will not be kept in the final output. This step allows users to obtain the map of grains subdivided per mineral phase (Figure 6c) and quantify texture characteristics for single mineral phases (Table 3);
- (iv)
- The vectorization step to derive a map of grain boundaries, where each boundary maintains information about the contact between a specific couple of minerals (Figure 6d).
3. Results
3.1. Amphibolite
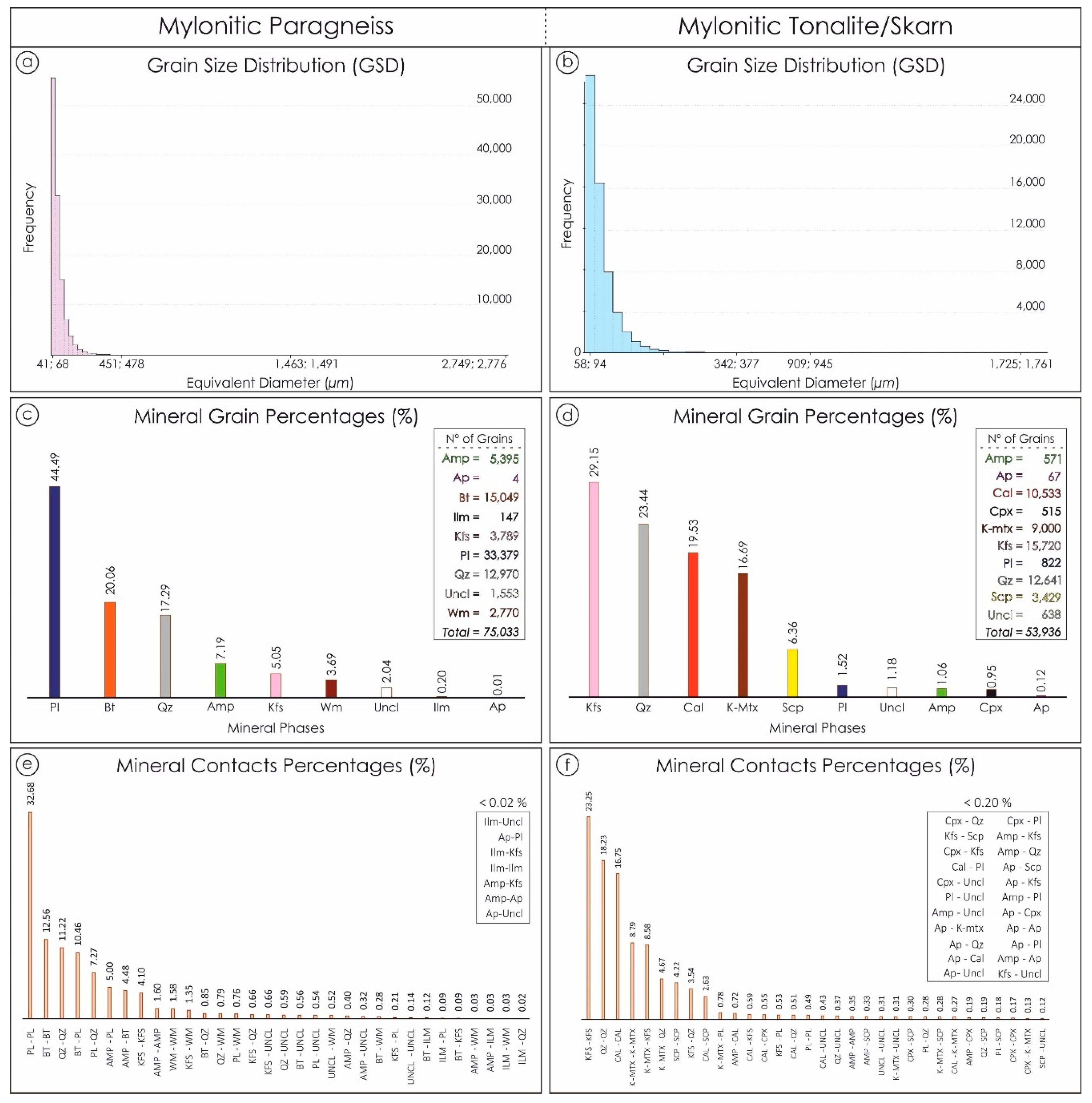
3.2. Mylonitic Paragneiss
3.3. Mylonitic Tonalite
3.4. Quartzarenite
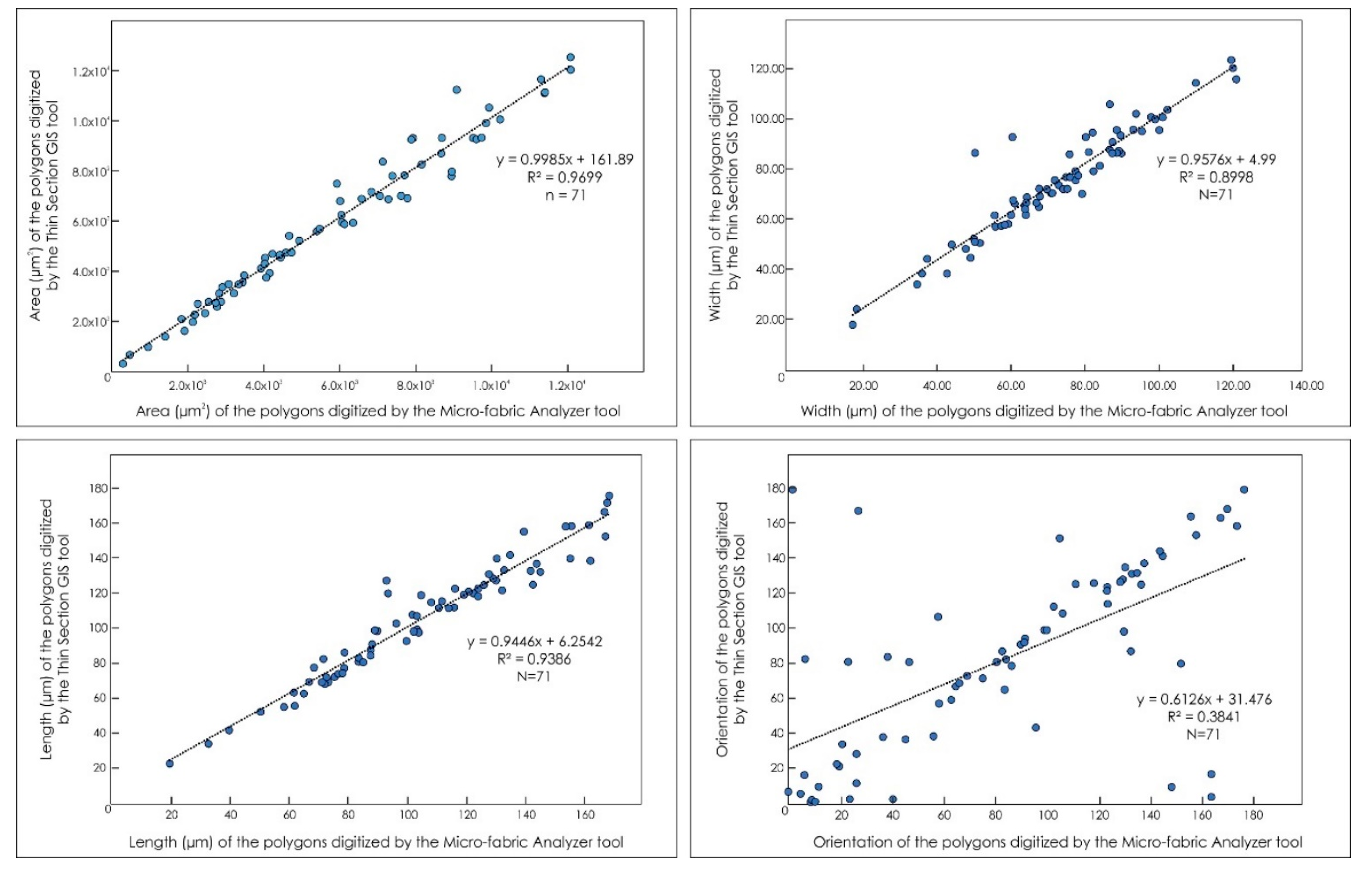
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- Area (A)
- Perimeter (P)
- Length (L)
- Width (W)
- Length Orientation (Clockwise from vertical direction: from 0° to 180°)
- Aspect Ratio (AsR)
- Equivalent Diameter (DEQU)
- Roundness (R)
- Shape Factor 1 (SF1)
- Shape Factor 2 (SF2)
References
- Heilbronner, R. Automatic grain boundary detection and grain size analysis using polarization micrographs or orientation images. J. Struct. Geol. 2000, 22, 969–981. [Google Scholar] [CrossRef]
- Tarquini, S.; Armienti, P. Quick determination of crystal size distributions of rocks by means of a color scanner. Image Anal. Stereol. 2002, 22, 27–34. [Google Scholar] [CrossRef]
- Abràmoff, M.D.; Magalhaes, P.J.; Ram, S.J. Image processing with ImageJ. Biophotonics Int. 2004, 11, 36–42. [Google Scholar]
- Li, Y.; Onasch, C.M.; Guo, Y. GIS-based detection of grain boundaries. J. Struct. Geol. 2008, 30, 431–444. [Google Scholar] [CrossRef]
- DeVasto, M.A.; Czeck, D.M.; Bhattacharyya, P. Using image analysis and ArcGIS® to improve automatic grain boundary detection and quantify geological images. Comput. Geosci. 2012, 49, 38–45. [Google Scholar] [CrossRef]
- Tarquini, S.; Favalli, M. A microscopic information system (MIS) for petrographic analysis. Comput. Geosci. 2010, 36, 665–674. [Google Scholar] [CrossRef] [Green Version]
- Heilbronner, R.; Barrett, S. Image Analysis in Earth Sciences, 1st ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Baker, D.R.; Mancini, L.; Polacci, M.; Higgins, M.D.; Gualda, G.A.R.; Hill, R.J.; Rivers, M.L. An introduction to the application of X-ray microtomography to the three-dimensional study of igneous rocks. Lithos 2012, 148, 262–276. [Google Scholar] [CrossRef]
- Cnudde, V.; Boone, M.N. High-resolution X-ray computed tomography in geosciences: A review of the current technology and applications. Earth-Sci. Rev. 2013, 123, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Raneri, S.; Cnudde, V.; De Kock, T.; Derluyn, H.; Barone, G.; Mazzoleni, P. X-ray computed micro-tomography to study the porous structure and degradation processes of a building stone from Sabucina (Sicily). Eur. J. Mineral. 2015, 27, 279–288. [Google Scholar] [CrossRef]
- Bloise, A.; Ricchiuti, C.; Lanzafame, G.; Punturo, R. X-ray synchrotron microtomography: A new technique for characterizing chrysotile asbestos. Sci. Total Environ. 2020, 703, 135675. [Google Scholar] [CrossRef]
- Borghi, A.; Spiess, R. Studying metamorphic microstructures: A brief insight on modern methodological approaches. Period. Mineral. 2004, 73, 235–247. [Google Scholar]
- Liu, J.L.; Cao, S.Y.; Zou, Y.X.; Song, Z.J. EBSD analysis of rock fabrics and its application. Geol. Bull. China 2008, 27, 1638–1645. [Google Scholar]
- Prior, D.J.; Mariani, E.; Wheeler, J. EBSD in the Earth Sciences: Applications, Common Practice, and Challenges. In Electron Backscatter Diffraction in Materials Science; Schwartz, A., Kumar, M., Adams, B., Field, D., Eds.; Springer: Boston, MA, USA, 2009. [Google Scholar] [CrossRef]
- Panozzo Heilbronner, R.; Pauli, C. Integrated spatial and orientation analysis of quartz c-axes by computer-aided microscopy. J. Struct. Geol. 1993, 15, 369–382. [Google Scholar] [CrossRef]
- Stöckhert, B.; Duyster, J. Discontinuous grain growth in recrystallised vein quartz-implications for grain boundary structure, grain boundary mobility, crystallographic preferred orientation, and stress history. J. Struct. Geol. 1999, 21, 1477–1490. [Google Scholar] [CrossRef]
- Fueten, F.; Goodchild, J.S. Quartz c-axes orientation determination using the rotating polarizer microscope. J. Struct. Geol. 2001, 23, 895–902. [Google Scholar] [CrossRef]
- Hassanpour, R. The use of ArcGIS for determination of quartz optical axis orientation in thin section images. J. Microsc. 2012, 245, 276–287. [Google Scholar] [CrossRef]
- Bachmann, F.; Hielscher, R.; Schaeben, H. Grain detection from 2d and 3d EBSD data-Specification of the MTEX algorithm. Ultramicroscopy 2011, 111, 1720–1733. [Google Scholar] [CrossRef]
- Ortolano, G.; Zappalà, L.; Mazzoleni, P. X-ray Map Analyzer: A new ArcGIS® based tool for the quantitative statistical data handling of X-ray maps (Geo- and material-science applications). Comput. Geosci. 2014, 72, 49–64. [Google Scholar] [CrossRef]
- Ortolano, G.; Visalli, R.; Godard, G.; Cirrincione, R. Quantitative X-ray Map Analyser (Q-XRMA): A new GIS-based statistical approach for Mineral Image Analysis. Comput. Geosci. 2018, 115, 56–65. [Google Scholar] [CrossRef]
- Cossio, R.; Borghi, A. PETROMAP: MS-DOS software package for quantitative processing of X-ray maps of zoned minerals. Comput. Geosci. 1998, 24, 797–803. [Google Scholar] [CrossRef]
- Lanari, P.; Vidal, O.; De Andrade, V.; Dubacq, B.; Lewin, E.; Grosch, E.; Schwartz, S. XMapTools: A MATLAB©-based program for electron microprobe Xray image processing and geothermobarometry. Comput. Geosci. 2014, 62, 227–240. [Google Scholar] [CrossRef] [Green Version]
- Tinkham, D.K.; Ghent, E.D. XRMapAnal: A program for analysis of quantitative X-ray maps. Am. Mineral. 2005, 90, 737–744. [Google Scholar] [CrossRef]
- Goodchild, J.S.; Fueten, F. Edge detection in petrographic images using the rotating polarizer stage. Comput. Geosci. 1998, 24, 745–751. [Google Scholar] [CrossRef]
- Bartozzi, M.; Boyle, A.P.; Prior, D.J. Automated grain boundary detection and classification in orientation contrast images. J. Struct. Geol. 2000, 22, 1569–1579. [Google Scholar] [CrossRef]
- McEwan, I.K.; Sheen, T.M.; Cunningham, G.J.; Allen, A.R. Estimating the size composition of sediment surfaces through image analysis. Proc. Inst. Civ. Eng. Water Marit. Energy 2000, 142, 189–195. [Google Scholar] [CrossRef]
- Thompson, S.; Fueten, F.; Bockus, D. Mineral identification using artificial neural network and the rotating polarizer stage. Comput. Geosci. 2001, 27, 1081–1089. [Google Scholar] [CrossRef]
- Gu, Y. Automated scanning electron microscope based mineral liberation analysis: An introduction to JKMRC/FEI mineral liberation analyser. J. Miner. Mater. Charact. Eng. 2003, 2, 33–41. [Google Scholar] [CrossRef]
- Miriello, D.; Crisci, G.M. Image analysis and flatbed scanners. A visual procedure in order to study the macro-porosity of the archaeological and historical mortars. J. Cult. Herit. 2006, 7, 186–192. [Google Scholar] [CrossRef]
- Perring, C.S.; Barnes, S.J.; Verrall, M.; Hill, R.E.T. Using automated digital image analysis to provide quantitative petrographic data on olivine-phyric basalts. Comput. Geosci. 2004, 30, 183–195. [Google Scholar] [CrossRef]
- Sardini, P.; Moreau, E.; Sammartino, S.; Touchard, G. Primary mineral connectivity of polyphasic igneous rocks by high-quality digitisation and 2D image analysis. Comput. Geosci. 1999, 25, 599–608. [Google Scholar] [CrossRef]
- Lexa, O.; Štípská, P.; Schulmann, K.; Baratoux, L.; Kröner, A. Contrasting textural record of two distinct metamorphic events of similar P-T conditions and different durations. J. Metamorph. Geol. 2005, 23, 649–666. [Google Scholar] [CrossRef]
- Martìnez-Martìnez, J.; Benavente, D.; Garcìa del Cura, M.A. Petrographic quantification of brecciated rocks by image analysis. Application to the interpretation of elastic wave velocities. Eng. Geol. 2007, 90, 41–54. [Google Scholar] [CrossRef]
- Beggan, C.; Hamilton, C.W. New image processing software for analyzing object size-frequency distributions, geometry, orientation, and spatial distribution. Comput. Geosci. 2010, 36, 539–549. [Google Scholar] [CrossRef]
- Berger, A.; Herwegh, M.; Schwarzm, J.O.; Putlitz, B. Quantitative analysis of crystal/grain sizes and their distributions in 2D and 3D. J. Struct. Geol. 2010, 33, 1751–1763. [Google Scholar] [CrossRef]
- Zucali, M.; Corti, L.; Delleani, F.; Zanoni, D.; Spalla, M.I. 3D reconstruction of fabric and metamorphic domains in a slice of continental crust involved in the Alpine subduction system: The example of Mt. Mucrone (Sesia–Lanzo Zone, Western Alps). Int. J. Earth Sci. 2020, 109, 1337–1354. [Google Scholar] [CrossRef]
- Launeau, P.; Cruden, A.R.; Bouchez, J.L. Mineral recognition in digital images of rocks: A new approach using multichannel classification. Can. Mineral. 1994, 32, 919–933. [Google Scholar]
- Coutelas, A.; Godard, G.; Blanc, P.; Person, A. Les mortiers hydrauliques: Synthèse bibliographique et premiers résultats sur des mortiers de Gaule romaine. Rev. d’Archéom. 2004, 28, 127–139. [Google Scholar] [CrossRef]
- Friel, J.J.; Lyman, C.E. X-ray mapping in electron-beam instruments. Microsc. Microanal. 2006, 12, 2–25. [Google Scholar] [CrossRef] [Green Version]
- Mouchi, V.; Crowley, Q.G.; Ubide, T. AERYN: A simple standalone application for visualizing and enhancing elemental maps. Appl. Geochem. 2016, 75, 44–53. [Google Scholar] [CrossRef] [Green Version]
- Lanari, P.; Vho, A.; Bovay, T.; Airaghi, L.; Centrella, S. Quantitative compositional mapping of mineral phases by electron probe micro-analyser. Geol. Soc. Lond. Spec. Publ. 2019, 478, 39–63. [Google Scholar] [CrossRef]
- Cirrincione, R.; Fazio, E.; Heilbronner, R.; Kern, H.; Mengel, K.; Ortolano, G.; Pezzino, A.; Punturo, R. Microstructure and elastic anisotropy of naturally deformed leucogneiss from a shear zone in Montalto (southern Calabria, Italy). Geol. Soc. Lond. Spec. Publ. 2010, 332, 49–68. [Google Scholar] [CrossRef]
- Barraud, J. The use of watershed segmentation and GIS software for textural analysis of thin sections. J. Volcanol. Geotherm. Res. 2006, 154, 17–33. [Google Scholar] [CrossRef]
- Kocabas, V.; Dragicevic, S. Enhancing a GIS cellular automata model of land use change: Bayesian networks, influence diagrams and causality. Trans. GIS 2007, 11, 681–702. [Google Scholar] [CrossRef]
- Gorsevski, P.V.; Onasch, C.M.; Farver, J.R.; Ye, X. Detecting grain boundaries in deformed rocks using a cellular automata approach. Comput. Geosci. 2012, 42, 136–142. [Google Scholar] [CrossRef]
- Ortolano, G.; Visalli, R.; Cirrincione, R.; Rebay, G. PT-path reconstruction via unravelling of peculiar zoning pattern in atoll shaped garnets via image assisted analysis: An example from the Santa Lucia del Mela garnet micaschists (Northeastern Sicily-Italy). Period. Mineral. 2014, 83, 257–297. [Google Scholar] [CrossRef]
- Fiannacca, P.; Ortolano, G.; Pagano, M.; Visalli, R.; Cirrincione, R.; Zappalà, L. IG-Mapper: A new ArcGIS® toolbox for the geostatistics-based automated geochemical mapping of igneous rocks. Chem. Geol. 2017, 470, 75–92. [Google Scholar] [CrossRef]
- Fazio, E.; Ortolano, G.; Visalli, R.; Cirrincione, R.; Fiannacca, P.; Kern, H.; Mengel, K.; Pezzino, A.; Punturo, R. Strain rates of the syn-tectonic Symvolon pluton (Southern Rhodope Core Complex, Greece): An integrated approach combining quartz paleopiezometry, flow laws and PT pseudosections. Ital. J. Geosci. 2018, 137, 219–237. [Google Scholar] [CrossRef]
- Ortolano, G.; Zappala, L. Management and deployment of rock-analysis data from thin section—to field-scale. Rend. Online Soc. Geol. Ital. 2012, 21, 726–728. [Google Scholar] [CrossRef]
- Asmussen, P.; Conrad, O.; Günter, A.; Kirsch, M.; Riller, U. Semi-automatic segmentation of petrographic thin section images using a “seeded-region growing algorithm” with as application to characterize weathered subarkose sandstone. Comput. Geosci. 2015, 83, 89–99. [Google Scholar] [CrossRef]
- Berrezueta, E.; Domínguez-Cuesta, M.J.; Rodríguez-Rey, Á. Semi-automated procedure of digitalization and study of rock thin section porosity applying optical image analysis tools. Comput. Geosci. 2019, 124, 14–26. [Google Scholar] [CrossRef]
- Ortolano, G.; Fazio, E.; Visalli, R.; Alsop, I.G.; Pagano, M.; Cirrincione, R. Quantitative microstructural analysis of mylonites formed during Alpine tectonics in the western Mediterranean realm. J. Struct. Geol. 2020, 131. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, B.; Wang, J.; Zhang, Z.; Shi, K.; Wu, S. Adobe photoshop quantification (PSQ) rather than point-counting: A rapid and precise method for quantifying rock textural data and porosities. Comput. Geosci. 2014, 69, 62–71. [Google Scholar] [CrossRef]
- Zhan, C. A Hybrid Line Thinning Approach. In Proceedings of the Auto-Carto 11, Minneapolis, MN, USA, 30 October–1 November 1993; pp. 396–405. [Google Scholar]
- Whitney, D.L.; Evans, B.W. Abbreviations for names of rock-forming minerals. Am. Mineral. 2010, 95, 185–187. [Google Scholar] [CrossRef]
- Clementini, E.; Sharma, J.; Egenhofer, M.J. Modelling topological spatial relations: Strategies for query processing. Comput. Graph. 1994, 18, 815–822. [Google Scholar] [CrossRef]
- Caracciolo, L.; Tolosana-Delgado, R.; Le Pera, E.; Von Eynatten, H.; Arribas, J.; Tarquini, S. Influence of granitoid textural parameters on sediment composition: Implications for sediment generation. Sediment. Geol. 2012, 280, 93–107. [Google Scholar] [CrossRef] [Green Version]
- Ortolano, G.; Visalli, R.; Fazio, E.; Fiannacca, P.; Godard, G.; Pezzino, A.; Punturo, R.; Sacco, V.; Cirrincione, R. Tectono-metamorphic evolution of the Calabria continental lower crust: The case of the Sila Piccola Massif. Int. J. Earth Sci. 2020, 109, 1295–1319. [Google Scholar] [CrossRef]
- Ortolano, G.; D’Agostino, A.; Pagano, M.; Visalli, R.; Zucali, M.; Fazio, E.; Alsop, I.; Cirrincione, R. ArcStereoNet: A new ArcGIS® toolbox for projection and analysis of structural and microstructural data. ISPRS Int. J. Geo.-Inf. 2021, 10. [Google Scholar]
- Fazio, E.; Punturo, R.; Fazio, E.; Cirrincione, R.; Ker, H.; Pezzino, A.; Wenk, H.R.; Goswami, S.; Mamtani, M.A. Quartz preferred orientation in naturally deformed mylonitic rocks (Montalto shear zone–Italy): A comparison of results by different techniques, their advantages and limitations. Int. J. Earth Sci. (Geol. Rundsch.) 2017, 106, 2259–2278. [Google Scholar] [CrossRef]
- Corti, L.; Zucali, M.; Visalli, R.; Mancini, M.; Sayab, M. Integrating X-Ray computed tomography with chemical imaging to quantify mineral re-crystallization from granulite to eclogite metamorphism in the Western Italian Alps (Sesia-Lanzo Zone). Front. Earth Sci. 2019, 7. [Google Scholar] [CrossRef]
- Ortolano, G.; D’Agostino, A.; Visalli, R.; Cirrincione, R. Plutonic rocks classification: A child’s play. Rend. Online Soc. Geol. Ital. 2019, 49, 46–54. [Google Scholar] [CrossRef]
- Belfiore, C.M.; Fichera, G.V.; Ortolano, G.; Pezzino, A.; Visalli, R.; Zappalà, L. Image processing of the pozzolanic reactions in Roman mortars via X-ray Map Analyser. Microchem. J. 2016, 125, 242–253. [Google Scholar] [CrossRef]






| Optical Scan Resolution (dpi) | Pixel Size (µm × px−1) | Input Hard Drive Space Allocation (MB) | Output Hard Drive Space Allocation (MB) | Processing Time (Minutes) |
|---|---|---|---|---|
| 2400 | ≈10.58 | ≈5–15 | ≈40–80 | ≈10–15′ |
| 3200 | ≈7.94 | ≈5–25 | ≈60–150 | ≈20–80′ |
| 4800 | ≈5.29 | ≈10–30 | ≈100–300 | ≈30–120′ |
| 6400 | ≈3.97 | ≈30–50 | ≈200–400 | ≈60–180′ |
| 12,800 | ≈1.98 | ≈65–100 | >400 | >240′ |
| Attributes | Values | ||||
|---|---|---|---|---|---|
| Object ID | 1 | 2 | 3 | 4 | …n |
| Length Orientation (clockwise from vertical direction: 0°; 180°) | 95.86 | 30.16 | 100.65 | 80.98 | 104.07 |
| Width | 82.02 | 71.58 | 62.57 | 81.98 | 60.09 |
| Length | 144.24 | 118.94 | 128.25 | 188.97 | 138.57 |
| Area | 8449.21 | 5720.06 | 6166.03 | 12175.11 | 5658.97 |
| Aspect Ratio | 1.76 | 1.66 | 2.05 | 2.31 | 2.31 |
| Equivalent Diameter | 103.75 | 85.36 | 88.63 | 124.54 | 84.91 |
| Perimeter | 384.96 | 300.38 | 354.36 | 464.03 | 319.46 |
| Roundness | 0.57 | 0.60 | 0.49 | 0.43 | 0.43 |
| Shape Factor 1 | 1.18 | 1.12 | 1.27 | 1.19 | 1.20 |
| Shape Factor 2 | 0.72 | 0.80 | 0.62 | 0.71 | 0.70 |
| Attributes | Values | ||||
|---|---|---|---|---|---|
| Object ID | 1 | 2 | 3 | 4 | …n |
| Length Orientation (clockwise from vertical direction: 0°; 180°) | 95.86 | 30.16 | 100.65 | 80.98 | 104.07 |
| … | … | ||||
| Same of Table 2 | Same of Table 2 | ||||
| … | … | ||||
| Mineral | Pl | Ilm | Ttn | Amp | Pl |
| Amphibolite | Mylonitic Paragneiss | Mylonitic Tonalite | Quartzarenite | |
|---|---|---|---|---|
| Spectral Detail | 14 | 15 | 15 | 14 |
| Spatial Detail | 12 | 18 | 19 | 6 |
| Minimum Segment Size | 200 | 50 | 100 | 100 |
| Number of Classes | 32 | 16 | 16 | 40 |
| Gradient Filter | 3 × 3 | 3 × 3 | 3 × 3 | 3 × 3 |
| Dilation Filter #1 | 4 × 4 | 2 × 2 | 2 × 2 | 7 × 7 |
| Dilation Filter #2 | 4 × 4 | 2 × 2 | 2 × 2 | 5 × 5 |
| Pixel Size (µm × px−1) | 5.29 | 5.29 | 5.29 | 0.665 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Visalli, R.; Ortolano, G.; Godard, G.; Cirrincione, R. Micro-Fabric Analyzer (MFA): A New Semiautomated ArcGIS-Based Edge Detector for Quantitative Microstructural Analysis of Rock Thin-Sections. ISPRS Int. J. Geo-Inf. 2021, 10, 51. https://doi.org/10.3390/ijgi10020051
Visalli R, Ortolano G, Godard G, Cirrincione R. Micro-Fabric Analyzer (MFA): A New Semiautomated ArcGIS-Based Edge Detector for Quantitative Microstructural Analysis of Rock Thin-Sections. ISPRS International Journal of Geo-Information. 2021; 10(2):51. https://doi.org/10.3390/ijgi10020051
Chicago/Turabian StyleVisalli, Roberto, Gaetano Ortolano, Gaston Godard, and Rosolino Cirrincione. 2021. "Micro-Fabric Analyzer (MFA): A New Semiautomated ArcGIS-Based Edge Detector for Quantitative Microstructural Analysis of Rock Thin-Sections" ISPRS International Journal of Geo-Information 10, no. 2: 51. https://doi.org/10.3390/ijgi10020051
APA StyleVisalli, R., Ortolano, G., Godard, G., & Cirrincione, R. (2021). Micro-Fabric Analyzer (MFA): A New Semiautomated ArcGIS-Based Edge Detector for Quantitative Microstructural Analysis of Rock Thin-Sections. ISPRS International Journal of Geo-Information, 10(2), 51. https://doi.org/10.3390/ijgi10020051







