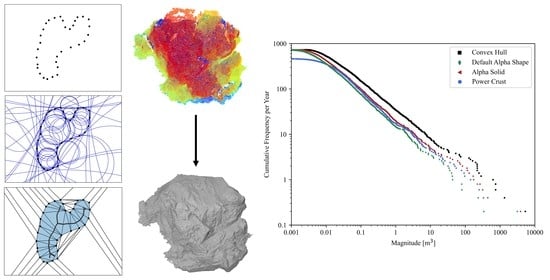
Computational Geometry-Based Surface Reconstruction for Volume Estimation: A Case Study on Magnitude-Frequency Relations for a LiDAR-Derived Rockfall Inventory
Abstract
1. Introduction
1.1. Rockfall Hazard
1.2. Rockfall Magnitude-Frequency Relations in the Digital Age
| Study | Timespan [Years] | Median Frequency | Site Dimensions | Change Detection Method | Clutter Removal | Clustering | Volume |
|---|---|---|---|---|---|---|---|
| Guerin et al. [34] | 11 | 365 days | ~160 × 600 m | C2M 1 | Neighbour averaging | DBSCAN | SfR 2: Manually w/3D software |
| Hartmeyer et al. [35] | 6 | yearly | 5-rockwalls: 234,700 m2 | M3C2 3 | - | Region growing | Sum of raster cells |
| DiFrancesco et al. [36] | 5.0 | 69 days | 240 × 120 m | M3C2 | Manual | DBSCAN 4 | SfR: Alpha Solid |
| Benjamin et al. [26] | 2.6 | 309 days | 20.5 km × (30–150 m) | M3C2 | Manual | DBSCAN | SfR: Power Crust |
| Guerin et al. [37] | 40 | 34 years–1 month | ~0.8 × 0.6 km; ~1.5 × 0.8 km; ~1.8 × 0.8 km; | C2M | Neighbour averaging | DBSCAN | SfR: Manually w/3D software |
| Williams et al. [18,38] | 0.8 | 1 h–30 days | 210 × 60 m | M3C2 (variable search lengths) | Waveform + edge filter; Noise mask | Region growing | Sum of raster cells |
| Van Veen et al. [39] | 1.3 | 76 days | 1.1 km × 500 m | M3C2 (nearest neighbors) | - | DBSCAN | SfR: Alpha Shapes * |
| Olsen et al. [40] | 1.8 | 11 months | 340 × 170 m; 110 × 11 m; 90 × 8 m | DoD 5 | Raster averaging | Region growing | Sum of triangulated raster cells |
| Carrea et al. [41] | 3.0 | 6 months | ~80 × 40 m | C2M | - | DBSCAN | SfR: Alpha Shapes * |
1.3. Surface Reconstruction Challenges and Requirements
1.4. Digital Surface Representation and Reconstruction Methods Background
1.5. Study Objectives
2. Materials and Methods
2.1. LiDAR-Derived 3D Rockfall Database
2.2. Computational Geometry Tools
2.3. Computational Geometry Surface Reconstruction for Volume Estimation
2.3.1. Convex Hull
2.3.2. Three Dimensional Alpha Shapes
2.3.3. Power Crust
- Poles: A subset of the Voronoi vertices, located on the interior and exterior of the object, but not along the object’s surface;
- Polar balls: The balls centered at the poles, each with radii such that they are touching the nearest input point sample;
- Medial axis: The skeleton of a closed shape, along which, points are equidistant to two or more locations along the shape’s boundary.
2.3.4. Power Crust Mesh Volume Computation
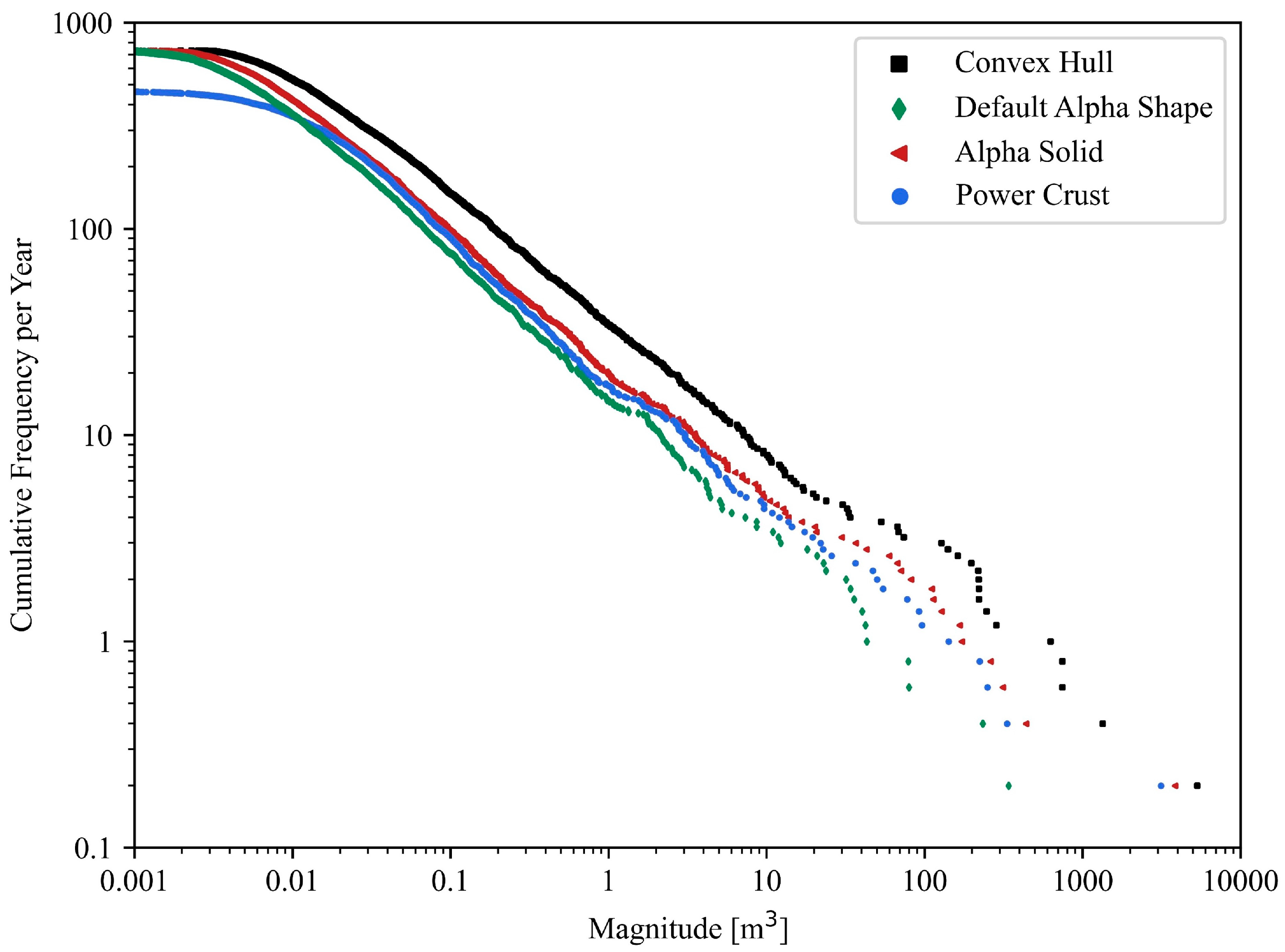
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Magnitude-Frequency Visualization and Power-Law Fitting
References
- Varnes, D.J. Slope Movement Types and Processes. Transp. Res. Board Natl. Acad. Sci. Spec. Rep. 1978, 176, 11–33. [Google Scholar]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes Classification of Landslide Types, an Update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Volkwein, A.; Schellenberg, K.; Labiouse, V.; Agliardi, F.; Berger, F.; Bourrier, F.; Dorren, L.; Gerber, W. Rockfall Characterisation and Structural Protection—A Review. Nat. Hazards Earth Syst. Sci. 2011, 2617–2651. [Google Scholar] [CrossRef]
- Corominas, J.; Moya, J. A Review of Assessing Landslide Frequency for Hazard Zoning Purposes. Eng. Geol. 2008, 102, 193–213. [Google Scholar] [CrossRef]
- Corominas, J.; Copons, R.; Moya, J.; Vilaplana, J.M.; Altimir, J.; Amigó, J. Quantitative Assessment of the Residual Risk in a Rockfall Protected Area. Landslides 2005, 2, 343–357. [Google Scholar] [CrossRef]
- Guzzetti, F.; Reichenbach, P.; Ghigi, S. Rockfall Hazard and Risk Assessment Along a Transportation Corridor in the Nera Valley, Central Italy. Environ. Manag. 2004, 34, 191–208. [Google Scholar] [CrossRef] [PubMed]
- Hungr, O.; Evans, S.G.; Hazzard, J. Magnitude and Frequency of Rock Falls and Rock Slides along the Main Transportation Corridors of Southwestern British Columbia. Can. Geotech. J. 1999, 36, 224–238. [Google Scholar] [CrossRef]
- Corominas, J.; Mavrouli, O.; Ruiz-Carulla, R. Magnitude and Frequency Relations: Are There Geological Constraints to the Rockfall Size? Landslides 2018, 15, 829–845. [Google Scholar] [CrossRef]
- Malamud, B.D.; Turcotte, D.L.; Guzzetti, F.; Reichenbach, P. Landslide Inventories and Their Statistical Properties. Earth Surf. Process. Landf. 2004, 711, 687–711. [Google Scholar] [CrossRef]
- Guthrie, R.H.; Evans, S.G. Analysis of Landslide Frequencies and Characteristics in a Natural System, Coastal British Columbia. Earth Surf. Process. Landf. 2004, 29, 1321–1339. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-Law Distributions in Empirical Data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Brardinoni, F.; Church, M. Representing the Landslide Magnitude–Frequency Relation: Capilano River Basin, British Columbia. Earth Surf. Process. Landf. 2004, 29, 115–124. [Google Scholar] [CrossRef]
- Hovius, N.; Stark, C.P.; Hao-Tsu, C.; Jiun-Chuan, L. Supply and Removal of Sediment in a Landslide-Dominated Mountain Belt: Central Range, Taiwan. J. Geol. 2000, 108, 73–89. [Google Scholar] [CrossRef] [PubMed]
- Martin, Y.; Rood, K.; Schwab, J.W.; Church, M. Sediment Transfer by Shallow Landsliding in the Queen Charlotte Islands, British Columbia. Can. J. Earth Sci. 2002, 39, 189–205. [Google Scholar] [CrossRef]
- Pelletier, J.D.; Malamud, B.D.; Blodgett, T.; Turcotte, D.L. Scale-Invariance of Soil Moisture Variability and Its Implications for the Frequency-Size Distribution of Landslides. Eng. Geol. 1997, 48, 255–268. [Google Scholar] [CrossRef]
- Guthrie, R.H.; Evans, S.G. Magnitude and Frequency of Landslides Triggered by a Storm Event, Loughborough Inlet, British Columbia. Nat. Hazards Earth Syst. Sci. 2004, 4, 475–483. [Google Scholar] [CrossRef]
- Stark, C.P.; Hovius, N. The Characterization of Landslide Size Distributions. Geophys. Res. Lett. 2001, 28, 1091–1094. [Google Scholar] [CrossRef]
- Williams, J.G.; Rosser, N.J.; Hardy, R.J.; Brain, M.J. The Importance of Monitoring Interval for Rockfall Magnitude-Frequency Estimation. J. Geophys. Res. Earth Surf. 2019, 124, 2841–2853. [Google Scholar] [CrossRef]
- Stoffel, M.; Schneuwly, D.; Bollschweiler, M.; Lièvre, I.; Delaloye, R.; Myint, M.; Monbaron, M. Analyzing Rockfall Activity (1600–2002) in a Protection Forest—A Case Study Using Dendrogeomorphology. Geomorphology 2005, 68, 224–241. [Google Scholar] [CrossRef]
- Rosser, N.J.; Lim, M.; Petley, D.; Dunning, S.; Allison, R. Patterns of Precursory Rockfall Prior to Slope Failure. J. Geophys. Res. 2007, 112, F04014. [Google Scholar] [CrossRef]
- Nichol, J.; Wong, M.S. Satellite Remote Sensing for Detailed Landslide Inventories Using Change Detection and Image Fusion. Int. J. Remote Sens. 2005, 26, 1913–1926. [Google Scholar] [CrossRef]
- Lu, P.; Stumpf, A.; Kerle, N.; Casagli, N. Object-Oriented Change Detection for Landslide Rapid Mapping. IEEE Geosci. Remote Sens. Lett. 2011, 8, 701–705. [Google Scholar] [CrossRef]
- Kromer, R.A.; Hutchinson, D.J.; Lato, M.J.; Gauthier, D.; Edwards, T. Identifying Rock Slope Failure Precursors Using LiDAR for Transportation Corridor Hazard Management. Eng. Geol. 2015, 195, 93–103. [Google Scholar] [CrossRef]
- Warrick, J.A.; Ritchie, A.C.; Adelman, G.; Adelman, K.; Limber, P.W. New Techniques to Measure Cliff Change from Historical Oblique Aerial Photographs and Structure-from-Motion Photogrammetry. J. Coast. Res. 2017, 33, 39. [Google Scholar] [CrossRef]
- Lato, M.J.; Hutchinson, D.J.; Gauthier, D.; Edwards, T.; Ondercin, M. Comparison of Airborne Laser Scanning, Terrestrial Laser Scanning, and Terrestrial Photogrammetry for Mapping Differential Slope Change in Mountainous Terrain. Can. Geotech. J. 2015, 52, 129–140. [Google Scholar] [CrossRef]
- Benjamin, J.; Rosser, N.J.; Brain, M.J. Emergent Characteristics of Rockfall Inventories Captured at a Regional Scale. Earth Surf. Process. Landf. 2020, 45, 2773–2787. [Google Scholar] [CrossRef]
- Kromer, R.A.; Abellán, A.; Hutchinson, D.J.; Lato, M.J.; Chanut, M.A.; Dubois, L.; Jaboyedoff, M. Automated Terrestrial Laser Scanning with Near-Real-Time Change Detection—Monitoring of the Séchilienne Landslide. Earth Surf. Dyn. 2017, 5, 293–310. [Google Scholar] [CrossRef]
- Kromer, R.A.; Walton, G.; Gray, B.; Lato, M.J.; Group, R. Development and Optimization of an Automated Fixed-Location Time Lapse Photogrammetric Rock Slope Monitoring System. Remote Sens. 2019, 11, 1890. [Google Scholar] [CrossRef]
- Eltner, A.; Kaiser, A.; Abellan, A.; Schindewolf, M. Time Lapse Structure-from-Motion Photogrammetry for Continuous Geomorphic Monitoring. Earth Surf. Process. Landf. 2017, 42, 2240–2253. [Google Scholar] [CrossRef]
- Telling, J.; Lyda, A.; Hartzell, P.; Glennie, C.L. Review of Earth Science Research Using Terrestrial Laser Scanning. Earth Sci. Rev. 2017, 169, 35–68. [Google Scholar] [CrossRef]
- Abellán, A.; Oppikofer, T.; Jaboyedoff, M.; Rosser, N.J.; Lim, M.; Lato, M.J. Terrestrial Laser Scanning of Rock Slope Instabilities. Earth Surf. Process. Landf. 2014, 39, 80–97. [Google Scholar] [CrossRef]
- Smith, M.W.; Carrivick, J.L.; Quincey, D.J. Structure from Motion Photogrammetry in Physical Geography. Prog. Phys. Geogr. Earth Environ. 2016, 40, 247–275. [Google Scholar] [CrossRef]
- Anderson, K.; Westoby, M.J.; James, M.R. Low-Budget Topographic Surveying Comes of Age: Structure from Motion Photogrammetry in Geography and the Geosciences. Prog. Phys. Geogr. Earth Environ. 2019, 43, 163–173. [Google Scholar] [CrossRef]
- Guerin, A.; Ravanel, L.; Matasci, B.; Jaboyedoff, M.; Deline, P. The Three-Stage Rock Failure Dynamics of the Drus (Mont Blanc Massif, France) since the June 2005 Large Event. Sci. Rep. 2020, 10. [Google Scholar] [CrossRef]
- Hartmeyer, I.; Keuschnig, M.; Delleske, R.; Krautblatter, M.; Lang, A.; Schrott, L.; Prasicek, G.; Otto, J.-C. A 6-Year Lidar Survey Reveals Enhanced Rockwall Retreat and Modified Rockfall Magnitudes/Frequencies in Deglaciating Cirques. Earth Surf. Dyn. 2020, 8, 753–768. [Google Scholar] [CrossRef]
- DiFrancesco, P.-M.; Bonneau, D.A.; Hutchinson, D.J. The Implications of M3C2 Projection Diameter on 3D Semi-Automated Rockfall Extraction from Sequential Terrestrial Laser Scanning Point Clouds. Remote Sens. 2020, 12, 1885. [Google Scholar] [CrossRef]
- Guerin, A.; Stock, G.M.; Radue, M.J.; Jaboyedoff, M.; Collins, B.D.; Matasci, B.; Avdievitch, N.; Derron, M.-H. Quantifying 40 Years of Rockfall Activity in Yosemite Valley with Historical Structure-from-Motion Photogrammetry and Terrestrial Laser Scanning. Geomorphology 2020, 356, 107069. [Google Scholar] [CrossRef]
- Williams, J.G.; Rosser, N.J.; Hardy, R.J.; Brain, M.J.; Afana, A.A. Optimising 4-D Surface Change Detection: An Approach for Capturing Rockfall Magnitude-Frequency. Earth Surf. Dyn. 2018, 6, 101–119. [Google Scholar] [CrossRef]
- van Veen, M.; Hutchinson, D.J.; Kromer, R.; Lato, M.; Edwards, T. Effects of Sampling Interval on the Frequency—Magnitude Relationship of Rockfalls Detected from Terrestrial Laser Scanning Using Semi-Automated Methods. Landslides 2017, 14, 1579–1592. [Google Scholar] [CrossRef]
- Olsen, M.J.; Wartman, J.; McAlister, M.; Mahmoudabadi, H.; O’Banion, M.; Dunham, L.; Cunningham, K. To Fill or Not to Fill: Sensitivity Analysis of the Influence of Resolution and Hole Filling on Point Cloud Surface Modeling and Individual Rockfall Event Detection. Remote Sens. 2015, 7, 12103–12134. [Google Scholar] [CrossRef]
- Carrea, D.; Abellan, A.; Derron, M.-H.; Jaboyedoff, M. Automatic Rockfalls Volume Estimation Based on Terrestrial Laser Scanning Data. In Engineering Geology for Society and Territory—Volume 2; Springer International Publishing: Cham, Switzerland, 2015; pp. 425–428. [Google Scholar] [CrossRef]
- Cignoni, P.; Rocchini, C.; Scopigno, R. Metro: Measuring Error on Simplified Surfaces. Comput. Graph. Forum 1998, 17, 167–174. [Google Scholar] [CrossRef]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D Comparison of Complex Topography with Terrestrial Laser Scanner: Application to the Rangitikei Canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; Simoudis, E., Fayyad, U., Han, J., Eds.; AAAI Press: Menlo Park, CA, USA, 1996; pp. 226–231. [Google Scholar]
- Tonini, M.; Abellán, A. Rockfall Detection from Terrestrial LiDAR Point Clouds: A Clustering Approach Using R. J. Spat. Inf. Sci. 2014, 8. [Google Scholar] [CrossRef]
- Hoppe, H.; DeRose, T.; Duchamp, T.; McDonald, J.; Stuetzle, W. Surface Reconstruction from Unorganized Points. Comput. Graph. 1992, 26, 71–78. [Google Scholar] [CrossRef]
- Benjamin, J.; Rosser, N.J.; Brain, M. Rockfall Detection and Volumetric Characterisation Using LiDAR. In Landslides and Engineered Slopes. Experience, Theory and Practice; CRC Press: Naples, Italy, 2016; pp. 389–395. [Google Scholar] [CrossRef]
- Berger, M.; Tagliasacchi, A.; Seversky, L.M.; Alliez, P.; Levine, J.A.; Sharf, A.; Silva, C.T. State of the Art in Surface Reconstruction from Point Clouds. In Eurographics 2014—State of the Art Reports; Lefebvre, S., Spagnuolo, M., Eds.; The Eurographics Association: Strasbourg, France, 2014; pp. 161–185. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Harer, J. Computational Toplogy an Introduction; American Mathematical Society: Providence, RI, USA, 2010. [Google Scholar]
- Bonneau, D.A.; DiFrancesco, P.-M.; Hutchinson, D.J. Surface Reconstruction for Three-Dimensional Rockfall Volumetric Analysis. ISPRS Int. J. Geo Inf. 2019, 8, 548. [Google Scholar] [CrossRef]
- Zhao, H.-K.; Osher, S.; Fedkiw, R. Fast Surface Reconstruction Using the Level Set Method. In Proceedings of the IEEE Workshop on Variational and Level Set Methods in Computer Vision, Vancouver, BC, Canada, 13 July 2001; IEEE Computer Society: Washington, DC, USA, 2001; pp. 194–201. [Google Scholar] [CrossRef]
- Kazhdan, M. Reconstruction of Solid Models from Oriented Point Sets. In Proceedings of the Third Eurographics Symposium on Geometry Processing, SGP ’05, Vienna, Austria, 4–6 July 2005; pp. 73–82. [Google Scholar]
- Lorensen, W.E.; Cline, H.E. Marching Cubes: A High Resolution 3D Surface Construction Algorithm. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques—SIGGRAPH ’87, Anaheim, CA, USA, 27–31 July 1987; ACM Press: New York, NY, USA, 1987; pp. 163–169. [Google Scholar] [CrossRef]
- Amenta, N.; Bern, M.; Kamvysselis, M. A New Voronoi-Based Surface Reconstruction Algorithm. In Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques—SIGGRAPH ’98, Orlando, FL, USA, 19–24 July 1998; ACM Press: New York, NY, USA, 1998; pp. 415–421. [Google Scholar] [CrossRef]
- Amenta, N.; Choi, S.; Kolluri, R.K. The Power Crust. In Proceedings of the Sixth ACM Symposium on Solid Modeling and Applications—SMA ’01, Ann Arbor, MI, USA, 4–8 June 2001; ACM Press: New York, NY, USA, 2001; pp. 249–266. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Mücke, E.P. Three-Dimensional Alpha Shapes. ACM Trans. Graph. 1994, 13, 43–72. [Google Scholar] [CrossRef]
- Boissonnat, J.-D. Geometric Structures for Three-Dimensional Shape Representation. ACM Trans. Graph. 1984, 3, 266–286. [Google Scholar] [CrossRef]
- MacLaurin, C.I.; Mahoney, J.B.; Haggart, J.W.; Goodin, J.R.; Mustard, P.S. The Jackass Mountain Group of South-Central British Columbia: Depositional Setting and Evolution of an Early Cretaceous Deltaic Complex. Can. J. Earth Sci. 2011, 48, 930–951. [Google Scholar] [CrossRef]
- Kromer, R.A.; Lato, M.J.; Hutchinson, D.J.; Gauthier, D.; Edwards, T. Managing Rockfall Risk through Baseline Monitoring of Precursors with a Terrestrial Laser Scanner. Can. Geotech. J. 2017, 967. [Google Scholar] [CrossRef]
- Sturzenegger, M.; Keegan, T.; Wen, A.; Willms, D.; Stead, D.; Edwards, T. LiDAR and Discrete Fracture Network Modeling for Rockslide Characterization and Analysis. In Engineering Geology for Society and Territory—Volume 6; Springer International Publishing: Cham, Switzerland, 2015; pp. 223–227. [Google Scholar] [CrossRef]
- Teledyne Optech. ILRIS Summary Specification Sheet; Teledyne Optech: Vaughan, ON, Canada, 2014. [Google Scholar]
- Pesci, A.; Teza, G.; Bonali, E. Terrestrial Laser Scanner Resolution: Numerical Simulations and Experiments on Spatial Sampling Optimization. Remote Sens. 2011, 3, 167–184. [Google Scholar] [CrossRef]
- Riegl Laser Measurement Systems. Riegl VZ-400i Datasheet; Riegl Laser Measurement Systems: Horn, Austria, 2017. [Google Scholar]
- Devert, A. 2D Laguerre-Voronoi Diagrams. Available online: https://gist.github.com/marmakoide/45d5389252683ae09c2df49d0548a627 (accessed on 10 January 2021).
- Royer, A. Mesh Generation with Alpha Complexes. Available online: http://ameroyer.github.io/projects/2018/03/01/alphacomplexes.html (accessed on 11 January 2021).
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Edelsbrunner, H. Voronoi Diagrams. In Algorithms in Combinatorial Geometry; Springer: Berlin/Heidelberg, Germany, 1987; pp. 293–335. [Google Scholar] [CrossRef]
- Mathworks. MATLAB—Version 9.9 (r2020b). 2020. Available online: https://www.mathworks.com/ (accessed on 15 November 2020).
- Bernardini, F.; Bajaj, C.L.; Chen, J.; Schikore, D.R. A Triangulation-Based Object Reconstruction Method. In Proceedings of the Thirteenth Annual Symposium on Computational Geometry—SCG ’97, Nice, France, 4–6 June 1996; ACM Press: New York, NY, USA, 1997; pp. 481–484. [Google Scholar] [CrossRef]
- Amenta, N.; Choi, S.; Kolluri, R.K. The Power Crust, Unions of Balls, and the Medial Axis Transform. Comput. Geom. 2001, 19, 127–153. [Google Scholar] [CrossRef]
- Alhashim, I. Power Crust—A Port for Windows. 2012. Available online: https://github.com/ialhashim/powercrust (accessed on 15 November 2020).
- Clarkson, K. A Program for Convex Hulls. 1995. Available online: http://www.netlib.org/voronoi/hull.html (accessed on 10 December 2020).
- Clarkson, K.L.; Shor, P.W. Applications of Random Sampling in Computational Geometry, II. Discret. Comput. Geom. 1989, 4, 387–421. [Google Scholar] [CrossRef]
- Liepa, P. Filling Holes in Meshes. In Eurographics Symposium on Geometry Processing; Kobbelt, L., Schroeder, P., Hoppe, H., Eds.; The Eurographics Association: Genoa, Italy, 2003. [Google Scholar] [CrossRef]
- Sieger, D.; Botsch, M. The Polygon Mesh Processing Library—Version 1.2.1. 2020. Available online: https://www.pmp-library.org/ (accessed on 23 December 2020).
- Lien, S.; Kajiya, J.T. A Symbolic Method for Calculating the Integral Properties of Arbitrary Nonconvex Polyhedra. IEEE Comput. Graph. Appl. 1984, 4, 35–42. [Google Scholar] [CrossRef]
- Blender Foundation and Community. Blender—A 3D Modelling and Rendering Package—Version 2.90.0; Stichting Blender Foundation: Amsterdam, The Netherlands, 2020; Available online: https://www.blender.org/ (accessed on 22 September 2020).
- Menegoni, N.; Giordan, D.; Perotti, C. Reliability and Uncertainties of the Analysis of an Unstable Rock Slope Performed on RPAS Digital Outcrop Models: The Case of the Gallivaggio Landslide (Western Alps, Italy). Remote Sens. 2020, 12, 1635. [Google Scholar] [CrossRef]
- Kazhdan, M.; Hoppe, H. Screened Poisson Surface Reconstruction. ACM Trans. Graph. 2013, 32, 1–13. [Google Scholar] [CrossRef]
- Goldstein, M.L.; Morris, S.A.; Yen, G.G. Problems with Fitting to the Power-Law Distribution. Eur. Phys. J. B 2004, 41, 255–258. [Google Scholar] [CrossRef]
- Benjamin, J. Regional-Scale Controls on Rockfall Occurrence. Ph.D. Thesis, Durham University, Durham, UK, 2018. Available online: http://etheses.dur.ac.uk/12813/ (accessed on 17 June 2020).








| Convex Hull | Default Alpha Shape | Alpha Solid | Power Crust | Power Crust Substituted 1 | |
|---|---|---|---|---|---|
| [m3] | 0.0501 | 0.0272 | 0.0339 | 0.0279 | 0.0217 |
| 1.6315 | 1.7193 | 1.6808 | 1.7012 | 1.7080 | |
| [Rockfalls per Year] | |||||
| 494 | 327 | 374 | 366 | 382 | |
| 115 | 62.4 | 77.9 | 72.8 | 74.8 | |
| 26.9 | 11.9 | 16.2 | 14.5 | 14.6 | |
| Convex Hull | Default Alpha Shape | Alpha Solid | Power Crust 1 | |
|---|---|---|---|---|
| [m3] | 1 | 1 | 1 | 1 |
| 1.6001 | 1.6471 | 1.5743 | 1.5757 | |
| [Rockfalls per Year] | ||||
| 25.6 | 11.3 | 14.3 | 12.6 | |
| 6.41 | 2.54 | 3.82 | 3.35 | |
| 1.61 | 0.573 | 1.02 | 0.890 | |
| 0.403 | 0.129 | 0.272 | 0.236 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
DiFrancesco, P.-M.; Bonneau, D.A.; Hutchinson, D.J. Computational Geometry-Based Surface Reconstruction for Volume Estimation: A Case Study on Magnitude-Frequency Relations for a LiDAR-Derived Rockfall Inventory. ISPRS Int. J. Geo-Inf. 2021, 10, 157. https://doi.org/10.3390/ijgi10030157
DiFrancesco P-M, Bonneau DA, Hutchinson DJ. Computational Geometry-Based Surface Reconstruction for Volume Estimation: A Case Study on Magnitude-Frequency Relations for a LiDAR-Derived Rockfall Inventory. ISPRS International Journal of Geo-Information. 2021; 10(3):157. https://doi.org/10.3390/ijgi10030157
Chicago/Turabian StyleDiFrancesco, Paul-Mark, David A. Bonneau, and D. Jean Hutchinson. 2021. "Computational Geometry-Based Surface Reconstruction for Volume Estimation: A Case Study on Magnitude-Frequency Relations for a LiDAR-Derived Rockfall Inventory" ISPRS International Journal of Geo-Information 10, no. 3: 157. https://doi.org/10.3390/ijgi10030157
APA StyleDiFrancesco, P.-M., Bonneau, D. A., & Hutchinson, D. J. (2021). Computational Geometry-Based Surface Reconstruction for Volume Estimation: A Case Study on Magnitude-Frequency Relations for a LiDAR-Derived Rockfall Inventory. ISPRS International Journal of Geo-Information, 10(3), 157. https://doi.org/10.3390/ijgi10030157