Mapping Very-High-Resolution Evapotranspiration from Unmanned Aerial Vehicle (UAV) Imagery
Abstract
:1. Introduction
2. Materials and Methods
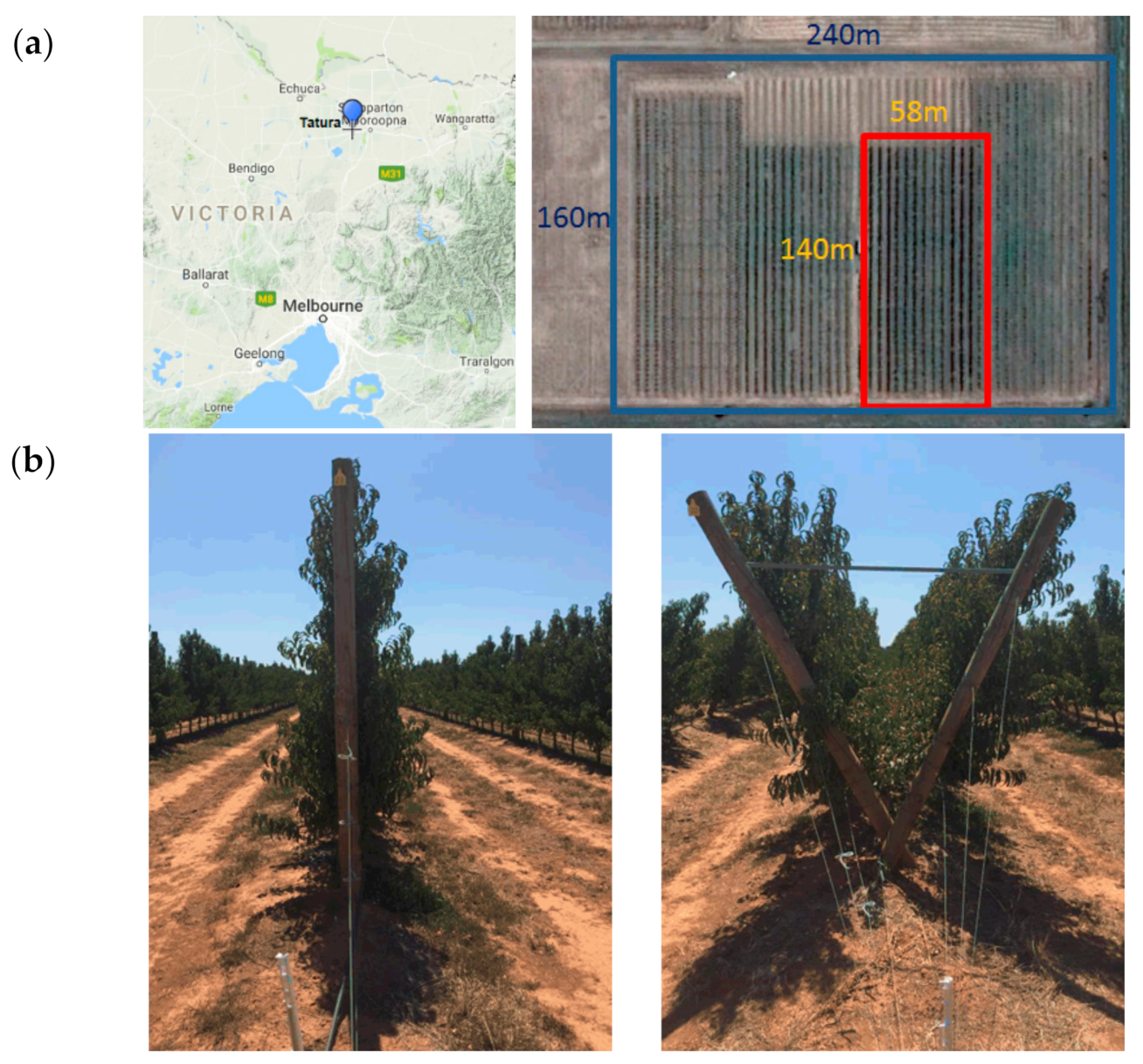
2.1. Study Site
2.2. Data Acquisition
2.2.1. Net Radiation and Micrometeorological Data
2.2.2. Crop Physiology and Solar Radiation Interception Data
2.2.3. UAV Field Campaign
2.3. Remote Sensing Data Processing and ET Modelling
2.3.1. Aerial Imagery Processing
2.3.2. Leaf Area Index (LAI) Estimation
2.3.3. Tree Segmentation
2.3.4. RSEB Algorithm in ET Modeling
2.3.5. Site-Specific Crop ET
3. Results and Discussions
3.1. Canopy Temperatures and NDVI
3.2. Tree-By-Tree Segmentation
3.3. Energy Balance Components
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qureshi, M.E.; Hanjra, M.A.; Ward, J. Impact of water scarcity in australia on global food security in an era of climate change. Food Policy 2013, 38, 136–145. [Google Scholar] [CrossRef]
- Mitchell, P.D.; Chalmers, D.J. The effect of reduced water supply on peach tree growth and yields [irrigation levels]. J. Am. Soc. Hortic. Sci. 1982, 107, 853–856. [Google Scholar]
- Goodwin, I.; O Connell, M.G. Drought water management: An australian perspective. In ActaHortic, 1150th ed.; International Society for Horticultural Science (ISHS): Lleida, Spain, 2017; pp. 219–232. [Google Scholar]
- Tognetti, R.; d’Andria, R.; Morelli, G.; Alvino, A. The effect of deficit irrigation on seasonal variations of plant water use in Olea europaea L. Plant Soil 2005, 273, 139–155. [Google Scholar] [CrossRef]
- Buesa, I.; Perez, D.; Castel, J.; Intrigliolo, D.S.; Castel, J.R. Effect of deficit irrigation on vine performance and grape composition of Vitis vinifera L. Cv. Muscat of alexandria. Aust. J. Grape Wine Res. 2017, 23, 251–259. [Google Scholar] [CrossRef]
- Nouri, H.; Beecham, S.; Anderson, S.; Hassanli, A.M.; Kazemi, F. Remote sensing techniques for predicting evapotranspiration from mixed vegetated surfaces. Urban Water J. 2015, 12, 380–393. [Google Scholar] [CrossRef]
- Kustas, W.; Anderson, M. Advances in thermal infrared remote sensing for land surface modeling. Agric. For. Meteorol. 2009, 149, 2071–2081. [Google Scholar] [CrossRef]
- Xia, T.; Kustas, W.; Anderson, M.; Alfieri, J.; Gao, F.; McKee, L.; Prueger, J.; Geli, H.; Neale, C.; Sanchez, L.; et al. Mapping evapotranspiration with high-resolution aircraft imagery over vineyards using one- and two-source modeling schemes. Hydrol. Earth Syst. Sci. 2016, 20, 1523–1545. [Google Scholar] [CrossRef] [Green Version]
- Courault, D.; Seguin, B.; Olioso, A. Review on estimation of evapotranspiration from remote sensing data: From empirical to numerical modeling approaches. Irrig. Drain. Syst. 2005, 19, 223–249. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (sebal). 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Roerink, G.J.; Su, Z.; Menenti, M. S-sebi: A simple remote sensing algorithm to estimate the surface energy balance. Phys. Chem. Earth Part B Hydrol. Ocean. Atmos. 2000, 25, 147–157. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (metric)-model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Norman, J.M.; Becker, F. Terminology in thermal infrared remote sensing of natural surfaces. Agric. For. Meteorol. 1995, 77, 153–166. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agric. For. Meteorol. 1999, 94, 13–29. [Google Scholar] [CrossRef]
- Zipper, S.C.; Loheide Ii, S.P. Using evapotranspiration to assess drought sensitivity on a subfield scale with hrmet, a high resolution surface energy balance model. Agric. For. Meteorol. 2014, 197, 91–102. [Google Scholar] [CrossRef]
- Ortega-Farías, S.; Ortega-Salazar, S.; Poblete, T.; Kilic, A.; Allen, R.; Poblete-Echeverría, C.; Ahumada-Orellana, L.; Zuñiga, M.; Sepúlveda, D. Estimation of energy balance components over a drip-irrigated olive orchard using thermal and multispectral cameras placed on a helicopter-based unmanned aerial vehicle (uav). Remote Sens. 2016, 8, 638. [Google Scholar] [CrossRef] [Green Version]
- Berni, J.A.J.; Zarco-Tejada, P.J.; Sepulcre-Cantó, G.; Fereres, E.; Villalobos, F. Mapping canopy conductance and cwsi in olive orchards using high resolution thermal remote sensing imagery. Remote Sens. Environ. 2009, 113, 2380–2388. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; González-Dugo, V.; Berni, J.A.J. Fluorescence, temperature and narrow-band indices acquired from a uav platform for water stress detection using a micro-hyperspectral imager and a thermal camera. Remote Sens. Environ. 2012, 117, 322–337. [Google Scholar] [CrossRef]
- Roy, S.; Ophori, D. Estimation of crop water stress index in almond orchards using thermal aerial imagery. J. Spat. Hydrol. 2014, 12, 29. [Google Scholar]
- Rud, R.; Cohen, Y.; Alchanatis, V.; Levi, A.; Brikman, R.; Shenderey, C.; Heuer, B.; Markovitch, T.; Dar, Z.; Rosen, C.; et al. Crop water stress index derived from multi-year ground and aerial thermal images as an indicator of potato water status. Precis. Agric. 2014, 15, 273–289. [Google Scholar] [CrossRef]
- Matese, A.; Toscano, P.; Gennaro, S.F.D.; Genesio, L.; Vaccari, F.P.; Primicerio, J.; Belli, C.; Zaldei, A.; Bianconi, R.; Gioli, B. Intercomparison of uav, aircraft and satellite remote sensing platforms for precision viticulture. Remote Sens. 2015, 7, 2971–2990. [Google Scholar] [CrossRef] [Green Version]
- Chalmers, D.J.; Van den Ende, B. Tatura Trellis Peaches: Productivity over Fifteen Year; International Society for Horticultural Science (ISHS): Clemson, SC, USA, 1989; pp. 303–306. [Google Scholar]
- Elkins, R.B.; DeJong, T.M. Effect of Training System and Rootstock on Growth and Productivity of Golden Russet® Bosc Pear Trees; International Society for Horticultural Science (ISHS): Leuven, Belgium; Ferrar-Bologna, Italy, 2002; pp. 603–607. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; p. 300. [Google Scholar]
- FLIRSystems. User’s Manual Flir ax5 Series; T559770; FLIR Systems: Wilsonville, OR, USA, 2013. [Google Scholar]
- Fan, L.; Gao, Y.; Brück, H.; Bernhofer, C. Investigating the relationship between ndvi and lai in semi-arid grassland in inner mongolia using in-situ measurements. Theor. Appl. Climatol. 2009, 95, 151–156. [Google Scholar] [CrossRef]
- Stenberg, P.; Rautiainen, M.; Manninen, T.; Voipio, P.; Smolander, H. Reduced simple ratio better than ndvi for estimating lai in finnish pine and spruce stands. Silva Fenn. 2004, 38, 3–14. [Google Scholar] [CrossRef] [Green Version]
- Steltzer, H.; Welker, J.M. Modeling the effect of photosynthetic vegetation properties on the ndvi-lai relationship. Ecology 2006, 87, 2765–2772. [Google Scholar] [CrossRef]
- Norman, J.M.; Jarvis, P.G. Photosynthesis in sitka spruce (Picea sitchensis (bong.) carr.). V. Radiation penetration theory and a test case. J. Appl. Ecol. 1975, 12, 839–878. [Google Scholar] [CrossRef]
- DecagonDevicesInc. Decagon Accupar Ceptometer Operating Manual; Decagon Devices Inc.: Pullman, WA, USA, 2001. [Google Scholar]
- Park, S.; Ryu, D.; Fuentes, S.; Chung, H.; Hernández-Montes, E.; O’Connell, M. Adaptive Estimation of Crop Water Stress in Nectarine and Peach Orchards Using High-Resolution Imagery from an Unmanned Aerial Vehicle (UAV). Remote Sens. 2017, 9, 828. [Google Scholar] [CrossRef] [Green Version]
- Goodwin, I.; Whitfield, D.M.; Connor, D.J. Effects of tree size on water use of peach (Prunus persica L. Batsch). Irrig. Sci. 2006, 24, 59–68. [Google Scholar] [CrossRef]
- Chávez, J.L.; Neale, C.M.U.; Prueger, J.H.; Kustas, W.P. Daily evapotranspiration estimates from extrapolating instantaneous airborne remote sensing et values. Irrig. Sci. 2008, 27, 67–81. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, C.; Lei, Y.; Tang, Y.; Yu, Q.; Shen, Y.; Sun, H. An integrated algorithm for estimating regional latent heat flux and daily evapotranspiration. Int. J. Remote Sens. 2006, 27, 129–152. [Google Scholar] [CrossRef]
- Hadiwijaya, B.; Pepin, S.; Isabelle, P.-E.; Nadeau, D.F. The dynamics of transpiration to evapotranspiration ratio under wet and dry canopy conditions in a humid boreal forest. Forests 2020, 11, 237. [Google Scholar] [CrossRef] [Green Version]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.; Ryu, D.; Fuentes, S.; Chung, H.; O’Connell, M.; Kim, J. Mapping Very-High-Resolution Evapotranspiration from Unmanned Aerial Vehicle (UAV) Imagery. ISPRS Int. J. Geo-Inf. 2021, 10, 211. https://doi.org/10.3390/ijgi10040211
Park S, Ryu D, Fuentes S, Chung H, O’Connell M, Kim J. Mapping Very-High-Resolution Evapotranspiration from Unmanned Aerial Vehicle (UAV) Imagery. ISPRS International Journal of Geo-Information. 2021; 10(4):211. https://doi.org/10.3390/ijgi10040211
Chicago/Turabian StylePark, Suyoung, Dongryeol Ryu, Sigfredo Fuentes, Hoam Chung, Mark O’Connell, and Junchul Kim. 2021. "Mapping Very-High-Resolution Evapotranspiration from Unmanned Aerial Vehicle (UAV) Imagery" ISPRS International Journal of Geo-Information 10, no. 4: 211. https://doi.org/10.3390/ijgi10040211
APA StylePark, S., Ryu, D., Fuentes, S., Chung, H., O’Connell, M., & Kim, J. (2021). Mapping Very-High-Resolution Evapotranspiration from Unmanned Aerial Vehicle (UAV) Imagery. ISPRS International Journal of Geo-Information, 10(4), 211. https://doi.org/10.3390/ijgi10040211







