Maximizing Impacts of Remote Sensing Surveys in Slope Stability—A Novel Method to Incorporate Discontinuities into Machine Learning Landslide Prediction
Abstract
:1. Introduction
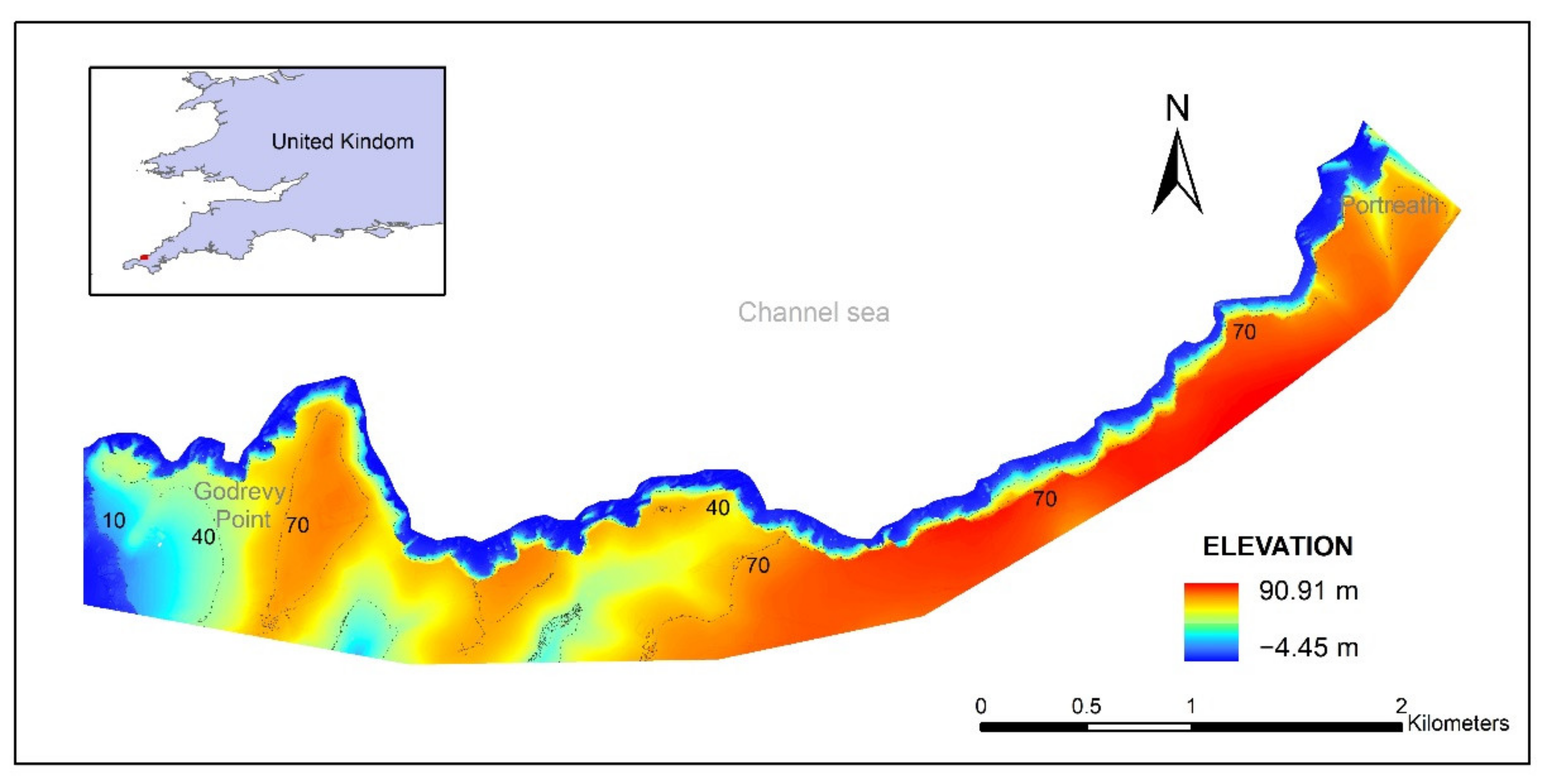
2. Study Area Description
3. Data and Methods
3.1. Landslide Detection and Sampling Strategy
3.2. Geological Structure Extraction from Remote Sensing Surveys
3.3. Variables Associated with Geometric Conditions, Sea Erosion and Geological Conditions
3.4. Variables Associated with Discontinuities
3.4.1. Planar Sliding Kinematic Analysis
- The dip of the major discontinuity is greater than the friction angle (30° was assumed for the mixture of sandstone and mudstone [48]).
- The apparent dip of a slope as seen from the dip direction of the critical discontinuity plane is greater than the dip of the discontinuity plane to allow the discontinuity to daylight on the slope face.
- The slope must be dipped in the same direction as the critical discontinuity plane (a lateral limit of 20° was assumed).

3.4.2. Wedge Sliding Kinematic Analysis
3.4.3. Direct Toppling Kinematic Analysis
- Two joint sets intersect such that the intersection lines dip into the slope and can form discrete toppling blocks.
- A third joint set exists that acts as a release plane or a sliding plane, allowing the blocks to topple.
- The dip of the slope is greater than the dip of the discontinuity plane.
- The slope dips in the same direction as the discontinuity plane (a lateral limit of 20° was assumed).
3.4.4. Flexural Toppling Kinematic Analysis
- The dip of the slope is greater than the friction angle (30° was assumed).
- The apparent dip of the slip limit plane as seen from the dip direction of a critical discontinuity plane is greater than ‘90°− dip of the critical discontinuity plane’.
- The slope dips in the opposite direction to the critical discontinuity plane (a 20° lateral limit was assumed).
3.5. ML Analysis
3.5.1. Random Forest
3.5.2. Support Vector Machine
3.5.3. Multilayer Perceptron
3.5.4. Deep Learning Neural Network
3.6. Frequency Ratio Analysis
4. Results
4.1. Frequency Ratio Analysis
4.2. Machine Learning Analysis
- For the RF model, ntree was assigned as 500 (500), and mtry was 3 (4).
- For the SVM model, the kernel was specified as the radial basis function (‘rbf’), and the regularization parameter C was assigned as 100 (100).
- For the MLP model, the activation function was specified as being ‘logistic’ (‘logistic’); the weight optimization algorithm was specified as ‘lbfgs’ (‘lbfgs’); the regularization parameter alpha was assigned as 0.1 (0.1); 10 (9) nodes were contained in the hidden layer.
- For the DLNN model, a Keras sequential model with 3 (3) hidden layers was configured. Each layer contained 64 (128) neurons. The optimizer used in this model was ‘Adadelta’ for the adaptive learning rate. An EarlyStopping callback was used in conjunction with model training to save optimal epoch the batch size of 1 to prevent overfitting.
5. Validation and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dilley, M.; Chen, R.; Deichmann, U.; Lerner-Lam, A.; Arnold, M.; Agwe, J.; Yetman, G. Natural Disaster Hotspots: A Global Risk; The World Bank: Washington, DC, USA, 2005. [Google Scholar]
- Van Tien, P.; Sassa, K.; Takara, K.; Fukuoka, H.; Dang, K.; Shibasaki, T.; Ha, N.D.; Setiawan, H.; Loi, D.H. Formation process of two massive dams following rainfall-induced deep-seated rapid landslide failures in the Kii Peninsula of Japan. Landslides 2018, 15, 1761–1778. [Google Scholar] [CrossRef]
- Xu, Y.; George, D.L.; Kim, J.; Lu, Z.; Riley, M.; Griffin, T.; de la Fuente, J. Landslide monitoring and runout hazard assessment by integrating multi-source remote sensing and numerical models: An application to the Gold Basin landslide complex, northern Washington. Landslides 2021, 18, 1131–1141. [Google Scholar] [CrossRef]
- Gao, Y.; Li, B.; Gao, H.; Chen, L.; Wang, Y. Dynamic characteristics of high-elevation and long-runout landslides in the Emeishan basalt area: A case study of the Shuicheng “7.23”landslide in Guizhou, China. Landslides 2020, 17, 1663–1677. [Google Scholar] [CrossRef]
- Bolla, A.; Paronuzzi, P. Geomechanical Field Survey to Identify an Unstable Rock Slope: The Passo della Morte Case History (NE Italy). Rock Mech. Rock Eng. 2019, 53, 1521–1544. [Google Scholar] [CrossRef]
- Yilmaz, I. Comparison of landslide susceptibility mapping methodologies for Koyulhisar, Turkey: Conditional probability, logistic regression, artificial neural networks, and support vector machine. Environ. Earth Sci. 2009, 61, 821–836. [Google Scholar] [CrossRef]
- Xu, C.; Dai, F.; Xu, X.; Lee, Y.H. GIS-based support vector machine modeling of earthquake-triggered landslide susceptibility in the Jianjiang River watershed, China. Geomorphology 2012, 145-146, 70–80. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Landslide susceptibility mapping using GIS-based multi-criteria decision analysis, support vector machines, and logistic regression. Landslides 2013, 11, 425–439. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Khosravi, K.; Yang, Y.; Pham, B.T. Assessment of advanced random forest and decision tree algorithms for modeling rainfall-induced landslide susceptibility in the Izu-Oshima Volcanic Island, Japan. Sci. Total Environ. 2019, 662, 332–346. [Google Scholar] [CrossRef] [PubMed]
- Behnia, P.; Blais-Stevens, A. Landslide susceptibility modelling using the quantitative random forest method along the northern portion of the Yukon Alaska Highway Corridor, Canada. Nat. Hazards 2017, 90, 1407–1426. [Google Scholar] [CrossRef]
- Chen, W.; Peng, J.; Hong, H.; Shahabi, H.; Pradhan, B.; Liu, J.; Zhu, A.-X.; Pei, X.; Duan, Z. Landslide susceptibility modelling using GIS-based machine learning techniques for Chongren County, Jiangxi Province, China. Sci. Total Environ. 2018, 626, 1121–1135. [Google Scholar] [CrossRef] [PubMed]
- Huang, F.; Cao, Z.; Guo, J.; Jiang, S.-H.; Li, S.; Guo, Z. Comparisons of heuristic, general statistical and machine learning models for landslide susceptibility prediction and mapping. Catena 2020, 191, 104580. [Google Scholar] [CrossRef]
- Bui, D.T.; Tsangaratos, P.; Nguyen, V.-T.; Van Liem, N.; Trinh, P.T. Comparing the prediction performance of a Deep Learning Neural Network model with conventional machine learning models in landslide susceptibility assessment. Catena 2020, 188, 104426. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B.; Lee, S. Application of convolutional neural networks featuring Bayesian optimization for landslide susceptibility assessment. Catena 2020, 186, 104249. [Google Scholar] [CrossRef]
- Lucchese, L.V.; De Oliveira, G.G.; Pedrollo, O.C. Attribute selection using correlations and principal components for artificial neural networks employment for landslide susceptibility assessment. Environ. Monit. Assess. 2020, 192, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Gilbert, G.; Cepeda, J.M.; Lysdahl, A.O.K.; Piciullo, L.; Hefre, H.; Lacasse, S. Modelling of shallow landslides with machine learning algorithms. Geosci. Front. 2021, 12, 385–393. [Google Scholar] [CrossRef]
- Nhu, V.-H.; Hoang, N.-D.; Nguyen, H.; Ngo, P.T.T.; Bui, T.T.; Hoa, P.V.; Samui, P.; Bui, D.T. Effectiveness assessment of Keras based deep learning with different robust optimization algorithms for shallow landslide susceptibility mapping at tropical area. Catena 2020, 188, 104458. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y. GIS-based evaluation of landslide susceptibility using hybrid computational intelligence models. Catena 2020, 195, 104777. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Singh, S.K.; Shirzadi, A.; Shahabi, H.; Bui, D.T. Landslide susceptibility modeling using Reduced Error Pruning Trees and different ensemble techniques: Hybrid machine learning approaches. Catena 2019, 175, 203–218. [Google Scholar] [CrossRef]
- Stead, D.; Wolter, A. A critical review of rock slope failure mechanisms: The importance of structural geology. J. Struct. Geol. 2015, 74, 1–23. [Google Scholar] [CrossRef]
- Ferrero, A.M.; Migliazza, M.R.; Pirulli, M.; Umili, G. Some Open Issues on Rockfall Hazard Analysis in Fractured Rock Mass: Problems and Prospects. Rock Mech. Rock Eng. 2016, 49, 3615–3629. [Google Scholar] [CrossRef]
- Francioni, M.; Coggan, J.; Eyre, M.; Stead, D. A combined field/remote sensing approach for characterizing landslide risk in coastal areas. Int. J. Appl. Earth Obs. Geoinformation 2018, 67, 79–95. [Google Scholar] [CrossRef]
- Francioni, M.; Salvini, R.; Stead, D.; Coggan, J. Improvements in the integration of remote sensing and rock slope modelling. Nat. Hazards 2018, 90, 975–1004. [Google Scholar] [CrossRef] [Green Version]
- Meng, F.; Wong, L.N.Y.; Zhou, H.; Wang, Z. Comparative study on dynamic shear behavior and failure mechanism of two types of granite joint. Eng. Geol. 2018, 245, 356–369. [Google Scholar] [CrossRef]
- Vatanpour, N.; Ghafoori, M.; Talouki, H.H. Probabilistic and sensitivity analyses of effective geotechnical parameters on rock slope stability: A case study of an urban area in northeast Iran. Nat. Hazards 2014, 71, 1659–1678. [Google Scholar] [CrossRef]
- Havaej, M.; Wolter, A.; Stead, D. The possible role of brittle rock fracture in the 1963 Vajont Slide, Italy. Int. J. Rock Mech. Min. Sci. 2015, 78, 319–330. [Google Scholar] [CrossRef]
- Vanneschi, C.; Eyre, M.; Venn, A.; Coggan, J.S. Investigation and modeling of direct toppling using a three-dimensional distinct element approach with incorporation of point cloud geometry. Landslides 2019, 16, 1453–1465. [Google Scholar] [CrossRef]
- Shail, R.K.; Coggan, J.S.; Stead, D. Coastal landsliding in Cornwall, UK: Mechanisms, modelling and implications. In Proceedings of the 8th International Congress IAEG, Vancouver, BC, Canada, 21–25 September 1998; pp. 1323–1330. [Google Scholar]
- Leveridge, B.; Shail, R. The Gramscatho Basin, south Cornwall, UK: Devonian active margin successions. Proc. Geol. Assoc. 2011, 122, 568–615. [Google Scholar] [CrossRef] [Green Version]
- Hollick, L.; Shail, R.; Leveridge, B. Devonian Rift-Related Sedimentation and Variscan Tectonics—New Data on the Looe and Gramscatho Basins from the Resurvey of the Newquay District; The Ussher Society, 2006. Geosci. South-West Engl. 2006, 11, 191–198. [Google Scholar]
- Turner, D.; Lucieer, A.; De Jong, S.M. Time Series Analysis of Landslide Dynamics Using an Unmanned Aerial Vehicle (UAV). Remote. Sens. 2015, 7, 1736–1757. [Google Scholar] [CrossRef] [Green Version]
- Maurer, J.; Rupper, S. Tapping into the Hexagon spy imagery database: A new automated pipeline for geomorphic change detection. ISPRS J. Photogramm. Remote. Sens. 2015, 108, 113–127. [Google Scholar] [CrossRef]
- Kim, M.-K.; Sohn, H.-G.; Kim, S. Incorporating the effect of ALS-derived DEM uncertainty for quantifying changes due to the landslide in 2011, Mt. Umyeon, Seoul. GIScience Remote. Sens. 2019, 57, 287–301. [Google Scholar] [CrossRef]
- Digimap. Available online: https://digimap.edina.ac.uk/lidar (accessed on 6 February 2021).
- Agisoft. Metashape; Agisoft LLC: Brooklyn, NY, USA, 2016.
- Channel Coastal Observatory. Available online: https://www.channelcoast.org/ (accessed on 6 February 2021).
- Split Engineering LLC. Split-FX. 2016. Available online: https://www.spliteng.com/ (accessed on 6 February 2021).
- Poluga, S.L.; Shakoor, A.; Bilderback, E.L. Rock Mass Characterization and Stability Evaluation of Mount Rushmore National Memorial, Keystone, South Dakota. Environ. Eng. Geosci. 2018, 24, 385–412. [Google Scholar] [CrossRef]
- Lato, M.; Diederichs, M.S.; Hutchinson, D.J.; Harrap, R. Optimization of LiDAR scanning and processing for automated structural evaluation of discontinuities in rockmasses. Int. J. Rock Mech. Min. Sci. 2009, 46, 194–199. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Hong, H. Comparison of convolutional neural networks for landslide susceptibility mapping in Yanshan County, China. Sci. Total Environ. 2019, 666, 975–993. [Google Scholar] [CrossRef]
- Shao, X.; Ma, S.; Xu, C.; Zhang, P.; Wen, B.; Tian, Y.; Zhou, Q.; Cui, Y. Planet Image-Based Inventorying and Machine Learning-Based Susceptibility Mapping for the Landslides Triggered by the 2018 Mw6.6 Tomakomai, Japan Earthquake. Remote. Sens. 2019, 11, 978. [Google Scholar] [CrossRef] [Green Version]
- Abanades, J.; Greaves, D.; Iglesias, G. Coastal defence using wave farms: The role of farm-to-coast distance. Renew. Energy 2015, 75, 572–582. [Google Scholar] [CrossRef] [Green Version]
- Levin, N.; Kidron, G.J.; Ben-Dor, E. The spatial and temporal variability of sand erosion across a stabilizing coastal dune field. Sedimentology 2006, 53, 697–715. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Sadhasivam, N.; Kariminejad, N.; Collins, A.L. Gully erosion spatial modelling: Role of machine learning algorithms in selection of the best controlling factors and modelling process. Geosci. Front. 2020, 11, 2207–2219. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, T. Underground Excavations in Rock, 1st ed.; The Institution of Mining and Metallurgy: London, UK, 1980. [Google Scholar]
- Yilmaz, I.; Marschalko, M.; Yildirim, M.; Dereli, E.; Bednárik, M.; Yıldırım, M. GIS-based kinematic slope instability and slope mass rating (SMR) maps: Application to a railway route in Sivas (Turkey). Bull. Int. Assoc. Eng. Geol. 2011, 71, 351–357. [Google Scholar] [CrossRef]
- Hoek, E.; Bray, J.W. Rock Slope Engineering, 3rd ed.; The Institute of Mining and Metallurgy: London, UK, 1981. [Google Scholar]
- Barton, N. Review of a new shear-strength criterion for rock joints. Eng. Geol. 1973, 7, 287–332. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.-M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef] [Green Version]











| Joint Set | Dip (°) / Dip Direction (°) | Description |
|---|---|---|
| S0 | 26/114 | Bedding. Smooth, undulating, planar. |
| J1 | 51/309 | Rough, undulating, stepped. |
| J2 | 90/322 | Smooth, undulating, planar. |
| J3 | 74/141 | Rough, undulating, planar. |
| J4 | 70/264 | Smooth, undulating, planar. |
| J5 | 84/242 | Smooth, undulating, planar. |
| Category | Variable | Description |
|---|---|---|
| Geometric conditions | Aspect | Aspect is the dip direction of slopes, and used to analyze effects of weather/sea conditions (such as wind directions) or unfavorable orientations of discontinuities |
| Profile curvature | Two types of curvatures indicate the amount of overburden on a failure plane (convex terrain of slope surface could result in more overburden than concave terrain | |
| Plan curvature | ||
| Slope angle | Slope angle indicates the potential for kinematic failures of slopes together with unfavorable orientated discontinuities | |
| Cliff height | As the slope height increases, the shear stress within the toe of the slope increases due to added weight | |
| Sea erosion conditions | Distance from sea | Distance from sea partially characterizes the conditions of sea erosion, which may cause physical and chemical change of coastal slopes, such as the removal of mass on the lower part, providing increases in the shear stress of the slopes and thus decreases in the factor of safety |
| Geological condition | Material of bedrock | This component influences the shear strength of a rock mass |
| Mechanism | Joint Set | Dip/DD (Plunge/Trend) | Failure Criteria | |
|---|---|---|---|---|
| Planar | P1 | J1 | 51°/309° | |
| P2 | J4 | 70°/264° | ||
| Wedge | W1 | J1/J4 | 49°/329° | |
| W2 | J1/J5 | 50°/325° | ||
| W3 | J2/J4 | 67°/232° | ||
| W4 | J3/J4 | 56°/206° | ||
| W5 | J4/J5 | 54°/324° | ||
| Direct toppling | DT1 (oblique) | Sliding: J1 | 51°/309° | |
| LOI: J3/J5 | 72°/171° | |||
| DT2 (oblique) | Sliding: J4 | 70°/264° | ||
| LOI: J3/J5 | 72°/171° | |||
| Flexural toppling | F1 | J3 | 74°/141° | |
| Mechanism | Class | LSi | ai | Pi | bi | FR |
|---|---|---|---|---|---|---|
| Planar_J1 | Class 1: [0, 0.05] | 156 | 0.31 | 573 | 0.56 | 0.54 |
| Class 2: (0.05, 0.1] | 213 | 0.42 | 283 | 0.28 | 1.51 | |
| Class 3: (0.1, max] | 141 | 0.28 | 164 | 0.16 | 1.72 | |
| Planar_J4 | Class 1: [0, 0.02] | 242 | 0.47 | 721 | 0.71 | 0.67 |
| Class 2: (0.02, 0.04] | 109 | 0.21 | 123 | 0.12 | 1.77 | |
| Class 3: (0.04, max] | 159 | 0.31 | 176 | 0.17 | 1.81 | |
| Wedge_J1/J4 | Class 1: [0, 0.1] | 69 | 0.14 | 359 | 0.35 | 0.38 |
| Class 2: (0.1, 0.2] | 208 | 0.41 | 364 | 0.36 | 1.14 | |
| Class 3: (0.2, max] | 233 | 0.46 | 297 | 0.29 | 1.57 | |
| Wedge_J2/J4 | Class 1: [0, 0.03] | 261 | 0.51 | 742 | 0.73 | 0.70 |
| Class 2: (0.03, 0.06] | 119 | 0.23 | 132 | 0.13 | 1.80 | |
| Class 3: (0.06, max] | 130 | 0.25 | 146 | 0.14 | 1.78 | |
| Wedge_J3/J4 | Class 1: [0,0.03] | 307 | 0.60 | 794 | 0.78 | 0.77 |
| Class 2: (0.03, 0.06] | 93 | 0.18 | 101 | 0.10 | 1.84 | |
| Class 3: (0.06, max] | 110 | 0.22 | 125 | 0.12 | 1.76 | |
| Flexural_J3 | Class 1: [0, 0.03] | 271 | 0.53 | 726 | 0.71 | 0.75 |
| Class 2: (0.03, 0.06] | 188 | 0.37 | 233 | 0.23 | 1.61 | |
| Class 3: (0.06, max] | 51 | 0.10 | 61 | 0.06 | 1.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, L.; Coggan, J.; Francioni, M.; Eyre, M. Maximizing Impacts of Remote Sensing Surveys in Slope Stability—A Novel Method to Incorporate Discontinuities into Machine Learning Landslide Prediction. ISPRS Int. J. Geo-Inf. 2021, 10, 232. https://doi.org/10.3390/ijgi10040232
He L, Coggan J, Francioni M, Eyre M. Maximizing Impacts of Remote Sensing Surveys in Slope Stability—A Novel Method to Incorporate Discontinuities into Machine Learning Landslide Prediction. ISPRS International Journal of Geo-Information. 2021; 10(4):232. https://doi.org/10.3390/ijgi10040232
Chicago/Turabian StyleHe, Lingfeng, John Coggan, Mirko Francioni, and Matthew Eyre. 2021. "Maximizing Impacts of Remote Sensing Surveys in Slope Stability—A Novel Method to Incorporate Discontinuities into Machine Learning Landslide Prediction" ISPRS International Journal of Geo-Information 10, no. 4: 232. https://doi.org/10.3390/ijgi10040232
APA StyleHe, L., Coggan, J., Francioni, M., & Eyre, M. (2021). Maximizing Impacts of Remote Sensing Surveys in Slope Stability—A Novel Method to Incorporate Discontinuities into Machine Learning Landslide Prediction. ISPRS International Journal of Geo-Information, 10(4), 232. https://doi.org/10.3390/ijgi10040232







