Copyright Protection Based on Zero Watermarking and Blockchain for Vector Maps

Abstract

Zero watermarking does not alter the original information contained in vector map data and provides perfect imperceptibility. The use of zero watermarking for data copyright protection has become a significant trend in digital watermarking research. However, zero watermarking encounters tremendous obstacles to its development and application because of its requirement to store copyright information with a third party and its difficulty in confirming copyright ownership. Aiming at the shortcomings of the existing zero watermarking technology, this paper proposes a new zero watermarking construction method based on the angular features of vector data that store the zero watermarking and copyright information on the blockchain after an XOR operation. When the watermark is being extracted, the copyright information can be extracted with the XOR operation to obtain the information stored on the blockchain. Experimental results show that the combination of zero watermarking and blockchain proposed in this paper gives full play to the advantages of the two technologies and protects the copyright of data in a lossless fashion. Compared with the traditional zero watermarking algorithms, the proposed zero watermarking algorithm exhibits stronger robustness. Moreover, the proposed data copyright protection framework with a combination of zero watermarking and blockchain can also be applied to other data types, such as images, audio, video, and remote sensing images.

1. Introduction

Vector data are widely used in the geographic information industry. Because of the small amount of data stored in vectors, as well as their fast updates and ease of copying and distribution, such data is vulnerable to illegal infringement and embezzlement. Effective copyright protection has always been the main focus in the field of data security. Digital watermark technology provides good technical support for protecting the copyrights of vector data [1]. The existing digital watermark algorithms for vector data are mainly divided into spatial domain [2,3,4] and frequency domain [5,6] algorithms. These two types of methods embed watermark information by modifying coordinate values directly or indirectly. This kind of embedding model will inevitably cause a loss of accuracy with respect to vector map data. Especially for vector data with high data accuracy requirements, the destruction of accuracy will directly reduce the data quality [7]. Under this circumstance, lossless watermark technology can provide copyright protection without losing the original data’s accuracy, so it has more advantages than the traditional watermark. Therefore, lossless copyright protection technology for vector data has become a research focus in data security.

Currently, there are three leading technologies for the lossless copyright protection of vector data. The first is the reversible watermark, which completely restores the original carrier data after extracting the watermark [8,9,10]. The data lose protection after being restored, although a reversible watermark avoids the loss of data accuracy. Therefore, the reversible watermark cannot provide permanent copyright protection for data, one of the existing issues faced by a reversible watermark.

The second lossless watermark technology embeds the watermark by modifying the attribute domain. This kind of method embeds the watermark information into vector data attributes and adjusts the storage order to achieve copyright protection [11,12,13]. For example, Sun et al. [11] hid watermark information in data attributes according to the TAB file structure, a file format for vector maps. The watermark is effectively concealed after embedding, since each vector object reserves redundant space when defining attributes. However, because their approach chooses a redundant space for the attribute data, which is most likely to be lost when processing the data to embed the watermark, the proposed method has poor practicality. Zhou et al. [12] proposed a lossless watermark algorithm based on stored features that determines the watermark position according to the chosen line’s length and angle. The storage order of the arc points in the line element is then changed according to the value of the watermark (zero or one). This algorithm realizes the copyright protection of vector map line elements by adjusting the arc points’ storage order. However, the algorithm is only applicable to vector line elements, not to vector points or area elements. Based on the work of Zhou, Ren et al. [13] gave the rules for constructing arc segments with vector points and area elements, and this improved the previously developed algorithm by allowing it to realize the copyright protection of all vector data elements; the new approach reflected strong robustness and imperceptibility. However, Ren and Zhou’s methods destroy the storage order when embedding a watermark, and this is not suitable for the situation where features or vertices reorder. Therefore, the functional objects of their algorithms are relatively limited. In other words, this kind of lossless watermark algorithm provides copyright protection without any loss of precision by embedding it into the attribute domain. Nevertheless, the embedded watermark is likely to be destroyed by pirates, and the lossless data obtained after destroying the watermark still have usefulness.

The third lossless watermark technique is zero watermarking. Zero watermarking algorithms are structural watermark algorithms whose key is to extract stable feature information from given data to construct watermarks [14]. The current research on zero watermarking for vector data can be divided into two types: spatial domain and frequency domain research. The spatial domain includes constructing the average coordinates of, for example, feature points [7], distance sequences [15], and angle sequences [16] through specific methods. This kind of algorithm has certain robustness to geometric attacks, cropping, compression, and other watermark attacks. The frequency domain includes constructing zero watermarks through frequency domain transformation methods such as the discrete Fourier transform (DFT) [17] and wavelet transform [18]. These kinds of methods have stronger robustness and higher computational complexity than spatial domain algorithms. Zero watermarking algorithms register their constructed watermarks with the intellectual property rights (IPR) to resist interpretation attacks [19,20,21] instead of embedding the watermark information into the data. The interpretation attack is a scheme for attacking watermarks proposed by International Business Machines Corporation (IBM). The attack scheme neither erases nor invalidates the target watermark. It generates copyright confusion by forging the original image or watermarking the image [22]. Unfortunately, the actual application of zero watermarking is often restricted by a series of factors, such as the required registration period, cost, and the credibility of the IPR.

In other words, the reversible watermark can restore data after extraction, but the restored data lose copyright protection at the same time. In addition, although modifying the attribute domain to embed a watermark can protect the data and ensure accuracy, the accuracy of the data is destroyed, which may lead to data theft. Zero watermarking can provide permanent copyright protection for data without damage. Moreover, the constructed watermark information is closely related to the coordinate accuracy, which makes up for the deficiencies of the two methods above. However, zero watermarking technology has tremendous practical application limitations due to its heavy reliance on centralized third-party copyright agencies. If the demand for third-party copyright agency certifications is solved, zero watermarking can become an ideal solution in the domain of lossless copyright protection technology.

Therefore, based on the above research, this paper thoroughly analyzes vector data’s spatial relationships and proposes a robust zero watermarking algorithm based on angular features. Besides that, we introduce blockchain technology to solve the issue such that zero watermarking fundamentally relies on the IPR. This will be a new exploration that will provide a new opportunity to further study and develop zero watermarking for vector data.

2. Basic Idea and Preliminaries

This paper introduces blockchain technology into the process of copyright protection for zero watermarking for the first time. It proposes a zero watermarking storage framework for vector data based on blockchain. Under this framework, the distribution of the given data is synchronized and chained with zero watermarking. When distributing the data to the user, the data’s zero watermark information is linked to the blockchain with both sides’ information to generate and save the certificate of copyright. This framework introduces blockchain into zero watermarking, providing an effective, safe, and traceable copyright protection scheme.

Moreover, the basic idea of a zero watermarking algorithm based on the angular feature proposed in this paper is as follows: First, the vector map line and surface are compressed to extract the feature points. Then, the angle sequence of the feature points is extracted by constructing concentric circles. Finally, an XOR operation is performed between the copyright image and angle sequence to obtain multiple zero watermarks. Experiments show that the proposed algorithm completely resists translation, rotation, and scaling attacks and has good robustness to compression, cropping, and adding attacks.

2.1. Zero Watermarking

Because several nodes connect the line segments of the vector line elements and surface elements, we regard the two types of elements as a set of nodes. The points that can reflect the full features of the vector data are regarded as feature points. To resist simplification attacks, we use the Douglas–Peucker algorithm to compress the vector data for selecting feature points and calculating the mean value of these feature points. We draw several concentric circles with the mean value as the center and a sequence of numbers determined by the length of the binary sequence of the copyright image as the radii. Then, we calculate the value of each point’s angles in each circle and binarize the sequence consisting of these values. After that, we can perform an XOR operation between the binary sequence of angles and the copyright image sequence to extract the zero watermarking. The algorithm ensures the even distribution of watermark features in space and improves the watermark’s ability to resist various attacks. The construction process of zero watermarking is shown in Figure 1.

2.2. Blockchain

Traditional zero watermarking algorithms send watermark information to the IPR for registration to ensure that the obtained watermark has a credible copyright attribute. When facing a copyright dispute, we can restore the copyright through a public algorithm designed for copyright protection. However, this method is unrealistic to apply to the protection of massive geographic data due to its long review cycle, high cost, and inability to trace infringement. The emergence of blockchain provides the right solution for the above issues.

2.2.1. Blockchain Technology

Blockchain technology was first proposed by a scholar named Satoshi Nakamoto in his paper “Bitcoin: A peer-to-peer e-cash system” published in 2008 [23].

2.2.2. Ant Blockchain Open Alliance

Nowadays, there are many mature blockchain applications, such as Bitcoin [24], Ethereum blockchain [25], and Antchain [26]. Among them, Antchain is the latest and most popular blockchain application in China. It is widely used in many fields, such as finance, digital copyright protection, and government affairs. The Ant Blockchain Open Alliance is a blockchain network for enterprises and developers in Antchain, which does not need to be built and can be linked quickly. We briefly introduce the Ant Blockchain Open Alliance from the following aspects:

• Smart contract

This is a computer protocol designed to disseminate, verify, or execute contracts in an information-based manner. A smart contract is a set of promises defined in digital form, including the agreements on which the contract participants can execute these promises. Smart contract allows trusted transactions without a third party, which is traceable and irreversible.

• Gas

Here, a smart contract is used to measure the consumption of computing and storage in a virtual machine, which can prevent malicious attacks and the waste of computing and storage.

• Virtual machine

A virtual machine is a high-level abstraction that simulates a physical machine based on a native operating system. It allows the same platform to run on many different hardware architectures and operating systems. Virtual machines in blockchain are mainly used to run intelligent contracts on the chain.

• World state

The storage status of blockchain accounts includes the basic storage status of all accounts and the internal storage status of contract accounts. The contract platform can be understood as a kind of "state machine" of transaction. The world state describes the current basic storage state. After executing the smart contract, the world state may change into another new world state.

• Consensus algorithm

This is the algorithm for data consistency assurance in the distributed system, which ensures the data consistency of multiple participants through certain protocol interactions. Standard algorithms include PDFT, RAFT, POW, POS, and so on.

As shown in Figure 2, a blockchain is a growing list of records, called blocks, linked through cryptography. Each block contains the encrypted hash value, timestamp, and transaction data of the previous block [24]. When applied to zero watermarking-based copyright protection, once the extracted watermark information is uploaded to the blockchain, each node in the blockchain will execute the smart contract code in the virtual machine. Then, the consensus can be reached on the execution result of the smart contract. Finally, the world state will be updated, and new blocks will be generated. Once the block is on the chain, each node in the blockchain will contain a block’s backup, eliminating the risk of data centralization [27]. Compared with traditional IPR, the application of blockchain makes the protection of vector data more credible.

3. Methods

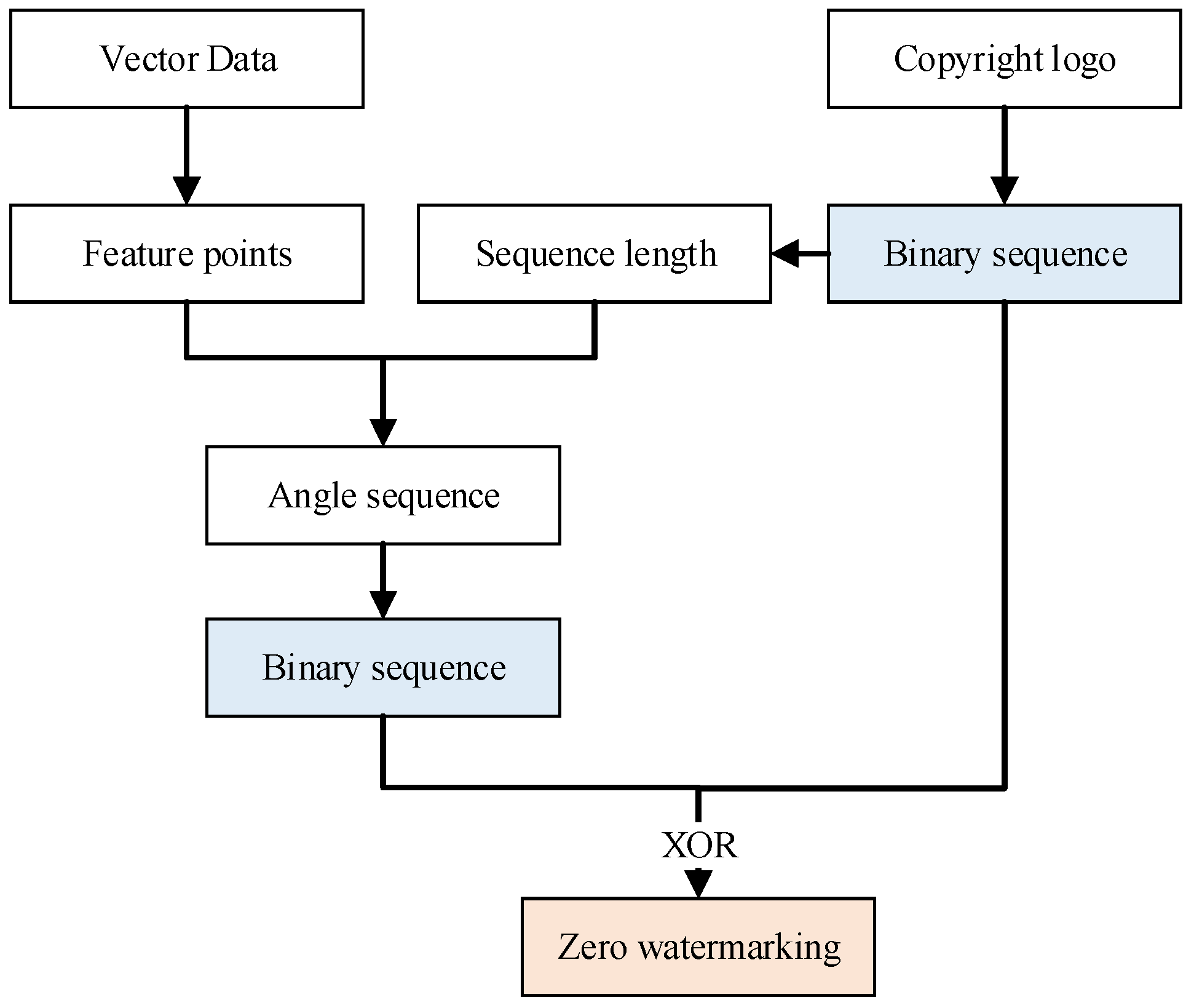
3.1. Zero Watermarking Algorithm

3.1.1. Feature Point Extraction

In this paper, the classic Douglas–Peucker algorithm was used for data compression. The basic idea is as follows: the first and last nodes of a curve are connected, and a straight line is determined for obtaining the maximum distance $d_{\max }$ from the curve’s middle point to the straight line. Comparing $d_{\max }$ and the pregiven threshold D, if $d_{\max }<D$, all the middle points are deleted, and the head and last nodes are reserved after processing. If $d_{\max }\ge D$, these nodes are divided into two groups, and then the steps above are repeated until all nodes are processed.

The Douglas–Peucker algorithm’s flow is shown in Figure 3, and the point set $u=\{1,2,3,4,5,6,7,8\}$ contains all the nodes representing a curve. According to the given threshold $D$, the curve is finally simplified as $U_D=\{1,4,6,7,8\}$. The contour of the original curve was still preserved.

3.1.2. Angle Calculation

As shown in Figure 4, $A(x_1,y_1)$, $B(x_2,y_2)$, $C(x_3,y_3)$, and $D(x_4,y_4)$ are the four endpoints of line segments $AB$ and $CD$. Then, we can define $\overrightarrow{AB}=(x_2-x_1,y_2-y_1)$ and $\overrightarrow{CD}=(x_4-x_3,y_4-y_3)$. Using Equation (1), we calculated the angle $\theta$ between the two line segments, where $\theta \in [0^{°},{180}^{°}]$.

$$\theta =\arccos (\frac{|\overrightarrow{AB}\ast \overrightarrow{CD}|}{\left|\overrightarrow{AB}\right|\ast \left|\overrightarrow{CD}\right|})$$

(1)

3.1.3. Construction of a Zero Watermark

The detailed construction process of zero watermarking is as follows:

Step 1: Select the binary image $I$ of the size $N\times N$ that contains the copyright information. The pixel of the image is $I(i,j)=\{0,1\}$, where $i,j\in \{1,2,3,\dots ,N\}$. The two-dimensional matrix $I$ is arranged into a one-dimensional copyright sequence $I^{\ast }$, which can be calculated from Equation (2):

$$I^{\ast }=N\times N$$

(2)

Step 2: Extract the feature points from the vector data with the Douglas–Peucker algorithm, where the number of feature points is $H$.

Step 3: The average point of the feature points is $O$, which can be calculated by Equation (3):

$$\{\begin{array}{l}{O}_x=\frac{{\displaystyle \sum _{i=1}^H{X}_i}}{H}\hfill \\ O_{\mathrm{y}}=\frac{{\displaystyle \sum _{i=1}^H{Y}_i}}{H}\hfill \end{array}$$

(3)

where $O_x$ and $O_{\mathrm{y}}$ are the X and Y coordinates of $O$, respectively, and $X_i$ and $Y_i$ are the X and Y coordinates of the feature points, respectively.

Step 4: Draw several concentric circles with $O$ as the center. The rule for dividing these circles is as follows: each feature point allocates 8 bits for storing the angle’s binary value. Moreover, the number of feature points needed in each circle $n$ can be calculated according to Equation (4):

$$\mathrm{n}=\frac{N\ast N}{8}$$

(4)

Step 5: Calculate the value of the vector of the angular feature points in turn and obtain the angle sequence $M=(m_1,m_2,\dots ,m_i,\dots ,m_n)$, where $m_i\in [0^{°},{180}^{°}]$, $1\le i\le n$.

Step 6: Binarize sequence $M$ to obtain a new sequence $M^{\ast }$ (with a length $N\times N$) that contains an angular feature. Then, perform an XOR operation bitwise between the binary copyright sequence $I^{\ast }$ and the binary angle sequence $M^{\ast }$ according to Equation (5) to obtain the zero watermarking sequence $W=(w_1,w_2,\dots ,w_i,\dots ,w_{N\times N})$, where $w_i\in \{0,1\}$, $1\le i\le N\times N$:

$$W=I^{\ast }\oplus M^{\ast }$$

(5)

Step 7: Repeat steps 4 and 5 and obtain $K$ zero watermarking sequences $Z=(W_1,W_2,\dots ,W_i,\dots ,W_K)$, where $1\le i\le K$ and $K$ is calculated by Equation (6):

$$K=\lfloor \frac{H}{n}\rfloor$$

(6)

Because the average point will be changed by cropping, adding points, or other attacks, the average point coordinate is binarized and stored together with the zero watermarking sequence $Z$.

3.1.4. Extraction of the Zero Watermark

The detection process of the watermark is the reverse of the construction process above. The angle sequence of the vector data is extracted, and an XOR operation is performed with the constructed zero watermarking information to generate the copyright image. Then, the similarity between the generated image and the original copyright image is checked as follows. First, the mode of attack being used against the vector map is determined. The original stored center point coordinate is used if the carrier is attacked by cropping or adding, and the center point’s coordinates are recalculated otherwise. Then, the binary angle sequence $M^{\ast }$ is extracted according to steps 2–5 above, and an XOR operation is performed with each zero watermarking sequence in $M^{\ast }$ to obtain the copyright sequence. Finally, each sequence’s value is calculated, and the copyright image $NC$ with the highest value is chosen as the watermark image. The extraction process is shown in Figure 5.

3.1.5. Zero Watermarking Forensics

When questionable data needs to be verified, as is shown in Figure 6, the distributor or receiver can query the zero watermarking of the original data in the blockchain and then calculate the similarity with the zero watermark extracted from the suspicious data to determine whether the suspicious data is infringing.

For one set of data with multiple distributions, the distributor in the first record of the distribution on the blockchain represents copyright ownership.

3.2. Smart Contract and Storage System Design

3.2.1. Smart Contract Design

The design of a smart contract is the key to the blockchain. To illustrate the design of the smart contract clearly, some abbreviations are listed in

Table 1. The abbreviations in smart contract design.

Abbreviation	Description
DU	Distribution Unit, the owner of data, responsible for the distribution of data
RU	Receiving Unit, the receiver of data
DU_AD	Account address of distribution unit
RU_AD	Account address of receiving unit
CONTRACT_BC	The byte code of the smart contract
BLOCK	The block constructed of ZW, DU_AD, and RU_AD
SERVER	The server is used to store vector geographic data and extract the zero watermarking algorithm
OV	Original vector map data
ZW	Zero watermarking extracted from the original vector map data
THX	The unique hash value generated after a successful transaction on the blockchain

.

In this part, we focus on designing the interfaces of the smart contract to meet the requirements of the DU and RU. The main interfaces of the contract are as follows:

• initContractData: only the DU can execute the interface, whose function is to compose the block with the DU_AD, RU_AD and ZW, and the return value is CONTRACT_BC;
• searchContract: both the DU and RU can execute this interface. Its function is to return the information of the contract. If it is not initialized, it will return null;
• dataDistribution: only the DU can execute the interface. Its function is to return the THX of the uploaded block.

After the smart contract is deployed, the above interfaces can be called normally.

3.2.2. Zero Watermarking Storage System Design

The alliance chain is jointly managed by several designated institutions or organizations [28]. Considering that most vector data are protected, the alliance chain ensures that the chain’s information is only open and transparent in a limited number of trusted nodes [29]. This design is better than the public chain in terms of efficiency and security.

In this paper, a zero watermarking storage system for vector data based on the Ant Blockchain Open Alliance is constructed for the DU and RU. The structure of the system is shown in Figure 7. Each step is listed below:

• RU sends RU_AD and the request for OV to the DU.
• After confirming the identity of the RU, the DU will use the proposed algorithm to extract the ZW of OV in SERVER.
• SERVER returns the extracted ZW to the DU.
• DU deploys the ZW, DU_AD, and RU_AD to the smart contract.
• The smart contract constructs information into the BLOCK and returns CONTRACT_BC to the DU.
• DU sends the CONTRACT_BC to the RU.
• RU uses the CONTRACT_BC to access the smart contract.
• The smart contract returns the ZW, DU_AD, and RU_AD to the RU.
• After confirming the RU_AD is correct, the RU returns the confirmation information to the DU.
• The DU sends the confirmation information to the smart contract.
• The smart contract uploads the BLOCK to the blockchain.
• The smart contract returns the THX to the DU.

The DU sends the THX and OV to the RU.

The function of the whole system can be divided into two categories. The RU has the functions of zero watermarking extraction, smart contract deployment, block upload, block query, and data distribution as a data distribution unit. As the data receiving unit, the DU only has the functions of data application, contract confirmation, block query, and data receiving. When questionable data needs to be verified, both the DU and RU can use the THX to query the ZW from the blockchain, which will protect the copyright of the OV and realize the traceability of its distribution and transaction process.

4. Experiments and Results

In this part, we tested the zero watermarking algorithm and the blockchain-based certificate storage system mentioned above. The certificate storage system was implemented based on the Ant Blockchain Open Alliance. The running environment was as follows: an i7-8700 CPU @ 3.20 GHz with 12 GB of RAM running on Windows 10. The program was written using Matlab, Java, and Solity.

4.1. Zero Watermarking Experiment and Results

4.1.1. Experimental Data and Parameter Settings

To verify the effectiveness of the proposed watermark algorithm, 1:5,000,000 “county-level administrative boundaries of Jiangsu province” were selected as the vector data for experimental purposes (shown in Figure 8a), the data format of which was shapfile. The coordinate system was the China Geodetic Coordinate System 2000, and the number of vertices was 100,251. This paper used a meaningful binary image logo of 32 × 32 pixels as the copyright information (shown in Figure 8b). The feature points were extracted by the Douglas–Peucker method, the threshold of which was set to 0.006 km. We extracted 9968 feature points and calculated the compression rate, which was approximately 90.05%.

Normalized correlation ($NC$) was used to evaluate the similarity between the extracted watermark and the original watermark in our experiment. The formula for doing so is shown in Equation (7):

$$NC=\frac{{\displaystyle \sum _{i=1}^{i=M}{\displaystyle \sum _{j=1}^{j=N}XNOR(W(i,j),W^{\prime }(i,j))}}}{M\times N}$$

(7)

where $W(i,j)$ is the original watermark and $W^{\prime }(i,j)$ is the extracted watermark. $M$ and $N$ are the numbers of pixels in each row and each column of the watermark image, respectively. The resulting $NC$ value represents the similarity between the extracted watermark image and the original watermark image. In our experiment, the threshold of $NC$ was given as 0.750.

4.1.2. Geometrical Attacks

As a zero watermarking algorithm with strong robustness, the proposed method should have been able to extract the watermark information after rotation, scaling, and translation (RST). Therefore, this experiment involved a series of RST attacks on the vector data. We processed the data by offsetting them with different distances (5 m, 10 m, and 15 m), scaling them with different ratios (1:0.5, 1:2, and 1:5) and rotating them with different angles (${30}^{°}$, ${60}^{°}$, and ${180}^{°}$). Then, we extracted the watermark information from the vector data after the attack.

Table 2. Watermark extraction results under translation, scaling, and rotating attacks.

Attack Type	Attack Degree or Mode	Extraction Result	NC
Translation	Translation 5 meter		1.000
	Translation 10 meter		1.000
	Translation 20 meter		1.000
Scaling	Scaling 0.5		1.000
	Scaling 2		1.000
	Scaling 5		1.000
Rotating	Rotate ${30}^{°}$		1.000
	Rotate ${60}^{°}$		1.000
	Rotate ${180}^{°}$		1.000

gives the results of the proposed algorithm against the attacks above. With the enhancement of the RST attack, the $NC$ value of the zero watermark extracted by the algorithm was always one. The RST attack did not change the relative positions between the feature points. It maintained the angle value of the inflection point, so the algorithm in this paper was completely resistant to the RST attack.

4.1.3. Cropping and Adding

Cropping and adding are standard data processing methods for vector data. A cropping attack characterizes itself by its cropping ratio, which is the percentage of data cropped from the entire dataset. Adding attacks are related to cropping attacks, where the adding ratio refers to the percentage of data that is added to the original data. As shown in Figure 9, we cropped and added adjacent areas with different cropping strengths (10%, 70%, and 80%) and adding strengths (10%, 50%, and 100%).

Table 3. Watermark extraction results under cropping and adding attacks.

Attack Type	Attack Degree or Mode	Extraction Result	NC
Cropping	Cut 10%		1.000
	Cut 70%		1.000
	Cut 80%		0.532
Adding	Add 10%		1.000
	Add 50%		1.000
	Add 100%		1.000

gives the results achieved by the proposed algorithm after the attack.

According to Table 3, when the cropping ratio was kept between 10% and 70%, the $NC$ value was always 1.000, because the original data center constructed the concentric circles under the cropping and adding attacks. As long as one of the sets of zero watermarking is detected, the purpose of copyright verification is achieved, even when part of the data is destroyed.

The last set of zero watermarking was destroyed and could not be extracted until the cropping ratio reached 80%. Therefore, the algorithm had a strong anti-cropping ability. The experimental results for the adding attack showed that the proposed algorithm could still extract the complete copyright image with an $NC$ value of one. This is because the data added to the original data in adjacent areas did not interfere with the ability of the algorithm to extract the zero watermarking from the center point of the original data. Therefore, the proposed algorithm was entirely resistant to adding attacks.

4.1.4. Compression Attacks

The purpose of vector data compression is to delete redundant data and reduce data storage. Its main task is to reduce the number of vertices in the point set of an arc in the vector coordinates. This paper used the Douglas–Peucker algorithm to perform compression attacks with different compression ratios (10%, 50%, and 90%) on the experimental data.

The results given in

Table 4. Watermark extraction results under compression attacks.

Attack Type	Attack Degree or Mode	Extraction Result	NC
Compression	Compressed 10%		1.000
	Compressed 50%		1.000
	Compressed 90%		1.000

show that the complete copyright image could always be extracted with an $NC$ value of one after compression. When the compression rate was between 10% and 90%, the algorithm in this paper extracted the data’s feature points with a compression preprocess, for which the compression ratio was over 90%. Therefore, zero watermarking should be constructed according to the size of the given vector data with a suitable compression ratio in practical applications. The smaller the compression ratio is, the stronger the algorithm’s ability against compression is. It can be seen that the algorithm in this paper could effectively resist the simplified attack. Obviously, the algorithm proposed in this paper resisted compression attacks.

4.2. Blockchain Experiment and Results

4.2.1. System Implementation

Based on the Ant Blockchain Open Alliance, we developed a blockchain certificate storage system for the DU. The system interface is shown in Figure 10. After receiving the confirmation from the RU, the DU can use the “Contract Call” module to upload the block. After clicking “submit,” the DU can get the THX of the uploaded block.

4.2.2. Gas Cost

To illustrate the advantage of the proposed system, we uploaded the zero watermark extracted from the data in Figure 8a to the Ant Open Alliance Blockchain. The THX and gas consumption are shown in Figure 11. According to the conversion rules of the Ant Blockchain Open Alliance [30], this transaction costed about CNY 0.368. The cost of this transaction was almost negligible.

5. Discussion

This paper proposed a robust zero watermarking algorithm and implemented the blockchain certificate storage system based on the Ant Blockchain Open Alliance. In this part, we will compare the robustness of the proposed algorithm with other algorithms. Furthermore, we will discuss the advantages and disadvantages of blockchain and IPR.

5.1. Comparison with Other Algorithms

To verify the advantages of the zero watermark constructed by the proposed algorithm under various attacks, we compared the algorithm with the four algorithms proposed in [20,31,32,33] by experimentation. The algorithm proposed in [20] constructs zero watermarking by dividing blocks and comparing the distance between points. The algorithm in [31] generates zero watermarking by using grid division and counting the numbers of points in the grids. In contrast, the algorithm in [32] constructs concentric circles. It counts the numbers of points in these circles to generate zero watermarking. Another algorithm proposed in [33] transforms the spatial topology information and spatial geometry information of the data into a zero watermark by establishing the graph complexity index.

5.1.1. Uniqueness Verification

A zero watermark is not directly added to the original data, and the watermark information must be unique. Therefore, it is necessary to verify the uniqueness of the algorithm. In this paper, we selected three different datasets of vector line features. Figure 12a shows the vector data for streets in the Gulou District, whereas Figure 12b and Figure 12c show the vector data for streets in the Qinhuai District and Xuanwu District, respectively. The detailed verification method was as follows: the $NC$ values of the zero watermark extracted in Figure 12a–c were calculated and compared as shown in

Table 5. Units for magnetic properties.

Vector Data		NC
	Proposed	[20]	[31]	[32]	[33]
Gulou District	1.000	1.000	1.000	1.000	1.000
Qinhuai District	0.523	0.972	0.480	0.828	0.671
Xuanwu District	0.541	0.981	0.454	0.831	0.557

.

According to Table 5, the algorithm proposed in this paper was proven to have the characteristic of uniqueness, and the same was true for the algorithms in [31,33]. The $NC$ values of the zero watermarks extracted by these three algorithms were under 0.750, whereas the $NC$ values of [20,32] were over 0.750, which did not satisfy the requirement of uniqueness. The block method of [20,32] would cause a lot of redundant space, filled by zero. This results in a high similarity of zero watermarking extracted from different data. Actually, [20,32] did not verify the uniqueness of their algorithms. Because neither of these two algorithms could guarantee the uniqueness of the zero watermarking, this paper only compared the proposed algorithm with [31,33].

5.1.2. Robustness Comparison

Our experiment selected the “provincial boundary of Jiangsu province” as the test data. Different watermark attacks were performed separately, such as rotation attacks, cropping attacks, adding attacks, and compression attacks. The experiments were designed as follows: the experimental data in the first series suffered from rotation attacks with different angles ranging from $0^{°}$ to ${180}^{°}$. The remaining three experiments separately performed cropping attacks, adding attacks, and compression attacks with corresponding factors ranging from 0% to 90%. The results are shown in Figure 13.

All algorithms mentioned, except the one proposed in [31], were entirely robust against rotation attacks, as shown in Figure 13a. The algorithm in [31] was vulnerable to rotation attacks because it constructed zero watermarking with a rectangular grid, so the construction result changed after rotation. The $NC$ values of the three algorithms decreased with the increasing cropping ratio, according to Figure 13b. This paper’s algorithm constructed multiple zero watermarks against cropping attacks so that the watermark information could still be extracted completely, even when the cropping ratio was up to 70%. As shown in Figure 13c, with the increase in redundant data, the watermark information extracted by the algorithms proposed in [31,33] was disturbed to some extent. When the adding ratio reached 40%, the $NC$ values of the algorithms in [31,33] were already lower than the given threshold of 0.750, so they could not wholly extract copyright information.

Moreover, this paper’s algorithm could always extract complete watermark information from the data under adding attacks, on the premise that the original data were not destroyed. It thus shows a strong ability to resist adding attacks. The algorithms in [31,33] did not preprocess the data with compression. Therefore, their $NC$ values decreased with the increasing compression ratio. When the compression ratio reached 20%, the $NC$ values of the algorithms in [31,33] were already lower than the given threshold. The algorithm in this paper reflected an ability to resist compression to some extent, because it applied a compression algorithm to extract the feature points. The watermark information could be wholly extracted when the compression ratio was lower than the feature points’ extraction rates.

In summary, the $NC$ value of the algorithm in [31] was lower than the given threshold, and it showed poor robustness. The algorithm proposed in [33] completely resisted rotation attacks. Nevertheless, its $NC$ values were below the threshold when the intensities of cropping, adding, and compression were over 30%. This paper’s algorithm completely resisted rotation, adding, and compression attacks and could extract copyright images even when the cropping ratio was over 70%. This algorithm showed the strongest robustness among the three algorithms.

5.2. Comparison between the Blockchain Framework and the Traditional IPR Framework

In addition to the high robustness requirement of the algorithm, it was also important to ensure that the obtained watermark information had credibility and legal validity for practical applications. As shown in

Table 6. Comparison between the blockchain and traditional IPR.

Evaluation Indicator	Blockchain Framework	Traditional IPR Framework
credibility	strong	common
audit cycle	not needed	long
cost	negligible	expensive
interpretation attack	can resist	unable to resist
traceability	yes	no

, this paper compares the advantages and disadvantages of the traditional IPR framework and the proposed blockchain framework in terms of zero watermarking copyright certification from five aspects. First, in terms of credibility, the blockchain is a decentralized distributed system with high credibility, where the watermark information cannot be modified on the chain [34]. The traditional IPR is essentially a centralized database that lacks credibility for the existing risk of artificial data tampering. The audit cycle refers to the time required for the copyright process, from registration to official enforcement. The copyright takes effect immediately without any auditing steps if the watermark information is written on a blockchain. The cost of the IPR’s services is high, and the charges are opaque. For example, the registration fee for each microfilm is approximately CNY 2000–3000, and at the same time, the registration process is very long, and the procedure is tedious [35]. However, the cost of copyright registration on the blockchain is relatively low compared with traditional copyright registration. In Section 4.2.1, only a CNY 0.385 cost was on the Ant Blockchain Open Alliance. Therefore, blockchain is undoubtedly the best choice for massive vector data that require copyright certification [36]. An interpretation attack refers to an infringement method by which multiple parties extract the same copyright, making it impossible to determine copyright ownership. The registration procedures, standards, and certificates stipulated by traditional IPR registration agencies are difficult to unify. Furthermore, it is difficult to determine the storage time of a copyright application given by one party. If there are multiple registrations from multiple parties, the copyright owner cannot be confirmed, so the copyright lacks authority.

Nevertheless, each block of a blockchain has its own timestamp. Once a copyright dispute occurs, the first data distribution of the information on the chain can be used to determine copyright ownership, so the blockchain framework completely resists interpretation attacks. The blockchain system designed in this paper for the data distribution and chaining synchronization of zero watermarking ensures data traceability. At the same time, traditional IPR copyright registration cannot trace the source of an infringement. Therefore, the long audit cycle and high cost of registration required by the traditional IPR framework mean that it cannot resist interpretation attacks and satisfy copyright traceability, which is one of the key reasons why zero watermarking has not been applied for practical use. The storage system of zero watermarking for vector data, based on the alliance chain proposed in this paper, provides a practical scheme for zero watermarking. This framework is not only limited to the copyright of vector data, but it is also applicable to any zero watermarking methods, including zero watermarking for images, videos, and audio.

6. Conclusions

The existing zero watermarking algorithm has the disadvantages of a long audit cycle, easy copyright loss, and difficult copyright ownership confirmation due to the requirement of copyright authentication by the IPR. We proposed a framework based on blockchain to solve these issues, making the resulting data distribution more traceable, more efficient, and cheaper than that yielded by registration with the traditional IPR. In addition, we proposed a zero watermarking algorithm based on the angular features of concentric circles with strong robustness. This algorithm constructs concentric circles with angular information from many inflection points in the line and area vector elements and generates multiple sequences of zero watermarking. The experiments show that the proposed algorithm reflects strong robustness under common watermark attacks, such as rotation, cropping, and compression, with different intensities and satisfies the requirement of uniqueness. This article fully combines zero watermarking and blockchain technology to achieve a lossless data protection scheme. When a copyright dispute occurs, the copyright information can be extracted with a public algorithm and compared with the same information stored on the blockchain to achieve copyright protection for the lossless vector map. This provides a new way of thinking about zero watermarking copyright authentication.