Vector Map Encryption Algorithm Based on Double Random Position Permutation Strategy
Abstract
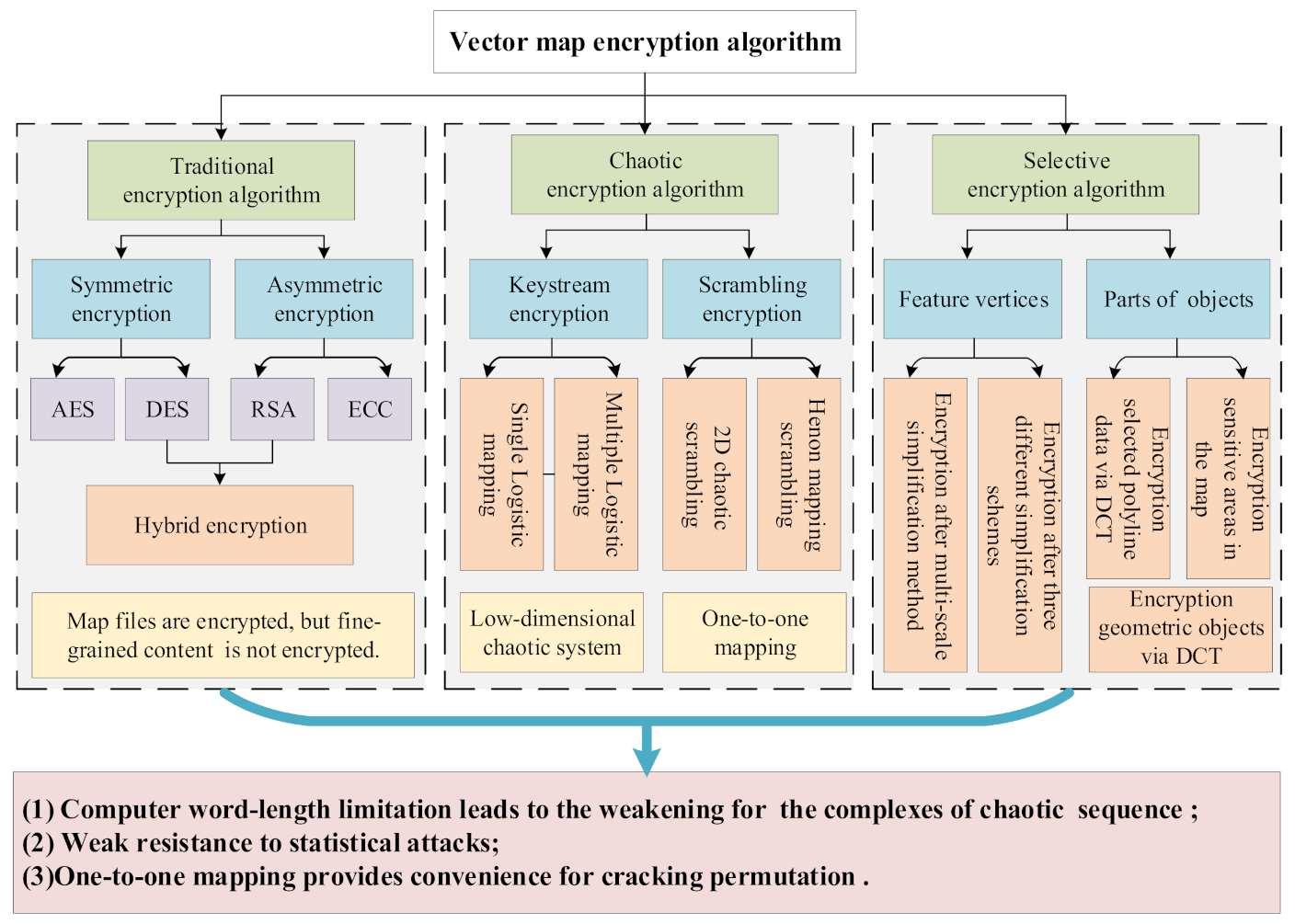
1. Introduction
2. Methods
2.1. Four-Dimension Hyperchaotic System
2.2. Generating the Initial Values and System Parameters for the 4-D Hyperchaotic System
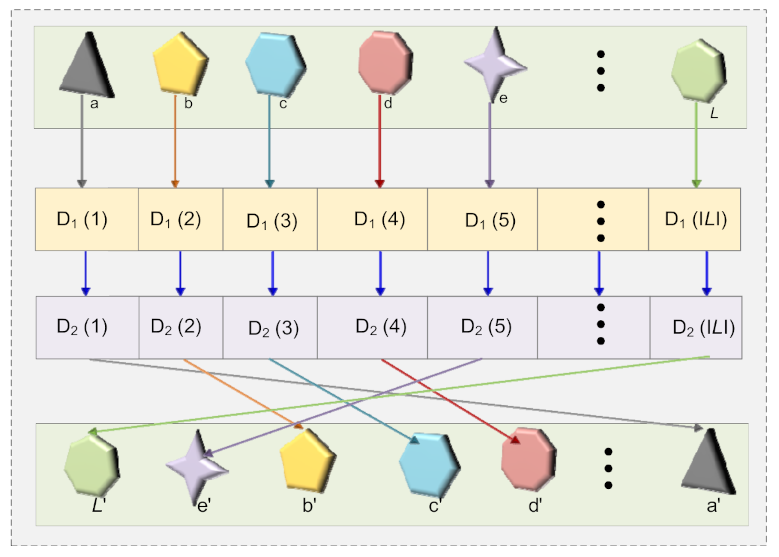
2.3. Double Random Position Permutation
2.4. Scrambling Encryption
2.5. Decryption Processing
3. Experimental Results and Performance Analysis
3.1. Encryption and Decryption Visualization
3.2. Correlation of the Adjacent Coordinates
3.3. Key Space
3.4. Key Sensitivity
3.5. Comparison of Different Scrambling Times
3.6. Comparison with Existing Studies
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Qiu, Y.; Duan, H. A novel multi-stage watermarking scheme of vector maps. Multimed. Tools Appl. 2021, 80, 877–897. [Google Scholar] [CrossRef]
- Qiu, Y.; Gu, H.; Sun, J. High-payload reversible watermarking scheme of vector maps. Multimed. Tools Appl. 2018, 77, 6385–6403. [Google Scholar] [CrossRef]
- Wang, Q.S.; Zhu, C.Q.; Fu, H.J. The digital watermarking algorithm for vector geographic data based on point positioning. Acta Geod. Cartogr. Sin. 2013, 42, 310–316. [Google Scholar]
- Li, H.; Zhu, H.; Hua, W. Key Technologies and Methods for Vector Geographic Data Security Protection. Earth Sci. 2020, 45, 4574–4588. [Google Scholar]
- Zhu, C. Research Progresses in Digital Watermarking and Encryption Control for Geographical Data. Acta Geod. Cartogr. Sin. 2017, 46, 1609–1619. [Google Scholar]
- Shekhar, S.; Huang, Y.; Djugash, J. Vector map compression: A clustering approach. In Proceedings of the 10th ACM International Symposium on Advances in Geographic Information Systems, McLean, VA, USA, 8–9 November 2002; pp. 74–80. [Google Scholar]
- Zhou, C. Prospects on pan-spatial information system. Prog. Geogr. 2015, 34, 129–131. [Google Scholar]
- Wang, J. Development of geographic information system and developing geographic information system. Eng. Sci. 2009, 11, 10–16. [Google Scholar]
- Li, A.; Wang, H.; Zhou, W. Scrambling encryption of vector digital map base on 2D chaos system. J. China Univ. Min. Technol. 2015, 44, 747–753. [Google Scholar]
- Oladipo, J.O.; Aboyeji, O.S.; Akinwumiju, A.S.; Adelodun, A.A. Fuzzy logic interference for characterization of surface water potability in Ikare rural community, Nigeria. J. Geovisualization Spat. Anal. 2020, 4, 1. [Google Scholar] [CrossRef]
- Biswas, K.; Chatterjee, A.; Chakraborty, J. Comparison of Air Pollutants Between Kolkata and Siliguri, India, and Its Relationship to Temperature Change. J. Geovisualization Spat. Anal. 2020, 4, 1–15. [Google Scholar] [CrossRef]
- Xu, J.; Zhou, H.; Nie, G.; An, J. Plotting earthquake emergency maps based on audience theory. Int. J. Disaster Risk Reduct. 2020, 47, 101554. [Google Scholar] [CrossRef]
- Du, M.; Zhang, X. Urban greening: A new paradox of economic or social sustainability? Land Use Policy 2020, 92, 104487. [Google Scholar] [CrossRef]
- Guida, C.; Carpentieri, G. Quality of life in the urban environment and primary health services for the elderly during the Covid-19 pandemic: An application to the city of Milan (Italy). Cities 2021, 110, 103038. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, L.; Yang, W. A normalization-based watermarking scheme for 2D vector map data. Earth Sci. Inform. 2017, 10, 471–481. [Google Scholar] [CrossRef]
- Yan, H.; Li, J.; Wen, H. A key points-based blind watermarking approach for vector geo-spatial data. Comput. Environ. Urban Syst. 2011, 35, 485–492. [Google Scholar] [CrossRef]
- López, C. Watermarking of digital geospatial datasets: A review of technical, legal and copyright issues. Int. J. Geogr. Inf. Syst. 2002, 16, 589–607. [Google Scholar] [CrossRef]
- Ren, N.; Wu, W.; Zhu, C.; Wang, D. An Accuracy Authentication Algorithm of Anti-Deleting Elements for Vector Geographic Data. Geogr. Geo-Inf. Sci. 2015, 17, 166–171. [Google Scholar]
- Zhu, C.; Zhou, W.; Wu, W. Research on the Policy and Law of China Geographic Information Security; Science Press: Beijing, China, 2015; pp. 1–18, 65–71. [Google Scholar]
- PRC NPC Web Site. Surveying and Mapping Law of the People’s Republic of China [EB/OL]. Available online: http://www.npc.gov.cn/wxzl/gongbao/2000-12/05/content_5004576.htm (accessed on 10 January 2021).
- Zhou, H.; Lv, Y. Research on Construction of Foreign Geographic Information Security Policies and Laws. Bull. Surv. Mapp. 2015, 115–118. [Google Scholar] [CrossRef]
- Zhou, Q.; Ren, N.; Zhu, C.; Zhu, A. Blind Digital Watermarking Algorithm against Projection Transformation for Vector Geographic Data. ISPRS Int. J. Geo-Inf. 2020, 9, 692. [Google Scholar] [CrossRef]
- Vybornova, Y.D.; Sergeev, V.V. Method for protection of copyright on vector data. Inform. Autom. 2021, 20, 181–212. [Google Scholar]
- Yang, C.; Zhu, C.; Wang, Y.; Rui, T.; Ding, K. A Robust Watermarking Algorithm for Vector Geographic Data Based on Qim and Matching Detection. Multimed. Tools Appl. 2020, 79, 30709–30733. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, L.; Jiang, M. A collusion-based vector spatial data fingerprinting scheme. Sci. Surv. Mapp. 2019, 45, 149–156. [Google Scholar] [CrossRef]
- Lv, W.; Zhang, L.; Ma, L.; Chen, J. A digital fingerprinting algorithm for vector spatial data using BIBD. Sci. Surv. Mapp. 2017, 42, 134–139. [Google Scholar]
- Chen, J.; Zhang, L.; Jiang, M. Digital fingerprint algorithm for vector spatial data using GD-PBIBD coding. Bull. Surv. Mapp. 2020, 81–86+100. [Google Scholar] [CrossRef]
- Sahoo, S.; Roshan, R.; Singh, V.; Halder, R. Bdmark: A blockchain-driven approach to big data watermarking. In Asian Conference on Intelligent Information and Database Systems; Springer: Singapore, 2020. [Google Scholar]
- Sahoo, S.; Halder, R. Traceability and ownership claim of data on big data marketplace using blockchain technology. J. Inf. Telecommun. 2021, 5, 35–61. [Google Scholar] [CrossRef]
- Sladić, G.; Milosavljević, B.; Nikolić, S. A Blockchain Solution for Securing Real Property Transactions: A Case Study for Serbia. ISPRS Int. J. Geo-Inf. 2021, 10, 35. [Google Scholar] [CrossRef]
- Zheng, Z.; Xie, S.; Dai, H.N. Blockchain challenges and opportunities: A survey. Int. J. Web Grid Serv. 2018, 14, 352–375. [Google Scholar] [CrossRef]
- Mao, J.; Zhu, C.; Zhang, X. A Fine-Granined access control model for vector geospatial data. Geogr. Geo-Inf. Sci. 2017, 33, 13–18. [Google Scholar]
- Zhang, A.; Gao, J.; Ji, C. Multi-Granularity spatial -temporal access control model for Web GIS. Trans. Nonferrous Met. Soc. China 2014, 24, 2946–2953. [Google Scholar] [CrossRef]
- Yu, G.; Li, R.; Lu, Z. Feature based spatial data access control model research. Comput. Sci. 2008, 35, 122–125+130.SS. [Google Scholar]
- Standard, Data Encryption. Federal Information Processing Standards Publication 46; National Bureau of Standards: Gaithersburg, MA, USA; US Department of Commerce: Washington, DC, USA, 1997; Volume 23.
- Daemen, J.; Rijmen, V. Reijndael: The Advanced Encryption Standard. Dr. Dobb’s J. Softw. Tools Prof. Program. 2001, 26, 137–139. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Zhang, S. Research on the Algorithm of Encryption in Network Transmission of Vector Graphic Data; Wuhan University: Wuhan, China, 2005. [Google Scholar]
- Van, B.N.; Lee, S.H.; Kwon, K.R. Selective Encryption Algorithm Using Hybrid Transform for GIS Vector Map. JIPS 2017, 13, 68–82. [Google Scholar]
- Zhao, Y.; Li, G.; Li, L. Electronic chart encryption method based on chaotic stream cipher. J. Harbin Eng. Univ. 2007, 28, 60–64. [Google Scholar]
- Wang, H. Scrambling Encryption Methods and Scrambling Performance Evaluation for Vector Geographic Data; Nanjing Normal University: Nanjing, China, 2014. [Google Scholar]
- Pham, G.N.; Ngo, S.T.; Bui, A.N. Vector Map Random Encryption Algorithm Based on Multi-Scale Simplification and Gaussian Distribution. Appl. Sci. 2019, 9, 4889. [Google Scholar] [CrossRef]
- Bang, N.V.; Lee, S.H.; Moon, K.S. Encryption Algorithm using Polyline Simplification for GIS Vector Map. J. Korea Multimed. Soc. 2016, 19, 1453–1459. [Google Scholar] [CrossRef][Green Version]
- Giao, P.N.; Kwon, O.J.; Lee, S.H. Perceptual encryption method for vector map based on geometric transformations. In Proceedings of the 2016 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA), Jeju, Korea, 13–16 December 2016. [Google Scholar]
- Pham, N.G.; Lee, S.H.; Kwon, K.R. Perceptual Encryption Based on Features of Interpolating Curve for Vector Map. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2017, 100, 1156–1164. [Google Scholar] [CrossRef]
- Jang, B.J.; Lee, S.H.; Lee, E.J. A crypto-marking method for secure vector map. Multimed. Tools Appl. 2017, 76, 16011–16044. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Zhao, J. Chaotic encryption algorithm based on alternant of stream cipher and block cipher. Nonlinear Dyn. 2011, 63, 587–597. [Google Scholar] [CrossRef]
- Zarei, A.; Tavakoli, S. Hopf bifurcation analysis and ultimate bound estimation of a new 4-D quadratic autonomous hyper-chaotic system. Appl. Math. Comput. 2016, 291, 323–339. [Google Scholar] [CrossRef]
- Chai, X.; Bi, J.; Gan, Z. Color image compression and encryption scheme based on compressive sensing and double random encryption strategy. Signal Process. 2020, 176, 107684. [Google Scholar] [CrossRef]









| Data | Correlation | |||||
|---|---|---|---|---|---|---|
| Original Map | Cipher Map | Decrypted Map | ||||
| X-Coordinates | Y-Coordinates | X-Coordinates | Y-Coordinates | X-Coordinates | Y-Coordinates | |
| Railways | 0.7486 | 0.7572 | −0.0013 | −0.0008 | 0.7486 | 0.7572 |
| Waterways | 0.8384 | 0.8498 | 0.0003 | 0.0004 | 0.8384 | 0.8498 |
| District | 0.9660 | 0.9618 | −0.0065 | −0.0009 | 0.9660 | 0.9618 |
| Times | 1 | 2 | 3 | 4 | 5 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Data | X | Y | X | Y | X | Y | X | Y | X | Y | |
| Railways | −0.0013 | −0.0008 | −0.0015 | 0.0016 | 0.0070 | 0.0054 | 0.0047 | −0.0013 | −0.0016 | −0.0036 | |
| Waterways | 0.0003 | 0.0004 | −0.0001 | 0.0016 | 0.0008 | 0.0019 | −0.0001 | −0.0008 | 0.0014 | 0.0028 | |
| District | −0.0065 | −0.0009 | 0.0136 | 0.1128 | −0.0036 | −0.0052 | −0.0018 | −0.0053 | −0.0028 | 0.0023 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Yan, H.; Zhang, L. Vector Map Encryption Algorithm Based on Double Random Position Permutation Strategy. ISPRS Int. J. Geo-Inf. 2021, 10, 311. https://doi.org/10.3390/ijgi10050311
Wang X, Yan H, Zhang L. Vector Map Encryption Algorithm Based on Double Random Position Permutation Strategy. ISPRS International Journal of Geo-Information. 2021; 10(5):311. https://doi.org/10.3390/ijgi10050311
Chicago/Turabian StyleWang, Xiaolong, Haowen Yan, and Liming Zhang. 2021. "Vector Map Encryption Algorithm Based on Double Random Position Permutation Strategy" ISPRS International Journal of Geo-Information 10, no. 5: 311. https://doi.org/10.3390/ijgi10050311
APA StyleWang, X., Yan, H., & Zhang, L. (2021). Vector Map Encryption Algorithm Based on Double Random Position Permutation Strategy. ISPRS International Journal of Geo-Information, 10(5), 311. https://doi.org/10.3390/ijgi10050311





