The Spatiotemporal Interaction Effect of COVID-19 Transmission in the United States
Abstract
:1. Introduction
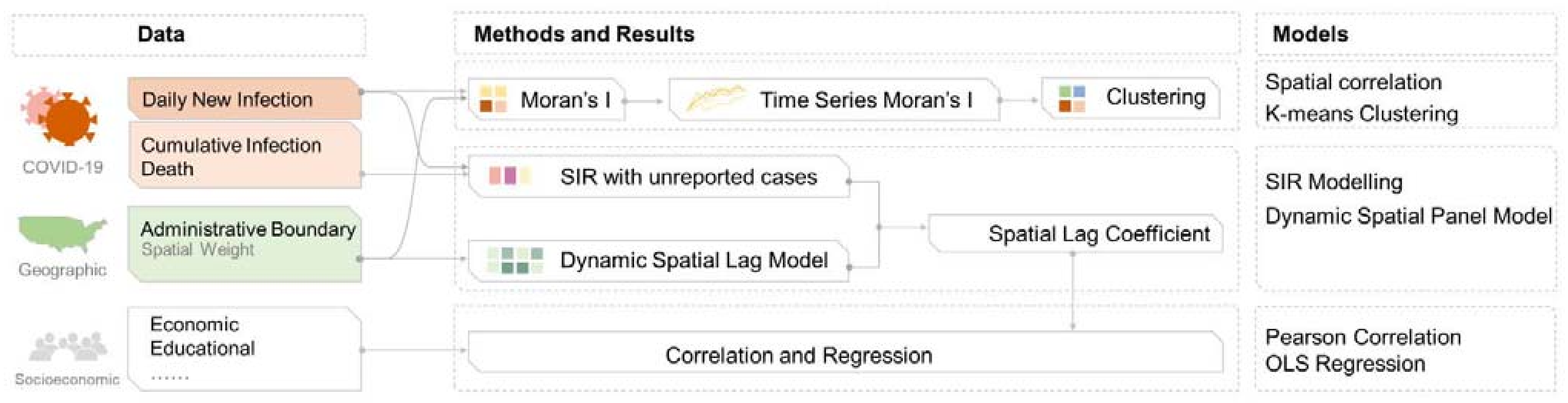
2. Materials and Methods
2.1. Global Moran’s I Index and K-Means Clustering
2.2. K-Means Clustering Algorithm
2.3. SIR with Unreported Infections
2.4. Dynamic Spatial Lag Model
2.5. Data
- (1)
- COVID-19 data of all counties in the United States from 22 January 2020 to 20 August 2020, including daily new infections, cumulative infections, deaths, and total population. The data were acquired from the GitHub repository of Johns Hopkins University (https://github.com/CSSEGISandData/COVID-19, accessed on 21August 2020).
- (2)
- Administrative boundary data at the state and county levels in the United States. These data are available in the Harvard Dataverse (https://dataverse.harvard.edu/dataverse/cdl_dataverse, accessed on 21August 2020).
- (3)
- Socioeconomic data of all states in the United States in 2019, including factors such as birth rate, death rate, international immigration rate, poverty rate, median age, average education level (high school graduation rate, undergraduate graduation rate, advanced education rate), and population density. Such data are available on the U.S. Census website (https://www.census.gov, accessed on 30 August 2020). Trump’s vote rate in the 2016 U.S. presidential election in the states was also included in the correlation analysis as a potential political variable of residents.
3. Results
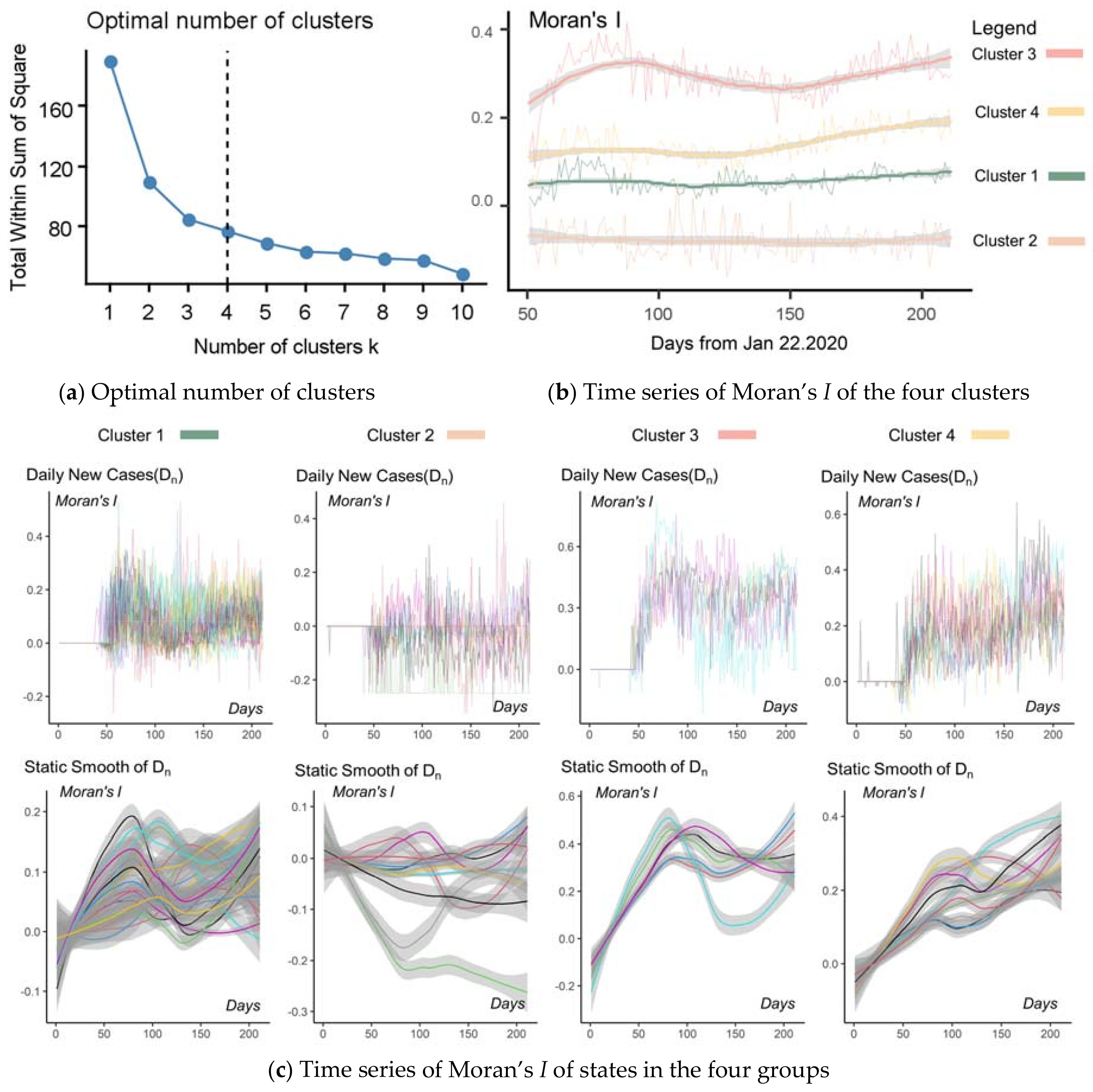
3.1. Time Series of Moran’s I
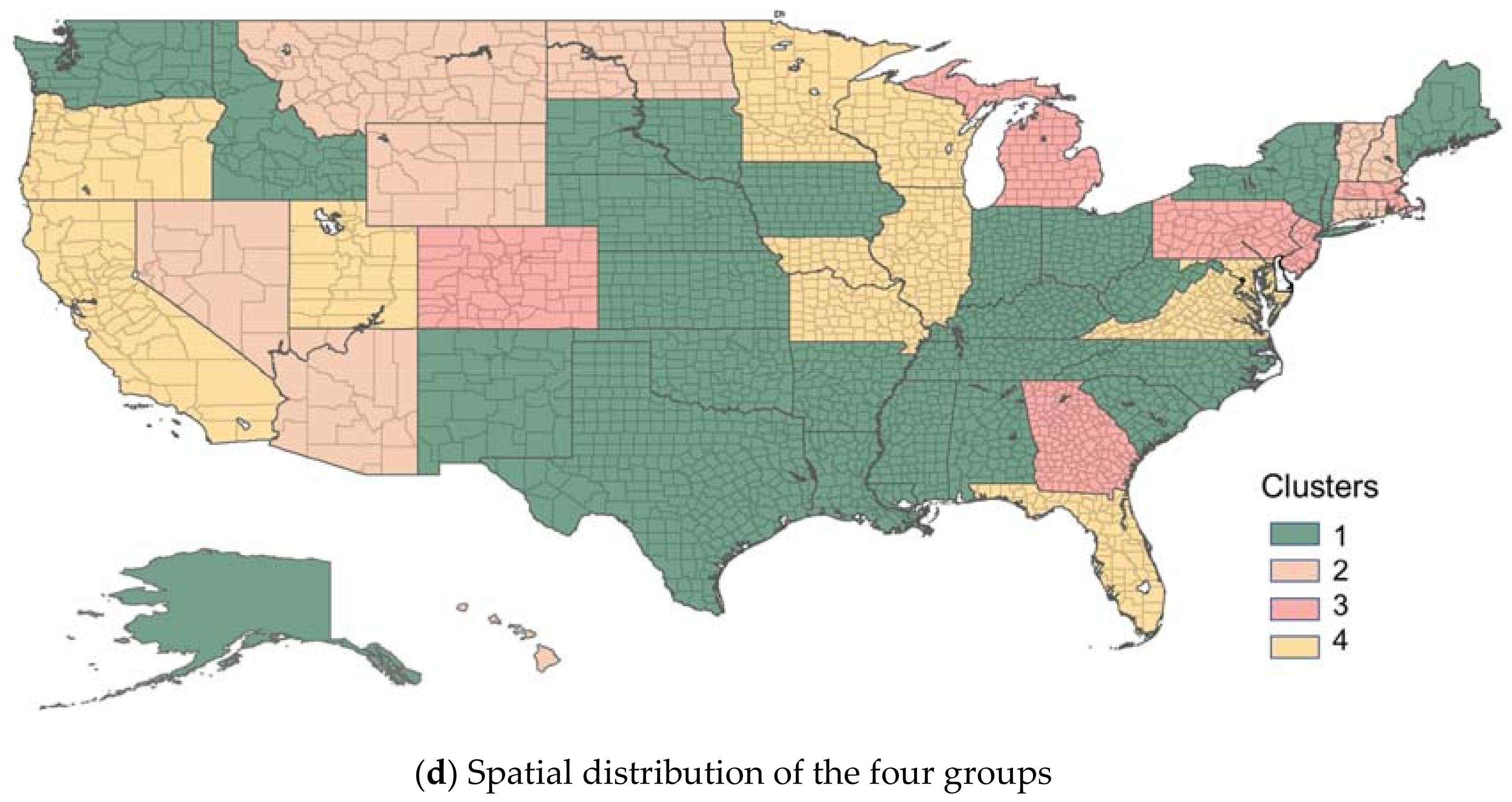
3.2. K-Means Clustering of Time Series of Moran’s I
3.3. SIRu Integrated with the Spatial Lag Model
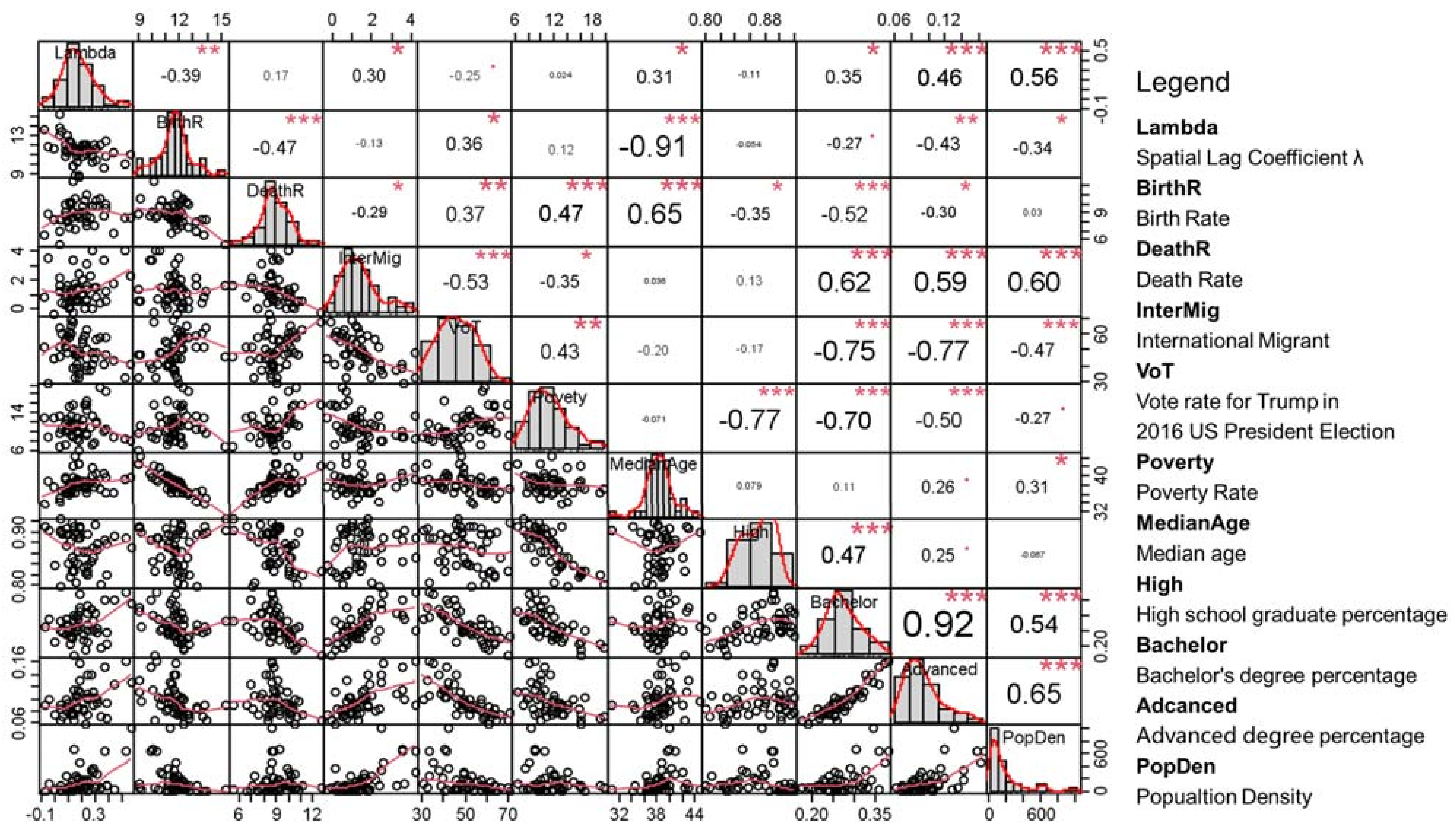
3.4. Correlation and Regression with Socioeconomic Variables
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, T.; Guan, W.W.; Zhu, X.; Shao, Y.; Liu, L.; Du, J.; Liu, H.; Zhou, H.; Wang, J.; She, B.; et al. Building an open resources repository for COVID-19 research. Data Inf. Manag. 2020, 4, 130. [Google Scholar] [CrossRef]
- Yang, C.; Sha, D.; Liu, Q.; Li, Y.; Lan, H.; Guan, W.W.; Hu, T.; Li, Z.; Zhang, Z.; Thompson, J.H.; et al. Taking the pulse of COVID-19: A spatiotemporal perspective. Int. J. Digit. Earth 2020, 13, 1186–1211. [Google Scholar] [CrossRef]
- Loeffler-Wirth, H.; Schmidt, M.; Binder, H. Covid-19 transmission trajectories–monitoring the pandemic in the worldwide context. Viruses 2020, 12, 777. [Google Scholar] [CrossRef]
- Walker, P.G.T.; Whittaker, C.; Watson, O.J.; Baguelin, M.; Winskill, P.; Hamlet, A.; Djafaara, B.A.; Cucunubá, Z.; Olivera Mesa, D.; Green, W.; et al. The impact of COVID-19 and strategies for mitigation and suppression in low- and middle-income countries. Science 2020, 369, 413–422. [Google Scholar] [CrossRef] [PubMed]
- Dowd, J.B.; Andriano, L.; Brazel, D.M.; Rotondi, V.; Block, P.; Ding, X.; Liu, Y.; Mills, M.C. Demographic science aids in understanding the spread and fatality rates of COVID-19. Proc. Natl. Acad. Sci. USA 2020, 117, 9696. [Google Scholar] [CrossRef] [Green Version]
- Merlo, J.; Chaix, B.; Ohlsson, H.; Beckman, A.; Johnell, K.; Hjerpe, P.; Råstam, L.; Larsen, K. A brief conceptual tutorial of multilevel analysis in social epidemiology: Using measures of clustering in multilevel logistic regression to investigate contextual phenomena. J. Epidemiol. Commun. H 2006, 60, 290. [Google Scholar] [CrossRef] [Green Version]
- Qi, H.; Xiao, S.; Shi, R.; Ward, M.P.; Chen, Y.; Tu, W.; Su, Q.; Wang, W.; Wang, X.; Zhang, Z. COVID-19 transmission in Mainland China is associated with temperature and humidity: A time-series analysis. Sci. Total Environ. 2020, 728, 138778. [Google Scholar] [CrossRef]
- Wu, X.; Yin, J.; Li, C.; Xiang, H.; Lv, M.; Guo, Z. Natural and human environment interactively drive spread pattern of COVID-19: A city-level modeling study in China. Sci. Total Environ. 2021, 756, 143343. [Google Scholar] [CrossRef]
- Rader, B.; Scarpino, S.V.; Nande, A.; Hill, A.L.; Adlam, B.; Reiner, R.C.; Pigott, D.M.; Gutierrez, B.; Zarebski, A.E.; Shrestha, M.; et al. Crowding and the shape of COVID-19 epidemics. Nat. Med. 2020, 26, 1829–1834. [Google Scholar] [CrossRef]
- Roques, L.; Bonnefon, O.; Baudrot, V.; Soubeyrand, S.; Berestycki, H. A parsimonious approach for spatial transmission and heterogeneity in the COVID-19 propagation. R. Soc. Open Sci. 2020, 7, 201382. [Google Scholar] [CrossRef]
- Viguerie, A.; Lorenzo, G.; Auricchio, F.; Baroli, D.; Hughes, T.J.R.; Patton, A.; Reali, A.; Yankeelov, T.E.; Veneziani, A. Simulating the spread of COVID-19 via a spatially-resolved susceptible–exposed–infected–recovered–deceased (SEIRD) model with heterogeneous diffusion. Appl. Math. Lett. 2021, 111, 106617. [Google Scholar] [CrossRef]
- Adekunle, I.A.; Onanuga, A.T.; Akinola, O.O.; Ogunbanjo, O.W. Modelling spatial variations of coronavirus disease (COVID-19) in Africa. Sci. Total Environ. 2020, 729, 138998. [Google Scholar] [CrossRef]
- Xiong, C.; Hu, S.; Yang, M.; Luo, W.; Zhang, L. Mobile device data reveal the dynamics in a positive relationship between human mobility and COVID-19 infections. Proc. Natl. Acad. Sci. USA 2020, 117, 27087. [Google Scholar] [CrossRef]
- Aleta, A.; Martín-Corral, D.; Pastore y Piontti, A.; Ajelli, M.; Litvinova, M.; Chinazzi, M.; Dean, N.E.; Halloran, M.E.; Longini, I.M., Jr.; Merler, S.; et al. Modelling the impact of testing, contact tracing and household quarantine on second waves of COVID-19. Nat. Hum. Behav. 2020, 4, 964–971. [Google Scholar] [CrossRef]
- Ascani, A.; Faggian, A.; Montresor, S. The geography of COVID-19 and the structure of local economies: The case of Italy. J. Reg. Sci. 2020. [Google Scholar] [CrossRef]
- Hellewell, J.; Abbott, S.; Gimma, A.; Bosse, N.I.; Jarvis, C.I.; Russell, T.W.; Munday, J.D.; Kucharski, A.J.; Edmunds, W.J.; Sun, F. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Glob. Health 2020, 8, e488–e496. [Google Scholar] [CrossRef] [Green Version]
- Abel, T.; Mcqueen, D. The COVID-19 pandemic calls for spatial distancing and social closeness: Not for social distancing! Int. J. Public Health 2020, 65, 231. [Google Scholar] [CrossRef] [Green Version]
- Lai, S.; Ruktanonchai, N.W.; Zhou, L.; Prosper, O.; Luo, W.; Floyd, J.R.; Wesolowski, A.; Santillana, M.; Zhang, C.; Du, X.; et al. Effect of non-pharmaceutical interventions to contain COVID-19 in China. Nature 2020, 585, 410–413. [Google Scholar] [CrossRef]
- Kraemer, M.U.G.; Yang, C.-H.; Gutierrez, B.; Wu, C.-H.; Klein, B.; Pigott, D.M.; du Plessis, L.; Faria, N.R.; Li, R.; Hanage, W.P.; et al. The effect of human mobility and control measures on the COVID-19 epidemic in China. Science 2020, 368, 493. [Google Scholar] [CrossRef] [Green Version]
- Flaxman, S.; Mishra, S.; Gandy, A.; Unwin, H.J.T.; Mellan, T.A.; Coupland, H.; Whittaker, C.; Zhu, H.; Berah, T.; Eaton, J.W.; et al. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature 2020, 584, 257–261. [Google Scholar] [CrossRef]
- Bertuzzo, E.; Mari, L.; Pasetto, D.; Miccoli, S.; Casagrandi, R.; Gatto, M.; Rinaldo, A. The geography of COVID-19 spread in Italy and implications for the relaxation of confinement measures. Nat. Commun. 2020, 11, 4264. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Wang, J.; Liu, J.; Li, Y.; Liu, D.; Tong, J.; Li, Z.; Yu, D.; Fan, Y.; Bi, X.; et al. Predicting and analyzing the COVID-19 epidemic in China: Based on SEIRD, LSTM and GWR models. PLoS ONE 2020, 15, e0238280. [Google Scholar] [CrossRef]
- Das, A.; Ghosh, S.; Das, K.; Basu, T.; Dutta, I.; Das, M. Living environment matters: Unravelling the spatial clustering of COVID-19 hotspots in Kolkata megacity, India. Sustain. Cities Soc. 2020, 102577. [Google Scholar] [CrossRef]
- Fingleton, B.; Olner, D.; Pryce, G. Estimating the local employment impacts of immigration: A dynamic spatial panel model. Urban. Stud. 2019, 57, 2646–2662. [Google Scholar] [CrossRef] [Green Version]
- Sannigrahi, S.; Pilla, F.; Basu, B.; Basu, A.S.; Molter, A. Examining the association between socio-demographic composition and COVID-19 fatalities in the European region using spatial regression approach. Sustain. Cities Soc. 2020, 62, 102418. Available online: https://www.sciencedirect.com/science/article/pii/S2210670720306399 (accessed on 21 December 2020). [CrossRef]
- Mollalo, A.; Vahedi, B.; Rivera, K.M. GIS-based spatial modeling of COVID-19 incidence rate in the continental United States. Sci. Total Environ. 2020, 728, 138884. [Google Scholar] [CrossRef]
- Anderson, R.M.; Heesterbeek, H.; Klinkenberg, D.; Hollingsworth, T.D. How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet 2020, 395, 931–934. [Google Scholar] [CrossRef]
- Lau, H.; Khosrawipour, V.; Kocbach, P.; Mikolajczyk, A.; Ichii, H.; Schubert, J.; Bania, J.; Khosrawipour, T. Internationally lost COVID-19 cases. J. Microbiol. Immunol. Infect. 2020, 53, 454–458. [Google Scholar] [CrossRef]
- Spychalski, P.; Błażyńska-Spychalska, A.; Kobiela, J. Estimating case fatality rates of COVID-19. Lancet Infect. Dis. 2020, 20, 774–775. [Google Scholar] [CrossRef]
- Wu, S.L.; Mertens, A.N.; Crider, Y.S.; Nguyen, A.; Pokpongkiat, N.N.; Djajadi, S.; Seth, A.; Hsiang, M.S.; Colford, J.M.; Reingold, A.; et al. Substantial underestimation of SARS-CoV-2 infection in the United States. Nat. Commun. 2020, 11, 4507. [Google Scholar] [CrossRef]
- Leon, D.A.; Shkolnikov, V.M.; Smeeth, L.; Magnus, P.; Pechholdová, M.; Jarvis, C.I. COVID-19: A need for real-time monitoring of weekly excess deaths. Lancet 2020, 395, e81. [Google Scholar] [CrossRef]
- Lipsitch, M.; Donnelly, C.A.; Fraser, C.; Blake, I.M.; Cori, A.; Dorigatti, I.; Ferguson, N.M.; Garske, T.; Mills, H.L.; Riley, S.; et al. Potential biases in estimating absolute and relative case-fatality risks during outbreaks. PLoS Neglect. Trop D 2015, 9, e0003846. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verity, R.; Okell, L.C.; Dorigatti, I.; Winskill, P.; Whittaker, C.; Imai, N.; Cuomo-Dannenburg, G.; Thompson, H.; Walker, P.G.T.; Fu, H.; et al. Estimates of the severity of coronavirus disease 2019: A model-based analysis. Lancet Infect. Dis. 2020, 20, 669–677. [Google Scholar] [CrossRef]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. A COVID-19 epidemic model with latency period. Infect. Dis. Model. 2020, 5, 323–337. [Google Scholar] [CrossRef] [PubMed]
- Cave, B.; Kim, J.; Viliani, F.; Harris, P. Applying an equity lens to urban policy measures for COVID-19 in four cities. Cities Health 2020, 1–5. [Google Scholar] [CrossRef]
- Hamidi, S.; Sabouri, S.; Ewing, R. Does density aggravate the COVID-19 pandemic? Early findings and lessons for planners. J. Am. Plan. Assoc. 2020, 1–15. [Google Scholar] [CrossRef]
- Peng, Z.; Ao, S.; Liu, L.; Bao, S.; Hu, T.; Wu, H.; Wang, R. Estimating unreported COVID-19 cases with a time-varying SIR regression model. Int. J. Environ. Res. Public Health 2021, 18, 1090. [Google Scholar] [CrossRef]
- Biglieri, S.; De Vidovich, L.; Keil, R. City as the core of contagion? Repositioning COVID-19 at the social and spatial periphery of urban society. Cities Health 2020, 1–3. [Google Scholar] [CrossRef]
- Sun, F.; Matthews, S.A.; Yang, T.-C.; Hu, M.-H. A spatial analysis of the COVID-19 period prevalence in U.S. counties through 28 June 2020: Where geography matters? Ann. Epidemiol. 2020, 52, 54–59. [Google Scholar] [CrossRef]
- Cole, H.V.S.; Anguelovski, I.; Baró, F.; García-Lamarca, M.; Kotsila, P.; Pérez del Pulgar, C.; Shokry, G.; Triguero-Mas, M. The COVID-19 pandemic: Power and privilege, gentrification, and urban environmental justice in the global north. Cities Health 2020, 1–5. [Google Scholar] [CrossRef]
- Yamey, G.; Gonsalves, G. Donald Trump: A political determinant of COVID-19. BMJ 2020, 369, m1643. [Google Scholar] [CrossRef] [Green Version]
- White, E.R.; Hébert-Dufresne, L. State-level variation of initial COVID-19 dynamics in the United States. PLoS ONE 2020, 15, e0240648. [Google Scholar] [CrossRef]
- Berkowitz, R.L.; Gao, X.; Michaels, E.K.; Mujahid, M.S. Structurally vulnerable neighbourhood environments and racial/ethnic COVID-19 inequities. Cities Health 2020, 1–4. [Google Scholar] [CrossRef]
- Dave, D.; Friedson, A.I.; Matsuzawa, K.; Sabia, J.J. When do shelter-in-place orders fight COVID-19 best? Policy heterogeneity across states and adoption time. Econ. Inq. 2021, 59, 29–52. [Google Scholar] [CrossRef]
- Cordes, J.; Castro, M.C. Spatial analysis of COVID-19 clusters and contextual factors in New York City. Spat. Spatio Temporal Epidemiol. 2020, 34, 100355. [Google Scholar] [CrossRef]

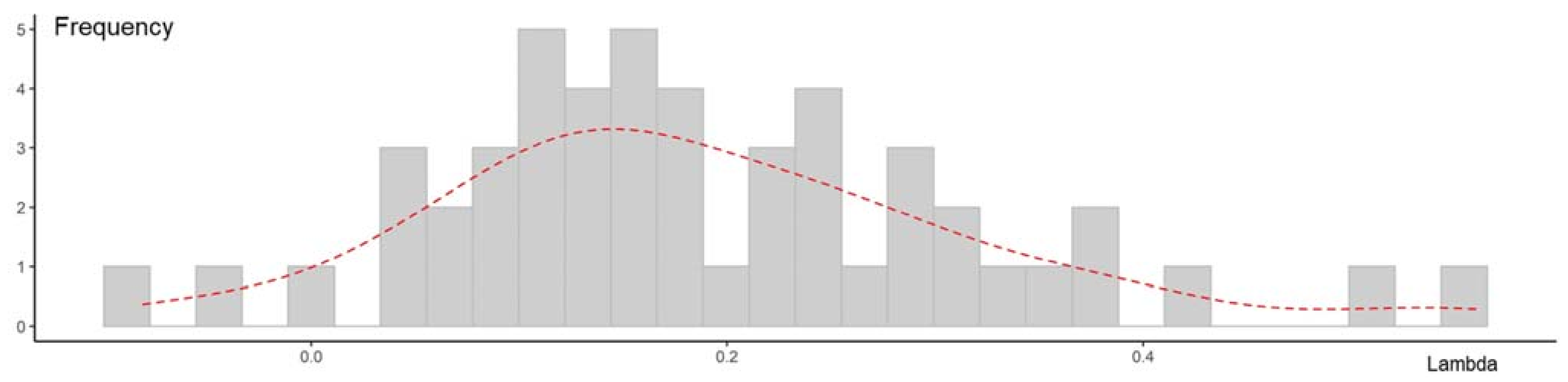

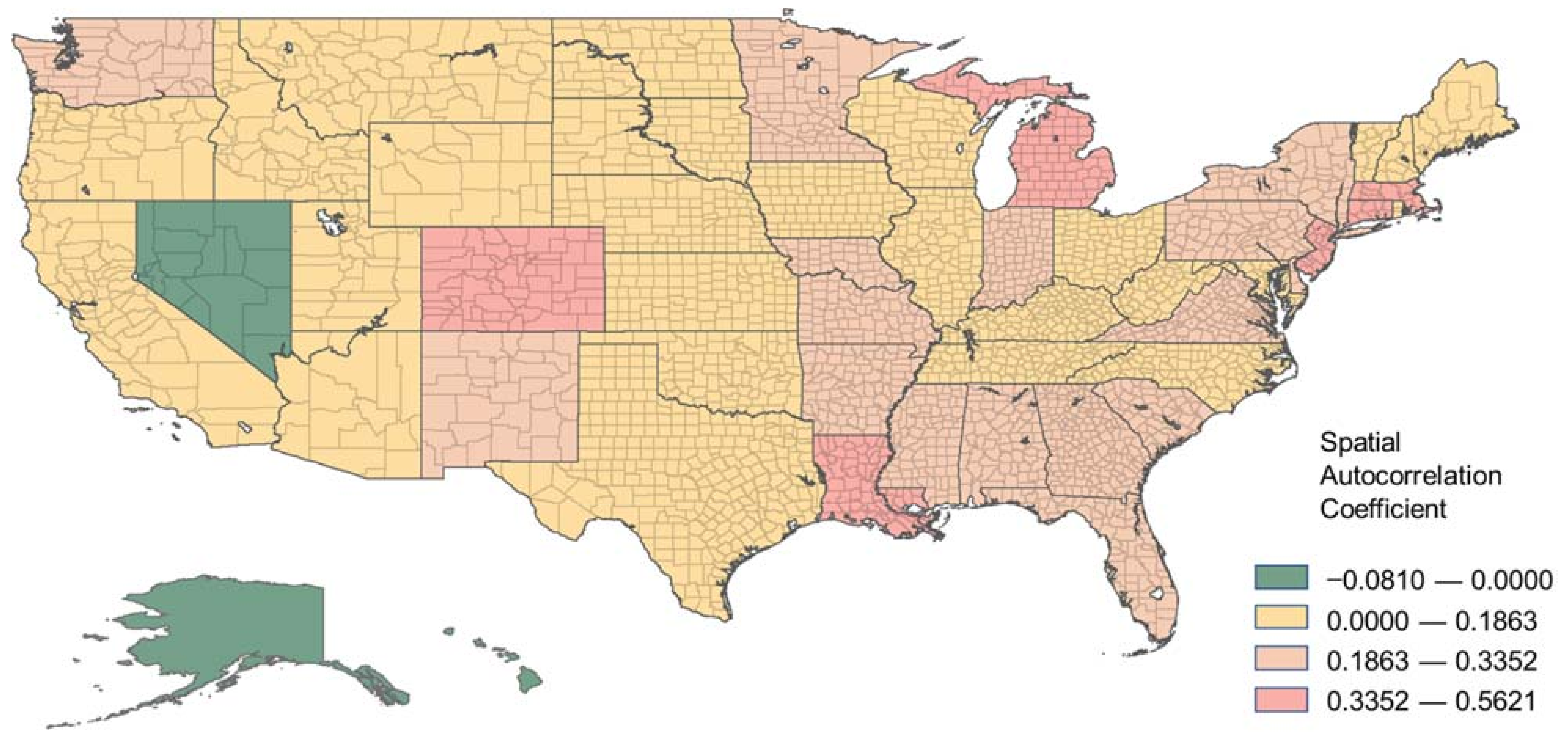
| State | Spatial Lag Coefficient | Stand Error | t-Value | p-Value |
|---|---|---|---|---|
| Alabama | 0.2297 *** | 0.0084 | 27.2015 | <0.001 |
| Alaska | −0.081 *** | 0.0126 | −6.4374 | <0.001 |
| Arizona | 0.09 *** | 0.0124 | 7.2636 | <0.001 |
| Arkansas | 0.2168 *** | 0.0099 | 21.8995 | <0.001 |
| California | 0.1472 *** | 0.0098 | 14.9829 | <0.001 |
| Colorado | 0.4275 *** | 0.0083 | 51.6714 | <0.001 |
| Connecticut | 0.3625 *** | 0.0233 | 15.5821 | <0.001 |
| Delaware | 0.278 *** | 0.0310 | 8.9794 | <0.001 |
| Florida | 0.2826 *** | 0.0081 | 34.6982 | <0.001 |
| Georgia | 0.2395 *** | 0.0051 | 47.2483 | <0.001 |
| Hawaii | −0.0489 ** | 0.0197 | −2.4883 | 0.0128 |
| Idaho | 0.1117 *** | 0.0088 | 12.7027 | <0.001 |
| Illinois | 0.1661 *** | 0.0066 | 25.0248 | <0.001 |
| Indiana | 0.2052 *** | 0.0084 | 24.3700 | <0.001 |
| Iowa | 0.1312 *** | 0.0087 | 15.0073 | <0.001 |
| Kansas | 0.0773 *** | 0.0081 | 9.5291 | <0.001 |
| Kentucky | 0.1032 *** | 0.0078 | 13.237 | <0.001 |
| Louisiana | 0.3791 *** | 0.0086 | 44.0066 | <0.001 |
| Maine | 0.1497 *** | 0.0214 | 7.004 | <0.001 |
| Maryland | 0.1864 *** | 0.0149 | 12.5354 | <0.001 |
| Massachusetts | 0.5202 *** | 0.0111 | 46.704 | <0.001 |
| Michigan | 0.3771 *** | 0.0075 | 50.2282 | <0.001 |
| Minnesota | 0.2892 *** | 0.0073 | 39.4947 | <0.001 |
| Mississippi | 0.3353 *** | 0.0081 | 41.2161 | <0.001 |
| Missouri | 0.3031 *** | 0.0065 | 46.2933 | <0.001 |
| Montana | 0.0859 *** | 0.0107 | 8.0393 | <0.001 |
| Nebraska | 0.1004 *** | 0.0085 | 11.7588 | <0.001 |
| Nevada | −0.0036 ** | 0.0168 | −0.2142 * | 0.0184 |
| New Hampshire | 0.1856 *** | 0.0265 | 7.0142 | <0.001 |
| New Jersey | 0.5621 *** | 0.0114 | 49.3291 | <0.001 |
| New Mexico | 0.2381 *** | 0.0128 | 18.5421 | <0.001 |
| New York | 0.2663 *** | 0.0090 | 29.7591 | <0.001 |
| North Carolina | 0.1598 *** | 0.0071 | 22.449 | <0.001 |
| North Dakota | 0.0348 ** | 0.0112 | 3.1114 ** | 0.0019 |
| Ohio | 0.0812 *** | 0.0090 | 9.0392 | <0.001 |
| Oklahoma | 0.1172 *** | 0.0075 | 15.6807 | <0.001 |
| Oregon | 0.1709 *** | 0.0126 | 13.5983 | <0.001 |
| Pennsylvania | 0.3031 *** | 0.0088 | 34.2476 | <0.001 |
| Rhode Island | 0.1400 *** | 0.0371 | 3.7685 | <0.001 |
| South Carolina | 0.2134 *** | 0.0095 | 22.4236 | <0.001 |
| South Dakota | 0.0560 *** | 0.0117 | 4.8008 | <0.001 |
| Tennessee | 0.1216 *** | 0.0079 | 15.3701 | <0.001 |
| Texas | 0.0376 *** | 0.0052 | 7.2084 | <0.001 |
| Utah | 0.0377 *** | 0.0089 | 4.2494 | <0.001 |
| Vermont | 0.1746 *** | 0.0243 | 7.1958 | <0.001 |
| Virginia | 0.2374 *** | 0.0063 | 37.9368 | <0.001 |
| Washington | 0.2351 *** | 0.0126 | 18.6703 | <0.001 |
| West Virginia | 0.1351 *** | 0.0119 | 11.3082 | <0.001 |
| Wisconsin | 0.1627 *** | 0.0078 | 20.7673 | <0.001 |
| Wyoming | 0.1288 *** | 0.0188 | 6.8477 | <0.001 |
| Estimate | Std. Error | t-Value | p-Value | VIF | |
|---|---|---|---|---|---|
| Intercept | 0.0000 | 0.1093 | 0.000 | 1.0000 | |
| BirthR | −0.2419 | 0.1214 | −1.992 | 0.0525 | 1.208749 |
| VoT | 0.2669 | 0.1752 | 1.523 | 0.1349 | 2.518246 |
| Poverty | 0.4468 ** | 0.1589 | 2.810 | 0.0073 | 2.072469 |
| Bachelor | 0.5706 * | 0.2292 | 2.489 | 0.0166 | 4.310079 |
| PopDen | 0.4089 ** | 0.1371 | 2.983 | 0.0046 | 1.541248 |
| Multiple R2 | 0.4633 | ||||
| Adjusted R2 | 0.4023 | ||||
| p-value | 0.00003247 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Hu, T.; Bao, S.; Wu, H.; Peng, Z.; Wang, R. The Spatiotemporal Interaction Effect of COVID-19 Transmission in the United States. ISPRS Int. J. Geo-Inf. 2021, 10, 387. https://doi.org/10.3390/ijgi10060387
Liu L, Hu T, Bao S, Wu H, Peng Z, Wang R. The Spatiotemporal Interaction Effect of COVID-19 Transmission in the United States. ISPRS International Journal of Geo-Information. 2021; 10(6):387. https://doi.org/10.3390/ijgi10060387
Chicago/Turabian StyleLiu, Lingbo, Tao Hu, Shuming Bao, Hao Wu, Zhenghong Peng, and Ru Wang. 2021. "The Spatiotemporal Interaction Effect of COVID-19 Transmission in the United States" ISPRS International Journal of Geo-Information 10, no. 6: 387. https://doi.org/10.3390/ijgi10060387
APA StyleLiu, L., Hu, T., Bao, S., Wu, H., Peng, Z., & Wang, R. (2021). The Spatiotemporal Interaction Effect of COVID-19 Transmission in the United States. ISPRS International Journal of Geo-Information, 10(6), 387. https://doi.org/10.3390/ijgi10060387








