Accuracy Evaluation of Ionospheric Delay from Multi-Scale Reference Networks and Its Augmentation to PPP during Low Solar Activity
Abstract
:1. Introduction
2. Methods
3. Data and Models
4. Results
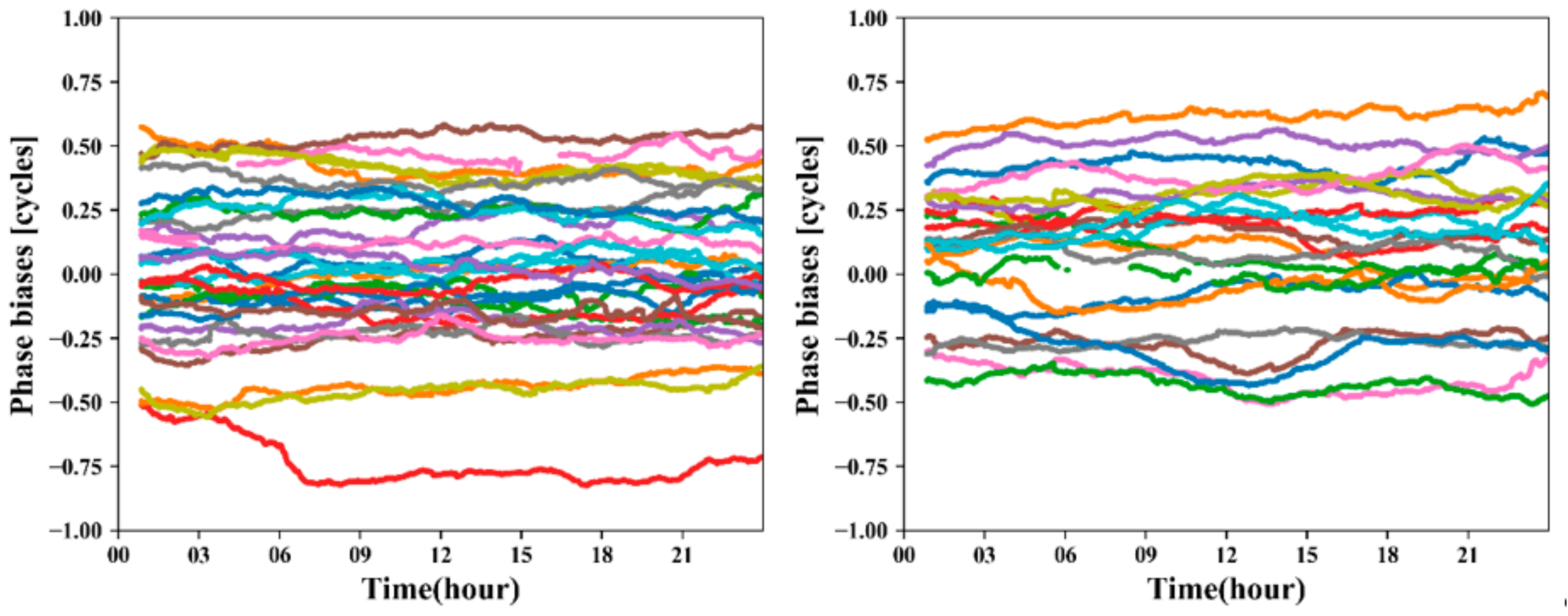
4.1. Convergence Analysis of Ambiguity-Float and Ambiguity-Fixed PPP
4.2. Ionospheric Delays Retrival from the Ambiguity-Fixed PPP
4.3. Using of CODE Global Ionosphere Products for PPP Ambiguity Resolution
4.4. PPP-RTK Using Ionospheric Delay from Multi-Scale Networks
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geoph. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- Geng, J.; Teferle, F.N.; Meng, X.; Dodson, A.H. Kinematic precise point positioning at remote marine platforms. GPS Solut. 2010, 14, 343–350. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Wabbena, G.; Schmitz, M.; Bagge, A. PPP-RTK: Precise Point Positioning using state-space representation in RTK networks. In Proceedings of the 18th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2005), Long Beach, CA, USA, 13–16 September 2005; Volume 5, pp. 13–16. [Google Scholar]
- De Oliveira, P.S.; Morel, L.; Fund, F.; Legros, R.; Monico, J.F.G.; Durand, S.; Durand, F. Modeling tropospheric wet delays with dense and sparse network configurations for PPP-RTK. GPS Solut. 2017, 21, 237–250. [Google Scholar] [CrossRef] [Green Version]
- Psychas, D.; Verhagen, S.; Liu, X.; Memarzadeh, Y.; Visser, H. Assessment of ionospheric corrections for PPP-RTK using regional ionosphere modelling. Meas. Sci. Technol. 2018, 30, 014001. [Google Scholar] [CrossRef] [Green Version]
- Teunissen, P.J.G.; Odijk, D.; Zhang, B. PPP-RTK: Results of CORS network-based PPP with integer ambiguity resolution. J. Aeronaut. Astronaut. Aviat. 2010, 42, 223–230. [Google Scholar]
- Li, X.; Zhang, X.; Ge, M. Regional reference network augmented precise point positioning for instantaneous ambiguity resolution. J. Geod. 2011, 85, 151–158. [Google Scholar] [CrossRef]
- Zhang, B.; Teunissen, P.J.G.; Odijk, D. A Novel Un-differenced PPP-RTK Concept. J. Navig. 2011, 64, S180–S191. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Chen, W.; Ruan, R.; Liu, X. Evaluation of PPP-RTK based on BDS-3/BDS-2/GPS observations: A case study in Europe. GPS Solut. 2020, 24, 1–12. [Google Scholar] [CrossRef]
- Psychas, D.; Verhagen, S. Real-time PPP-RTK performance analysis using ionospheric corrections from multi-scale network configurations. Sensors 2020, 20, 3012. [Google Scholar] [CrossRef] [PubMed]
- BeiDou Navigation Satellite System Signal in Space Interface Control Document: Precise Point Positioning Service Signal PPP-B2b (Version 1.0). Available online: http://en.beidou.gov.cn/SYSTEMS/Officialdocument/202008/P020200803544810243992.pdf (accessed on 12 April 2021).
- Galileo High Accuracy Service (HAS). Available online: https://www.gsc-europa.eu/sites/default/files/sites/all/files/Galileo_HAS_Info_Note.pdf (accessed on 12 April 2021). [CrossRef]
- Schaer, S.; Beutler, G.; Rothacher, M.; Springer, T.A. Global ionosphere maps based on GPS carrier phase data routinely produced by the code analysis center. In Proceedings of the IGS Analysis Center Workshop 1996, Silver Spring, MD, USA, 19–21 March 1996. [Google Scholar]
- Bruyninx, C.; Legrand, J.; Fabian, A.; Pottiaux, E. GNSS metadata and data validation in the EUREF Permanent Network. GPS Solut. 2019, 23, 106. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, B.; Yuan, Y.; Li, Z.; Wang, N. Multi-GNSS triple-frequency differential code bias (DCB) determination with precise point positioning (PPP). J. Geod. 2019, 93, 765–784. [Google Scholar] [CrossRef]
- Zhang, B.; Teunissen, P.J.G. Characterization of multi-GNSS between-receiver differential code biases using zero and short baselines. Sci. Bull. 2015, 60, 1840–1849. [Google Scholar] [CrossRef] [Green Version]
- Zha, J.; Zhang, B.; Yuan, Y.; Zhang, X.; Li, M. Use of modified carrier-to-code leveling to analyze temperature dependence of multi-GNSS receiver DCB and to retrieve ionospheric TEC. GPS Solut. 2019, 23, 103. [Google Scholar] [CrossRef]
- Jin, S.; Su, K. PPP models and performances from single-to quad-frequency BDS observations. Satell. Navig. 2020, 1, 1–13. [Google Scholar] [CrossRef]
- Laurichesse, D.; Blot, A. Fast PPP convergence using multi-constellation and triple-frequency ambiguity resolution. In Proceedings of the ION GNSS 2016, Portland, OR, USA, 12–16 September 2016. [Google Scholar]
- Deng, Z.; Fritsche, M.; Uhlemann, M.; Wickert, J.; Schuh, H. Reprocessing of GFZ multi-GNSS product GBM. In Proceedings of the IGS Workshop 2016, Sydney, Australia, 8–12 February 2016. [Google Scholar]
- Vaclavovic, P.; Nesvatba, O. Comparison and assessment of float, fixed, and smoothed Precise Point Positioning. Acta Geodyn. Geomat. 2020, 17, 329–340. [Google Scholar] [CrossRef]
- Václavovic, P.; Douša, J.; Gyori, G. G-Nut software library—State of development and first results. Acta Geodyn. Geomat. 2013, 10, 431–436. [Google Scholar] [CrossRef] [Green Version]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P. Differential code bias estimation using multi-GNSS observations and global ionosphere maps. In Proceedings of the 2014 International Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 27–29 January 2014; pp. 802–812. [Google Scholar]
- Laurichesse, D. Phase Biases for Ambiguity Resolution: From an Undifferenced to an Uncombined Formulation; CNES White Paper; CNES: Paris, France, 2015. [Google Scholar]
- Seeber, G. Satellite Geodesy: Foundations, Methods and Applications. Int. Hydrogr. Rev. 2003, 4, 92–93. [Google Scholar]
- Mungufeni, P.; Habarulema, J.B.; Jurua, E. Modeling of ionospheric irregularities during geomagnetically disturbed conditions over African low-latitude region. Space Weather. 2016, 14, 710–723. [Google Scholar] [CrossRef]
- Dach, R.; Schaer, S.; Arnold, D.; Orliac, E.; Prange, L.; Susnik, A.; Villiger, A.; Jäggi, A. CODE Final Product Series for the IGS; Astronomical Institute, University of Bern: Bern, Switzerland, 2016. [Google Scholar]
- Deng, Z.; Bender, M.; Dick, G.; Ge, M.; Wickert, J.; Ramatschi, M.; Zou, X. Retrieving tropospheric delays from GPS networks densified with single frequency receivers. Geophys. Res. Lett. 2009, 36, 308. [Google Scholar] [CrossRef]
- Hong, J.; Tu, R.; Zhang, R.; Fan, L.; Han, J.; Zhang, P.; Lu, X. Analysis of dual-frequency solution method for single-frequency precise point positioning based on SEID model for GPS and BDS. Measurement 2021, 175, 109102. [Google Scholar] [CrossRef]






















| Modeling | Strategies |
|---|---|
| Observation combination | Raw double-frequency |
| Orbits/Clocks/Phase bias | GFZ final orbit/clock products, estimated biases CNES real-time orbit/clock/biases products |
| Ionosphere corrections | Iono-No: estimated as unknown parameter Iono-Interp: Interpolated from network side |
| Zenith troposphere delay | Estimated as random walk parameter |
| Satellite DCB | Corrected using products provided by DLR [24] |
| Receiver DCB | Estimated as random unknown parameter |
| Elevation cutoff | 7° |
| Sampling | 30 s |
| Attitude corrections | Steering attitude model for GFZ products Nominal attitude model for CNES PPP |
| Ambiguity resolution | Partial ambiguity resolution |
| Coordinates | Service side: Static User side: Kinematic |
| Station | Receiver Type | Antenna Type | Lon | Lat | Dist. (m) |
|---|---|---|---|---|---|
| YARR | SEPT POLARX5 | LEIAT504 NONE | 115.3472 | 29.0465 | 20.2 |
| YAR3 | SEPT POLARX5 | LEIAR25 NONE | |||
| GOP6 | SEPT POLARX5 | LEIAR25.R4 LEIT | 14.7856 | 49.9137 | 4.1 |
| GOPE | TRIMBLE SPS855 | TPSCR.G3 TPSH | |||
| PRD2 | TPS NET-G5 | NOV750.R4 NONE | −114.2929 | 50.8713 | 77.6 |
| PRD3 | TPS NET-G5 | TPSCR.G3 NONE |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Douša, J.; Václavovic, P. Accuracy Evaluation of Ionospheric Delay from Multi-Scale Reference Networks and Its Augmentation to PPP during Low Solar Activity. ISPRS Int. J. Geo-Inf. 2021, 10, 516. https://doi.org/10.3390/ijgi10080516
Zhao L, Douša J, Václavovic P. Accuracy Evaluation of Ionospheric Delay from Multi-Scale Reference Networks and Its Augmentation to PPP during Low Solar Activity. ISPRS International Journal of Geo-Information. 2021; 10(8):516. https://doi.org/10.3390/ijgi10080516
Chicago/Turabian StyleZhao, Lewen, Jan Douša, and Pavel Václavovic. 2021. "Accuracy Evaluation of Ionospheric Delay from Multi-Scale Reference Networks and Its Augmentation to PPP during Low Solar Activity" ISPRS International Journal of Geo-Information 10, no. 8: 516. https://doi.org/10.3390/ijgi10080516
APA StyleZhao, L., Douša, J., & Václavovic, P. (2021). Accuracy Evaluation of Ionospheric Delay from Multi-Scale Reference Networks and Its Augmentation to PPP during Low Solar Activity. ISPRS International Journal of Geo-Information, 10(8), 516. https://doi.org/10.3390/ijgi10080516






