Encoding Conversion Algorithm of Quaternary Triangular Mesh
Abstract
:1. Introduction
2. The Encoding of QTM
2.1. The Encoding
2.1.1. Goodchild Encoding
2.1.2. LS Encoding
2.1.3. Modified Direction Encoding
2.1.4. Quaternary Encoding
2.1.5. TRQ Encoding
2.1.6. Arithmetic Layer Encoding
2.2. Encoding Classification
2.2.1. Hierarchical Encoding
2.2.2. Other Encoding
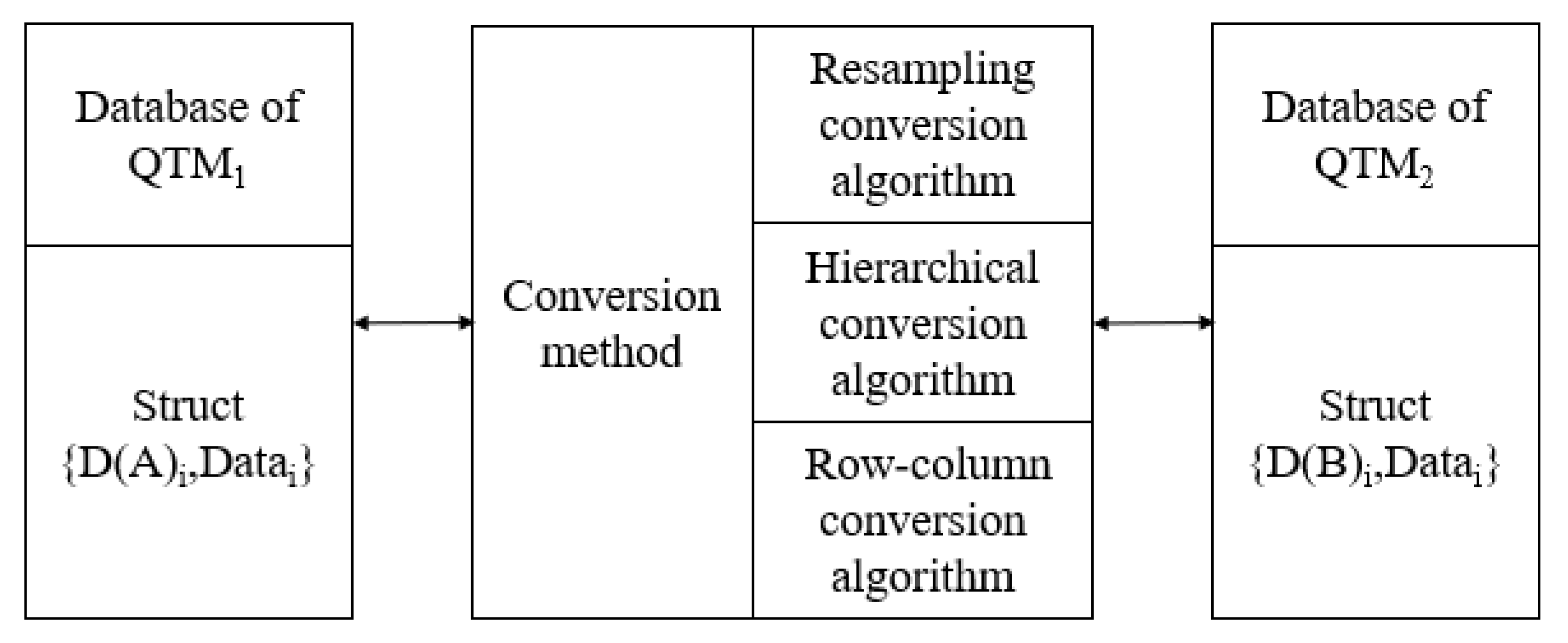
3. Conversion Method
3.1. Resampling Conversion Algorithm
3.2. Hierarchical Conversion Algorithm
3.2.1. Conversion Rules between Goodchild Encoding and LS Encoding
3.2.2. Conversion Rules between Goodchild Encoding and Modified Direction Encoding
3.2.3. Conversion Rules between Goodchild Encoding and Quaternary Encoding
3.3. Row–Column Conversion Method
3.3.1. Conversion Algorithm of the QTM Encoding and Row–Column Number
- ①
- If CODE[i] = 0, then κ = κ + [2 × (φ − m/2) + 1], φ = m − φ − 1, m = m/2;
- ②
- If CODE[i] = 1, then κ = κ, m = m/2;
- ③
- If CODE[i] = 2, then κ = κ, m = m/2, φ = φ − m;
- ④
- If CODE[i] = 3, then κ = κ + m, m = m/2, φ = φ − m;
- ⑤
- Repeat the above calculations until i = 2n−1 and output the value of κ.
- ①
- If φ < m/2, then CODE[i] = 1, m = m/2, φ = φ − m;
- ②
- If φ ≥ m/2, and κ < (φ+1−m/2), then CODE[i] = 2, m = m/2;
- ③
- If φ ≥ m/2, and κ ≥ m ∩ κ ≥ (φ + 1− m/2), then CODE[i] = 3, κ = κ − 2m;
- ④
- If φ ≥ m/2, and (φ + 1 − m/2) ≤ κ < m, then CODE[i] = 0, κ = κ + m − 2φ −1, m = m/2, φ = φ − m;
- ⑤
- Repeat the above calculations until i = 2n−1 and output CODE.
- ①
- Convert α, β, γ into n-bit binary strings Strα, Strβ, Strγ, where n is the subdivision level;
- ②
- According to the rules in Table 4, the encoding are calculated from Strα[i], Strβ[i], and Strγ[i], and the same value in the encodings corresponding to the three level identifiers is the desired encoding;
- ③
- Repeat the above steps until the calculation is completed.
3.3.2. Conversion Algorithm of the TRQ Encoding and Row–Column Number
- ①
- First the rhombic grid coordinates φD, κD; in the φκ coordinate system can be obtained by inverse calculation using Equation (8) and the row–column number of the triangular grid;
- ②
- Then it uses the Equation (9) and φD, κD to obtain the coordinates of the rhombic grid in the IJ coordinate system, and converts I and J to the diamond grid encoding;
- ③
- Finally, according to the orientation of the triangle and the encoding rules, the TRQ encoding of the triangular grid can be obtained.
4. Comparison and Analysis of Algorithm Efficiency
4.1. Comparative Analysis of Conversion Algorithms of Hierarchical Encoding
4.2. Comparison and Analysis of Conversion Algorithm Efficiency of Other Types of Encoding
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Purss, M.B.; Peterson, P.R.; Strobl, P.; Dow, C.; Sabeur, Z.A.; Gibb, R.G.; Ben, J. Datacubes: A discrete global grid systems perspective. Cartogr. Int. J. Geogr. Inf. Geovis. 2019, 54, 63–71. [Google Scholar] [CrossRef]
- Yao, X.; Li, G.; Xia, J.; Ben, J.; Cao, Q.; Zhao, L.; Ma, Y.; Zhang, L.; Zhu, D. Enabling the big earth observation data via cloud computing and DGGS: Opportunities and challenges. Remote Sens. 2019, 12, 62. [Google Scholar] [CrossRef] [Green Version]
- Kolar, J. Representation of the geographic terrain surface using global indexing. In Proceedings of the 12th International Conference on Geoinformatics, Gävle, Sweden, 7–9 June 2004; pp. 321–328. [Google Scholar]
- Zhao, X.S.; Ben, J.; Sun, W.B.; Tong, X. Overview of the research progress in the earth tessellation grid. Acta Geod. Et Cartogr. Sin. 2016, 45, 1–14. [Google Scholar]
- Dutton, G.H. A Hierarchical Coordinate System for Geoprocessing and Cartography; Spring: Berlin/Heidelberg, Germany, 1999; p. 23. [Google Scholar]
- Goodchild, M.F. Reimagining the history of GIS. Ann. GIS 2018, 24, 1–8. [Google Scholar] [CrossRef]
- Dutton, G. Modeling Locational Uncertainty via Hierarchical Tesselation: Accuracy of Spatial Database; Taylor and Francis: London, UK, 1989; pp. 125–140. [Google Scholar]
- Hou, M.; Xing, H.; Zhao, X.; Chen, J. Computing of complicated topological relation in spherical surface quaternary triangular mesh. Geomat. Inf. Sci. Wuhan Univ. 2012, 37, 468–470. [Google Scholar]
- Fekete, G. Rendering and managing spherical data with sphere quadtrees. In Proceedings of the First 1990 IEEE Conference on Visualization, San Francisco, CA, USA, 23–26 October 1990; pp. 176–186. [Google Scholar]
- Goodchild, M.F.; Yang, S. A hierarchical spatial data structure for global geographic information systems. CVGIP Graph. Models Image Processing 1992, 54, 31–44. [Google Scholar] [CrossRef] [Green Version]
- Dutton, G. Digital map generalization using a hierarchical coordinate system. In Proceedings of the Auto Carto 13, Bethesda, MD, USA, 7–10 April 1997; ACSM/AS-PRS. pp. 367–376. [Google Scholar]
- Dutton, G. Scale, sinuosity and point selection in digital line generalization. Cartogr. Geogr. Inf. Sci. 1999, 26, 33–53. [Google Scholar] [CrossRef]
- Lee, M.; Samet, H. Navigating through triangle meshes implemented as linear quadtree. ACM Trans. Graph. 2000, 19, 79–121. [Google Scholar] [CrossRef]
- Chen, Y.H.; Wang, J.X.; Cao, Z.N. The uniform encoding and generation method of structure elements of Discrete Global Grid Systems. J. Geo-Inf. Sci. 2021, 23, 1382–1390. [Google Scholar]
- Amiri, A.M.; Samavati, F.; Peterson, P. Categorization and conversions for indexing methods of discrete global grid systems. Int. J. Geo-Inf. 2015, 4, 320–336. [Google Scholar] [CrossRef]
- Du, L.Y.; Ben, J.; Maq, H. An algorithm for generating discrete line transformation of planar triangular grid based on weak duality. Geomat. Inf. Sci. Wuhan Univ. 2020, 45, 105–110. [Google Scholar]
- Amiri, A.M.; Harrison, E.; Samavati, F. Hexagonal connectivity maps for Digital Earth. Int. J. Digit. Earth 2015, 8, 750–769. [Google Scholar] [CrossRef]
- Ben, J.; Tong, X.C.; Zhou, C.H.; Zhang, K.X. Construction algorithm of octahedron based hexagon grid systems. J. Geo-Inf. Sci. 2015, 17, 789–797. [Google Scholar]
- Gold, C.; Mostafavi, M.A. Towards the global GIS. ISPRS J. Photogramm. Remote Sens. 2000, 55, 150–163. [Google Scholar] [CrossRef]
- Bartholdi, J.J.; Goldsman, P. Continuous indexing of hierarchical subdivisions of the globe. Int. J. Geogr. Inf. Sci. 2001, 15, 489–522. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.X.; Chen, Y.H.; Cao, Z.N.; Qin, Z.; Shi, Y. Algorithm of neighbor finding on quaternary triangular mesh with modified direction coding. Sci. Surv. Mapp. 2021, 46, 196–202. [Google Scholar]
- Bai, J.J.; Zhao, X.S.; Chen, J. Indexing of discrete global grids using linear quadtree. Geomat. Inf. Sci. Wuhan Univ. 2005, 30, 805–808. [Google Scholar]
- Zhao, X.S.; Chen, J. Fast translating algorithm between QTM code and longitude/latitude coordination. Acta Geod. Cartogr. Sin. 2003, 32, 272–277. [Google Scholar]
- Tong, X.C.; Zhang, Y.S.; Ben, J. Three orientation translating algorithm of long./lat. coordination and QTM code along with its criterion judge of precision. Geomat. Inf. Sci. Wuhan Univ. 2006, 31, 27–30. [Google Scholar]
- White, D. Global grids from recursive diamond subdivisions of the surface of an octahedron or icosahedron. Environ. Monit. Assess. 2000, 64, 93–103. [Google Scholar] [CrossRef]







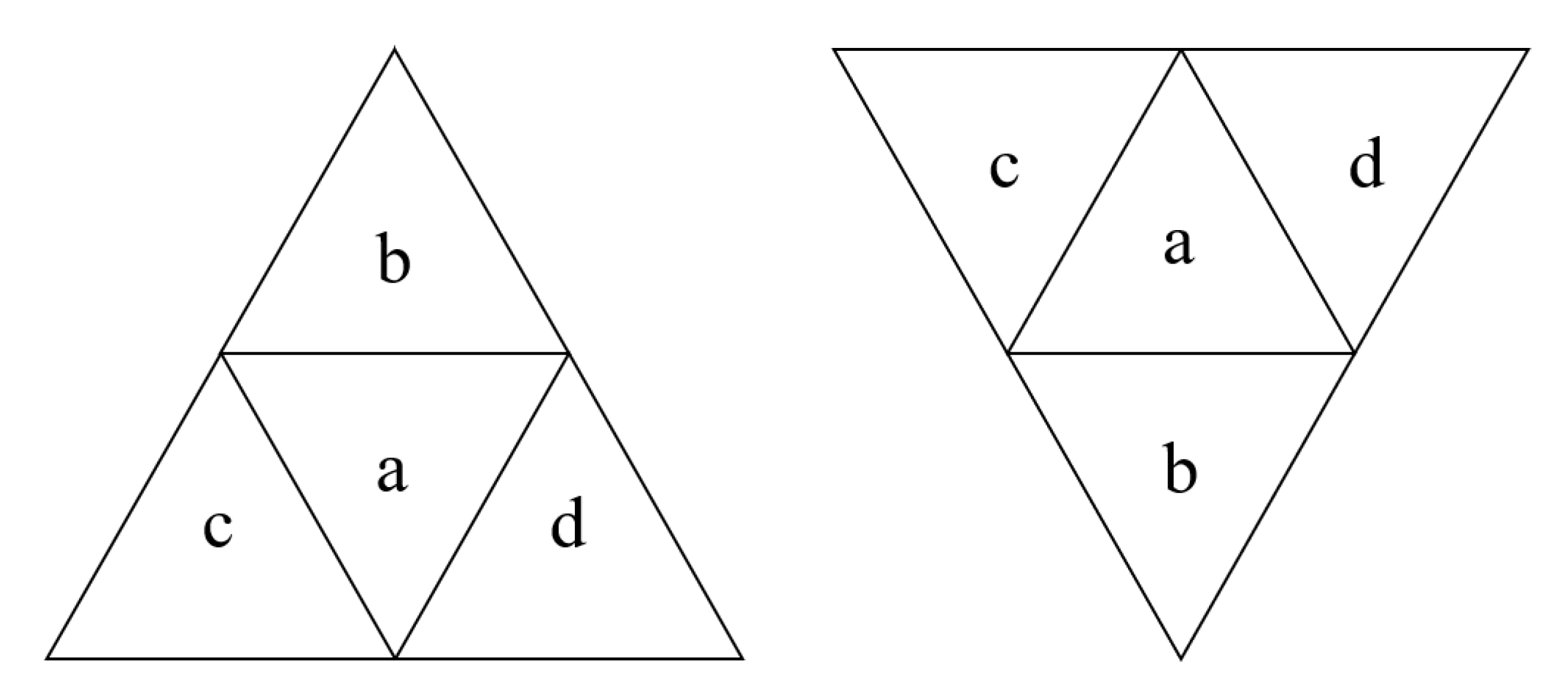

















| Encoding Method | Hierarchically Nesting | Type | Supported Applications |
|---|---|---|---|
| Goodchild encoding | √ | Hierarchical encoding | Spatial data hierarchical indexing |
| LS encoding | √ | Hierarchical encoding | Global navigation |
| Quaternary encoding | √ | Hierarchical encoding and filling curve encoding | Data storage |
| Dutton encoding | √ | Hierarchical encoding | Global spatial data extraction and multi-resolution management |
| TRQ encoding | × | Integer coordinate encoding and filling curve encoding | Establish the relation between rhombus grid and triangular grid |
| Arithmetic layer encoding | × | Integer coordinate encoding | The uniform encoding and generation method of structure elements of DGGS |
| Encoding Method | a | b | c | d | Arrangement Situation |
|---|---|---|---|---|---|
| Goodchild encoding | 0 | 1 | 2 | 3 | 1 |
| LS encoding | 10 | 00 | 01 | 11 | 1 |
| Modified direction encoding | 0 | 1 | 2 | 3 | 2 |
| 0 | 1 | 3 | 2 | ||
| Quaternary encoding | 1 | 2 | 0 | 3 | 4 |
| 1 | 2 | 3 | 0 | ||
| 1 | 0 | 2 | 3 | ||
| 1 | 0 | 3 | 2 |
| CODE[i] | Direction | CODE[i−1] | a | b | c | d |
|---|---|---|---|---|---|---|
| 0 | Upward | 0, 1, 2 | 1 | 2 | 0 | 3 |
| 3 | 1 | 0 | 2 | 3 | ||
| Downward | 0, 1, 2 | 1 | 0 | 3 | 2 | |
| 3 | 1 | 2 | 3 | 0 | ||
| 1 | Upward | 0, 1, 2 | 1 | 2 | 0 | 3 |
| 3 | 1 | 0 | 2 | 3 | ||
| Downward | 0, 1, 2 | 1 | 0 | 3 | 2 | |
| 3 | 1 | 2 | 3 | 0 | ||
| 2 | Upward | 0, 1, 2 | 1 | 2 | 0 | 3 |
| 3 | 1 | 0 | 2 | 3 | ||
| Downward | 0, 1, 2 | 1 | 0 | 3 | 2 | |
| 3 | 1 | 2 | 3 | 0 | ||
| 3 | Upward | 0, 1, 2 | 1 | 0 | 2 | 3 |
| 3 | 1 | 2 | 0 | 3 | ||
| Downward | 0, 1, 2 | 1 | 2 | 3 | 0 | |
| 3 | 1 | 0 | 3 | 2 |
| Identifiers at Each Level | Encoding of Triangles | |
|---|---|---|
| Upward Triangle | Downward Triangle | |
| Strα[i] = 0 | 1 | 0, 2, 3 |
| Strα[i] = 1 | 0, 2, 3 | 1 |
| Strβ[i] = 0 | 3 | 0, 1, 2 |
| Strβ[i] = 1 | 0, 1, 2 | 3 |
| Strγ[i] = 0 | 2 | 0, 1, 3 |
| Strγ[i] = 1 | 0, 1, 3 | 2 |
| Subdivision Level | The Number of Cells in the Grid | Time (s) | Average Number of Conversions of 1s | Algorithm (1) 1 Time/Algorithm (2) 2 Time | ||
|---|---|---|---|---|---|---|
| Algorithm (1) 1 | Algorithm (2) 2 | Algorithm (1) 1 | Algorithm (2) 2 | |||
| 6 | 4096 | 0.013 | 0.008 | 315,077 | 512,000 | 62% |
| 7 | 16,384 | 0.057 | 0.035 | 287,439 | 468,114 | 61% |
| 8 | 65,536 | 0.246 | 0.149 | 266,407 | 439,839 | 61% |
| 9 | 262,144 | 1.050 | 0.643 | 249,661 | 407,689 | 61% |
| 10 | 1,048,576 | 4.506 | 2.715 | 232,707 | 386,216 | 60% |
| 11 | 4,194,304 | 17.789 | 10.695 | 235,781 | 392,174 | 60% |
| 12 | 16,777,216 | 72.894 | 43.565 | 230,159 | 385,108 | 60% |
| Subdivision Level | The Number of Cells in the Grid | Time (s) | Average Number of Conversions of 1s | Algorithm (1) 1 Time/Algorithm (2) 2 Time | ||
|---|---|---|---|---|---|---|
| Algorithm (1) 1 | Algorithm 2) 2 | Algorithm (1) 1 | Algorithm (2) 2 | |||
| 6 | 4096 | 0.006 | 0.014 | 682,667 | 292,571 | 43 |
| 7 | 16,384 | 0.025 | 0.058 | 655,360 | 282,483 | 43 |
| 8 | 65,536 | 0.103 | 0.243 | 638,504 | 269,695 | 42 |
| 9 | 262,144 | 0.436 | 1.048 | 601,248 | 250,137 | 42 |
| 10 | 1,048,576 | 1.844 | 4.534 | 568,642 | 231,270 | 41 |
| 11 | 4,194,304 | 7.568 | 18.459 | 554,216 | 227,223 | 41 |
| 12 | 16,777,216 | 30.589 | 74.973 | 548,472 | 223,777 | 41 |
| Subdivision Level | The Number of Cells in the Grid | Time (s) | Average Number of Conversions of 1s | Algorithm (1) 1 time/Algorithm (2) 2 Time | ||
|---|---|---|---|---|---|---|
| Algorithm (1) 1 | Algorithm (2) 2 | Algorithm (1) 1 | Algorithm (2) 2 | |||
| 9 | 3455 | 0.019 | 0.004 | 181,842 | 909,211 | 20% |
| 10 | 14,653 | 0.084 | 0.017 | 174,440 | 861,941 | 20% |
| 11 | 57,087 | 0.357 | 0.072 | 159,908 | 792,875 | 20% |
| 12 | 225,264 | 1.445 | 0.290 | 155,892 | 776,772 | 20% |
| 13 | 894,665 | 5.849 | 1.171 | 152,960 | 764,018 | 20% |
| 14 | 3,587,606 | 23.688 | 4.766 | 151,452 | 752,750 | 20% |
| 15 | 14,386,302 | 96.056 | 19.334 | 149,770 | 744,093 | 20% |
| Subdivision Level | The Number of Cells in the Grid | Time (s) | Average Number of Conversions of 1s | Algorithm (1) 1 Time/Algorithm (2) 2 Time | ||
|---|---|---|---|---|---|---|
| Algorithm (1) 1 | Algorithm (2) 2 | Algorithm (1) 1 | Algorithm (2) 2 | |||
| 9 | 3455 | 0.016 | 0.008 | 215,938 | 431,875 | 50% |
| 10 | 14,653 | 0.07 | 0.035 | 209,329 | 418,657 | 50% |
| 11 | 57,087 | 0.283 | 0.142 | 201,721 | 402,021 | 50% |
| 12 | 225,264 | 1.177 | 0.579 | 191,388 | 389,057 | 49% |
| 13 | 894,665 | 4.944 | 2.398 | 180,960 | 373,088 | 49% |
| 14 | 3,587,606 | 20.918 | 10.25 | 171,508 | 350,010 | 49% |
| 15 | 14,386,302 | 88.692 | 43.637 | 162,205 | 329,681 | 49% |
| Subdivision Level | The Number of Cells in the Grid | Time (s) | Average Number of Conversions of 1s | Algorithm (1) 1 Time/Algorithm (2) 2 Time | ||
|---|---|---|---|---|---|---|
| Algorithm (1) 1 | Algorithm (2) 2 | Algorithm (1) 1 | Algorithm (2) 2 | |||
| 9 | 3455 | 0.021 | 0.013 | 164,524 | 265,769 | 62% |
| 10 | 14,653 | 0.092 | 0.056 | 159,272 | 261,661 | 61% |
| 11 | 57,087 | 0.399 | 0.239 | 143,075 | 238,858 | 60% |
| 12 | 225,264 | 1.632 | 0.958 | 138,029 | 235,140 | 59% |
| 13 | 894,665 | 6.669 | 3.883 | 134,153 | 230,406 | 58% |
| 14 | 3,587,606 | 27.276 | 15.820 | 131,530 | 226,777 | 58% |
| 15 | 14,386,302 | 112.104 | 64.796 | 128,330 | 222,025 | 58% |
| Subdivision Level | Number of Grids | Time (s) | Average Number of Conversions of 1s | Algorithm (1) 1/Algorithm(2) 2 | ||
|---|---|---|---|---|---|---|
| Algorithm (1) 1 | Algorithm (2) 2 | Algorithm (1) 1 | Algorithm (2) 2 | |||
| 9 | 3455 | 0.016 | 0.014 | 215,938 | 246,786 | 88 |
| 10 | 14,653 | 0.072 | 0.063 | 203,514 | 232,587 | 88 |
| 11 | 57,087 | 0.306 | 0.268 | 186,559 | 213,011 | 88 |
| 12 | 225,264 | 1.243 | 1.080 | 181,226 | 208,578 | 87 |
| 13 | 894,665 | 5.116 | 4.476 | 174,876 | 199,880 | 87 |
| 14 | 3,587,606 | 21.054 | 18.103 | 170,400 | 198,177 | 86 |
| 15 | 14,386,302 | 87.051 | 74.863 | 165,263 | 192,168 | 86 |
| Subdivision Level | Number of Grids | Time (s) | Average Number of Conversions of 1s | Algorithm (1) 1/Algorithm(2) 2 | ||
|---|---|---|---|---|---|---|
| Algorithm (1) 1 | Algorithm (2) 2 | Algorithm (1) 1 | Algorithm (2) 2 | |||
| 9 | 3455 | 0.018 | 0.012 | 191,944 | 287,917 | 67 |
| 10 | 14,653 | 0.079 | 0.052 | 185,481 | 280,709 | 66 |
| 11 | 57,087 | 0.341 | 0.225 | 167,411 | 253,720 | 66 |
| 12 | 225,264 | 1.395 | 0.919 | 161,480 | 245,119 | 66 |
| 13 | 894,665 | 5.638 | 3.703 | 158,685 | 241,605 | 66 |
| 14 | 3,587,606 | 23.061 | 14.992 | 155,570 | 239,301 | 65 |
| 15 | 14,386,302 | 93.355 | 60.680 | 154,103 | 237,085 | 65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Cao, Z.; Wang, J.; Shi, Y.; Qin, Z. Encoding Conversion Algorithm of Quaternary Triangular Mesh. ISPRS Int. J. Geo-Inf. 2022, 11, 33. https://doi.org/10.3390/ijgi11010033
Chen Y, Cao Z, Wang J, Shi Y, Qin Z. Encoding Conversion Algorithm of Quaternary Triangular Mesh. ISPRS International Journal of Geo-Information. 2022; 11(1):33. https://doi.org/10.3390/ijgi11010033
Chicago/Turabian StyleChen, Yihang, Zening Cao, Jinxin Wang, Yan Shi, and Zilong Qin. 2022. "Encoding Conversion Algorithm of Quaternary Triangular Mesh" ISPRS International Journal of Geo-Information 11, no. 1: 33. https://doi.org/10.3390/ijgi11010033
APA StyleChen, Y., Cao, Z., Wang, J., Shi, Y., & Qin, Z. (2022). Encoding Conversion Algorithm of Quaternary Triangular Mesh. ISPRS International Journal of Geo-Information, 11(1), 33. https://doi.org/10.3390/ijgi11010033





