Development and Application of a QGIS-Based Model to Estimate Monthly Streamflow
Abstract
:1. Introduction
2. Materials and Methods
2.1. Direct Runoff Calculation
2.2. Baseflow Calculation
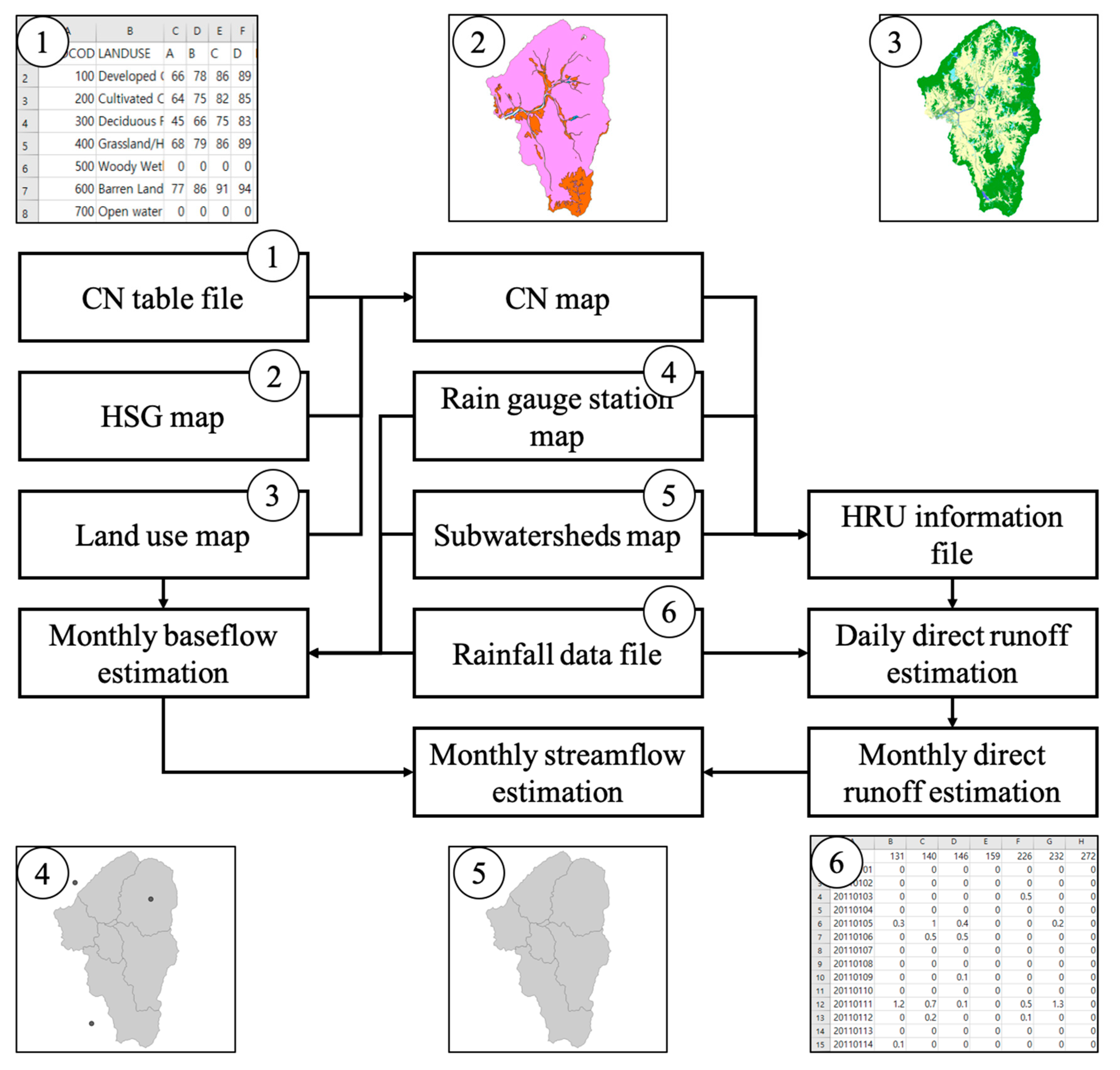
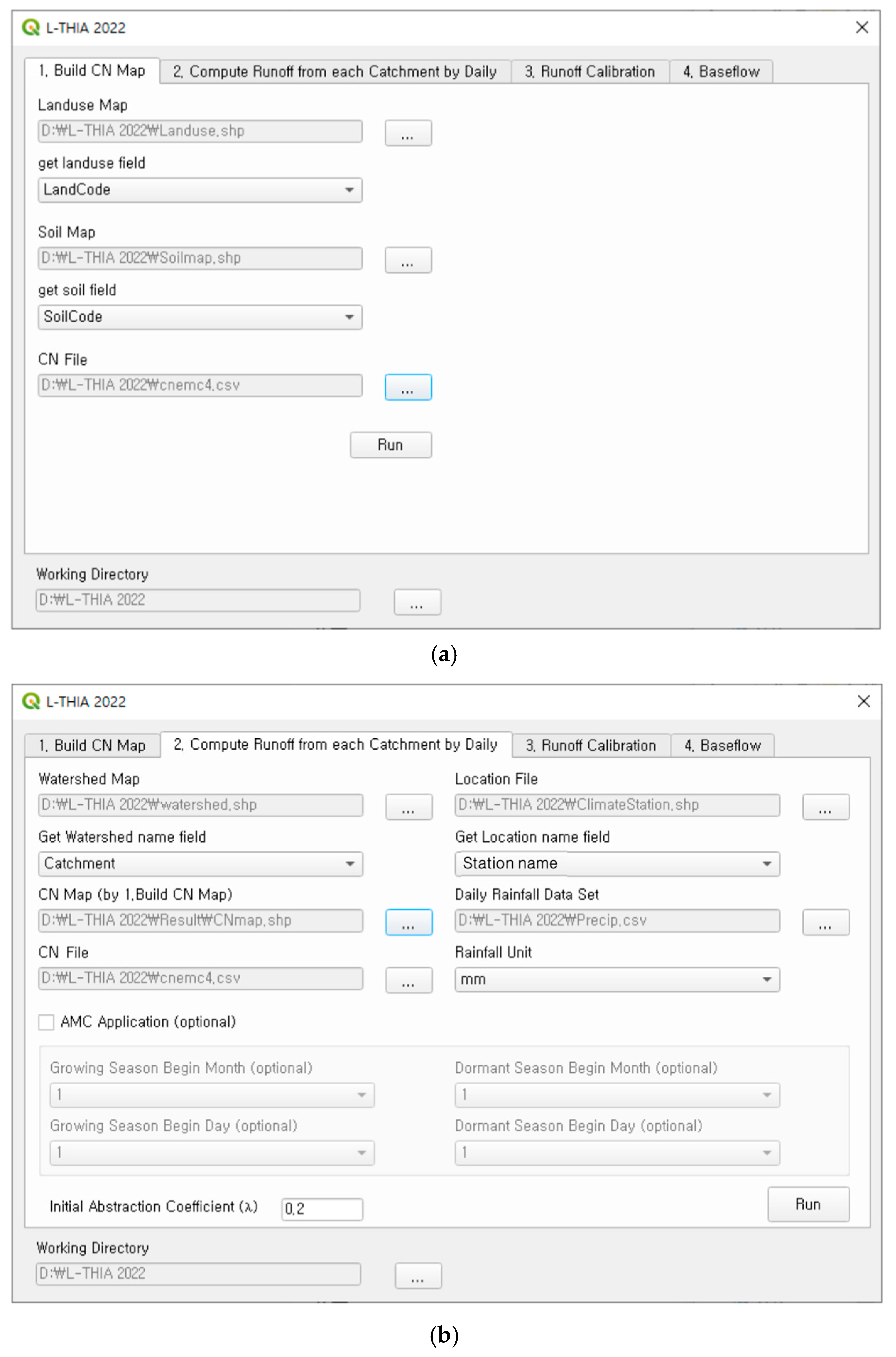
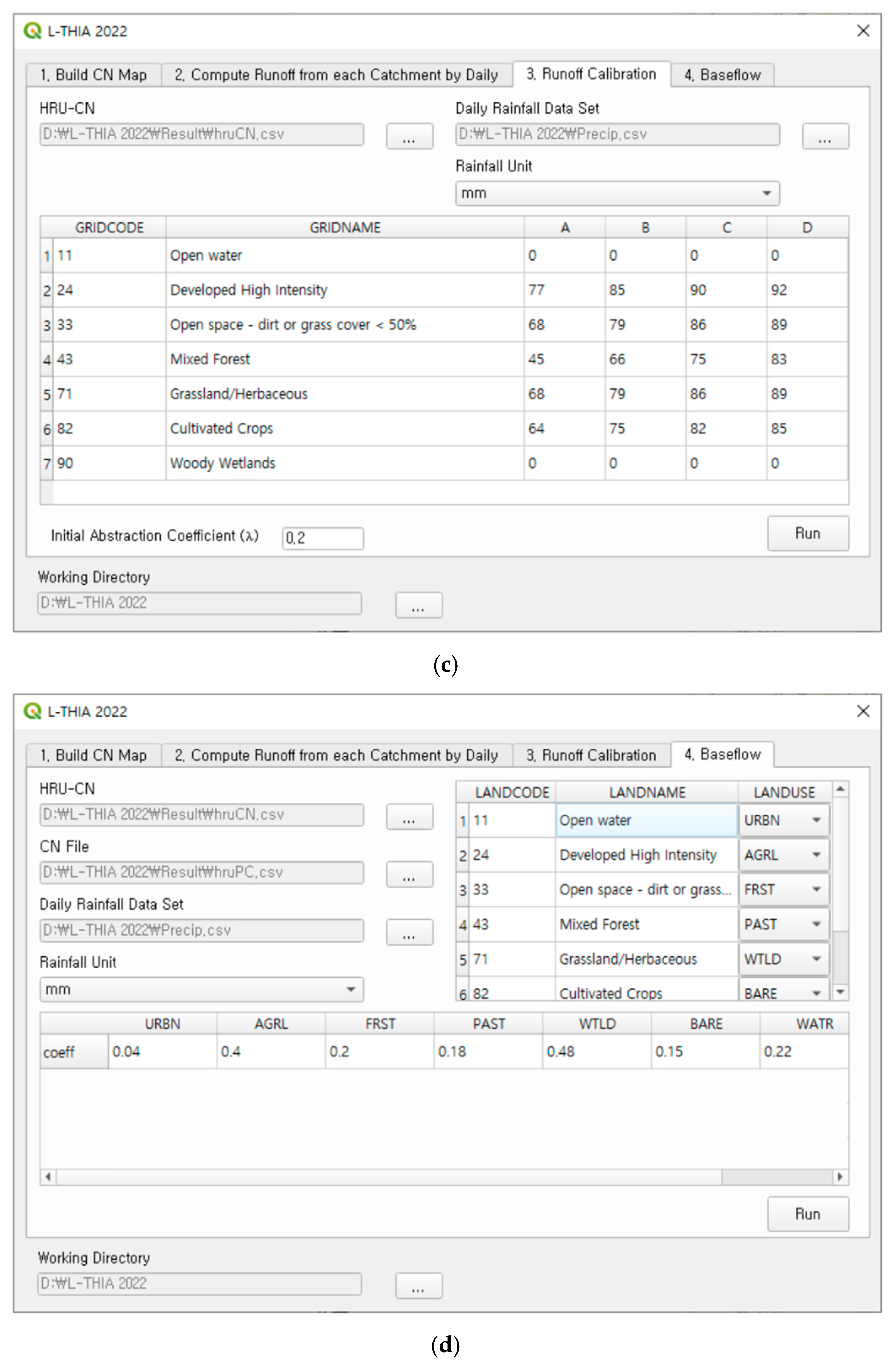
2.3. Development of L-THIA 2022 Model
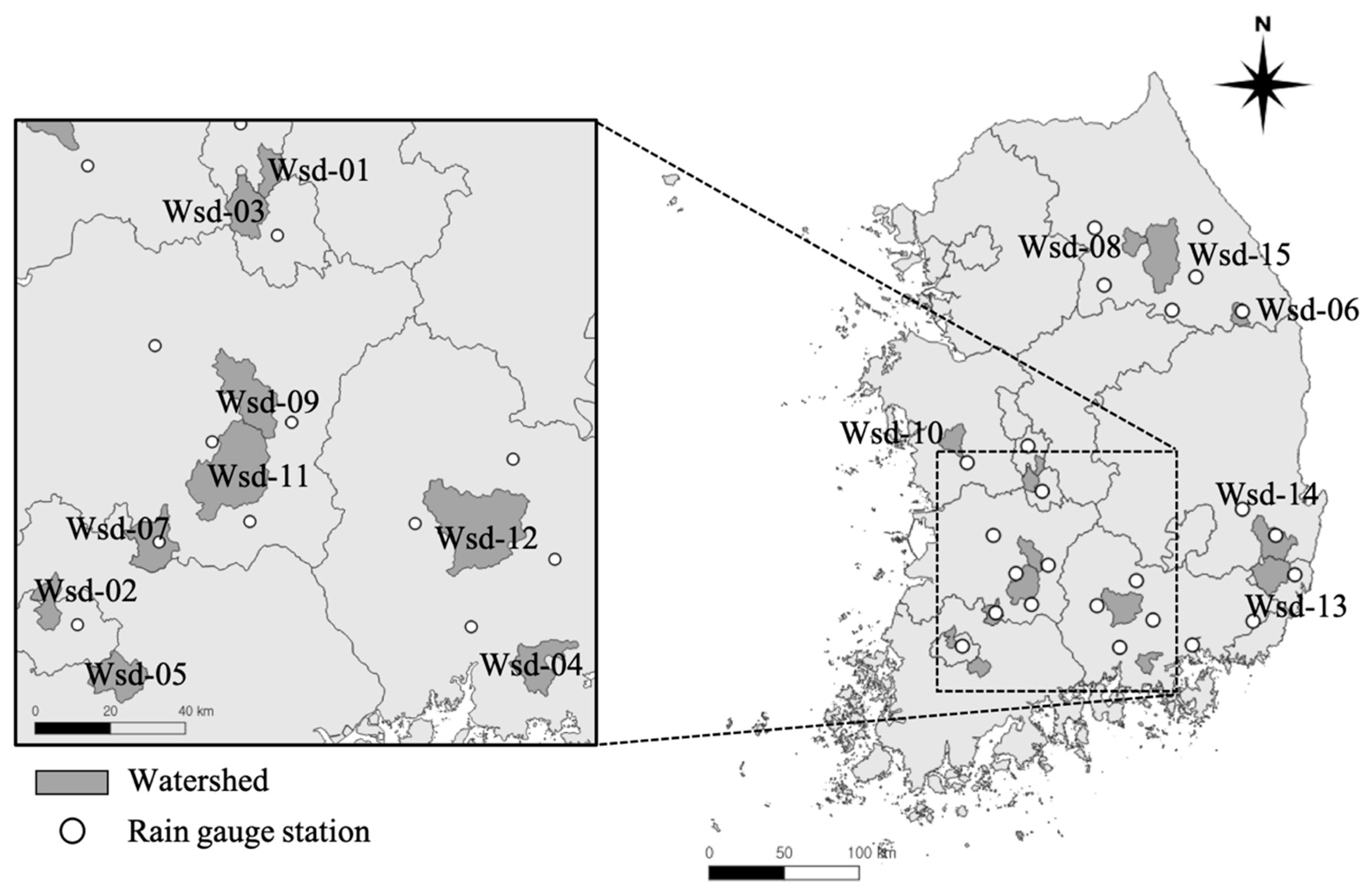
2.4. Application of L-THIA 2022
3. Results
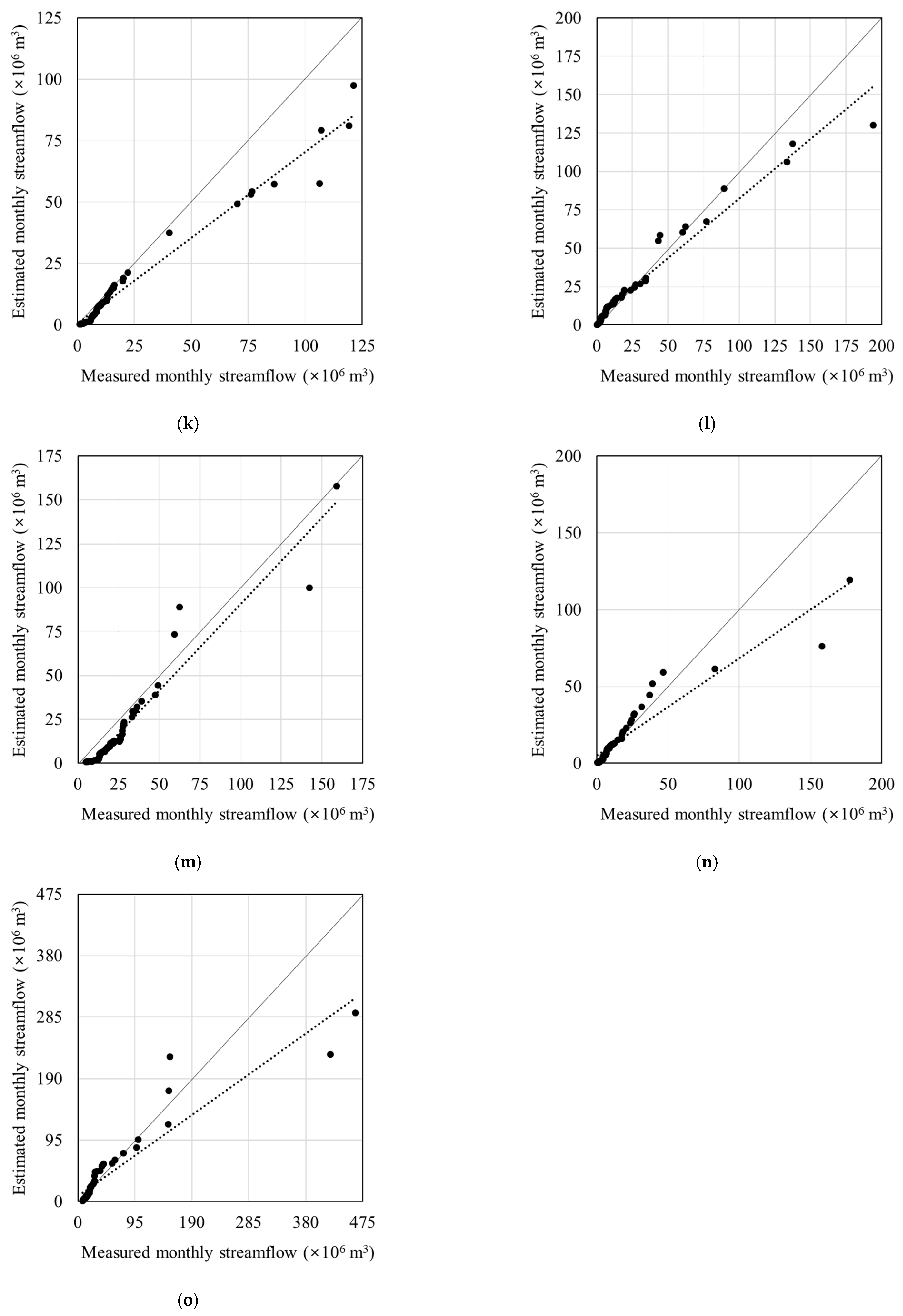
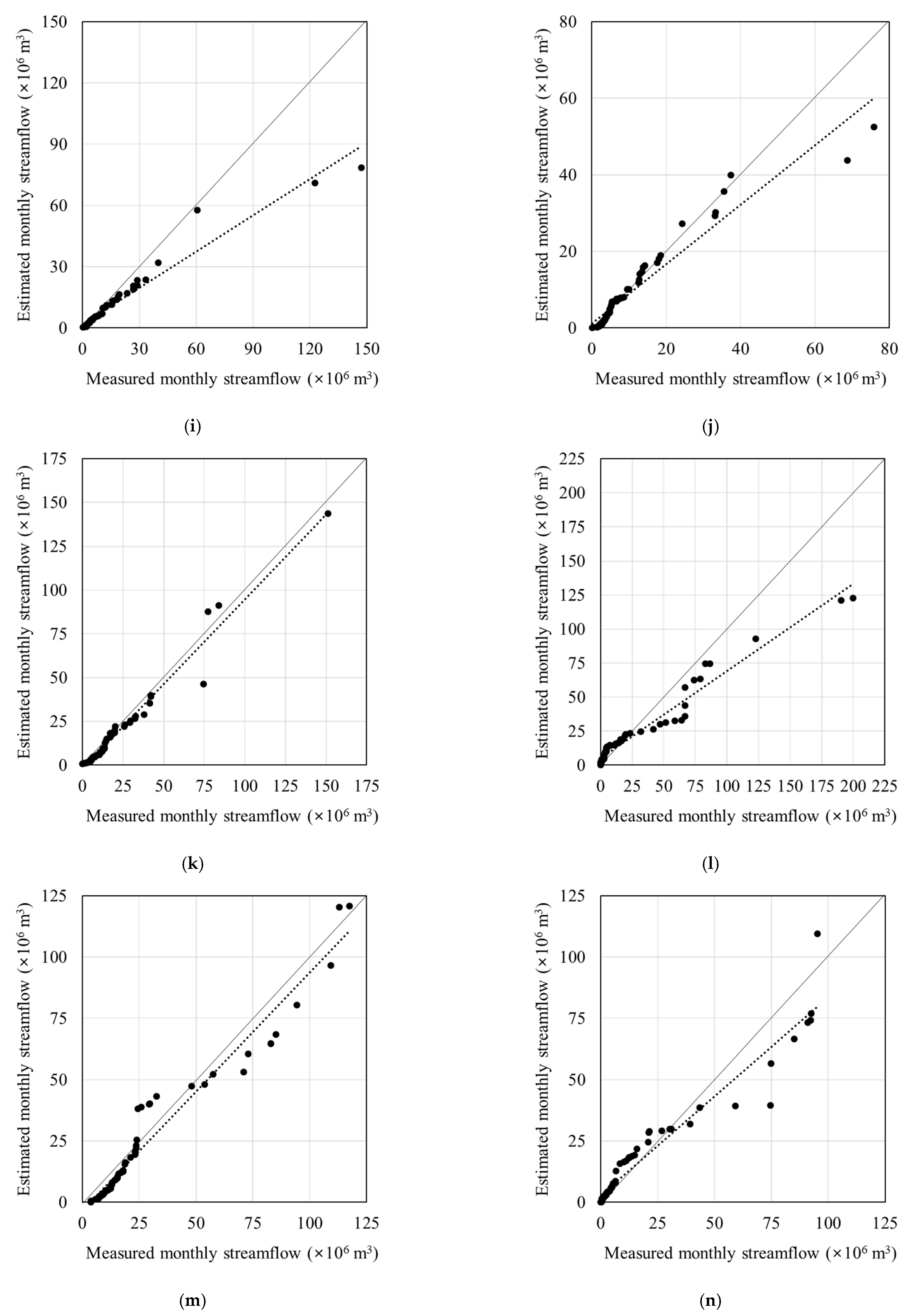
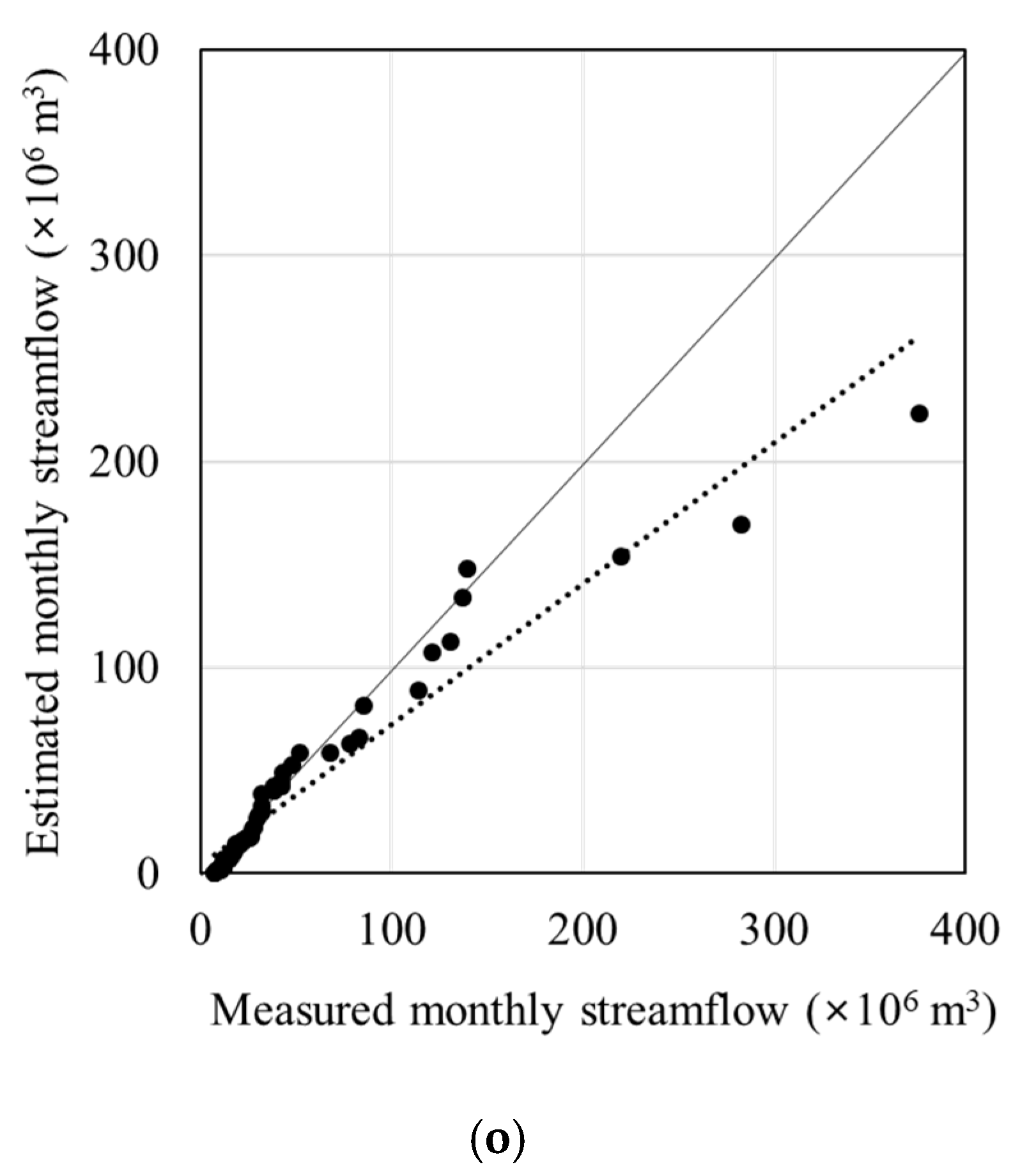
3.1. Model Calibration
3.2. Model Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thakur, P.K.; Patel, P.; Garg, V.; Roy, A.; Dhote, P.; Bhatt, C.M.; Nikam, B.R.; Chouksey, A.; Aggarwal, S.P. Role of Geospatial Technology in Hydrological and Hydrodynamic Modeling with Focus on Floods Studies; Springer: Cham, Switzerland, 2022; pp. 483–503. [Google Scholar] [CrossRef]
- Pochaievets, O.; Obodovsky, O.; Lukianets, O.; Gerbin, V. Algorithm Research and Evaluation of Minimum Water Flow of Mountain Rivers Using GIS; Geoinformatics: Kyiv, Ukraine, 11–14 May 2021. [Google Scholar] [CrossRef]
- Sentas, A.; Karamoutsou, L.; Charizopoulos, N.; Psilovikos, T.; Psilovikos, A.; Loukas, A. The use of stochastic models for short-term prediction of water parameters of the Thesaurus dam, River Nestos, Greece. Proceedings 2018, 2, 634. [Google Scholar] [CrossRef] [Green Version]
- Harbor, J. A practical method for estimating the impact of land-use change on surface runoff, groundwater recharge, and wetland hydrology. J. Am. Plann. Assoc. 1994, 60, 95–108. [Google Scholar] [CrossRef]
- Bhaduri, B. A GIS-Based Model to Assess the Long-Term Impacts of Land Use Change on Hydrology and Nonpoint Source Pollution. Ph.D. Thesis, Department of Earth and Atmospheric Sciences, Purdue University, West Lafayette, IN, USA, 1998. [Google Scholar]
- Grove, M. Development and Application of a GIS-Based Model for Assessing the Long-Term Hydrologic Impacts of Land Use Change. Master’s Thesis, Department of Earth and Atmospheric Sciences, Purdue University, West Lafayette, IN, USA, 1997. [Google Scholar]
- Lim, K.J.; Engel, B.; Kim, Y.; Bhaduri, B.; Harbor, J. Development of the Long Term Hydrologic Impact Assessment (L-THIA) WWW systems. In Proceedings of the 10th International Soil Conservation Organization Meeting, Purdue University and USDA-ARS National Soil Erosion Research Laboratory, West Lafayette, IN, USA, 24–29 May 1999. [Google Scholar]
- Tang, Z.; Engel, B.A.; Lim, K.J.; Pijanowski, B.C.; Harbor, J. Minimizing the impact of urbanization of long term runoff. J. Am. Water Resourc. Assoc. 2005, 41, 1347–1359. [Google Scholar] [CrossRef]
- Wilson, C.; Weng, Q. Assessing surface water quality and its relation with urban land cover changes in the Lake Calumet area, Greater Chicago. Environ. Manag. 2010, 45, 1096–1111. [Google Scholar] [CrossRef] [PubMed]
- Eaton, T.T. Approach and case-study of green infrastructure screening analysis for urban stormwater control. J. Environ. Manag. 2018, 209, 495–504. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Chen, J.; Liu, Y.; Xu, P.; Sun, H.; Engel, B.A.; Wang, S. Assessment of the impact of land use/cover change and rainfall change on surface runoff in China. Sustainability 2019, 11, 3535. [Google Scholar] [CrossRef] [Green Version]
- Park, Y.S.; Lim, K.J.; Larry, T.; Engel, B.A. Long-Term Hydrologic Impact Assessment. Department of Agricultural and Biological Engineering, 2013. Available online: http://npslab.kongju.ac.kr/models/LTHIA2013_Manual.pdf (accessed on 1 November 2021).
- Arnold, J.G.; Allen, P.M. Automated methods for estimating baseflow and ground water recharge from streamflow records. J. Am. Water Resour. Assoc. 1999, 35, 411–424. [Google Scholar] [CrossRef]
- Ahiablame, L.M.; Engel, B.A.; Chaubey, I. Representation and evaluation of low impact development practices with L-THIALID: An example for site planning. Environ. Pollut. 2012, 1, 1. [Google Scholar] [CrossRef]
- Ahiablame, L.; Chaubey, I.; Engel, B.; Cherkauer, K.; Merwade, V. Estimation of annual baseflow at ungauged sites in Indiana USA. J. Hydrol. 2013, 476, 13–27. [Google Scholar] [CrossRef]
- Brown, L.C.; Barnwell, T.O. The Enhanced Stream Water Quality Models QUAL2E and QUAL2E-UNCAS: Documentation and User Manual; U.S. Environmental Protection Agency: Athens, GA, USA, 1987. [Google Scholar]
- Srinivasan, R.; Arnold, J. Integration of a basin-scale water quality model with GIS. J. Am. Water Resourc. Assoc. 1994, 30, 453–462. [Google Scholar] [CrossRef]
- Tetra Tech, Inc. The Environmental Fluid Dynamics Code; Tetra Tech, Inc.: Fairfax, VA, USA, 2007. [Google Scholar]
- United States Environmental Protection Agency (U.S.EPA). Estimating Hydrology and Hydraulic Parameters for HSPF, Technical Note 6; U.S.EPA: Washington DC, USA, 2000. [Google Scholar]
- Rossman, L.A. Modeling low impact development alternatives with SWMM. J. Water Manag. Model. 2010, 6062, 167–182. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Choi, H.S.; Chae, M.S.; Park, Y.S. A study to suggest monthly baseflow estimation approach for the Long-Term Hydrologic Impact Analysis models: A case study in South Korea. Water 2021, 13, 2043. [Google Scholar] [CrossRef]
- USDA. Urban Hydrology for Small Watersheds, National Resources Conservation Service; United States Department of Agriculture: Washington, DC, USA, 1986. [Google Scholar]
- QGIS Development Team. QGIS Geographic Information System, Open Source Geospatial Foundation Project. 2009. Available online: http://qgis.osgeo.org (accessed on 1 July 2021).
- Environmental Geographic Information Service. Available online: https://egis.me.go.kr/main.do (accessed on 5 January 2021).
- Korea Meteorological Administration. Available online: https://www.weather.go.kr/w/index.do (accessed on 7 January 2021).
- Water Resources Management Information System. Available online: http://water.nier.go.kr/main/mainContent.do (accessed on 7 January 2021).
- Duda, P.B.; Hummel, P.R.; Donigian, A.S.; Imhoff, J.C. BASINS/HSPF: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1523–1547. [Google Scholar] [CrossRef]
- Skaggs, R.W.; Youssef, M.A.; Chescheir, G.M. DRAINMOD: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1509–1522. [Google Scholar] [CrossRef]
- Wang, X.; Williams, J.; Gassman, P.; Baffaut, C.; Izaurralde, R.; Jeong, J.; Kiniry, J. EPIC and APEX: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1447–1462. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Am. Soc. Agric. Biol. Eng. 2015, 58, 1763–1785. [Google Scholar]




| AMC | Description | ||
|---|---|---|---|
| Growing Season | Dormant Season | ||
| AMC I | Dry soil | ||
| AMC II | |||
| AMC III | Wet soil | ||
| Watershed | Area (ha) | |||||||
|---|---|---|---|---|---|---|---|---|
| Urban | Agriculture | Forest | Pasture | Wetland | Bare land | Water | Total | |
| Wsd-01 | 657 | 493 | 3931 | 568 | 50 | 123 | 18 | 5841 |
| Wsd-02 | 2022 | 2473 | 1067 | 1035 | 61 | 270 | 82 | 7012 |
| Wsd-03 | 475 | 1204 | 8204 | 1474 | 110 | 286 | 68 | 11,821 |
| Wsd-04 | 420 | 2263 | 8631 | 788 | 197 | 133 | 149 | 12,581 |
| Wsd-05 | 831 | 1701 | 7743 | 1936 | 139 | 302 | 120 | 12,772 |
| Wsd-06 | 630 | 456 | 10,526 | 817 | 41 | 384 | 66 | 12,919 |
| Wsd-07 | 904 | 3811 | 6209 | 1733 | 154 | 428 | 130 | 13,370 |
| Wsd-08 | 246 | 1520 | 14,725 | 1059 | 190 | 374 | 75 | 18,189 |
| Wsd-09 | 560 | 2919 | 12,907 | 1900 | 183 | 507 | 190 | 19,166 |
| Wsd-10 | 888 | 4278 | 13,011 | 2573 | 330 | 319 | 258 | 21,658 |
| Wsd-11 | 1377 | 9267 | 19,252 | 4141 | 479 | 846 | 414 | 35,775 |
| Wsd-12 | 1393 | 6160 | 29,910 | 2967 | 489 | 755 | 573 | 42,246 |
| Wsd-13 | 2835 | 5424 | 29,165 | 2911 | 548 | 1033 | 843 | 42,759 |
| Wsd-14 | 2552 | 8745 | 28,863 | 3615 | 716 | 881 | 596 | 45,968 |
| Wsd-15 | 1566 | 6316 | 65,558 | 4638 | 663 | 1750 | 615 | 81,107 |
| Watershed | Monthly Streamflow (×106 m3) | Number of Used Rain Gauge Stations | ||
|---|---|---|---|---|
| Minimum | Maximum | Mean | ||
| Wsd-01 | 0.14 | 30.38 | 3.44 | 2 |
| Wsd-02 | 1.05 | 44.82 | 5.12 | 1 |
| Wsd-03 | 0.003 | 69.72 | 7.39 | 1 |
| Wsd-04 | 0.14 | 79.58 | 9.27 | 3 |
| Wsd-05 | 0.18 | 57.88 | 6.52 | 2 |
| Wsd-06 | 0.42 | 41.99 | 8.42 | 2 |
| Wsd-07 | 0.22 | 214.75 | 11.32 | 2 |
| Wsd-08 | 0.06 | 121.00 | 8.14 | 1 |
| Wsd-09 | 0.10 | 147.04 | 14.11 | 4 |
| Wsd-10 | 0.17 | 104.68 | 10.73 | 3 |
| Wsd-11 | 0.90 | 151.18 | 20.41 | 1 |
| Wsd-12 | 0.13 | 199.93 | 23.94 | 2 |
| Wsd-13 | 3.71 | 158.96 | 26.86 | 3 |
| Wsd-14 | 0.21 | 177.73 | 17.78 | 1 |
| Wsd-15 | 7.38 | 462.88 | 46.50 | 1 |
| Watershed | NSE | R2 |
|---|---|---|
| Wsd-01 | 0.834 | 0.867 |
| Wsd-02 | 0.729 | 0.873 |
| Wsd-03 | 0.868 | 0.917 |
| Wsd-04 | 0.755 | 0.865 |
| Wsd-05 | 0.766 | 0.795 |
| Wsd-06 | 0.813 | 0.863 |
| Wsd-07 | 0.601 | 0.765 |
| Wsd-08 | 0.739 | 0.882 |
| Wsd-09 | 0.799 | 0.879 |
| Wsd-10 | 0.866 | 0.867 |
| Wsd-11 | 0.776 | 0.861 |
| Wsd-12 | 0.854 | 0.874 |
| Wsd-13 | 0.770 | 0.875 |
| Wsd-14 | 0.776 | 0.808 |
| Wsd-15 | 0.713 | 0.743 |
| Watershed | NSE | R2 |
|---|---|---|
| Wsd-01 | 0.785 | 0.808 |
| Wsd-02 | 0.917 | 0.946 |
| Wsd-03 | 0.746 | 0.878 |
| Wsd-04 | 0.611 | 0.726 |
| Wsd-05 | 0.780 | 0.805 |
| Wsd-06 | 0.753 | 0.817 |
| Wsd-07 | 0.641 | 0.823 |
| Wsd-08 | 0.687 | 0.700 |
| Wsd-09 | 0.714 | 0.834 |
| Wsd-10 | 0.719 | 0.729 |
| Wsd-11 | 0.900 | 0.913 |
| Wsd-12 | 0.730 | 0.797 |
| Wsd-13 | 0.718 | 0.754 |
| Wsd-14 | 0.865 | 0.868 |
| Wsd-15 | 0.636 | 0.676 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Chae, M.S.; Park, J.-Y.; Lim, K.J.; Park, Y.S. Development and Application of a QGIS-Based Model to Estimate Monthly Streamflow. ISPRS Int. J. Geo-Inf. 2022, 11, 40. https://doi.org/10.3390/ijgi11010040
Lee H, Chae MS, Park J-Y, Lim KJ, Park YS. Development and Application of a QGIS-Based Model to Estimate Monthly Streamflow. ISPRS International Journal of Geo-Information. 2022; 11(1):40. https://doi.org/10.3390/ijgi11010040
Chicago/Turabian StyleLee, Hanyong, Min Suh Chae, Jong-Yoon Park, Kyoung Jae Lim, and Youn Shik Park. 2022. "Development and Application of a QGIS-Based Model to Estimate Monthly Streamflow" ISPRS International Journal of Geo-Information 11, no. 1: 40. https://doi.org/10.3390/ijgi11010040
APA StyleLee, H., Chae, M. S., Park, J.-Y., Lim, K. J., & Park, Y. S. (2022). Development and Application of a QGIS-Based Model to Estimate Monthly Streamflow. ISPRS International Journal of Geo-Information, 11(1), 40. https://doi.org/10.3390/ijgi11010040







